1 Introduction: From PMT to SiPM in PET

The invention of the first photomultiplier tube (PMT) in 1934, the Kubetsky’s tube [1], and the discovery of the scintillation properties of thallium-doped sodium iodide crystals (NaI/Tl) by Hofstadter in 1948 [2] have paved the way for the development of a new class of ionization radiation detectors, which have become the basic blocks of scintigraphy, single-photon emission computed tomography (SPECT) and positron emission tomography (PET) detectors of the emerging field of nuclear medical imaging.

One of the first PET detector, the Headshrinker [3], developed in 1961 at the Brookhaven National Laboratory (BNL) in the USA was made of 32 1" diameter NaI crystals read out by PMTs inserted alternatively radially and axially in a hexagonal gantry around the head of a patient in a sitting position (Fig. 1a). Later on, this machine was moved by Chris Thompson to the Montreal Neurological Institute in Canada and rearranged under the new name Positome [4], so that patients could be scanned in supine position like in a computed tomography (CT) scanner (Fig. 1b).

Fig. 1
figure 1

a The Headshrinker developed at BNL in 1961. b The Positome in Montreal showing the arrangement of the 32 NaI(Tl) PMT detectors around the patient’s head

Full size image

PMTs have been the photodetectors of choice for a long time because of the possibility to produce large-area photocathodes with a reasonable quantum efficiency (typically in the range of 15 to 25%), and because of a large single photo-electron amplification factor of about 106, making possible the use of cheap of-the shelf electronics, and of reasonable timing properties, allowing selecting a coincidence time window of about 2 ns and reducing therefore the number of random coincidences. Moreover, thanks to their relatively low cost, large advances in PET scanners with larger geometrical coverage and hence, sensitivity, could be made possible. Not only the axial field could be increased by the addition of more rings in the scanners, but the spatial resolution was improved by using smaller crystals and introducing more channels per ring.

There was, however, a limitation to this approach, as the finite size of PMTs was a physically limiting factor and expensive means for one-to-one crystal–PMT coupling, when sub-centimeter spatial resolution and large axial coverage were desired.

This limitation was overcome by Casey and Nutt, who introduced in 1986 the concept of block detector [5], using only four PMTs to read out the scintillation light produced in a matrix of 8 × 4 (32) BGO crystals (5.6 mm transaxial, 12.9 mm axial and 30 mm depth). This was using the well-established method of light sharing between photomultipliers, pioneered by Anger in the gamma camera. The principle of the block detector is shown in Fig. 2 for an 8 × 8 (64) array coupled to four photomultipliers. The first commercial block-based PET scanner, which had a 10 cm axial length and 15 transaxial-plane readout, was acquired by the Hammersmith group in London [6].

Fig. 2
figure 2

Image courtesy of D. Townsend, Ref. [1]

The block detector concept of Casey and Nutt, where the crystal pixel, in which the gamma interacted, is identified by the light sharing between four PMTs.

Full size image

Silicon pin diodes could have been a more compact alternative to PMTs, with the additional advantage of working at a low bias voltage, preventing the use of kilovolt power supplies needed for PMTs. Unfortunately, the absence of gain in pin diodes was not compatible with the low light level produced by the conversion of 511 keV gamma rays in the NaI(Tl) or BGO scintillators. However, the situation changed in the 1980s with the emergence of avalanche photodiodes (APD) through the pioneer work of McIntyre [7]. APDs allowed for one-to-one coupling of millimeter-scale scintillators with the photodetector, offering a granularity which cannot be achieved with PMTs. Moreover, compared to PMTs, APDs are insensitive to strong magnetic fields, which allows for dual-modality PET and MRI. The first PET scanner to use APDs was realized by Roger Lecomte's team at the University of Sherbrooke in 1994 and is shown in Fig. 3 [8].

Fig. 3
figure 3

The Sherbrooke small animal PET, the first PET with APDs

Full size image

This new photodetector triggered interest in the high-energy physics community at a time where the Large Hadron Collider (LHC) project was launched. Indeed, the huge scintillator-based electromagnetic calorimeter of the CMS experiment had to work in a 4 T magnetic field preventing the use of PMTs. Moreover, the selected scintillating crystal, lead tungstate (PWO), is characterized by a relatively low light yield, necessitating the use of a photodetector with gain. An impressive several-year-long R&D effort has been therefore organized with several institutes and companies worldwide, in order to prepare the mass production of 120,000 APDs with consistent and reliable characteristics [9].

As a result of this, APDs became a credible and affordable photodetector that several groups tried to introduce in prototype PET scanners, mostly for small animal or organ-specific PETs. Among those, the ClearPEM [10] has successfully integrated 12,288 APDs, one-to-one coupled to LYSO crystals in a dedicated breast PET scanner. The ClearPEM-Sonic, combining in a multimodal approach the ClearPEM and the ultrasonic Aixplorer device from the company SuperSonic Imaging, is shown in Fig. 4 [11].

Fig. 4
figure 4

The ClearPEM-Sonic with 12,288 APDs. From Ref. [10]

Full size image

However, APDs have not been widely used and they have not been adopted by PET industry. The reason is due to a still high cost of the one-to-one scintillator–photodetector coupling approach, the modest amplification gain (typically 50 to 200), and most importantly to timing properties (in the ns range), which could not compete with fast PMTs and a rapidly developing class of photodetectors named silicon photomultipliers, SiPM.

The situation progressively changed in the years 2000 with the growing interest for PET/MRI multimodality, requiring magnetic field immunity of the photodetectors and with an increasing demand for time-of-flight capabilities with a strong impact on effective PET sensitivity and image quality.

At the same time, the development of Geiger-mode avalanche photodiodes initiated by Cova [12], also named single-photon avalanche diodes (SPADs), opened new perspectives for single-photon detection and leads to a substantial improvement in sensitivity. Later on, thousands of SPADs have been assembled in arrays of few millimeters square (named SiPMs) [13] using the technological solution proposed firstly by Golovin [14]. Since then, impressive progress has been made on the SiPM technology, leading to a dramatic improvement in the photodetection efficiency (PDE) from about 15% to more than 60% today, a strong reduction in dark count rate (DCR) and inter-SPAD cross talk, and impressive progress on timing properties, with a significant reduction in the single-photon time response (SPTR).

The quest for single-photon counting with ultimate timing resolution has pushed several groups to develop digital, or even multi-digital SiPMs. A review of the different attempts is given in [15].

As a result of this, SiPMs are progressively becoming the photodetectors of choice for a new generation of time-of-flight PET (TOF-PET) scanners, as demonstrated by the development in 2013 of the Philips Vereos PET scanner, with a coincidence time resolution (CTR) of 325 ps [16], and of the Siemens Biograph Vision scanner in 2018 with an unprecedented CTR of 214 ps [17].

2 SiPM working principle

As already mentioned, the silicon photomultiplier (SiPM) is an array of single-photon avalanche diodes (SPADs). In the analog case, the passive quenching circuit is normally integrated within each SPAD, whereas the digital SiPM can have passive or active quenching combined with the front-end readout electronics. The SPAD is simply speaking a p–n junction or diode operated in reverse direction above the so-called breakdown voltage, where self-sustained avalanche processes can occur.

In Fig. 5, the different modes of operation of a SPAD can be seen. Applying a small reverse voltage to the diode, the generated electron–hole (e–h) pairs are separated with no additional gain and the measured current is proportional to the impinging light flux on the diode. This is the photodiode operation regime, and because of gain 1 it is not suitable to detect the dim light from scintillators upon 511 keV gamma interaction, as already mentioned in the Introduction. If the reverse voltage is increased, the operation enters the avalanche photodiode (APD) range. Here, the electrical field is strong enough for electrons to gain enough kinetic energy in order to produce secondary e–h pairs via impact ionization. The measured current is multiplied by the APD gain and proportional to the impinging light flux on the device. Because the electric field is still below the breakdown voltage, the heavier holes do not obtain enough kinetic energy and the avalanche is only supported by the lighter electrons flowing in one direction, which gives rise to a natural self-quenching of the avalanche. APDs show a medium gain in the order of few tens to hundreds and a high excess noise factor, inherent in the avalanche multiplication, which scales with the gain.

Fig. 5
figure 5

Operation regimes of a solid-state p–n junction, i.e., photodiode, avalanche photodiode (APD) and single-photon avalanche diode (SPAD) or SiPM range

Full size image

Increasing the reverse voltage even further, above the so-called breakdown voltage, holes obtain enough kinetic energy to perform also impact ionization. This is the regime of the Geiger-mode avalanche operation. Because the avalanche is supported by holes and electrons flowing in both directions, the avalanche diverges and must be quenched by an external quenching circuit, lowering the reverse voltage after the detection of the avalanche. In analog SiPMs, this is done by a series quenching resistor Rq connected to each SPAD. The diverging current after an avalanche provokes a voltage drop across Rq and, hence, quenches the avalanche by reducing the reverse voltage below the breakdown voltage. After the quenching of the avalanche, the SPAD has to be recharged via Rq leading to a certain dead time, while the SPAD is blind for further photon detection.

Because the current diverges upon creation of a single e–h pair, the SPAD is sensitive to single photons with an excellent electronic signal-to-noise ratio. The drawback is that a SPAD cannot give a difference between one or several photons detected. In order to overcome this saturation and the recharging problem, and to be able to count photons, as in the case of PMTs, several (up to thousands) of SPADs are connected in parallel in the so-called analog SiPM, as can be seen in Fig. 6a. The analog SiPM has excellent photon separation and counting abilities due to its high gain (several millions). One particular advantage of the Geiger-mode regime, exploited by the SiPM, is that the excess noise factor is much lower as compared to APDs, being close to the theoretical limits given by Poisson statistics [18].

Fig. 6
figure 6

a Picture of an analog SiPM (HPK S10931-3050P) with a zoom on the individual SPADs. b All SPADs with integrated quenching resistor are connected in parallel in the analog SiPM

Full size image

Nowadays, the analog SiPM is the dominant photodetector used in TOF-PET due to its impressive developments made in the past few years. Figure 6a shows a picture taken of an analog SiPM from Hamamatsu with a zoom on the individual SPADs. All these SPADs are connected in parallel to form the analog SiPM, as can be seen in Fig. 6b.

Despite the many advantages of the SiPM in view of high gain, excellent excess noise factor, photon counting ability, etc., there are some disadvantages. The SiPM has a limited dynamic range which is directly correlated with the number of SPADs integrated. Hence, saturation effects are observed for an impinging light flux higher than the available SPAD density. This is deteriorating the energy resolution when coupled to a scintillator. However, this limitation is mitigated by the development of SiPMs with a high density of SPADs, such that the energy resolution of L(Y)SO/Ce crystals, currently used in PET scanners, remains within the range of its intrinsic resolution.

The SiPM shows also higher dark count rates (DCRs), single-photon signals generated by thermally generated electron–hole pairs as compared to PMTs for example. As generally the leading-edge trigger level in TOF-PET detectors must be low to achieve best timing performance, this calls for the need of clever validation electronics in order to reduce electronic dead time.

Another source of noise in SiPMs, not present in PMTs, is the so-called cross talk. Upon an avalanche in the SPAD, the vast amount of electrons and holes generated can recombine radiatively, producing secondary red and near-IR photons, which can trigger secondary avalanches within the SPAD or in SPADS nearby [19]. The amount has been estimated to 3 · 10−5 photons per avalanche carrier [20, 21]. Three main types of optical cross talk can be distinguished, (a) prompt or direct cross talk, (b) delayed cross talk and (c) external cross talk [22]. Prompt or direct cross talk describes the secondary photons traversing directly to neighboring cells with subsequent triggering of an avalanche. Delayed cross talk or delayed optical cross talk is generated by secondary avalanche photons, which are absorbed in the un-depleted region of a neighboring SPAD. This results in photon-generated minority carriers which can reach the multiplication region of the SPAD by diffusion and consequently can trigger additional avalanches after some delay. External cross talk describes the reflection of the secondary photons in the protective glass or epoxy window on top of the SiPM, or in the coupled (glued) scintillator. This effect is deemed to be the most important in PET, as the contribution of the external cross talk cannot be mitigated by clever SiPM designs, but has to be done jointly with the crystal and optical coupling design. Especially in view of achieving highest timing but also energy resolution, the reduction in optical cross talk in SiPMs is important. For example, a too high cross talk probability can severely limit the highest bias voltage at which the SiPM is operational and, therefore, limits the SiPM gain, photon detection efficiency and single-photon time resolution [23].

One of the most important parameters of SiPMs is the photon detection efficiency (PDE), which quantifies the ability of the SiPM to sense photons. The PDE is defined as the probability of a photon impinging at the SiPM to deliver a measurable electronic signal and defined in Eq. (1). It includes the quantum efficiency (QE), the avalanche triggering probability (PT) and the geometric fill factor (FFeff). The PDE is generally a function of the overvoltage Vov (operational bias voltage minus the breakdown voltage) and the wavelength λ.

$$ {\text{PDE}}({\text{Vov}},\lambda ) = {\text{QE}}(\lambda ) \cdot {\text{PT}}({\text{Vov}},\lambda ) \cdot {\text{FFeff}}({\text{Vov}},\lambda ). $$
(1)

The quantum efficiency gives the probability of a photon to be absorbed in silicon and generating an electron–hole pair (accounting for the loss of electrons or holes by recombination or capture at defects) and the avalanche trigger probability giving the likelihood of an electron or hole to ignite an avalanche. The fill factor is mostly defined by boarder regions and dead spaces around the SPADs, i.e., the pure geometrical fill factor, but also includes secondary effects like an increasing detection area by a higher electrical field saturation in the SPAD due to a higher operational bias voltage or overvoltage. As already mentioned, the PDE has a strong dependence of the detected photon wavelength and applied SiPM operation voltage. State-of-the-art devices can reach values of up to 60% at 410 nm [24], which make them almost ideal candidates to detect the light emitted from L(Y)SO/Ce crystals. In Fig. 7, an overview of the PDE versus the applied SiPM overvoltage can be seen for different devices currently available on the market and by high-level research institutes.

Fig. 7
figure 7

Reproduction from [24]

PDE as a function of the SiPM overvoltage (SiPM bias voltage minus SiPM breakdown voltage) measured at 410 nm. a Hamamatsu S13360 and S14160 with a photograph of HPK S14160 showing the center wire-bond connection and individual SPADs with 50 μm pitch. b Comparison of the PDE for Broadcom, FBK, Ketek and SensL (now part of ON semiconductors).

Full size image

Another important parameter of SiPMs, especially for timing applications, is the so-called single-photon time resolution (SPTR). As the name indicates, the SPTR gives the ability and intrinsic accuracy on recording the arrival time of a detected single photon. In order to achieve ultimate timing with scintillators or prompt photon emitters (e.g., Cherenkov radiation in BGO), the SPTR has to be as small as possible, i.e., lowest values in the order of 10 ps FWHM are desired [25]. Because the single-photon signal of a SPAD can be fairly small (depending on the SiPM and SPAD size), the readout electronics plays a crucial role in achieving lowest measured SPTR [24].

This can be understood by the well-known Eq. (2):

$$ \sigma_{{{\text{SPTR}}\_{\text{electronic}}\_{\text{part}}}} = \, \sigma_{{{\text{vnoise}}}} /\left({{\text{d}}v/{\text{d}}t_{{@{\text{threshold}}}} } \right) $$
(2)

expressing the part of the single-photon time resolution (SPTR) only caused by the electronic readout with σvnoise, the r.m.s of the electronic noise floor, and dv/dt@threshold, the slew rate of the signal at a given leading-edge threshold.

As shown in Fig. 8a, modern SiPMs can reach measured SPTR values of 90 ps FWHM with FBK NUV-HD SiPMs, having a 40 µm SPAD pitch, illuminating the whole 4 × 4mm2 device area [24]. The electronic noise plays a crucial role, especially in view of achieving best SPTR. Recently, it has been shown that high-frequency readout of the SiPMs can give significant improvements in this respect [26]. The main idea is that via the passive quenching capacitance Cq a high-frequency path is established, allowing for GHz bandwidths of a voltage-based readout scheme [18]. However, even with this optimized readout there is still a non-negligible impact on electronic noise to the SPTR, which in Fig. 8b was accounted for. In the figure, the picosecond laser pulse width of 42 ps FWHM was subtracted in addition to give the intrinsic SPTR of the SiPM. In fact, the intrinsic SPTR of the different tested SiPMs is the parameter of interest for PET applications and is further directly linked to the best achievable CTR, as will be discussed more in detail in chapter 4. In Fig. 8b, it can be observed that the different SiPMs from the different producers offer very different SPTR performances. The main reason of these differences lies in the internal SPAD structure and technology. For example, Hamamatsu SiPMs typically employ deeper junctions (thicker structures) which, besides advantages of higher PDE values for light detection in the red part of the spectrum, have some disadvantages in a homogenous field distribution, especially at the edges, leading therefore to a worse overall SPTR. On the other hand, the very uniform field distribution in the SPADs from FBK (also at the edges) allows for record SPTRs in these devices. A more shallower SPAD structure in these devices further allows for a faster avalanche development and better SPTR in addition.

Fig. 8
figure 8

From Ref. [24]

State-of-the--art SPTR of SiPMs from different producers. (a) Measured SPTR including laser pulse width of 42 ps FWHM, electronic noise. (b) Intrinsic SPTR after subtracting the laser and electronic noise contribution. The intrinsic SPTR is a sole SiPM property.

Full size image

These examples show that in order to go to ultimate time resolution, the SPAD electric field configuration has to be considered. Especially on the edges of the SPAD, where the field has to go from zero to the high fields applied in the central region of the SPAD, the SPTR is strongly deteriorated, which was recently demonstrated by focused laser measurements [27]. A sharper field transition and the use of larger SPAD sizes can help to mitigate this effect, as was impressively shown by FBK NUV-HD devices, achieving intrinsic SPTR values of 70 ps. Novel methods to overcome these limitations even further, applying ideas from the rapidly evolving field of metamaterials, will be discussed in chapter 5.

3 Time-of-flight PET

Although the idea of using time of flight in PET has been proposed as early as in 1966 by Anger [28], it is only in the recent years that the interest for TOF-PET scanners has been growing at the point that the major PET manufacturers are now concentrating their efforts in improving PET time-of-flight performance.

One reason is related to the limited timing properties of scintillators, photomultipliers and electronics used until recently. The situation changed with the introduction of the much faster LSO/Ce crystal scintillator, the development of SiPM photodetectors and fast readout electronics.

Moreover, a number of clinical considerations and new medical challenges are calling for significant improvement in noise reduction in PET images.

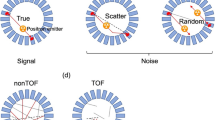
T. Tominati analyzed the influence of TOF in the noise propagation of filtered back-projection (FBP) image reconstruction algorithms [29]. As shown in Fig. 9, in the case of non-TOF-PET, all the volume elements (voxels) along a line of response (LOR) defined by the two interacting γ-rays emitted by the positron decay contribute to the same projection data. In other terms, the noise associated with each of these voxels is added to the signal from the voxel of interest.

Fig. 9
figure 9

Principle of time-of-flight PET

Full size image

On the other hand, each event is TOF-tagged if time of flight is implemented. It means that only the voxels along the LOR, which are associated with this TOF information, will contribute in the back-projection reconstruction, and the signal-to-noise ratio of the image (SNR) is improved by a factor given by the TOF kernel, with a probability function having a width Δx = cΔt/2.

As a result, a significant improvement in the image signal-to-noise ratio (SNR) is expected, according to Eq. (3):

$$ {\raise0.7ex\hbox{${{\text{SNR}}_{{{\text{TOF}}}} }$} \!\mathord{\left/ {\vphantom {{{\text{SNR}}_{{{\text{TOF}}}} } {{\text{SNR}}_{{{\text{NONTOF}}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${{\text{SNR}}_{{{\text{NONTOF}}}} }$}} = \sqrt {\frac{2D}{{c \cdot {\text{CTR}}}}} $$
(3)

where D is the diameter of the field of view (FOV), c is the speed of light in vacuum, and CTR is the coincidence time resolution.

The corresponding gain in image variance, also called effective sensitivity gain, is the square of the SNR gain, corrected by a factor 1.47 to take into account the fact that the TOF kernel around the measured TOF position on the LOR is not a square but rather a Gaussian [30].

The variance being proportional to the diameter D of the volume of interest, one first evidence of the interest of TOF-PET was the improvement in the image quality for overweight patients in the first generation of TOF-PET scanners with a timing resolution of 500–600 ps [17, 31].

Less noisy images also translate to higher quantitative accuracy of lesions uptake and allow taking full advantage of higher spatial resolution with a smaller number of counts in smaller voxels.

But one of the most spectacular advantages of TOF-PET is the gain in effective sensitivity, opening the way for longitudinal examinations over more radio-isotope lifetimes, which turns out to be very important for some clinical indications, such as immunotherapy studies. This effective sensitivity gain can also be exploited by reducing the doses injected to the patients, opening therefore PET applications to new categories of patients, such as pediatric and even prenatal examinations.

Additional advantages of TOF-PET are related to the extra time information recorded for each event, which increases the robustness of PET image reconstruction in case of inconsistent, incomplete or even incorrect data [32]. It has been shown, for instance, that TOF-PET reconstruction is more immune to unprecise attenuation corrections, which could help mitigating the problem of attenuation corrections in PET/MR as compared to PET/CT [33]. In a similar way, inaccurate normalization and scatter corrections have a smaller impact in the presence of good timing information [33].

4 SiPMs for TOF-PET

SiPMs were evaluated for TOF-PET in the early 2005 with the first commercial PET scanners using SiPMs appearing around 2014 and the latest machines even showing time resolutions in the 210 ps range [34, 35].

Hybrid scanners like SPECT/MR (single-photon emission computed tomography, combined with magnetic resonance imaging) and PET/MR were one of the main drivers of applying SiPMs in medical applications and paved the way for advanced TOF-PET systems discussed before [34]. The idea to combine PET with MR was evident after the success of PET/CT hybrid scanners in clinical applications. However, due to the magnetic fields present in MR systems and the demand of having a simultaneous hybrid system, PMTs were not an option anymore [35]. The first PET/MR systems were built using APDs as photodetectors, which could operate inside the MR. As already mentioned, the development on APDs was largely driven by high-energy physics, as some calorimeters (e.g., CMS) operate in high magnetic fields and thus PMTs are not an option either [36]. In the long run, SiPMs comprised an attractive alternative to APDs, because of their much higher gain, faster rise time and much lower bias supply voltage, which make the integration in a system easier. After first attempts were made by several groups (e.g., [37]), the first commercial PET/MR system based on SiPMs was produced by GE Healthcare [38]. Preclinical PET/MR systems equipped with the Philips d-SiPM were studied around 2012 with impressive CTR results of 213 ps FWHM and a spatial resolution of 0.73 mm FWHM [39, 40].

Nowadays, popular state-of-the-art SiPMs available on the market show a difference of maximum 25% in the best achievable CTR performance [24]. This significant difference in the measured CTR with different devices is mainly explained by the very different single-photon time resolution of the SiPMs. The intrinsic SPTR can change by as much as 100%, whereas the best PDE at 410 nm only varies maximally by 18% for the different SiPMs tested in [24]. In Fig. 10, the CTR performance of different analog SiPMs available on the market is shown, as a function of the SiPM SPTR. This plot concentrates on the inherent performance of different SiPMs, and therefore the PET timing was tested with small 2 × 2 × 3mm3 LSO/Ce/Ca crystals. As said previously, the best intrinsic SPTR measured with modern analog SiPMs is 70 ps FWHM achieved with NUV-HD SiPMs from FBK [25, 41], which is the reason for the best CTR performance achieved by this device to be seen in Fig. 10. In full generality, it was shown by Vinogradov [42] that the CTR can be parametrized as stated in Eq. (4):

$$ {\text{CTR}}_{{{\text{analytic}}}} = 3.33\cdot\sqrt {\frac{{\tau_{{{\text{deff}}}}\cdot \left( {1.57\cdot \tau_{r} + 1.13\cdot \sigma_{{{\text{SPTR}} + {\text{PTS}}}} } \right)}}{{{\text{PDE}} \cdot {\text{LTE}} \cdot {\text{ILY}}_{{@{\text{Energy}}}} }}}. $$
(4)
Fig. 10
figure 10

CTR shown as a function of the SPTR. CTR was measured with 2 × 2 × 3mm3 LSO/Ce/0.4%Ca crystals wrapped in Teflon coupled with Meltmount and normalized, as if all the SiPMs would have a PDE of 59%. Monte Carlo simulations of the CTR were performed for an analog SiPM with high-frequency readout and a hypothetical digital SiPM combining all time stamps via maximum likelihood estimation

Full size image

One can see that all relevant parameters in the system have a very similar impact on the CTR. These parameters in Eq. (4) are: the scintillation-related parameters, such as effective scintillation decay time (τdeff), intrinsic light yield (ILY) and scintillation rise time (τr), the SiPM-related parameters, such as photon detection efficiency (PDE) and single-photon time resolution (SPTR), and the light transport-related parameters, such as light transfer efficiency (LTE) and photon transfer time spread (PTS) [43]. It is also important to notice that the SPTR and PTS have the same impact on the CTR which is usually one convolved quantity in the system. The direct consequence of Eq. (4) is that by improving the SPTR also the PTS has to be improved. This can be done either by shortening the pixel sizes (like in Fig. 10) or by determining the gamma impact point in the crystal, with consequent correction of this so-called depth-of-interaction timing bias.

Figure 10 further shows Monte Carlo simulation studies using a fully multi-digital SiPM, where each photon detected can be time-stamped and recorded. Indeed, the digital SiPM offers some further improvements in the best achievable CTR, especially if the SPTR can be improved as well [24, 44]. This can easily be understood, as the fully multi-digital SiPM overcomes the problem of electronic noise. This has two main reasons: 1) In this device, each SPAD is connected to its own readout electronics and the rather large gain of a single SPAD can be utilized to its full potential, allowing for highest signal-to-noise ratio and 2) potentially remaining electronic noise only would increase the intrinsic SPTR and not deteriorate the signal formation, as the treatment of arriving photon times is shifted to a purely mathematical problem in the multi-digital SiPM.

The given values are only selective examples, and many groups around the world are working on fast timing with scintillators, especially in the field of PET, achieving very similar results. For example, [45] showed a time resolution of 80 and 122 ps FWHM with 3- and 20-mm-long LGSO/Ce crystals coupled to NUV-HD SiPMs, respectively. Further studies can be found in [27, 43,44,45,46,47,48].

Knowing the best timing performance achievable with laboratory setups is important in order to have a reliable benchmark for the later construction of optimized systems. The integration of thousands of channel (e.g., in a full-body TOF-PET) sets unavoidably compromises on the performance. One prominent example is the optimization of a manageable power consumption versus the timing performance of the system. Hence, a trade-off has to be found between best achievable timing performance by increasing the electronic bandwidth of the front-end, which also increases the power consumption substantially, and system integration also in view of other important parameters in PET, e.g., energy resolution and granularity. Going to ultimate TOF performance also sets further requirements on the used time-to-digital converters (TDCs), clock distribution, signal routing, only to name a few. Another important aspect of the integration into a PET machine is the sensitivity and cost, which have also to be considered.

In order to improve the PET sensitivity, it is necessary to use crystals of 20 mm and longer which, however, deteriorate the CTR performance, as compared to shorter crystals of, for example, 3 mm. This is due to a decrease in the light transfer efficiency (LTE) and an increase in the photon transfer time spread (PTS) with increasing crystal length [49]. Nevertheless, recently it has been shown that even with 20-mm-long crystal a coincidence time resolutions of 100 ps FWHM can be achieved in the laboratory [41]. Such CTR is considered to be the next step envisaged in TOF-PET systems expected to leading to further game-changing improvements in image quality, image reconstruction and reduction in dose applied to the patients (and radiologists).

Another way to improve the sensitivity even further and at the same time to reduce the system cost significantly is the use of different scintillation materials. For example, BGO was the preferred material in PET for a long time due to its high density, high photo-fraction and relatively low cost of production. Nevertheless, BGO was replaced by L(Y)SO which offered much better timing performance with PMTs and earlier generations of SiPMs. Nowadays, with the impressive improvements made in SiPMs, especially in the domain of the achievable SPTR, it was successfully shown that by using the prominent Cherenkov emission in BGO excellent timing can be achieved in TOF-PET configurations [50, 51].

The past and ongoing intensive research made in SiPMs, leading to impressive performance boosts, is one of the reasons of continued CTR records achieved with TOF-PET detectors over the last decade. Many novel ideas are currently evaluated and pave new ways to ultimate time resolution, subject for discussion in the next chapter.

5 Toward a new generation of ultrafast SiPMs

SiPMs provide outstanding performance in constant progress in terms of single-photon sensitivity, signal speed and timing. In recent years, two transformative technologies in integrated circuitry (IC) have revolutionized the field of silicon imaging sensors: backside illuminated devices (BSI) and 3D integration. These technologies have now matured enough that they have become industry standard in the field of consumer and professional imaging sensors.

However, an important bottleneck remains at the photoconversion level, particularly when ultimate single-photon detection precision is required.

Recent years have seen impressive progress in the performance of SiPMs.

In 2016, the authors have conducted a detailed study of the performance of a large quantity of SiPMs from different producers and have shown that the single-photon time resolution (SPTR) was in the range of 200 ps FWHM or higher [27].

Since that time, impressive improvements have been realized on the SPTR, which now reaches 70 ps FWHM for the most recent NUV-HD series from FBK (Fig. 8) [24].

However, this remains an important limitation for most applications. Detailed analysis of the factors limiting the SiPM timing resolution as well as impressive progress in the domain of nanophotonics opens new perspectives for the development of a new concept of SiPM, integrating in a metamaterial structure microelectronic and nanophotonic features, for a better handling of the photon–electron interactions.

By their very nature, SiPMs are composed of many separated single avalanche photodiodes (SPADs), which require some dead border at the edges for electrical and optical isolation and to prevent edge breakdown. This reduces the so-called fill factor (FF) of the device and sets an intrinsic limit to its photodetection efficiency (PDE).

One solution is to use plasmonic metasurfaces to overcome the FF limitations. Plasmonics is the domain of resonant interaction between light and free electrons in metals. Usually, two types of resonances are identified depending on if they are delocalized (typically propagating along a metal interface) or localized (typically on a metallic particle, often designed as a nanoantenna). Localized plasmons and nanoantennas have the unique ability to enhance and concentrate light at a subwavelength scale. The potential of metasurfaces to be used as light concentrators has been studied for several years and has been demonstrated in many other applications. In this regard, achieving light concentration by means of resonant plasmonic structures will constitute a true paradigm shift in the field of single-photon detection.

Indeed, it will be possible to focus light in a very small central spot of the microcell, obtaining almost 100% FF for light detection while leaving plenty of space to increase the width of the dead border even in very small cells (≤ 5 μm). The paradigm shift allowed by these structures, thus, will be essentially decoupling FF, cell size and dead border. With this new design freedom, it will be possible to design SiPMs with: (i) very small cell size, thus reduced gain, primary and correlated noise, dead time and much increased cell density; (ii) increased dead border with room for better intra-cell optical isolation and separation between active area and cell edge, allowing to further reduce primary and correlated noise.

Another source of time jitter in a SiPM is related to the statistical variation of the depth of interaction of the photon in the SiPM structure, as a function of its wavelength and incident angle. The use of hyperbolic metamaterials gives the possibility to create strong spot-like photoconversion region in a well-defined position of the SPAD, making the detection process tunable and the electronic avalanche generation independent from the photon’s impinging point, wavelength and direction. The integration of such hyperbolic metamaterial layers in the SiPM structure is expected to improve SPTR and PDE of the device.

In summary, combining light concentration and SPTR/PDE increase will be a disruptive technological change, tailored and optimized for the SiPM structure. The ultimate goal will be creating a new generation of quantum sensors, with close to 100% PDE, ultra-high cell density, negligible correlated noise and beyond state-of-the-art primary noise.

Finally, the progress in microelectronics technology nodes as well as in 3D electronic integration with Trough VIA and bump-bonded technologies opens new perspectives for the development of highly integrated dedicated front-end ASIC with unprecedented intrinsic timing performance. The electronics can be formed by a very front-end part, reading out the signal of the individual SPADs or group of SPADs, and transforming it into a digital pulse, and a back-end, that time-stamps the digital pulse with ps resolution and manages the data formatting and off-chip data transmission.

More details about these new perspectives can be found in [52].

6 Conclusion

The rapid development of SiPMs in the 1990s has opened the way to a new generation of PET scanners. First introduced because of their immunity to the magnetic field at a time of growing interest for multimodal PET/MR imaging, they have rapidly supplanted the photomultiplier tubes, because of many other advantages, such as compactness, low bias voltage, low noise, high gain and good single-photon timing resolution.

Moreover, they have been developed in many different sizes and packaging options, from single units of 1 × 1mm2 to 6 × 6mm2 to linear arrays or up to 12 × 12 matrices. The introduction of through via technology has minimized the dead gap between matrix elements. Four-side buttable systems are now available, allowing a high flexibility in multichannel detector designs.

A much higher density of individual SPADS considerably increased the dynamic range of SiPMs, without compromising the photodetection efficiency, reaching now impressive values in excess of 60%, thanks to a clever arrangement of the SPADs, much thinner trenches to optically isolate them and more transparent metal quenching than poly-Si resistors.

The emergence of time-of-flight PET scanners has boosted the research for improving the SiPM’s timing performance. Better than 100 ps SPTR values (FWHM) are now achievable. In parallel, several groups are developing multi-digital SiPMs allowing single-photon counting with a sub-100 ps time tag of up to the 48 first photons produced by the scintillator pulse in a PET scanner [25].

SiPM technology has reached enough maturity in the first two decades of this century to be adopted as the standard photodetector by the PET industry. But we are still in the slope of enlightenment, and the plateau of the hype cycle of disruptive technologies has not been reached yet. More progresses are therefore to be expected in the next future with a direct impact on positron emission tomography.