1 Introduction

Silicon Drift Detectors (SDDs) are flexible solid state devices characterised by fast timing and excellent energy resolution (close to the Fano limit in silicon). Thanks to these features and to a well-established technology, SDDs have revolutionized X-ray spectrometry in the last 40 years [1,2,3,4,5].

The recent proposal of applying them to electron spectroscopy is motivated by the need of accurate and precise measurements of the beta spectrum of isotopes with keV-MeV end-points. As an example, in the case of the well know spectrum of \(^3\)H the observation of a spectral deformation can unveil the existence of new particles [6,7,8]. For these application, a resolution of less then 200 eV at the \(^{55}\)Fe line with counting rates in the hundreds of kHz range is required. These requirements are not matched, for example, by the focal plane detectors currently used by experiments using high intensity tritium sources, like KATRIN [9], where the focal plane detector only acts as a counter (with poor energy resolution in the keV range and a count rate of few counts per second). On the contrary, in the case of heavier isotopes, for which nuclear models give uncertain results, spectral measurements can help in understanding the effects of approximations and simplifications introduced in the theory and can constrain model free parameters [10, 11]. In both cases the key factors are a good energy resolution a high sustainable rate (both matched by SDD’s) as well as an accurate control of detector (and source) systematics. As a final remark it is worth to observe that also in the field of applied Physics e.g. radio-protection and metrology SDDs could represent a cheap and compact alternative to classical instruments and methods (see for example [12,13,14]).

As always when electrons are concerned, the challenge is to be able to infer with the required accuracy the energy of the impinging electron. Physics phenomena like back-scattering and bremsstrahlung and instrumental effects like a dead layer are among the worrisome effects that can give rise to dramatic systematic errors such as sizable distortions of the energy spectra or biased determination of the real source rate. The task is particularly tricky because an accurate reconstruction of the detector response function implies the use of a very well known source, devoid of any distortion in the emitted electron energy spectrum. In this paper, we discuss a technique based on the use of monochromatic electron beams as electron source whereas a GEANT4 simulation is used to model electron behaviour. The technique proves to be effective for the study of both the instrumental and the physics effects.

2 Experimental setup

The hereby presented study uses, as detector, a single pixel SDD. This is illuminated by a mono-energetic electron beam generated by a Scanning Electron Microscope (SEM), as well as by an \(^{55}\)Fe X-ray source. A very detailed description of the setup and a full report on the results of measurements done at different beam energies, incident angles and beam position on the detector surface can be found in [15]. In the cited paper, the process of optimization of the detector working point for X-rays and electrons is also described. The SDD surface has been scanned with the electron beam to identify the regions where the response (in terms of energy resolution, charge collection and detection efficiency) becomes sub-optimal. In order to restrict the study of the response function presented here to a single geometrical dimension (i.e. the penetration depth), only data collected with the beam hitting the SDD at the center of the fully active area (i.e. half way between the anode and the border of the device) are considered.

2.1 SDD assembly and read-out

The SDD, fabricated by MPG-HLL, has a circular design with 1600 \(\upmu \)m radius active area (Fig. 1) and the wafer is 450 \(\upmu \)m thick. The electric field is generated by polarizing a set of circular electrodes on the back of the device, while the front surface (where the radiation to be measured is supposed to hit the detector) is an equi-potential contact realized with a very shallow (of the order of tens of nanometers) implantation, covered with a 22 nm thick silicon oxide passivated layer. The entrance window has no metallic deposition in order to minimize the amount of passive material that the radiation must penetrate. Five small aluminum markers, four placed 100\(\upmu \)m away from the edge of the active area and one in the very center, are deposited on the surface as reference points. At the very center of the circular active area, where the collection anode is situated, an integrated transistor acts as the first stage of the charge integration and signal amplification chain. The SDD is glued to a PCB (called detector board in the following) where the anode signal is collected and routed to the front-end electronics. This board also hosts the detector and transistor bias lines. In the front-end an ASIC is used as pre-amplifier [16] and the signal is routed towards a DAQ system. The ASIC is mounted on a second board, called ASIC board. Detector board and ASIC board are connected with a flexible PCB and are both placed inside the SEM vacuum chamber. The DAQ, situated outside the SEM vacuum chamber, consists of an XGLab Dante DPP (digital pulse processing unit) [17] based on a 125 MHz, 16 bit digitizer. The programmable DPP applies a digital flat-top (trapezoidal) filter to the digitized waveform. The peaking time is A histogram with the amplitude of the filtered events is finally filled.

Fig. 1
figure 1

SDD entrance window with the polarization contacts and the five reference aluminum markers visible on the surface. The anode and integrated transistor sit below the central dot. The picture was realised with the SEM in imaging mode

Full size image
Fig. 2
figure 2

Experimental setup with the SDD assembly on the SEM (Tescan VEGA TS 5136XM) stage, inside the vacuum chamber. The setup consists of: a detector board with single-pixel SDD, b preamplifier board, c routing of the signal and biases towards the vacuum feed-through, d electron beam source

Full size image

The SDD and detector board are covered with an aluminum protective case that also acts as the holder for the \(^{55}\)Fe source. A hole in the cover allows the electron beam to hit the detector surface. The hole is shaped so that the beam doesn’t hit the cover in the whole range of incidence angles to be investigated.

2.2 SEM and electron beam

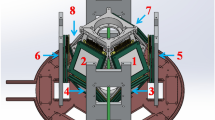
The electron beam used is generated by a Tescan VEGA TS 5136XM SEM. The detector and front-end electronics are placed on the sample stage of the SEM (see Fig. 2), and connected via vacuum-compatible feed-throughs to the bias generators and DPP, placed outside the SEM vacuum chamber. The SEM stage can be moved with \(\sim \) 1\(\upmu \)m precision along the x, y and z axis, rotated and tilted. The possibility of tilting the detector with respect to the electron beam axis is crucial for this study: the analysis of the energy spectra acquired in a wide range of incidence angles proves very sensitive to the profile of the entrance window energy-to-signal conversion. The larger is the beam angle w.r.t. the surface normal, the longer the effective thickness of the insensitive (or partially sensitive) part of the detector that the electrons must penetrate. This allows us to explore the incidence-angle/energy phase-space and optimize our detector response model so that it is able to reproduce the detector behaviour in the most general case. As discussed in Sect. 3.2 this implies that a single set of model parameters must be able to describe the detector response whatever the energy and direction of the impinging electron is.

The beam cross section of  100 nm, as well as the uncertainty on its energy of the order of few eV, are negligible compared to the size and energy resolution of the detector (\(\sim \)270 eV FWHM at 20 keV as extrapolated from X-ray calibration). The beam is therefore considered perfectly collimated and mono-energetic in the following analysis.

During the measurements, the current of the SEM beam has been reduced well below the minimum settings by reducing the heating current of the electrons source. In this way the event rate on the detector was low enough (below 10 kHz) to make pile-up completely negligible. No relevant pile-up is expected to affect the reconstructed energy spectrum until hundreds of kHz of counting rate are reached.

2.3 \(^{55}\)Fe X-ray source

In all the SEM measurements, the SDD is illuminated by a \(^{55}\)Fe source. The two full energy X-ray peaks at 5.9 and 6.5 keV of Fe are used for calibration of the energy scale and provide a real-time monitor of the energy resolution of the SDD. The calibration is extrapolated up to the maximum beam energy of 20 keV. Both the detector and part of the surrounding material are uniformly illuminated by this source that contributes for about one-tenth of the overall counting rate measured by the detector (\(\sim \)3 kHz)

3 Detector response model

As already discussed, one of the most tricky aspects of SDD characterization is the reconstruction of their energy-response function, \(R(E;E_0,\alpha )\), that is defined as the probability of measuring an energy E when the incoming electron energy is \(E_0\) and the incident angle is \(\alpha \). The main structures in this function are:

  1. (1)

    a “full energy” peak, with a FWHM that measures the energy resolution of the device. The position of this peak is slightly below the electron beam energy, due to a DC polarization of the entrance window of -110 V and to the effect of a partial signal generation efficiency at the surface (Sect. 3.2);

  2. (2)

    a roughly flat and featureless continuum at low energy due to energy losses outside the detector volume, both from bremsstrahlung X-ray emission and electron back-scattering;

  3. (3)

    few silicon X-ray escape peaks generated when a silicon X-ray produced by the electron interaction leaves the detector;

  4. (4)

    a tail on the left-side of the “full energy” peak due to an incomplete collection of the charges produced by particle interaction.

The structures described by (1), (2) and (3) are a consequence of the mechanism of interaction of the electrons with matter, and would be present also with an ideal detector with the ability of convert all the deposited energy into a readable signal. Their relative magnitude is obtained with the GEANT4 simulation described in Sect. 3.1.

The width of the full energy peak (1) is dominated by the combination of electron-hole pairs statistics and electronic noise. It is reproduced by convolving the output of the simulation with a gaussian function whose width is energy (E) dependent and is defined by

$$\begin{aligned} \sigma ^2(E) = \sigma _{\mathrm {noise}}^2 + \sigma _{\mathrm {e-h}}^2 E \end{aligned}$$
(1)

where \(\sigma _{\mathrm {noise}}\) and \(\sigma _{\mathrm {e-h}}\) are obtained by the analysis of X-ray calibration data.

The detector entrance window is the major source of the effect 4). Its treatment is described in Sect. 3.2. We build and optimize an effective analytical model to account for the impact of the entrance window on the electrons energy reconstruction. An alternative approach to account for it would be an event-by-event simulation of the full device that describes charge production, drift and collection. This approach would be too computationally demanding and complex to be implemented in a real-life application, where an effective model is much more efficient when dealing with a large number of events of the typical applications [6, 7, 10].

In the energy range of interest for this work (5–20 keV) the entrance window has a mild effect on R(E) when dealing with X-rays: most of the photons interact in the very bulk of the detector where charge collection is fully efficient. The R(E) still features a gaussian peak, corresponding to the X-ray nominal energy, and the low energy continuum, but the effect of the entrance window is observed to be negligible in our measurements. In the case of electrons, the effect of the entrance window is more dramatic because no electron can reach the fully active detector volume without experiencing an energy loss in the shallower layers. The peak is shifted toward lower energies (by an amount proportional to the minimum amount of energy that the electron can loose in the inactive volume when crossing it perpendicularly with minimal deviations) and deformed. The low energy continuum is also more pronounced, mostly because of the high probability of electron back-scattering. Finally, by changing the incidence angle of the electron beam with the SDD surface, the relative importance of the different effects can be changed. The further from normal incidence, the larger the amount of energy lost in the inactive and partially active parts of the entrance window, and the larger the probability of back-scattering. For this reason an electron beam, whose incidence angle can be controlled precisely, is an optimal solution for this characterisation.

3.1 MonteCarlo simulation of beam interaction

We use GEANT4 [18] version 10.4.p02 to simulate the interaction of an electron of energy \(E_0\) entering the SDD with an angle \(\alpha \). The simulation predicts the local energy depositions \(E_i(x_i,y_i,z_i)\) along the electron track inside the material (i runs over the propagation steps of the particles in the simulation, and \((x_i,y_i,z_i)\) are the coordinates of the i-th interaction step where energy \(E_i\) is deposited). At each step the different energy-depositing processes (continuous energy loss, nuclear diffusion) as well as the production and propagation of secondary radiation (bremsstrahlung, photo-electric effect, Rayleigh and Thomson scattering, X-ray escape) are considered. The detector is modeled as a homogeneous layer of silicon. Relevant parts of the setup located near the detector active volume (PCB, detector holders, etc.) are also included in the simulation in order to account for the contribution to the signal of escaping radiation re-entering the detector after interacting with the surrounding material. For each value of \(E_0\) and \(\alpha \) a large number of electrons (\(2\times 10^6\) events, about twice the statistics of the data) is simulated, and for each event the coordinates of each energy deposition are recorded. This information is later weighted for the energy-to-signal conversion, or quantum efficiency (Q.E. from now on) to extract the expected signal magnitude (Sect. 3.2). The Q.E. accounts for the efficiency with which an energy deposition in a given position in the detector volume actually contributes to the formation of the signal.

As the energy of the electrons is relatively low (few keV) and the required spatial accuracy of the simulation very high (the SDD Q.E. is expected to show relevant variations on the scale of tens of nanometers), the default statistical treatment of the energy depositions can lack the required accuracy. For this reason we decided to use the G4EmLivermorePhysics physics list (optimised for low energy electrons) and enabled the G4StepLimiter feature in order to ensure that each propagation step isn’t longer than 10 nm.

3.2 Energy-to-signal conversion efficiency

Once the information about the energy deposited by each event at different coordinates inside the SDD is generated by the GEANT4 simulation and recorded, an analytical model (\(f_{\mathrm {QE}}(z;\theta )\)) of the Q.E. is applied to the electron sample in order to build the expected spectrum of recorded amplitudes. The recorded amplitude is defined as a weighted sum of the energy depositions:

$$\begin{aligned} E=\sum _i E_i(x_i,y_i,z_i) \cdot f_{\mathrm {QE}}(z_i;\theta ) \end{aligned}$$
(2)

The Q.E. model \(f_{\mathrm {QE}}(z;\theta )\), acting as a weight function, is assumed to depend only on the z coordinate (i.e. the penetration depth) but the study could, in principle, be extended with the same method to a higher dimensional model. This would allow to model, for example, non-ideal charge collection at the edge of the active area or in proximity of the central anode. For the sake of this work, however, the electron beam was steered to hit only the region where these effects are not present (half way between the anode and the edge of the device), therefore a mono-dimensional Q.E. model is sufficient to describe the detector response. \(f_{\mathrm {QE}}\) also depends on a set of parameters, \(\theta \).

The general shape of the Q.E. reflects the technology used to build the SDD entrance window: an oxide layer exists on the device surface (any electron-hole pair produced here contributes to the signal formation with a constant probability, \(p_0\), that is expected to be zero). For this particular device the thickness of the oxide dead layer, t, is expected to be \(\sim \)22 nm. Moving forward along the z axis beyond the boundary between the oxide and the active silicon, a volume where the implantation of the entrance window contact occurred is encountered. In this volume the charge collection is at work but not fully efficient. Here the Q.E. is assumed to start from a value \(p_1\) and gradually approaches a unitary value with a regular behaviour that we decided to model as an exponential with scale parameter \(\lambda \) [19, 20]. Once the free parameters of the model, \(\theta = \{t,p_0,p_1,\lambda \}\), are defined, the Q.E. \(f_\mathrm {QE}(z;\theta ) = f_\mathrm {QE}(z;t,p_0,p_1,\lambda )\) can be written as:

$$\begin{aligned} f_\mathrm {QE}(z;\theta ) = {\left\{ \begin{array}{ll} p_0 &{} z < t \\ 1+(p_1-1)\exp {\left( -\frac{z-t}{\lambda }\right) } &{} z > t \end{array}\right. } \end{aligned}$$

   A representation of the Q.E. as a function of the depth (z coordinate) is reported in Fig. 3 both in a generic case with dummy parameters and in the case of the model developed in this work (as calculated in Sect. 3.3).

Fig. 3
figure 3

Energy-to-signal conversion efficiency (Q.E.) parametric model. In blue the most generic form of the Q.E. (with dummy parameters), with a shallow layer of partial efficiency followed by an exponentially increasing region with free intercept. The green curve is the configuration eventually found to better fit the data, with gray bands representing the curves obtained by varying by \(\pm 1\sigma \) the free parameters in an uncorrelated way. In the lower panel a conceptual sketch of a recorded MonteCarlo event for a low energy electron. The total signal is evaluated as the energy E\(_i\) deposited along each step, weighted for the Q.E. evaluated at the corresponding coordinates

Full size image

The aim of this study is to show that a set of optimized parameters, \({\hat{\theta }}\), can be obtained by comparing the simulated spectra with real data. The resulting response function can be used to predict the shape of the measured spectrum for any source of electrons illuminating the SDD. In this particular work we assume \(p_0 = 0\) and \(t = 22\) nm, as the oxide layer thickness is known from the design of the device and fabrication process. It is worth noting that the described method can be applied to an arbitrary number of free, unknown parameters of the model, with an obvious increase in the computing complexity.

3.3 Fitting procedure and estimation of model parameters

The estimation of the best parameters \({\hat{\theta }}\) is performed with a simultaneous least square fit of the simulations to the available data-sets (different energies and angles). The data used for this analysis have been collected with three beam energy settings (5, 10 and 20 keV) and incidence angles varied between \(5^\circ \) and \(60^\circ \) with a step of \(5^\circ \). It’s worth noting that the real energy \(E_0\) of the beam is assumed to be 110 eV smaller than the energy setting of the SEM, due to the polarization of the entrance window contact. For each beam condition (defined by energy \(E_0\) and incidence angle \(\alpha \)) we run a high statistics simulation (in order to make the statistical errors of the model subdominant) recording the local energy depositions \(E_i(x_i,y_i,z_i)\) occurring in the SDD. We then process each event in the simulation with the selected \(f(z,\theta _j)\) model (j index runs over all the combinations of free parameters that are tested). The obtained simulated energy spectrum is the one that we would expect to measure if the Q.E. were described by the set of parameters \(\theta _j\). For each \(\theta _j\) we finally compare the simulated spectrum with the experimental one.

In order to extend the comparison below 6 keV we also include the contribution from the \({}^{55}\)Fe source. Since the source illuminates the detector evenly the spectral shape it produces is affected by more non-idealities than the electron beam (e.g. loss of efficiency close to the detector border, X-ray interactions in materials close to the SDD). For this reason we do not use a MC simulation to estimate this contribution, but a beam-off measured spectrum properly scaled to match the X-ray peaks areas. From this point onward we’ll refer to ’simulated spectrum’ as the combination of the electron simulation and the measured \({}^{55}\)Fe contribution.

We sample the \(\theta \) parameter space and for each point (\(\theta _j\)) we perform a simultaneous comparison of the real and simulated spectra for all available \(E_0\) and \(\alpha \). From this comparison we extract a \(\chi ^2\) value for each point j in the \(\theta \) space as:

$$\begin{aligned} \chi ^2_j = \sum _{E_0,\alpha } \chi ^2_{E_0,\alpha ;j}. \end{aligned}$$
(3)

Each term in the sum in Eq. 3 is defined as

$$\begin{aligned} \chi ^2_{E_0,\alpha ;j} = \sum _n \frac{(D_n(E_0,\alpha ) - S_n(E_0,\alpha ;\theta _j))^2}{D_n(E_0,\alpha )}, \end{aligned}$$
(4)

where \(D_n(E_0,\alpha )\) is the number of events in the n-th bin of the data with beam energy \(E_0\) and incidence angle \(\alpha \). \(S_n(E_0,\alpha ;\theta _j)\) is the content of the n-th bin in the corresponding simulation, processed with a the j-th set of model parameters \(\theta _j\). We exclude the bins corresponding to energies smaller than 3 keV from the \(\chi ^2\) calculation as DAQ threshold effects, as well as random triggers of noise fluctuations introduce distortion in this energy region that we don’t model in our simulation. Similarly, we consider only energies up to 200 eV (1 keV) above the beam energy for the 5 keV (10 and 20 keV) data-sets since we don’t expect any relevant information above these thresholds.

The minimum value among the \(\chi ^2_j\) corresponds to the best set of parameters \({\tilde{\theta }}\). We marginalize the \(\chi ^2\) distribution with respect to each parameter and interpolate the resulting graphs with parabolic functions around the minima in order to extract statistical uncertainties.

Fig. 4
figure 4

Values of the two free parameters \(\lambda \) and \(p_1\) obtained from the fits of the single angle (\(\alpha \)) data-sets. For reference, the average of the points (dashed), as well as the global fit result (solid black) and the associated errors (solid grey) are reported. The result of the fit is stable with respect to the choice of the subset of analyzed data, and the spread of the results is therefore used as a measure of the error associated to the global fit outcome

Full size image
Fig. 5
figure 5

Projection of the reduced \(\chi ^2\) in the \((\lambda ,p_1)\) plane. Minimum and correlations between parameters can be extracted from these projections. The error bars are dominated by systematic effects that have been evaluated as the RMS of the results obtained by repeating the fit on the 12 independent subsets of data corresponding to single incident angles

Full size image

A possible source of bias in the estimation of the parameters derives from the fact that the model that we used might be an over-simplification of the real response. In order to account for this we repeat the fitting procedure on reduced data-sets corresponding to single angles (summing over the different energies). We therefore obtain a total of 12 best fit values (Fig. 4), and we report their RMS as an estimation of the systematic error associated to the best fit from the simultaneous fit. The resulting values for the free parameters are the following:

$$\begin{aligned} \lambda= & {} (59.8 \pm 3.1) \mathrm {~nm} \\ p_1= & {} (9 \pm 5)\% \end{aligned}$$

As expected, given the large amount of statistics in the single spectra, the statistical error is negligible. The uncertainty on the parameters is completely dominated by the systematics contribution, accounting for the small deviations of the model from the data perceivable in some regions of the spectrum. The relative uncertainty on \(p_1\) is large, indicating that the procedure is not sensitive to this parameter of the model, i.e. its effect on the shape of the reconstructed spectrum is small.

In Fig. 5 a bi-dimensional projection of the reduced \(\chi ^2\) in the \((\lambda ,p_1)\) plane is reported for reference. Together with the minimum, corresponding to \({\tilde{\chi }}^2 = 3.3\), correlations between the parameters can be extracted with this method.

Fig. 6
figure 6

Top: data (red) and MonteCarlo (MC) reconstruction (blue) of the response function to 20 keV electrons hitting the surface of the SDD with a 60\(^{\circ }\) angle. The reconstruction is obtained with the best fit response function from the global analysis of the different energies and incidence angles. The \(\chi ^2\) is calculated only in the non-shaded regions. The region below 3 keV is always excluded because threshold and random trigger (noise) effects are not modelled in our simulation, while the upper limit is slightly above the beam energy. Bottom: residuals normalized to the bin error (black) and to the highest bin in the fitted region (green)

Full size image

Figures 6, 7 and 8 show three examples of comparison between data (red) and the MonteCarlo reconstruction (blue). The reconstructed spectra reported here are the ones obtained by processing the MonteCarlo simulation with the best set of parameters \({\hat{\theta }}\) of the Q.E. model. The \(\chi ^2\) is calculated only in the non-shaded regions. The residuals normalized to the bin error (black) and to the highest bin in the fit region (green) are also reported.

Fig. 7
figure 7

Top: data (red) and MC reconstruction (blue) of the response function to 10 keV electrons hitting the surface of the SDD with a 45\(^{\circ }\) angle. Bottom: residuals normalized to the bin error (black) and to the highest bin in the fitted region (green)

Full size image
Fig. 8
figure 8

Top: data (red) and MC reconstruction (blue) of the response function to 5 keV electrons hitting the surface of the SDD with a 30\(^{\circ }\) angle. Bottom: residuals normalized to the bin error (black) and to the highest bin in the fitted region (green)

Full size image

The agreement between the data and the model is remarkably good for the 20 and 10 keV spectra in the wide range of energies and angles analysed, with the maximum deviation over all the 24 spectra being of the order of \(10\%\) of the peak intensity over few (out of many thousands) energy bins. The reconstruction of the 5 keV data is the least accurate. This is a clear indication that the capability of the simulation to model the physics effects involving electrons at the lower end of the considered energy range is still lacking the required accuracy.

4 Conclusions

This work presents a method to develop a model of the response of an SDD to keV electrons. The response function is built by comparing GEANT4 simulations, processed with an analytical model of the energy-to-signal conversion efficiency (or quantum efficiency, Q.E.) of the SDD entrance window with data acquired when illuminating a device with mono-energetic electron beams and X-rays. We proof that with a simple Q.E. model based on few parameters and Geant4 simulations it is possible to describe the SDD response to electrons over a wide range of energies and incident angles. This result can in principle be used to perform a deconvolution of the detector response from a measured spectrum and infer the original energy distribution of the electrons with a good accuracy. A future step will be to verify the power of this approach and the level of accuracy that can be reached by reconstructing well known beta spectra from superallowed transitions and compare them with the reliable theoretical expectations.