Skip to main content
SpringerLink
Log in

Vibration analysis of stress-driven nonlocal integral model of viscoelastic axially FG nanobeams

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

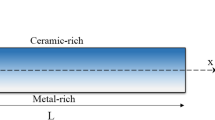
Finite element method (FEM) and generalized differential quadrature method (GDQM) are developed for damping vibration analysis of viscoelastic axially functionally graded (VAFG) nanobeams within the framework of stress-driven nonlocal integral model (SDM). The equivalent differential law of SDM and two constitutive non-classic boundary conditions (CBCs) are utilized to construct FE and GDQ models. In FEM, three different types of beam elements are derived: two different types for the both ends of the nanobeam and another type for elements located in the middle of nanobeam. Convergence and accuracy of the present FEM and GDQM are evaluated, and it is shown that the present results and formulations are efficient and reliable. Also, in the damping vibration analysis of VAFG nanobeams by SDM, variations of the mechanical properties are considered as a power-law function. After validation of present results and mathematical modeling, various benchmark results are presented to determine the influences of several parameters, such as nonlocal SDM parameter, FG index and damping factor on both parts of size-dependent complex frequencies of VAFG nanobeams with different boundary conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Abbreviations

\( E_{\text{l}} \), \( E_{\text{r}} \) :

Young’s modulus in left and right side of nanobeam

\( \rho_{\text{l}} \), \( \rho_{\text{r}} \) :

Mass density in left and right side of nanobeam

\( \eta_{\text{l}} \), \( \eta_{\text{r}} \) :

Damping factor in left and right side of nanobeam

\( E\left( x \right) \) :

Variable Young’s modulus

\( \rho \left( x \right) \) :

Variable mass density

\( \eta \left( x \right) \) :

Variable damping factor

c :

Non-dimensional damping parameter

L :

Length of nanobeam

b :

Width of nanobeam

H :

Thickness of nanobeam

x, y, z :

Cartesian coordinate system

\( \Im_{\text{eff}} \) :

Effective material properties of nanobeam

\( \Im_{\text{l}} \), \( \Im_{\text{r}} \) :

Material properties in left and right side of nanobeam

\( V_{\text{l}} \left( x \right) \) :

Volume fraction of material in left side of nanobeam

np :

FG index

\( \varepsilon_{xx} \) :

Axial strain

\( \sigma_{xx} \) :

Normal stress

k :

Nonlocal parameter

\( \mu \) :

Non-dimensional nonlocal parameter

I :

Moment of inertia of the cross section

M :

Bending moment

A :

Area of the cross section

\( w\left( {x,t} \right) \) :

Transverse displacement

\( T\left( t \right) \) :

Time response function

t :

Time

\( m_{1} \) :

Mass distribution per length

\( \omega \) :

Vibration frequency

\( \left[ M \right] \) :

Mass matrix

\( \left[ {Ks} \right] \) :

Strain stiffness matrix

\( \left[ D \right] \) :

Damping matrix

\( ng \) :

Number of grid points

\( x_{i} \) :

Location of grid points

\( H_{ij}^{\left( r \right)} \) :

Hermite shape functions

\( U_{\text{b}} \), \( U_{\text{d}} \) :

Boundary and domain grid points

\( {\mathbb{Z}} \) :

State vector

\( \left[ S \right] \) :

State matrix

\( \bar{\mathbb{Z}} \) :

Eigenvectors

\( \left[ I \right] \) :

Identity matrix

\( \zeta \) :

Ratio of \( \eta_{\text{r}} /\eta_{\text{l}} \)

References

  1. A.C. Eringen, Nonlocal polar elastic continua. Int. J. Eng. Sci. 10, 1–16 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  2. A.C. Eringen, D. Edelen, On nonlocal elasticity. Int. J. Eng. Sci. 10, 233–248 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  3. A.C. Eringen, On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54, 4703–4710 (1983)

    Article  ADS  Google Scholar 

  4. J. Reddy, Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 45, 288–307 (2007)

    Article  MATH  Google Scholar 

  5. M. Ece, M. Aydogdu, Nonlocal elasticity effect on vibration of in-plane loaded double-walled carbon nano-tubes. Acta Mech. 190, 185–195 (2007)

    Article  MATH  Google Scholar 

  6. M. Eltaher, S.A. Emam, F. Mahmoud, Free vibration analysis of functionally graded size-dependent nanobeams. Appl. Math. Comput. 218, 7406–7420 (2012)

    MathSciNet  MATH  Google Scholar 

  7. S. Sahmani, A. Fattahi, Small scale effects on buckling and postbuckling behaviors of axially loaded FGM nanoshells based on nonlocal strain gradient elasticity theory. Appl. Math. Mech. 39, 561–580 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  8. B. Zhang, H. Shen, J. Liu, Y. Wang, Y. Zhang, Deep postbuckling and nonlinear bending behaviors of nanobeams with nonlocal and strain gradient effects. Appl. Math. Mech. 2019, 1–34 (2019)

    ADS  MATH  Google Scholar 

  9. F. Khosravi, S.A. Hosseini, A. Tounsi, Torsional dynamic response of viscoelastic SWCNT subjected to linear and harmonic torques with general boundary conditions via Eringen’s nonlocal differential model. Eur. Phys. J. Plus 135, 183 (2020)

    Article  Google Scholar 

  10. B.A. Hamidi, S.A. Hosseini, R. Hassannejad, F. Khosravi, Theoretical analysis of thermoelastic damping of silver nanobeam resonators based on Green–Naghdi via nonlocal elasticity with surface energy effects. Eur. Phys. J. Plus 135, 1–20 (2020)

    Article  Google Scholar 

  11. Y. Lei, S. Adhikari, M. Friswell, Vibration of nonlocal Kelvin–Voigt viscoelastic damped Timoshenko beams. Int. J. Eng. Sci. 66, 1–13 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  12. Y. Lei, T. Murmu, S. Adhikari, M. Friswell, Dynamic characteristics of damped viscoelastic nonlocal Euler–Bernoulli beams. Eur. J. Mech. A/Solids 42, 125–136 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. R. Talebitooti, S.O. Rezazadeh, A. Amiri, Comprehensive semi-analytical vibration analysis of rotating tapered AFG nanobeams based on nonlocal elasticity theory considering various boundary conditions via differential transformation method. Compos. B Eng. 160, 412–435 (2019)

    Article  Google Scholar 

  14. J. Phadikar, S. Pradhan, Variational formulation and finite element analysis for nonlocal elastic nanobeams and nanoplates. Comput. Mater. Sci. 49, 492–499 (2010)

    Article  Google Scholar 

  15. S. Thai, H.-T. Thai, T.P. Vo, V.I. Patel, A simple shear deformation theory for nonlocal beams. Compos. Struct. 183, 262–270 (2017)

    Article  Google Scholar 

  16. J. Fernández-Sáez, R. Zaera, J. Loya, J. Reddy, Bending of Euler–Bernoulli beams using Eringen’s integral formulation: a paradox resolved. Int. J. Eng. Sci. 99, 107–116 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  17. A.D. Polyanin, A.V. Manzhirov, Handbook of Integral Equations (CRC Press, Boca Raton, 2008)

    Book  MATH  Google Scholar 

  18. J. Fernández-Sáez, R. Zaera, Vibrations of Bernoulli–Euler beams using the two-phase nonlocal elasticity theory. Int. J. Eng. Sci. 119, 232–248 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. S. Hosseini-Hashemi, S. Behdad, M. Fakher, Vibration analysis of two-phase local/nonlocal viscoelastic nanobeams with surface effects. Eur. Phys. J. Plus 135, 190 (2020)

    Article  Google Scholar 

  20. M. Fakher, S. Behdad, A. Naderi, S. Hosseini-Hashemi, Thermal vibration and buckling analysis of two-phase nanobeams embedded in size dependent elastic medium. International Journal of Mechanical Sciences. 2019, 105381 (2019)

    Google Scholar 

  21. G. Romano, R. Barretta, Nonlocal elasticity in nanobeams: the stress-driven integral model. Int. J. Eng. Sci. 115, 14–27 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  22. M.F. Oskouie, R. Ansari, H. Rouhi, Bending of Euler–Bernoulli nanobeams based on the strain-driven and stress-driven nonlocal integral models: a numerical approach. Acta Mech. Sin. 2018, 1–12 (2018)

    MathSciNet  Google Scholar 

  23. G. Romano, R. Barretta, Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. B Eng. 114, 184–188 (2017)

    Article  Google Scholar 

  24. R. Barretta, S. Fazelzadeh, L. Feo, E. Ghavanloo, R. Luciano, Nonlocal inflected nano-beams: a stress-driven approach of bi-Helmholtz type. Compos. Struct. 200, 239–245 (2018)

    Article  Google Scholar 

  25. H. Darban, F. Fabbrocino, L. Feo, R. Luciano, Size-dependent buckling analysis of nanobeams resting on two-parameter elastic foundation through stress-driven nonlocal elasticity model. Mech. Adv. Mater. Struct. 2020, 1–9 (2020)

    Article  Google Scholar 

  26. R. Barretta, R. Luciano, F.M. de Sciarra, G. Ruta, Stress-driven nonlocal integral model for Timoshenko elastic nano-beams. Eur. J. Mech. A/Solids 72, 275–286 (2018)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. R. Barretta, M. Diaco, L. Feo, R. Luciano, F.M. de Sciarra, R. Penna, Stress-driven integral elastic theory for torsion of nano-beams. Mech. Res. Commun. 87, 35–41 (2018)

    Article  Google Scholar 

  28. R. Barretta, S.A. Faghidian, R. Luciano, Longitudinal vibrations of nano-rods by stress-driven integral elasticity. Mech. Adv. Mater. Struct. 2018, 1–9 (2019)

    Article  Google Scholar 

  29. A. Apuzzo, R. Barretta, R. Luciano, F.M. de Sciarra, R. Penna, Free vibrations of Bernoulli–Euler nano-beams by the stress-driven nonlocal integral model. Compos. B Eng. 123, 105–111 (2017)

    Article  Google Scholar 

  30. R. Barretta, M. Čanadija, L. Feo, R. Luciano, F.M. de Sciarra, R. Penna, Exact solutions of inflected functionally graded nano-beams in integral elasticity. Compos. B Eng. 142, 273–286 (2018)

    Article  Google Scholar 

  31. R. Barretta, S.A. Faghidian, R. Luciano, C. Medaglia, R. Penna, Free vibrations of FG elastic Timoshenko nano-beams by strain gradient and stress-driven nonlocal models. Compos. B Eng. 154, 20–32 (2018)

    Article  Google Scholar 

  32. E. Mahmoudpour, S. Hosseini-Hashemi, S. Faghidian, Nonlinear vibration analysis of FG nano-beams resting on elastic foundation in thermal environment using stress-driven nonlocal integral model. Appl. Math. Model. 57, 302–315 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  33. M.F. Oskouie, R. Ansari, H. Rouhi, Stress-driven nonlocal and strain gradient formulations of Timoshenko nanobeams. Eur. Phys. J. Plus 133, 336 (2018)

    Article  Google Scholar 

  34. M.F. Oskouie, R. Ansari, H. Rouhi, A numerical study on the buckling and vibration of nanobeams based on the strain-and stress-driven nonlocal integral models. Int. J. Comput. Mater. Sci. Eng. 7, 1850016 (2018)

    Google Scholar 

  35. T.H.G. Megson, Aircraft Structures for Engineering Students (Butterworth-Heinemann, Oxford, 2016)

    Google Scholar 

  36. Y. Zhang, M. Pang, L. Fan, Analyses of transverse vibrations of axially pretensioned viscoelastic nanobeams with small size and surface effects. Phys. Lett. A 380, 2294–2299 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  37. M. Arefi, A.M. Zenkour, Nonlocal electro-thermo-mechanical analysis of a sandwich nanoplate containing a Kelvin–Voigt viscoelastic nanoplate and two piezoelectric layers. Acta Mech. 228, 475–493 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  38. M.F. Oskouie, R. Ansari, F. Sadeghi, Nonlinear vibration analysis of fractional viscoelastic Euler–Bernoulli nanobeams based on the surface stress theory. Acta Mech. Solida Sin. 30, 416–424 (2017)

    Article  Google Scholar 

  39. O. Martin, Nonlocal effects on the dynamic analysis of a viscoelastic nanobeam using a fractional Zener model. Appl. Math. Model. 73, 637–650 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  40. A. Norouzzadeh, R. Ansari, Isogeometric vibration analysis of functionally graded nanoplates with the consideration of nonlocal and surface effects. Thin-Walled Struct. 127, 354–372 (2018)

    Article  Google Scholar 

  41. H.B. Khaniki, On vibrations of FG nanobeams. Int. J. Eng. Sci. 135, 23–36 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  42. R. Barretta, F. Fabbrocino, R. Luciano, F.M. de Sciarra, Closed-form solutions in stress-driven two-phase integral elasticity for bending of functionally graded nano-beams. Phys. E 97, 13–30 (2018)

    Article  Google Scholar 

  43. R. Ansari, R. Rajabiehfard, B. Arash, Nonlocal finite element model for vibrations of embedded multi-layered graphene sheets. Comput. Mater. Sci. 49, 831–838 (2010)

    Article  Google Scholar 

  44. S. Pradhan, Nonlocal finite element analysis and small scale effects of CNTs with Timoshenko beam theory. Finite Elem. Anal. Des. 50, 8–20 (2012)

    Article  Google Scholar 

  45. M. Eltaher, S.A. Emam, F. Mahmoud, Static and stability analysis of nonlocal functionally graded nanobeams. Compos. Struct. 96, 82–88 (2013)

    Article  Google Scholar 

  46. Ö. Civalek, C. Demir, A simple mathematical model of microtubules surrounded by an elastic matrix by nonlocal finite element method. Appl. Math. Comput. 289, 335–352 (2016)

    MathSciNet  MATH  Google Scholar 

  47. X. Zhu, L. Li, On longitudinal dynamics of nanorods. Int. J. Eng. Sci. 120, 129–145 (2017)

    Article  Google Scholar 

  48. S. Rajasekaran, H.B. Khaniki, Bending, buckling and vibration analysis of functionally graded non-uniform nanobeams via finite element method. J. Braz. Soc. Mech. Sci. Eng. 40, 549 (2018)

    Article  Google Scholar 

  49. M. Faraji-Oskouie, A. Norouzzadeh, R. Ansari, H. Rouhi, Bending of small-scale Timoshenko beams based on the integral/differential nonlocal-micropolar elasticity theory: a finite element approach. Appl. Math. Mech. 2019, 1–16 (2019)

    MATH  Google Scholar 

  50. A. Pisano, A. Sofi, P. Fuschi, Nonlocal integral elasticity: 2D finite element based solutions. Int. J. Solids Struct. 46, 3836–3849 (2009)

    Article  MATH  Google Scholar 

  51. M. Taghizadeh, H. Ovesy, S. Ghannadpour, Beam buckling analysis by nonlocal integral elasticity finite element method. Int. J. Struct. Stab. Dyn. 16, 1550015 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  52. P. Khodabakhshi, J. Reddy, A unified integro-differential nonlocal model. Int. J. Eng. Sci. 95, 60–75 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  53. M. Tuna, M. Kirca, Bending, buckling and free vibration analysis of Euler–Bernoulli nanobeams using Eringen’s nonlocal integral model via finite element method. Compos. Struct. 179, 269–284 (2017)

    Article  Google Scholar 

  54. K. Eptaimeros, C.C. Koutsoumaris, G. Tsamasphyros, Nonlocal integral approach to the dynamical response of nanobeams. Int. J. Mech. Sci. 115, 68–80 (2016)

    Article  Google Scholar 

  55. A. Norouzzadeh, R. Ansari, Finite element analysis of nano-scale Timoshenko beams using the integral model of nonlocal elasticity. Phys. E 88, 194–200 (2017)

    Article  Google Scholar 

  56. M. Fakher, S. Rahmanian, S. Hosseini-Hashemi, On the carbon nanotube mass nanosensor by integral form of nonlocal elasticity. Int. J. Mech. Sci. 150, 445–457 (2018)

    Article  Google Scholar 

  57. H.M. Sedighi, M. Malikan, Stress-driven nonlocal elasticity for nonlinear vibration characteristics of carbon/boron-nitride hetero-nanotube subject to magneto-thermal environment. Phys. Scr. 95, 055218 (2020)

    Article  ADS  Google Scholar 

  58. H.M. Sedighi, H.M. Ouakad, R. Dimitri, F. Tornabene, Stress-driven nonlocal elasticity for the instability analysis of fluid-conveying C-BN hybrid-nanotube in a magneto-thermal environment. Phys. Scripta 95(6), 065204 (2020)

    Article  ADS  Google Scholar 

  59. Y. He, H. Qing, C.-F. Gao, Theoretical analysis of free vibration of microbeams under different boundary conditions using stress-driven nonlocal integral model. Int. J. Struct. Stab. Dyn. 20, 2050040 (2020)

    Article  MathSciNet  Google Scholar 

  60. L. Meirovitch, Fundamentals of Vibrations (Waveland Press, Long Grove, 2010)

    Google Scholar 

  61. T. Wu, G. Liu, Application of generalized differential quadrature rule to sixth-order differential equations. Commun. Numer. Methods Eng. 16, 777–784 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  62. A. Shahba, R. Attarnejad, S. Hajilar, Free vibration and stability of axially functionally graded tapered Euler–Bernoulli beams. Shock Vib. 18, 683–696 (2011)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Iran University of Science and Technology, 16846-13114, Narmak, Tehran, Iran

    Mahmood Fakher, Shahin Behdad & Shahrokh Hosseini-Hashemi

  2. Center of Excellence in Railway Transportation, Iran University of Science and Technology, 16846-13114, Narmak, Tehran, Iran

    Shahrokh Hosseini-Hashemi

Authors
  1. Mahmood Fakher
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shahin Behdad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shahrokh Hosseini-Hashemi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mahmood Fakher.

Appendix

Appendix

1.1 Shape functions of element-1

$$ \begin{aligned} N_{1}^{1} & = \frac{{\left( {l_{e} - x} \right)^{4} \left( {l_{e}^{3} + 4l_{e}^{2} x + 10l_{e} x^{2} + 20x^{3} } \right)}}{{l_{e}^{7} }},\,N_{2}^{1} = \frac{{x\left( { - x + l_{e} } \right)^{4} \left( {10x^{2} + 4xl_{e} + l_{e}^{2} } \right)}}{{l_{e}^{6} }} \\ N_{3}^{1} & = \frac{{x^{2} \left( { - x + l_{e} } \right)^{4} \left( {xl_{e} + 3k\left( {4x + l_{e} } \right)} \right)}}{{6kl_{e}^{5} }},N_{4}^{1} = \frac{{x^{4} \left( { - 20x^{3} + 70x^{2} l_{e} - 84xl_{e}^{2} + 35l_{e}^{3} } \right)}}{{l_{e}^{7} }} \\ N_{5}^{1} & = \frac{{x^{4} \left( {10x^{3} - 34x^{2} l_{e} + 39xl_{e}^{2} - 15l_{e}^{3} } \right)}}{{l_{e}^{6} }},N_{6}^{1} = \frac{{x^{4} \left( { - x + l_{e} } \right)^{2} \left( { - 4x + 5l_{e} } \right)}}{{2l_{e}^{5} }} \\ N_{7}^{1} & = - \frac{{x^{4} \left( { - x + l_{e} } \right)^{3} }}{{6l_{e}^{4} }} \\ \end{aligned} $$

1.2 Shape functions of element-2

$$ \begin{aligned} N_{1}^{2} & = \frac{{\left( { - x + l_{e} } \right)^{4} \left( {20x^{3} + 10x^{2} l_{e} + 4xl_{e}^{2} + l_{e}^{3} } \right)}}{{l_{e}^{7} }},\,N_{2}^{2} = \frac{{x\left( { - x + l_{e} } \right)^{4} \left( {10x^{2} + 4xl_{e} + l_{e}^{2} } \right)}}{{l_{e}^{6} }} \\ N_{3}^{2} & = \frac{{x^{2} \left( { - x + l} \right)_{e}^{4} \left( {4x + l_{e} } \right)}}{{2l_{e}^{5} }},N_{4}^{2} = \frac{{x^{3} \left( { - x + l_{e} } \right)^{4} }}{{6l_{e}^{4} }} \\ N_{5}^{2} & = \frac{{x^{4} \left( { - 20x^{3} + 70x^{2} l_{e} - 84xl_{e}^{2} + 35l_{e}^{3} } \right)}}{{l_{e}^{7} }},N_{6}^{2} = \frac{{x^{4} \left( {10x^{3} - 34x^{2} l_{e} + 39xl_{e}^{2} - 15l_{e}^{3} } \right)}}{{l_{e}^{6} }} \\ N_{7}^{2} & = \frac{{x^{4} \left( { - x + l_{e} } \right)^{2} \left( {l_{e} \left( { - x + l_{e} } \right) + 3k\left( { - 4x + 5l_{e} } \right)} \right)}}{{6kl_{e}^{5} }} \\ \end{aligned} $$

1.3 Shape functions of element-3

$$ \begin{aligned} N_{1}^{3} & = \frac{{\left( { - x + l_{e} } \right)^{4} \left( {20x^{3} + 10x^{2} l_{e} + 4xl_{e}^{2} + l_{e}^{3} } \right)}}{{l_{e}^{7} }},\,N_{2}^{3} = \frac{{x\left( { - x + l_{e} } \right)^{4} \left( {10x^{2} + 4xl_{e} + l_{e}^{2} } \right)}}{{l_{e}^{6} }} \\ N_{3}^{3} & = \frac{{x^{2} \left( { - x + l_{e} } \right)^{4} \left( {4x + l_{e} } \right)}}{{2l_{e}^{5} }},N_{4}^{3} = \frac{{x^{3} \left( { - x + l_{e} } \right)^{4} }}{{6l_{e}^{4} }} \\ N_{5}^{3} & = \frac{{x^{4} \left( { - 20x^{3} + 70x^{2} l_{e} - 84xl_{e}^{2} + 35l_{e}^{3} } \right)}}{{l_{e}^{7} }},N_{6}^{3} = \frac{{x^{4} \left( {10x^{3} - 34x^{2} l_{e} + 39xl_{e}^{2} - 15l_{e}^{3} } \right)}}{{l_{e}^{6} }} \\ N_{7}^{3} & = \frac{{x^{4} \left( { - x + l_{e} } \right)^{2} \left( { - 4x + 5l_{e} } \right)}}{{2l_{e}^{5} }},\,N_{8}^{3} = - \frac{{x^{4} \left( { - x + l_{e} } \right)^{3} }}{{6l_{e}^{4} }} \\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fakher, M., Behdad, S. & Hosseini-Hashemi, S. Vibration analysis of stress-driven nonlocal integral model of viscoelastic axially FG nanobeams. Eur. Phys. J. Plus 135, 905 (2020). https://doi.org/10.1140/epjp/s13360-020-00923-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-020-00923-6

Search

Navigation