Tolerance versus synaptic noise in dense associative memories

Abstract

The retrieval capabilities of associative neural networks are known to be impaired by fast noise, which endows neuron behavior with some degree of stochasticity, and by slow noise, due to interference among stored memories; here, we allow for another source of noise, referred to as “synaptic noise,” which may stem from i. corrupted information provided during learning, ii. shortcomings occurring in the learning stage, or iii. flaws occurring in the storing stage, and which accordingly affects the couplings among neurons. Indeed, we prove that this kind of noise can also yield to a break-down of retrieval and, just like the slow noise, its effect can be softened by relying on density, namely by allowing p-body interactions among neurons.

1 Introduction

Associative memories (AM) are devices able to store and then retrieve a set of information (see, e.g., [1]). Since the 70’s, several models of AM have been introduced, among which the Hopfield neural network (HNN) probably constitutes the best known example [2, 3]. In this model, one has N units, meant as stylized (on/off) neurons, able to process information through pairwise interactions. The performance of an AM is usually measured as the ratio $\alpha$ between the largest extent of information safely retrievable and the amount of neurons employed for this task; in the HNN, this ratio is order of 1. In the last decades, many efforts have been spent trying to raise this ratio (see, e.g., [4, 5] and references therein). For instance, in the so-called dense associative memories (DAMs) neurons are embedded on hyper-graphs in such a way that they are allowed to interact in p-tuples and $\alpha \sim {\mathcal {O}}(N^{p-1})$. However, this model also requires more resources as the number of connections encoding the learned information scales as $N^{p}$ instead of $N^{2}$ as in the standard pairwise model [6, 7].

Clearly, whatever the AM model considered, limitations on $\alpha$ are intrinsic given that the amount of resources (in terms of number of neurons and number of connections) available necessarily yields to bounds in the extent of information storable. In particular, by increasing the pieces of information to be stored, the interference among them generates a so-called slow noise which requires a relatively large number of neurons or of connections to be resolved. Beyond this, one has also to face another kind of noise, which has been less investigated in the last years and which is the focus of the current work.

In fact, classical AM models assume that learning and storing stages rely on exact knowledge of information and work without flaws, whereas, in general, the information provided may be corrupted and communication among neurons can be disturbed (see, e.g., [8, 9]). We refer to the noise stemming from this kind of shortcomings as synaptic noise, and, as we will explain, we envisage different ways to model it, mimicking different physical situations (i.e., respectively, noisy patterns, noisy learning, and noisy storing). In each case, we investigate the effects of such a noise on the retrieval capabilities of the system and on the existence of bounds on the amount of noise above which the network can not work as an AM any longer. More precisely, our analysis is led on (hyper-)graphs with $p \ge 2$ and we highlight an interplay between slow noise, synaptic noise and network density: by increasing p one can exploit some of the additional resources to soften the effect of slow noise and make higher load affordable, and some to soften the effect of synaptic noise and make the system more robust. On the other hand, here, possible effects due to fast noise (also referred to as temperature) are discarded and, since it typically makes neurons more prone to failure, our results provide an upper bound for the system performance. Also, this particular setting allows addressing the problem analytically via a signal-to-noise approach [2].

In the following Sect. 2, we will frame the problem more quantitatively exploiting, as a reference model, the HNN: we will review the signal-to-noise approach and introduce the necessary definitions. Next, in Sect. 3, we will consider the p-neuron Hopfield model and we will find that i. when the information to be stored is provided with some mistakes (noisy patterns), then the machine will store the defective pieces of information and retrieving the correct ones is possible as long as mistakes are “small”; ii. when the information is provided exactly, but the learning process is imperfect (noisy learning), then retrieval is possible, but the capacity $\alpha$ turns out to be downsized; iii. when information is provided exactly and it is correctly learned, but communication among neurons during retrieval is faulty (noisy storing), then retrieval is still possible, but $\alpha$ is “moderately” reduced. These results are also successfully checked versus numerical simulations. Finally, Sect. 4 is left for our conclusive remarks. Since calculations for the p-neuron Hopfield model are pretty lengthy, they are not shown in details for arbitrary p, instead, we report explicit calculations for the case $p=4$ in Appendix.

2 Noise tolerance

In this section, we introduce the main players of our investigations taking advantage of the HNN as a reference framework.

The HNN is made of N neurons, each associated with a variable $\sigma _i \in \{-1, +1 \}$, with $i=1, \ldots , N$ representing the related status (either active or inactive), embedded in a complete graph with weighted connections. An HNN with N neurons is able to learn pieces of information which can be encoded in binary vectors of length N, also called patterns. After the learning of K such vectors $\{ \varvec{\xi }^1, \ldots , \varvec{\xi }^K \}$, with $\varvec{\xi }^{\mu } \in \{-1, +1\}^N$ for $\mu =1,\ldots ,K$, the weight for the coupling between neuron i and j is given by the so-called Hebbian rule $J^{\mathrm{Hebb}}_{ij}= \frac{1}{N} \sum _{\mu =1}^K \xi _i^{\mu } \xi _j^{\mu }$ for any $i \ne j$, while self-interactions are not allowed, i.e., $J_{ii}=0$, for any i.

In the absence of external noise and external fields, the neuronal state evolves according to the dynamic

$$\begin{aligned} \sigma _i(t+1) = \text {sign}[h_i(\varvec{\sigma }(t))], \end{aligned}$$

(1)

where

$$\begin{aligned} h_i(\varvec{\sigma }(t)) = \sum _{j=1}^N J_{ij} \sigma _j(t) \end{aligned}$$

(2)

is the internal field acting on the i-th neuron. This dynamical system corresponds to a steepest descent algorithm where

$$\begin{aligned} H(\varvec{\sigma }, \varvec{\xi }) = - \sum _{i>j}^N h_i(\varvec{\sigma }) \sigma _ i = - \frac{1}{2N} \sum _{\begin{array}{c} i,j \\ i \ne j \end{array}}^{N,N} \sum _{\mu =1}^K \xi _i^{\mu } \sigma _i \sigma _j \xi _j^{\mu } \end{aligned}$$

(3)

plays as a Lyapunov function or, in a statistical-mechanics setting, as the Hamiltonian of the model (see, e.g., [2, 3]).

The retrieval of a learned pattern $\varvec{\xi }^{\mu }$, starting from a certain input state $\varvec{\sigma }(t=0)$, is therefore assured as long as this initial state belongs to the attraction basin of $\varvec{\xi }^{\mu }$, according to the dynamic (1), in such a way that, eventually, the neuronal configuration will reach the stable state $\varvec{\sigma }= \varvec{\xi }^{\mu }$. With these premises, the signal-to-noise analysis ascertains the stability of the configuration corresponding to the arbitrary pattern $\varvec{\xi }^{\mu }$ by checking whether the inequality

$$\begin{aligned} h_i(\varvec{\xi }^{\mu }) \xi _i^{\mu } >0 \end{aligned}$$

(4)

is verified for any neuron $i=1,\ldots ,N$. Of course, this kind of analysis can be applied to an arbitrary AM model, by suitably defining the internal field in the condition (4), as $h_i$ issues from the architecture characterizing the considered model.

Before proceeding, a few remarks are in order.

The expression “signal-to-noise” refers to the fact that, as we will see, the l.h.s. in (4) can be split into a “signal” term S and a “noise” term R, the latter typically stemming from interference among patterns and growing with K. Thus, the largest amount of patterns that the system can store and retrieve corresponds to the largest value of K which still ensures $S/R \gtrsim 1$.¹ Further, since we are interested in storing the largest amount of information, rather than the largest amount of patterns, recalling the Shannon–Fano coding, the pattern entries shall be drawn according to

$$\begin{aligned} P\left( \xi _i^{\mu }\right) = \frac{1}{2}\left[ \delta \left( \xi _i^{\mu } + 1\right) + \delta \left( \xi _i^{\mu } -1\right) \right] , \end{aligned}$$

(5)

for any $i, \mu$, that is, entries are taken as i.i.d. Rademacher random variables.

Remarkably, the above-mentioned Hebbian rule accounts for an “ideal” situation, where i. the dataset $\{ \varvec{\xi }^{\mu } \}_{\mu =1,\ldots ,P}$, ii. the learning of this dataset, and iii. the related storage are devoid of any source of noise which may lead to some errors, while in general shortcomings may take place and we accordingly revise $J^{\mathrm{Hebb}}$ as explained hereafter; we stress that, in order to see how noise can effectively affect the couplings in the HNN, we will exploit a formal analogy between HNNs and restricted Boltzmann machines (RBMs) [8, 10,11,12,13,14, 23].

Fig. 1

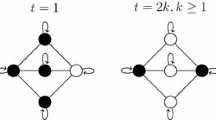
RBM corresponding to faulty patterns. The machine is built over a hidden layer made of Gaussian neurons $\{z_{\mu }\}_{\mu =1,\ldots ,K}$ and a visible layer made of binary neurons $\{ \sigma _i \}_{i=1,\ldots ,N}$; in this case, a neuron $z_{\mu }$ belonging to the hidden layer can interact with one neuron $\sigma _i$ belonging to the visible layer and the coupling is $\eta _i^{\mu } = \xi _i^{\mu } + \omega {\tilde{\xi }}_i^{\mu }$, as described by Eq. 6. Since the machine is restricted, intra-layer interactions are not allowed. In the dual associative network, the neurons interact pairwise ($p=2$) and the synaptic weight for the couple ($\sigma _i, \sigma _j$) is $J_{ij} = \sum _{\mu } ( \xi _i^{\mu } + \omega {\tilde{\xi }}_i^{\mu })( \xi _i^{\mu } + \omega {\tilde{\xi }}_i^{\mu })$, as reported also in Eq. 7. This structure can be straightforwardly generalized for $p>2$. In this figure, seeking for clarity, only a few connections are drawn for illustrative purposes

Fig. 2

RBM corresponding to shortcomings in the learning stage. The machine is built over a hidden layer made of Gaussian neurons $\{z_{\mu }\}_{\mu =1,\ldots ,K}$ and a visible layer made of binary neurons $\{ \sigma _i \}_{i=1,\ldots ,N}$; in this case, a neuron $z_{\mu }$ belonging to the hidden layer can interact simultaneously with two neurons $(\sigma _i, \sigma _j)$ belonging to the visible layer and the coupling is $\xi _i^{\mu }\xi _j^{\mu } + \omega {\tilde{\xi }}_{ij}^{\mu }$, mimicking a situation where the correct patterns are learnt, yet interaction among the two layers is disturbed. Since the machine is restricted, intra-layer interactions are not allowed. In the dual associative network, the neurons interact via 4-body interactions ($p=4$) and the synaptic weight for the 4-tuple ($\sigma _i, \sigma _j, \sigma _k, \sigma _l$) is $J_{ijkl} = \sum _{\mu } ( \xi _i^{\mu } \xi _j^{\mu } + \omega {\tilde{\xi }}_{ij}^{\mu })( \xi _k^{\mu } \xi _l^{\mu } + \omega {\tilde{\xi }}_{kl}^{\mu })$, as reported also in Eq. 18. Notice that this kind of noise is intrinsically defined only for associative networks where p is even and that when $p=2$ we recover the case depicted in Fig. 1. Also in this figure, seeking for clarity, only a few connections are drawn for illustrative purposes

Fig. 3

RBM corresponding to shortcomings in the storage case. The machine is built over a hidden layer made of Gaussian neurons $\{z_{\mu }\}_{\mu =1,\ldots ,K}$ and a visible layer made of binary neurons $\{ \sigma _i \}_{i=1,\ldots ,N}$; in this case, a neuron $z_{\mu }$ belonging to the hidden layer can interact with one neuron $\sigma _i$ belonging to the visible layer and the coupling is $\xi _i^{\mu }$, namely the patterns are correctly learnt and communications between the two layers is devoid of flaws. Since the machine is restricted, intra-layer interactions are not allowed. In the dual associative network, the neurons interact pairwise ($p=2$) and the synaptic weight for the pair ($\sigma _i, \sigma _j$) is $J_{ij} = \sum _{\mu } \xi _i^{\mu } \xi _j^{\mu } + \omega {\tilde{\xi }}_{ij}^{\mu }$, as reported also in Eq. 8. This structure can be straightforwardly generalized for $p>2$. In this figure, again, seeking for clarity, only a few connections are drawn for illustrative purposes

• (i) Noisy patterns. The first kind of noise we look at allows for corrupted patterns, referred to as $\{\varvec{\eta }^{\mu }\}_{\mu =1,\ldots ,K}$, and defined as

  $$\begin{aligned} \eta _i^{\mu }=\xi _i^{\mu }+\omega ~ {\tilde{\xi }}_i^{\mu }, \end{aligned}$$

  (6)

  where ${\tilde{\xi }}_i^{\mu }$ is a standard Gaussian random variable and $\omega$ is a real parameter that tunes the noise level. The Hebbian rule, in the case $p=2$, is therefore revised as

  $$\begin{aligned} J_{ij} = \frac{1}{N}\sum _{\mu =1}^K \eta _i^{\mu } \eta _j^{\mu }. \end{aligned}$$

  (7)

  Since this kind of noise directly affects the information we feed the machine with, we expect strong effects and, in fact, as we will show, even in a low-load regime (i.e., $K/N^{p-1} \rightarrow 0$) and for relatively small values of $\omega$, it implies the breakdown of pattern recognition capability. It is intuitive to see that this kind of noise leads to such a dramatic effect if one looks at the dual representation of the associative neural network in terms of a RBM, see Fig. 1. In fact, the coupling (7) is reminiscent of the fact that, during the learning stage, the system is fed by noisy patterns and therefore it learns patterns along with their noise. Notice that, for p-body interactions, the coupling $J_{ij}$ turns out to be a polynomial order p in $\omega$.

• (ii) Noisy learning. The second kind of noise we look at can be thought of as due to flaws during the learning stage. Still looking at the RBM representation, in this case the couplings between visible and hidden units are noisy² and, again, we quantify this noise by $\omega$ times a standard Gaussian variable, see Fig. 2. Notice that, when $p=2$ (as for the classical HNN), this kind of noise coincides with the previous one and, in general, it yields to a revision in the coupling $J^{\mathrm{Hebb}}_{ij}$ given by additional terms up to second order in $\omega$. This suggests that, in this case, effects are milder with respect to the previous one. In fact, as we will see, in a low-load regime, the degree of noise $\omega$ can grow algebraically with the system size, without breaking retrieval capabilities.

• (iii) Noisy storing. The third kind of noise we look at can be thought of as due to effective shortcomings in storage as it directly affects the coupling among neurons in the AM system as

  $$\begin{aligned} J_{ij} = \frac{1}{N}\sum _{\mu =1}^K\left( \xi _i^{\mu } \xi _j^{\mu } + \omega {\tilde{\xi }}_{ij}^{\mu }\right) , \end{aligned}$$

  (8)

  where, again, ${\tilde{\xi }}_{ij}^{\mu }$ is a standard Gaussian random variable and $\omega$ is a real parameter that tunes the noise level. In the RBM representation, this corresponds to a perfect learning, while defects emerge just in the associative network, see Fig. 3. Notice that the coupling in (8) is linear in $\omega$ and it yields to relatively weak effects. In fact, we will show that in a low-load regime, $\omega$ can grow “fast” with the system size, without breaking retrieval capabilities.

It is worth recalling that the problem of a HNN endowed with noisy couplings like in (8) has already been addressed in the past (see, e.g., [2, 15,16,17,18]). In particular, Sompolinsky [15, 16] showed that, in the high-load regime (i.e., $K \sim N$), the strength of noise affecting couplings still preserving retrieval is of order one. More precisely, denoting by $\delta _{ij}$ a centered Gaussian variable with variance $\delta ^2$ and setting $J^s_{ij} = \sum _{\mu } \xi _i^{\mu } \xi _j^{\mu }/N + \delta _{ij}/\sqrt{N}$, he found that, as $\delta$ is fine tuned, the system capacity $\alpha$ is lowered and it vanishes for $\delta \approx 0.8$. From this result, one can conclude that the HNN is relatively robust to the presence of “moderate levels” of effective synaptic noise. These findings are recovered in our investigations and suitably extended for $p>2$. Notably, this kind of noise also includes, as a special example, the diluted network, where a finite fraction of the connections are cut randomly, still retaining a giant component [2, 15, 16, 19].

Before concluding, we need a few more definitions. As aforementioned, we distinguish the tolerance with respect to interference among patterns (slow noise), which grows with K, and with respect to errors during learning or storing (synaptic noise), which grows with $\omega$. More quantitatively, we set

$$\begin{aligned} K= & {} N^a,\quad a \ge 0 \end{aligned}$$

(9)

$$\begin{aligned} \omega= & {} N^b,\quad b \ge 0, \end{aligned}$$

(10)

and we introduce

$$\begin{aligned} \alpha (b):= & {} \max _{a ~ \text {s.t.} ~ \frac{S}{R} \lesssim 1} \frac{K}{N}, \end{aligned}$$

(11)

$$\begin{aligned} \beta (a):= & {} \max _{b ~ \text {s.t.} ~ \frac{S}{R} \lesssim 1} \omega . \end{aligned}$$

(12)

Finally, the Mattis magnetization, defined as

$$\begin{aligned} m_{\mu } := \frac{1}{N} \sum _{i=1}^N \sigma _i \xi _i^{\mu }, \quad \mu =1,\ldots ,K, \end{aligned}$$

(13)

is used to assess the retrieval of the $\mu$-th pattern.

3 The p-neuron Hopfield model with synaptic noise

The p-neuron Hopfield model is described by the Hamiltonian

$$\begin{aligned} H^{(p)}(\varvec{\sigma }, \varvec{\xi })=-\frac{1}{p!N^{p-1}}\sum _{\mu =1}^K\sum _{i_1,\ldots ,i_p}\xi _{i_1}^{\mu } \cdots \xi _{i_p}^{\mu }\sigma _{i_1}\cdots \sigma _{i_p}, \end{aligned}$$

(14)

where the sum runs over all possible p-tuples and self-interactions are excluded³. This kind of model provides an example of dense AMs, which have been intensively studied in the last years (see, e.g., [7, 8, 20, 21]).

For even p, this model is thermodynamically equivalent to a RBM equipped with a hidden layer made of K Gaussian neurons $\{z_{\mu }\}_{\mu =1,\ldots ,K}$ and with a visible layer made of N binary neurons $\{ \sigma _i \}_{i=1,\ldots ,N}$, but now couplings in the RBM are $(1+p/2)$-wise and include one hidden neuron and p/2 visible neurons, say $(z_{\mu }, \sigma _{i_1}, \ldots , \sigma _{i_{p/2}})$, and the related coupling in the p-neuron Hopfield model is $\xi _{i_1}^{\mu } \cdots \xi _{i_{p/2}}^{\mu }$.

To see the equivalence between this RBM and the model described by (14), we look at the RBM partition function and we perform the Gaussian integration to marginalize over the hidden units as

$$\begin{aligned} Z_{\text {RBM}}^{(p)}(\varvec{\xi })= & {} \sum _{\varvec{\sigma }} \prod _{\mu =1}^K \int d z_{\mu } \frac{e^{- \frac{\beta z_{\mu }^2}{2}}}{\sqrt{2\pi }} e^{ \beta N^{\frac{1-p}{2}} \left( \prod _{j=1}^{p/2}\sum _{i_j} \sigma _{i_j} \xi _{i_j}^{\mu }\right) z_{\mu }} \nonumber \\= & {} \sum _{\varvec{\sigma }} \prod _{\mu =1}^K e^{\frac{\beta '}{p!} N^{1-p} \prod _{j=1}^{p} \sum _{i_j} \sigma _{i_j} \xi _{i_j}^{\mu } }, \end{aligned}$$

(15)

where the inverse temperature $\beta$ has been properly rescaled into $\beta '$.

Let us start the study of this system in the presence of slow noise only and let us check stability of the configuration $\varvec{\xi }^1$, without loss of generality. By signal to noise analysis, we write

$$\begin{aligned} h_i^{(p)}\xi _i^1=S+R^{(0)}, \end{aligned}$$

where the signal term S includes the field contribution which tends to align the network configuration with the pattern $\varvec{\xi }^1$, while the noise term $R^{(0)}$ includes the remaining contributions, which tend to destroy the correlation of the neural configuration and the first pattern; more precisely,

$$\begin{aligned} S&= \frac{1}{p!N^{p-1}} \sum _{i_2,\ldots ,i_p}^N\xi _{i}^{1}\xi _{i_2}^{1}\cdots \xi _{i_p}^{1}.\xi ^1_i \xi _{i_2}^1\cdots \xi _{i_p}^1,\\ R^{(0)}&=\frac{1}{p!N^{p-1}}\sum _{\mu =2}^K\sum _{i_2,\ldots ,i_p}^N\xi _{i}^{\mu } \xi _{i_2}^{\mu }\cdots \xi _{i_p}^{\mu }\cdot \xi ^1_i\xi _{i_2}^1\cdots \xi _{i_p}^1. \end{aligned}$$

Now, the signal term can be evaluated straightforwardly as $S\sim 1$; as for the noise term, it contains a sum of, approximately, $N^{p-1}K$ binary variables and, since pattern entries are uncorrelated, its mean value is zero and we can assess its magnitude in terms of the square root of the variance, that is, for large N and exploiting the central limit theorem,

$$\begin{aligned} R^{(0)}\sim \frac{1}{N^{p-1}}\sqrt{KN^{p-1}}=\sqrt{\frac{K}{N^{p-1}}}. \end{aligned}$$

(16)

Recalling that the condition for retrieval is $R^{(0)}\lesssim S$, the highest load corresponds to $K \sim N^{p-1}$, namely

$$\begin{aligned} \alpha ^{(p)} = N^{p-2}, \end{aligned}$$

(17)

as previously proved in [7].

This result shows that increasing the number of interacting spins allows to arbitrary increase the tolerance versus slow noise. It is then natural to question if an analogous robustness can be obtained versus synaptic noise too.

In the next subsections, we address this question for the three sources of noise outlined in Sect. 2.

3.1 Noisy patterns

When the noise affects directly patterns constituting the dataset, using Eq. (6) we can write the product between the local field and a pattern, according to Eq. 2, as

$$\begin{aligned} h_i^{(p)}\xi _i^1&=\frac{1}{p!N^{p-1}}\sum _{\mu }^K\sum _{i_2,\ldots ,i_p}^N\\&\quad \left( \xi _{i}^{\mu }+\omega {\tilde{\xi }}_{i}^{\mu }\right) \left( \xi _{i_2}^{\mu } +\omega {\tilde{\xi }}_{i_2}^{\mu }\right) \cdots \left( \xi _{i_p}^{\mu } +\omega {\tilde{\xi }}_{i}^{\mu }\right) \xi _{i}^1\xi _{i_2}^1\cdots \xi _{i_p}^1. \end{aligned}$$

Splitting the sum into a signal S and a noise R term, we obtain $h_i^{(p)}\xi _i^1=S+R$, with

$$\begin{aligned} S\sim 1, \quad R=\sum _{n=0}^pR^{(n)}. \end{aligned}$$

The quantity $R^{(0)}$ is the standard contribution due to slow noise given by Eq. (16), while ${\tilde{R}}=\sum _{n=1}^pR^{(n)}$ derives from the presence of synaptic noise. To simplify the following formulas, we rename i as $i_1$ and write this last contribution as

$$\begin{aligned} {\tilde{R}}&=\frac{1}{p!N^{p-1}}\sum _{\mu }^K\sum _{i_2,\ldots ,i_p}^N \xi _{i_1}^1\xi _{i_2}^1\cdots \xi _{i_p}^1\\&\quad \left\{ \underbrace{\omega \sum _{(i_x)}\xi _{i_1}^{\mu } \cdots {\tilde{\xi }}_{i_x}^{\mu }\cdots \xi _{i_p}^{\mu }}_{R^{(1)}}\right. \\&\quad +\underbrace{\omega ^2\sum _{(i_x, i_y)}\xi _{i_1}^{\mu } \cdots {\tilde{\xi }}_{i_x}^{\mu }\cdots {\tilde{\xi }}_{i_y}^{\mu } \cdots \xi _{i_p}^{\mu }}_{R^{(2)}}\\&\quad +\underbrace{\omega ^3\sum _{(i_x, i_y, i_z)}\xi _{i_1}^{\mu } \cdots {\tilde{\xi }}_{i_x}^{\mu }\cdots {\tilde{\xi }}_{i_y}^{\mu } \cdots {\tilde{\xi }}_{i_z}^{\mu }\cdots \xi _{i_p}^{\mu }}_{R^{(3)}}\\&\quad \vdots \\&\quad \left. +\ \underbrace{\omega ^p{\tilde{\xi }}_{i_1}^{\mu }{\tilde{\xi }}_{i_2}^{\mu } {\tilde{\xi }}_{i_3}^{\mu }\cdots {\tilde{\xi }}_{i_p}^{\mu }}_{R^{(p)}}\right\} , \end{aligned}$$

where $\sum _{(i_{a_1}\ldots i_{a_n})}$ denotes the sum over all possible permutations of n indices chosen from $i_1\ldots i_p$. Using the central limit theorem (as explained in details for $p=4$ in the Appendix A), we obtain that

$$\begin{aligned} R^{(n)}\sim \frac{\omega ^n}{N^{p-1}}\left[ N^{p-n}\left( N^{1/2}\right) ^{n-1} +N^{p-(n-1)}\left( N^{1/2}\right) ^n+\sqrt{KN^{p-1}}\right] . \end{aligned}$$

Then, at leading order, it holds

$$\begin{aligned} {\tilde{R}}\sim \frac{1}{N^{p-1}}\left[ \left( \sum _{n=1}^p\omega ^nN^{p-n} \left( N^{1/2}\right) ^{n-1}\right) +\omega ^p\sqrt{KN^{p-1}}\right] . \end{aligned}$$

Therefore, overall, the noise $R=R^{(0)}+{\tilde{R}}$ scales as

$$\begin{aligned} R\sim \left[ \sum _{n=1}^p\omega ^nN^{1-n}\left( N^{1/2}\right) ^{n-1}\right] +\omega ^p \sqrt{\frac{K}{N^{p-1}}}. \end{aligned}$$

Recalling that $S\sim 1$, we conclude that retrieval is possible provided that $\omega \sim 1$, independently of the number K of stored patterns (up to $K\sim N^{p-1}$). This implies that a diverging synaptic noise (i.e., $\omega \sim {\mathcal {O}} (N^b), b>0$) cannot be handled by the system even if the number p of spins interacting and, accordingly, the number of links, is arbitrarily increased.

This result is checked numerically as shown in Fig. 4. In particular, we notice that, as long as $\omega$ remains finite (or vanishing) while the size N is increased, i.e., as long as $b \le 0$, the Mattis magnetization corresponding to the input pattern is non-null and the system can retrieve. The transition between a retrieval and a non-retrieval regime is sharper when the network size is larger. In Fig. 5, we focus on $p=2$ and we set the ratio $K/N < \alpha (b=0) \approx 0.14$, while we perform a fine tuning by varying $\omega \in [0,3]$. As expected, even small values of $\omega$ are sufficient to break down retrieval capabilities.

Fig. 4

Numerical simulations for the p-neuron Hopfield model endowed with noisy patterns ($p>2$). We simulated the evolution of a p-neuron Hopfield model, with $p=3$ ($\triangle$), $p=4$ ($\square$), and $p=5$ ($\star$), under the dynamics (1) and using as starting state $\varvec{\sigma }= \varvec{\xi ^{\mu }}$, finally collecting the Mattis magnetization $m_{\mu }^{(\mu )}$ (where the superscript highlights the initial state; we also check that $m_{\nu }^{(\mu )} \approx 0$ for $\nu \ne \mu$). Here, we set $K=N$ and $\omega =N^b$, where b is varied in $[-0.5, 0.5]$, and we plot the mean magnetization $\langle m \rangle$ versus b; the mean magnetization $\langle m \rangle$ is obtained by averaging $m_{\mu }^{(\mu )}$ with respect to $\mu$ and over $M=10$ realizations of the patterns $\varvec{\eta }$, as defined in (6), the standard deviation is represented by the errorbar. Three different sizes are considered $N=20$, $N=40$, $N=80$, as explained by the legend. The vertical dashed line is set at $b=0$ and highlights the threshold for retrieval, as stated in the main text

Fig. 5

Numerical simulations for the Hopfield model with pairwise couplings ($p=2$) endowed with noisy patterns. We run numerical simulation as explained in the caption of Fig. 4 but setting $p=2$ and varying $\omega$ linearly in [0, 3]. We compare two loads: $K/N = 0.125$ ($\times$) and $K/N=0.04$ ($+$). Notice that, in both cases, even small values of $\omega$ yield to a breakdown of retrieval

3.2 Noisy learning

Let us now consider the AM corresponding to imperfect learning as depicted in Fig. 2. This equals to say that the noise affects the $(p/2+1)$-component tensor

$$\begin{aligned} \eta _{i_1\ldots i_{p/2}}^{\mu }=\xi _{i_1}^{\mu }\cdots \xi _{i_{p/2}}^{\mu } +\omega {\tilde{\xi }}^{\mu }_{i_1\ldots i_{p/2}}, \end{aligned}$$

in such a way that the coupling between neurons is

$$\begin{aligned} J_{i_1, \ldots , i_p} = \sum _{\mu } \left( \xi _{i_1}^{\mu }\cdots \xi _{i_{p/2}}^{\mu } +\omega {\tilde{\xi }}^{\mu }_{i_1\ldots i_{p/2}}\right) \times \left( \xi _{i_{1+p/2}}^{\mu }\cdots \xi _{i_{p}}^{\mu } +\omega {\tilde{\xi }}^{\mu }_{i_{1+p/2}\ldots i_{p}}\right) \end{aligned}$$

(18)

Notice that this picture is possible only for even p and constitutes a generalization of the system studied in [22]. The product between the local field and the pattern $\varvec{\xi ^1}$ candidate for retrieval reads

$$\begin{aligned} \xi _i^1h_i&=\frac{1}{p!N^{p-1}}\sum _{\mu }^K\sum _{i_2,\ldots ,i_p}^N \left( \xi _{i_1}^{\mu }\cdots \xi _{i_{p/2}}^{\mu } +\omega {\tilde{\xi }}^{\mu }_{i_1\ldots i_{p/2}}\right) \\&\quad \left( \xi _{i_{p/2+1}}^{\mu }\cdots \xi _{i_{p}}^{\mu } +\omega {\tilde{\xi }}^{\mu }_{i_{p/2+1}\ldots i_{p}}\right) \xi _{i}^1\xi _{i_2}^1\cdots \xi _{i_p}^1. \end{aligned}$$

Again, we can split this quantity into a signal S and a noise $R=\sum _{n=0}^2R^{(n)}$ term, the signal and the zeroth order of noise are, as already shown,

$$\begin{aligned} S\sim 1, \quad R^{(0)}\sim \sqrt{\frac{K}{N^{p-1}}}. \end{aligned}$$

The first-order contribution is

$$\begin{aligned} R^{(1)}=\frac{\omega }{p!N^{p-1}}\sum _{\mu =1}^K\sum _{i_2,\ldots ,i_p}^N \left( \xi _{i_1}^{\mu }\cdots \xi _{i_{p/2}}^{\mu }{\tilde{\xi }}^{\mu }_{i_{p/2+1} \ldots i_{p}}+\xi _{i_{p/2+1}}^{\mu }\cdots \xi _{i_{p}}^{\mu }{\tilde{\xi }}^{\mu }_{i_1\ldots i_{p/2}}\right) \xi _{i}^1\xi _{i_2}^1\cdots \xi _{i_p}^1, \end{aligned}$$

and, in the limit of large network size (for more details, we refer to Appendix A where calculations for $p=4$ are reported),

$$\begin{aligned} R^{(1)}\sim \frac{\omega }{N^{p-1}}\left[ N^{p/2}\left( N^{1/2}\right) ^{p/2-1}+N^{p/2-1} \left( N^{1/2}\right) ^{p/2}+\sqrt{KN^{p-1}}\right] . \end{aligned}$$

Similarly, the second-order contribution is of the form

$$\begin{aligned} R^{(2)}&=\frac{\omega ^2}{p!N^{p-1}}\sum _{\mu =1}^K \sum _{i_2,\ldots ,i_p}^N{\tilde{\xi }}^{\mu }_{i_1\ldots i_{p/2}} {\tilde{\xi }}^{\mu }_{i_{p/2+1}\ldots i_p}\xi _{i}^1\xi _{i_2}^1\cdots \xi _{i_p}^1\\&\sim \frac{\omega ^2}{N^{p-1}}\sqrt{KN^{p-1}}. \end{aligned}$$

We then deduce that the noise R scales as

$$\begin{aligned} R&\sim \frac{1}{N^{p-1}}\left\{ \omega \left[ N^{p/2}\left( N^{1/2}\right) ^{p/2-1} +N^{p/2-1}\left( N^{1/2}\right) ^{p/2}\right] \right. \\&\quad \left. +\sqrt{KN^{p-1}}\left( 1+\omega +\omega ^2\right) \right\} , \end{aligned}$$

and therefore, neglecting subleading contributions, we can write

$$\begin{aligned} R\sim \omega N^{1/2-p/4}+\omega ^2\sqrt{K}N^{1/2-p/2}. \end{aligned}$$

Setting $K\sim N^a$ and $\omega \sim N^b$, the condition for retrieval reads

$$\begin{aligned} N^{1/2-p/4+b}+N^{(1-p+a)/2+2b}\lesssim 1. \end{aligned}$$

By comparing the scaling of the two terms in the r.h.s. of the previous equation, we see that the former diverges with N if $b>p/4-1/2$, while the latter diverges if $b>p/4-(1+a)/4$. This implies that when $a\le 1$ the first term dominates the signal-to-noise analysis and the extremal condition for retrieval reads $b=(p-2)/4$. Therefore, the tolerance versus synaptic noise is

$$\begin{aligned} \beta _p(a)\sim N^{p/4-1/2}\quad \text {for}\quad a\le 1. \end{aligned}$$

Conversely, if $a>1$, the second term prevails and consequently the extremal condition for retrieval becomes $b=(p-1-a)/4$, and the tolerance is

$$\begin{aligned} \beta _p(a)\sim N^{p/4-(1+a)/4} \quad \text {for}\quad 1<a<p-1. \end{aligned}$$

Note that in this case the tolerance depends on a, that is, on the network load. This shows that storing and tolerance are intimately tangled: the larger the load and the smaller the synaptic noise that can be handled. In particular, at low load, so for $a=1$, the tolerance reads

$$\begin{aligned} \beta _p(1)\sim N^{p/4-1/2}, \end{aligned}$$

(19)

as corroborated numerically in Fig. 6.

For $p=2$, this kind of noise reduces to the case discussed in Sect. 3.1 and consistently we get $\beta _2(1)\sim 1$.

Fig. 6

Numerical simulations for the p-neuron Hopfield affected by noisy learning ($p>2$). We simulated the evolution of a p-neuron Hopfield model, with $p=4$ ($\square$) and $p=6$ ($*$), under the dynamics (1) and using as starting state $\varvec{\sigma }= \varvec{\xi ^{\mu }}$, finally collecting the Mattis magnetizations $m_{\mu }^{(\mu )}$ (where the superscript highlights the initial state; we also check that $m_{\nu }^{(\mu )}$ for $\nu \ne \mu$). Here, we set $K=N$ and $\omega =N^b$, where b is varied in, respectively, [0, 1] and in [0, 2], and we plot the mean magnetization $\langle m \rangle$ versus b; the mean magnetization $\langle m \rangle$ is obtained by averaging $m_{\mu }^{(\mu )}$ with respect to $\mu$ and over $M=10$ realizations of the patterns $\varvec{\eta }$, as defined in (6), the standard deviation is represented by the errorbar. Three different sizes are considered $N=20$, $N=40$, $N=80$, as explained by the legend. The dashed and dotted vertical lines are set at $b=0.5$ and $b=1.0$, which represent the thresholds for retrieival for, respectively, $p=4$ and $p=6$, according to (19)

3.3 Noisy storing

Finally, we consider noise acting directly on couplings,

$$\begin{aligned} J_{i_1\ldots i_p}^{\mu } = \sum _{\mu } \eta _{i_1\ldots i_p}^{\mu }, \end{aligned}$$

(20)

where $\eta _{i_1\ldots i_p}^{\mu }$ is the $(p+1)$-component tensor

$$\begin{aligned} \eta _{i_1\ldots i_p}^{\mu }=\xi _{i_1}^{\mu }\cdots \xi _{i_p}^{\mu }+\omega {\tilde{\xi }}_{i_1\ldots i_p}^{\mu }. \end{aligned}$$

Still following the prescription coded by Eq. 2, the product between the local field $h_i$ and $\xi _i^1$ is

$$\begin{aligned} h_i\xi _i^1=\frac{1}{p!N^{p-1}}\sum _{\mu =1}^K\sum _{i_2\ldots i_p}^N\left( \xi _{i_1}^{\mu }\cdots \xi _{i_p}^{\mu }+\omega {\tilde{\xi }}_{i_1\ldots i_p}^{\mu }\right) \xi _{i_1}^1\cdots \xi _{i_p}^1 \end{aligned}$$

The signal scales as $S\sim 1$, while the noise is composed on solely two contributions: zeroth and first order. We have already computed the former

$$\begin{aligned} R^{(0)}\sim \sqrt{\frac{K}{N^{p-1}}}, \end{aligned}$$

and, as for the latter, it holds

$$\begin{aligned} R^{(1)}=\frac{\omega }{p!N^{p-1}}\sum _{\mu =1}^K\sum _{i_2\ldots i_p}^N{\tilde{\xi }}_{i_1\ldots i_p}^{\mu }\xi _{i_1}^1\cdots \xi _{i_p}^1\sim \omega \sqrt{\frac{K}{N^{p-1}}}. \end{aligned}$$

Therefore,

$$\begin{aligned} R=R^{(0)}+R^{(1)}\sim \sqrt{\frac{K}{N^{p-1}}}\left( 1+\omega \right) \sim \omega \sqrt{\frac{K}{N^{p-1}}}. \end{aligned}$$

Setting, as before, $K\sim N^a$ and $\omega \sim N^b$ the condition for retrieval becomes

$$\begin{aligned} N^{(a-p+1)/2+b}\sim 1\rightarrow b=\frac{p-1-a}{2}. \end{aligned}$$

This implies that the tolerance versus synaptic noise is

$$\begin{aligned} \beta _p(a)\sim N^{(p-1-a)/2}\quad \text {for}\quad a\le p-1. \end{aligned}$$

(21)

This is successfully checked numerically in Fig. 7. The particular case $p=2$ is considered in Fig. 8. Again, as pointed out in the previous section, tolerance versus synaptic noise and load are intrinsically related and, for a given amount of resources, cannot be simultaneously enhanced: an increase in the latter results in a decrease in the former.

A similar problem, for the $p=2$ Hopfield model, has been studied by Sompolinsky [15, 16]. In particular, the following couplings have been considered

$$\begin{aligned} J^s_{ij}=\left( \frac{1}{N}\sum _{\mu =1}^K\xi _i^{\mu }\xi _j^{\mu }\right) +\underbrace{\frac{\delta _{ij}}{\sqrt{N}}}_{{\tilde{J}}_{ij}^s}. \end{aligned}$$

Here, $\delta _{ij}$ are Gaussian variables with null mean and variance $\delta ^2$, while ${\tilde{J}}_{ij}^s$ represents the correction to Hebbian couplings due to noise. Focusing on the high load regime, that is $K\sim N$, retrieval was found to be possible provided that $\delta \lesssim 0.8$. We can easily map noise defined by Eq. (8) into this notation, indeed

$$\begin{aligned} J_{ij} = \frac{1}{N}\sum _{\mu =1}^K\left( \xi _i^{\mu } \xi _j^{\mu } + \omega {\tilde{\xi }}_{ij}^{\mu }\right) =\frac{1}{N}\sum _{\mu =1}^K\xi _i^{\mu } \xi _j^{\mu }+\underbrace{\frac{\omega }{N} \sum \nolimits _{\mu =1}^K{\tilde{\xi }}_{ij}^{\mu }}_{{\tilde{J}}_{ij}}. \end{aligned}$$

As a consequence, in our framework the noisy contribution to couplings reads

$$\begin{aligned} {\tilde{J}}_{ij}=\frac{\omega }{N}\sum _{\mu =1}^K{\tilde{\xi }}_{ij}^{\mu } =\frac{\omega _{ij}\sqrt{K}}{N}, \end{aligned}$$

where $\omega _{ij}$ are Gaussian variables with null mean and variance $\omega ^2$. Considering the high load regime, we then obtain

$$\begin{aligned} {\tilde{J}}_{ij}\sim \frac{\omega _{ij}\sqrt{N}}{N}=\frac{\omega _{ij}}{\sqrt{N}}. \end{aligned}$$

This shows that $\omega _{ij}$ is the counterpart of $\delta _{ij}$ and, therefore, that $\omega$ plays the same role of $\delta$. Recalling Eq. (21) and setting $p=2$ and $a=1$, we conclude that retrieval is possible provided that $\omega \lesssim 1$. This result is in perfect agreement with Sompolinsky’s bound $\delta \lesssim 0.8$ and also with the simulations we run.

Fig. 7

Numerical simulations for the p-neuron Hopfield affected by noisy storing ($p>2$). We simulated the evolution of a p-neuron Hopfield model, with $p=3$ ($\triangle$), $p=4$ ($\square$), and $p=5$ ($\star$), under the dynamics (1) and using as starting state $\varvec{\sigma }= \varvec{\xi ^{\mu }}$, finally collecting the Mattis magnetizations $m_{\mu }^{(\mu )}$ (where the subscript highlights the initial state; we also check that $m_{\nu }^{(\mu )}=0$ for $\nu \ne \mu$). Here, we set $K=N$ and $\omega =N^b$, where b is varied in [0, 2], and we plot the mean magnetization $\langle m \rangle$ versus b; the mean magnetization $\langle m \rangle$ is obtained by averaging $m_{\mu }^{(\mu )}$ with respect to $\mu$ and over $M=10$ realizations of the couplings ${\varvec{J}}$, as defined in (8), the standard deviation is represented by the errorbar. Three different sizes are considered $N=20$, $N=40$, $N=80$, as explained by the legend

Fig. 8

Numerical simulations for the Hopfield model with pairwise couplings ($p=2$) endowed with noisy couplings. We run numerical simulation as explained in the caption of Fig. 7 but setting $p=2$ and varying $\omega$ linearly in [0, 5]. We compare two loads: $K/N = 0.125$ ($\times$) and $K/N=0.04$ ($+$). Notice that, in both case, as $\omega$ is relatively large the retrieval is lost

4 Conclusions

In this work, we considered dense AMs and we investigated the role of density in preventing retrieval break-down due to noise. In particular, we allow for noise stemming from pattern interference (i.e., slow noise) and for noise stemming from uncertainties during learning or storing (i.e., synaptic noise), while fast noise is neglected. Synaptic noise ultimately affects the synaptic couplings among neurons making up the network and we envisage different ways to model it, mimicking different physical situations. In fact, since couplings encode for the pieces of information previously learned, we can account for the following scenarios: i. information during learning is provided corrupted, ii. information is supplied correctly, but is imperfectly learned, iii. information is well supplied and learned but storing is not accurate. These cases are discussed leveraging on the duality between AM and RBMs [8, 10,11,12,13,14].

Investigations were led analytically (via signal-to-noise approach) and numerically (via Monte Carlo simulations) finding that, according to the way synaptic noise is implemented, effects on retrieval can vary qualitatively. As long as the dataset is provided correctly during learning, synaptic noise can be annihilated by increasing redundancy (i.e., by letting neurons interact in relatively large cliques or work in a low-load regime); this would “protect” information content of the patterns much as like done in the error-correcting codes. On the other hand, if, during learning, the machine was presented to corrupted pieces of information, it will learn noise as well and the correct information can be retrieved only if the original corruption is non-diverging, no matter how redundant the network is.

The 4-neuron Hopfield model

In this appendix, we set $p=4$ and we go through signal-to-noise calculations in detail.

The 4-neuron Hopfield model is described by the Hamiltonian

$$\begin{aligned} H^{(4)}(\varvec{\sigma })=-\frac{1}{4!N^{3}}\sum _{\mu =1}^K\sum _{i,j,k,l}^{N}\xi _{i}^{\mu } \xi _{j}^{\mu }\xi _{k}^{\mu }\xi _{l}^{\mu }\sigma _{i}\sigma _{j}\sigma _{k}\sigma _{l}. \end{aligned}$$

(22)

where the sum is meant without self-interaction. Let us start the study of this system in the presence of slow noise only and let us check stability of the configuration $\varvec{\xi }^1$, without loss of generality. By signal to noise analysis, we write

$$\begin{aligned} h_i\xi _i^1=S+R^{(0)}, \end{aligned}$$

with

$$\begin{aligned} S&=\frac{1}{N^{3}}\sum _{j,k,l}\xi _{i}^{1}\xi _{j}^{1}\xi _{k}^{1}\xi _{l}^{1} \xi _{i}^{1}\xi _{j}^{1}\xi _{k}^{1}\xi _{l}^{1}\sim 1,\\ R^{(0)}&=\frac{1}{N^{3}}\sum _{\mu =2}^K\sum _{jkl}^N\xi _{i}^{\mu }\xi _{j}^{\mu } \xi _{k}^{\mu }\xi _{l}^{\mu }\xi ^1_i\xi _k^1\xi ^1_l \sim \frac{\sqrt{KN^3}}{N^3}=\sqrt{\frac{K}{N^3}}, \end{aligned}$$

where asymptotic expressions are obtained exploiting the central limit theorem. Recalling that the condition for retrieval is $R^{(0)}\lesssim S$, the highest load corresponds to $K \sim N^3$, namely

$$\begin{aligned} \alpha ^{(4)} = N^{2}. \end{aligned}$$

(23)

1.1 Noisy patterns

We now turn to the case in which the network is affected by pattern noise. We begin considering a situation in which the noise arises directly from patterns, in particular we suppose that the network stores the following vectors

$$\begin{aligned} \eta _i^{\mu }=\xi _i^{\mu }+\omega {\tilde{\xi }}_i^{\mu }, \end{aligned}$$

(24)

where $\xi _i^{\mu }$ are the patterns we would like to memorize, while ${\tilde{\xi }}_i^{\mu }$ are i.i.d. Gaussian variables with null mean and unitary variance. In order to study the stability of $\xi _i^1$, we consider the local field acting on it

$$\begin{aligned} h_i\xi _i^1&=\frac{1}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\left( \xi _i^{\mu } +\omega {\tilde{\xi }}_{i}^{\mu }\right) \left( \xi _j^{\mu }+\omega {\tilde{\xi }}_{j}^{\mu }\right) \\&\quad \left( \xi _k^{\mu }+\omega {\tilde{\xi }}_{k}^{\mu }\right) \left( \xi _l^{\mu } +\omega {\tilde{\xi }}_{l}^{\mu }\right) \xi _i^1\xi _j^1\xi _k^1\xi _l^1. \end{aligned}$$

We split this sum in signal S ad noise $R=\sum _{i=0}^4R^{(i)}$. The signal and the zeroth order of noise are straightforward

$$\begin{aligned} S\sim & {} 1,\\ R^{(0)}\sim & {} \sqrt{\frac{K}{N^3}}. \end{aligned}$$

The first order is

$$\begin{aligned} R^{(1)}=\frac{\omega }{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1\left( {\tilde{\xi }}_i^{\mu }\xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu } +\xi _i^{\mu }{\tilde{\xi }}_j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\xi _i^{\mu }\xi _j^{\mu }{\tilde{\xi }}_k^{\mu }\xi _l^{\mu } +{\tilde{\xi }}_i^{\mu }\xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\right) . \end{aligned}$$

That is

$$\begin{aligned} R^{(1)}=\frac{\omega }{2N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1\left( \underbrace{{\tilde{\xi }}_i^{\mu }\xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu }}_{(a)} +3\underbrace{\xi _i^{\mu }{\tilde{\xi }}_j^{\mu }\xi _k^{\mu }\xi _l^{\mu }}_{(b)}\right) . \end{aligned}$$

Let us study the two terms separately

$$\begin{aligned} (a)&=\frac{\omega }{N^3}\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1{\tilde{\xi }}_i^{1} \xi _j^{1}\xi _k^{1}\xi _l^{1}\\&\quad +\frac{\omega }{N^3}\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1{\tilde{\xi }}_i^{\mu }\xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\\&=\frac{\omega }{N^3}\left( \sum _{j,k,l}^N\xi _i^1{\tilde{\xi }}_i^{1} +\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1 {\tilde{\xi }}_i^{\mu }\xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\right) , \end{aligned}$$

it then follows

$$\begin{aligned} (a)\sim \omega \left( 1+\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

For what concerns the other term

$$\begin{aligned} (b)&=\frac{\omega }{N^3}\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1\xi _i^{1} {\tilde{\xi }}_j^{1}\xi _k^{1}\xi _l^{1}\\&\quad +\frac{\omega }{N^3}\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1 \xi _i^{\mu }{\tilde{\xi }}_j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\\&=\frac{\omega }{N^3}\left( \sum _{j,k,l}^N\xi _j^1{\tilde{\xi }}_j^{1} +\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1\xi _i^{\mu } {\tilde{\xi }}_j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\right) , \end{aligned}$$

therefore

$$\begin{aligned} (b)\sim \omega \left( \frac{1}{\sqrt{N}}+\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

Combining the two terms, we get

$$\begin{aligned} R^{(1)}=(a)+3(b)\sim \omega \left( 1+\frac{1}{\sqrt{N}}+\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

We can now turn to the second order of pattern noise, proceeding as before it is easy to show that

$$\begin{aligned} R^{(2)}=\frac{\omega ^2}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1\left( 3\underbrace{{\tilde{\xi }}_i^{\mu }{\tilde{\xi }}_j^{\mu }\xi _k^{\mu } \xi _l^{\mu }}_{(a)}+3\underbrace{\xi _i^{\mu }{\tilde{\xi }}_j^{\mu } {\tilde{\xi }}_k^{\mu }\xi _l^{\mu }}_{(b)}\right) . \end{aligned}$$

The first term is

$$\begin{aligned} (a)&=\frac{\omega ^2}{N^3}\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1 {\tilde{\xi }}_i^{1}{\tilde{\xi }}_j^{1}\xi _k^{1}\xi _l^{1}\\&\quad +\frac{\omega ^2}{N^3}\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1{\tilde{\xi }}_i^{\mu }{\tilde{\xi }}_j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\\&=\frac{\omega ^2}{N^3}\left( \sum _{j,k,l}^N\xi _i^1{\tilde{\xi }}_i^{1} \xi _j^1{\tilde{\xi }}_j^{1}+\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1{\tilde{\xi }}_i^{\mu }{\tilde{\xi }}_j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\right) . \end{aligned}$$

Consequently

$$\begin{aligned} (a)\sim \omega ^2\left( \frac{1}{\sqrt{N}}+\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

Analogously

$$\begin{aligned} (b)&=\frac{\omega ^2}{N^3}\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1\xi _i^{1} {\tilde{\xi }}_j^{1}{\tilde{\xi }}_k^{1}\xi _l^{1}\\&\quad +\frac{\omega ^2}{N^3}\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1\xi _i^{\mu }{\tilde{\xi }}_j^{\mu }{\tilde{\xi }}_k^{\mu }\xi _l^{\mu }\\&=\frac{\omega ^2}{N^3}\left( \sum _{j,k,l}^N\xi _k^1{\tilde{\xi }}_k^{1} \xi _j^1{\tilde{\xi }}_j^{1}+\sum _{\mu =2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1 \xi _k^1\xi _l^1\xi _i^{\mu }{\tilde{\xi }}_j^{\mu }{\tilde{\xi }}_k^{\mu }\xi _l^{\mu }\right) . \end{aligned}$$

That is

$$\begin{aligned} (b)\sim \omega ^2\left( \frac{1}{N}+\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

We then obtain

$$\begin{aligned} R^{(2)}=3(a)+3(b)\sim \omega ^2\left( \frac{1}{\sqrt{N}}+\frac{1}{N} +\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

The third order of noise is of the form

$$\begin{aligned} R^{(3)}=\frac{\omega ^3}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1 \xi _k^1\xi _l^1\left( 3\underbrace{{\tilde{\xi }}_i^{\mu } {\tilde{\xi }}_j^{\mu }{\tilde{\xi }}_k^{\mu }\xi _l^{\mu }}_{(a)} +\underbrace{\xi _i^{\mu }{\tilde{\xi }}_j^{\mu }{\tilde{\xi }}_k^{\mu } {\tilde{\xi }}_l^{\mu }}_{(b)}\right) , \end{aligned}$$

where the two terms scale as

$$\begin{aligned}&(a)\sim \omega ^3\left( \frac{1}{N}+\sqrt{\frac{K}{N^3}}\right) ,\\&(b)\sim \omega ^3\left( \sqrt{\frac{1}{N^3}}+\sqrt{\frac{K}{N^3}}\right) \sim \sqrt{\frac{K}{N^3}}. \end{aligned}$$

Therefore,

$$\begin{aligned} R^{(3)}=3(a)+(b)\sim \omega ^3\left( \frac{1}{N}+\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

Finally, the fourth order is

$$\begin{aligned} R^{(4)}=\frac{\omega ^4}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1 \xi _k^1\xi _l^1{\tilde{\xi }}_i^{\mu }{\tilde{\xi }}_j^{\mu }{\tilde{\xi }}_k^{\mu } {\tilde{\xi }}_l^{\mu }, \end{aligned}$$

whose scaling is simply

$$\begin{aligned} R^{(4)}\sim \omega ^4\sqrt{\frac{K}{N^3}}. \end{aligned}$$

Combining the four contribution, we obtain the following scaling for the noise

$$\begin{aligned} R&=\sum _{i=0}^4R^{(i)}\sim \omega \left( 1+\frac{1}{\sqrt{N}}\right) +\omega ^2 \left( \frac{1}{\sqrt{N}}+\frac{1}{N}\right) \\&\quad +\omega ^3\frac{1}{N}+\sqrt{\frac{K}{N^3}}\left( 1+\omega +\omega ^2 +\omega ^3+\omega ^4\right) . \end{aligned}$$

Recalling that $S\sim 1$, we deduce that the network can tolerate, at most, $\omega \sim 1$. In other words, the tolerance versus pattern noise satisfies

$$\begin{aligned} \beta (a)\sim 1\quad \text {for}\quad a\le 3. \end{aligned}$$

1.2 Noisy learning

At second level, we can consider the following form of synaptic noise

$$\begin{aligned} \eta _{ij}^{\mu }=\xi _i^{\mu }\xi _j^{\mu }+\omega {\tilde{\xi }}_{ij}^{\mu }. \end{aligned}$$

(25)

The local field is defined as

$$\begin{aligned} h_i=\frac{1}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\eta _{ij}^{\mu }\eta _{kl}^{\mu } \sigma _j\sigma _k\sigma _l, \end{aligned}$$

where, even if not specified, the sum does not contain self-interaction among spins. In these terms, the Hamiltonian is

$$\begin{aligned} H=-\sum _i^Nh_i\sigma _i. \end{aligned}$$

We want to study the stability of pattern $\xi _i^1$. Recalling that $\eta _{ij}^{\mu }=\xi _i^{\mu }\xi _j^{\mu }+\omega {\tilde{\xi }}_{ij}^{\mu }$, we get

$$\begin{aligned} h_i\xi _i^1&=\frac{1}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\eta _{ij}^{\mu }\eta _{kl}^{\mu } \xi _i^1\xi _j^1\xi _k^1\xi _l^1\\&=\frac{1}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\left( \xi _i^{\mu }\xi _j^{\mu } +\omega {\tilde{\xi }}_{ij}^{\mu }\right) \left( \xi _k^{\mu }\xi _l^{\mu } +\omega {\tilde{\xi }}_{kl}^{\mu }\right) \xi _i^1\xi _j^1\xi _k^1\xi _l^1, \end{aligned}$$

that is

$$\begin{aligned} h_i\xi _i^1=\frac{1}{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1\left( \xi _i^{\mu }\xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu } +\omega \xi _i^{\mu }\xi _j^{\mu }{\tilde{\xi }}_{kl}^{\mu }+\omega \xi _k^{\mu }\xi _l^{\mu }{\tilde{\xi }}_{ij}^{\mu } +\omega ^2{\tilde{\xi }}_{ij}^{\mu }{\tilde{\xi }}_{kl}^{\mu }\right) . \end{aligned}$$

We can split this sum into a signal S and a noise $R=R^{(0)}+R^{(1)}+R^{(2)}$. The signal is

$$\begin{aligned} S=\frac{1}{2N^3}\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1\xi _i^{1} \xi _j^{1}\xi _k^{1}\xi _l^{1}\sim 1. \end{aligned}$$

The contribution to noise due to interference among patterns $R^{(0)}$ is

$$\begin{aligned} R^{(0)}=\frac{1}{N^3}\sum _{\mu =2}^k\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1\xi _i^{\mu }\xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu }\sim \frac{\sqrt{N^3K}}{N^3}\sim \sqrt{\frac{K}{N^3}}. \end{aligned}$$

As expected, in the absence of pattern noise, the network can store up to $N^3$ vector patterns. At first-order synaptic noise contributes with $R^{(1)}$, whose expression is

$$\begin{aligned} R^{(1)}=\frac{\omega }{N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1 \xi _l^1\left( \xi _i^{\mu }\xi _j^{\mu }{\tilde{\xi }}_{kl}^{\mu }+\xi _k^{\mu } \xi _l^{\mu }{\tilde{\xi }}_{ij}^{\mu }\right) . \end{aligned}$$

Distinguishing between $\mu =1$ and $\mu >2$, we get

$$\begin{aligned} R^{(1)}&=\frac{\omega }{N^3}\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1 \left( \xi _i^{1}\xi _j^{1}{\tilde{\xi }}_{kl}^{1}+\xi _k^{1}\xi _l^{1} {\tilde{\xi }}_{ij}^{1}\right) \\&\quad +\frac{\omega }{N^3}\sum _{\mu>2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1 \left( \xi _i^{\mu }\xi _j^{\mu }{\tilde{\xi }}_{kl}^{\mu }+\xi _k^{\mu }\xi _l^{\mu } {\tilde{\xi }}_{ij}^{\mu }\right) \\&=\frac{\omega }{N^3}\sum _{j,k,l}^N\left( \xi _k^1\xi _l^1{\tilde{\xi }}_{kl}^{1} +\xi _i^{1}\xi _j^{1}{\tilde{\xi }}_{ij}^{1}\right) \\&\quad +\frac{\omega }{N^3}\sum _{\mu >2}^K\sum _{j,k,l}^N\xi _i^1\xi _j^1\xi _k^1\xi _l^1 \left( \xi _i^{\mu }\xi _j^{\mu }{\tilde{\xi }}_{kl}^{\mu }+\xi _k^{\mu } \xi _l^{\mu }{\tilde{\xi }}_{ij}^{\mu }\right) . \end{aligned}$$

We then obtain

$$\begin{aligned} R^{(1)}&\sim \frac{\omega }{N^3}\left( N\sqrt{N^2}+N^2\sqrt{N}+\sqrt{KN^3}\right) \\&\sim \omega \left( \frac{1}{N}+\frac{1}{\sqrt{N}}+\sqrt{\frac{K}{N^3}}\right) . \end{aligned}$$

Finally, the second order of the pattern noise $R^{(2)}$ is

$$\begin{aligned} R^{(2)}=\frac{\omega ^2}{N^3}\sum _{\mu }^K\sum _{j,k,l}^N\xi _i^1\xi _j^1 \xi _k^1\xi _l^1{\tilde{\xi }}_{ij}^{\mu }{\tilde{\xi }}_{kl}^{\mu }\sim \omega ^2 \sqrt{\frac{K}{N^3}}. \end{aligned}$$

In conclusion, the noise can be written as

$$\begin{aligned} R&\sim R^{(0)}+R^{(1)}+R^{(2)}\\&\sim \sqrt{\frac{K}{N^3}}\left( 1+\omega +\omega ^2\right) +\omega \left( \frac{1}{N} +\frac{1}{\sqrt{N}}\right) . \end{aligned}$$

We set $K\sim N^a$ and $\omega \sim N^b$, in this way we obtain, at leading order

$$\begin{aligned} R\sim \sqrt{\frac{K}{N^3}}\omega ^2+\frac{\omega }{\sqrt{N}}\sim N^{(a-3)/2+2b}+N^{b-1/2}. \end{aligned}$$

Recalling that retrieval is possible provided that $R\lesssim S\sim 1$ we see that there are two different regimes: if $a\le 1$ noise is dominated by the second term and the extremal condition for retrieval reads

$$\begin{aligned} N^{b-1/2}\sim 1\rightarrow b=\frac{1}{2}, \end{aligned}$$

therefore the tolerance versus pattern noise is

$$\begin{aligned} \beta (a)\sim N^{1/2} \quad \text {for}\quad a\le 1; \end{aligned}$$

if $a>1$, increasing the load reduces the tolerance versus pattern noise, indeed we obtain

$$\begin{aligned} N^{(a-3)/2+2b}\sim 1\rightarrow b=\frac{3}{4}-\frac{a}{4}, \end{aligned}$$

and then it follows

$$\begin{aligned} \beta (a)\sim N^{(3-a)/4} \quad \text {for}\quad 1<a<3. \end{aligned}$$

1.3 Noisy storing

Finally, the less challenging noise is the one applied on 4-tensors or, analogously, on the couplings. This is of the form

$$\begin{aligned} \eta _{ijkl}^{\mu }=\xi _{i}^{\mu }\xi _{j}^{\mu }\xi _{k}^{\mu }\xi _{l}^{\mu } +\omega {\tilde{\xi }}_{ijkl}^{\mu }. \end{aligned}$$

(26)

Again, we consider the product between the local field $h_i$ and $\xi _i^1$

$$\begin{aligned} h_i\xi _i^1=\frac{1}{2N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N\left( \xi _i^{\mu } \xi _j^{\mu }\xi _k^{\mu }\xi _l^{\mu }+\omega {\tilde{\xi }}_{ijkl}^{\mu }\right) \xi _i^1\xi _j^1\xi _k^1\xi _l^1. \end{aligned}$$

The signal, as already shown, scales as $S\sim 1$, while the noise is composed of two contributions: zeroth and first order. We have already computed the former

$$\begin{aligned} R^{(0)}\sim \sqrt{\frac{K}{N^3}}\sim \sqrt{\frac{K}{N^3}}. \end{aligned}$$

For what concerns the first order, it holds

$$\begin{aligned} R^{(1)}=\frac{\omega }{2N^3}\sum _{\mu =1}^K\sum _{j,k,l}^N{\tilde{\xi }}_{ijkl}^{\mu } \xi _i^1\xi _j^1\xi _k^1\xi _l^1\sim \omega \sqrt{\frac{K}{N^3}}. \end{aligned}$$

Therefore,

$$\begin{aligned} R=R^{(0)}+R^{(1)}\sim \sqrt{\frac{K}{N^3}}\left( 1+\omega \right) \sim \omega \sqrt{\frac{K}{N^3}}. \end{aligned}$$

Setting, as before, $K\sim N^a$ and $\omega \sim N^b$ the condition for retrieval becomes

$$\begin{aligned} N^{(a-3)/2+b}\sim 1\rightarrow b=\frac{3-a}{2}, \end{aligned}$$

which implies that the tolerance versus pattern noise is

$$\begin{aligned} \beta (a)\sim N^{(3-a)/2}\quad \text {for}\quad a\le 3. \end{aligned}$$