Surface energy layers investigation of intelligent magnetoelectrothermoelastic nanoplates through a vibration analysis

Abstract

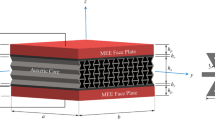
Intelligent materials such as magnetoelectrothermoelastic (METE) nanoplates offer great potential to supply more efficient energy harvesting devices, transducers, sensors, and actuators. In this study, the influences of slanted angle of the METE nanoplate and orthotropic angle of Pasternak foundation on the magnitude of surface energy layers are investigated through a vibrational analysis. The nanoplate is exposed to outer thermal, electric, magnetic and in-plane loadings. For modeling the plate’s nonlocal behavior and surface stresses, the governing equations are constructed based on Hamilton’s principle. Galerkin method is implemented to solve the equilibrium motions, and also for the authenticity of the solution, the equations are resolved by the Navier’s method. Obtained results are deemed useful for the mechanical analysis and design of nano-/microelectromechanical system nanostructures constructed from the METE materials. The numerical examples indicated that after a particular value of slanted angle of the nanoplate, α ≥ 80, the magnitude of surface energy layers in the vibration behavior becomes opposite to the case when the slanted angles are 0° < α < 80°. In addition, the value of the slanted angle of the nanoplate can cause the harmonic responses of the vibration due to the orthotropic angle of Pasternak foundation to shift in harmony with the slanted angle degree.

Appendices

Appendix 1

K and χ matrixes can be written as follows:

$$ \begin{aligned} K_{ij}^{b,11} & = \int\limits_{ - 1}^{ + 1} \int\limits_{ - 1}^{ + 1} {\varPsi_{{^{i} }}^{b} } \left\{ {\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{4} }} + \frac{{2\,(D_{12}^{b} + 2D_{66}^{b} )}}{{D_{11}^{b} }}\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} \partial \eta^{2} }} + \frac{{D_{22}^{b} }}{{D_{11}^{b} }}\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{4} }}} \right. \\ & \quad\left. - \left( {\frac{{2\tau^{s} a^{2} }}{{D_{11}^{b} }} + \frac{{N_{\text{total}} a^{2} }}{{D_{11}^{b} }} + \frac{{K_{w} a^{4} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} } \right)\;\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{2} }}} \right) + \left( {\frac{{K_{w} a^{4} }}{{D_{11}^{b} }}} \right)\;(\varPsi_{{^{j} }}^{b} ) \right. \\ & \quad \left. + \left( {\frac{{2\tau^{s} a^{2} }}{{D_{11}^{b} }} + \frac{{N_{\text{total}} a^{2} }}{{D_{11}^{b} }}} \right)\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{4} }} + 2\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} \partial \eta^{2} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{4} }}} \right) \right. \\ & \quad \left. - \frac{{K_{gX1} a^{2} }}{{D_{11}^{b} }}\left( {\,\cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} }}} \right) + 2\cos \beta \sin \beta \,\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{\partial \xi \partial \eta }} \right) + \sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{2} }}} \right)} \right) \right. \\ & \quad \left. - \frac{{K_{gY1} a^{2} }}{{D_{11}^{b} }}\left( {\,\sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} }}} \right) - 2\sin \beta \cos \beta \,\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{\partial \xi \partial \eta }} \right) + \cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{2} }}} \right)} \right) \right. \\ & \quad \left. + \frac{{K_{gX1} a^{2} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( \,\cos^{2} \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right.\right. \\ &\quad \left.\left. + 2\cos \beta \sin \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{3} \partial \eta }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi \partial \eta^{3} }}} \right) + \sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right) \right.\\ & \quad \left. + \frac{{K_{gY1} a^{2} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( \sin^{2} \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right.\right.\\ &\quad \left.\left. - 2\sin \beta \cos \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{3} \partial \eta }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi \partial \eta^{3} }}} \right) + \cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right) \right\}\left| J \right|{\text{d}}\xi {\text{d}}\eta \\ \end{aligned} $$

$$ \begin{aligned} K_{ij}^{s,12} & = K_{ij}^{b,21} \left( {{\text{put}}\,\,\varPsi^{b} \;{\text{instead}}\,\;{\text{of}}\,\,\varPsi^{s} } \right) \\ & = \int\limits_{ - 1}^{ + 1} \int\limits_{ - 1}^{ + 1} {\varPsi_{{^{i} }}^{s} } \left\{ - \left( {\frac{{2\tau^{s} a^{2} }}{{D_{11}^{b} }} + \frac{{N_{\text{total}} a^{2} }}{{D_{11}^{b} }} + \frac{{K_{w} a^{4} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} } \right)\;\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right) \right. \\ & \quad \left. + \left( {\frac{{K_{w} a^{4} }}{{D_{11}^{b} }}} \right)\;\left( {\varPsi_{{^{j} }}^{s} } \right) + \left( {\frac{{2\tau^{s} a^{2} }}{{D_{{^{{_{11} }} }}^{b} }} + \frac{{N_{\text{total}} a^{2} }}{{D_{{^{{_{11} }} }}^{b} }}} \right)\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + 2\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }}} \right) \right. \\ & \quad \left. - \frac{{K_{gX1} a^{2} }}{{D_{11}^{b} }}\left( {\,\cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }}} \right) + 2\cos \beta \sin \beta \,\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{\partial \xi \partial \eta }} \right) + \sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right)} \right) \right. \\ & \quad \left. - \frac{{K_{gY1} a^{2} }}{{D_{11}^{b} }}\left( {\,\sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }}} \right) - 2\sin \beta \cos \beta \,\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{\partial \xi \partial \eta }} \right) + \cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right)} \right) \right. \\ & \quad \left. + \frac{{K_{gX1} a^{2} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( \cos^{2} \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right.\right. \\ & \quad \left.\left. + 2\cos \beta \sin \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{3} \partial \eta }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi \partial \eta^{3} }}} \right) + \sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right) \right. \\ & \quad \left. + \frac{{K_{gY1} a^{2} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( \sin^{2} \beta \left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right.\right. \\ & \quad \left.\left. - 2\sin \beta \cos \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{3} \partial \eta }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi \partial \eta^{3} }}} \right) + \cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right) \right\}\left| J \right|{\text{d}}\xi {\text{d}}\eta \\ \end{aligned} $$

$$ \begin{aligned} K_{ij}^{s,22} & = \int\limits_{ - 1}^{ + 1} \int\limits_{ - 1}^{ + 1} {\varPsi_{i}^{s} } \left\{ \frac{{D_{11}^{s} }}{{D_{11}^{b} }}\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + \frac{{2\,(D_{12}^{s} + 2D_{66}^{s} )}}{{D_{{^{{_{11} }} }}^{b} }}\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }} \right.\\ &\quad \left. + \frac{{D_{22}^{s} }}{{D_{11}^{b} }}\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }} - \left( {\frac{{D_{{_{55} }}^{s} a^{2} }}{{D_{{^{{_{11} }} }}^{b} }} + \frac{{2\tau^{s} a^{2} }}{{D_{{^{{_{11} }} }}^{b} }}} \right)\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }} - \left( {\frac{{D_{44}^{s} a^{2} }}{{D_{11}^{b} }} + \frac{{2\tau^{s} a^{2} }}{{D_{11}^{b} }}} \right)\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }} \right.\\ &\quad \left. - \left( {\frac{{2\tau^{s} a^{2} }}{{D_{11}^{b} }} + \frac{{N_{\text{total}} a^{2} }}{{D_{11}^{b} }} + \frac{{K_{w} a^{4} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} } \right)\;\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right) + \left( {\frac{{K_{w} a^{4} }}{{D_{11}^{b} }}} \right)\;(\varPsi_{{^{j} }}^{s} ) \right.\\ &\quad \left. + \left( {\frac{{2\tau^{s} a^{2} }}{{D_{11}^{b} }} + \frac{{N_{\text{total}} a^{2} }}{{D_{11}^{b} }}} \right)\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + 2\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }}} \right) \right.\\ &\quad \left. - \frac{{K_{gX1} a^{2} }}{{D_{11}^{b} }}\left( {\,\cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }}} \right) + 2\cos \beta \sin \beta \,\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{\partial \xi \partial \eta }} \right) + \sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right)} \right) \right.\\ &\quad \left. - \frac{{K_{gY1} a^{2} }}{{D_{11}^{b} }}\left( {\,\sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }}} \right) - 2\sin \beta \cos \beta \,\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{\partial \xi \partial \eta }} \right) + \cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right)} \right) \right.\\ &\quad \left. + \frac{{K_{gX1} a^{2} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( \cos^{2} \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right.\right.\\ &\quad \left.\left. + 2\cos \beta \sin \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{3} \partial \eta }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi \partial \eta^{3} }}} \right) + \sin^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right) \right.\\ &\quad \left. + \frac{{K_{gY1} a^{2} }}{{D_{11}^{b} }}\left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( \sin^{2} \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right.\right.\\ &\quad \left. \left. - 2\sin \beta \cos \beta \,\left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{3} \partial \eta }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi \partial \eta^{3} }}} \right) + \cos^{2} \beta \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }}} \right) \right) \right\}\left| J \right|{\text{d}}\xi {\text{d}}\eta \\ \end{aligned} $$

$$ \begin{aligned} \chi_{ij}^{b,11} & = \int\limits_{ - 1}^{ + 1} {\int\limits_{ - 1}^{ + 1} {\varPsi_{{_{i} }}^{b} } \left\{ {\frac{{\rho ha^{4} }}{{D_{11} }}\left( {\varPsi_{{_{j} }}^{b} - \left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{2} }}} \right)} \right)} \right.} \\ & \quad \left. { - \frac{{\rho h^{3} a^{2} }}{{12 \times D_{11} }}\left( {\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{2} }}} \right) - \left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{4} }} + 2\frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \xi^{2} \partial \eta^{2} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{b} }}{{\partial \eta^{4} }}} \right)} \right)} \right\}\left| J \right|{\text{d}}\xi {\text{d}}\eta \\ \chi_{ij}^{s,12} & = \chi_{ij}^{b,12} ({\text{put}}\,\,\varPsi^{b} \;{\text{instead}}\,\;{\text{of}}\,\,\varPsi^{s} ) = \int\limits_{ - 1}^{ + 1} {\int\limits_{ - 1}^{ + 1} {\varPsi_{i}^{s} } } \left\{ {\frac{{\rho ha^{4} }}{{D_{11} }}\left( {\varPsi_{{_{j} }}^{s} - \left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right)} \right)} \right\}\left| J \right|{\text{d}}\xi {\text{d}}\eta \\ \chi_{ij}^{s,22} & = \int\limits_{ - 1}^{ + 1} {\int\limits_{ - 1}^{ + 1} {\varPsi_{i}^{s} } } \left\{ {\frac{{\rho ha^{4} }}{{D_{11} }}\left( {\varPsi_{{_{j} }}^{s} - \left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right)} \right)} \right. \\ & \quad \left. { - \frac{{\rho h^{3} a^{2} }}{{12 \times 84 \times D_{11} }}\left( {\left( {\frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{2} }}} \right) - \left( {\frac{{e_{0} a_{0} }}{a}} \right)^{2} \left( {\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{4} }} + 2\frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \xi^{2} \partial \eta^{2} }} + \frac{{\partial^{4} \varPsi_{{^{j} }}^{s} }}{{\partial \eta^{4} }}} \right)} \right)} \right\}\left| J \right|{\text{d}}\xi {\text{d}}\eta \\ N_{\text{total}} & = N_{\text{t}} + N_{\text{p}} + N_{\text{e}} + N_{\text{m}} \\ \end{aligned} $$

(33)

Appendix 2

Navier’s method For an exact solution of the equations, Navier’s method can be used for obtaining the natural frequency of nanoplates with simply supported boundary conditions in all edges:

$$ W^{*b} = \sum\limits_{m = 1}^{\infty } {{\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{n = 1}^{\infty } {W_{mn}^{b} } } \sin {\kern 1pt} (\zeta {\kern 1pt} x)\;\sin {\kern 1pt} (\gamma {\kern 1pt} y),\quad W^{*b} = \sum\limits_{m = 1}^{\infty } {{\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{n = 1}^{\infty } {W_{mn}^{s} } } \sin {\kern 1pt} (\zeta {\kern 1pt} x)\;\sin {\kern 1pt} (\gamma {\kern 1pt} y), $$

(34)

where ζ = mπ/a, and γ = nπ/b. Furthermore, m and n could be introduced the half-wave number alongside x and y directions. By replacing Eq. (34) into Eq. (21) and without considering orthotropic Pasternak foundation, the following matrix is derived as:

$$ \left[ {\begin{array}{*{20}c} {I_{11} } & {I_{12} } \\ {I_{21} } & {I_{22} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {W_{mn}^{b} } \\ {W_{mn}^{s} } \\ \end{array} } \right\}{\kern 1pt} \, = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \right\}, $$

(35)

where

$$ \begin{aligned} I_{11} & = D_{{^{{_{11} }} }}^{b} \zeta^{4} + 2\,(D_{{^{12} }}^{b} + 2D_{{^{66} }}^{b} )\zeta^{2} \gamma^{2} + D_{{_{22} }}^{b} \gamma^{4} + 2\,\tau^{\text{s}} \left\{ {\,(\zeta^{2} + \gamma^{2} ) + (e_{0} a_{0} )^{2} (\zeta^{2} + \gamma^{2} ){\kern 1pt}^{2} } \right\} \\ & \quad + \,(N_{xt} + N_{xp} + N_{xe} + N_{xm} )\;\left\{ {\;\zeta^{2} + (e_{0} a_{0} )^{2} (\zeta^{4} + \zeta^{2} \gamma^{2} )} \right\} \\ &\quad + (N_{yt} + N_{yp} + N_{ye} + N_{ym} )\left\{ {\;\gamma^{2} + (e_{0} a_{0} )^{2} (\gamma^{4} + \alpha^{2} \gamma^{2} )} \right\} \\ & \quad - \,\omega^{2} \rho \;h{\kern 1pt} \,\left\{ {\;1 + (e_{0} a_{0} )^{2} (\zeta^{2} + \gamma^{2} )} \right\} - \omega^{2} \frac{{\rho \,h^{3} }}{12}{\kern 1pt} {\kern 1pt} \left\{ {\;(\zeta^{2} + \beta^{2} ) + (e_{0} a_{0} )^{2} (\zeta^{4} + \gamma^{4} + 2{\kern 1pt} \zeta^{2} \gamma^{2} )} \right\} \\ I_{12} & = I_{21} = 2\,\tau^{\text{s}} \left\{ {\;(\zeta^{2} + \gamma^{2} ) + (e_{0} a_{0} )^{2} (\zeta^{4} + \gamma^{4} + 2{\kern 1pt} \zeta^{2} \gamma^{2} )} \right\} \\ &\quad + (N_{xt} + N_{xp} + N_{xe} + N_{xm} )\left\{ {\;\zeta^{2} + (e_{0} a_{0} )^{2} (\zeta^{4} + \zeta^{2} \gamma^{2} )} \right\} \\ & \quad + \,(N_{yt} + N_{yp} + N_{ye} + N_{ym} )\left\{ {\;\gamma^{2} + (e_{0} a_{0} )^{2} (\gamma^{4} + \zeta^{2} \gamma^{2} )} \right\} - \omega^{2} \rho \;h{\kern 1pt} \,\left\{ {1 + (e_{0} a_{0} )^{2} (\zeta^{2} + \gamma^{2} )} \right\} \\ I_{22} & = D_{{^{{_{11} }} }}^{s} \zeta^{4} + 2\,(D_{{^{12} }}^{s} + 2D_{{^{66} }}^{s} )\zeta^{2} \gamma^{2} + D_{{_{22} }}^{s} \gamma^{4} + 2\,\tau^{\text{s}} \left\{ {\;(\zeta^{2} + \gamma^{2} ) + (e_{0} a_{0} )^{2} (\zeta^{4} + \gamma^{4} + 2{\kern 1pt} \zeta^{2} \gamma^{2} )} \right\} \\ & \quad + \,(N_{xt} + N_{xp} + N_{xe} + N_{xm} )\left\{ {\;\zeta^{2} + (e_{0} a_{0} )^{2} (\zeta^{4} + \zeta^{2} \gamma^{2} )} \right\} \\ &\quad + (N_{yt} + N_{yp} + N_{ye} + N_{ym} )\left\{ {\gamma^{2} + (e_{0} a_{0} )^{2} (\gamma^{4} + \zeta^{2} \gamma^{2} )} \right\} \\ & \quad - \,\omega^{2} \rho \,h\,\left\{ {\,\;1 + (e_{0} a_{0} )^{2} (\zeta^{2} + \gamma^{2} )} \right\}\, - \omega^{2} \frac{{\rho \,h^{3} }}{12 \times 84}\,\left\{ {(\zeta^{2} + \gamma^{2} ) + (e_{0} a_{0} )^{2} (\zeta^{4} + \gamma^{4} + 2{\kern 1pt} \zeta^{2} \gamma^{2} )\,} \right\} \\ \end{aligned} $$

(36)