Skip to main content
SpringerLink
Log in

Dynamic transverse vibration characteristics of nonuniform nonlocal strain gradient beams using the generalized differential quadrature method

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract.

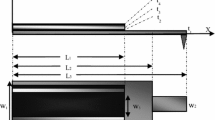
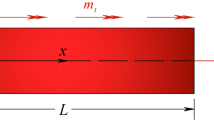
In this study, vibration response of small-scale tapered beams is investigated. Size-dependent effects are modeled in the framework of the nonlocal strain gradient theory and three different types of linearly cross-section variation are proposed by having width variation, thickness variation and a combination of them both. The small-scale beam is formulated using Euler-Bernoulli beam theory, nonlocal strain gradient theory and Hamilton’s principle. Equations of motion for all three types of nonuniformity are solved using the generalized differential quadrature method (GDQM). Results are presented and compared to those achieved for simplified models and effects of having different slenderness ratio are presented. Moreover, a comprehensive parametric study is proposed and the effects of varying nonuniformity terms, nonlocal and strain gradient parameters are precisely studied. Accordingly, with the vast application of tapered small-scale beams in many devices, especially scanning tunneling microscopes (STM) and atomic force microscopes (AFM), this study could be a step forward in understanding, predicting and controlling such kind of behaviors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Zhang, C.M. Wang, E. Ruocco, N. Challamel, Eng. Struct. 126, 252 (2016)

    Article  Google Scholar 

  2. S.M. Abdelghany, K.M. Ewis, A.A. Mahmoud, M.M. Nassar, Beni-Suef Univ. J. Basic Appl. Sci. 4, 192 (2015)

    Article  Google Scholar 

  3. H. Malaeke, H. Moeenfard, J. Sound Vib. 366, 211 (2016)

    Article  ADS  Google Scholar 

  4. M. Ahmadi, A. Nikkhoo, Appl. Math. Modell. 38, 2130 (2014)

    Article  Google Scholar 

  5. W. He, S.S. Ge, IEEE/ASME Trans. Mechatron. 20, 237 (2015)

    Article  Google Scholar 

  6. J.R. Banerjee, J. Phys.: Conf. Ser. 721, 012005 (2016)

    Google Scholar 

  7. Z. Qian, Y. Hui, F. Liu, S. Kar, M. Rinaldi, Single Transistor Oscillator Based on a Graphene-Aluminum Nitride Nano Plate Resonator, in Proceedings of the 2013 IEEE International Frequency Control Symposium (IFCS 2013), Prague, Czech Republic (IEEE, 2013) pp. 559--561

  8. X. Tong, G.A. DiLabio, O.J. Clarkin, R.A. Wolkow, Nano Lett. 4, 357 (2004)

    Article  ADS  Google Scholar 

  9. R. Reddy, B.R. Dorvel, J. Go, P.R. Nair, O.H. Elibol, G.M. Credo, J.S. Daniels, E.K.C. Chow, X. Su, M. Varma, M.A. Alam, R. Bashir, Biomed. Microdev. 13, 335 (2011)

    Article  Google Scholar 

  10. Y. Zhang, G. Chang, S. Liu, W. Lu, J. Tian, X. Sun, Biosensors Bioelectron. 28, 344 (2011)

    Article  Google Scholar 

  11. J. Ding, K. Zhang, G. Wei, Z. Su, RSC Adv. 5, 69745 (2015)

    Article  Google Scholar 

  12. Z. Jing, J. Zhan, Adv. Mater. 20, 4547 (2008)

    Article  Google Scholar 

  13. E. Detsri, Chin. Chem. Lett. 27, 1635 (2016)

    Article  Google Scholar 

  14. X. Tang, K.W.C. Lai, Quantitative Study of AFM-based Nanopatterning of Graphene Nanoplate, in 14th IEEE International Conference on Nanotechnology (IEEE, 2014) pp. 54--57

  15. W. Jeong, M. Lee, H. Lee, H. Lee, B. Kim, J.Y. Park, Nanotechnology 27, 215601 (2016)

    Article  ADS  Google Scholar 

  16. T. Nan, Y. Hui, M. Rinaldi, N.X. Sun, Sci. Rep. 3, 1985 (2013)

    Article  ADS  Google Scholar 

  17. Y. Hui, J.S. Gomez-Diaz, Z. Qian, A. Alu, M. Rinaldi, Nat. Commun. 7, 11249 (2016)

    Article  ADS  Google Scholar 

  18. E. Kröner, Int. J. Solids Struct. 3, 731 (1967)

    Article  Google Scholar 

  19. A.C. Eringen, J. Appl. Phys. 54, 4703 (1983)

    Article  ADS  Google Scholar 

  20. A.C. Eringen, Nonlocal Continuum Field Theories (Springer-Verlag, New York, 2002) https://doi.org/10.1007/b97697

  21. J.N. Reddy, Int. J. Eng. Sci. 45, 288 (2007)

    Article  Google Scholar 

  22. H.B. Khaniki, S. Hosseini-Hashemi, Int. J. Eng. Sci. 115, 51 (2017)

    Article  Google Scholar 

  23. C.M. Wang, Y.Y. Zhang, X.Q. He, Nanotechnology 18, 105401 (2007)

    Article  ADS  Google Scholar 

  24. S.H. Hashemi, H.B. Khaniki, J. Mech. 33, 559 (2017)

    Article  Google Scholar 

  25. S.H. Hashemi, H.B. Khaniki, Alex. Eng. J. (2017) https://doi.org/10.1016/j.aej.2016.12.015

  26. S.C. Pradhan, J.K. Phadikar, J. Sound Vib. 325, 206 (2009)

    Article  ADS  Google Scholar 

  27. T. Murmu, S.C. Pradhan, Physica E 41, 1451 (2009)

    Article  ADS  Google Scholar 

  28. J. Aranda-Ruiz, J. Loya, J. Fernández-Sáez, Compos. Struct. 94, 2990 (2012)

    Article  Google Scholar 

  29. S.H. Hashemi, H.B. Khaniki, Int. J. Eng. Trans. B: Appl. 29, 688 (2016)

    Google Scholar 

  30. S.H. Hashemi, H.B. Khaniki, Int. J. Nano Dimens. 8, 70 (2017)

    Google Scholar 

  31. J. Aranda-Ruiz, J. Loya, J. Fernández-Sáez, Compos. Struct. 94, 2990 (2012)

    Article  Google Scholar 

  32. G. Romano, R. Barretta, M. Diaco, F.M. de Sciarra, Int. J. Mech. Sci. 121, 151 (2017)

    Article  Google Scholar 

  33. G. Romano, R. Barretta, Int. J. Eng. Sci. 109, 240 (2016)

    Article  Google Scholar 

  34. G. Romano, R. Barretta, Int. J. Eng. Sci. 115, 14 (2017)

    Article  Google Scholar 

  35. G. Romano, R. Barretta, Compos. Part B: Eng. 114, 184 (2017)

    Article  Google Scholar 

  36. A. Apuzzo, R. Barretta, R. Luciano, F.M. de Sciarra, R. Penna, Compos. Part B: Eng. 123, 105 (2017)

    Article  Google Scholar 

  37. G. Romano, R. Barretta, M. Diaco, Int. J. Mech. Sci. 131, 490 (2017)

    Article  Google Scholar 

  38. R.M. Bergman, J. Appl. Math. Mech. 32, 1085 (1968)

    Article  Google Scholar 

  39. R.A. Toupin, Arch. Ration. Mech. Anal. 11, 385 (1962)

    Article  MathSciNet  Google Scholar 

  40. R.D. Mindlin, H.F. Tiersten, Arch. Ration. Mech. Anal. 11, 415 (1962)

    Article  Google Scholar 

  41. N.A. Fleck, G.M. Muller, M.F. Ashby, J.W. Hutchinson, Acta Metallur. Mater. 42, 475 (1994)

    Article  Google Scholar 

  42. D.C.C. Lam, F. Yang, A.C.M. Chong, J. Wang, P. Tong, J. Mech. Phys. Solids 51, 1477 (2003)

    Article  ADS  Google Scholar 

  43. H.M. Ma, X.L. Gao, J.N. Reddy, J. Mech. Phys. Solids 56, 3379 (2008)

    Article  ADS  MathSciNet  Google Scholar 

  44. H.B. Khaniki, S. Hosseini-Hashemi, Eur. Phys. J. Plus 132, 200 (2017)

    Article  Google Scholar 

  45. S.K. Park, X.L. Gao, J. Micromech. Microeng. 16, 2355 (2006)

    Article  ADS  Google Scholar 

  46. B. Akgöz, Ö. Civalek, Int. J. Eng. Sci. 49, 1268 (2011)

    Article  Google Scholar 

  47. B. Akgöz, Ö. Civalek, Struct. Eng. Mech. 48, 195 (2013)

    Article  Google Scholar 

  48. B. Akgöz, Ö. Civalek, Compos. Struct. 98, 314 (2013)

    Article  Google Scholar 

  49. G. Romano, R. Barretta, M. Diaco, Continuum Mech. Thermodyn. 28, 1659 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  50. C.W. Lim, G. Zhang, J.N. Reddy, J. Mech. Phys. Solids 78, 298 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  51. F. Ebrahimi, M.R. Barati, J. Vib. Control (2016) https://doi.org/10.1177/1077546316678511

  52. L. Li, Y. Hu, L. Ling, Physica E 75, 118 (2016)

    Article  ADS  Google Scholar 

  53. H. Zeighampour, Y.T. Beni, I. Karimipour, Microfluid. Nanofluid. 21, 85 (2017)

    Article  Google Scholar 

  54. L. Lu, X. Guo, J. Zhao, Int. J. Eng. Sci. 116, 12 (2017)

    Article  Google Scholar 

  55. X.J. Xu, X.C. Wang, M.L. Zheng, Z. Ma, Compos. Struct. 160, 366 (2017)

    Article  Google Scholar 

  56. L. Li, Y. Hu, X. Li, Int. J. Mech. Sci. 115, 135 (2016)

    Article  Google Scholar 

  57. L. Li, Y. Hu, Int. J. Eng. Sci. 97, 84 (2015)

    Article  Google Scholar 

  58. T.Y. Wu, G.R. Liu, Comput. Mech. 24, 197 (1999)

    Article  MathSciNet  Google Scholar 

  59. T.Y. Wu, G.R. Liu, Int. J. Numer. Methods Biomed. Eng. 16, 777 (2000)

    Google Scholar 

  60. L. Li, X. Li, Y. Hu, Int. J. Eng. Sci. 102, 77 (2016)

    Article  Google Scholar 

  61. C.M. Wang, Y.Y. Zhang, X.Q. He, Nanotechnology 18, 105401 (2007)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Impact Research Laboratory, Department of Mechanical Engineering, Iran University of Science and Technology, 16846-13114, Tehran, Iran

    H. Bakhshi Khaniki & Sh. Hosseini-Hashemi

  2. Center of Excellence in Railway Transportation, Iran University of Science and Technology, 16842-13114, Tehran, Iran

    Sh. Hosseini-Hashemi

Authors
  1. H. Bakhshi Khaniki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sh. Hosseini-Hashemi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. Bakhshi Khaniki.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bakhshi Khaniki, H., Hosseini-Hashemi, S. Dynamic transverse vibration characteristics of nonuniform nonlocal strain gradient beams using the generalized differential quadrature method. Eur. Phys. J. Plus 132, 500 (2017). https://doi.org/10.1140/epjp/i2017-11757-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/i2017-11757-4

Search

Navigation