Novel and topical business news and their impact on stock market activity

Abstract

We propose an indicator to measure the degree to which a particular news article is novel, as well as an indicator to measure the degree to which a particular news item attracts attention from investors. The novelty measure is obtained by comparing the extent to which a particular news article is similar to earlier news articles, and an article is regarded as novel if there was no similar article before it. On the other hand, we say a news item receives a lot of attention and thus is highly topical if it is simultaneously reported by many news agencies and read by many investors who receive news from those agencies. The topicality measure for a news item is obtained by counting the number of news articles whose content is similar to an original news article but which are delivered by other news agencies. To check the performance of the indicators, we empirically examine how these indicators are correlated with intraday financial market indicators such as the number of transactions and price volatility. Specifically, we use a dataset consisting of over 90 million business news articles reported in English and a dataset consisting of minute-by-minute stock prices on the New York Stock Exchange and the NASDAQ Stock Market from 2003 to 2014, and show that price volatility, transaction volumes, and the number of transactions exhibited a significant response to a news article when it was novel and topical.

Introduction

Financial markets can be regarded as a non-equilibrium open system. Understanding how they work remains a great challenge to researchers in finance, economics, and statistical physics. Fluctuations in financial market prices are sometimes driven by endogenous forces and sometimes by exogenous forces. Business news is a typical example of exogenous forces. Casual observation indicates that stock prices respond to news articles reporting on new developments concerning companies’ circumstances. Market reactions to news have been extensively studied by researchers in several different fields [1–14], with some researchers attempting to construct models that capture static and/or dynamic responses to endogenous and exogenous shocks [15, 16]. The starting point for neoclassical financial economists typically is what they refer to as the ‘efficient market hypothesis,’ which implies that stock prices respond at the very moment that news is delivered to market participants. A number of empirical studies have attempted to identify such an immediate price response to news but have found little evidence supporting the efficient market hypothesis [17–22].

Investors seek to forecast what will happen in the near future, and buy and sell securities based on such forecasts. Through this process, some newsworthy developments are factored into market prices before they occur, so that stock prices do not respond at all when they are reported [23]. This means that it is important for researchers to distinguish between anticipated and unanticipated news and focus only on unanticipated news in detecting the immediate response to news. To do this, we need to measure the extent to which a news article is novel to market participants, which is the first issue we will discuss in this paper. On the other hand, even if a particular piece of news is unanticipated, market responses differ depending on the importance of that piece of news to market participants. Specifically, it has been shown that market reaction to news differs depending on how it is interpreted by market participants [24], on how it is reported by the media (i.e., whether it is reported in a pessimistic or an optimistic context) [25], and on how many times the same news item is reported [26]. It has also been shown that transaction volumes tend to be greater for stocks with a larger number of searches on the internet [27]. All of these pieces of evidence suggest that we need to distinguish news that attract a lot of attention from market participants and news that receive little attention, and focus on news attracting a lot of attention in assessing the market response to such news. This means that we need to measure the extent to which a news item attracts attention from market participants, which is the second issue we will discuss in this paper.

Our approach to measure the novelty and topicality of news is closely related to recent studies on the application of text mining techniques to the analysis of financial market activities. Specifically, it has been shown that linguistic and statistical characteristics of news articles extracted using text mining techniques contain useful information to predict future stock price changes and trading volumes [28–33]. Also, in the context of information filtering, several new methods for detecting and eliminating redundant text in blogs and on twitters have been developed and applied to the identification of the novelty content of social networking service (SNS) texts [34–39].

In this paper, we measure the novelty of a news article by comparing it with other news articles reported before that article in terms of linguistic similarity: the article is regarded as novel if there was no linguistically similar news article before it. On the other hand, we say a news item attracts a lot of attention and thus is highly topical if it is simultaneously reported by multiple news agencies and read by many investors who acquire news from those agencies. The topicality measure for a news article is obtained by counting the number of news articles which have a similar content to the original news article but are delivered by other news agencies.

To check the usefulness of these two indicators, we empirically examine how they are correlated with intraday financial market indicators such as the number of transactions and price volatility. Specifically, we use a dataset consisting of over 90 million business news articles reported in English and a dataset consisting of minute-by-minute stock prices on the New York Stock Exchange (NYSE) and the NASDAQ Stock Market from 2003 to 2014, and show that stock price volatility and transaction volumes exhibited a significant response to a news article when it was novel and topical.

Our novelty measure is closely related to the one proposed by the Thomson Reuters Corporation ([40, 41]). They measure the novelty of news by counting the number of linguistically similar news articles that are found in the recent past (e.g. 12 hours, 24 hours, 3 days, etc.). Based on this method, it was shown that financial market activities respond more strongly to follow-up news than to the initial news [42]. Unfortunately, the details on their methodology, including how they define similarity between news articles, is not made available to the public, so that we cannot directly compare it with our methodology. The approach we employ is to use cosine similarity between news articles reported at different points in time to construct a novelty measure. We empirically show that this novelty measure is closely correlated with stock price volatility and transaction volumes. These are our contribution to the literature. Turning to the measure of topicality, our measure is related in some sense to the measure adopted by [43], which proposes to measure the importance of a news article by counting the number of retweets of a tweet mentioning the article. Their measure differs from ours in that they rely on information from Twitter users in evaluating the importance of news articles while we rely on information from news agencies. Also, it should be noted that our measure is able to capture the extent to which a news article is topical immediately after it is delivered, while the measure proposed by [43] does not work that quickly because the number of retweets increases only gradually.

The rest of the paper is organized as follows. We first provide a detailed description of our dataset containing over 90 million English-language business news articles, and show that breaking news have much more impact on stock price volatility and transaction volume than other news. Next, we examine the statistical laws regarding linguistic similarity among news articles, and propose a measure for the novelty of a news article as well as a measure for the topicality of an article. We then examine how these indicators are correlated with intraday financial market indicators.

News dataset

The Thomson Reuters Corporation (RTRS) and the Dow Jones & Company Inc. (DJ) deliver news to market participants around the world within fractions of a second through electronic systems [44, 45]. News items published by over 300 third parties are displayed on the RTRS electronic trading platform. In this paper, we use only English-language news articles published by RTRS, the Business Wire News Service (BSW), the Canada Newswire News Service (CNW), Marketwire (MKW), the PR Newswire News Service (PRN), and Market News Publishing Inc. (VMN) on the RTRS platform as well as all of the English-language news articles by DJ from 2003 to 2014. The total number of news articles exceeds 90 million. Journalists include keywords in their articles on the RTRS platform. For example, news articles for General Motors Company, LLC have a keyword, GM.N, where .N refers to the NYSE.

There are three types of news events on the RTRS platform. ALERT articles, which provide a one-line summary of breaking news, are displayed in red. HEADLINE articles provide a one-line summary of non-breaking news. An ALERT and a HEADLINE are up to 80-100 characters long. A STORY shows a complete news article. The percentages of ALERTs and HEADLINEs in our dataset are about 12% and 42%, respectively. On the other hand, the DJ news articles also contain keywords like GM.

Some remarks on ALERT and HEADLINE articles are in order. First, market reactions to news typically occur when the first report is delivered to market participants, and the first report typically takes the form of an ALERT or a HEADLINE. Second, although ALERT and HEADLINE articles are very short, they contain all relevant information available at the time. Given this, we focus our analysis in this paper on ALERTs, HEADLINEs, and the titles of DJ news articles. Third, news agencies deliver news articles as breaking news when they regard them as very important. Such article are classified as ALERTs in our dataset. If a news article is regarded as less important by news agencies, then it is delivered as non-breaking news and classified in our dataset as HEADLINE.

Market reaction to ALERT and HEADLINE articles

To observe the intraday market reaction to news, we measure market activity using the price volatility, the number of transactions, and the transaction volume every minute for each stock. Price volatility is defined by the absolute value of the stock price log-return over one minute:

$$ V'(d,t)=\big|\log{P(d,t+1)}-\log{P(d,t)}\big|, $$

(1)

where d and t represent the date and the time of day (by the minute) (e.g., $d=\text{5/18/2015}$, $t=\text{9:30 a.m.}$), respectively. Note that the three market activity indicators considered here are highly correlated with each other [46].

Market activity has seasonal and daytime variations. We remove these variations from typical market cycles to correctly estimate the market impact on market activity for a day by introducing the normalized volatility, the normalized number of transactions, and the normalized volume as follows:

$$\begin{aligned}& V(d,t)=\frac{\frac{V'(d,t)}{\langle V'(d,t) \rangle_{d}}}{\langle\frac {V'(d,t)}{\langle V'(d,t) \rangle_{d}} \rangle_{t}}, \end{aligned}$$

(2)

$$\begin{aligned}& N(d,t)=\frac{\frac{N'(d,t)}{\langle N'(d,t) \rangle_{d}}}{\langle\frac {N'(d,t)}{\langle N'(d,t) \rangle_{d}} \rangle_{t}}, \end{aligned}$$

(3)

$$\begin{aligned}& \mathit{Vol}(d,t)=\frac{\frac{\mathit{Vol}'(d,t)}{\langle \mathit{Vol}'(d,t) \rangle_{d}}}{\langle \frac{\mathit{Vol}'(d,t)}{\langle \mathit{Vol}'(d,t) \rangle_{d}} \rangle_{t}}, \end{aligned}$$

(4)

where $N'(d,t)$ and $\mathit{Vol}'(d,t)$ are the number of transactions and their volume at time t on date d. Since $\langle\cdots\rangle _{d}$ expresses the mean on date d, daily seasonality is removed from the level of market activity by the first term in each of the equations. $\langle \cdots\rangle_{t}$ also expresses the mean at time t in all sample periods. The second term removes the intraday cycles in market activity.

Next, we investigate the intraday market reaction to news displayed on the RTRS electronic trading platform. For illustration, we focus on GM stocks traded on the NYSE. We observe the three indicators of market activity in GM stocks on the NYSE at time Δt (i.e., $V(\Delta t)$, $N(\Delta t)$, $\mathit{Vol}(\Delta t)$), knowing that there was an ALERT or a HEADLINE with ‘GM.N’ at time $\Delta t=0$. Figure 1 shows the mean of each of the market activity measures, i.e., $\langle V(\Delta t) \rangle$, $\langle N(\Delta t) \rangle$, and $\langle \mathit{Vol}(\Delta t) \rangle$. In the ALERT case, the mean jumped by about 60% at time $\Delta t=0$ and slowly decayed in an exponential function ($=0.45 \exp(-0.073 \Delta t)+1$). On the other hand, when a HEADLINE was displayed the mean hardly moved.

Figure 1

Market activity in GM stocks before and after an ALERT and a HEADLINE for GM are displayed. When $\Delta t=0$, news articles with the keyword ‘GM.N’ are displayed on the RTRS electronic trading platform. (a), (b), and (c) show the normalized number of transactions, $\langle N(\Delta t) \rangle$, the normalized volume, $\langle V(\Delta t) \rangle$, and the normalized volatility, $\langle \mathit{Vol}(\Delta t) \rangle$. (d) is a semi-logarithmic figure, where the solid and dashed lines respectively represent the market response to an ALERT and a HEADLINE news item. The black line in (d) is a reference line ($=0.45 \exp(-0.073 \Delta t)+1$). The error bars shown in (a), (b), and (c) are for ALERTs and are calculated using randomized data (i.e., the timing of the arrival of news is randomized). The error bars for HEADLINEs are not shown in (a), (b), and (c) to make the figures easier to read. For (d), only the upper bound of the error bar is shown.

Figure 2 shows the intraday market reaction to the news of 64 NYSE stocks and 14 NASDAQ stocks. The correspondence between the stock numbers in Figure 2 and ticker symbols is provided in Table 1. Note that the stocks we analyze here are reststricted to those satisfying the following requirements: (1) the number of ALERTs is above 500, (2) the number of HEADLINEs is above 500, and (3) the sum of the two is above 3000. Specifically, each of the panels in Figure 2 presents the conditional mean of one of our measures of market activity in the three minutes after a particular news item was displayed, i.e., $\langle V(\Delta t)|0 \le\Delta t < 3 \rangle$, $\langle N(\Delta t)|0 \le\Delta t < 3 \rangle$, $\langle \mathit{Vol}(\Delta t)|0 \le\Delta t < 3 \rangle$. In the case of ALERTs, we observe a jump in market activity in almost all stocks. The mean of these jumps is 36.5%. On the other hand, none of the stocks responded much to HEADLINE news.

Figure 2

Market activity in 78 stocks in the three minutes after an ALERT or a HEADLINE are displayed. The ticker symbol corresponding to each stock number is provided in Table 1. (a), (b), and (c) show the normalized number of transactions, $\langle N(0 \le\Delta t<3) \rangle$, the normalized volume, $\langle V(0 \le\Delta t<3) \rangle$, and the normalized volatility, $\langle \mathit{Vol}(0 \le\Delta t<3) \rangle$. The error bars shown are for ALERTs and are calculated using randomized data (i.e., the timing of the arrival of news is randomized). The error bars for HEADLINEs are not shown to make the figures easier to read.

Table 1 Ticker that corresponds to stock number in Figure  2

To check the statistical significance of these results, we randomize the timing of the arrival of a news item and repeat the same exercises as in Figures 1 and 2. We then use the randomized data to calculate the mean and the standard deviation of the market activity measures. The error bars shown in the two figures are for ALERTs. As seen in Figures 1 and 2, the reaction of the market activity indicators observed in the actual data is much greater than that calculated using the randomized data, implying that market reactions to news are statistically significant.

The results presented in Figures 1 and 2 suggest that we need to distinguish news that attract a lot of attention from market participants and news that receive little attention, and focus on news attracting a lot of attention in assessing the market response to such news. In the following sections, we examine the statistical laws regarding linguistic similarity among news articles, and propose measures for the novelty of a news article and for the topicality of an article.

Similarity among news articles

We use Inverse Document Frequency (IDF) and cosine similarity to measure the similarity among news articles. Stop words such as ‘and,’ ‘with,’ and ‘the’ are not good keywords to measure similarity, unlike less common words such as ‘Chevrolet,’ ‘antitrust,’ or ‘bankrupt.’ IDF, which is a widely used measure in natural language processing to determine whether a term is common or rare across documents, is defined as the logarithm of the ratio of the total number of articles in a news dataset to the number of articles containing the given word.

Let $A=\{a_{1},\ldots,a_{n}\}$ be a set of articles and $W=\{w_{1},\ldots ,w_{m}\}$ be a set of distinct words occurring in A. An article is represented as an m-dimensional vector $\vec{w_{a}}$. We use the idf value as word weights and define the vector as follows:

$$\begin{aligned}[b] &\vec{w_{a}}=\bigl(\delta(a,w_{1})\mathit{idf}(w_{1}), \ldots, \delta(a,w_{m})\mathit{idf}(w_{m})\bigr), \\ &\left\{ \textstyle\begin{array}{l@{\quad}l} \delta(a,w_{k})=1 & (w_{k}\in a), \\ \delta(a,w_{k})=0 & (w_{k}\notin a) . \end{array}\displaystyle \right.\end{aligned} $$

(5)

When articles are represented as vectors, the similarity of two articles can be measured by the correlation between the vectors. The correlation is quantified as the cosine of the angle between the two vectors: this is referred to as cosine similarity. The cosine similarity between two articles $a_{i}$ and $a_{j}$ is given by

$$ \mathit{SIM}(a_{i},a_{j})=\frac{\vec{w_{a_{i}}}\vec{w_{a_{j}}}}{|\vec{w_{a_{i}}}||\vec{w_{a_{j}}}|}. $$

(6)

Note that given the definition above, the value of cosine similarity ranges between 0 and 1.

Employing Eq. (6), we use two different indicators of similarity between articles. The first gauges the similarity of news articles reported at different points in time. Function $S_{a} (\Delta t)$ expresses the mean of the cosine similarity between articles reported at different points in time, t and $t+\Delta t$. We refer to this as an auto cosine similarity function. Figure 3(a) shows the auto cosine similarity functions of RTRS news articles with the keywords ‘GM.N,’ ‘IBM.N,’ ‘PFE.N,’ ‘AAPL.O,’ and ‘YHOO.O’ (PFE.N and AAPL.O stand for Pfizer Inc. and Apple Inc., where .O stands for the NASDAQ stock exchange). For example, we collect articles with ‘GM.N’ and then calculate the cosine similarity between articles reported at t and at $t+\Delta t$ to obtain the auto cosine similarity function for GM. The functions are almost constant, $S_{a} (\Delta t)=0.3$, for $\Delta t \le200$ minutes. For Δt greater than 200 minutes, the functions decay slowly until about $\Delta t=5 \times10^{5}$ minutes ≈ 1 year and are $S_{a} (\Delta t) \approx0.02$ at $\Delta t=1$ year. The decay follows a power law, $S_{a} (\Delta t) \propto\Delta t^{-0.35}$ when $10^{2} \le \Delta t \le10^{5}$ minutes. These results suggest that news content tends to be remembered for several months. To check the statistical significance of these results, we conduct the same exercise using the randomized data (i.e., the timing of the arrival of news is randomized). The dotted lines in Figure 3(a) represent the cosine similarity calculated in this way. The lines show that cosine similarity calculated using the actual data is much greater than that calculated using the randomized data for $\Delta t < 5 \times10^{5}$.

Figure 3

Cosine similarity functions for GM, IBM, PFE, AAPL, and YHOO. Panels (a) and (b) show auto cosine similarity functions and cross cosine similarity functions, respectively. The dashed lines represent the result obtained using the randomized data (i.e., the timing of news arrival is randomized). The solid line in (a) is a reference line representing a power law with an exponent of −0.35.

The second indicator of similarity focuses on the similarity of news articles reported by different news agencies. Function $S_{c} (\Delta t)$ expresses the mean of the cosine similarity between a news article delivered by an agency at time t and another article delivered by another agency at time $t+\Delta t$. We refer this as the cross cosine similarity function. Figure 3(b) shows the cross cosine similarity functions for articles with the keywords ‘GM.N,’ ‘IBM.N,’ ‘PFE.N,’ ‘AAPL.O,’ and ‘YHOO.O’ for various values of Δt. For example, we collect articles with ‘GM.N’ and then calculate the cosine similarity between an article reported by agency i at t and an article reported by agency j at $t+\Delta t$ to obtain the cross cosine similarity for GM. The functions decay quickly with Δt. Specifically, $S_{c} (\Delta t) \le0.03$ for $|\Delta t| \ge 60$ minutes. An important thing to note is that the peak of the function is observed around $\Delta t=0$, where $S_{c} (\Delta t)$ is approximately equal to 0.3, and that this value is almost the same as the value of the auto cosine similarity function for $\Delta t \le200$ minutes. This indicates that news agencies tend to report similar news with almost no time lag ($\Delta t=0$). We repeat this exercise using the randomized data to confirm the statistical significance of the results.

Novelty and topicality detection

In this section, we introduce our novelty and topicality measures for news articles. News articles on similar topics frequently use similar words. Based on this, we define the novelty of news article $a_{t}$ at time t by counting the number of linguistically similar news articles reported before article $a_{t}$ as follows:

$$ \mathit{Nov}(a_{t})= \sum_{0 < \Delta t \le\tau}\mathit{SIM}(a_{t},a_{t-\Delta t}). $$

(7)

Note that news articles at time t and $t-\Delta t$ exist in our news dataset. Novelty is high when $\mathit{Nov}(a_{t})$ is close to 0. In this paper, we set maximum time lag τ to one week at which the auto cosine similarity function is around 0.1 (Figure 3(a)).

We check whether novel news articles are correctly identified by our novelty measure using RTRS’s follow-up articles. Figure 4(a) shows how the value of $\mathit{Nov}(a_{t})$ for an article depends on the rank of the article (i.e., whether it is a first report or a second one, etc). It shows that the mean of $\mathit{Nov}(a_{t})$ increases in proportion to the rank, indicating that our novelty indicator correctly distinguishes news articles with different ranking. We also compare the conditional mean for ALERT and HEADLINE follow-ups to find that the novelty of ALERTs is higher than that of HEADLINEs except for initial news.

Figure 4

Novelty of follow-up news articles for GM, IBM, and PFE. (a) Mean of novelty. (b) PDF of novelty for the 1st, 5th, 10th, and more than 20th follow-up ALERT news articles for GM.

One may wonder if these results come from a limited number of news articles with an extremely high novelty value, which have a dominant impact on the mean of $\mathit{Nov}(a_{t})$. To examine whether this is the case, we show in Figure 4(b) the entire distribution of $\mathit{Nov}(a_{t})$ for ALERTs associated with GM. In the figure, we show four distributions for different ranks (i.e., for the 1st, 5th, and 10th rank and for ranks of greater than 20). For example, the distribution for the novelty measure for the first rank has a peak at $\mathit{Nov}(a_{t})=0$, indicating that most of the news items of this rank are highly novelty. However, the lower the rank is, the more the distribution shifts to the right, implying lower novelty. These findings on changes in the distribution of the novelty measure clearly reject the notion that the results in Figure 4(a) are driven by outliers in the novelty measure.

Next, we define our measure of the topicality of news. We denote a news article reported by news agency k at time t by $a_{t,k}$, and then define the measure of news topicality $\mathit{Top}(a_{t,k})$ in terms of the number of news articles which have a similar content to the original news article but are provided by other news agencies:

$$ \mathit{Top}(a_{t,k})= \sum_{j\neq k, j\in K}\mathit{SIM}(a_{t,k},a_{t,j}). $$

(8)

Note that news articles $a_{t,k}$ and $a_{t,j}$ exist in our news dataset, and $K=\{k_{1}, \ldots, k_{l}\}$ is the set of news agencies. Topicality is high when $\mathit{Top}(a_{t,k})$ takes a large value. To take GM as an example, we collect articles with ‘GM.N’ and calculate the cosine similarity between an article reported by agency k at time t and another article reported by agency j at time t. Note that the articles in this example are both reported at time t. In the empirical exercise we conduct in this paper, we compare an article reported by agency k at t and another article reported by agency j in the time interval between 30 minutes before t and 30 minutes after t. The rationale for this choice of time interval is that, as we saw in Figure 3(b), the cross cosine similarity function peaks at $\Delta t=0$ and decays quickly as Δt deviates from zero.

To check whether our topicality measure correctly capture topical news articles, we compare the value of $\mathit{Top}(a_{t,k})$ for ALERTs and that for HEADLINEs. As explained in Section 2, news agencies deliver a news article as breaking news when they regard it as very important. Such articles are classified as ALERTs in our dataset. If a news article is regarded as less important by the news agency, it is delivered as non-breaking news and classified in our dataset as HEADLINE. Given this, it is reasonable to expect the value of $\mathit{Top}(a_{t,k})$ to be higher for ALERTs than for HEADLINEs. The results presented in Table 2 shows that $\mathit{Top}(a_{t,k})$ is indeed substantially higher for ALERTs than for HEADLINEs for all of the four companies examined.

Table 2 Mean of topicality $\pmb{\mathit{Top}(a_{t,k})}$ of RTRS news for GM, IBM, PFE, AAPL, and YHOO

Difference in market reaction by novelty and topicality of news

Using our novelty and topicality measures of news articles, we investigate the intraday market reactions to both novel and topical news. As an illustration, we focus on Apple shares (AAPL.O). Figure 5 shows our measures of market activity (i.e., volatility $\langle V(\Delta t) \rangle$, number of transactions $\langle N(\Delta t) \rangle$, and transaction volume $\langle \mathit{Vol}(\Delta t) \rangle$ defined in Eqs. (2)-(4)) for Apple stocks before and after ALERTs for ‘AAPL.O’ were released. When $\mathit{Nov}(a_{t}) \ge\langle \mathit{Nov} \rangle$, market activity sharply increases just after an ALERT is released at $\Delta t=0$. In contrast, when $\mathit{Nov}(a_{t}) < \langle \mathit{Nov} \rangle$, the market has already responded to the previous ALERTs and HEADLINEs before the additional current ALERT is released.

Figure 5

Response of AAPL stock to ALERT news with high and low novelty. The solid (dashed) lines represent the level of market activity when the novelty measure is above (below) the average.

The results shown in Figure 5 suggest that there is asymmetry in market activity before and after the arrival of news. To investigate this in more detail, we calculate the cumulative response of transaction volumes after the news by adding up transaction volumes for $0<\Delta t<120$. Similarly, we calculate the cumulative value before the news by adding up transaction volumes for $-120<\Delta t<0$. Finally, we define an index indicating the extent of asymmetry as $S_{\mathrm{after}}/(S_{\mathrm{after}}+S_{\mathrm{before}})$ where $S_{\mathrm{before}}$ and $S_{\mathrm{after}}$ represent the cumulative transaction volumes before and after the news. We conduct the same calculation for the other two market activity indicators. Figure 6 shows the result for AAPL, GM, and YHOO, with the degree of novelty shown on the horizontal axis and the degree of asymmetry shown on the vertical axis. As can be seen, market activity is highly asymmetric for novel news but not so asymmetric when news is not that novel. In fact, the asymmetry index defined above is very close to 0.5 (i.e., no asymmetry before and after the news) for news with $\mathit{Nov}(a_{t})$ greater than one. We obtained similar results for all other firms listed in Table 1.

Figure 6

Asymmetry in market activity before and after the arrival of news for AAPL, GM, and YHOO.

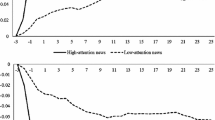
Finally, we turn to the relationship between the topicality of news and the market reaction. As shown in Figure 7(a), for $\mathit{Top}(a_{t,k}) \ge\langle \mathit{Top} \rangle$, the market activity indicators exhibit a significant response to news; however, for $\mathit{Top}(a_{t,k}) < \langle \mathit{Top} \rangle$, they show almost no response to news. Furthermore, Figure 7(b) shows how the magnitude of the market response to news within three minutes of the arrival of news (i.e., $\langle V(\Delta t)|0 \le\Delta t < 3 \rangle$, $\langle N(\Delta t)|0 \le\Delta t < 3 \rangle$, $\langle \mathit{Vol}(\Delta t)|0 \le \Delta t < 3 \rangle$) is related to the degree of news topicality. The figure shows that the market response to a news article is positively related to $\mathit{Top}(a_{t,k})$, indicating a greater market response to news with higher topicality. We found similar relationships between the market response and news topicality for the other firms listed in Table 1 and that the relationship observed in the data can not be reproduced if we use the randomized data.

Figure 7

Relationship between topicality of news and market reaction. (a) Response of GM stock to news with high and low topicality. (b) Relationship between news topicality and market activity three minutes after the news. The solid (dashed) lines in (a) show the level of market activity when the topicality measure is above (below) the average. For IBM, PFE, AAPL, YHOO in (b), the market activity indicator is the average of the three indicators (number of transaction, transaction volume, and price volatility).

Why is the market reaction to news greater if it is more topical? To consider this question, suppose that a news article contains highly valuable information for market participants. In that case, it will be reported simultaneously by many news agencies, and the key words used in the news articles by the different agencies will overlap with each other. In this case, our measure signals very high topicality. The empirical results shown above suggest that it is in such a situation that investors respond actively to such news article. An alternative interpretation is that simultaneous news reports by a number of agencies themselves stimulate market activity. An examination of this causality is beyond the scope of this paper, but our measure of news topicality allows market participants to detect a news article that is likely to have a large impact on market activity, and therefore provides useful information to investors.

Conclusion

In this paper, we examined the stock market response to news items displayed on the RTRS electronic trading platform. We found that whereas stocks responded strongly to news items categorized as ALERTs, they did not respond greatly to news items categorized as HEADLINEs, which make up the majority of news items. These results suggest that we need to measure the importance of news to predict market responses to it. To this end, we proposed two novel indicators to measure the importance of news: an indicator measuring the degree to which a particular news article is novel, and another measuring the degree to which a particular news article is topical. The novelty measure is obtained by comparing a news article with other news articles reported before that article in terms of linguistic similarity. On the other hand, we say a news article is highly topical if it is simultaneously reported by other news agencies. The topicality measure for a news article is obtained by counting the number of news articles which have similar content to the original news article but are delivered by other news agencies.

Using these two new measures, we investigated how market activity (i.e., the number of transactions, the transaction volume, volatility) respond to both novel and topical news. We found that, for a news article with high novelty, market activity sharply increased just after the news article was reported. On the other hand, for a news article with low novelty, we did not find any significant increase in market activity, since the market had already responded to a similar news article reported earlier. We also found that market activity responded more to news with higher topicality.

The contribution of this paper can be summarized as follows. We proposed two new measures to efficiently summarize news articles on individual companies and empirically showed that the two measures are closely correlated with indicators of market activity such as the transaction volume and price volatility. Our methodology is closely related to approaches adopted in previous studies but differs from them in some important respects. First, our novelty measure is closely related to the notion in economics and finance that stock prices are affected by unanticipated news components, but not by anticipated news components. Studies have, for example, examined the impact of the release of government statistics such as the unemployment rate on stock prices. These studies deal with a situation in which the release of statistics is prescheduled and is therefore known to the public; however, the numbers that will be released are not known to the public, although people may have some prior information on them. A similar situation arises when a company makes an earnings announcement. In contrast, the news that we focus on in this paper differ from such anticipated events in that the timing and nature of the events is not known to the public in advance. That is, most important business-related news events are not prescheduled, and our methodology to identify novel news can be applied even to those events. Second, the topicality measure we introduce is based on the simple idea that a news article that receives more attentions from news agencies and market participants should have a larger impact on stock prices and transaction volumes. While this is probably a widely held presumption among market participants, somewhat surprising no serious academic research has been conducted on this. An important exception is [43], which proposes to measure the importance of a news article by counting the number of retweets of a tweet mentioning the article. Our approach differs from this in that we assess the importance of news based on information from news agencies (i.e., how many agencies report it), while their measure is based on information from Twitter users (i.e., how many users retweet it). We believe information coming from news agencies is more reliable and quicker than information based on retweets. However, carefully comparing these two information sources is a task we hope to tackle in the future.

Although the empirical analysis in this paper demonstrates the usefulness of our methodology, there still remain some issues that were not fully addressed here. First, our topicality measure is based on the idea that important news should be reported simultaneously by many news agencies. However, it is possible that different agencies use different terminologies even when they report about the same event. If this is the case, our topicality measure wrongly signals that this event is not that important. To avoid this, we need to pay more careful attention to the relationship among individual words and the sentence structure in defining similarity among news articles. Second, we examined how the measures we introduce are related with the three indicators for stock market activity (price volatility, transaction volume, and the number of transactions). However, as we mentioned in Section 3, the three market activity indicators are closely correlated with each other [46]. The empirical results reported in this paper all show that the three indicators respond in a similar fashion to the news, but it is still possible that each of the three indicators responds differently depending on the characteristics of the news. Third, the empirical analysis of this paper used ALERTs and HEADLINEs. We believe that such news items contain important information from the viewpoint of investors, but they are much shorter than complete news articles. It may be worthwhile to conduct a similar empirical exercise as in this paper using complete news articles such as STORY articles on the RTRS platform. These issues are left for future research.