1 Introduction

The present report focuses on high precision aspects met when studying the hyperfine structure (hfs) of atomic protactinium (Pa i). Our analysis is in continuation of work performed during decades at Laboratoire Aimé Cotton (LAC) by the classification team (see [1] and references therein). Since the late 60s, classification of very complex spectra is making considerable progress at LAC with the development of both Fourier-transform (FT) spectroscopy [2] and theoretical interpretation in the Condon–Slater–Racah formalism for which dedicated codes have been developed [3].

\(^{231}\)Pa\(_{\,91}\) is the only natural isotope of the third element in the group of actinides. It is radioactive with a half-life of \(3.25\times 10^4\) y [4]. It is used as a marker for radiometric dating in recent geological evolution. Its nuclear spin is \(I=3/2\). Due to the relatively large value of the nuclear magnetic dipole moment of this isotope \(\mu _I=2.01\,\mu _N\) [4], many fine structure lines show a noticeable hyperfine splitting. The influence of the nuclear electric quadrupole moment \(Q=-1.72\) barn [4] on the line hyperfine splitting is often relatively small, however, visible in many lines of the FT spectrum.

Due to the low value \(I=3/2\) of the nuclear spin, each line splits up in four main hfs components only, which leads to three hfs intervals. Based on these three experimental values is not possible to determine four hfs constants, i.e. the A and B constants for both levels involved in the transition. Therefore, a new strategy is required: the simultaneous fit of several lines. This is done in the present work. With this method not only the problems are solved but also high precision could be achieved.

The early steps of the classification of the very complex spectrum of Pa are described in references [5, 6]. As only available high resolution experimental reference for Pa, a magnetic resonance study by Marrus et al. [7] provides hfs constants of the atomic ground state of another isotope \(^{233}\)Pa (with same nuclear spin \(I=3/2\) and nuclear moments of similar order of magnitude [4]).

An infrared Fourier-transform (FT) spectrum of Pa was recorded by G.Guelachvili [8] in the early days of FT spectroscopy at LAC. This was an example of short time handling of radioactive material providing a valuable amount of information concerning a very complex spectrum. Small Doppler effect associated with high atomic mass highlights the high resolution achieved in FT spectroscopy. Our hfs study is mainly based on this IR recording, which is rich of transitions between low lying energy levels with a maximum resolution. It is supplemented by some lines from a Pa spectrum in the visible range, which was recorded ten years later J.Vergès [9].

Results on Pa I presented by Blaise et al. [10] focus on the parametric interpretation of fine structure for lower even energy levels. This reference [10] provides historical information on recorded spectra and classification as well as data for 64 even energy levels belonging to the mixed configurations \(f^{2}ds^{2}\) and \(f^{2}d^{2}s\); total hfs splitting of levels is presented relative to an arbitrary origin for the ground level. These quantities do not describe the disposition of energy sublevels but are useful tools for line classification because they obey the combination principle which links wavenumbers and energies.

Later, reporting extensively on classification in their Tables of Actinides [11], Blaise and Wyart gave a list of strong lines of Pa and a description of the energy levels including a term analysis. Complementary archives have been made available by J.Blaise [12] for a continuation of the analysis at LAC.

Up to now published hfs data of Pa i seem limited to relative values of total splitting of levels for \(^{231}\)Pa [10], and to hfs constants A and B for the ground state of \(^{233}\)Pa [7]. Preliminary results, namely values of hfs constants A and B for more than one hundred levels of atomic \(^{231}\)Pa were presented by A.G. in Brussels in 1994 [13].

In the last few years, only a few works have been added that deal with atomic Pa and they all focus on other aspects: In [14] the focus is on the ionization potentials of the lanthanides and actinides and in [15] high lying levels located around the first-ionization potential were investigated by resonance ionization spectroscopy.

Here, the re-analysis of FT hfs data in the IR range [8] is described and the method which makes possible the determination of accessible fine and hyperfine characteristics of levels with the high precision. The interpretation of the hfs spectrum relies on the study of hfs components in sets of many spectral lines fitted together by overdetermined systems of linear equations. Weighted least-squares fits limit the influence of perturbations due to blended components. In a first step a collective analysis of sets of hfs intervals in selected lines provides a determination of hfs constants A and B with a high precision for many levels. As a continuation, the interpretation of hfs wavenumbers includes fine structure energies and shows a need for adjusted small systematic corrections on wavenumbers. Finally an very high level of consistency is obtained in the interpretation over the whole recorded spectrum.

2 Fine and hyperfine structure in lines and levels

Wavenumbers in lines \(\sigma \) are linked to the level energies E of the two levels involved in the transition through the Ritz combination principle:

$$\begin{aligned} \sigma = E^{\textrm{upper}} - E^{\textrm{lower}} \end{aligned}$$
(1)

This applies to both fine structure and hyperfine structure (hfs). For the fine structure, this concerns the centre of gravity of lines and levels, which is obtained by weighting hfs components according to their intensities and sublevels according to multiplicity. For the hfs, it concerns the hyperfine sublevel energies in levels and the wavenumber of the corresponding hfs component.

A fine structure energy level E is characterized by the total electronic angular momentum quantum number J. If an isotope has a nuclear spin quantum number I greater than zero a fine structure energy levels splits into hfs sublevels, caused by higher order interactions of the nuclear moments with the magnetic and electric fields produced by the electrons at the site of the nucleus. The hfs sublevels are characterized by the total angular momentum quantum number F, which can take values from \(|J-I|\) to \((J+I)\). The number of hfs sublevels is equal to the minimum of \((2J+1)\) or \((2I+1)\).

The hfs interactions are much smaller than interactions associated to fine structure. Our study of Pa i relies on the extensive FT description which concerns both scales of fine structure and hfs.

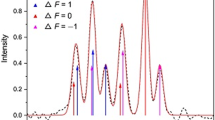
As exemplified in Fig. 1, due to the nuclear spin of \(I=3/2\) hfs patterns of Pa lines contain maximal \(2I +1 = 4\) strong main components.

In the next subsections, the classical elements of atomic theory is shortly described.

Fig. 1
figure 1

Intensity profiles in the Pa FT spectra at around 6 130 cm\(^{-1}\) (excerpt from the 400 m long paper chart where in the original 10 cm represent 2 cm\(^{-1}\)). The superimposed profiles represent recordings with two different excitation conditions

Full size image

2.1 The Casimir formula and hfs constants A and B

As concerns hfs sublevels of a given energy level (with total electronic momentum J), the Casimir formula describes the effects of magnetic dipole and electric quadrupole in the hyperfine structure as follows:

$$\begin{aligned} E_F= & {} \, E_{\textrm{cg}} +\, A\,\frac{K}{2} +\, B\,\frac{3\,K(K+1)\, -4\,I(I+1)J(J+1)}{8\,I(2I-1)J(2J-1)}\nonumber \\{} & {} \textrm{with} \,\, K\,=\,F(F+1)\, -I(I+1)\, -J(J+1) \end{aligned}$$
(2)

\(E_F\) denotes the energy of the hfs sublevel designated with the total quantum number F and \(E_{\textrm{cg}}\) the energy of the centre of gravity. This formula means that the distance of an hyperfine sublevel to the centre of gravity of a fine structure energy level depends on hfs interaction constants associated to each energy level, namely A for the magnetic dipole interaction, and B for the electric quadrupole interaction.

As concerns a transition between two energy levels, wavenumbers differences between hfs components of the line depend on four hfs constants (A and B of the upper and lower fine structure level) and on quantum numbers of sublevels in upper and lower levels. The main hfs components are those with \(\Delta J = \Delta F\). In transitions with \(\Delta J = 0 \), wavenumbers of main components depend only of the differences in A and B constants between upper and lower levels.

2.2 The Landé rule

If the contributions of quadrupole interaction is negligible (as for levels with a relatively small B constant), formula 2 simplifies into the Landé rule

$$\begin{aligned} \Delta W_{F,F-1} =\, E_F - E_{F-1} =\, A \,F \end{aligned}$$
(3)

which says that intervals \(\Delta W\) between hfs sublevels with F and \(F-1\) are proportional to the quantum number F.

When both energy levels in a transition have the same J value (\(\Delta J = 0 \)), wavenumbers of main hfs components obey the Landé rule similarly and intervals decrease linearly with decreasing F values.

In Pa, because of the ratio of the electric quadrupole moment Q to the magnetic dipole moment \(\mu \) both hyperfine effects associated to magnetic dipole and electric quadrupole have to be taken into account. In the FT spectrum this is manifested by obvious deviations from the Landé rule.

2.3 Intensities of lines and hfs components

The relative intensity of a hfs component characterized by the quantum numbers J and F of the upper level and \(J'\) and \(F'\) of the lower level is given by [16]:

$$\begin{aligned} \textrm{Int} = (2F+1)(2F'+1)\,\left\{ \begin{array}{ccc} J &{} I &{} F \\ F' &{} 1 &{} J' \end{array} \right\} ^2 \end{aligned}$$
(4)

The strong components of the hfs pattern correspond to hfs transitions with \(\Delta F = \Delta J\). Almost always a typical decrease in intensities with decreasing F values is observed up or down the wavenumber scale. In these so-called flag patterns, the main components are conveniently numbered in the order of this decrease (first, second, third and fourth main hfs component). Higher J-values correspond to a lower decrease in intensity for the strong components. Therefore, intensity patterns of the four main components give information for approximate J assignment which are useful for line classification. In the present work on Pa, we use the convention where a line is characterized by the wavenumber and intensity of the second main hfs component (see Sect. 2.4).

Fine structure line intensities correspond to similar rules for L, S, J quantum numbers. But due to an intermediate coupling, atomic states are a combination of pure LS basis terms. Therefore, the calculation of intensities may be comprised by a large number of transitions of LS basis states and the intensity scheme is complex. The fine structure intensities also depend on the excitation conditions in the plasma. Furthermore, in the FT recordings comparison is limited to the local scale because the arbitrary intensity scale has not been corrected for sensitivity of detectors in the IR range. Nevertheless the intensities deliver important information on transitions according to transition probabilities and selection rules. However, explicit interpretation of line intensities has not been undertaken.

2.4 Definition of level energy and line wavenumber

When hfs is present, it is a current convention (in particular at LAC) to use as wavenumber of a line (respectively energy of a level) the wavenumber of a hyperfine component (respectively energy of a hyperfine sublevel) close to the centre of gravity. This was meant initially as an approximation for the wavenumber of the centre of gravity of a line. These definitions (implicitly used in the Tables of Actinides [11]) actually allow exact combinations of wavenumbers and energies according to the Ritz combination principle (formula 1), which is valid equally for centres of gravity or for hfs components and energies of sublevels. Numbering line components and sublevels according to decreasing F values, the second main component (i.e. second highest in intensity) and second sublevel with \(F = F_{\textrm{max}} - 1\) are chosen for Pa.

In our analysis, the centre of gravity for levels and lines is calculated after the determination of hfs characteristics of the energy levels and their fine structure energy. Considering that the wavenumber is the difference of the upper and lower level energies for centre of gravity assumes that excitation conditions do not favour some of the sublevels; this seems reasonable here.

In the structure of a level x, according to the Casimir formula (2), the energy of the centre of gravity is linked to that of the sublevel with second largest F value as follows for \(I=3/2\):

$$\begin{aligned} E_{\textrm{cg}} (x) = E_{F_{\textrm{max}}-1} (x) -\, A \,\frac{J-3}{2} -\, B \,\frac{3-2J^2-5J}{4(2J^2-J)} \nonumber \\ \end{aligned}$$
(5)

The difference between \(E_{\textrm{cg}} (x)\) and \(E_{F_{\textrm{max}}-1}(x)\) can be calculated when hfs constants A and B are known. In rough approximation \(E_{\textrm{cg}} (x)\) can be equated with \(E_{F_{\textrm{max}}-1}(x)\).

As concerns the values listed for the level energies in the different conventions, they belong to two different reference systems. In the present paper, level energies in the convention of centres of gravity are marked by an asterisk (\(E^*_{\textrm{cg}}\)) and level energies in the convention of second sublevel are noted without asterisk (\(E_{\textrm{cg}}\)). It should be noted, that both systems differ by a general shift because zero energy of the ground state is either at centre of gravity or at second sublevel in the respective systems, namely:

$$\begin{aligned} E^*_{\textrm{cg}}(0)\,=\,0 \,\,\,\, \textrm{or} \,\,\,\,E_{F_{\textrm{max}}-1}(0)\,=\,0\, \end{aligned}$$
(6)

Therefore the following conversion between both systems is valid:

$$\begin{aligned} E^*_{\textrm{cg}}(x)\, = E_{\textrm{cg}}(x)\,-\,E_{\textrm{cg}}(0) \end{aligned}$$
(7)

The general shift \(-\,E_{\textrm{cg}}(0)\) is according to formula (5):

$$\begin{aligned} -\,E_{\textrm{cg}}(0) = A (0)\,\frac{J(0)-3}{2} +\,B(0) \,\frac{3-2J(0)^2-5J(0)}{4(2J(0)^2-J(0))} \end{aligned}$$

I.e. with \(J(0)=11/2\) for the ground levels:

$$\begin{aligned} -\,E_{\textrm{cg}}(0) = 5/4\,A (0)\, + \,17/44 \,B(0) \end{aligned}$$
(8)

Therefore values in the lists are linked as follows:

$$\begin{aligned} E^*_{\textrm{cg}}(x)\,= & {} \,E_{F_{\textrm{max}}-1}(x)\,+ [\,E_{\textrm{cg}}(x)\,- \,E_{F_{\textrm{max}}-1}(x)\,]\nonumber \\{} & {} -\,[\,E_{\textrm{cg}}(0)\,-\,E_{F_{\textrm{max}}-1}(0)\,] \end{aligned}$$
(9)

involving quantities to be obtained according to formula (5) for both level x and the ground state.

Because of its importance in the definition of the energy reference, the hfs of the ground state has been the object of a special study discussed in Sect. 4.9. The general shift due to the choice of origin of the energy scale has no influence on the calculated wavenumber of the centre of gravity of a line!

3 Experimental basis

Our detailed study of hfs in Pa i is mainly based on an experimental Fourier-transform (FT) spectrum in the infrared (IR) spectral range, namely from 3 100 cm\(^{-1}\) up to 11 900 cm\(^{-1}\). This spectrum is rich of transitions between low lying energy levels with a maximum resolution. It have been recorded in the early 70s at LAC by Guelachvili [8] with a line width around \(20 \times 10^{-3}\) cm\(^{-1}\).

When the study presented here was carried out in the years 2003 to 2010, only a printed list of peak wavenumbers and a printed paper chart of the intensity profile are still available. (Files of calculated spectrum are missing due to lack of storage at that time.) Unfortunately, even this data is no longer accessible. The peak wavenumbers have been calculated with a sophisticated method of peak finding developed at LAC long before 2003. The paper chart of the intensity profile of the IR recording has a length of about 400 m. The resolution is given by the plotting scale: 10 cm in the paper chart represent 2 cm\(^{-1}\). Both the paper copy of the peak wavenumber list and of the intensity profile are annotated by Blaise [12].

In the 80s Vergès [9] recorded a FT spectrum of Pa in the visible range. For this FT recording only the paper copy of the peak wavenumber is preserved; printed intensity profile is absent. The visible FT spectrum is actually less favourable to the study of hfs because of both a larger Doppler effect and the absence of printed intensity profile. However, some lines from FT data in the visible range supplement our study. This is required due to the fact that the ground state, which has a important role as origin of the energies, is poorly linked to other levels in the IR spectrum. Including additional lines from visible FT spectrum improves the precision for data of the ground (see Subsection 4.9).

The light source was an electrode-less tube operated with successively two different excitation conditions. Profiles corresponding to both excitation conditions have been superimposed on the paper charts as illustrated in Fig. 1. Intensity ratios in neighbouring lines are visibly different for different excitation conditions, e.g. comparing lines at 6 126 cm\(^{-1}\) and 6 130 cm\(^{-1}\) equal intensities in the less intense spectrum correspond to different values in the more intense spectrum, with a ratio around two. This effect is linked to the types of transition.

4 Weighted least-squares fits

In our parametric study of transitions, a theoretical linear representation of the wavenumbers of hfs components is fitted to the available experimental wavenumbers using adjustable parameters. Practically, this is inspired from the least-squares fit studies of fine and hyperfine structure in the Condon–Racah–Slater scheme performed at LAC with the devoted chain of codes already mentioned [3].

4.1 Program codes

At LAC, the code GRAMAC (part of the chain of codes [3]) is designated for least-squares fits of overdetermined systems of linear equations. It is particularly suited to use and label large numbers of data and therefore adequate to our study of wavenumbers. It has been complemented as needed in order to use labelled hfs coefficients as input by A. Bachelier-Carlier and J. Sinzelle. Additionally, it has been modified to implement a more variable use of weights and finally the dimensions have been increased [17]. The display of input and output data sorted by transitions allows detailed control of the output and comparison with the experimental material.

4.2 Stages of optimization

The individual steps of the optimization process are described in the following sections. At the same time, Fig. 2 shows the process graphically.

\(\underline{{\textbf {Step 1:}}(A,\,B)}\)

In a first step, only the hfs intervals in line patterns (i.e. the distances of the hfs components within each line) were adjusted, without taking the absolute wavenumbers and energies into account. As origin of hfs intervals, the hfs sublevel with maximum F value of \(F_{\textrm{max}} = I+J\) is chosen, which has two advantages:

  • it gives a simple expression when the Landé rule is valid

  • the first hfs component of a line is more intense and more separated (than the other hfs components), thus more precisely observed.

This approach provides the advantage that initially a limited number of parameters occur, i.e. only the hfs constants A and B are used as adjustable parameters. In this representation, two parameters per level (i.e. A and B) appear in the fit:

$$\begin{aligned} \text {number of parameters} = 2 \times \text {numbers of levels} \end{aligned}$$

No information about absolute position of levels and lines, i.e. about the fine structure, is available in the approach.

Fig. 2
figure 2

Flow chart of the optimization process

Full size image

\(\underline{{\textbf {Step 2:}}(A,\,B,\,R)}\)

In a second step, in order to account for possibly perturbed of first components which could influence all hfs intervals, absolute wavenumbers of hfs components have been used for the fits. For this purpose, a parameter R representing the absolute wavenumber of the hfs first component (with \(F_{\textrm{max}}\)) has been added for each line. Thus, the number of parameters is increased from twice the number levels by the number of lines, i.e.:

$$\begin{aligned} \mathrm{number\,\, of\,\, parameters}= & {} 2 \times \mathrm{numbers\,\, of\,\, levels} \\ {}{} & {} + \mathrm{numbers\,\, of\,\, lines} \end{aligned}$$

In fact, pre-decimal places have been deleted from wavenumbers. This corresponds to the subtraction of the truncated integer of the wavenumbers (in cm\(^{-1}\)). As a consequence, the parameter R is kept as only a quantity which carries information on the same order of magnitude as hfs intervals. This eliminates problems of precision in calculations and saves memory space in the treatment. This cutting off just needs some attention and corresponding corrections in specific cases, when a pre-decimal position switches to the next digit within an hfs interval.

\(\underline{{\textbf {Step 3:}}(A,\,B,\,N)}\)

In a third step, instead of the parameters for absolute wavenumber R of the line, the energy of the sublevel with maximum F value (\(F_{\textrm{max}} = I+J\)) is represented by an adjustable parameter N. Thus, additional to the hfs data, information about fine structure is extracted from the fits. Also here (as in the second stem for the parameter R and for the same reasons) decimal position preceding the decimal point (in cm\(^{-1}\)) is cut, i.e. the parameter N represents the post decimal positions of the absolute hfs wavenumbers. The truncate value (pre-decimal positions) is used as a label for the parameters. In this representation, the number of parameters is:

$$\begin{aligned} \mathrm{number\,\, of\,\, parameters} = 3 \times \mathrm{numbers\,\, of\,\, levels} \end{aligned}$$

The degree of over-determination in the systems of linear equations in step 2 \((A,\,B,\,R)\) and step 3 \((A,\,B,\,N)\) depends on the number of levels and the number of lines, connecting these levels. When few lines are taken into account, the degree of over-determination is higher in the \((A,\,B,\,R)\)-system. In a dense array (which means many lines per level), the degree of over-determination is higher in the \((A,\,B,\,N)\)-system.

\(\underline{{\textbf {Step 4:}}(A,\,B,\,N,\,D)}\)

The extension of the representation \((A,\,B,\,N)\) to wide spectral range revealed new problems: A wavelength-dependent systematic deviation of the wavenumbers was found, which could be solved only by introduction of an addition wavenumber-scale correction parameters D (see Sect. 4.6).

4.3 Hfs parameters and coefficients

Table 1 Examples for the coefficients (\(K_A\), \(K_B\), \(K_N)\) associated to adjustable hfs parameters A, B and fine structure parameter N in the representation level energies (for explanation, see text in Sect. 4.3)
Full size table

In the following, we use a tilde to pointing out when a wavenumber or energy parameter is represented by the post decimal positions only, i.e.:

$$\begin{aligned} \sigma= & {} \mathrm{pre\,\,decimal\,\,positions}(\sigma ) + {\tilde{\sigma }} \nonumber \\ E= & {} \mathrm{pre\,\,decimal\,\,positions}(E) + {\tilde{E}} \end{aligned}$$
(10)

The general formula for any hfs interval or hfs energy is a linear function of A and B. The coefficients \(K_A\) and \(K_B\) have been calculated according to the Casimir formula (2) and depend on the I, J and F values of the energy level. As explained in Sect. 4.2 (Step 3), the calculation was performed relative to the position of the sublevel with \(F_{\textrm{max}}\) (which is labelled N). \(K_A\) and \(K_B\) were therefore calculated as the difference between the Casimir factor for the hfs sublevel i and the Casimir factor for the hfs sublevel \(i=1\) (with \(F=F_{\textrm{max}}\)). Examples of these coefficient values are shown in Table 1 for the J values 7/2 to 11/2. This table gives the complete display of the linear representation used in the computer codes. \(K_N\) is the coefficient for the parameter N, which is the post decimal positions of the absolute hfs wavenumber in cm\(^{-1}\). Any quantity Y listed in the header of the table can be written as a linear function of A, B and N using the listed coefficients:

$$\begin{aligned} Y = K_A \cdot A + K_B \cdot B + K_N \cdot N. \end{aligned}$$
(11)

Hence we find:

$$\begin{aligned} {{\tilde{E}}}_i= & {} K_{A_i} \cdot A + K_{B_i} \cdot B + N\,\,\,\, \textrm{for}\,\,\,i=1\,\,\, \textrm{to}\,\,\, 4 \end{aligned}$$
(12)
$$\begin{aligned} {{\tilde{E}}}_{\textrm{cg}}= & {} K_{A_{\textrm{cg}}} \cdot A + K_{B_{\textrm{cg}}} \cdot B + N \end{aligned}$$
(13)
$$\begin{aligned} W= & {} K_{A_W} \cdot A + K_{B_W} \cdot B \end{aligned}$$
(14)

All values E, W, A, B and N are given in the same unit: \(10^{-3}\) cm\(^{-1}\).

According to the Ritz combination principle (1), the contribution of the lower level is obtained by changing the signs of all coefficients. Hence, a linear equation in the system of \((A,\,B,\,N)\) (corresponding to one hfs component of one fine structure line) is given by:

$$\begin{aligned} \sigma _{\textrm{hfs}} = \Delta E= & {} K_{A_x} A_x + K_{B_x} B_x +N_x \nonumber \\{} & {} - K_{A_y} A_y + K_{B_y} B_y\,-N_y \end{aligned}$$
(15)

The indices x and y refer to the lower and upper level, respectively.

4.4 Sets of transitions

Initially, data have been organized in sets of transitions where a limited number of levels are connected by many resolved lines. This fragmentation of the interpretation of data was due to the need for preliminary exploration and selection, and because of the limited dimensions allowed for fits in the primary version of the program code. Later, using the new version of program code [17] and increased memory space, the data set concerns more than ten thousand wavenumbers, including thousands of fitted data, and almost a thousand of parameters.

For a determination of the characteristics of easily accessible levels, a selection of around 300 resolved lines linking nearly 140 levels has been studied. In this set, the number of good lines describing a level of odd parity varies from one to ten with an average of four. For even parity up to 20 lines accrue per level. This dense core of transitions is representative for the high level of precision available in FT data. The corresponding adjusted values of level characteristics form a basis for the extension of the study.

Fig. 3
figure 3

Dense array of transitions selected for a demonstration of consistency: calculated level energies \(E^*_{\textrm{cg}}\) (in the general convention of centres of gravity) and experimental line wavenumbers \(\sigma _{\mathrm{cg\,exp}}\) (corresponding to \(\Delta E^*_{\textrm{cg}} + D\)) in cm\(^{-1}\); total hyperfine splitting W and \(\Delta W\) in mK\(\,=\,10^{-3}\) cm\(^{-1}\); FT line intensity for the second hfs component

Full size image

As an illustration of the high-level consistency achieved with this set, an extract of the transition array with seven levels of odd and four levels of even parity and corresponding transitions is presented in Fig. 3. It is noticeable that all the 24 transitions allowed by the \(\Delta J\) selection rule are observed in the FT spectra – which is not the case for all 300 levels involved in the array.

In order to extend the description of lines and levels, other sets of selected lines in the IR range have been studied. In addition, we have studied a few transitions to the ground state in the FT spectrum of the visible range recorded by Vergès [9] (see Sect. 4.9).

4.5 Outliers and weights

The major effect of least-squares fits is obtaining parameter values which represent experimental data with limited deviations. This is satisfying when all data are supposedly of similar quality. The process of least-squares fits is not expected to favour small deviations, because of their small influence on the sum of squared deviations. If the degree of over-determination is high adequate, small deviations are due to good data which allow good parameters to represent them. Eliminating outliers as due to perturbations is a way to obtain good parameters. This provides a representation which reflects the quality of recorded unperturbed data. This general method explicitly included in the present study is proved to be efficient.

The whole trick is to recognize the outliers. First fits are usually devoted to detecting any kind of mistakes (mistype, misinterpretation, misidentification, etc.). After eliminating real mistakes, smaller weights have been assigned to data represented with larger deviations. Typical weights assigned are:

  • 5000 for very good main components (\(\Delta F = \Delta J\)) in a well-represented line;

  • 1000 for good component maybe in a line with blend somewhere;

  • 10 or 1 for low confidence or for non-principal components;

  • 1 for unresolved lines.

Detailed control by reading on both paper charts of the intensity profile and lists of wavenumbers is made for all lines with larger deviations from fitted values. By comparing the printed the intensity profile with calculated positions of hfs components or with a simulation of the hfs profiles causes for outliers are searched – and mostly found: After corrections, most of the components considered perturbed (outliers in fits) occur where blends are predicted within the hfs pattern of a line.

Weighting based on deviations is very efficient if the provided equations remain sufficiently overdetermined. This tends to give importance to best data. If a sufficient number of good data are available and good data are predominant, reliable values for adjustable parameter can be achieved. In other cases, data with lower weights just influence the corresponding specific parameters.

Intensities have no role in the assignment of weights. Nevertheless, it was found that well-resolved lines with high intensity form a large part of best data. At both ends of the recorded range, lines recorded with smaller intensities are of similar quality because of a less dense spectrum.

4.6 Wavenumber-scale correction parameters

In an early step of the interpretation of hfs wavenumbers, the exclusion of one line (at 4 618 cm\(^{-1}\)), within a set of 50 lines, dramatically improved the fit of the other lines. Large systematic deviations on all its hfs components (visualized when fitting this line with a weight of 0) evidenced that the interpretation of this line could not be consistent with the system of level energies adjusted in the fit.

Information was lacking concerning the experimental set-up, especially concerning the optimization performed 30 years earlier on the wavenumbers scale. Nevertheless, an attempt was done with a correction of the wavenumbers scale, leading to amazing improvement of the quality of the fit. Parameters for a possible linear correction on wavenumbers are defined by:

$$\begin{aligned} \sigma _{\textrm{corr}} = C_0 + C_1 \times \sigma _{\textrm{exp}} \end{aligned}$$

This seems to explains the problems of consistency of the line 4 618 cm\(^{-1}\) in the system of 50 lines: the line at 4 618 cm\(^{-1}\) (classified as transition from the levels 7585 cm\(^{-1}\) to 2966 cm\(^{-1}\)) completes a circle, formed by a series of transitions starting and ending on the same level:

$$\begin{aligned}{} & {} 2966 \xrightarrow [\textrm{up}]{\sigma _1} 7585 \xrightarrow [\textrm{up}]{\sigma _2} 12777 \xrightarrow [\textrm{up}]{\sigma _3} 18620 \\{} & {} \quad \xrightarrow [\textrm{down}]{\sigma _4} 7000 \xrightarrow [\textrm{up}]{\sigma _5} 10444 \xrightarrow [\textrm{down}]{\sigma _6} 2966 \end{aligned}$$

At this point in the investigation, in this system of 50 lines, this is the unique case, where a multi-transition-change from an level of even parity to an level of odd parity (or opposite) is done by three succession increasing transitions (which means from lower to higher level): \(\sigma _1\), \(\sigma _2\) and \(\sigma _3\). All other changes of parity are build up by series of increasing-decreasing-increasing transitions (which means one transition from lower to higher level, next transition from higher to lower level, and then again from lower to higher level or opposite).

Corrected wavenumbers \(\sigma _{\mathrm{corr,\, n}}\) in the above presented series of the successive transitions appear with plus or minus signs in the balance of energy differences, resulting in:

$$\begin{aligned}{} & {} - \sigma _{\mathrm{corr,\, 1}} - \sigma _{\mathrm{corr,\, 2}} - \sigma _{\mathrm{corr,\, 3}} \\ {}{} & {} \quad + \sigma _{\mathrm{corr,\, 4}} - \sigma _{\mathrm{corr,\, 5}} + \sigma _{\mathrm{corr,\, 6}} = 0 \end{aligned}$$

This has the following consequences for the experimental wavenumbers:

$$\begin{aligned}{} & {} - \sigma _{\mathrm{exp,\, 1}} - \sigma _{\mathrm{exp,\, 2}} - \sigma _{\mathrm{exp,\, 3}} + \sigma _{\mathrm{exp,\, 4}} - \sigma _{\mathrm{exp,\, 5}}\\ {}{} & {} \quad + \sigma _{\mathrm{exp,\, 6}} = 2\cdot C_0 / C_1 \end{aligned}$$

where \(C_1\) is almost 1.

Just by this combination of transition, by chance the shift in wavenumbers becomes noticeable. The experimental wavenumbers of these transitions yields to a shift of around \(C_0 = 10\times 10^{-3}\) cm\(^{-1}\), which should be added to the differences between sublevel energies in order to represent the experimental wavenumbers of hfs components.

This algebraic sum of six terms is of questionable precision but the interpretation has been verified later: when extending the system of transitions by adding less intense transitions, similar effects appear. In the transition array with 1 300 lines, the high precision of our analysis proves that the shift in wavenumbers is not a simple offset but a nonlinear function. Because in least-squares fits of linear equations it is not possible to fit nonlinear functions, a step function with a few adjustable parameters \(D(\sigma )\) was used instead.

Resulting wavenumber corrections fitted as adjusted parameters D are shown in Fig. 4. Error bars shown in the figure are standard deviations resulting from the fit. A parabola is proposed for interpolation of the step function. With this correction, corrected wavenumbers are obtained, which correspond to the energy difference \(\Delta E\) between upper and lower energy levels:

$$\begin{aligned} \Delta E = E_{\textrm{upper}} - E_{\textrm{lower}} = \sigma _{\textrm{corr}} = \sigma _{\textrm{exp}}-D \end{aligned}$$

Actually, a similar problem seems to exist in the visible range recorded later by Vergès [9]. A shift – even larger than in the IR – is found for the hfs components when studied transitions to the ground state in the visible for the determination of A and B values. Observed experimental wavenumbers are smaller than the differences of energies obtained from the IR spectrum with a discrepancy of around \(40\times 10^{-3}\) cm\(^{-1}\).

Fig. 4
figure 4

Parameters D (\(10^{-3}\) cm\(^{-1}\)) for systematic shifts on FT wavenumbers, as adjusted in a weighted fit of experimental wavenumbers \(\sigma _{\textrm{exp}}\). A parabola is proposed for interpolation

Full size image

4.7 Fixed and free parameters; standard deviations

Although empirical, the use of weighted least-squares fits is validated by the unexpected precision and the consistency obtained. As described in Sect. 4.3, parameters for A and B hfs constants have been introduced in a first step together with R parameters assigned to each line The coupling between fine structure and hfs parameters only comes from perturbations in some wavenumbers of first component which perturbs hfs intervals. Such a separate determination of hfs constants has been found to prevent perturbations of the parameters N which represent fine structure energy. This is how A and B parameter values have been determined for 140 levels from the experimental description of around 300 selected lines. These parameters were fixed for the subsequent adjustment of the corresponding N values.

Providing a large number of values is another positive aspect of FT analysis, even if some values have less precision. In order to take advantage of all data and to keep high precision of the initial values, the introduction of data with lower quality and poorer links requires to fix some of these initial parameters. The remaining levels are treated as particular cases, and during the fit of their characteristics parameters of well-described levels are fixed. B constants for some of these seem inaccessible and were fixed to zero.

Standard deviations obtained in a progression of weighted least-squares fits poorly represent the uncertainty, because of weights and fixed values in successive fits. From step to step, values may change. Indeed, some cases are found where determinations differ by more than the sum of standard deviations when comparing different steps of the exploration. Standard deviations may be indicative but the number of good lines or hfs components, respectively, used for determination of a parameter is significant, too.

In a final step, an unweighted fit performed with a large number of transitions assumed to be unperturbed (lines with at least all 4 main components calculated with small deviations) has been performed. The absence weights simplifies the evaluation, but leads to results with a lower precision. The standard deviations calculated in the unweighted fit are a better indicator for the uncertainty of the parameters.

4.8 Identification of small hfs components

Fig. 5
figure 5

Example in the Pa FT spectrum at around 6 700 cm\(^{-1}\). The very intense line at 6 701.5 cm\(^{-1}\) perturbs the profile. In the lower part, classification of the 3 major lines is illustrated by levels characteristics, simulated profiles and sublevel schemes. The transitions are from left to right: \(\sigma =6\,701.5\) cm\(^{-1}\): 16 463 cm\(^{-1}\), \(J=9/2\) to 9 762 cm\(^{-1}\), \(J=9/2\) \(\sigma =6\,702.7\) cm\(^{-1}\): 8 320 cm\(^{-1}\), \(J=3/2\) to 1 618 cm\(^{-1}\), \(J=5/2\) \(\sigma =6\,703.4\) cm\(^{-1}\): 21 085 cm\(^{-1}\), \(J=13/2\) to 14 382 cm\(^{-1}\), \(J=13/2\)

Full size image

In the fitting procedure, we calculate intervals or wavenumbers for all the hfs components, main components and non-principal components (except the smallest ones in \(\Delta J \not = 0\) transitions, i.e. with \(\Delta F = - \Delta J \)). Main components of good lines are calculated in the fits within 0.4 \(\times 10^{-3}\) cm\(^{-1}\) of the listed values used as input. The identification of corresponding smaller components confirms the interpretation. An example is given in Fig. 5, where the hfs of three lines is clearly visible, including smaller components for two lines. For illustrated simulated profiles and sublevel schemes are shown in the lower part of the figure.

Figure 5 also illustrates how two different intensity scaling (printed together) are adequate for either low or high intensity lines.

Wavenumbers of weak hfs components originate from the list of peak wavenumbers or from the printed chart of intensity profile. Peaks are only included in the list of peak wavenumbers if their intensity exceeds a certain value. Other weak components with low intensity could be identified in the printed chart of intensity profile. They are read off with a ruler in relation to neighbouring peaks, which are included in the list of peak. An uncertainty around 2/10 mm in reading the charts corresponds to \(4\times 10^{-3}\) cm\(^{-1}\).

In Fig. 5, perturbations of the profile due to a very intense line at 6 701 cm\(^{-1}\) are visible. For that strong line and for the neighbouring line at 6 702 cm\(^{-1}\), all hfs wavenumbers are well resolved and identified.

4.9 Importance of the ground level

The ground state has a specific role as origin of the energies – as discussed in Sect. 2.4. But in fact it is poorly linked to other levels in the IR spectrum: only two partially resolved lines exist as transitions to the ground level for a determination of its hfs constants A(0) and B(0). In order to get a better precision in this determination, FT data recorded by Vergès [9] in the visible range have been added in the study. There are 13 resolved lines out of which 6 lines were found to be good enough. Unfortunately, information about these lines is no longer available. However, the results of the investigation are still available [18] and results in the following values for the ground state:

$$\begin{aligned}A(0) = 19.78\,(0.02)\cdot 10^{-3}\,\,\textrm{cm}^{-1} \end{aligned}$$

and

$$\begin{aligned}B(0) = -75.7\,(0.5)\cdot 10^{-3}\,\,\textrm{cm}^{-1} \end{aligned}$$

The general shift for changing to the convention of centre of gravity (see formula 8 in Sect. 2.4) is thus described by

$$\begin{aligned} E_{\textrm{cg}}(0) = -54.0\,(0.2)\cdot 10^{-3}\,\,\textrm{cm}^{-1} \end{aligned}$$

We use this value for calculated values \(E^*\) (energies with the convention of centres of gravity).

As concerns the fine structure energy of the ground level, the study of these lines in the visible range shows that wavenumbers are not consistent with the energies obtained from the IR range. Some wavenumber-scale parameters should be introduced, which are of lower precision. Therefore, we prefer a determination of fine structure parameter fully consistent with the more precise wavenumber scale in the IR by use of the only two transitions available in the IR. The first (most intense) component needed for the determination of the \(E_{F_{\textrm{max}}}(0)\) is less perturbed than the other partially resolved components in both lines, but nevertheless the determination is less precise than in other levels of the core.

In order not to fix the hole high precision system on this ‘unreliable’ level and to preserve the degree of consistency accessible in the fits, the even level at 7 000 cm\(^{-1}\) is chosen as an arbitrary reference with a fixed fine structure parameter value N. The value \(N(7\,000)\) was selected in such a way that the ground level is calculated with a zero energy. This yields small standard deviations in the fits which correspond to small uncertainty on all calculated energy values. The uncertainty of the energy difference between the level 7\(\dot{0}\)00 cm\(^{-1}\) and the ground state remains, however, and affects all levels.

4.10 Further classification and new levels

In each of the different steps of the optimization process, there were feedback loops in which further classifications were made and thus further lines were included in the system.

Search for new levels could be done be looking for coincidences in the list of energy differences, calculated by the wavenumber of all unclassified lines added (or subtracted) by the energy of each level. For such a search computer codes are used, taking into account the selection rules for \(\Delta J\). They are supplemented by hfs data. The precision of line wavenumbers and level energies obtained on the large scale was an advantage of FT data which is made accessible by our analysis. Only by the high precision in our characterization of hfs and fine structure energy makes classification possible even with only very few lines.

In Fig. 6, an example is shown, where a new odd level classifies three lines with uncommon patterns, and confirms a new additional even level found similarly by precise coincidences. For the new even energy level at 7 516 cm\(^{-1}\), eight meaningful coincidences for both energy and hfs splitting were found. The spread in energies was \(22~\times 10^{-3}\) cm\(^{-1}\) (5 coincidences within \(8~\times 10^{-3}\) cm\(^{-1}\)). This includes only 2 resolved lines, with a coincidence within \(10^{-3}\) cm\(^{-1}\) for energy and \(3~\times 10^{-3}\) cm\(^{-1}\) for hfs total splitting.

Fig. 6
figure 6

Examples for high precision coincidences involving low J values. Experimental profiles are compared with a simulation with approximate level characteristics adjusted in fits of wavenumbers (contribution of B value assumed negligible in the new levels). Transitions between sublevels are visible on the level schemes

Full size image

In extreme examples, hfs alone is used for classification of a line, as, for example, for the line at 6 702.7 cm\(^{-1}\) presented in Fig. 5. The intensities of non-principal components and decrease in intensities in the flag pattern of this hitherto unclassified line are typical of low J values around 5/2. Trying reasonable hypotheses, the hfs wavenumber intervals of this line have been successfully interpreted together with those of another line involving the even level at 1 618 cm\(^{-1}\) with \(J = 5/2\) assumed as common to both transitions.

It is to be noticed that levels with small J values are particularly beneficial of hfs study in individual lines.

High precision may also suggest some changes in J-values, e.g. J = 5/2 rather than 7/2 seems necessary for the levels at 16 310 and 16 870 which both appear in probable transitions to new levels at 7516 and 8641. The value J = 3/2 seems correct for these new levels, according to hfs patterns in the intensity profile (see Fig. 6). However, some transitions to levels with J =9/2 support J = 7/2 for the level at 16 310. The investigation of the hfs wavenumbers is not decisive because of the small splitting of this plane.

Table 2 List of levels of even parity of Pa I; energy values E in cm\(^{-1}\) and hfs constants A and B resulting from an unweighted fit of peak wavenumbers of 2588 hfs components belonging to 646 spectral lines; new: new level; and f: parameter fixed, not fitted in the equations system presented here. This table is also available as machine-readable ASCII table
Full size table

5 Results

At this point, I would like to point out once again that the calculations presented here were made around 15 to 20 years ago. I described here what we did back then. The investigation was documented at the time – more or less well. I am now not in a position to repeat and further optimize the calculations.

Tables 2 and 3 present lists of levels with even and odd parity, respectively, the results of an unweighted fit including 645 lines as well as 73 levels of even and 176 levels of odd parity. The 645 lines contain a total of 2588 hfs components, resulting in a system of 2588 linear equations. The number of parameters corresponds to three times the numbers of levels, i.e. 747 parameters for N, A and B supplemented by nine wavenumber-scale correction parameters D (see Sect. 4.6). The calculated wavenumbers of the hfs components mostly agree with the observed values within \(10^{-3}\) cm\(^{-1}\).

The centre of gravity energy values \(E_{\textrm{cg}}\) given in this both tables is calculated from the N parameters using the A and B values to calculate the distance of \(E_{\textrm{cg}}\) from the first hfs component. As described in Sect. 4.9, the level 7000 cm\(^{-1}\) is chosen as an arbitrary reference with a fixed fine structure parameter value N. The entire system has been shifted so that the origin is at the centre of gravity of the ground state. The uncertainties \(u_E\) of the energy values given in the tables were calculated as the sum of the standard deviation of the corresponding N parameter of the level and the uncertainty in the determination of the centre of gravity energy of the ground state relative to the level 7000 cm\(^{-1}\).

In addition to the 249 levels involved in this set of lines, 56 further levels are listed in Tables 2 and 3, 27 levels of even parity and 29 levels of odd parity. As these levels have not been adjusted in the equations system presented here, the corresponding E, A and B values in the tables are labelled with f. Six of the levels do not appear in the final list of lines (Table 4, see below). The results of these levels are still available to me, and I have included these levels in the tables nevertheless. These levels are marked with an asterisk.

The levels presented here include 20 new levels, 14 levels of even and six levels of odd parity, which are neither listed in reference [6] nor in [11].

Table 4 provides a list of the Pa I lines from the FT spectrum. The list contains the 645 lines mentioned above (marked by ‘a’), which were used for the calculation presented here. In addition, the list contains 632 other lines that were analysed in earlier steps. Detailed information about the intermediate results is no longer available for these earlier steps, only the overview of the lines with the corresponding intensities still exists. The wavenumbers for these lines are therefore given with one digit less than for the lines marked with ‘a’.

Table 4 contains two columns each for the wavenumber and the energy of levels of odd and even parity. The data relating to the centre of gravity of the line and the levels (\(\sigma _{\textrm{cg}}\), \(E_{\mathrm{o,\,cg}}\), \(E_{\mathrm{e,\,cg}}\)) as well as the data relating to the second strongest hfs component of the line and the sublevel with \(F_{\mathrm{{max}}-1}\) (\(\sigma _{F_{\mathrm{{max}}-1}}\), \(E_{\textrm{o,}\,F_{\mathrm{{max}}-1}}\), \(E_{\textrm{e,}\,F_{\mathrm{{max}}-1}}\)) are listed. Most users are probably primarily interested in the data for the centre of gravity. However, data relating to \(F_{\mathrm{{max}}-1}\) are necessary to demonstrate the high level of precision. The wavenumber data for the centre of gravity were calculated from the fit results, while the wavenumber data for \(F_{\mathrm{{max}}-1}\) originates from the experiment. It should be noted that the experimental wavenumber \(\sigma _{F_{\mathrm{{max-1}}},\,\textrm{FT}}\) listed in Table 4 is shifted be the wavenumber-scale correction parameter D (see Subsection 4.6). The shift is in the order of \(10^{-3}\) cm\(^{-1}\). For the sake of clarity, we have refrained from inserting an additional column with the uncorrected experimental value for the wavenumber in the table.

Table 3 List of levels of odd parity of Pa I; energy values E in cm\(^{-1}\) and hfs constants A and B resulting from an unweighted fit of peak wavenumbers of 2588 hfs components belonging to 646 spectral lines; new: new level; and f: parameter fixed, not fitted in the equations system presented here. This table is also available as machine-readable ASCII table
Full size table

6 Conclusion

Here, I report on a re-analysis, carried out about 20 years ago, of experimental FT data, measured more than 50 years ago. Both colleagues who worked with me at the time have since passed away, much to my regret.

The re-analysis resulted in an extensive description with a high precision and concerns the fine as well as the hyperfine structures in lines and energy levels. In the evaluation reported here, more than 750 parameters are involved in a linear representation of more than 2500 peak wavenumbers of hfs components These includes adjusted hfs constants A and B and fine structure energies of about 250 levels.

High precision in this analysis is due to a strategy of detailed parametric interpretation: best data are selectively used owing to weighted least-squares fits. Well-linked levels provide a secure basis for the expansion of the system. This high precision analysis decouples experimental data of lower or higher quality. In particular, the high quality of the FT wavenumbers for unblended hfs components supports the choice of analysing wavenumbers. Therefore, fits including thousands of hfs components remain reasonable.

Among the many advantages of FT spectroscopy, the quality of the experimental wavenumbers is to make accessible simultaneous in a same record properties which concern hfs in the RF range as well as levels energies in transitions, which are larger by about five orders of magnitude. The high accuracy of the levels data has facilitated the search for new levels.

As mentioned in the foreword, the investigation of this spectrum was like a bottomless pit. However, a continuation of the investigation and further optimization is no longer possible, as I have no access to the measurement data, the printed list of peak wavenumbers and the printed paper chart of the intensity profile. But the results already contain a great deal of information, even in the current ‘degree of maturity’.

Table 4 List of Pa I lines from FT spectra. All values except int. and J are given in cm\(^{-1}\). This table contains 1 277 lines and is available in its entirety as machine readable ASCII table. Only a portion is shown here for guidance regarding its form and content
Full size table