Abstract
The ionising interactions of high-energy particles with molecules have applications in many areas. Despite this, some areas, including positron scattering, lack experimental data due to difficulties in performing experiments. Here, quick and simple methods for computing direct electron and positron impact ionisation cross sections are presented. These calculations, performed using the open-source software RAPID-CS, can provide a complete data set as a first approximation for when experimental, or more detailed computational work is not available. The cross-sectional data set includes the total, partial/fragment-specific, single-differential, average secondary electron energy and stopping power cross sections. The molecules N\(_2\), O\(_2\) and CO were chosen to study due to the availability of positron scattering data. An overall good agreement with experimental and other computational results is presented.
Graphical abstract
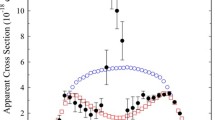
Direct electron (left) and positron right) impact partial ionisation cross sections for N2. Total cross section: red, \(N^{+}_{2}\) partial cross section: blue, N\(^{+}\) partial cross section: green.electron: solid lines: BEB, experimental measurements by Lindsay and Mangan [36]:Ürosses, Straub et al. [37]: stars, Opel et al. [39]: squares. Positron: solid lines: BEB0, Dashed lines: BEBA, Marler and Surko [23]: red crosses, Bluhme et al. [24]: stars
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
High-energy electron and positron interactions with molecules have applications in many areas including in medical settings [1], plasma physics [2], atmospheric science [3, 4] and interstellar chemistry [5]. An important high-energy scattering interaction is direct impact ionisation. In lepton scattering, this is when a molecule is ionised due to a direct impact of a lepton. In electron scattering, this is the only straightforward mechanism that can lead to ionisation. However, for positron scattering positronium formation and annihilation can also lead to ionisation. In this work, the focus is on direct impact ionisation and dissociative ionisation, if the collision energy is sufficiently high.
A popular and frequently used method for computing electron impact ionisation cross section is the Binary-Encounter-Bethe method (BEB) proposed by Kim et al. [6] This is a semiempirical method that has been found to give reliable results for a range of molecules [7]. As the BEB method computes the total ionisation cross section (TICS), various modifications have been proposed which can be used to compute partial, fragmentation-specific, ionisation cross section (PICS) as well. These frequently utilise branching ratios from a mass spectrum at a given energy and generalise them over an energy range [8,9,10,11]. However, all of these methods rely on some experimental data as an input. A method proposed by Huber et al. [12] uses a simple relationship between the formation energy of the fragment and the PICS to get good approximations without the need for experimental input. This method was applied to polyatomic molecules where, after careful selection of the fragment pathways, the method was shown to still produce good first approximations to the branching ratios [10]. This method forms the basis of the work presented here.
Alternative methods to BEB are available including Deutch-Mark [13, 14], Spherical Complex Optical Potential (SCOP) approaches [15] and the Jain-Khare method [16]. All of these methods focus on computing the TICS. However, a modification to the Jain-Khare method (mJK) [17] can be used to compute the PICS directly and then sum them to get the TICS. Difficulty in the mJK method arises from the need to know the dipole oscillator strength. If this is not known experimentally then it can be calculated from photoionisation cross section. However, this still relies on experimental, or computationally reliable, photoionisation cross sections to be known.
Beyond electron scattering, the BEB method has been modified to compute direct positron impact ionisation. This was first done by Fedus and Karwasz [18] who devised the BEB0 and BEBW approaches but various modifications (BEBA and BEBB) were followed by Franz et al. [19]. Here, the PICS method by Huber et al. is combined with the positron scattering BEB0 and BEBA methods to produce positron PICS. The focus on BEB0 and BEBA was chosen as BEB0 seems to work best for polar molecules and BEBA for non-polar [19]. However, investigations with more molecules are needed to confirm this.
More details about the ionisation event can be gained from the single-differential cross section (SDCS) which is a function of the ejected electron energy. Garkoti et al. [20] proposed a method for computing the BEB-SDCS. The SDCS can be used to compute the average secondary electron energy (ASEE) and the stopping cross section (SCS) [1, 20]. The SCS can, for example, be used to probe the extent of potential damage to DNA [1]. Here, partial -SDCS, -ASEE and -SCS are presented for electron and positron scattering. The benefit to this dataset is that the cross sections are quick and easy to compute but also that all the cross sections are computed at the same level. As a result, their accuracy should be comparable and can be used to fill in gaps in databases.
The historical lack of research into positron scattering means that the only measurements for direct positron impact ionisation are for H\(_2\) [21, 22], N\(_2\) [23, 24], O\(_2\) [23], CO [23, 25] and tetrahydrofuran [26]. This is unlikely to change in the coming years due to the difficulty in distinguishing between Ps formation and direct ionisation. [19] The work presented here could be used to infer the Ps formation channel from the measured total cross section. A comprehensive review of all data available for positron scattering has been done by Brunger et al. [27]. In this work, the molecules studied are N\(_2\), O\(_2\) and CO as, aside from the positron cross sections, there is also a reasonable amount of experimental data available for electron scattering.
The remaining paper is outlined as follows: In the next section, there is an explanation of the theory for all of the BEB-based methods used here. This is followed by computational details including a short description of the software implementation that enabled this work. Results for the three molecules studied are then discussed and finally, conclusions are presented.
2 Theory
2.1 Fragment formation energies
The dissociation pathway and associated formation energy due to electron or positron impact ionisation are shown below. This is for an arbitrary diatomic molecule AB and leads to a single ion,
the charged fragment \(A^+\) is produced with the related formation energy \(D_{A^+}\). Here, the formation energy is the dissociation threshold. The ground state energy of species X (where here \(X = A^+\), B or \(AB^+\)) is shown as E(X) and IP is the ionisation potential of the parent species (AB). For direct ionisation with no fragmentation, this pathway would be
The formation energy of this pathway is the ionisation energy of the molecule. Typically, a good approximation is to shift this ionisation energy to match the Koopmans theorem [28] energy. The other formation energies should also be shifted to maintain the dissociation energy thresholds.
2.2 Branching ratios
Using the formation energy, the probability that a fragment will form can be computed using a method outlined by Huber et al. [12]. This method requires only the formation energy as input and results in an un-normalised probability.
Here, \(b_i\) is the un-normalised probability of fragment i forming with the corresponding formation energy \(D_i\). Huber et al. determined \(\beta \) to be approximately 3 for electron scattering. However, here a value of 6 is used for electron scattering and 20 is used for positron scattering. These higher values were used to compensate for the accuracy of the formation energies computed in this work (see below for more details).
To normalise these values, the following conditions are imposed,
where n is the total number of fragments. The parameter \(\Gamma _i\) is the branching ratio of fragment i now dependent on whether the energy, T, of the impacting particle (an electron or positron) meets the criteria: \(T \ge D_i\). At the moment, this energy dependence is only valid at very high energies. This dependency can be made more general for any value of T by using an asymptotic dependency.
The power term \(\gamma \) was determined to be \(1.5 \pm 0.2\) by Janev and Reiter [29]. A value of 1.5 is used in this work.
2.3 Fragmentation selection process
In this section, it is assumed that the scattering particle is an electron but the same process for selecting the fragments is applied for positron scattering.
As the fragment formation pathways used in this work are simple, the fragments which are included must be carefully selected. Note that the focus is on the ionic fragment. For example, ABC is an arbitrary linear triatomic molecule, with the structure of \(A-B-C\), (i.e. A is not bonded to C). All of the possible (single ionisation) pathways are
Here, double ionisation pathways are not included due to their added complexity. Doubly charged ions could undergo a Coulombic explosion which is too complex for the simple theory presented.
The first 8 of these fragmentation pathways require no new bonds to be formed. Instead, one, or two, bonds that were present in the parent molecule break. As a result, these fragmentation pathways can be included in the computations. However, as the last two pathways require the formation of a new bond, \(A-C\), they cannot be included. This is because the dynamics here would be more complex, relying on post-ionisation collisions and/or transition states. This is outside of the scope of the current approximation. Furthermore, if two fragmentation pathways lead to the same charged fragment then only the lowest energy pathway is included. In the above pathways, No.3 and No.6 both produce the \(C^+\) fragment. As the breaking of a single bond typically takes less energy, only pathway No.6 would be included.
From ABC, the included pathways are
In this work, the molecules investigated are diatomic. All of the possible fragments are considered. They include:
2.4 Cross sections
The relationship between a total (\(\sigma _F\)) and its corresponding fragment-specific partial (\(\sigma _i\)) cross sections at a given particle impact energy (T) is
with the relation between the cross sections and the branching ratios being
Several types of cross sections are investigated in this work. They are outlined as follows.
2.4.1 Electron—ionisation
A widely regarded electron impact ionisation cross section method is the Binary–Encounter–Bethe (eBEB) method. [6] The TICS is computed as the sum of the eBEB for each molecular orbital. The orbital eBEB uses three orbital constants and is given as
with,
The constants \(a_0\) is the Bohr radius and R is the Rydberg energy. The orbital constants are the binding energy B, kinetic energy U and occupation number N. Some variations of the eBEB formulation use a fourth orbital constant, \({\mathcal {W}}\) which is the oscillator strength. Here, this constant is assumed to be 1 as a further approximation.
If the scattering electron exceeds the IP of an orbital, a secondary electron could be emitted via an Auger-Meitner process. This is included by doubling the contribution from an orbital if the scattering energy is over double the IP of the orbital [30].
2.4.2 Electron—single differential
Single Differential Cross Sections (SDCS) can be computed within the eBEB formalism as proposed by Garkoti et al. [20]. The method uses the same orbital constants as the eBEB method but also includes the variable \(w = W/B\) where W is the energy of the ejected electron. The SDCS is given as,
Here the SDCS is dependent on both the energy of the scattering electron, given by T, and on the energy of the ejected electron, given by W.
2.4.3 Positron—ionisation
The standard eBEB formula can be modified to compute positron scattering. A simple modification, referred to as BEB0 is presented below [18]
where the parameters t, u and S are the same as in the eBEB formulation. As before, the total cross section is the sum over all molecular orbitals.
Here, the only modification is that the exchange term in eBEB is dropped. An alternative modification, proposed by Franz et al. [19], imposes the threshold law proposed by Jansen et al. [31]. This, referred to as BEBA, is given as,
with,
The constant \(C_a\) is not known directly from the Jansen et al. threshold law and so it is assumed that \(C_a = 1\) [19].
2.4.4 Positron—single differential
In the same way that the eBEB method can be modified to compute positron scattering ionisation cross section, the eBEB-SDCS can be modified to compute SDCS for positron scattering. Within the BEB0 model, the SDCS would be,
where once again, the exchange term has been dropped. Similarly, for BEBA the SDCS can be given as,
2.4.5 Average secondary electron energy
The average secondary electron energy (ASEE) can be computed from the SDCS as [1, 20],
In the case of electron scattering, the ejected electron cannot be distinguished from the scattering electron. As a result, the SDCS is symmetric about \(\frac{T-B}{2}\). Typically, it’s assumed that the faster of the two outgoing electrons is scattering electron. This results in the term a in the upper limit of the integral being 2. [20] However, for positron scattering there is only one outgoing electron and as a result, the integration can be performed with a = 1. [18]
The SDCS used in this work to compute the ASEE uses the eBEB, BEB0 and BEBA models outlined above.
2.4.6 Stopping
The stopping cross section can also be computed from the SDCS as [1],
As was the case for the ASEE, for electron scattering a = 2 and for positron scattering a = 1. This cross section (and the ASEE) is computed for each occupied molecular orbital with the total given as the sum. This is in line with the BEB formalism outlined above.
3 Computational details
All branching ratios and cross sections were computed using the open-source Fortran program RAPID-CS: Relative and Absolute Partial Ionisation and Dissociation Cross Section [32]. This program is designed to be a quick and easy implementation of the theory outlined above. It can be used to provide sets of cross sections as a first approximation. It uses a quantum chemistry driver (either Psi4 [33] or Molpro [34]) to perform the energy calculations required, which can be done in serial or parallel with MPI.
A minimal input would include a molecular geometry, basis set and the level of detail requested for the energy calculations. The program can then generate the allowed fragmentation pathways, formation energies, branching ratios, and cross sections required.
In this work, experimental geometries were taken from CCCBDB [35] and the basis set used throughout was cc-pVDZ. The formation energies of the closed/open shell fragments were computed to a CCSD(T)/RCCSD(T) level and shifted to match Koopmans theorem (as described above). Whereas the orbital constants used in the total cross section were computed at a HF/RHF level. The quantum chemistry calculations were conducted using Molpro [34].
The basis set and level of computational detail were chosen to ensure that the computations would be quick and easy on widely available computers. Better/more accurate formation energies could have been computed using a different setup. However, it has been shown that BEB calculations yield excellent results at HF level using small basis sets for a wide range of molecules [20].
RAPID-CS is designed to run with minimal input but also has several parameters which allow the user more freedom.
4 Results
4.1 Fragment formation energies
The branching ratios are determined as an approximation based on the formation energies. There is, therefore, a need for reasonably good-quality formation energies (\(D_i\)). Presented in Table 1 are the formation energies compared to the appearance energies from various experiments.
Appearance energies are the first energy that a fragment is observed in an experimental measurement. The upper values in the ranges presented in Table 1 are the first measurements that the fragments were present. The lower value is the energy of the previous measurement. This gives a range that the fragment formation energy should be within. As mentioned above, the formation energies computed here were done so using quick and easy methods. Hence, the comparison presented in Table 1 is with experimental formation energies and not with highly accurate values.
The computed formation energies are consistently lower than the experimental appearance energies. Except for N\(_2^+\) which is \(\approx \) 0.8 eV higher than the appearance energy of Lindsay and Mangan [36] but lower than the appearance energy of Straub et al. [37]. The thresholds have been shifted such that the parent ion is equal to the Koopmans [28] ionisation energy. The parent ions are in a much closer agreement with the experiment than the other fragments are.
This could result in the branching ratios for those fragments to be larger than expected. The parameter \(\beta \) in Eq. 2 can be used to compensate for the error in the formation energies. This is the reason that values > 3 are used in this work despite 3 being used in previous works [10, 12]. However, it should be noted that the order of the branching ratio, in terms of magnitude, is solely dependent on the order of the formation energise. It is crucial that this is correct. The branching ratios themselves are approximated, and so the formation energies only have to be approximations.
4.2 Nitrogen molecule
4.2.1 Branching ratios and ionisation cross sections
As the branching ratios and the TICS underpin all of the cross section data presented, they are the crucial factors in determining the accuracy of the results presented. The branching ratios for electron and positron scattering from N\(_2\) are shown in Fig. 1 along with experimental results. The electron scattering (solid lines) shows an underestimation of the parent ion, N\(_2^+\), but an overestimation of the fragment N\(^+\) when compared to the crosses of Lindsay and Mangan [36]. Despite this, the error is approximately 10% showing a good overall agreement. For positron scattering (dashed lines), the results are well within 10% of the stars of Bluhme et al. [24] showing a fantastic agreement. In this case, the parent is slightly overestimated and the fragment, N\(^+\) is slightly underestimated.
Branching ratios (left) and TICS (right) of N\(_2\). For branching ratios, blue data: N\(_2^+\), green: N\(^+\). Solid lines: e\(^-\) work presented here, dashed lines: e\(^+\) work presented here, e\(^-\) experimental measurements by Lindsay and Mangan [36]: crosses, e\(^+\) experimental measurements by Bluhme et al. [24]: stars. For TICS, red data is electron scattering. Solid lines: eBEB, stars: Straub et al. [37], crosses: Lindsay and Mangan [36], squares: Opel et al. [39]. Black data positron scattering, crosses: Marler and Surko [23], stars: Bluhme et al. [24], solid lines: BEB0 and dashed lines: BEBA
Electron (left) and positron (right) PICS for N\(_2\). TICS: red, N\(_2^+\) PICS: blue, N\(^+\) PICS: green. Electron: solid lines: eBEB, measurements by Lindsay and Mangan [36]: crosses, Straub et al. [37]: stars, Opel et al. [39]: squares. Positron: solid lines: BEB0, dashed lines: BEBA, Marler and Surko [23]: red crosses, Bluhme et al. [24]: stars
The electron scattering TICS has a good overall agreement with the experiment. Agreement pre-maxima is better than post-maxima where eBEB overestimates the cross section. Experimental positron scattering results by Marler and Surko [23] and Bluhme et al. [24] are presented. The agreement below the maxima is good with BEBA being slightly better. Above the maxima, both BEB0 and BEBA overestimate the experiment.
Electron scattering PICS are presented in Fig. 2 on the left. Here, the overestimation of the TICS has led to the fragment N\(_2^+\) being very well estimated when compared to the experimental results. The fragment N\(^+\), is not as well described. This is due to both the N\(^+\) branching ratio and the TICS being overestimated. Despite this, the overall shapes, fragment orders and approximate magnitudes are well approximated.
For the positron scattering shown on the right of Fig. 2, both fragments are in reasonably good agreement with the experiment [24]. For N\(_2^+\), the fragment is overestimated above the maxima, as was the TICS. The agreement with the N\(^+\) fragment is very good as well. As a result, the positron scattering results presented here are in better agreement with the experiment than the electron scattering results for N\(_2\).
4.2.2 SDCS, ASEE and stopping cross sections
SDCS are presented in Figs. 3 and 4 for electron and positron scattering respectively. The step-like features are due to the summation over all molecular orbitals. As the ejected electron energy increases, the number of orbitals that the ejected electron could originate from decreases which results in a drop in the cross section. For electron scattering, the eBEB model often overestimates the number of low-energy electrons ejected when compared with measurements by Opel et al. [39]. However, measurements by Ogurtsov [40] agree much better with the eBEB results for the entire energy range. In comparison with mJK results by Pal and Bhatt [41], the results presented here show a better agreement with the experiment. The mJK underestimates the experimental for the low-energy ejected electrons. At higher secondary electron energies, both theories agree with the experiments.
Positron scattering results are presented in Fig. 4. No experimental or other computational work is available. At lower impact energies, the differences between the BEB0 and BEBA results are more important. At high energy, the threshold effect isn’t as important and so the two models give almost identical results.
The ASEE and stopping cross sections for scattering from N\(_2\) are presented in Fig. 5. No experimental or computational data is available here for direct electron or positron ionisation, only computational total positron impact ionisation mass stopping power cross section are available by Gumus et al. [42]. This further emphasises the lack of data in this area.
4.3 Oxygen molecule
4.3.1 Branching ratios and ionisation cross sections
The O\(_2\) branching ratios (left) and the TICS (right) are presented in Fig. 6. Comparison is made with experimental and theoretical results from electron and positron scattering. No experimental positron scattering branching ratios are available, as a result, it is assumed that the positron scattering accuracy is approximately as good as the electron scattering results.
Branching ratios (left) and TICS (right) of O\(_2\). For branching ratios, blue data: O\(_2^+\), green: O\(^+\). Solid lines: work presented here, dashed lines: mJK by Sharma and Sharma [43], experimental measurements by Lindsay and Mangan [36]: crosses. For TICS, red data is electron scattering. Solid lines: eBEB, dashed lines: mJK by Sharma and Sharma [43], stars: Straub et al. [37], crosses: Lindsay and Mangan [36], squares: Opel et al. [39]. Black data: positron scattering, crosses: Marler and Surko [23], solid lines: BEB0 and dashed lines: BEBA
The branching ratios computed here underestimate the parent fragment, O\(_2^+\), and overestimate O\(^+\) when compared to the experiment. Despite this, the results presented are, once again, within \(\approx \) 10 % of the experiment giving a good approximation. Interestingly, the mJK results by Sharma and Sharma [43] give the opposite result with O\(_2^+\) being overestimated and O\(^+\) underestimated.
For the TICSs, the positron scattering results (black) show a good agreement with Marler and Surko [23] with BEB0 having a slightly better agreement than BEBA. For electron scattering, the eBEB results are in a better agreement with Opel et al. [39] than the other experimental results but still give a reasonably good agreement. Particularly in terms of the shape of the curve. A comparison of electron and positron results shows the positron scattering cross section as being larger than the electron results. This is consistent with previous findings [24]. Here, BEB0 and BEBA are larger than eBEB due to the dropped repulsive exchange term.
The partial cross sections are expected to be in good agreement with the experiment as the branching ratios and TICS are in reasonably good agreement. PICS can be seen in Fig. 7.
Electron (left) and positron (right) PICS for O\(_2\). TICS: red, O\(_2^+\) PICS: blue, O\(^+\) PICS: green. Electron: solid lines: eBEB, dashed lines: mJK by Sharma and Sharma [43], measurements by Lindsay and Mangan [36]: crosses, Straub et al. [37]: stars, Opel et al. [39]: squares. Positron: solid lines: BEB0, dashed lines: BEBA, Marler and Surko [23]: red crosses
For electron scattering, the underestimation of the O\(_2^+\) fragment in the branching ratios has been compensated for by the slight overestimation of the total cross section. As a result, the O\(_2^+\) fragment is in reasonably good agreement with the experiment. The O\(^+\) fragment is overestimated. A similar level of agreement is seen between the results presented here and the mJK results. No experimental comparison is available for positron scattering.
4.3.2 SDCS, ASEE and stopping cross sections
SDCS for electron scattering are presented in Fig. 8 at 50, 100, 500 and 2000 eV. The same level of agreement between the eBEB model and the experimental result is seen as was seen for electron scattering N\(_2\). A comparison of the total SDCS with experimental results is made with an overall good agreement seen. In particular in the mid-secondary electron energy range. Also presented are mJK total and partial SDCS [41] which have a smaller magnitude than the eBEB results presented here. At low secondary electron energies, the eBEB SDCS have a slightly better agreement with the experiment than the mJK does. At higher energies, the two theories are in good agreement with the experiment.
No experimental or other computational results have been conducted for positron scattering SDCS. The BEB0 and BEBA results are presented in Fig. 9. As the electron scattering is in good agreement, it is expected that the positron scattering will also be. The differences in threshold description between BEB0 and BEBA can be seen at lower energies (50 eV top left figure), with the BEB0 and BEBA SDCS being virtually identical at 500 and 2000 eV (bottom left and bottom right), hence only BEB0 is presented.
The different threshold effects between BEB0 and BEBA can also be seen clearly in the average energy of the secondary (ejected) electron (ASEE) shown in Fig. 10 (left). The BEB0 (black) more closely follows the eBEB (red) cross section at very low energies. As the impact energy increases and the threshold effects become less important, the BEB0 and BEBA (cyan) curves agree. Higher energies are also where the largest differences are between the electron and positron scattering results. This is in contradiction to the total cross section which shows the electron and positron results converging at high energy. Differences in the ASEE could be due to positron scattering having an attractive electron-positron potential and no repulsive exchange term which allows for more energy to transfer to the ejected electron. This is in contrast to electron scattering which has a repulsive electron–electron potential and includes the exchange interaction.
Branching ratios (left) and TICS (right) of CO. For branching ratios, blue data: CO\(^+\), green: C\(^+\), purple: O\(^+\). Solid lines: electron scattering work presented here, dashed lines: positron scattering work presented here, experimental electron measurements by Mangan et al. [38]: crosses, positron measurements by Bluhme et al. [25]: stars. For TICS, red data is electron scattering. Solid lines: eBEB, stars: Tian and Vidal [45], crosses: Mangan et al. [38]. Black data: positron scattering, crosses: Marler and Surko [23], stars: Bluhme et al. [25], solid lines: BEB0 and dashed lines: BEBA
Electron (left) and positron (right) PICS for N\(_2\). TICS: red, N\(_2^+\) PICS: blue, N\(^+\) PICS: green. Electron: solid lines: eBEB, measurements by Mangan [38]: crosses, Tian and Vidal [45]: stars. Positron: solid lines: BEB0, dashed lines: BEBA, Marler and Surko [23]: red crosses, Bluhme et al. [25]: stars
Electron scattering stopping cross sections are shown in Fig. 10 (right). For positron scattering, BEB0 and BEBA gave very similar results and so only BEB0 is presented in Fig. 10. No experimental or computational results are available for comparison. Mass stopping cross sections, i.e. the average energy loss by the particle per unit length divided by the density, is available [42, 44] but was not computed as a part of this work.
In comparison with N\(_2\), the same trends and curve shapes are seen. This is with the expectation of the small structure in the O\(_2\) ASEE cross section seen at around 20 eV. For N\(_2\), there is a small defect but all three cross sections (eBEB, BEB0 and BEBA) are in closer agreement at low energies. The threshold effect implemented in BEBA must have a smaller effect for N\(_2\) than here.
4.4 Carbon monoxide
4.4.1 Branching ratios and ionisation cross sections
The final molecule to be studied is CO. Here, there are three fragments: CO\(^+\), C\(^+\) and O\(^+\) and the molecule is polar. The branching ratios and TICS are presented in Fig. 11. As the branching ratios sum to unity, they are dependent on each other. As a result, the large overestimation of the electron scattering C\(^+\) ratio when compared to experiments by Mangan et al. [38], leads to an underestimation of CO\(^+\). The results for O\(^+\) are the closest to the experiment. For positron scattering however, the fragments CO\(^+\) is in good agreement with the experiment by Bluhme et al. [25]. The slight overestimation of the C\(^+\) fragment leads to an underestimation of O\(^+\). As the latter fragment is experimentally very small, the underestimation results in the branching ratio computed here to be almost 0.
The electron scattering TICS is in reasonably good agreement with the experiments of Mangan et al. [38] and Tian and Vidal [45]. The agreement becomes slightly worse above the maxima as was the case for N\(_2\) and O\(_2\). The positron scattering results also show a good agreement with the experiments, performed by Marler and Surko [23] and Bluhme et al. [25]. Here, BEB0 is in slightly better agreement.
The PICS shown in Fig. 12 reflect what’s seen in the branching ratios. The worst agreement for electron scattering is C\(^+\) which overestimates the experiments [38, 45]. Leading to an underestimation of the parent CO\(^+\) fragment. Finally, the O\(^+\) is in the best agreement. Despite this, the order of the fragments has been replicated. For positron scattering, the C\(^+\) is overestimated and O\(^+\) is underestimated. Here, the parent CO\(^+\) is best described with an underestimation at only the peak of the cross section.
4.4.2 SDCS, ASEE, stopping cross sections
Very little experimental data is available here for both electron and positron scattering. There are measurements by Opel et al. [39] for the electron SDCSs at 500 eV and by Ogurtsov [40] at 100 and 500 eV. The SDCS are presented for electron scattering in Fig. 13 and for positron scattering in Fig. 14. A good agreement is seen between the experiment of Opel et al. [39] and Ogurtsov [40] 100 and 500 eV. The remaining energies have the same trends and curve shapes for both electron and positron scattering as seen for N\(_2\) and O\(_2\).
As with the SDCS, the same curve shape and trends seen for N\(_2\) and O\(_2\) are seen for the ASEE and SCS in Fig. 15. The threshold behaviour seen in O\(_2\) is seen here again in the positron scattering ASEE.
5 Conclusion
The work presented emphasises the lack of experimental and computational results in this area. Even for simple, small molecules. To help fill this gap, a series of BEB-based methods were presented for computing electron and positron TICS, PICS, SDCS, ASEE and SCS. These methods are simple, quick, require no experimental input, and have no fitting parameters that need to be tuned for each molecule. The value \(\beta \) in Eq. 2 can be used to optimise results, particularly when the formation energies are known to be poorly described. The computational implementation of this work is the open-source code RAPID-CS.
The three diatomics investigated, N\(_2\), O\(_2\) and CO were chosen due to the available positron scattering experimental results. Despite the small basis set used, a good agreement was seen for electron scattering when compared to various experiments and for positron scattering when a comparison was possible. These methods proved to be useful for giving first approximations when no other data is available. Their accuracy and quality are reflected in the simple theory they are based.
There are limitations to the methods presented here, specifically in the computation of the branching ratios. The various total cross sections can be extended to compute larger systems. However, as the size of the molecule increases, the number of fragmentation pathways will increase. The fragmentation selection process will lead to some pathways being ignored regardless of their importance. This in turn will limit the accuracy of the branching ratios and, by extension, the partial cross sections produced.
Data Availibility Statement
The manuscript has associated data in a data repository. [Authors’ comment: Data corresponding to the calculations presented here, along with parameters used in the BEB calculations, are openly available at (https://doi.org/10.21954/ou.rd.24961971.v2).]
References
E. Surdutovich, O.I. Obolensky, E. Scifoni, I. Pshenichnov, I. Mishustin, A.V. Solov’yov, W. Greiner, Ion-induced electron production in tissue-like media and DNA damage mechanisms. Eur. Phys. J. D 51(1), 63–71 (2009). https://doi.org/10.1140/epjd/e2008-00207-y
H. Kim, J. Lim, M. Kim, H. Oh, D. Ko, G. Kim, W. Shin, J. Park, Investigation of oxide layer removal mechanism using reactive gases. Microelectron. Eng. 135, 17–22 (2015). https://doi.org/10.1016/j.mee.2015.02.025
R.K. Asundi, J.D. Craggs, Electron capture and ionization phenomena in SF6and C7F14. Proc. Phys. Soc. 83(4), 611–618 (1964). https://doi.org/10.1088/0370-1328/83/4/314
M. Shih, W.J. Lee, C.H. Tsai, P.J. Tsai, C.Y. Chen, Decomposition of SF6 in an RF plasma environment. J. Air Waste Manag. Assoc. 52(11), 1274–1280 (2002). https://doi.org/10.1080/10473289.2002.10470864
J.C. Higdon, R.E. Lingenfelter, R.E. Rothschild, The galactic positron annihilation radiation and the propagation of positrons in the interstellar medium. Astrophys. J. 698(1), 350 (2009). https://doi.org/10.1088/0004-637X/698/1/350
Y.K. Kim, W. Hwang, N.M. Weinberger, M.A. Ali, M.E. Rudd, Electron-impact ionization cross sections of atmospheric molecules. J. Chem. Phys. 106(3), 1026–1033 (1997). https://doi.org/10.1063/1.473186
H. Tanaka, M. Brunger, L. Campbell, H. Kato, M. Hoshino, A. Rau, Scaled plane-wave Born cross sections for atoms and molecules. Reviews of Modern Physics 88(2), 025004 (2016). https://doi.org/10.1103/RevModPhys.88.025004
J.R. Hamilton, J. Tennyson, S. Huang, M.J. Kushner, Calculated cross sections for electron collisions with NF3, NF2 and NF with applications to remote plasma sources. Plasma Sources Sci. Technol. 26(6), 065010 (2017). https://doi.org/10.1088/1361-6595/aa6bdf
M. Luthra, K. Goswami, A.K. Arora, A. Bharadvaja, K.L. Baluja, Mass spectrometry-based approach to compute electron-impact partial ionization cross-sections of methane, water and nitromethane from threshold to 5 keV. Atoms 10(3), 74 (2022). https://doi.org/10.3390/atoms10030074
V. Graves, B. Cooper, J. Tennyson, Calculated electron impact ionisation fragmentation patterns. J. Phys. B Atom. Mol. Opt. Phys. 54(23), 235203 (2022). https://doi.org/10.1088/1361-6455/ac42db
R. Snoeckx, J. Tennyson, M.S. Cha, Theoretical cross sections for electron collisions relevant for ammonia discharges part 1: NH3, NH2, and NH. Plasma Sources Sci. Technol. 32(11), 115020 (2023). https://doi.org/10.1088/1361-6595/ad0d07
S. Huber, A. Mauracher, D. Suß, I. Sukuba, J. Urban, D. Borodin, M. Probst, Total and partial electron impact ionization cross sections of fusion-relevant diatomic molecules. J. Chem. Phys. 150(2), 024306 (2019). https://doi.org/10.1063/1.5063767
H. Deutsch, K. Becker, R. Basner, M. Schmidt, T.D. Mark, Application of the modified additivity rule to the calculation of electron-impact ionization cross sections of complex molecules. J. Phys. Chem. A 102(45), 8819–8826 (1998). https://doi.org/10.1021/jp9827577
H. Deutsch, K. Becker, S. Matt, T.D. Mark, Theoretical determination of absolute electron-impact ionization cross sections of molecules. Int. J. Mass Spectrom. 197(1), 37–69 (2000). https://doi.org/10.1016/S1387-3806(99)00257-2
K.N. Joshipura, B.K. Antony, Total (including ionization) cross sections of electron impact on ground state and metastable Ne atoms. Phys. Lett. A 289(6), 323–328 (2001). https://doi.org/10.1016/S0375-9601(01)00636-3
D.K. Jain, S.P. Khare, Ionizing collisions of electrons with CO\(_{2}\), CO, H\(_{2}\)O, CH\(_{4}\) and NH\(_{3}\). J. Phys. B At. Mol. Phys. 9(8), 1429 (1976). https://doi.org/10.1088/0022-3700/9/8/023
S.P. Khare, W.J. Meath, Cross sections for the direct and dissociative ionisation of NH\(_{3}\), H\(_{2}\)O and H\(_{2}\)S by electron impact. J. Phys. B At. Mol. Phys. 20(9), 2101 (1987). https://doi.org/10.1088/0022-3700/20/9/021
K. Fedus, G.P. Karwasz, Binary-encounter dipole model for positron-impact direct ionization. Phys. Rev. A 100(6), 062702 (2019). https://doi.org/10.1103/PhysRevA.100.062702
M. Franz, K. Wiciak-Pawlowska, J. Franz, Binary-encounter model for direct ionization of molecules by positron-impact. Atoms 9(4), 99 (2021). https://doi.org/10.3390/atoms9040099
P. Garkoti, M. Luthra, K. Goswami, A. Bharadvaja, K.L. Baluja, The binary-encounter-Bethe model for computation of singly differential cross sections due to electron-impact ionization. Atoms 10(2), 60 (2022). https://doi.org/10.3390/atoms10020060
D. Fromme, G. Kruse, W. Raith, G. Sinapius, Ionisation of molecular hydrogen by positrons. J. Phys. B At. Mol. Opt. Phys. 21(10), L261 (1988). https://doi.org/10.1088/0953-4075/21/10/005
J. Moxom, G. Laricchia, M. Charlton, Ionization of He, Ar and H2 by position impact at intermediate energies. J. Phys. B At. Mol. Opt. Phys. 28(7), 1331 (1995). https://doi.org/10.1088/0953-4075/28/7/024
J.P. Marler, C.M. Surko, Positron-impact ionization, positronium formation, and electronic excitation cross sections for diatomic molecules. Phys. Rev. A 72(6), 062713 (2005). https://doi.org/10.1103/PhysRevA.72.062713
H. Bluhme, N.P. Frandsen, F.M. Jacobsen, H. Knudsen, J. Merrison, K. Paludan, M.R. Poulsen, Non-dissociative and dissociative ionization of nitrogen molecules by positron impact. J. Phys. B At. Mol. Opt. Phys. 31(20), 4631 (1998). https://doi.org/10.1088/0953-4075/31/20/020
H. Bluhme, N.P. Frandsen, F.M. Jacobsen, H. Knudsen, J.P. Merrison, R. Mitchell, K. Paludan, M.R. Poulsen, Non-dissociative and dissociative ionization of CO, CO\(_{2}\) and CH\(_{4}\) by positron impact. J. Phys. B At. Mol. Opt. Phys. 32(24), 5825 (1999). https://doi.org/10.1088/0953-4075/32/24/316
L. Chiari, E. Anderson, W. Tattersall, J.R. Machacek, P. Palihawadana, C. Makochekanwa, J.P. Sullivan, G. Garcia, F. Blanco, R.P. McEachran, M.J. Brunger, S.J. Buckman, Total, elastic, and inelastic cross sections for positron and electron collisions with tetrahydrofuran. J. Chem. Phys. 138(7), 074301 (2013). https://doi.org/10.1063/1.4789584
M.J. Brunger, S.J. Buckman, K. Ratnavelu, Positron scattering from molecules: an experimental cross section compilation for positron transport studies and benchmarking theory. J. Phys. Chem. Ref. Data 46(2), 023102 (2017). https://doi.org/10.1063/1.4982827
T. Koopmans, Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den Einzelnen Elektronen Eines Atoms. Physica 1(1), 104–113 (1934). https://doi.org/10.1016/S0031-8914(34)90011-2
R.K. Janev, D. Reiter, Collision processes of C2,3Hy and C2,3Hy+ hydrocarbons with electrons and protons. Phys. Plasmas 11(2), 780–829 (2004). https://doi.org/10.1063/1.1630794
V. Graves, B. Cooper, J. Tennyson, The efficient calculation of electron impact ionization cross sections with effective core potentials. J. Chem. Phys. 154(11), 114104 (2021). https://doi.org/10.1063/5.0039465
K. Jansen, S.J. Ward, J. Shertzer, J.H. Macek, Absolute cross section for positron-impact ionization of hydrogen near threshold. Phys. Rev. A 79(2), 022704 (2009). https://doi.org/10.1103/PhysRevA.79.022704
V. Graves. RAPID-CS (2023). https://gitlab.com/vhgraves/RAPID-CS
D.G.A. Smith, L.A. Burns, A.C. Simmonett, R.M. Parrish, M.C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio, A. Alenaizan, A.M. James, S. Lehtola, J.P. Misiewicz, M. Scheurer, R.A. Shaw, J.B. Schriber, Y. Xie, Z.L. Glick, D.A. Sirianni, J.S. O’Brien, J.M. Waldrop, A. Kumar, E.G. Hohenstein, B.P. Pritchard, B.R. Brooks, H.F. Schaefer, III, A.Y. Sokolov, K. Patkowski, A.E. DePrince, III, U. Bozkaya, R.A. King, F.A. Evangelista, J.M. Turney, T.D. Crawford, C.D. Sherrill, PSI4 1.4: Open-source software for high-throughput quantum chemistry. The Journal of Chemical Physics 152(18), 184108 (2020). https://doi.org/10.1063/5.0006002
H. Werner, P.J. Knowles, G. Knizia, F.R. Manby, M. Schutz, Molpro: a general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2(2), 242–253 (2012). https://doi.org/10.1002/wcms.82
R.D. Johnson. Computational Chemistry Comparison and Benchmark Database, NIST Standard Reference Database 101 (2023). https://doi.org/10.18434/T47C7Z. http://cccbdb.nist.gov/
B.G. Lindsay, M.A. Mangan. Interactions of Photons and Electrons with Molecules \(\cdot \) 5.1 Ionization: Datasheet from Landolt-Börnstein - Group I Elementary Particles, Nuclei and Atoms \(\cdot \) Volume 17C: “Interactions of Photons and Electrons with Molecules” in SpringerMaterials . https://doi.org/10.1007/10874891_2
H.C. Straub, P. Renault, B.G. Lindsay, K.A. Smith, R.F. Stebbings, Absolute partial cross sections for electron-impact ionization of H\(_{2}\), N\(_{2}\), and O\(_{2}\) from threshold to 1000 eV. Phys. Rev. A 54(3), 2146–2153 (1996). https://doi.org/10.1103/PhysRevA.54.2146
M.A. Mangan, B.G. Lindsay, R.F. Stebbings, Absolute partial cross sections for electron-impact ionization of CO from threshold to 1000 eV. J. Phys. B At. Mol. Opt. Phys. 33(17), 3225 (2000). https://doi.org/10.1088/0953-4075/33/17/305
C.B. Opal, E.C. Beaty, W.K. Peterson, Tables of secondary-electron-production cross sections. Atom. Data Nucl. Data Tables 4, 209–253 (1972). https://doi.org/10.1016/S0092-640X(72)80004-4
G.N. Ogurtsov, Differential cross sections for ionization of atmospheric gases by electron impact. J. Phys. B. At. Mol. Opt. Phys. 31(8), 1805 (1998). https://doi.org/10.1088/0953-4075/31/8/029
S. Pal, J. Kumar, P. Bhatt, Electron impact ionization cross-sections for the N\(_{2}\) and O\(_{2}\) molecules. J. Electron Spectrosc. Relat. Phenomena 129(1), 35–41 (2003). https://doi.org/10.1016/S0368-2048(03)00033-1
H. Gumus, T. Namdar, A. Bentabet, Positron stopping power in some biological compounds for intermediate energies with generalized oscillator strength model. Int. J. Mol. Biol. Open Access (2018). https://doi.org/10.15406/ijmboa.2018.03.00057
R. Sharma, S. Sharma, Direct and dissociative ionization cross section of oxygen molecule from threshold to 10 KeV. Int. J. Eng. Adv. Technol. (IJEAT) 8(6s3), 1365–1368 (2019)
A. Williart, P.A. Kendall, F. Blanco, P. Tegeder, G. Garcia, N.J. Mason, Inelastic scattering and stopping power for electrons in O2 and O3 at intermediate and high energies, 0.3–5 keV. Chem. Phys. Lett. 375(1), 39–44 (2003). https://doi.org/10.1016/S0009-2614(03)00801-7
C. Tian, C.R. Vidal, Cross sections of the electron impact dissociative ionization of CO, and. J. Phys. B At. Mol. Opt. Phys. 31(4), 895 (1998). https://doi.org/10.1088/0953-4075/31/4/031
Acknowledgements
V.Graves would like to acknowledge support from the EPSRC Doctoral Training Partnership EP/T518165/1. A special thanks to Professor Jimena Gorfinkiel for their help and advice in the writing and submission process.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Graves, V. BEB-based models for ionisation cross sections of electron and positron impact with diatomic molecules. Eur. Phys. J. D 78, 56 (2024). https://doi.org/10.1140/epjd/s10053-024-00852-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-024-00852-4