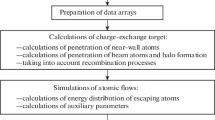
Abstract
In the present work, we describe a new method, dressed cross-section model (DCSM), enabling implementation of large number of atomic transitions (~106 and more) in the kinetic simulations. The effective collision cross-sections derived from the DCSM show expected asymptotic behaviour: (i) For low plasma density, they reduce to the conventional cross-sections for single-step transitions from the ground state; (ii) the Maxwell-averaged rate coefficients are equal to the corresponding rate coefficients obtained from the Collisional-Radiative Model. We describe implementation of ionization and recombination DCSM into the PIC MC code BIT1 and present new results for tokamak plasma edge modelling.
Graphical abstract
Realistic simulations of the plasma edge require precise treatment of plasma–impurity and plasma–neutral particle interactions. Full fluid, or fluid plasma—kinetic neutral models employ effective collision rates derived from the Collisional-Radiative Models (CRM) precalculated by different atomic data providers (e.g. see Summers and O’Mullane (AIP Conf. Proc. 1344:179, 2011)). These CRM incorporate large number of atomic states (103 and more) and corresponding transitions (~106), but assume Maxwellian energy distribution functions (EDF) for colliding particles. In order to describe processes in a non-Maxwellian plasma, kinetic models are applied. Such models operate with collision cross-sections and due to limited computing power of present-day computing facilities can simulate just a few dozens of interaction channels, see Tskhakaya (Plasma Phys Contr Fusion 59:114001, 2017), Mijin et al. (Comput Phys Commun 258:107600, 2021) and references there.

The DCSM consists of two steps: calculation of averaged cross-sections for excitation collisions from the ground state and introduction of effective cross-sections based on CRM rate coefficients. The effective cross-sections derived from the DCSM show expected asymptotic behaviour: i. For low plasma density, they reduce to the direct transition cross-sections from the ground state; and ii. the Maxwell-averaged rate coefficients obtained from the DCSM are equal the corresponding CRM rate coefficients.
We demonstrate application of the DCSM in simulations of the tokamak scrape-off layer
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Realistic modelling of the plasma edge requires precise treatment of plasma–impurity and plasma–neutral particle interactions. The fluid plasma models employ effective collision rate coefficients derived from the Collisional-Radiative Models (CRM) precalculated by different atomic data providers (e.g. see [1]). These CRM incorporate a large number of atomic states (~103) and the corresponding transitions (~106), but assume Maxwellian velocity distribution functions (VDF) for colliding particles. In order to describe processes in a non-Maxwellian plasma, kinetic models have to be applied. Such models operate with collision cross-sections and due to limited computing power of present-day computing facilities could simulate only up to few hundreds of interaction channels (see [2, 3] and references there). In the present work, we introduce a new model of the collision operator Dressed Cross-Section Model (DCSM) enabling effective treatment of a large number of atomic transitions in kinetic modelling of the plasma edge.
2 Description of DCSM
In a low-density plasma edge, atomic collision is relatively rare and the excited states of particles de-excite spontaneously before suffering new collisions. Therefore, particles are mostly in a ground state, and the transitions from this ground state A to some final state C happen during a single collision event. This represents a so-called coronal approximation. Starting from the first kinetic models of the plasma edge [4, 5] up to resent [2, 6], the absolute majority of plasma edge kinetic codes treat atomic and molecular processes within the coronal approximation. With increasing plasma density, the coronal approximation is not valid any more as the particles in excited states can collide multiple times. As a result, the effective rate of the transition from the state A into the state C can increase significantly. One of such examples represents a multi-step ionization process of atoms:
when the first collision excites the atom from the ground state and the second ionizes it.
The effective rate coefficients of e + H ionization collision as a function of electron density and temperature are plotted in Fig. 1, indicating importance of multi-step processes in a high-density plasmas. Figure 2 shows electron density and temperature profiles along the magnetic field in a so-called divertor plasma of different tokamaks. Figures 1 and 2 indicate the importance of multi-step processes in the divertor plasma of large fusion devices, such as JET and ITER (see also [10]) and to be implemented into the kinetic plasma edge models.
Normalized rate coefficients for e + H ionization collisions derived from the ADAS database [1]
One of such examples represents a recently developed kinetic plasma edge code SOL-KiT [3]. SOL-KiT follows 30 excited states of hydrogen atoms and incorporates different transition processes between these states. The number of important excited stated increases drastically when one considers impurity particles, N, Ne, Ar. C, W, etc. As an example, Table 1 shows numbers of the excited states of Ne atoms and ions, up to the 4th ionized state, and of the corresponding transition channels treated in ADAS [1].
For the computing power, available at present day, it is impossible to follow such a large number of particle species (> 103) and treat the corresponding atomic collisions. Moreover, complete sets of collision cross-sections for all these transitions are hard to access.
One possibility is to introduce state bundles and reduce the number of simulated particle species as it is done for different ionized states of high nuclear charge impurities (e.g. see [11]). But the number of excited states of particles exceeds the number of possible ionized states by order(s) of magnitude and a proper choice of the bundled states becomes extremely difficult. Therefore, other approach, different from the conventional bundling, has to be introduced.
In our previous work, we made the first attempt to develop a new collision model allowing the treatment of multi-step atomic transitions [12]. In the present work, we generalize this method and call it DCSM.
The main idea of the DCSM is simple: we consider a transition of particles A and B in their ground states to some new states
where “\(\Rightarrow\)” denotes all possible channels of this transition. The corresponding total rate coefficient \(R\left( {n_{A} ,T_{A} ,\gamma } \right)\) depends in general on the projectile particle temperature, TA, density, nA and a set of some additional parameters, γ. We introduce a dressed cross-section as
where E is the relative energy of the colliding particles, \(\sigma \left( E \right)\) is the cross-section of the single-step transition corresponding to the collision (2) and \(R_{0} = \left\langle {\sigma V} \right\rangle\) is the rate coefficient averaged over the distribution function of projectile particles. It is easy to check that the dressed cross-section has the following features:
-
1.
It accounts for multi-step transition processes;
-
2.
in a low-density plasma limit, it reduces to a single-step transition cross-section
$$ \sigma_{{{\text{DCS}}}} \left( {E,T,n \to 0} \right) = \sigma \left( E \right); $$(4) -
3.
the rate coefficient obtained by integration of the dressed cross-section corresponds to the total rate coefficient of the transition (2):
$$ \left\langle {\sigma_{{{\text{DCS}}}} \left( {E,n,T} \right)V} \right\rangle = R\left( {n,T} \right), $$(5)here (and below) for simplicity, we omitted sub-indexes and γ, and used the equality
$$ R\left( {n = 0,T} \right) = R_{0} \left( T \right). $$(6)
The DCSM assumes that target particles are in a ground state, and the transitions between these states are described by the dressed cross-sections (3). The projectile particle velocity distribution function (VDF) in general can be arbitrary. In reality, the available collision rate coefficients, \(R\left( {n,T,\gamma } \right)\), are obtained from the CRM assuming that the VDF are Maxwellians. Therefore, the DCSM is valid when the projectile particle VDF does not deviate from the Maxwellian significantly. The estimation of the possible error for the non-Maxwellian VDF requires full kinetic treatment of the exited states and out of the scope of this work. We just note that in two limited cases, for low density, when R ~R0, and very high-density plasmas, when electron Coulomb collision mean free path < < characteristic gradient scales, the error reduces to zero.
Another effect, not accounted by the ionization DCSM, is the cooling of electrons with sub-ionization-threshold energy, which does not contribute to the ionization in this model.
Below we consider the DCSM for electron impact ionization and recombination processes.
3 Electron impact ionization DCSM
The transition corresponds to the following process:
We distinguish a multi-step and a direct (i.e. single-step) ionizations events. The schematic of the DCSM is given in Fig. 3. Any multi-step ionization is initiated by an excitation collision; therefore, the colliding particle pairs are analysed first for the excitation collisions. If the excitation collision takes place, then the colliding particle pare is analysed for the probability of multi-step ionization. If this condition is satisfied, then the multi-step ionization takes place; otherwise, the excitation collision takes place. If the condition for excitation collision is not satisfied, then the colliding particle papers are analysed for the direct ionization event and so on. In order to exclude double accounting of the direct ionization events, the expression for dressed cross-section (3) has to be substituted by
where the index “i” corresponds to ionization event.
The scheme of the multi-step ionization collision event itself is similar to the direct ionization one and implementation dependent (e.g. see [5, 13] and references their). The ionization energy to be subtracted from the primary election energy is same for multi-step and direct ionization events.
The ionization DCSM has been implemented into the electrostatic PIC MC (Particle-in Cell Monte Carlo) code BIT1, which is frequently used for modelling of the scrape-off layer (SOL) of different tokamaks [2, 14, 15]. The implementation of the DCSM required also generalization of the existing excitation collision module, which is be described below.
The original BIT1 code, as majority of the kinetic plasma edge codes, treats each type of the excitation collision separately. For extremely large number of excitation collision types (e.g. see Table 1), a new approach was employed, the average excitation model. In this model, all excitation transitions from the given ground states are substituted by one average transition with an effective cross-section and average threshold energy given as follows:
Here, the “j” index runs all over possible excitation channels. It has to be noted that the average threshold energy is not a constant and depends on the energy of a primary electron, see Fig. 4.
We implemented H isotope and Ne+i, i = 0,.. 6, ionization DCSM into the BIT1 code. One has to emphasize the importance of a proper choice of the direct ionization cross-section. The problem is following: The cross-sections and the effective ionization rate coefficients are usually provided by the different atomic data sources, so that the satisfaction of the condition (6) cannot be guaranteed a priory. As a “good” example, Fig. 5 shows plotted e + H ionization collision rate coefficients obtained from the ADAS database for low-density limit and by integration over the Maxwell VDF of the direct ionization cross-section implemented in BIT1.
Dressed cross-sections for e + H ionization collisions for different plasma density and electron temperatures are plotted in Fig. 6.
For validation of the ionization DCSM, we consider D ionization process in an unbounded plasma without the electric field and compare the obtained growth rates of ionized particles to the corresponding analytic expression:
where, for simplicity, we considered short time interval and assume υi to be constant. Simulation results for different neutral particle densities are plotted in Fig. 7 indicating a good agreement with the analytic model (10).
4 Electron impact ion recombination DCSM
The recombination in a low-temperature plasma, contrary to the ionization, can take place via two different channels—the radiative (RR) and the three-body (TBR) recombinations:
The kinematic of these collisions is different and has to be considered separately [17]. The RR is the dominant recombination process practically for all impurity atoms and ions, while TBR is the dominant recombination channel for H (isotope) ions [10]. The RR DCSM is similar to the ionization DCSM described by Eq. (8) and will not be considered here. The generalization of the DCSM to TBR represents the application of the two-body collision cross-section to the three-body one:
where \(R_{{{\text{TBR}}}} \left( {n,T} \right)\) and \(\sigma_{{{\text{TBR}}}} \left( {E_{1} ,E_{2} ,n} \right)\) are the TBR effective rate coefficient obtained from the CRM in ADAS [1] and the TBR cross-section from [17], n is the quantum index of the recombined H atom. The choice n = 1 in Eq. (12) was defined by the requirement to use the smallest possible cross-section \((\sigma_{{{\text{TBR}}}} \left( {E_{1} ,E_{2} ,n} \right)\sim n^{6} )\) in order to ensure satisfaction of the inequality \(R_{{{\text{TBR}}}} \left( {n_{e} ,T_{e} } \right) \le n_{e} R_{n} \left( {T_{e} } \right)\).
The dressed cross-section (12) satisfies the conditions similar to (4) and (5),
The implementation of the TBR DCSM in BIT1 is done by substitution of the conventional TBR cross-section by the expression (12).
As it was done for ionization collisions, we performed tests for unbounded D plasma without the electric field and compared the obtained growth rates of D atom density to the corresponding analytic expression:
where, the index “0” denotes values at t = 0, and we assumed constant RTBR. The simulation results plotted in Fig. 8 show a good agreement between the simulation and the analytic estimates.
Growth rate of D atoms due to 2e + D+ TBR collisions. Analytic curve corresponds to Eq. (14)
5 Simulation of the tokamak SOL
In order to test a newly developed DCSM for realistic applications and study effects of multi-step atomic transitions in tokamak plasma edge, we performed a set of BIT1 SOL modelling for JET and ITER relevant plasma conditions. In the both cases, the simulations included e, D, D+ and seeded impurity particles, Ne+i, i = 0,..,6. BIT1 SOL simulation details can be found in [2, 14, 15].
For simulation of the JET SOL, three different models were considered: i) The original BIT1 model including D and Ne+i excitation (conventional model) and the ionization collisions without the DCSM, ii) as the former, but with the D ionization DCSM, and iii) as the former, but with the D and Ne+i, i = 0,…5, ionization DCSM. The recombination DCSM was not activated as it was expected to be negligibly small due to relatively high electron temperature exceeding 9 eV. Figure 9 shows density profiles for electrons and Ne+2,+3 ions and the electron temperature profile in the inner divertor plasma. As one can see, electron parameters are only slightly influenced by multi-step ionization processes, while Ne+i impurity densities change significantly.
For the simulation of the ITER SOL, we also consider three cases: (i) the original case including excitation, ionization and recombination processes without the DCSM, (ii) the case with the ionization DCSM for D and impurity particles Ne+i, i = 0,…5, and (iii) the case including ionization, as well as the recombination DCSM (the latter only for D+ ions). The election density and temperature profiles indicate no significant influence of the DCSM on the plasma profiles (see Fig. 10), as it was for JET SOL, but show strong reduction of the electron heat flux to the divertor plates shown in Table 2.
The mechanism of the divertor heat flux reduction is explained from Fig. 11; in the original model, the divertor heat is curried mainly by the fraction of collisionless high-energy electrons originating from the hot upstream SOL [2], while in the model with the DCSM, the fraction of these collisionless electrons is reduced, leading to the reduction of the divertor heat flux.
6 Discussion
A new collision operator, DCSM, introduced in this work, incorporates multi-step atomic transitions and relatively easy to be implemented into the plasma edge modelling kinetic codes. It bridges two approaches: present-day coronal approximation-based collision models with the full kinetic models following individual excited states of particles to be developed in future.
Our simulations did not show any significant influence of multi-step transition processes in a JET relevant relatively hot divertor plasma. Contrary to this, the electron heat loads to the ITER divertor plates were strongly affected by the multi-step ionization and recombination processes in the divertor plasma and have to be accounted for in future simulations.
Data Availability Statement
This manuscript has associated data in a data repository. [Authors’ comment: The datasets generated in this study are available from the corresponding author, D. Tskhakaya, upon reasonable request.]
References
H.P Summers and M.G. O’Mullane, AIP Conference Proceedings, 1344, 179 (2011); ADAS: https://open.adas.ac.uk/
D. Tskhakaya, Plasma. Phys. Contr. Fusion. 59, 114001 (2017). https://doi.org/10.1088/1361-6587/aa8486
S. Mijin, A. Antonya, F. Militello, R.J. Kingham, Comput. Phys. Commun. 258, 107600 (2021). https://doi.org/10.1016/j.cpc.2020.107600
M. Surendra et al., Phys. Rev. A 41(2), 1112–1126 (1990). https://doi.org/10.1103/PhysRevA.41.1112
C.K. Birdsall, IEEE Trans. Plasma Sci. 19, 65–85 (1991). https://doi.org/10.1109/27.106800
T. Takizuka, Plasma Phys. Control. Fusion 59, 034008 (2017). https://doi.org/10.1088/1361-6587/59/3/034008
R. Panek et al., Plasma Phys. Control. Fusion 58, 014015 (2016). https://doi.org/10.1088/0741-3335/58/1/014015
P.C. Stangeby, The Plasma Boundary of Magnetic Fusion Devices, ed S Laurenson, Bristol: IOP Publishing (2000).
S. Gao et al., AIP Adv. 11, 025233 (2021). https://doi.org/10.1063/5.0037381
L. Popova et al., Contrib. Plasma Phys. 44(1–3), 252–255 (2004). https://doi.org/10.1002/ctpp.200410037
D. Tskhakaya et al., Contrib. Plasma Phys. 47(8–9), 563–594 (2007). https://doi.org/10.1002/ctpp.200710072
D. Tskhakaya et al., J. Nucl. Materials 415, S860–S864 (2011). https://doi.org/10.1016/j.jnucmat.2010.10.090
D. Tskhakaya et al., Nucl. Mater. Energy 26, 100893 (2021). https://doi.org/10.1016/j.nme.2020.100893
R.K. Janev (ed.), Atomic and Molecular Processes in the Fusion Edge Plasmas (Plenum Press, New York and London, 1995)
D. Tskhakaya et al., Contr. Plasma Phys. 56(6–8), 698–704 (2016). https://doi.org/10.1002/ctpp.201611004
Acknowledgements
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200—EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. This work has been supported by MYES project CZ.02.1.01/0.0/0.0/16 013/0001551 and Czech Science Foundation project GA20-28161S. PIC simulations were performed on Marconi and IFERC supercomputers.
Author information
Authors and Affiliations
Contributions
DT introduced the new collision operator, implemented it into the BIT1 code, performed kinetic simulations, analysed obtained results and wrote the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The author has no relevant financial or non-financial interests to disclose.
Additional information
T.I.: Atomic and Molecular Data and Their Applications: ICAMDATA 2022.
Guest editors: Annarita Laricchiuta, Iouli E. Gordon, Christian Hill, Gianpiero Colonna, Sylwia Ptasinska.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Tskhakaya, D. Implementation of dressed cross-section model into the BIT1 code. Eur. Phys. J. D 77, 135 (2023). https://doi.org/10.1140/epjd/s10053-023-00682-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-023-00682-w