Quantum gradient evaluation through quantum non-demolition measurements

Abstract

We discuss a quantum non-demolition measurement (QNDM) protocol to estimate the derivatives of a cost function with a quantum computer. The cost function, which is supposed to be classically hard to evaluate, is associated with the average value of a quantum operator. Then a quantum computer is used to efficiently extract information about the function and its derivative by evolving the system with a so-called variational quantum circuit. To this aim, we propose to use a quantum detector that allows us to directly estimate the derivatives of an observable, i.e., the derivative of the cost function. With respect to the standard direct measurement approach, this leads to a reduction of the number of circuit iterations needed to run the variational quantum circuits. The advantage increases if we want to estimate the higher-order derivatives. We also show that the presented approach can lead to a further advantage in terms of the number of total logical gates needed to run the variational quantum circuits. These results make the QNDM a valuable alternative to implementing the variational quantum circuits.

Appendices

Appendix A

Unitary evolution in the parameter space

In the main text, we have written the total unitary transformation to measure the gradient as $U_{tot} = e^{ i \lambda {\hat{p}} \otimes {\hat{M}} } U_2 e^{-i \lambda {\hat{p}} \otimes {\hat{M}} } U_1$. The $U_1$ and $U_2$ operation can be thought of as a sequence of non-commuting logical quantum gates or, alternatively using a more physical language, generated by a time-dependent Hamiltonian $H(\theta (t))$.

We consider the change in ${\vec \theta }$ along a single direction $\textbf{e}_{j_1}$ so that the difference between the points ${\vec \theta } \pm s \textbf{e}_{j_1}$ is parametrized only by s. To build the operator $U({\vec \theta })$, we divide the transformation into N steps as usually done for the evolution of a quantum system or the implementation in a quantum circuit. Similarly, we suppose that to implement the operators $U({\vec \theta } - s \textbf{e}_{j_1})$ and $U({\vec \theta } + s \textbf{e}_{j_1})$ we need $N-N_1$ and $N+N_2$ operations, respectively. Denoting the single unitary operation a $u_k$, we can write

$$\begin{aligned} U_1 = u_{N-N_1} ... u_{1} = U({\vec \theta } - s \textbf{e}_{j_1}) \end{aligned}$$

(S1)

and $U_2 = \Pi _{j=1}^{N+N_2} u_j = \Pi _{j=N-N_1}^{N+N_2} u_j U_1$. Therefore, we can obtain $U_2$ by implementing first $U_1$ and then applying other $N_2+N_1$ operators.

Using the mapping $U_1= U({\vec \theta } - s \textbf{e}_{j_1})$ and $U_2= U({\vec \theta } + s \textbf{e}_{j_1})$, we rewrite the above equation as

$$\begin{aligned} U({\vec \theta } + s \textbf{e}_{j_1}) = U({\vec \theta } + s \textbf{e}_{j_1}, {\vec \theta } - s \textbf{e}_{j_1}) U({\vec \theta } - s \textbf{e}_{j_1}) \end{aligned}$$

(S2)

where we have implicitly denoted with $U({\vec \theta } + s \textbf{e}_{j_1}, {\vec \theta } - s \textbf{e}_{j_1})$ the operator that allows us to pass from ${\vec \theta } - s \textbf{e}_{j_1}$ to ${\vec \theta } + s \textbf{e}_{j_1}$ with $N_2+N_1$ operators.

In a similar way, we can implement the series of operators ${\mathcal {U}}_\lambda = e^{ i \lambda {\bar{p}} {\hat{M}} } U_4 e^{-i \lambda {\bar{p}} {\hat{M}} } U_3 e^{ i \lambda {\bar{p}} {\hat{M}} } U_2 e^{-i \lambda {\bar{p}} {\hat{M}} } U_1$ to measure the second derivative. The $U_j$ operators (with $j=1,..,4$) correspond to the operators working in the $\vec \theta$ space.

We define the quasi-characteristic function as in Eq. (9) and use the above expression for ${\mathcal {U}}_\lambda$. Taking the first derivative with respect to $\lambda$, and using the mapping

$$\begin{aligned} U (\vec \theta + s (\textbf{e}_{j_1}-\textbf{e}_{j_2}))&= U_1 \nonumber \\ U (\vec \theta - s (\textbf{e}_{j_1}+\textbf{e}_{j_2}))&= U_2 U_1\nonumber \\ U (\vec \theta + s (-\textbf{e}_{j_1}+\textbf{e}_{j_2}))&= U_3 U_2 U_1 \nonumber \\ U (\vec \theta + s (\textbf{e}_{j_1}+\textbf{e}_{j_2}))&= U_4 U_3 U_2 U_1, \end{aligned}$$

(S3)

we obtain

$$\begin{aligned}&-i \partial _\lambda {\mathcal {G}}_\lambda \Big |_{\lambda =0} \\&\quad = \textrm{Tr}_S [U^\dagger (\vec \theta + s (\textbf{e}_{j_1}+\textbf{e}_{j_2})) M U (\vec \theta + s (\textbf{e}_{j_1}+\textbf{e}_{j_2})) \rho _S^0 +\\&\qquad -U^\dagger (\vec \theta + s (-\textbf{e}_{j_1}+\textbf{e}_{j_2})) M U (\vec \theta + s (-\textbf{e}_{j_1}+\textbf{e}_{j_2})) \rho _S^0 +\\&\qquad -U^\dagger (\vec \theta + s (\textbf{e}_{j_1}-\textbf{e}_{j_2})) M U (\vec \theta + s (\textbf{e}_{j_1}-\textbf{e}_{j_2})) \rho _S^0 \\&\qquad +U^\dagger (\vec \theta - s (\textbf{e}_{j_1}+\textbf{e}_{j_2})) M U (\vec \theta - s (\textbf{e}_{j_1}+\textbf{e}_{j_2})) \rho _S^0 ] \\&\quad = f(\vec \theta +s (\textbf{e}_{j_1}+\textbf{e}_{j_2})) - f(\vec \theta +s(-\textbf{e}_{j_1}+\textbf{e}_{j_2})) \\&\qquad - f(\vec \theta +s (\textbf{e}_{j_1}-\textbf{e}_{j_2})) + f(\vec \theta -s (\textbf{e}_{j_1}+\textbf{e}_{j_2})) \end{aligned}$$

(S4)

where in the last line we have used the definition of $f(\vec \theta )$ in Eq. (3). A part from a $2 \sin s$ factor, this is the second derivative as in Eq. (5). By denoting with $U(\vec \theta _2, \vec \theta _1)$ the operator that allows us to pass from $\vec \theta _1$ to $\vec \theta _2$, we obtain the explicit form of the $U_j$ operators as in Eq. (22) of the main text.

Appendix B

Detection with a qubit

We consider the case in which a qubit, i.e., a two-level system, is used as a detector. The initial state of the detector is fixed at $|\eta _0\rangle = \cos \alpha /2 |0\rangle + \sin \alpha /2 |1\rangle$. The initial contribution to ${\mathcal {G}}_\lambda$ is $\langle 0|\eta _0 \rangle \langle \eta _0|1 \rangle = 1/2~\sin \alpha$.

After the evolution the detector acquires a phase $\phi (\lambda )$ so that its final state is $|\eta _f\rangle = \cos \alpha /2 |0\rangle + \sin \alpha /2 e^{- i \phi (\lambda )} |1\rangle$. The numerator of the ${\mathcal {G}}_\lambda$ is $\langle 0|\eta _f \rangle \langle \eta _f|1 \rangle = 1/2~\sin \alpha e^{ i \phi (\lambda )}$ and

$$\begin{aligned} {\mathcal {G}}_\lambda = e^{i \phi (\lambda )}. \end{aligned}$$

(S5)

is exactly the phase accumulated during the evolution.

We can verify that ${\mathcal {G}}_\lambda$ has the properties discussed in the previous section recalling that for $\lambda =0$ there is no system–detector interaction and, thus, no phase is accumulated, i.e., $\phi (0) = 0$.

In particular, $-i \partial _\lambda {\mathcal {G}}_\lambda |_{\lambda =0 } = \partial _\lambda \phi (\lambda )|_{\lambda =0}$; therefore, the average value and the gradient are related to the derivative of the accumulated phase evaluated in the origin.

In the experiments, we need to calculate $\partial _\lambda \phi (\lambda )|_{\lambda =0}$ numerically. We can approximate it as

$$\begin{aligned} -i \partial _\lambda {\mathcal {G}}_\lambda |_{\lambda =0 } = \partial _\lambda \phi (\lambda )|_{\lambda =0} \approx \frac{\phi (\Delta \lambda ) - \phi (0)}{\Delta \lambda } = \frac{\phi (\Delta \lambda ) }{\Delta \lambda } \end{aligned}$$

(S6)

We can calculate the desired quantity by evaluating the protocol and the phase at a small $\Delta \lambda \ll 1$.

Appendix C

Measuring the Pauli string—QNDM and DM circuit implementation

Fig. 4

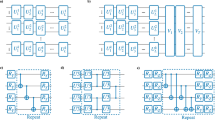
The circuit to implement the operator $\exp \{ i \lambda \sigma _z^D \prod _i \sigma _i^j \}$. We need a maximum of $2(n+1)$ Hadamard-like gates (to diagonalize the $\sigma _x^k$ or $\sigma _y^k$), $2(n+1)$ CNOT gates and a phase gate (denoted as ph) for a total of $\approx 4n$ elementary gates. Notice that if the $\sigma _z^k$ operator appears in ${{\hat{P}}}_j$, we do not need to apply any Hadamard operator and, thus, the $2(n+1)$ is the estimated maximum number of Hadamard-like operators needed

Let us consider the implementation of the exponential operator $\exp \{ i \lambda {{\hat{p}}} \otimes {\hat{P}}_j \}$ where the Pauli string ${\hat{P}}_j$ is a product of Pauli operators: ${\hat{P}}_j = \prod _i \sigma _i^j$.

Having in mind the implementation in a quantum computer, we can substitute the detector ${\hat{p}}$ operator with a Pauli operator $\sigma _z^D$. The exponential operator reads $\exp \{ i \lambda \sigma _z^D \prod _i \sigma _i^j \}$; therefore, the presence of the detector simply increases the dimension of the Pauli string of one qubit.

To implement the exponential operator, we first rotate the Pauli operator to have a product of $\sigma _z$ operators. This can be done by applying Hadamard operators $H_{had, x}$ for the $\sigma _x$ and the corresponding $H_{had, y}$ for the $\sigma _y$. That is $\left( \prod H_{had, l} \right) \exp \{ i \lambda \sigma _z^D {\hat{P}}_j \} \left( \prod H_{had, l} \right) = \exp \{ i \lambda \sigma _z^D \prod _p \sigma _z^p \}$.

The diagonalized exponential operator generates a phase factor $\exp \{\pm i \lambda \}$ depending on the logical string to whom it is applied. More specifically, taking $\sigma _z |0\rangle = - |0\rangle$ and $\sigma _z |1\rangle = |1\rangle$, the transformation is $|x_1 x_2... x_n\rangle \rightarrow \exp \{ i \lambda \} |x_1 x_2... x_n\rangle$ if the number of $x_i=0$ is even and $|x_1 x_2... x_n\rangle \rightarrow \exp \{- i \lambda \} |x_1 x_2... x_n\rangle$ if the number of $x_i=0$ is odd.

To count the parity of $x_i=0$ in a string, we add an ancilla qubit in position $n+2$ (the $n+1$ qubit is the detector) and apply a sequence of n $\textrm{C}_i \textrm{NOT}_{n+2}$ logical gate with $i=1,2,..., n+1$. The $\textrm{C}_i \textrm{NOT}_{n+2}$ is controlled on the i-th logical qubit and acts always in the ancilla qubit. As a consequence, if we have an even number of $x_i=0$, the ancilla qubit will end up in the $|0\rangle$ state, otherwise, i.e., for an odd number of $x_i=0$, in the $|1\rangle$ state. Then we apply a phase gate on the ancilla qubit $\exp \{ i \lambda \sigma _z^a \}$ and reverse the $\textrm{C}_i \textrm{NOT}_{n+2}$ operations to reset the ancilla qubit to its original state $|0\rangle$. The full circuit is shown in Fig. 4.

To implement this operator, we need $2(n+1)$ Hadamard gates, $2(n+1)$ CNOT gates and a phase gate for a total of $4(n+1)+1\approx 4n$ elementary gates for $n \gg 1$. Notice that this is the worst case where we have to apply 2n Hadamard gates. In many cases, the Pauli string operators are the product of a limited number of Pauli operators so the number of Hadamard gates can be significantly reduced. For example, in physical problems where we need to find the energy of the ground state of a Hamiltonian, the Pauli strings are usually the product of only four Pauli operators [20, 29].

For the DM approach, we have an analogous situation. In quantum computers, the measurement is performed in a fixed basis (usually the one in which $\sigma _z$ is diagonal). Since we cannot directly measure an alternative Pauli observable ($\sigma _x$ or $\sigma _y$), we have to rotate the qubit state and perform the measurement in the predetermined basis. As above, this is done by applying an Hadarmard $H_{had,l}$ operator. Therefore, to measure the average of a Pauli string, we need a maximum of n $H_{had,l}$ logical gates.