Abstract
The absolute densities of O and O\(_3\) in the effluent of a kINPen, an atmospheric pressure plasma jet, are determined by molecular beam mass spectrometry. A nitrogen gas curtain surrounding the effluent provides a stable environment and prevents interactions with the ambient air. Both He and Ar were used as feed gas with admixtures of O\(_2\) up to 1%. Measurements are performed at discharge voltages from 1600 to 3000 \({\textrm{V}}_{\textrm{pp}}\) and at distances from 5.5 to 10.5 mm from the nozzle of the gas shielding device to the orifice of the mass spectrometer. The measured O atom densities are in the order of 1 \(\times \) \(10^{14}~{\textrm{cm}}^{-3}\) to 2 \(\times \) \(10^{15}~{\textrm{cm}}^{-3}\), whereas the O\(_3\) molecule densities are in the order of 1 \(\times \) \(10^{14}~{\textrm{cm}}^{-3}\) to 5 \(\times \) \(10^{14}~{\textrm{cm}}^{-3}\), respectively, when operated in argon the plasma generates higher densities of reactive species. Additionally, a novel molecular beam chopper design with linear movement has been successfully tested in the mass spectromerty setup as an alternative to a rotating chopper.
Graphic Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the past decades, a wide variety of cold atmospheric pressure plasma jets (APPJ) have been developed and studied [1,2,3]. Their unique properties are used for different applications in plasma medicine [4, 5], thin film deposition [6, 7], production of nanoparticles [8] and surface modification [2, 9, 10].
Cold (or non-equilibrium) plasmas have different temperatures for hot electrons and cold heavy particles (neutrals and ions). The electron temperature of these jets is in the order of 1 eV [9, 11] (\({1}~{\textrm{eV}} \approx {11000}~{\textrm{K}}\) [12]) while the temperature of the heavy particles is still close to room temperature. Due to inelastic collisions, the electron kinetics enables chemical processes that normally require high temperatures [13]. The plasma produces different species like ions, radical species, excited atoms/radicals/molecules and VUV radiation.
In APPJs, the feed gas flows through a discharge volume. The reactive particles produced in the plasma zone are carried outside of the discharge volume by the gas flow with diffusion much slower compared to convection. This effect leads to the formation of the so-called effluent outside of the actual discharge volume. Often, a distinction is made between three regions: the core plasma, the effluent and the far field further down the gas stream.
APPJs are often operated with Ar or He as feed gas with admixtures of molecular gases up to a few percent [2]; sometimes they are even operated with air [3]. One focus of research is on the description and diagnostics of radicals and excited species. When operated with N\(_2\)/O\(_2\) admixtures or in air, respectively, so-called reactive oxygen and nitrogen species (RONS [5]), like, e.g., O, NO, NO\(_2\) and O\(_3\), are produced by the APPJs [14,15,16].
Absolute particle densities of RONS have been measured by means of optical methods [16,17,18,19,20,21] or by molecular beam mass spectrometry (MBMS) [17, 22,23,24,25] for different plasma sources and various experimental conditions. The particle densities are dependent on gas composition, humidity of the feed gas, applied discharge voltage and geometry of the jet [11].
For the kINPen, the densities of many different RONS have been measured for different conditions (distance to nozzle, far-field vs. effluent, different admixtures, different gas curtain, etc.) [9, 16,17,18], but most of these measurements have been performed in the far-field region with Ar as feed gas. Most of the studies are conducted by optical methods like absorption spectroscopy or laser-induced fluorescence (LIF), but only very few have employed mass spectrometry [17, 26, 27].
In the present study, measurements of absolute densities determined by MBMS in the effluent of a kINPen operated with Ar and He are described. Since an extensive overview for MBMS of APPJs is given in [28, 29], only a brief summary of the theory is provided here. In particular, a novel setup for particle extraction MBMS is described in more detail, whereas the kINPen itself is described elsewhere [9].
2 Experimental setup
2.1 Plasma jet
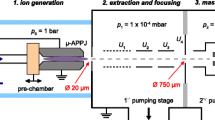
The kINPen was designed at the the Leibniz Institute for Plasma Science and Technology (INP) Greifswald. It is a radio-frequency (RF)-driven APPJ, the plasma is ignited at a central high-voltage needle inside a dielectric capillary (see Fig. 1). At present, different modifications and commercially available designs of this jet type exist [9].
The plasma jet used in this study is a kINPen Sci [26]. In contrast to other kINPen designs, this version has an output for voltage and current measurements for electric diagnostics [9]. Its operating frequency is about 900 kHz. The amplitude of the applied voltage is in the range of 1300–3000 \({\textrm{V}}_{\textrm{pp}}\) at a flow rate of 3 slm of Ar or He, respectively, with admixtures of O\(_2\) up to 1%. In order to produce a controlled atmosphere around the effluent, a shielding gas device is mounted on top of the RF head [30, 31]. It produces a gas curtain and, thus, shields the effluent during operation from the ambient air. The influence of the gas admixture on the absorbed power has been characterized for similar jets before [32,33,34,35], and its dependence has to be kept in mind when comparing results among different admixtures.
The length of the effluent depends on the applied voltage and the gas composition [18]. The higher the applied voltage the longer the effluent becomes and the higher the O\(_2\) admixture to the feed gas the shorter the effluent. When the effluent comes close to the aperture of the MS, filaments between the kINPen and the aperture can be sometimes observed. These filaments should be avoided, because they alter the plasma properties [36]. The gas flow is regulated by MKS flow controllers. A photograph of the kINPen in front of the mass spectrometer is shown in Fig. 2.
2.2 Plasma chemical processes in the kINPen
Occurring processes of ionization, excitation and fragmentation of molecules/atoms by the jet plasma and the formation of particles are studied in several papers related to the plasma chemistry. The most important reactions leading to the formation of atomic O and O\(_3\) molecules are
where \(\text {X}^*\) may be an exited particle, a fast electron or a UV photon with sufficient energy. M is an arbitrary third particle, \(k_{\text {Ar}}\) is the rate coefficient for Ar, \(k_{\text {He}}\) for He as third particle. Competing, but slower reactions for the destruction of O are:
More information on collisions at elevated pressure for plasma chemical processes of APPJs can be found in the literature, e.g. [3, 37, 38, 40,41,42,43], rate coefficients can be found at NIST kinetics database [44] or IUPAC AERIS [45].
2.3 Molecular beam mass spectrometry
2.3.1 The mass spectrometer
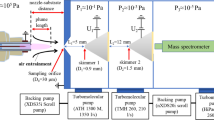
The setup of the mass spectrometer is based on the HPR60 differential pumping stage by HIDEN Analytical Ltd [46]. The two-stage-HPR60 pumping stage was equipped with an additional first stage containing a chopper. The design is based on the principle of the rotating skimmer described in [47]. The rotating skimmer was already successfully demonstrated for investigations by other research groups [22, 34, 48].
In this novel setup, a linear moving skimmer is placed on a moving slide driven by a stepper motor outside the vacuum. The setup of the chopper is shown in Fig. 3. The chopper is placed in the first stage. The used mass spectrometer is an EPIC1000. It consists of an ionizer, a quadrupol mass filter and a secondary electron multiplier (SEM) detector. An integrated multichannel scaler (MCS) is used to achieve a time resolution of 5 \(\upmu {\textrm{s}}\).
To prevent UV radiation produced by the plasma from reaching the detector, the EPIC1000 is mounted under a small angle of 4\(^{\circ }\). This measure is necessary because the EPIC1000 does not have an energy filter, which is otherwise blocking the line-of-sight from the ionizer to detector. Common energy filters are a Bessel box or a sector field electrostatic energy analyzer.
The ambient atmosphere can enter into first stage through an orifice (diameter \(d = {50}~{\upmu {\textrm{m}}}\)). When the skimmer is aligned with the orifice, a molecular beam (MB) forms behind the skimmer and expands into the second stage (see [28, 49]). When the skimmer is not aligned with the orifice the movable stage is blocking the incoming gas from directly entering the second stage and it is confined to the first stage and exhausted only. A small fraction of it enters the subsequent stages leading to a slight increase in the gas pressure compared to a fully sealed second stage. The stepper motor’s frequency was tested in the range up to 20 Hz. Higher frequencies might harm the mechanical construction and have not been tested. The synchronisation of the chopper and the measurement is done by a photoelectric sensor. During one cycle, the chopper is opened twice.
The particle composition along the MB axis is not constant and changes due to composition distortion effects [28, 29, 50]. This effects include acceleration into the sampling orifice, strong radial gradients in the MB and Mach number focusing. Particles inside the ionizer are ionized by electron impact ionization (EII). Often, there is a shift between the selected energy in the software and the real (peak) electron energy [23, 24]. For our ionizer, this shift is 1.5 V. This difference was determined by comparing the measured ionization potentials of different gases (Ar, O\(_2\), N\(_2\)) to their literature values (taken from NIST [51]).
2.3.2 Evaluation of a signal
The signal \(S_i\) of species i at the detector consists of two contributions: the background signal due to residual gas particles inside the ionizer and the contribution from the MB related to the APPJ operation [24, 28, 29, 52]. Only the contribution from the MB is the desired signal of interest. The background is not constant over time, but rises when the chopper is partially or fully opened and decreases exponentially with time when the chopper is closed. When the chopper is fully open, the increase in the signal is solely determined by the rising background. At a chopper frequency of 20 Hz, this increase can be approximated as linearly.
To determine the signal S, an assumption for the background has to be made. Here the background before the time-resolved signal is assumed constant and after the time-resolved signal to decrease linear (approximation of the exponential decrease). To avoid an influence of different transit times or geometrical effects of the sampling region, the fit is made 1 ms after the chopper is closed. The interval for the fit is 1 ms. The backgrounds are then extrapolated to the time when the chopper is fully opened. The contribution of the MB is determined as difference of the average signal during the time when the chopper is fully open and the mean of the background. Examples for the evaluation of CO\(_2\), O and O\(_3\) are shown in Fig. 4.
Exemplary measurements for the evaluation of the signal. Only the first opening time is shown. The counts are black (1, 5), when the chopper is closed, orange when the chopper is partially opened (2, 4) and blue when the chopper is fully opened (3). The approximated background and the fit region are plotted in red. The top shows a CO\(_2\) signal, the second an O signal and the last one an O\(_3\) signal. The feed gas was He for all three measurements
2.3.3 Calibration for absolute densities
The signal \(S_i\) of species i at the detector is given by [28, 53]
The particle density inside the ionizer is denoted by \(n_i\), \(\sigma _i\) denotes the energy-dependent cross section for electron impact ionisation (EII), \(\beta \) the extraction efficiency of the ionizer, I the electron current and L the length of the ionizer. T and \(\Theta \) are the mass-dependent transmission function and detection probability, respectively.
Because \(T(m_i)\), \(\Theta (m_i)\) and \(\beta \) are unknown, a calibration is performed for each species. This calibration process is similar to the one described in [26, 34]: A gas box is placed in front of the mass spectrometer. A constant gas flow creates a controlled atmosphere inside the gas box, which is determined by the ratio of the gas flows of the different gases. The composition has to be similar to the situation for the kINPen operation (He/N\(_2\) or Ar/N\(_2\), respectively) to have the same disturbing effects in the MB. A stable gas (Ne, CO\(_2\)) is then added in different amounts up to 1% of the total gas flow to this atmosphere. The particle density of the calibration species \(n_{\textrm{cal}}\) is calculated as its fraction of the total flow.
A linear fit
is performed. In an ideal case, the offset should be 0, but for some gases a small signal can be observed even without admixture (either from impurities or from a small fraction of air still entering the mass spectrometer). This offset is ignored for the calibration procedure, because the radical species do not have an offset in the signal.
The density \(n_i\) of species i is then given by
with \(f_{\textrm{cal}}\) and \(f_i\) being the mass-dependent transmission function. The function f(m) is assumed to follow the relation \(f \propto m^{-z}\) [34, 54].
The calibration is performed for each of the two opening signals separately. The shape of the time-resolved signal depends on the chopper velocity. Additionally, small misalignments from the center (either along or perpendicular to the direction of chopper motion) can cause that the measured profiles look different for the two directions of the chopper motion and can provide different signal intensities (within 10% difference). An average of both is, therefore, taken as the measured signal intensity. A list with each measured species and its calibration gas is provided in Table 1. The used cross sections are given in Table 2.
2.4 Alignment of the kINPen
To correctly align the kINPen with the orifice of the MS, the plasma jet is mounted on two perpendicular X–Y tables. The kINPen can thereby be moved in three dimensions. First, the kINPen is positioned to be in line with the MS. The precise alignment is done by monitoring the N\(_2\) signal with the mass spectrometer and adjusting the kINPen to minimize it. This is the same as maximizing the feed gas signal, but more precise.
To avoid temperature drifts having an effect on the measurements, the parameter variations are performed in random order. Therefore, the observed trends are real trends and not effects of temporal or temperature drifts.
The aging of the secondary electron multiplier detector is negligible for the time duration of our measurement campaigns. The absolute values of the cross sections are known with a certain accuracy. For most species the uncertainty of their absolute cross sections is in the range of 5%. But for Ne there are two values provided in literature with different cross sections at 25 eV that differ by a factor of 1.48 [56, 59]. Following [60], the higher value is used.
3 Results
In this section at first, the ratio of feed gas to gas curtain as well as the dependence of the signal on the MS emission current, both without the plasma, are described. Then, the variation of the applied voltage, the variation of the distance between nozzle and orifice of the MS and the variation of the oxygen admixture are presented. All measurements are performed at a gas flow of 3 slm for the feed gas and a flow of 5 slm N\(_2\) for the gas curtain. For these measurements, the signals of O, O\(_2\), N\(_2\), O\(_3\) and the feed gas have been recorded. To achieve an acceptable signal-to-noise ratio, the accumulation times for one species were between 3 s (Ar, N\(_2\)) and up to 20 min (O).
3.1 Ratio feed gas to gas curtain
For the calibration, the ratio of feed gas to curtain gas must be known. To obtain the ratio for Ar, the composition of Ar and N\(_2\) in the gas box was varied from 100% Ar to 100% N\(_2\) within 10 steps. The ratio was compared to the ratio when using the kINPen (3 slm Ar as feed gas and 5 slm N\(_2\) curtain). For Ar, the atmosphere in front of the orifice consists of \(18 \pm 3\)% Ar and, thus, of \(82 \pm 3\)% N\(_2\).
For He, only small admixtures of N\(_2\) are used. The ratio in the gas box was varied from 0 to 0.7% N\(_2\) in 7 steps. Again, the ratio of the N\(_2\) signal to the He signal is compared to the ratio when using the kINPen. For He the atmosphere in front of the orifice consists of \(99.85 \pm 0.05\)% He and \(0.25 \pm 0.05\)% N\(_2\), respectively. The differences are mainly due to a laminar flow for He and a turbulent flow for Ar.
These results cannot be compared to free-flow simulations or measurements, because the aperture does disturb the gas flow. The results for Ar are in agreement with measurements by Dünnbier et al. [26] who also used MS. When comparing the results, it should be noted that Dünnbier et al. measured the distance from the nozzle of the quartz tube to the orifice while in this study the distance is measured from the nozzle of the gas shielding device. Thus, the distance from the quartz tube to the nozzle of the gas shielding device (2 mm) must be added and the densities must be compared to 9.5 mm distance in Dünnbier et al. [26].
3.2 Influence of the emission current
The signal S is dependent on the emission current I in the MS. The time to perform one measurement could therefore be decreased by using a higher current. However, by large emission current a large space charge is formed in the ionizer and the scaling of the measured signal to the emission current is not linear anymore. To check, if S scales proportionally with I, the Ar signal was determined for different I from 5 to 200 \({\upmu {\textrm{A}}}\). When S is proportional to I, then S/I is constant. The ratio S/I is displayed in Fig. 5. The ratio S/I does change only marginally. But to exclude this as an additional source of error, all calibrations are performed at the same emission current as their respective species.
3.3 Voltage variation
The applied voltage was varied at a constant distance of 7.5 mm and 1% O\(_2\) admixture to the feed gas. For He, the voltage of the kINPen could be changed between 1600 and 2180 \({\textrm{V}}_{\textrm{pp}}\), and for Ar 1760 \({\textrm{V}}_{\textrm{pp}}\) to 3000 \({\textrm{V}}_{\textrm{pp}}\). The O and O\(_3\) densities are shown in Fig. 6. With increasing voltage the O density rises for He from 1.1 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 1300 \({\textrm{V}}_{\textrm{pp}}\) to 4.7 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 2180 \({\textrm{V}}_{\textrm{pp}}\). The O\(_3\) density rises from 1.2 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) to 1.6 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\). For Ar the O density rises from 3.7 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 1760 \({\textrm{V}}_{\textrm{pp}}\) to 1.9 \(\times \) \(10^{15}~{\mathrm{cm^{-3}}}\) at 3000 \({\textrm{V}}_{\textrm{pp}}\).
Densities of O and O\(_3\) at different applied voltages. The distance was fixed at 7.5 mm and 1% O\(_2\) admixture to the feed gas. The top figure shows the O and O\(_3\) densities for Ar as feed gas and the bottom figure the densities for He as feed gas, respectively. The y-axes are scaled differently
The O\(_3\) density remains here almost constant in the range of 3.6 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 3000 \({\textrm{V}}_{\textrm{pp}}\) and 5.1 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 2000 \({\textrm{V}}_{\textrm{pp}}\). The uncertainties are too large to confirm any trend. The trend for He is similar to the trend observed with the COST-jet [34] and can be explained by O formation in reaction 1 and its recombination into O\(_3\) in reaction 2 where the O density is increasing with the increasing applied voltage (power) but O\(_3\) stays more or less constant due to its dissociation in the plasma and lower rate of the reaction 2 at higher temperatures.
The densities of O and O\(_3\) are about 5 times as high in Ar as they are in He considering the interval from ignition to maximum adjustable voltage. It is reported that Ar can dissociate molecular gases more efficient compared to He [61]. It is assumed that the main reason for the different dissociation is a higher electron density in an Ar plasma compared to a He plasma [62].
3.4 Variation of O\(_2\) admixture
As seen from the voltage variation, the kINPen has different voltage ranges for He and Ar. Therefore, no attempt was made to measure at the same voltage. The voltage for both Ar and He was chosen to be as high as possible without producing sparks at 0% O\(_2\) admixture. The applied voltage was 1580 \({\textrm{V}}_{\textrm{pp}}\) for He and 2000 \({\textrm{V}}_{\textrm{pp}}\) for Ar. The densities are displayed in Fig. 7.
Densities of O and O\(_3\) at different O\(_2\) admixtures. The applied voltage was 1580 V for He and 2000 V for Ar. The distance between nozzle and aperture was 7.5 mm. The top figure shows the O and O\(_3\) densities for Ar as feed gas and the bottom figure the densities for He as feed gas, respectively. The y-axes are scaled differently
For He the O density rises from 0 \({\textrm{cm}}^{-3}\) at 0% admixture to 2 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 1% admixture of O\(_2\) in He. The O\(_3\) density increases from 0 \({\textrm{cm}}^{-3}\) to 1.5 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\). For Ar the O density remains nearly constant between 4.5 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 0.17% admixture and 7.7 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 0.5% admixture. The O\(_3\) density is monotonically increasing from 3 \(\times \) \(10^{13}~{\mathrm{cm^{-3}}}\) at 0.17% admixture to 4.9 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) at 1% admixture.
It should be kept in mind that the applied voltage was kept constant, not the power.
The O\(_3\) density is by a factor 5 smaller than FTIR measurements by Schmidt-Blecker et al. [16]. This could be due to the fact that FTIR measurements are performed in the far effluent, where all O has recombined into O\(_3\). In our case, the O density is much higher than the O\(_3\) density at the distance of 7.5 mm.
Again, the general trend for He is similar to the COST-jet. For Ar, the trend is similar to simulations [42].
3.5 Distance variation
The distance was varied between 5.5 and 10.5 mm for an admixture of 1% O\(_2\) to the feed gas and an applied voltage of 2300 \({\textrm{V}}_{\textrm{pp}}\) for He and 2600 \({\textrm{V}}_{\textrm{pp}}\) for Ar. The voltage was chosen that no sparks between the jet and the mass spectrometer occur at 5.5 mm. The results are shown in Fig. 8.
With increasing distance, the densities of O decreases and the densities of O\(_3\) increase for both He and Ar. For He, the decrease is smaller (3.1 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) to 2.4 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\)) than for Ar (18 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) to 7.5 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\)). The O\(_3\) density increases for He from 1 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) to 2.1 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) and for Ar from 4.6 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\) to 5.6 \(\times \) \(10^{14}~{\mathrm{cm^{-3}}}\).
An interesting result is the higher increase in the O\(_3\) density than the decrease in the O density for He as feed gas. This could be explained by accumulation of O\(_3\) in the background gas and its diffusion towards the axis at increasing distance. A potential source for O could be the dissociation of O\(_2\) by UV-radiation or by collisions with excited (metastable) He atoms. The general trend is again known from the COST-jet [34].
4 Conclusion
The densities of O and O\(_3\) in the effluent of a kINPen for both He and Ar as feed gases have been measured by MBMS for different experimental conditions. The densities have been determined for oxygen admixtures to the feed gas from 0 to 1%, for distances from 5.5 to 10.5 mm and voltages from 1300 to 2180 \({\textrm{V}}_{\textrm{pp}}\) for He and 1760 \({\textrm{V}}_{\textrm{pp}}\) to 3000 \({\textrm{V}}_{\textrm{pp}}\) for Ar, respectively. For all settings, the O and O\(_3\) densities are higher for Ar than for He. The O\(_3\) densities determined here in the effluent differ from measurements in the far effluent [16] by a factor of about 5. The absolutely calibrated measurements presented in this article are important for the quantitative analysis of this plasma interaction with any surfaces. Additionally, a new version of the beam chopper with integrated skimmer has been successfully constructed and tested showing that a construction with linear movement is a possible alternative to rotating chopper.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The data that support the findings of this study are available from the corresponding author upon reasonable request.]
References
M. Laroussi, T. Akan, Plasma Process. Polym. 4, 777–788 (2007). (ISSN 0022-3727)
J. Winter, R. Brandenburg, K.D. Weltmann, Plasma Sources Sci. Technol. 24, 064001 (2015). (ISSN 0963-0252)
X. Lu, S. Reuter, M. Laroussi, D. Liu, Nonequilibrium Atmospheric Pressure Plasma Jets: Fundamentals, Diagnostics, and Medical Applications (CRC Press/Taylor and Francis Group, Boca Raton, 2019). (ISBN 978-0-429-62072-0)
T. von Woedtke, S. Reuter, K. Masur, K.D. Weltmann, Phys. Rep. 530, 291–320 (2013). (ISSN 03701573)
D.B. Graves, J. Phys. D Appl. Phys. 45(263001), 1361–6463 (2012). (ISSN 0022-3727)
J. Schäfer, R. Foest, A. Quade, A. Ohl, K.D. Weltmann, J. Phys. D Appl. Phys. 41(194010), 1361–6463 (2008). (ISSN 0022-3727)
D. Merche, N. Vandencasteele, F. Reniers, Thin Solid Films 520, 4219–4236 (2012). (ISSN 00406090)
D. Mariotti, R.M. Sankaran, J. Phys. D Appl. Phys. 43(323001), 1361–6463 (2010). (ISSN 0022-3727)
S. Reuter, T. von Woedtke, K.D. Weltmann, J. Phys. D Appl. Phys. 51(233001), 1361–6463 (2018). (ISSN 0022-3727)
M. Laroussi, IEEE Trans. Plasma Sci. 37(714–725), 1939–9375 (2009). (ISSN 0093-3813)
P.J. Bruggeman, F. Iza, R. Brandenburg, Plasma Sources Sci. Technol. 26, 123002 (2017). (ISSN 1361-6595)
M.A. Lieberman, A.J. Lichtenberg, Principles of Plasma Discharges and Materials Processing: Lieberman/Plasma 2e (Wiley, Hoboken, 2005). (ISBN 978-0-471-72425-4 978-0-471-72001-0)
J.C. Whitehead, J. Phys. D Appl. Phys. 49, 243001 (2016). (ISSN 0022-3727)
M.G. Kong, G. Kroesen, G. Morfill, T. Nosenko, T. Shimizu, J. van Dijk, J.L. Zimmermann, New J. Phys. 11, 115012 (2009). (ISSN 1367-2630)
P. Bruggeman, R. Brandenburg, J. Phys. D Appl. Phys. 46(464001), 1361–6463 (2013). (ISSN 0022-3727)
A. Schmidt-Bleker, R. Bansemer, S. Reuter, K.D. Weltmann, Plasma Process. Polym. 13, 1120–1127 (2016). (ISSN 16128850)
S. Iseni, S. Zhang, A.F.H. van Gessel, S. Hofmann, B.T.J. van Ham, S. Reuter, K.D. Weltmann, P.J. Bruggeman, New J. Phys. 16, 123011 (2014). (ISSN 1367-2630)
S. Reuter, J. Winter, S. Iseni, S. Peters, A. Schmidt-Bleker, M. Dünnbier, J. Schäfer, R. Foest, K.D. Weltmann, Plasma Sources Sci. Technol. 21(034015), 1361–6595 (2012). (ISSN 0963-0252)
A.F.H. van Gessel, K.M.J. Alards, P.J. Bruggeman, J. Phys. D Appl. Phys. 46, 265202 (2013). (ISSN 0022-3727)
P. Preissing, I. Korolov, J. Schulze, V. Schulz-von der Gathen, M. Böke, Plasma Sources Sci. Technol. 29(125001), 1361–6595 (2020). (ISSN 0963-0252)
S. Schröter, J. Bredin, A.R. Gibson, A. West, J.P. Dedrick, E. Wagenaars, K. Niemi, T. Gans, D. O’Connell, Plasma Sources Sci. Technol. 29(105001), 1361–6595 (2020). (ISSN 0963-0252)
D. Ellerweg, J. Benedikt, A. von Keudell, N. Knake, V. Schulz-von der Gathen, New J. Phys. 12, 013021 (2010). (ISSN 1367-2630)
B.T.J. van Ham, S. Hofmann, R. Brandenburg, P.J. Bruggeman, J. Phys. D Appl. Phys. 47(224013), 1361–6463 (2014). (ISSN 0022-3727)
J. Jiang, Y.A. Gonzalvo, P.J. Bruggeman, Plasma Sources Sci. Technol. 29, 045023 (2020). (ISSN 1361-6595)
G. Willems, J. Benedikt, A. von Keudell, J. Phys. D Appl. Phys. 50(335204), 1361–6463 (2017). (ISSN 0022-3727)
M. Dünnbier, A. Schmidt-Bleker, J. Winter, M. Wolfram, R. Hippler, K.D. Weltmann, S. Reuter, J. Phys. D Appl. Phys. 46(435203), 1361–6463 (2013). (ISSN 0022-3727)
M. Dünnbier, Plasma Jets for Life Science Applications: Characterisation and Tuning of the Reactive Species Composition. Ph.D. Thesis Ernst-Moritz-Arndt-Universität (2015)
J. Benedikt, A. Hecimovic, D. Ellerweg, A. von Keudell, J. Phys. D Appl. Phys. 45(403001), 1361–6463 (2012). (ISSN 0022-3727)
S. Große-Kreul, S. Hübner, S. Schneider, D. Ellerweg, A. von Keudell, S. Matejčík, J. Benedikt, Plasma Sources Sci. Technol. 24(044008), 1361–6595 (2015). (ISSN 0963-0252)
S. Reuter, J. Winter, A. Schmidt-Bleker, H. Tresp, M.U. Hammer, K.D. Weltmann, IEEE Trans. Plasma Sci. 40(2788–2794), 1939–9375 (2012). (ISSN 0093-3813)
A. Schmidt-Bleker, J. Winter, S. Iseni, M. Dünnbier, K.D. Weltmann, S. Reuter, J. Phys. D Appl. Phys. 47(145201), 1361–6463 (2014). (ISSN 0022-3727)
D. Marinov, N.S.J. Braithwaite, Plasma Sources Sci. Technol. 23(062005), 1361–6595 (2014). (ISSN 0963-0252)
V. Léveillé, S. Coulombe, Plasma Sources Sci. Technol. 14(467–476), 1361–6595 (2005). (ISSN 0963-0252)
G. Willems, J. Golda, D. Ellerweg, J. Benedikt, A. von Keudell, N. Knake, V. Schulz-von der Gathen, New J. Phys. 21, 059501 (2019). (ISSN 1367-2630)
C. Douat, S. Hübner, R. Engeln, J. Benedikt, Plasma Sources Sci. Technol. 25(025027), 1361–6595 (2016). (ISSN 0963-0252)
S. Bornholdt, M. Wolter, H. Kersten, Eur. Phys. J. D 60(653–660), 1434–6079 (2010). (ISSN 1434-6060)
K. Niemi, J. Waskoenig, N. Sadeghi, T. Gans, D. O’Connell, Plasma Sources Sci. Technol. 20, 055005 (2011). https://doi.org/10.1088/0963-0252/20/5/055005
W.V. Gaens, A. Bogaerts, J. Phys. D Appl. Phys. 46, 275201 (2013). (ISSN 0022-3727)
R. Atkinson, D.L. Baulch, R.A. Cox, J.N. Crowley, R.F. Hampson, R.G. Hynes, M.E. Jenkin, M.J. Rossi, J. Troe, Atmos. Chem. Phys. 4, 1461–1738 (2004). (ISSN 1680-7324)
Y. Sakiyama, D.B. Graves, H.W. Chang, T. Shimizu, G.E. Morfill, J. Phys. D Appl. Phys. 45, 425201 (2012). (ISSN 0022-3727)
T. Murakami, K. Niemi, T. Gans, D. O’Connell, W.G. Graham, Plasma Sources Sci. Technol. 23, 025005 (2014). (ISSN 0963-0252)
W.V. Gaens, S. Iseni, A. Schmidt-Bleker, K.D. Weltmann, S. Reuter, A. Bogaerts, New J. Phys. 17, 033003 (2015). (ISSN 1367-2630)
G.V. Naidis, Plasma Sources Sci. Technol. 22(035015), 1361–6595 (2013). (ISSN 0963-0252)
J.A. Manion, R.E. Huie, R.D.L.D.R.B.J.V.L. Orkin, W. Tsang, W.S. McGivern, J.W. Hudgens, V.D. Knyazev, D.B. Atkinson, E. Chai, A.M. Tereza, C.Y. Lin, T.C. Allison, W.G. Mallard, F. Westley, J.T. Herron, R.F. Hampson, D.H. Frizzell, NIST Chemical Kinetics Database, NIST Standard Reference Database 17 https://kinetics.nist.gov/
IUPAC: Task Group on Atmospheric Chemical Kinetic Data Evaluation https://iupac.aeris-data.fr/
Hiden Analytical Ltd. website https://www.hidenanalytical.com/
J. Benedikt, D. Ellerweg, A. von Keudell, Rev. Sci. Instrum. 80(055107), 1089–7623 (2009). (ISSN 0034-6748)
D. Ellerweg, A. von Keudell, J. Benedikt, Plasma Sources Sci. Technol. 21(034019), 1361–6595 (2012). (ISSN 0963-0252)
J.H. Gross, Massenspektrometrie (Springer, Berlin, 2013). (ISBN 978-3-8274-2980-3 978-3-8274-2981-0)
E.L. Knuth, Combust. Flame 103, 171–180 (1995). (ISSN 00102180)
P. Linstrom, NIST Chemistry WebBook. NIST Standard Reference Database 69 (1997)
T. Krähling, D. Ellerweg, J. Benedikt, Rev. Sci. Instrum. 83(045114), 1089–7623 (2012). (ISSN 0034-6748)
H. Singh, J.W. Coburn, D.B. Graves, J. Vac. Sci. Technol. A Vac. Surf. Films 17(2447–2455), 1520–8559 (1999). (ISSN 0734-2101)
J. Benedikt, A. Consoli, M. Schulze, A. von Keudell, J. Phys. Chem. A 111(10453–10459), 1520–5215 (2007). (ISSN 1089-5639)
W.R. Thompson, M.B. Shah, H.B. Gilbody, J. Phys. B At. Mol. Opt. Phys. 28(1321–1330), 1361–6455 (1995). (ISSN 0953-4075)
K. Stephan, H. Helm, T.D. Märk, J. Chem. Phys. 73(3763–3778), 1089–7690 (1980). (ISSN 0021-9606)
Y. Itikawa (ed.), Interactions of Photons and Electrons with Molecules (Landolt-Börnstein - Group I Elementary Particles, Nuclei and Atoms, vol. 17C (Springer, Berlin, 2003). (ISBN 978-3-540-44338-4)
H.C. Straub, B.G. Lindsay, K.A. Smith, R.F. Stebbings, J. Chem. Phys. 105(4015–4022), 1089–7690 (1996). (ISSN 0021-9606)
R. Rejoub, B.G. Lindsay, R.F. Stebbings, Phys. Rev. A 65(042713), 1094–1622 (2002). (ISSN 1050-2947)
G. Willems, Reaction Chemistry in Non-Equilibrium Atmospheric Pressure Plasmas. Ph.D. Thesis (2018)
C. Stewig, S. Schüttler, T. Urbanietz, M. Böke, A. von Keudell, J. Phys. D Appl. Phys. 53, 125205 (2020). (ISSN 0022-3727)
J. Golda, J. Held, V.S.V. der Gathen, Plasma Sources Sci. Technol. 29, 025014 (2020). (ISSN 0963-0252)
Acknowledgements
We would like to thank our technicians Frank Brach, Volker Rohwer and Michael Poser. The work was supported by the DFG (Project Number 426208229).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
TAH contributed to conceptualization, performing the experiments, examining the results, and writing—the original draft. JB contributed to conceptualization, design of the chopper, supervision, examining the results, writing—reviewing, and editing. HK contributed to supervision, writing—reviewing, and editing.
Corresponding author
Ethics declarations
Conflict of interest
There is no conflict of interest.
Additional information
Electron-Driven Processes from Single Collisions to High-Pressure Plasmas. Guest editors: Jose L Lopez, Michael Brunger, Holger Kersten.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hahn, T.A., Benedikt, J. & Kersten, H. Absolute densities of O and O\(_3\) in the effluent of an atmospheric pressure plasma jet (kINPen) operated with He and Ar determined by molecular beam mass spectrometry. Eur. Phys. J. D 77, 47 (2023). https://doi.org/10.1140/epjd/s10053-023-00627-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-023-00627-3