1 Introduction

The experimental demonstration of entanglement between two photons is a landmark contribution of Alain Aspect that led to the emergence of the second quantum revolution and to the development of quantum technologies [1]. Today, these technologies exploit a broad diversity of quantum systems that can be isolated and manipulated at the individual level. Among them, nuclear spins in solids stand out for their extremely long coherence time, which results from a high level of isolation from the environment. This property has opened many perspectives in quantum information science [2,3,4,5], metrology [6,7,8] and, more recently, quantum simulations [9]. Despite such interesting prospects, individual nuclear spins have long remained difficult to detect owing to their very low gyromagnetic ratio. A solution to this problem consists in using an ancillary single-electron spin as a quantum sensor allowing to probe remote nuclei coupled by hyperfine interaction [10,11,12]. A prominent example is the single-shot detection and coherent control of individual nuclear spins in diamond obtained by mapping their quantum states onto the electron spin of a single nitrogen-vacancy (NV) color center [13,14,15,16,17]. This atomic-sized impurity has a spin triplet ground state, which can be efficiently polarized by optical pumping, coherently manipulated with microwave magnetic fields and read-out through optically detected magnetic resonance methods [18]. Due to its long coherence time [19], the NV’s electronic spin provides a robust interface to detect and control the quantum state of nuclear spins localized at neighboring lattice sites in the diamond matrix. During the last decade, these nuclei have been extensively used as memory qubits, both for advanced quantum information protocols [20,21,22,23] and for quantum sensing applications [24,25,26,27].

The NV’s electronic spin is always coupled with the nucleus of the nitrogen atom constituting the defect, whose majority isotope \(^{14}\)N (\(> 99.6\%\)) has a nuclear spin \(I_N=1\). Moreover, the lattice sites of the diamond crystal are randomly occupied by \(^{13}\)C atoms (\(I=1/2\)) with a natural isotopic content around \(1.1\%\). These paramagnetic impurities constitute a dilute nuclear spin bath, whose fluctuations are responsible for the decoherence of the NV defect electron spin [28,29,30,31]. However, when a \(^{13}\)C atom is sufficiently close to the NV center, the hyperfine interaction is strong enough to be resolved in electron spin resonance (ESR) spectra, thus allowing nuclear-spin selective control of the coupled quantum system [12,13,14]. Systematic studies of the hyperfine structure of individual NV defects have shown that the hyperfine coupling strength with nearby \(^{13}\text {C}\) nuclei can only take discrete values, which correspond to different neighboring lattice sites in the diamond matrix [32,33,34,35]. To detect such \(^{13}\text {C}\) atoms in ESR spectra, it is however necessary that the strength of the hyperfine coupling exceeds the spectral width of the magnetic resonance, which is intrinsically limited by the decoherence rate \(\gamma _2^{\star }\) of the NV electron spin. For a high-purity diamond crystal with a natural content of \(^{13}\text {C}\) isotope, \(\gamma _2^{\star }\sim 200\) kHz [29]. As a result, only one or two strongly coupled \(^{13}\text {C}\) are at best detected in the vicinity of a given NV defect [34], limiting the size of the quantum register to few qubits. A powerful approach to further increase the size of the quantum register is offered by dynamical decoupling spectroscopy [36,37,38], which enables to detect and control weakly coupled \(^{13}\text {C}\) from the bath. Using such methods, up to ten spin qubits have been recently included in a diamond-based quantum register [39].

Any use of individual \(^{13}\text {C}\) nuclear spin for quantum technologies requires first a reliable initialization of its quantum state. Depending on the strength of the hyperfine interaction, different nuclear spin polarization methods can be employed. For \(^{13}\text {C}\) nuclei featuring a strong hyperfine coupling with the NV’s electron spin (\(\ge 2\) MHz), an efficient polarization can be obtained by exploiting an excited-state level anti-crossing of the NV defect [34, 40]. In this case, electron-nuclear-spin flip-flops mediated by the hyperfine interaction in the NV’s excited state lead to a transfer of electron spin polarization to the nuclear spin by optical pumping. Such a polarization transfer can also be obtained by using nuclear spin selective microwave excitations combined with an applied magnetic field providing a \(^{13}\text {C}\) Larmor precession conditional on the NV electron spin state [14]. For weakly coupled \(^{13}\text {C}\) (\(<200\) kHz), polarization is rather obtained through single-shot readout methods [17, 21, 41] or dynamical decoupling protocols [36].

In this work, we focus on individual \(^{13}\text {C}\) with intermediate hyperfine coupling strengths (\(\sim 1\) MHz), for which the polarization techniques mentioned above are ineffective. We describe two different methods providing an efficient polarization of these peculiar \(^{13}\text {C}\) nuclear spins under ambient conditions. The first one is based on a polarization transfer from the NV electron spin to the \(^{13}\text {C}\) nucleus which is mediated by the anisotropic component of the hyperfine interaction [42,43,44,45]. The second one relies on coherent population trapping within a \(\Lambda \)-type energy-level configuration in the microwave domain [46], which enables to initialize the nuclear spin in any quantum state superposition on the Bloch sphere. For these two techniques, we investigate the impact of optical illumination on the nuclear spin polarization efficiency. This work adds new methods to the quantum toolbox used for coherent control of individual nuclear spins in diamond, which might find applications in quantum metrology [47].

The paper is organized as follows. In Sect. 2, we first introduce the Hamiltonian describing the electron spin of a single NV defect in diamond coupled by hyperfine interaction with a nearby \(^{13}\)C nuclear spin and we give details about the experimental setup. We then describe in Sect. 3 the nuclear spin polarization protocol relying on the \(^{13}\text {C}\) Larmor precession mediated by anisotropic hyperfine coupling. Section 4 is finally devoted to room-temperature initialization of a single nuclear spin via coherent population trapping methods.

2 Spin system

2.1 Spin Hamiltonian

We start by introducing the spin Hamiltonian describing a single NV defect coupled by hyperfine interaction with a nearby \(^{13}\)C nuclear spin (Fig. 1a) [33, 34].

Fig. 1
figure 1

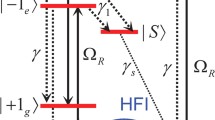
a Energy-level structure of a single NV defect in diamond coupled by hyperfine interaction with a nearby \(^{13}\text {C}\) nuclear spin. All notations are defined in the main text. In this diagram, we consider \({\mathcal {A}}_{zz}<0\) and \(\gamma _n B + {\mathcal {A}}_{zz} \sim 0\), leading to nuclear spin mixing in the \(m_s=-1\) electron spin manifold. The ESR transitions are labeled from to . b ESR spectrum recorded at \(B=850\) G for a single NV defect coupled with a \(^{13}\text {C}\) nuclear spin from ’family I.’ c Same experiment performed at \(B=535\) G for a single NV defect coupled with a \(^{13}\text {C}\) nuclear spin from ’family N.’ Here \({\mathcal {A}}_{zz}>0\) such that nuclear spin mixing occurs in the \(m_s=+1\) electron spin manifold

Full size image

The ground level of the NV defect is an electronic spin triplet (\(S=1\)) with a characteristic zero-field splitting \(D\sim 2.87\) GHz between a singlet state \(m_s=0\) (\(\left| 0_e \right. \rangle \)) and a doublet \(m_s=\pm 1\) (\(\left| \pm 1_e \right. \rangle \)) [18]. Here \(m_s\) denotes the spin projection along the intrinsic quantization axis (z) of the NV defect, which corresponds to the [111] crystal axis joining the nitrogen and the vacancy. For a magnetic field B applied along this axis, the ground-state spin Hamiltonian in frequency units reads

$$\begin{aligned} \hat{{\mathcal {H}}}_0=D{\hat{S}}_{z}^2 - \gamma _eB{\hat{S}}_{z} \, \end{aligned}$$
(1)

where \(\gamma _e\approx -2.8\) MHz/G is the electronic spin gyromagnetic ratio. When a neighboring lattice site of the NV defect is occupied by a \(^{13}\)C nuclear spin (\(I=1/2\)), the spin Hamiltonian describing the coupled spin system is given by

$$\begin{aligned} \hat{{\mathcal {H}}}=\hat{{\mathcal {H}}_{0}} - \gamma _{n}B{\hat{I}}_{z}+\mathbf {{\hat{S}}}\cdot {{\mathcal {A}}}\cdot \mathbf {{\hat{I}}} \, \end{aligned}$$
(2)

where \(\gamma _n=1.07\) kHz/G is the gyromagnetic ratio of the \(^{13}\)C nuclear spin and \({\mathcal {A}}\) denotes the hyperfine interaction tensor. In the secular approximation for the electron spin, this Hamiltonian simplifies as

$$\begin{aligned} \hat{{\mathcal {H}}}= & {} \hat{{\mathcal {H}}}_0 - \gamma _nB{\hat{I}}_z+{\hat{S}}_z{\mathcal {A}}_{zz}{\hat{I}}_z \end{aligned}$$
(3)
$$\begin{aligned}{} & {} +\frac{1}{2}{\mathcal {A}}_{ani}{\hat{S}}_z(e^{-i\phi }{\hat{I}}_++e^{i\phi }{\hat{I}}_-) \, \end{aligned}$$
(4)

where \({\hat{I}}_{\pm }={\hat{I}}_{x}\pm i{\hat{I}}_{y}\) are the nuclear spin ladder operators, \({\mathcal {A}}_{ani}=({\mathcal {A}}_{zx}^{2}+{\mathcal {A}}_{zy}^{2})^{1/2}\) is the anisotropic component of the hyperfine interaction, and \(\tan \phi = {\mathcal {A}}_{zy}/{\mathcal {A}}_{zx}\). We note that the hyperfine interaction with the intrinsic \(^{14}\textrm{N}\) nuclear spin (\(I_N=1\)) of the NV defect is not included in the Hamiltonian since it is not playing any role in the experiments reported in this work. We thus consider a fixed \(^{14}\)N nuclear spin projection, e.g., \(m_{I_{N}}=+1\).

In the following we assume that \({\mathcal {A}}_{zz} < 0\), and the eigenstates of the \({\hat{I}}_z\) operator are denoted as \(\left| \uparrow \right. \rangle \) and \(\left| \downarrow \right. \rangle \). In the \(m_s=0\) electron spin subspace, the eigenstates of the coupled spin system are \(|0_e,\uparrow \rangle \) and \(|0_e,\downarrow \rangle \) with eigenenergies separated by \(\Delta _0=\gamma _nB\) (Fig. 1a). In the \(m_s=-1\) manifold, the eigenstates are expressed as

$$\begin{aligned} |-1_e,+\rangle= & {} \cos (\theta /2)|-1_e,\downarrow \rangle -\sin (\theta /2)e^{-i\phi }|-1_e,\uparrow \rangle \\ |-1_e,-\rangle= & {} \sin (\theta /2) e^{i\phi }|-1_e,\downarrow \rangle +\cos (\theta /2)|-1_e,\uparrow \rangle \, \end{aligned}$$

with

$$\begin{aligned} \tan \theta =\frac{{\mathcal {A}}_{ani}}{\gamma _nB+{\mathcal {A}}_{zz}} . \end{aligned}$$
(5)

and eigenenergies separated by

$$\begin{aligned} \Delta _{-1}=\sqrt{{\mathcal {A}}_{ani}^2+(\gamma _nB+{\mathcal {A}}_{zz})^2} . \end{aligned}$$
(6)

The nuclear spin mixing parameter \(\theta \) can be experimentally controlled by tuning the magnetic field B applied along the NV defect axis. When \(\gamma _n B + {\mathcal {A}}_{zz}\sim 0\), i.e., when \(\theta \sim \pi /2\) and \(\Delta _{-1}\sim {\mathcal {A}}_{ani}\), four ESR transitions can be driven from \(m_s=0\) to \(m_s=-1\). These transitions are labeled from to in Fig. 1a. Such a coupled spin configuration corresponds to a double \(\Lambda \)-scheme in the microwave domain that will be used to perform coherent population trapping of a single nuclear spin in Sect. 4.

In the \(m_s=+1\) electron spin manifold, the eigenstates of the coupled spin system are given by

$$\begin{aligned} |+1_e,+^{\prime }\rangle= & {} \cos (\theta ^{\prime }/2)|+1_e,\downarrow \rangle +\sin (\theta ^{\prime }/2)e^{-i\phi }|+1_e,\uparrow \rangle \\ |+1_e,-^{\prime }\rangle= & {} -\sin (\theta ^{\prime }/2)e^{i\phi }|+1_e,\downarrow \rangle +\cos (\theta ^{\prime }/2)|+1_e,\uparrow \rangle \, \end{aligned}$$

where

$$\begin{aligned} \tan \theta ^{\prime }=\frac{{\mathcal {A}}_{ani}}{\gamma _nB-{\mathcal {A}}_{zz}}. \end{aligned}$$
(7)

Assuming \({\mathcal {A}}_{zz}<0\), the condition \(|{\mathcal {A}}_{zz}-\gamma _nB| \gg {\mathcal {A}}_{ani}\) is always fulfilled, so that \(\theta ^{\prime }\approx 0\) and

$$\begin{aligned} |+1_e,+^{\prime }\rangle= & {} |+1_e,\downarrow \rangle \end{aligned}$$
(8)
$$\begin{aligned} |+1_e,-^{\prime }\rangle= & {} |+1_e,\uparrow \rangle . \end{aligned}$$
(9)

The \(^{13}\)C nuclear spin projections are therefore identical in the \(m_s=0\) and \(m_s =+1\) electron spin manifolds, and only two nuclear-spin conserving ESR transitions can be driven by a microwave excitation. These transitions are labeled and in Fig. 1a. In the following, such ESR transitions without nuclear spin mixing will be used to evaluate the efficiency of nuclear spin polarization.

We note that for a \(^{13}\)C nuclear spin with \({\mathcal {A}}_{zz}>0\), nuclear spin mixing is instead obtained in the \(m_s=+1\) electron spin manifold.

2.2 Experimental details

We investigate native NV defects hosted in a high-purity diamond crystal grown by chemical vapor deposition (Element 6) with a natural abundance of \(^{13}\text {C}\) isotopes (\(1.1\%\)). Individual NV defects are optically isolated at room temperature with a scanning confocal microscope using a laser excitation at 532 nm whose power is set at the saturation intensity of the NV’s optical transition. Under optical illumination, the NV defect is efficiently polarized in the \(m_s=0\) ground state. In addition, it exhibits a spin-dependent PL signal enabling electron spin readout through optically detected magnetic resonance methods [18, 48]. In this work, these properties will be exploited to polarize and readout individual \(^{13}\text {C}\) nuclear spins. A permanent magnet mounted on a three-axis translation stage is used to apply a static magnetic field along the NV defect axis and ESR transitions are driven by a microwave excitation applied through a copper microwire deposited on the crystal surface. Optically detected ESR spectra are recorded by monitoring the spin-dependent PL signal of the NV defect while sweeping the microwave frequency. More details about the experimental setup can be found in Ref. [49].

All experiments reported in this work are performed on two different NV defects. The first one is coupled to a \(^{13}\text {C}\) nuclear spin localized on a neighboring lattice site referred to as ’family I’ in Ref. [34], whose hyperfine interaction is characterized by a longitudinal component \({\mathcal {A}}^{\textrm{I}}_{zz}\sim -1\) MHz. Figure 1b shows the ESR spectrum recorded for this NV defect at a magnetic field \(B=850\) G, i.e., such that \(\gamma _n B + {\mathcal {A}}^{\textrm{I}}_{zz}\sim 0\). As expected, the \(m_s=0\rightarrow m_s=-1\) transition features four hyperfine lines owing to nuclear spin mixing induced by the anisotropic component of the hyperfine interaction. The second NV defect studied below is coupled to a \(^{13}\text {C}\) nuclear spin belonging to ’family N’ that correspond to \({\mathcal {A}}_{zz}^{\textrm{N}}\sim +0.5\) MHz [34]. In this case, nuclear spin mixing occurs in the \(m_s=+1\) manifold. The ESR spectrum recorded at \(B=535\) G is shown in Fig. 1c. Although the four hyperfine lines cannot be properly resolved, the observed broadening of the \(m_s=0\rightarrow m_s=+1\) transition is a signature of nuclear spin mixing.

Fig. 2
figure 2

a Pulse sequence used to detect the nuclear spin Larmor oscillation induced by the anisotropic component of the hyperfine interaction. The microwave \(\pi \)-pulse, which duration is set to \(T_{\pi ,e}=2 \ \mu \)s, selectively excites the nuclear spin projection \(\left| \uparrow \right. \rangle \) (i.e., transitions and  shown in Fig. 1a). b PL signal recorded during the readout laser pulse as a function of the free precession time \(\tau \). The blue solid line is data fitting with a cosine function. The free precession time corresponding to an optimal nuclear spin flip is referred to as \(T_{\pi ,n}\). c,d Larmor frequency as a function of the magnetic field for a \(^{13}\text {C}\) nuclear spin from ‘family I’(c) and from ‘family N’ (d). The black dashed lines are data fitting with Eq. (10)

Full size image

3 Nuclear-spin polarization via anisotropic hyperfine coupling

3.1 Nuclear spin Larmor precession

The anisotropic component of the hyperfine interaction can be exploited to perform coherent manipulation of the nuclear spin [42,43,44]. To illustrate this, we apply the experimental sequence sketched in Fig. 2a to the NV defect coupled with a \(^{13}\text {C}\) belonging to ’family I’ (\({\mathcal {A}}_{zz}<0\)). A laser pulse is first used to initialize the electron spin in \(m_s=0\) by optical pumping. A nuclear-spin selective microwave \(\pi \)-pulse is then applied to transfer the population with nuclear spin state \(\left| \uparrow \right. \rangle \) from the \(m_s=0\) to the \(m_s=-1\) electron spin manifold. After this microwave pulse, the nuclear spin projection is tilted with respect to its quantization axis in the \(m_s=-1\) subspace. As a result, it starts to precess under the effect of the anisotropic hyperfine interaction with a characteristic Larmor frequency

$$\begin{aligned} \nu _{\textrm{R}}=\Delta _{-1}=\sqrt{{\mathcal {A}}_{ani}^2+({\mathcal {A}}_{zz}+\gamma _nB)^2} . \end{aligned}$$
(10)

Following a free precession time \(\tau \), a second microwave \(\pi \)-pulse is applied to bring the remaining population in \(\left| \uparrow \right. \rangle \) from \(m_s=-1\) to \(m_s=0\). A laser pulse is finally used to readout the population in \(m_s=0\) through a measurement of the spin-dependent PL signal. This sequence is repeated continuously to average the PL signal while increasing the free precession time.

Fig. 3
figure 3

a Nuclear spin polarization and readout sequence. b,c Polarization of a \(^{13}\text {C}\) nuclear spin from ‘family I’ (b) and from ‘family N’ (c). The top panels correspond to the ESR spectra obtained without applying the nuclear spin polarization step. The middle (resp. bottom) panels show the ESR spectra obtained by including the polarization step with a microwave \(\pi \)-pulse exciting selectively the nuclear spin projection \(\left| \downarrow \right. \rangle \) (resp. \(\left| \uparrow \right. \rangle \)). Solid lines are data fitting with Gaussian functions. The duration of the laser pulses used for polarization transfer and spin readout are set to 300 ns. d Probability \({\mathcal {P}}_{\left| \uparrow \right. \rangle }\) plotted as a function of the total duration \(T_{\textrm{tot}}\) of the laser pulses used in the experimental sequence. The measurements are performed for the \(^{13}\text {C}\) from ’family I’ at two different magnetic fields. The data are plotted on a semi-log scale

Full size image

The result of this experiment performed at \(B\sim 900\) G is depicted in Fig. 2b. We observe an oscillation of the PL signal that corresponds to a Larmor precession at the frequency \(\nu _{\textrm{R}}\) between the \(\left| \uparrow \right. \rangle \) and \(\left| \downarrow \right. \rangle \) nuclear spin states in the \(m_s=-1\) spin subspace. The evolution of the Larmor frequency with the magnetic field is shown in Fig. 2c. By fitting the data with Eq. (10), we infer the hyperfine interaction components for a \(^{13}\text {C}\) nuclear spin belonging to ’family I,’ \({\mathcal {A}}_{zz}^{\textrm{I}}=-1047\pm 6\) kHz and \({\mathcal {A}}_{ani}^{\textrm{I}}=360\pm 3\) kHz. These values are in fair agreement with previous experimental work using different measurement methods [34] and with ab initio theoretical calculations [35]. The same experiments were also performed for a single NV defect coupled to a \(^{13}\text {C}\) from ’family N’ (Fig. 2d), leading to \({\mathcal {A}}_{zz}^{\textrm{N}}=+565\pm 7\) kHz and \({\mathcal {A}}_{ani}^{\textrm{N}}=209\pm 5\) kHz.

Besides providing an alternative method to characterize the components of the hyperfine interaction, these measurements enable to infer the free precession time \(T_{\pi ,n}\) that corresponds to a nuclear spin inversion induced by the anisotropic hyperfine coupling (Fig. 2b). Obtaining an optimal nuclear spin flip involves several experimental constraints. First the magnetic field must fulfill the condition \(\gamma _nB+{\mathcal {A}}_{zz}\sim 0\) to achieve maximum nuclear spin mixing, thus optimizing the amplitude of the Rabi oscillation. Second, the microwave \(\pi \)-pulse has to selectively excite a given nuclear spin projection. To drive the nuclear spin state \(\left| \uparrow \right. \rangle \) (resp. \(\left| \downarrow \right. \rangle \)), the \(\pi \)-pulse must excite simultaneously the ESR transitions and  (resp. and ). Such a nuclear spin selectivity is fulfilled if the \(\pi \)-pulse duration \(T_{\pi ,e}\) is such that \(\Delta _{-1}\ll T_{\pi ,e}^{-1}\ll \Delta _0\) (see Fig. 1a). For a magnetic field maximizing nuclear spin mixing, this condition can be expressed as

$$\begin{aligned} {\mathcal {A}}_{ani}\ll T_{\pi ,e}^{-1}\ll |{\mathcal {A}}_{zz}| \, \end{aligned}$$
(11)

which is hard to satisfy for \(^{13}\text {C}\) nuclear spins featuring a weak hyperfine coupling strength. For the experiments described above, the microwave power was adjusted to obtain a \(\pi \)-pulse duration \(T_{\pi ,e}=2 \ \mu \)s that corresponds to a spectral width around 500 kHz. Given the hyperfine coupling strength considered in this work, Eq. (11) is not perfectly satisfied in our experiments, leading to a reduced fidelity of the nuclear spin flip. This is one of the limiting factor of the nuclear spin polarization protocol described in the next section.

3.2 Nuclear spin polarization

The experimental sequence used to achieve nuclear spin polarization is depicted in Fig. 3a. Starting with the electron spin initialized in \(m_s=0\), a nuclear spin-selective microwave \(\pi \)-pulse is followed by a free precession time \(T_{\pi ,n}\) which results in a nuclear spin flip in the \(m_s=-1\) electron spin subspace. Such a nuclear spin flip is then transferred to the \(m_s=0\) manifold through optical pumping with a green laser pulse. If the selective microwave \(\pi \)-pulse is applied on the nuclear spin projection \(\left| \downarrow \right. \rangle \) (resp. \(\left| \uparrow \right. \rangle \)), this simple sequence leads to nuclear spin pumping in state \(\left| \uparrow \right. \rangle \) (resp. \(\left| \downarrow \right. \rangle \)). In order to measure the resulting polarization without disturbing it, we perform pulsed ESR spectroscopy of the hyperfine transitions without nuclear spin mixing, which are labeled and in Fig. 1. To this end, the nuclear spin polarization step is followed by a microwave \(\pi \)-pulse and a readout laser pulse (Fig. 3a). ESR spectra are recorded by continuously repeating the whole sequence while sweeping the frequency of the readout microwave \(\pi \)-pulse across the transitions and , and monitoring the spin-dependent PL signal.

The resulting ESR spectra are gathered in Fig. 3b for the NV defect coupled to a \(^{13}\text {C}\) nuclear spin from ’family I.’ When the nuclear spin polarization step is not introduced in the experimental sequence, the amplitudes of the ESR transitions and are identical (top panel), showing that the nuclear spin is in a thermal state with equal populations in \(\left| \uparrow \right. \rangle \) and \(\left| \downarrow \right. \rangle \), as expected. By including the polarization step, one of the ESR lines almost cancels out whereas the amplitude of the other becomes two times higher, revealing an efficient nuclear spin polarization. As discussed above, the nuclear spin can be polarized either in state \(\left| \uparrow \right. \rangle \) (middle panel) or in state \(\left| \downarrow \right. \rangle \) (bottom panel), by changing the nuclear-spin selectivity of the microwave excitation. As shown in Fig. 3c, similar results are obtained for the \(^{13}\text {C}\) nuclear spin from ’family N,’ thus illustrating the generality of the method.

The probability \({\mathcal {P}}_{\left| \uparrow (\downarrow ) \right. \rangle }\) to find the nuclear spin in state \(\left| \uparrow (\downarrow ) \right. \rangle \) can be measured as

$$\begin{aligned} {\mathcal {P}}_{\left| \uparrow (\downarrow ) \right. \rangle }=\frac{{\mathcal {I}}_{\left| \uparrow (\downarrow ) \right. \rangle }}{{\mathcal {I}}_{\left| \downarrow \right. \rangle }+{\mathcal {I}}_{\left| \uparrow \right. \rangle }} \, \end{aligned}$$
(12)

where \({\mathcal {I}}_{\left| \uparrow (\downarrow ) \right. \rangle }\) is the integral of the ESR line corresponding to the nuclear spin state \(\left| \uparrow (\downarrow ) \right. \rangle \). For the \(^{13}\text {C}\) nuclear spin from ’family I,’ we obtain \({\mathcal {P}}^{\textrm{I}}_{\left| \uparrow \right. \rangle }=84 \pm 3 \%\) and \({\mathcal {P}}^{\textrm{I}}_{\left| \downarrow \right. \rangle }=83 \pm 3 \%\). The polarization is slightly less efficient for ’family N,’ \({\mathcal {P}}^{\textrm{N}}_{\left| \uparrow \right. \rangle }=78 \pm 3 \%\) and \({\mathcal {P}}^{\textrm{N}}_{\left| \downarrow \right. \rangle }=76 \pm 3 \%\), because Eq. (11) is more difficult to fulfill for weakly coupled \(^{13}\text {C}\) nuclei.

The nuclear spin polarization efficiency is governed by several parameters of the spin system. First, it is limited by the electron spin polarization efficiency of the NV defect under optical pumping [50], a parameter measured around \(90 \%\) at room temperature [51]. Besides this intrinsic limit, the steady-state nuclear spin polarization obtained in our experiments is linked to (i) the selectivity of the microwave excitation, (ii) the efficiency of the nuclear spin flip induced by the anisotropic hyperfine interaction and (iii) the fidelity of its transfer to the \(m_s=0\) electron spin manifold by optical pumping. The laser pulse used for this transfer is known to depolarize the nuclear spin during optical cycles [14, 44, 52], leading to an overall reduction of the polarization efficiency. Such an optically induced nuclear spin relaxation also occurs during the laser pulse employed for polarization readout. To illustrate this effect, the probability \({\mathcal {P}}_{\left| \uparrow \right. \rangle }\) was measured while increasing the total duration \(T_{\textrm{tot}}\) of the laser pulses used in the experimental sequence. The results obtained at two different magnetic fields for the \(^{13}\text {C}\) from ’family I’ are shown in Fig. 3d. We observe an exponential decrease of the nuclear spin polarization with \(T_{\textrm{tot}}\). We note that the duration of each laser pulse cannot be reduced below \(\sim 300\) ns in order to ensure both efficient polarization transfer and spin readout [49]. In addition, we observe that the polarization efficiency vanishes faster when the magnetic field is detuned from the condition \(\gamma _nB+{\mathcal {A}}_{zz}\sim 0\), owing to a reduced fidelity of the nuclear spin flip in the \(m_s=-1\) manifold. A more quantitative analysis of nuclear spin relaxation under optical illumination will be given in Sect. 4.3.

The polarization protocol described above makes it possible to initialize the nuclear spin state either in state \(\left| \uparrow \right. \rangle \) or in state \(\left| \downarrow \right. \rangle \). To obtain full control over the nuclear spin state, it is however necessary to prepare any coherent superposition on the Bloch sphere. Although this can be achieved through coherent manipulation of the nuclear spin state with a resonant radio-frequency excitation, we will describe in the next section an alternative approach based on coherent population trapping methods.

4 Nuclear spin polarization via coherent population trapping with controlled dissipation

4.1 Coherent population trapping of a single nuclear spin

Coherent population trapping (CPT) is a quantum interference effect that occurs in three-level quantum systems featuring a \(\Lambda \)-type configuration, i.e., with two fundamental levels coupled to the same excited level. The simultaneous coherent excitation of the two transitions leads to the pumping into a coherent superposition of the fundamental levels, which is commonly referred to as dark state because it is perfectly decoupled from the excitation of the quantum system [53]. Since its discovery in the seventies [54,55,56], CPT has found numerous applications in atomic physics, from laser cooling of atoms and molecules [57, 58], to metrology [59, 60] and quantum information storage [61, 62]. More recently, this powerful method has been extended to various solid-state quantum systems including optically active electron spin impurities [63,64,65] and superconducting circuits [66, 67].

Below, we make use of CPT methods to polarize a single \(^{13}\text {C}\) nuclear spin in diamond at room temperature [46]. All the experiments described in this section make use of a single NV defect coupled with a \(^{13}\text {C}\) nuclear spin from ’family I’ at a magnetic field \(B=850\) G. As discussed in Sect. 2.1, nuclear spin mixing induced by the anisotropic hyperfine interaction results in two \(\Lambda \)-level configurations in the microwave domain (Fig. 1a). One of these \(\Lambda \)-level structures \(\{\left| 0_e,\uparrow \right. \rangle ,\left| 0_e,\downarrow \right. \rangle ,\left| -1_e,+ \right. \rangle \}\) can be isolated and its ESR transitions coherently driven with two microwave excitations, MW\(_1\) and MW\(_2\). As sketched in Fig. 4a, the frequency of MW\(_1\) is set on resonance while MW\(_2\) is detuned by \(\delta \). When the two-photon resonance condition \(\delta =0\) is satisfied, the eigenstates of the coupled spin system are given by [53]

$$\begin{aligned} \left| B\right. \rangle= & {} \frac{1}{\sqrt{\Omega _1^2+\Omega _2^2}}\left( \Omega _1\left| 0_e,\downarrow \right. \rangle +\Omega _2\left| 0_e,\uparrow \right. \rangle \right) \end{aligned}$$
(13)
$$\begin{aligned} \left| D\right. \rangle= & {} \frac{1}{\sqrt{\Omega _1^2+\Omega _2^2}}\left( \Omega _2\left| 0_e,\downarrow \right. \rangle -\Omega _1\left| 0_e,\uparrow \right. \rangle \right) \end{aligned}$$
(14)

where \(\Omega _1\) and \(\Omega _2\) are the Rabi frequencies characterizing the strength of the microwave coupling on each branch of the \(\Lambda \)-scheme. The dark state \(\left| D\right. \rangle \) is perfectly decoupled from the microwave excitations. Conversely, the population of the bright state \(\left| B\right. \rangle \) is efficiently coupled to the \(\left| -1_e,+\right. \rangle \) level with an effective Rabi frequency \(\Omega =\sqrt{\Omega _1^2+\Omega _2^2}\), and then partially transferred to the dark state by relaxation (Fig. 4b). After several excitation cycles, the system is thus trapped in the dark state. The relaxation process in atomic systems is commonly provided by spontaneous emission. For our coupled spin system, relaxation is rather controlled externally by applying a laser pulse which triggers the decay of populations from the \(\left| -1_e,+\right. \rangle \) states towards \(\left| D\right. \rangle \) and \(\left| B\right. \rangle \) in the \(m_s=0\) manifold (Fig. 4b) [46].

Fig. 4
figure 4

a \(\Lambda \)-level configuration in the microwave domain. b Sketch illustrating the coupling between the eigenstates of the \(\Lambda \) scheme at the two-photon resonance condition \(\delta =0\). All notations are defined in the main text. The relaxation from the excited level \(\left| -1_e,+ \right. \rangle \) is triggered by a green laser excitation (green arrows). c ESR spectrum recorded by applying the pulse sequence shown in inset with a duration of the laser pulse \(T_L=300\) ns. The dip observed at \(\delta =0\) is the signature of CPT in the dark state

Full size image

CPT of a single nuclear spin is revealed by recording an ESR spectrum while applying the experimental sequence sketched in Fig. 4c. The two branches of the \(\Lambda \)-scheme are simultaneously excited with two microwave pulses to obtain a quantum interference between the transition probabilities. A laser pulse is subsequently applied both to trigger relaxation of the spin system into the dark state and to perform electron spin readout by recording the spin dependent PL signal. The laser pulse duration is set to \(T_L=300\) ns in order to optimize the readout contrast while minimizing nuclear spin dephasing induced by optical cycles. By repeating continuously this simple sequence, an ESR spectrum can be recorded by monitoring the PL signal while sweeping the detuning \(\delta \) across the resonance (Fig. 4c). The observation of a highly contrasted dip at two-photon resonance \(\delta =0\) indicates an efficient polarization of the spin system in the dark state. Interestingly, it was shown in a previous work that the composition of the dark state can be modified by changing \(\Omega _1\) and \(\Omega _2\) [see Eq. (14)], providing an efficient way to directly prepare the nuclear spin in any quantum state superposition on the Bloch sphere [46]. In the following sections, we investigate the dynamics of nuclear spin dephasing induced by the laser pulse that is employed to trigger relaxation in the \(\Lambda \)-level configuration.

4.2 Rabi oscillations within the \(\Lambda \)-scheme

Fig. 5
figure 5

a Pulse sequence used to record Rabi oscillations within the \(\Lambda \)-scheme. The PL signal is integrated during the first 300 ns of the laser pulse, whose duration is fixed to \(100 \ \mu \)s in order to reset the nuclear spin in a thermal state at the end of the sequence. b PL signal plotted as a function of the duration \(\tau \) of the dual microwave excitation. The top panel is obtained for \(\Omega _1=0\) and the bottom panel for \(\Omega _1/\Omega _2=1.08\). Solid lines are data fitting with cosine functions. The data are vertically shifted for the sake of clarity. c Evolution of the effective Rabi frequency \(\Omega /2\pi \) as a function of \(\Omega _1/\Omega _2\). The red dashed line corresponds to \(\Omega =\Omega _2\sqrt{1+(\Omega _1/\Omega _2)^2}\)

Full size image

To optimize the efficiency of dark state pumping, we first perform Rabi oscillations within the \(\Lambda \)-level configuration using the sequence sketched in Fig. 5a. Starting with the electron spin polarized in the \(m_s=0\) subspace and the \(^{13}\text {C}\) nuclear spin in a thermal state, we apply simultaneously the two microwaves excitations at two-photon resonance \(\delta =0\) during a time \(\tau \). A laser pulse is then used for optical readout of the electron spin state. The duration of this laser pulse is set to \(100 \ \mu \)s in order to start the next sequence with the nuclear spin reset to a thermal distribution. This measurement is repeated for different durations of the microwave pulse to reveal the Rabi oscillation at frequency \(\Omega =\sqrt{\Omega _1^2+\Omega _2^2}\) between the levels \(\left| B\right. \rangle \) and \(\left| -1_e,+\right. \rangle \). The experiment is reproduced by tuning the Rabi frequency \(\Omega _1\) while keeping \(\Omega _2\) constant.

Figure 5b shows the results obtained for two different values of \(\Omega _1\). The top curve is recorded for \(\Omega _1=0\), such that \(\left| B\right. \rangle =\left| 0_e,\uparrow \right. \rangle \) and \(\left| D\right. \rangle =\left| 0_e,\downarrow \right. \rangle \). From these data, we infer \(\Omega /2\pi =\Omega _2/2\pi =136\pm 4\) kHz. The bottom curve is recorded for \(\Omega _1\sim \Omega _2\), leading to \(\Omega /2\pi =200\pm 5\) kHz. It corresponds to an increase of the Rabi frequency by a factor \(\sqrt{2}\), which is a characteristic signature of the quantum interference between the transition probabilities in the \(\Lambda \)-level configuration. The effective Rabi frequency \(\Omega \) is plotted as a function of \(\Omega _1/\Omega _2\) in Fig. 5c. The experimental results are very well reproduced by the theoretical prediction \(\Omega =\sqrt{\Omega _1^2+\Omega _2^2}\).

Such measurements of the Rabi oscillation enable us to infer the duration of a dual microwave \(\pi \)-pulse which maximizes population transfer to the excited level of the \(\Lambda \)-scheme. Below, all measurements are performed with such a \(\pi \)-pulse on the transition \(\left| B\right. \rangle \rightarrow \left| -1_e,+\right. \rangle \).

4.3 Step-by-step dark state pumping

The pulsed-CPT protocol described above is performed in an unusual regime for which relaxation from the excited level of the \(\Lambda \)-scheme is externally triggered through incoherent optical pumping and well-separated in time from coherent microwave excitations [46]. This CPT method with controlled dissipation can be used to investigate the dynamics of the sequential accumulation of population in the dark state. To this end, the CPT sequence including a dual microwave \(\pi \)-pulse followed by a laser pulse of duration \(T_L\) is repeated N times, as sketched in the inset of Fig. 6.

At the beginning of the \(N^\textrm{th}\) pumping sequence, the populations in the ground levels of the \(\Lambda \)-scheme, \(\left| D\right. \rangle \) and \(\left| B\right. \rangle \), are the one obtained at the end of the \((N-1)^\textrm{th}\) sequence, \({\mathcal {P}}_{\left| D\right. \rangle }(N-1)\) and \({\mathcal {P}}_{\left| B\right. \rangle }(N-1)\). Considering an ideal polarization of the NV defect in the \(m_s=0\) manifold by optical pumping, these populations are linked by \({\mathcal {P}}_{\left| D\right. \rangle }(N-1)+{\mathcal {P}}_{\left| B\right. \rangle }(N-1)=1\). After applying the dual microwave \(\pi \)-pulse, the population in the excited-level \(\left| -1_e,+\right. \rangle \) is then given by

$$\begin{aligned} {\mathcal {P}}_{\left| -1_e,+\right. \rangle }(N)={\mathcal {P}}_{\left| B\right. \rangle }(N-1) \, \end{aligned}$$
(15)

such that the probability to find the spin system in the dark state simply reads

$$\begin{aligned} {\mathcal {P}}_{\left| D\right. \rangle }(N-1)=1-{\mathcal {P}}_{\left| -1_e,+\right. \rangle }(N) . \end{aligned}$$
(16)

The sequential accumulation of population in the dark state can thus be inferred by measuring the population in state \(\left| -1_e,+\right. \rangle \) through a spin-dependent PL measurement at each repetition of the CPT sequence [46]. Figure 6 shows the results of this experiment performed for different laser pulse durations \(T_L\) and a dual microwave excitation with \(\Omega _1/\Omega _2=0.26\). Starting from a thermal state \({\mathcal {P}}_{\left| D\right. \rangle }(0)=1/2\), the population of the dark state increases exponentially with the number of CPT steps and reaches a steady-state value that corresponds to the efficiency of dark state pumping. Here, the polarization efficiency reaches \(\sim 85\%\) for the shortest laser pulse duration \(T_L=300\) ns, and drops to \(\sim 58\%\) when \(T_L=8 \ \mu \)s. Such results are similar to the one reported in Sect. 3.2 (Fig. 3d).

Fig. 6
figure 6

Probability \({\mathcal {P}}_{\left| D\right. \rangle }\) to find the \(^{13}\text {C}\) nuclear spin in the dark state after N pumping steps (see inset) for a dual microwave \(\pi \)-pulse characterized by \(\Omega _1/\Omega _2=0.26\). The experiment is performed for different durations \(T_L\) of the laser pulse used to trigger the relaxation of the \(\Lambda \)-scheme. The solid lines are data fitting with Eq. (19) from which the parameters \(\alpha _p\) and \(\alpha _{dp}\) are extracted

Full size image

These dynamics can be understood by considering the competition between (i) dark state pumping with a probability \(\alpha _p\) per CPT step and (ii) nuclear spin dephasing induced by optical cycles, with a probability \(\alpha _{dp}\) per step expressed as

$$\begin{aligned} \alpha _{dp}=1-\exp (-\Gamma _{dp}T_L ) \, \end{aligned}$$
(17)

where \(\Gamma _{dp}\) denotes the nuclear-spin dephasing rate under optical illumination. Using the simple rate equation model introduced in Ref. [46], the dark state population after N pumping steps can then be written as

$$\begin{aligned} {\mathcal {P}}_{|D\rangle } (N)= & {} \frac{\alpha _p + \alpha _{dp}(0.5 - \alpha _p)}{\alpha _p + \alpha _{dp}(1 - \alpha _p)} \end{aligned}$$
(18)
$$\begin{aligned}- & {} 0.5\frac{\alpha _p(1-\alpha _{dp})}{\alpha _p + \alpha _{dp}(1 - \alpha _p)}\exp \left( -\frac{N}{N_s}\right) , \end{aligned}$$
(19)

where \(N_s = -1/\ln [1-\alpha _p - \alpha _{dp}(1-\alpha _p)]\) is the characteristic number of pumping steps to reach the steady state.

Sequential dark state pumping experiments were fitted with Eq. (19) to infer the evolution of the parameter \(\alpha _{dp}\) with the laser pulse duration \(T_L\). As shown in Fig. 7a [red curve], \(\alpha _{dp}\) increases exponentially with \(T_L\). Data fitting with Eq. (17) leads to \(\Gamma _{dp}=0.14\pm 0.01 \ \mu \textrm{s}^{-1}\). For these experiments, the dual microwave excitation is characterized by \(\Omega _1/\Omega _2\sim 0.26\) so that the dark state composition is close to a population state \(\left| D\right. \rangle \sim \left| 0_e,\downarrow \right. \rangle \) [see Eq. (14)]. As a result, the parameter \(\Gamma _{dp}\) extracted from these measurements mainly corresponds to the longitudinal nuclear spin relaxation time under optical illumination \(T_{1,n}^{\textrm{laser}}\sim 1/\Gamma _{dp}=7.0\pm 0.4 \ \mu \)s. The same experiments were then performed for a dual microwave excitation with \(\Omega _1/\Omega _2\sim 1.08\), yielding a much faster dephasing rate \(\Gamma _{dp}=0.66\pm 0.05 \ \mu \textrm{s}^{-1}\) (see Fig. 7a, blue curve). In this case, the dark state is close to an optimal coherent superposition \(\left| D\right. \rangle \sim \frac{1}{\sqrt{2}}\left( \left| 0_e,\downarrow \right. \rangle -\left| 0_e,\uparrow \right. \rangle \right) \). The dephasing rate \(\Gamma _{dp}\) is therefore linked to the transverse nuclear spin relaxation time under optical illumination \(T_{2,n}^{\textrm{laser}}\sim 1/\Gamma _{dp}=1.5\pm 0.1 \ \mu \)s. These results show that nuclear spin coherences are less robust than populations under optical illumination. This is further illustrated by Fig. 7b where the parameter \(\alpha _{dp}\) is plotted as a function of \(\Omega _1/\Omega _2\) for a fixed value of the laser pulse duration \(T_L=300\) ns. We observed that \(\alpha _{dp}\) reaches a maximum for \(\Omega _1/\Omega _2\sim 1\). As a result, the polarization efficiency is reduced for dark states corresponding to a coherent superposition of the \(^{13}\text {C}\) nuclear spin states (Fig. 7c).

Fig. 7
figure 7

a Probability \(\alpha _{dp}\) as a function of the duration \(T_L\) of the laser pulse obtained for \(\Omega _1/\Omega _2=0.26\) (red) and \(\Omega _1/\Omega _2=1.08\) (blue). Solid lines are data fitting with Eq. (17). b Probability \(\alpha _{dp}\) plotted as a function of \(\Omega _1/\Omega _2\) on a semi-log scale for a laser pulse duration fixed to \(T_L=300\) ns. The black dashed line is a fit to the data using Eq. (20). c Probability \({\mathcal {P}}_{\left| D\right. \rangle }\) to find the \(^{13}\text {C}\) nuclear spin in the dark state after N pumping steps for a dual microwave \(\pi \)-pulse characterized by \(\Omega _1/\Omega _2=0.26\) (red) and \(\Omega _1/\Omega _2=1.08\) (blue) using \(T_L=300\) ns. Solid lines are data fitting with Eq. (19)

Full size image

The behavior observed in Fig. 7b can be modeled by considering a pure nuclear spin dephasing process with rate \(\gamma _d\) and a thermalization process or spin flips with a symmetric rate \(\gamma \), both in the nuclear basis \(\{\left| \uparrow \right. \rangle ,\left| \downarrow \right. \rangle \}\) and under optical illumination. Using Bloch equation formalism, the expected behavior for \(\alpha _{dp}\) is given by

$$\begin{aligned} \alpha _{dp}T_L^{-1}\approx 2\gamma + 4(\gamma _d-\gamma )\left( \frac{\Omega _1/\Omega _2}{1+\left( \Omega _1/\Omega _2\right) ^2}\right) ^2. \end{aligned}$$
(20)

Note that this equation is only valid for \(\Gamma _{dp}T_L\ll 1\), such that \(\Gamma _{dp}\approx \alpha _{dp}T_L^{-1}\) [see Eq. (17)]. Fitting the data shown in Fig. 7b with Eq. (20) leads to a thermalization rate \(\gamma =200\pm 30\) kHz and a pure dephasing rate \(\gamma _d=790\pm 80\) kHz. These two processes are expected for a nuclear spin interacting with an electronic spin via hyperfine interaction where both nuclear spin precession (due to \({\mathcal {A}}_{zz}\)) and nuclear spin flips (due to \({\mathcal {A}}_{ani}\)) might take place. Furthermore, the obtained rates are of the order of the hyperfine interaction terms for a nuclear spin of ’family I’ (see Section IIIA). We finally note that these rates are related to the relaxation times \(T_{1,n}^{\text {laser}}\) and \(T_{2,n}^{\text {laser}}\) introduced above. Indeed, in the limit \(\Omega _1/\Omega _2\rightarrow 0\), only the thermalization rate \(\gamma \) plays a role leading to \(\Gamma _{dp} \approx 2\gamma \sim 1/T_{1,n}^{\text {laser}}\). Meanwhile, when \(\Omega _1/\Omega _2 = 1\), the thermalization rate \(\gamma \) and the pure dephasing rate \(\gamma _d\) participate, leading to \(\Gamma _{dp}\approx \gamma +\gamma _d\sim 1/T_{2,n}^{\text {laser}}\).

5 Conclusion

To summarize, we have described two different methods providing room-temperature polarization of individual \(^{13}\text {C}\) nuclear spins featuring a moderate hyperfine coupling strength (\(\sim 1\) MHz) with a single NV defect in diamond. For both approach, we have shown that the polarization efficiency remains limited by nuclear spin dephasing under optical illumination. The presented polarization and CPT techniques could be scaled up to more nuclei by using the hyperfine coupling between the NV electronic spin and the intrinsic \(^{14}\)N nuclear spin under transverse magnetic fields [68]. These methods could find use for efficient quantum information storage of microwave photons in superconducting resonators [69], quantum metrology [47] and coherent control of nuclear spins through stimulated Raman adiabiatic passage [70].