1 Introduction

One of the greatest challenges when describing a scientific revolution is to structure, from the future, a linear and coherent narrative of how ideas emerged, and how they were discussed, combined, proved and disproved so as to finally converge into a theory. This difficulty is particularly pronounced in what concerns quantum physics. Not only there is no complete consensus about its interpretation, but also it is not clear whether it is indeed possible to have a single only interpretation of it. In addition, and for some people, most importantly, many of the existing interpretations require completely abandoning some principles of physics which are known as “classical”. In spite of all that, we keep on doing research, predicting and confirming physical phenomena that would not have been imaginable if we hadn’t agreed at some point that controversial as it is, using whatever interpretation we chose, quantum physics is the most accurate theory to describe and predict physical phenomena at a given scale.

Nevertheless, and as a consequence of this debate, a recurrent question arises when observing and studying quantum phenomena: what is so quantum about all that? Is this really quantum? Indeed, it is a hard to answer question, which becomes even harder when followed by its twin sibling: “what’s the classical counterpart of the situation I am studying? ”, “what should I compare my results to?” “Is it possible to compare quantum to classical?”.

It is clear that quantum computing and quantum information science brought some light into these problems, by defining quantum advantage, or supremacy, as the power of some quantum algorithms and protocols to move problems from one complexity class to another. This is an objective method to separate quantum from non-quantum phenomena. Putting all this into work and using quantum mechanics to solve practical problems by designing quantum machines is what A. Aspect termed the second quantum revolution.

From the physics and quantum optics point of view, the quantum/classical frontier and questions about how to define it and place it seems less explicit, but we cannot avoid plunging into them when we thumb through Mr. A. Aspect’s lectures, in particular [1], seeking for inspiration for writing the introduction of a paper in his honor. What does he mean when he says something is quantum or classical? Does it make sense?

Starting from these questions, we concentrate on some interesting aspects of one of the experiments Mr. A. Aspect uses to illustrate the differences between quantum and classical physics in his lectures, the Hong–Ou–Mandel (HOM) experiment [2]. We’ll see how this experiment, which we briefly describe and discuss in Sect. 2, followed by its classical analog (Sect. 2.1), can be associated with the time-frequency phase space (Sect. 3), and finally we provide some applications of our results (Sect. 4).

2 The Hong–Ou–Mandel experiment

Quantum phenomena are usually, if not always, associated with interference effects. The Hong–Ou–Mandel experiment is an example of a clever way to use an interferometer to probe photon indistinguishability using a consequence of the bosonic commutation relations. Indeed, the experiment shows that indistinguishable photons (even when generated by independent sources with no a priori phase relation) interfere in such a way that they both exit the same output port of the interferometer. We call this behavior “bunching”, and its experimental signature is the absence of coincidence detections (the famous HOM dip). To understand this behavior, we consider two photons in different spatial modes, each one of them associated with one input arm of the interferometer. We define the following notation: \(\hat{a}_i^{\dagger }(\omega _i)|0 \rangle =|1_{\omega _i} \rangle =|\omega _i \rangle \), so that the corresponding state can be described in the general form

$$\begin{aligned} |\psi \rangle =\int \int f(\omega _1,\omega _2)|\omega _1, \omega _2 \rangle \textrm{d}\omega _1 \textrm{d}\omega _2, \end{aligned}$$
(1)

where the indices \(i=1,2\) denote different spatial modes and \(\omega \) is an arbitrary photonic degree of freedom, as the transverse position and momentum or frequency. In the present contribution, we consider pure states, while the general expressions are given in Sect. 2.1. As a representative case, we focus on the frequency degree of freedom. We will present our framework in the description of an experimental system consisting of semiconductor waveguides emitting frequency and/or polarization correlated photon pairs by spontaneous parametric down conversion (SPDC) [3,4,5]. A more detailed description of the experimental device can be found in Sect. 4.

In the particular case of indistinguishable photons emitted from independent sources, we have that \( f(\omega _1,\omega _2)=g(\omega _1)g(\omega _2)e^{i\phi }\) in Eq. (1), which means that the spectral amplitude of each photon is the same up to an arbitrary and random phase factor (a consequence from the fact that photons are independent).

In many experiments, the two photons come from a common source, as is the case in SPDC. For clarity, we’ll consider in the present contribution the situation where the two photons can be distinguished either by polarization or by propagation direction, so as they can be sent to different arms of an interferometer. This is illustrated in Fig. 1 (which corresponds to a modified version of the original HOM experiment), where two photons that have, say, orthogonal polarization, are spatially split by a polarizing beam splitter and take different propagation directions associated with different arms of an interferometer. Then, in the interferometer, one of the two photons polarization is rotated so as to become identical to the other’s. After a 50/50 beam-splitter, the input spatial modes are combined in the following way: \(\hat{a}_A(\omega ) = (\hat{a}_1(\omega )+\hat{a}_2(\omega ))/\sqrt{2}\) and \(\hat{a}_B(\omega ) = (\hat{a}_1(\omega )-\hat{a}_2(\omega ))/\sqrt{2}\), where A and B are the output spatial modes where photons are detected in coincidence after leaving the beam-splitter. Thus, the state described by Eq. (1) is transformed into:

$$\begin{aligned} |\psi \rangle= & {} \times \frac{1}{2}\int \int g(\omega _1)g(\omega _2)e^{i\phi } (\hat{a}_A^{\dagger }(\omega _1)\hat{a}_B^{\dagger }(\omega _2)\nonumber \\{} & {} -\hat{a}_A^{\dagger }(\omega _2)\hat{a}_B^{\dagger }(\omega _1) \nonumber \\{} & {} +\hat{a}_A^{\dagger }(\omega _1)\hat{a}_A^{\dagger }(\omega _2)-\hat{a}_B^{\dagger }(\omega _1)\hat{a}_B^{\dagger }(\omega _2))|0 \rangle \textrm{d}\omega _1 \textrm{d}\omega _2.\nonumber \\ \end{aligned}$$
(2)

Two single photon detectors are used to measure temporal correlations between the photons exiting the two output ports. We now focus on the coincidence detection probability. The terms in the third line of Eq. (2) correspond to photon bunching and do not lead to coincidence detections, since both photons leave the interferometer in the same spatial mode. They are thus ignored from now on, and we focus on the two first terms in the r.h.s. of Eq. (2). The coincidence detection probability \(\mathcal{C}\) between photons in modes A and B is given by the square of the absolute value of this term. We have thus:

$$\begin{aligned} \mathcal{C} = \frac{1}{2}- \frac{1}{2}\int \int |g(\omega _1)|^2 |g(\omega _2)|^2 \textrm{d}\omega _1 \textrm{d}\omega _2, \end{aligned}$$
(3)

and using the normalization condition \(\int \int |g(\omega _1)|^2 |g(\omega _2)|^2 \textrm{d}\omega _1 \textrm{d}\omega _2 =1\), we obtain that \(\mathcal{C}=0\) irrespectively of the phase \(\phi \). Consequently, we can conclude that independent photons sent in different arms of a balanced interferometer always bunch and exit the interferometer from the same port.

This important result can be made even more interesting if we add some spice to it, in the form of a controllable optical path difference between the input photons. In this case, the initial state right before impinging the beam splitter in Fig. 1 is characterized by the wave function \( f(\omega _1,\omega _2)=g(\omega _1)g(\omega _2)e^{i\omega _1 \tau }\), where we dropped the phase \(\phi \), since it does not play a role in the coincidence detection, and added a time- and frequency-dependent phase that comes from the path difference between the two arms. It is easy to verify that in this case

$$\begin{aligned} \mathcal{C}(\tau )= & {} \frac{1}{2}- \frac{1}{2}\int \int |g(\omega _1)|^2 |g(\omega _2)|^2 e^{i(\omega _1-\omega _2)\tau }\textrm{d}\omega _1 \textrm{d}\omega _2 \nonumber \\= & {} \frac{1}{2}\left( 1- |\int \tilde{g}(t) \tilde{g}^*(t-\tau )\textrm{d}t|^2\right) \end{aligned}$$
(4)

where \(\tilde{g}(t)\) is the Fourier transform of \(g(\omega )\) at point t. Equation (4) is in general different from zero. If the overlap between the Fourier transforms calculated at the two points appearing in Eq. (4) is different from one, we say that the two incoming photons are not completely indistinguishable, and in the limit of complete distinguishability, \(\mathcal{C}(\tau ) =1/2\). This result is the same one would expect to find if photons were billiard balls arriving into a path bifurcation in pairs and were randomly sent through one output path or the other, A or B. This is why we refer to this situation as the classical one.

In spite of having been initially difficult to probe the indistinguishability of photons coming from independent sources, the first experimental demonstrations of the Hong–Ou–Mandel effect used photon pairs generated by spontaneous down conversion (SPDC) processes [2]. The reason for that is the experimental difficulty at that time to build independent and yet sufficiently similar single photon sources, a difficulty overcame in [6]. Nevertheless, as we will see throughout the present contribution, the HOM effect presents many other facets than the one it was initially designed for. Its applications are numerous, and for presenting some of them it’s important to provide, for the general case of (1), the expression of the coincidence probability. Using the same manipulations to obtain (3), we have that

$$\begin{aligned} \mathcal{C}(\tau )= & {} \frac{1}{2}- \frac{1}{2}\int \int f(\omega _1,\omega _2) f^*(\omega _2, \omega _1) e^{i(\omega _1-\omega _2)\tau }\nonumber \\{} & {} \times \textrm{d}\omega _1 \textrm{d}\omega _2, \end{aligned}$$
(5)

which is the central equation of the present manuscript. Simple as it seems to be, Eq. (5) can provide information about entanglement [7], time-frequency phase space representation [8], and be used to characterize resources for quantum simulation [9, 10], metrology [11] and quantum error correction [12].

2.1 On the “quantumness” of the HOM experiment

Before moving to the central point of the present contribution, in this section we discuss in more detail the interpretation of the HOM experiment as probing quantum properties of light. In [13], an experiment involving intensity correlations between classical fields with a fixed, but random phase reference showed that it is indeed possible to reproduce the HOM dip with close to \(100 \%\) visibility. While the theoretical model presented in [13] uses a classical description of light, we provide here a theoretical description using intensity correlations between coherent states which are sent at the two input ports of a HOM-like interferometer and where intensity correlations are calculated between the signals recorded at the two output ports, as in [13].

Using the same spatial modes labelling given in the introduction, we have that, after the introduction of a time delay \(\tau \) in one arm (say, arm 2) of the HOM interferometer and recombination in the beam splitter, the normalized intensity correlation between modes A and B can be written as:

$$\begin{aligned} \mathcal{C}(\tau )= \frac{\langle \hat{N}_A \hat{N}_B \rangle }{\langle \hat{N}_A \rangle \langle \hat{N}_B \rangle }, \end{aligned}$$
(6)

where

$$\begin{aligned} \hat{N}_i=\int \hat{a}_i^{\dagger }(\omega )\hat{a}_i(\omega )\textrm{d}\omega , \end{aligned}$$
(7)

with \(i=A,B\), and where the average is taken both over classical parameters (as the phase \(\phi )\) and on the quantum state. Equation (6) can be rewritten using:

$$\begin{aligned} \hat{N}_{A(B)}= & {} \frac{1}{2}\int \left( \hat{a}_1^{\dagger }(\omega )e^{-i\omega \tau } \pm \hat{a}_2^{\dagger }(\omega )\right) \nonumber \\{} & {} \times \left( \hat{a}_1(\omega )e^{i\omega \tau }\pm \hat{a}_2(\omega )\right) \textrm{d}\omega \nonumber \\= & {} \frac{1}{2}\left[ \hat{N}_1 + \hat{N}_2 \pm (\hat{\mathcal{I}}_{1,2}(\tau ) +\hat{\mathcal{I}}_{1,2}^{\dagger }(\tau ))\right] , \end{aligned}$$
(8)

with \(\hat{\mathcal{I}}_{1,2}(t)= \int \hat{a}_1^{\dagger }(\omega )\hat{a}_2(\omega )e^{i\omega \tau } \textrm{d}\omega \) and \(\hat{N}_{1(2)}=\int \hat{a}_{1(2)}^{\dagger }(\omega )\hat{a}_{1(2)}(\omega )\textrm{d}\omega \). Finally, \(\mathcal{C}(\tau )\) can be written as:

$$\begin{aligned} \mathcal{C}(\tau )= \frac{\langle \hat{N} ^2 \rangle - \langle (\hat{\mathcal{I}}_{1,2}(\tau ) +\hat{\mathcal{I}}_{1,2}^{\dagger }(\tau ))^2 \rangle }{(\langle \hat{N} \rangle ^2 -\langle \hat{\mathcal{I}}_{1,2}(\tau ) +\hat{\mathcal{I}}_{1,2}^{\dagger }(\tau ) \rangle ^2)}, \end{aligned}$$
(9)

where \(\hat{N}=\hat{N}_1 + \hat{N}_2\) is related to the total field intensity. Expression (8) is general and can be used also for non-pure states [14], and a similar expression was obtained in [15] in the form of temporal correlations for microwave field temporal correlations for microwave fields. As a matter of fact, it is easy to verify that this expression reduces to the coincidence probability if we consider as input state a biphoton by noticing that in this case

$$\begin{aligned}{} & {} \hat{\mathcal{I}}_{1,2}(t)\hat{\mathcal{I}}_{1,2}^{\dagger }(\tau )= \hat{N}_1 \\{} & {} \quad + \int \int \hat{a}_1^{\dagger }(\omega _A)\hat{a}_2^{\dagger }(\omega _B)\hat{a}_1(\omega _B)\hat{a}_2(\omega _A) e^{i(\omega _A-\omega _B)\tau }\textrm{d} \omega _A \textrm{d} \omega _B,\nonumber \end{aligned}$$
(10)

and

$$\begin{aligned}{} & {} \hat{\mathcal{I}}_{1,2}^{\dagger }(t)\hat{\mathcal{I}}_{1,2}(\tau )= \hat{N}_2 \\{} & {} \quad +\int \int \hat{a}_1^{\dagger }(\omega _B)\hat{a}_2^{\dagger }(\omega _A)\hat{a}_1(\omega _A)\hat{a}_2(\omega _B) e^{i(\omega _B-\omega _A)\tau }\textrm{d} \omega _A \textrm{d} \omega _B, \nonumber \end{aligned}$$
(11)

and \(\langle \hat{\mathcal{I}}_{1,2}^{\dagger }(\tau ) \rangle = \langle \hat{\mathcal{I}}_{1,2}(t) \rangle = \langle \hat{\mathcal{I}}_{1,2}^{\dagger }(\tau )^2\rangle = \langle \hat{\mathcal{I}}_{1,2}(\tau )^2 \rangle = 0\).

2.1.1 Application to coherent states

We now compute (8) in the case where \(|\psi \rangle =|\alpha \rangle _1|\beta \rangle _2\) are coherent states with respective amplitudes \(\beta =|\alpha | e^{i\phi }\) and \(\alpha = |\alpha |\), in analogy to the calculations in [13] done using classical fields. We have that

$$\begin{aligned} \mathcal{C}(t)= & {} \frac{1}{\langle \hat{N} \rangle ^2_{\gamma } - 4(\textrm{Re}\left[ \int |\alpha (\omega )|^2 e^{i\phi }e^{i\omega \tau }\textrm{d}\omega \right] )^2} \nonumber \\{} & {} \times \left( \langle \hat{N} \rangle ^2_{\gamma } - 2 \textrm{Re}\left[ (\int |\alpha (\omega )|^2 e^{i\phi }e^{i\omega \tau }\textrm{d}\omega )^2\right] \right. \\{} & {} \left. -2 \textrm{Re}\left[ \int \int |\alpha (\omega _A)|^2 |\alpha (\omega _B)|^2 e^{i(\omega _A-\omega _B) \tau }\textrm{d}\omega _A\textrm{d}\omega _B\right] \right) \nonumber , \end{aligned}$$
(12)

where \(\langle \hat{N}\rangle _{\gamma }=2\int |\alpha (\omega )|^2\textrm{d}\omega \). Note that we haven’t averaged over \(\phi \) yet: in order to do so, let’s take a look to (12) for \(\tau =0\). In this case, we have that \(\mathcal{C}(0)= \frac{\langle \sin ^2 {\phi } \rangle _{\phi }}{1-\langle \cos {\phi }\rangle _{\phi }^2}\). From this expression, we see that if the phase \(\phi \) is uniformly distributed in the continuous interval ranging from 0 to \(2\pi \), we have \(\mathcal{C}(0)=1/2\) with a visibility of 1/2. If the phase can take only two values with equal probability and \(\phi \in \{0, \pi \}\), we have that \(\mathcal{C}(0)=0\) with a theoretical visibility of 1, which reproduces the two-photon coincidence case in the classical regime. Finally, if the two possible and equally probable phases are such that \(\phi \in \{\pi /2,3\pi /2\}\), \(\mathcal{C}(0)=1\) and the visibility is zero. These results are in agreement with the ones in [13], where the authors use them to argue that observing a near \(100 \%\) visibility dip in intensity correlations is not necessarily a quantum signature. Accordingly, the authors suggest that by adding a wave-particle duality-like experiment in the output of the HOM interferometer one could then obtain observable differences between quantum and classical properties, which is of course also true.

The conclusion that it is possible to mimic the HOM dip with classical fields should be put into perspective by inspecting Eqs. (9) and (12). We can see that the average zero correlation effect is caused by the \(\phi \) dependent term, which is a first-order interference term. One can thus easily identify and isolate it and argue that quantum effects are associated with second-order correlation terms only [16]. By keeping only these terms, it is clear that the HOM dip cannot be reproduced with classical fields. Another way to argue in this sense is by noticing that the \(\phi \) dependent term presents rapid oscillations that are averaged to zero depending on the detection sensibility to fluctuations in a given frequency range. This is precisely the situation of the Hanbury Brown and Twiss experiment, for instance, where only purely second-order correlation terms remain and such first-order phase-dependent effects do not play a role.

From our point of view, it is interesting to notice that the spectral intensity overlap between classical fields in Eq. (12) does not lead to \(100 \%\) visibility of the intensity correlations while being always \(\le 0\), so that in the absence of the first-order interference term intensity correlations are always \(1/2 \le \mathcal{C}(\tau ) \le 1/4\), with visibility 1/2.

As a conclusion, even though [13] presents an interesting classical situation analogous to the HOM dip, it is not clear in our view how to compare both situations and whether this classical result challenges the usual interpretation of the HOM experiment.

3 The Wigner function

We now turn back to the biphoton situation. Those working in optics, and used to interference effects, are familiar with expressions as (5), where two amplitudes overlap. This relation is such that it may ring a bell in those who are also familiar with the phase space representations of quantum mechanics. As a matter of fact, Eq. (5) is pretty similar to the Wigner function of a massive particle, or the Wigner function associated with the quadrature state of a single mode electromagnetic field, which is given by:

$$\begin{aligned} W(x,p)= \int \langle x-\frac{q}{2} |\hat{\rho }|x+\frac{q}{2} \rangle e^{ips}\textrm{dq} . \end{aligned}$$
(13)

For a pure state, Eq. (13) reduces to

$$\begin{aligned} W(x,p)=\int \psi ^*\left( x-\frac{q}{2}\right) \psi \left( x+\frac{q}{2}\right) e^{ipq}\textrm{d q}, \end{aligned}$$
(14)

where x and p are the position and momentum variables or, equivalently, two orthogonal quadratures of the electromagnetic field, and \(\psi (x)\) is the wave function in, say, the position basis. We see that Eqs. (14) and (5) are indeed very similar but still, not identical.

Indeed, when comparing (5)–(14) many differences appear: in the first place, it seems that we have the equivalent to a two-particle system in Eq. (5), since we have a two-variable integral (in \(\omega _1\) and \(\omega _2\) variables). Also, there is no displacement in the frequency variables, as there is in the position one in (14). Finally, (14) describes the quantum state of a particle or of the electromagnetic field, but what about (5)? We will handle these issues one by one to conclude that, indeed, (5) and (14) are pretty much the same, or at least provide the same type of information about the quantum state of a system if one limits the discussion to the case where each mode is occupied by one photon only.

To start with, and for pedagogical reasons, we perform a change of variables in (5) such that: \(\omega _{\pm }=(\omega _1 \pm \omega _2)/2\). In this case, \(f(\omega _1,\omega _2)=F(\omega _+,\omega _-)\) and \(f(\omega _2,\omega _1)=F(\omega _+,-\omega _-)\). Then, following [8], we define \(G( \omega _-)G^*(- \omega _-)=\int F(\omega _+, \omega _-)F^*(\omega _+, -\omega _-) \textrm{d}\omega _+\). In the case where \( F(\omega _+, \omega _-)\) is a separable function in the \(\omega _{\pm }\) variables, \(G( \omega _-)\) is the wave function associated with the \(\omega _-\) variable and provides all the information about this collective mode. In the general case, we are considering a marginal of the wave function. In any case, using the previously introduced definition, we have that:

$$\begin{aligned} \mathcal{C} (\tau )= \frac{1}{2}- \frac{1}{2}\textrm{Re}[\int G(\omega _-)G^*(-\omega _-) e^{i\omega _-\tau }\textrm{d}\omega _- ],\nonumber \\ \end{aligned}$$
(15)

where we have transformed the double integral of Eq. (5) into a single one, in the form of (14).

Fig. 1
figure 1

Modified HOM experiment including a time delay \(\tau \) in one input arm and frequency displacements of \(\mu \) in the other input arms. Photon pairs are generated by SPDC in orthogonal polarizations. For each pair, the photons are spatially separated with a polarizing beam splitter (PBS) and sent to two arms of an interferometer. A half wave-plate rotates the polarization on one of the two arms. A time delay \(\tau \) and a frequency displacement \(\mu \) are inserted. Photons are detected at the output of a 50/50 beam splitter, and coincidences are measured. As described in Sects. 4 and 4.3, the experiment can also be seen as composed of a preparation step (for state engineering and for an alternative to implement frequency displacements for quantum state measurement, red box), a manipulation step (that can be used to implement logical gates, as described in 4.3 or for quantum state measurement as well, green box) and a detection step based on coincidence measurements (blue box)

Full size image

Thanks to this transformations, the analogy between Eqs. (14) and (15) can be more easily carried out. In the first place, we can notice that the position displacement of (14) corresponds to a displacement in the \(\omega _-\) variable in (15). In the same way, the momentum displacement of (14) is equivalent to the time displacement appearing in (15). It is clear that transformations of the type \(\pm \omega _- \rightarrow \mu \pm \omega _-\) would transform (15) into the exact mathematical analog of (14) with the replacements \(\tau \rightarrow p\), \(\omega _- \rightarrow 2q\) and \(x \rightarrow \mu \). By analyzing the interferometer in Fig. 1, we see that a frequency displacement of \(\mu \) in one of the interferometer’s arms would modify the photonic state and its wave function in such a way that the coincidence detection at the outputs of the interferometer would give:

$$\begin{aligned}{} & {} \mathcal{C}(\mu , \tau ) = \frac{1}{2}- \frac{1}{2}\textrm{Re}\left[ \int G(\mu +\omega _-)G^*(\mu -\omega _-) e^{i\omega _-\tau }\textrm{d}\omega _-\right] .\nonumber \\ \end{aligned}$$
(16)

We leave the discussion about possible ways to experimentally implement such displacements to Sect. 4. The integral in Eq. (16) has now the same form as the one in (14). So, what’s the meaning of all that? Is this really a Wigner function, as (14)? And if it’s the case, what type of information can it provide about the state, or at least about the part of the state associated with variable \(\omega _-\)? These issues were addressed in [8, 17, 18], leading to the conclusion that indeed, the coincidence detection of the output of a HOM interferometer can be expressed as:

$$\begin{aligned} \mathcal{C} (\mu , \tau )= \frac{1}{2}-\frac{1}{2}W_-(\mu ,\tau ), \end{aligned}$$
(17)

where \(W_-(\mu ,\tau ) = \int G(\mu +\omega _-)G^*(\mu -\omega _-) e^{2i\omega _-\tau }\textrm{d}\omega _-\) is the chronocyclic Wigner function associated with the variable \(\omega _-\) of the photon pair. The chronocyclic Wigner function is currently used in classical optics to characterize the frequency state of classical fields. In this context, but at the intersection with the quantum optics community, interesting experiments revealing sub-Planck-like structures of the time-frequency phase space were performed in [19, 20]. For single photons, or pairs of single photons, and thanks to the statistics and symmetries of this particular field states, the chronocyclic Wigner function is directly connected to the measurement outcome statistic of time and frequency measurements taken on these states. It can thus be used to completely characterize the time/frequency state of individual photons and to display their statistical and entanglement properties [21, 22]

In the case of a biphoton wave function which is separable in the variables \(\omega _-\) and \(\omega _+\), this information completely characterizes the quantum state of the biphoton associated with the variable \(\omega _-\). In particular, we can notice that the usual shape of the HOM dip is nothing but a cut in the phase space of varying \(\tau \) and at \(\mu = 0\) of a Gaussian spectral function.

An important point to address is the fact that we’re dealing here with the quantum description of the photon pair detected in coincidence, so the Wigner function describes the photonic quantum state in frequency. The quantum statistics of the field it refers to gives to \(W_-(\mu , \tau )\) specific properties having a quantum interpretation. For instance, in [7], it was shown that if \(\mathcal{C} (0,\tau ) > 1/2\), then the photon pair is frequency entangled. We can show that having \(\mathcal{C} (\mu ,\tau ) > 1/2\) is also an entanglement witness, and this corresponds precisely to saying that the existence of negative points of \(W_-(\mu ,\tau )\) is a proof that the photon pair is frequency entangled.

Interpreting the integral in (16) as a Wigner function contributes to provide a physical picture of frequency and time of single photons as quantum continuous variables. Even though it is known that such degrees of freedom are continuous, in most protocols and applications they are either discretized [23,24,25] or distributed in the basis of discrete modes [26, 27] so that their genuine continuous character is not fully exploited. As shown in [12], the single photon time and frequency variables can also be used for quantum information, computing and communication protocols analogously to “usual” quantum continuous variables in quantum optics—as the vibrational state of trapped ions or the quadratures of the electromagnetic field. This opens the perspective to further expand the applications of single photon-based quantum information protocols, since frequency and time variables are shown to be the continuous versions of polarization degrees of freedom, for instance.

As a concluding remark for this part, we have seen that the coincidence probability in a HOM experiment is a direct measurement of the Wigner function associated with the \(\omega _-\) variable of a photon pair. This may seem restrictive, but it is only a consequence of the choice of the experimental system and its relevant degrees of freedom. We have shown in [8] that the HOM provides a way to characterize other photonic degrees of freedom as well, as for instance the Wigner function associated to the transverse position and momentum coordinates. For these degrees of freedom, it is easier to perform spatial rotations of the field’s profile so that one can directly access different combinations of variables, as for instance the one associated not only to the difference but also to the sum of the transverse coordinates of the photons.

It is also possible to adapt the ideas proposed in [8] so as to access the full Wigner function of a single photon. In this case, instead of seeing the photon pair generated by a SPDC process as produced by the physical device, we can interpret it as the product of a series of logical gates that are applied to a separable state. For this, it was shown in [22, 28] that the frequency beam-splitter operation defined as

$$\begin{aligned} \hat{U}|\omega _{1},\omega _{2} \rangle =|\omega _{+},\omega _{-} \rangle . \end{aligned}$$
(18)

plays the role of the entangling interaction that naturally occurs in the SPDC process. These entangling operations are physically associated with the phase matching condition and energy conversation. Thus, the produced entangled state emitted by the SPDC-based device can formally be obtained by starting from two initially separable single photons described by the wave function \(|\psi \rangle =\iint d\omega _{1} d\omega _{2} f(\omega _{1})g(\omega _{2}) |\omega _{1},\omega _{2} \rangle \), which are then entangled by a frequency beam-splitter operation.

As a result of this interpretation, we can interpret the function f (resp. g) of the separable initial photon pair as being the same as the function modeling the energy conservation (resp. the phase-matching conservation) of a SPDC process. Thus, the coincidence measurement corresponds to measuring the spectral function of an initial single photon that has been entangled (changed variables) by the device. In Ref. [28], we also proposed a direct way for implementing such an operation with nonlinear crystals in cascade. More efficient ways could also be investigated within light-matter interaction using split-ring resonators or with a quantum emitter embedded into a waveguide [29, 30].

Finally, if a separable two-photon state enters into the HOM interferometer, the coincidence probability corresponds to the spectrogram:

$$\begin{aligned} S(\mu ,\tau )=\frac{1}{2}\left( 1-\left|\int f^{*}(\omega _{1})g(\omega _{1}-\mu )e^{ i\omega _{1}\tau }\textrm{d}\omega _1\right|^{2}\right) .\nonumber \\ \end{aligned}$$
(19)

The spectrogram is the absolute value of the windowed Fourier transform. The amplitude and phase of the spectral function f of one single photon could be reconstructed using a phase-retrieval algorithm if the spectral function g, used as a window, is known.

As a conclusion, the HOM interferometer provides various ways for measuring the amplitude and phase of the spectral function of single- and two-photon states.

4 Quantum state manipulation and engineering

We have seen that interpreting the HOM experiment as a direct measurement of the Wigner function of the biphoton associated with the variable \(\omega _-\) requires being capable of implementing displacements in the time–frequency phase space. While time displacement is in practice easy to implement in quantum optics by temporal delay lines, frequency displacement requires more involved experimental techniques at the single photon level, some of them based on nonlinear optics. Nevertheless, frequency displacements are necessary not only to have access to the whole chronocyclic phase space and characterize the single photon state, but also for quantum state engineering. A possibility to implement frequency shifts is by using electro-optic modulators, which are commercially available, with performances compatible with single photon operation. Such devices were used to perform the spectral tomography of single photons [31] or measuring only their temporal envelope [32]. The direct signature of such frequency shifts was observed through the decrease of the visibility of the dip in HOM interferometry in [33]. In [34], the spectral tomography of an attenuated coherent optical field at the single photon level has been performed by using an electro-optics modulator as frequency shifter.

In this section, we take a different direction and provide solutions to implement phase space displacements using techniques as pump engineering and post-selection.

In order to fix the ideas, we provide the details of a specific experimental system to illustrate our method.

4.1 An experimental context

Counterpropagating phase-matching offers a high versatility to engineer the spectral wave-function and the exchange statistics of photon pairs, as probed in the HOM experiment. This configuration can be found, for instance, in semiconductor chip-integrated sources of photons pairs, as the one shown in Fig. 2a. A SEM image of it is shown in Fig. 2b. The source is a Bragg ridge microcavity made of a stack of AlGaAs layers with alternating aluminum concentrations [35, 36]. It is based on a transverse pump scheme, where a pulsed laser beam, impinging on top of the waveguide with an incidence angle \(\theta \), generates pairs of counterpropagating and orthogonally polarized photons (signal and idler) by SPDC. Along the epitaxial direction momentum conservation is implemented through a quasiphase-matching structure of AlGaAs layers (shown in orange in Fig. 2a), with alternating high and low values of the effective nonlinear coefficient. The Bragg mirrors provide both a vertical microcavity to enhance the pump field and a cladding for the twin-photon modes.

Fig. 2
figure 2

a Working principle and b SEM image of an AlGaAs ridge microcavity generating frequency-entangled photon pairs by SPDC in a transverse pump geometry

Full size image

Two nonlinear interactions can occur simultaneously in the device [36]; we consider here the one that generates a TE-polarized signal photon (propagating along \(z>0\), as sketched in Fig. 2a) and a TM-polarized idler photon (propagating along \(z<0\)). When the photons are generated close to degeneracy and for a narrow pump spectrum, the biphoton state can be written in the following form:

$$\begin{aligned} |\psi \rangle = \iint \mathrm{{d}} \omega _s \mathrm{{d}} \omega _i f_+(\omega _s+\omega _i) f_-(\omega _s-\omega _i) |\omega _s,\omega _i \rangle \end{aligned}$$
(20)

The joint spectral amplitude (JSA) \(\phi (\omega _s,\omega _i)= f_+(\omega _+) f_-(\omega _-)\), where \(\omega _\pm =\omega _s \pm \omega _i\), gives the probability amplitude to measure a signal photon at frequency \(\omega _s\) and an idler photon at frequency \(\omega _i\). The function \(f_+\), reflecting the condition of energy conservation, is given by the spectrum of the pump beam, while the function \(f_-\), corresponding to the phase-matching condition, is determined by the spatial properties of the pump beam:

$$\begin{aligned} f_-(\omega _-)=\int _{-L/2}^{L/2} \mathrm{{d}}z \, \Phi (z) e^{-i (k_\textrm{deg}+\omega _-/\bar{v}_\textrm{g})z} \end{aligned}$$
(21)

Here, \(\Phi (z)\) is the pump amplitude profile along the waveguide direction, L is length of the waveguide, \(\bar{v}_g\) is the harmonic mean of the group velocities of the twin-photon modes and \(k_\textrm{deg}=\omega _p\text {sin}(\theta _\textrm{deg})/c\), with \(\omega _p\) the pump central frequency, c the velocity of light and \(\theta _\textrm{deg}\) the pump incidence angle corresponding to the production of frequency-degenerate photons.

4.2 Pump beam engineering

Measurements in quantum physics can be performed in different ways. In textbooks, measurements can be taken in any basis, and all the basis states can be directly measured. In reality, experimental measurement apparatus can often only measure quantum states in a given specific basis, sometimes even only at some part of this basis, or at specific points of phase space. A solution to circumvent this and obtain full information about the state is to manipulate it, so as the basis transformation or the projector transformation is implemented on the state instead of being implemented on the measurement apparatus. Then, a measurement in a given state (the only directly accessible one for the measurement apparatus) means that, in fact, the system was previously in another state which is considered to be the measured one.

In the previous subsection, we have seen that the JSA of the produced photon pair can be controlled by modifying the pump laser beam properties, as its angle and position of incidence. In [37], we have exploited this fact to propose methods not only to engineer exotic and useful quantum states of the photon pair, but also to measure them by implementing displacements in different directions of the phase space. This technique modifies the state to be measured while keeping the measured projectors the same.

Using the results of the previous section, if the dimensions of the waveguide are large with respect to the pump waist, i.e., in the limit where \(L\rightarrow \infty \), \(f_-\) can be approximated as the Fourier transform of the spatial profile of the pump beam:

$$\begin{aligned} f_- (\omega _-) \approx \tilde{\varphi }\left( \frac{\omega _-}{\bar{v}_g}\right) \end{aligned}$$
(22)

We start by considering the situation depicted in Fig. 3 where a Gaussian pump beam with waist \(w_p\) impinges onto the source at an angle \(\theta \) and position \(z_0\). The field distribution along the z axis is \(\Phi (z) \propto e^{-{(z-z_0)^2 \cos ^2{\theta }}/{w_p^2}} e^{ i (k\sin \theta ) z}\), and therefore, \(f_-\) reads:

$$\begin{aligned} f_-(\omega _-)\propto e^{-i\omega _- \tau _0} e^{-\tfrac{\left( \omega _- - \omega _-^{(0)}\right) ^2 }{\Delta \omega ^2}} \end{aligned}$$
(23)

with \(\tau _0 = z_0/\bar{v}_g\), \(\Delta \omega = \bar{v}_g\cos {\theta }/\pi w_p\) and \(\omega _-^{(0)} = (k\sin \theta -k_{\textrm{deg}})\bar{v}_g\).

From a general complex amplitude representation describing a pure state \(f_-(\omega _-)\), the Wigner function \(W(\tau , \mu )\) at points \(\tau , \mu \) of the phase space is given by:

$$\begin{aligned} W(\tau , \mu )=\int _{-\infty }^{\infty }\mathrm{{d}}\omega _-f_-\left( \mu -\frac{\omega _-}{2}\right) f_-^*\left( \mu +\frac{\omega _-}{2}\right) e^{i\tau \omega _-}.\nonumber \\ \end{aligned}$$
(24)

Using, for instance, the expression obtained in (23), it is easy to see that this corresponds to a Gaussian Wigner function centered at point \(\tau =\tau _0\), \(\mu = \omega _-^{(0)}\). In this situation, shifting the pumping spot \(z_0\) is equivalent to realizing displacements in the \(\tau \) axis of the phase space while changing the angle of incidence \(\theta \) of the pump beam corresponds to shifting the state along the \(\mu \) axis.

More complex states can be obtained by engineering the pump beam. Indeed, two identical beams impinging at positions \(z_a\) and \(z_b\) generate a superposition of 2 coherent states displaced along the \(\tau \) axis, which is a state analogous to a Schrödinger cat in position and momentum phase space. The orthogonality between the two Gaussian states is ensured if \(\frac{(z_a - z_b)}{\bar{v}_g} \gg \frac{1}{\Delta \omega }\). A superposition of two Gaussian packets can also be obtained along axis \(\mu \) by using 2 different pump beam’s incidence angles \(\theta _a\) and \(\theta _b\) impinging at the same point \(z_0\) (see Fig. 3), and this type of state was shown to be a resource for quantum metrology in [11, 38]. We can generalize even more these Schrödinger cat-like to arbitrary configurations of pump beams, for instance a compass state, which is a superposition of four coherent states whose utility for metrology has been pointed out in [39] and studied in the context of SPDC in [38]. To obtain it, a set of 4 beams is required: 2 pairs of beams impinging at 2 different points separated by a distance \(\Delta z\), each pair consisting of 2 beams symmetrically tilted with respect to the degeneracy angle.

Fig. 3
figure 3

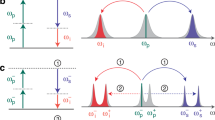
Pump engineering for producing a Schrödinger cat-like state in frequency. A divided pump that impinges on the medium at different angles leads to different phase matching conditions which are angle dependent and center the state’s frequency distribution at different values. By changing both pump’s angles while keeping their angular distance constant, one displaces the center of both frequency distributions in the same direction and by the same amount. This is equivalent to performing frequency displacements in phase space, a strategy that can be used both for quantum state engineering and for measuring the Wigner function using the HOM interferometer at different points of the time frequency phase space

Full size image

As a conclusion, we can see that pump engineering is a valuable tool not only to design interesting frequency-time entangled states but also to implement displacements in phase space, thus enabling quantum state measurements.

4.3 Exploiting cavity effects

Quantum state engineering of the photon pair emitted by SPDC can be implemented not only with pump engineering but also by exploiting the properties of the device itself. One example of this is by using the temperature dependency of the phase-matching condition, which can implement frequency displacements enabling the direct measurement of the Wigner function \(W_-(\mu ,\tau )\) [40]. Other ways to engineer the nonlinear susceptibility of a nonlinear crystal can be found in [41] for the single photon and in [42] for the two-mode squeezed regime.

In the following, we describe the possibilities of quantum state manipulation and engineering enabled by the interplay between cavity effects and temporal delay between photons of a pair. The method can be adapted and applied to a large variety of systems, either bulk or integrated, thus increasing their flexibility and the richness of the generated states. Here we illustrate these concepts by taking the example of the biphoton state generation in an AlGaAs waveguide based on a modal phase matching scheme in a collinear geometry. In this case, the phase-velocity mismatch among the three interacting fields is compensated by a multimode waveguide dispersion engineering by confining the modes using Bragg reflectors [23].

In this type of device, the facets of the nonlinear waveguide are reflective, due to the refractive index contrast between semiconductor and air. For this reason, a cavity effect occurs in the emitted photons propagation direction, which produces a temporal grating that generates a frequency comb in their spectrum. The peaks of the comb are spaced by \(\bar{\tau }/2\), where \(\bar{\tau }\) is the time a photon takes to make a roundtrip in the cavity, and in [23] we have shown that by changing the pump frequency we can engineer different phase profiles for the comb, with different symmetry properties. An example can be seen in Fig. 4, that shows as well the dependency of the peak visibility with the reflectivity of the cavity, and the expected HOM profile for the considered device, for which the reflectivity \(R \approx 0.3\). This cavity effect enables the discretization of such frequency combs, which are raising a considerable interest in the community, since they can be used as qudits [23], that can have applications in quantum key distribution, for instance [43]. The full physical analysis of the HOM experiment when photon pairs with a frequency comb are used has been studied in [44].

Fig. 4
figure 4

Simulated results of HOM interferometry for a biphoton frequency comb generated by an AlGaAs nonlinear cavity. Horizontal axis: time delay between peaks in units of \(\bar{\tau }\). Top panel: simulation of the dependency of the coincidence probability with the cavity reflectivity (vertical axis) and time. The color code refers to the coincidence probability that oscillates between 0 and 1 according to the time delay, \(P=1\) for an anti-symmetric state and \(P=0\) for a symmetric one. The symmetry of the produced state is related to the resonance or anti-resonance of the pump beam with the cavity frequency. On the top left, the pump beam frequency is resonant with the cavity frequency, and on the top right, the pump beam is anti-resonant with the cavity frequency. The corresponding produced states can be associated with GKP-like states in different bases. Bottom panel: Vertical axis: simulation of the coincidence probability for the same states at the top for \(R=0.3\). This figure is a reproduction from [23]

Full size image

From the continuous variables perspective, large superpositions of numerous highly localized states can be used to encode error-protected qubits. Such states present redundancy and translational symmetry in the ideal case of an infinite superposition of infinitely localized states. These properties are interesting for quantum error correction, as first proposed by Gottesman-Kitaev and Preskill (GKP) [45]. The so-called GKP states are robust against small displacements in phase space (small with respect to the comb spacing in position and momentum representation), and they can be used not only to encode quantum information but also as a resource to correct displacement errors that affect different states defined in continuous variables [46]. In addition, it has been shown that these states are sufficient non-Gaussian elements to complete Gaussian-based quantum computation and turn it universal [46].

In spite of its numerous applications and its fundamental interest for quantum computing with continuous variables, the experimental production of GKP states is extremely challenging in the quadrature representation, since it involves creating highly non-Gaussian states. Nevertheless, some experimental results exist using superconducting circuits operating in the microwave range [47] and using the motional state of trapped ions [48]. In [49], it was shown that spatial gratings can be used to engineer GKP states using the transverse position and momentum degrees of freedom of single photons. As for time and frequency variables, the cavity structure of AlGaAs semiconducting device naturally creates a comb structure, as mentioned. We have shown in [12] that such comb can, indeed, be seen as an entangled GKP state, and measuring time or frequency of one the photons enables correcting the errors of the other, in a reminiscence of a measurement-based quantum computing scheme.

The main idea behind our results is the fact that the effective nonlinear interaction producing the photon pair in a cavity can be seen as a combination of universal gates, as defined in [22], acting on a separable ideal pair of GKP states. The effect of such gates is to add noise to the ideal state, under the form of a classical distribution of displacement operators, and entangle both states. Such operations can be seen as a small quantum circuit that produces entangled GKP states, which were proven to be a resource for quantum error correction.

Additionally, frequency-encoded GKP states can also be manipulated thanks to the HOM interferometer. As a matter of fact, in the subspace formed by GKP states, time and frequency displacements of fixed amounts, corresponding to the combs’ interspacing, act as Pauli matrices do on qubits. Thus, fixing the time delay in one arm of the HOM interferometer is equivalent to applying a quantum gate analogous to the Pauli matrix \(\sigma _x\) to a GKP state, as was shown in [12].

Of course, one can use different techniques to generate frequency comb structures, as placing a cavity in one arm of the HOM interferometer, as done in [50]. Nevertheless, using the natural cavity-like structure in the device studied in [12] is interesting since it avoids extra sources of losses.

5 Discussion and conclusion

We have revisited the HOM experiment, a benchmark in quantum optics and quantum physics, taking a phase space perspective which enables interpreting time and frequency degrees of freedom of single photons as genuine quantum continuous variables, in perfect analogy with position and momentum. We also discussed the quantum nature of this experiment and how classical results reproducing the ones due to photon statistics may deserve to be interpreted under a different perspective.

We have focused on a specific experimental system and shown how exotic states can be engineered in such a device by manipulating a classical pump beam. Also, we identified the “natural” output of such a device as an entangled state with quantum properties, which were shown to be useful for quantum error correction. The presented original approach to the HOM experiment opens the possibility of novel applications of single photon-based protocols and shows that quantum phenomena have not stopped surprising us.

As an interesting perspective, we should also mention the extension of the presented results to the atomic version of the HOM experiment [51], performed by Alain Aspect and co-workers.

All the authors contributed equally to this work.