Revealing hidden steering nonlocality in a quantum network

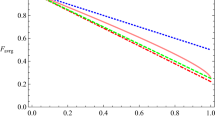
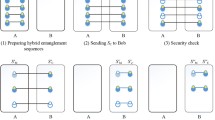
Abstract

By combining two objects with no quantum effect one can get an object with quantum effect. Such a phenomenon, often referred to as activation, has been analyzed for the notion of steering nonlocality. Activation of steering nonlocality is observed for different classes of mixed entangled states in linear network scenarios. Characterization of arbitrary two qubit states, in ambit of steering activation in network scenarios has been provided in this context. Using the notion of reduced steering, instances of steerability activation are also observed in nonlinear network. Present analysis involves three measurement settings scenario (for both trusted and untrusted parties) where steering nonlocality is distinguishable from Bell nonlocality.

Graphical abstract

Appendices

Appendix A

Proof of Theorem 1

Both $\rho _{AB}^{'}$ [Eq. (17)] and $\rho _{BC}^{'}$ [Eq.(18)] violate Eq. (5). Hence, $\sum _{j=1}^3{\sqrt{\mathfrak {t}^2_{1jj}}},{\sqrt{\mathfrak {t}^2_{2jj}}}\le 1$ which imply that $|\mathfrak {t}_{kjj}|\le 1,\forall k=1,2$ and $j=1,2,3.$ Let $\mathcal {V}_{b_1b_2}$ denote the correlation tensor of conditional state $\rho _{AC}^{(b_1b_2)}.$ Now, two cases are considered: either one or both the parties have no non-null local Bloch vectors. In both the cases, $Tr (\mathcal {V}_{b_1b_2}^T\mathcal {V}_{b_1b_2})= \sum _{k=1}^3(t_{1kk}t_{2kk})^2,\,\forall b_1,b_2=0,1.$ Hence, for each of $\mathcal {V}_{b_1b_2},$ $\sqrt{Tr (\mathcal {V}_{b_1b_2}^T\mathcal {V}_{b_1b_2})}$ takes the form:

$$\begin{aligned}&\sqrt{Tr (\mathcal {V}_{b_1b_2}^T\mathcal {V}_{b_1b_2})}=\sqrt{\sum _{k=1}^3(t_{1kk}t_{2kk})^2}\nonumber \\&\quad \le \sqrt{\sqrt{\sum _{k=1}^3}t^4_{1kk}.\sqrt{\sum _{k=1}^3}t^4_{2kk}}\nonumber \\&\quad \le \sqrt{\sqrt{\sum _{k=1}^3}t^2_{1kk}.\sqrt{\sum _{k=1}^3}t^2_{2kk}}\nonumber \\&\quad \le 1. \end{aligned}$$

(26)

The second inequality holds as $|\mathfrak {t}_{kjj}|\le 1,\forall k=1,2$ and $j=1,2,3$ and the last is due to the fact that none of the initial states satisfies Eq. (5). $\square$

Appendix B

Proof of Theorem 3

Here, $\vec {u_1}=\vec {u_2}=\Theta .$ $\rho _{AB}$ and $\rho _{BC}$ thus have the form:

$$\begin{aligned} \rho _{AB}={\frac{1}{4}(\mathbb {I}_{2\times 2}+\mathbb {I}_2\otimes \vec {\mathfrak {v}_1}. \vec {\sigma }+\sum _{j_1,j_2=1}^{3}w_{1j_1j_2}\sigma _{j_1}\otimes \sigma _{j_2})}, \end{aligned}$$

$$\begin{aligned} \rho _{BC}={\frac{1}{4}(\mathbb {I}_{2\times 2}+\mathbb {I}_2\otimes \vec {\mathfrak {v}_2}. \vec {\sigma }+\sum _{j_1,j_2=1}^{3}w_{2j_1j_2}\sigma _{j_1}\otimes \sigma _{j_2})}, \end{aligned}$$

Let $\Lambda$ [Eq. (20)] be applied on both $\rho _{AB}$ and $\rho _{BC}$ followed by local unitary operations(to diagonalize the correlation tensors). Let $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$ denote the respective canonical forms [Eq. (22)] of $\rho _{AB}$ and $\rho _{BC}$ [70]:

$$\begin{aligned} {\rho _{AB}^{(2)}}= & {} {\frac{1}{4}(\mathbb {I}_{2\times 2}+\sum _{j=1}^{3}w_{1jj}^{''}\sigma _{j}\otimes \sigma _{j})}, \end{aligned}$$

(27)

$$\begin{aligned} {\rho _{BC}^{(2)}}= & {} {\frac{1}{4}(\mathbb {I}_{2\times 2}+\sum _{j=1}^{3}w_{2jj}^{''} \sigma _{j}\otimes \sigma _{j})}, \end{aligned}$$

(28)

Now $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$ both satisfy unsteerability criterion given by Eq. (23). This in turn gives:

$$\begin{aligned} Max _{x_1,x_2,x_3}\sqrt{\sum _{j=1}^3}(x_jw_{kjj}^{''})^2\le \frac{1}{2},\,\,\,\,k=1,2 \end{aligned}$$

(29)

where $\hat{x}=(x_1,x_2,x_3)$ denotes a unit vector. $\square$

We next perform maximization over $\hat{x}$ so as to obtain a closed form of the unsteerability criterion in terms of elements of correlation tensors of the initial states $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$. Maximization over unit vector $\hat{x}$: Taking $\hat{x}=(\sin (\theta )\cos (\phi ), \sin (\theta )\sin (\phi ),\cos (\theta )),$ maximization problem in L.H.S. of Eq. (41) can be posed as:

$$\begin{aligned} Max _{\theta ,\phi }\sqrt{A(\theta ,\phi )} \end{aligned}$$

(30)

where,

$$\begin{aligned} {A(\theta ,\phi )}= & {} \sin ^2(\theta )(\cos ^2(\phi )(w_{k11}^{''})^2\nonumber \\&+\sin ^2(\phi )(w_{k22}^{''})^2)+\cos ^2(\theta )(w_{k33}^{''})^2\qquad \end{aligned}$$

(31)

Now for any $g_1,g_2\ge 0,$ $Max _{\kappa }(g_1\cos ^2(\kappa )+g_2\sin ^2(\kappa ))$ is $g_1$ if $g_1>g_2$ and $g_2$ when $g_2>g_1.$ This relation is used for maximizing $A(\theta ,\phi ).$ In order to consider all possible values of $(w_{k11}^{''})^2,$ $(w_{k22}^{''})^2$ and $(w_{k33}^{''})^2,$ we consider the following cases:

Case1:$(w_{k11}^{''})^2>(w_{k22}^{''})^2$: Then $Max _{\phi }A(\theta ,\phi )$ gives:

$$\begin{aligned} B(\theta )= {\sin ^2(\theta )(w_{k11}^{''})^2+\cos ^2(\theta )(w_{k33}^{''})^2} \end{aligned}$$

(32)

Subcase1: $(w_{k11}^{''})^2>(w_{k33}^{''})^2,i.e., \,(w_{k11}^{''})^2=Max _{j=1,2,3} (w_{kjj}^{''})^2:$ Then $Max _{\theta }B(\theta )=(w_{k11}^{''})^2.$ Hence,

$$\begin{aligned} Max _{\theta ,\phi }\sqrt{A(\theta ,\phi )}=|w_{k11}^{''}|. \end{aligned}$$

(33)

Subcase2:$(w_{k11}^{''})^2<(w_{k33}^{''})^2,i.e., \, (w_{k22}^{''})^2<(w_{k11}^{''})^2<(w_{k33}^{''})^2:\,Then \,Max _{\theta }B(\theta )=(w_{k33}^{''})^2.$ Hence,

$$\begin{aligned} Max _{\theta ,\phi }\sqrt{A(\theta ,\phi )}=|w_{k33}^{''}|. \end{aligned}$$

(34)

Case2:$(w_{k11}^{''})^2<(w_{k22}^{''})^2$: Then $Max _{\phi }A(\theta ,\phi )$ gives:

$$\begin{aligned} B(\theta )= {\sin ^2(\theta )(w_{k22}^{''})^2+\cos ^2(\theta )(w_{k33}^{''})^2} \end{aligned}$$

(35)

Subcase1:$(w_{k22}^{''})^2>(w_{k33}^{''})^2,i.e., \, (w_{k22}^{''})^2=Max _{j=1,2,3}(w_{kjj}^{''})^2:$ Then$\quad Max _{\theta }B(\theta )=(w_{k22}^{''})^2.$ Hence,

$$\begin{aligned} Max _{\theta ,\phi }\sqrt{A(\theta ,\phi )}=|w_{k22}^{''}|. \end{aligned}$$

(36)

Subcase2:$(w_{k22}^{''})^2<(w_{k33}^{''})^2, i.e., \,(w_{k11}^{''})^2<(w_{k22}^{''})^2<(w_{k33}^{''})^2:\,Then \, Max _{\theta }B(\theta )= (w_{k33}^{''})^2.$ Hence,

$$\begin{aligned} Max _{\theta ,\phi }\sqrt{A(\theta ,\phi )}=|w_{k33}^{''}|. \end{aligned}$$

(37)

So, combining all cases, we get:

$$\begin{aligned} Max _{\theta ,\phi }\sqrt{A(\theta ,\phi )}=Max _{j=1}^{3}|w_{kjj}^{''}|,\,\,k=1,2.\qquad \end{aligned}$$

(38)

So, the unsteerability criterion [Eq. (41)] turns out to be:

$$\begin{aligned} Max _{j=1,2,3}|w_{kjj}^{''}|\le \frac{1}{2}. \end{aligned}$$

(39)

where $k=1,2$ correspond to states $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$, respectively. So $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$ and therefore $\rho _{AB}$ and $\rho _{BC}$ are unsteerable. Steerability of state remaining invariant under application of linear map [Eq. (20)], considering the canonical forms $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$ as the initial states used in the network. Depending on the output of BSM obtained by Bob (and result communicated to Alice and Charlie), the conditional states shared between Alice and Charlie are given by $\rho _{AC}^{ij},\,i,j=0,1$ (see Table 4). $\forall i,j,$ $\rho _{AC}^{ij}$ has null local Blochs and diagonal correlation tensor.

Table 4 State parameters of each of the four conditional states are specified here

Hence, for each of the conditional states, L.H.S. of Eq. (23) turns out to be:

$$\begin{aligned} Max _{x_1,x_2,x_3}\sqrt{\sum _{j=1}^3(x_jw_{1jj}^{''}w_{2jj}^{''})^2} \end{aligned}$$

(40)

Following the same procedure of maximization as above, the optimal expression of the maximization problem [Eq. (40)] is given by:

$$\begin{aligned} Max _{j=1,2,3}|w_{1jj}^{''}w_{2jj}^{''}| \end{aligned}$$

Using Eq. (39), the maximum value of Eq. (40) turns out to be $\frac{1}{4}$. Each of the four conditional states thus satisfies the unsteerability criterion [Eq. (23)]. So if both the initial states satisfy Eq. (23) and have null local Bloch vector (corresponding to first party), then none of the conditional states generated in the network is steerable. Hence genuine activation of steering does not occur. States satisfies Eq. (5).

Appendix C

Details of the numerical observation given in Sect. 6: Without loss of any generality, of two initial states, let $\rho _{BC}$ has non-null Bloch vector corresponding to the first party, i.e., $\vec {u_1}=\Theta ,\vec {u_2}\ne \Theta .$ $\rho _{BC}$ thus has the form:

$$\begin{aligned} \rho _{BC}= & {} \frac{1}{4}(\mathbb {I}_{2\times 2}+\vec {\mathfrak {u}_2}.\vec {\sigma }\times \mathbb {I}_{2} +\mathbb {I}_2\otimes \vec {\mathfrak {v}_2}.\vec {\sigma }\\&+\sum _{j_1,j_2=1}^{3}w_{2j_1j_2}\sigma _{j_1}\otimes \sigma _{j_2}), \end{aligned}$$

After applying $\Lambda$ [Eq. (20)] followed by local unitary operations, the canonical form $\rho _{AB}^{(2)}$ of $\rho _{AB}$ is given by Eq. (27), whereas that of $\rho _{BC}$ is given by:

$$\begin{aligned} {\rho _{BC}^{(2)}}={\frac{1}{4}(\mathbb {I}_{2\times 2}+\vec {\mathfrak {u}_2^{''}}.\vec {\sigma }\times \mathbb {I}_{2} +\sum _{j=1}^{3}w_{2jj}^{''}\sigma _{j}\otimes \sigma _{j})},\qquad \end{aligned}$$

(41)

Now $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$ both satisfy unsteerability criterion given by Eq. (23). This in turn gives:

$$\begin{aligned} Max _{x_1,x_2,x_3}\sqrt{\sum _{j=1}^3(x_jw_{1jj}^{''})^2}\le \frac{1}{2} \end{aligned}$$

(42)

and

$$\begin{aligned} Max _{x_1,x_2,x_3}(\vec {\mathfrak {u}_2^{''}}.\hat{x})^2+ 2\sqrt{\sum _{j=1}^3(x_jw_{2jj}^{''})^2}\le 1 \end{aligned}$$

(43)

with $\hat{x}=(x_1,x_2,x_3)$ denoting unit vector. While the closed form of Eq. (42) is given by Eq. (39) for $k=1,$ the same for Eq. (43) is hard to derive owing to the complicated form of the maximization problem involved in it. Now as $\rho _{BC}^{(2)}$ satisfies an unsteerability criterion [Eq. (43)] so it is unsteerable and consequently violates Eq. (5):

$$\begin{aligned} \sum _{j=1}^3(w_{2jj}^{''})^2\le 1 \end{aligned}$$

(44)

As discussed above, the canonical forms $\rho _{AB}^{(2)}$ and $\rho _{BC}^{(2)}$ as the initial states used in the network. Depending on Bob’s output, the conditional states shared between Alice and Charlie are given by $\rho _{AC}^{ij},\,i,j=0,1$ (see Table 5).

Table 5 State parameters of each of the four conditional states are specified here

Let us consider $\rho _{AC}^{00}.$ Using state parameters (Table 5) of $\rho _{AC}^{00},$ L.H.S. of Eq. (23) becomes:

$$\begin{aligned}&Max _{x_1,x_2,x_3}((x_1\mathfrak {u}_{21}^{''}w_{111}^{''}-x_2\mathfrak {u}_{22}^{''}w_{122}^{''} +x_3\mathfrak {u}_{23}^{''}w_{133}^{''})^2\nonumber \\&\quad +sqrt{\sum _{j=1}^3(x_jw_{1jj}^{''}w_{2jj}^{''})^2}), \end{aligned}$$

(45)

where $\mathfrak {u}_{21}^{''},\mathfrak {u}_{22}^{''},\mathfrak {u}_{23}^{''}$ are the components of real valued vector Bloch vector $\vec {\mathfrak {u}_{2}^{''}}.$ In Eq. (45), maximization is to be performed over $x_1,x_2,x_3$, whereas the state parameters are arbitrary. Now the expression in Eq. (45) is numerically maximized over all the state parameters involved and also $x_1,x_2,x_3$ under the following restrictions:

• $w_{111}^{''}\le \frac{1}{2}$

• $w_{122}^{''}\le \frac{1}{2}$

• $w_{133}^{''}\le \frac{1}{2}$

• $\sum _{j=1}^3(w_{2jj}^{''})^2\le 1.$

While the first three restrictions are due to the unsteerability of $\rho _{AB}^{(2)},$ i.e., given by Eq. (39) for $k=1,$ the last restriction is provided by Eq. (44)(a consequence of unsteerability of $\rho _{BC}^{(2)}$). Maximum value of the above maximization problem [Eq. (45)] turns out to be 0.75, corresponding maxima (alternate maxima exists) given by $w_{111}^{''}=0.5,$ $w_{122}^{''}=0.454199,$ $w_{133}^{''}=0.46353,$ $w_{211}^{''}=-1,$ $w_{222}^{''}=0,$ $w_{233}^{''}=0,$ $\mathfrak {u}_{21}^{''}=1,$ $\mathfrak {u}_{22}^{''}=0,$ $\mathfrak {u}_{23}^{''}=0,$ $x_1=1,$ $x_2=0$ and $x_3=0.$ Maximum value less than 1 implies that the original maximization problem [Eq. (45)], where maximization is to be performed only over $x_1,x_2,x_3$(for arbitrary state parameters) under the above restrictions (resulting from unsteerability of $\rho _{AB}^{(2)},\rho _{BC}^{(2)}$), cannot render optimal value greater than 1. Consequently conditional state $\rho _{AC}^{00}$ satisfies the unsteerability criterion [Eq. (23)] and is therefore unsteerable. So, in case Bob’s particles get projected along $|\phi ^{+}\rangle ,$ genuine activation of steering does not occur in the linear network. In similar way, considering, other three conditional states, it is checked that the unsteerability criterion [Eq. (23)] is satisfied in each case. Genuine activation of steering is thus impossible for all possible outputs of Bob. Hence when one of the initial states has null local Bloch vector corresponding to first party, genuine activation of steering does not occur.

Appendix D

See Table 6.

Table 6 Bloch matrix parameters of each of the four conditional states generated in the linear swapping network using $\Omega _3,\Omega _4$ [Eq. (24)] as initial states are specified here