1 Introduction

The development of attosecond light sources since the beginning of the twenty-first century has opened the possibility to probe electronic dynamics with attosecond resolution. The absorption of an attosecond light pulse by matter leads to the emission of a photoelectron wavepacket (EWP) corresponding to the coherent superposition of continuum states. The measurement of the amplitude and phase of the EWPs, using attosecond streaking [1] or the reconstruction of attosecond beating by interference of two-photon transitions (RABBIT) technique [2], provides information on the photoionization dynamics in atoms and molecules in the gas phase [3,4,5,6,7,8,9,10] as well as in solids [11, 12] and liquids [13]. One of the successful applications of the RABBIT technique has been the study of the ionization dynamics close to an autoionization resonance [14,15,16,17,18,19]. The interpretation of these measurements relies on the assumption that the EWPs are fully coherent and can be represented by a complex-valued wavefunction, i.e., a pure quantum state.

In general, however, quantum experiments only probe a reduced number of degrees of freedom. As a result, measurements are averaged over the degrees of freedom outside of the studied subsystem. If the subsystem is entangled with some of the degrees of freedom that are not measured, averaging over the latter leads to a loss of coherence in the measurements. A typical example is the sudden excitation of a coherent superposition of electronic states in a molecule. The entanglement of the electronic and nuclear degrees of freedom results in a loss of its coherence on a timescale ranging from a few to hundreds of femtoseconds when the vibrational degrees of freedom are not accessible in the measurement [20,21,22].

Recently, several studies have investigated quantum effects in attosecond science. The generation of non-classical light via high harmonic generation has been experimentally demonstrated [23, 24], and a scheme for the generation of high-photon number entangled states has been proposed [25]. In the case of photoionization, following the seminal work of Akoury et al. on electron–electron entanglement in single-photon double ionization of H\(_2\) [26], several theoretical investigations of electron–ion entanglement and its effect on the degree of coherence of the individual subsystems have been reported [27,28,29,30]. Nonetheless, experimentally quantifying decoherence is a difficult task, often overlooked in attosecond photoionization experiments since coupling to the outside environment usually happens on a timescale much longer than that of the photoionization process. Recently, Koll et al. experimentally observed signatures of decoherence due to electron–ion entanglement in H\(_2\) [31] and Bourassin-Bouchet et al. measured the quantum state of photoelectrons emitted following the absorption of an attosecond pulse train, demonstrating the impact of experimental fluctuations and limited spectral resolution on the photoelectron coherence [32, 33].

As demonstrated by Bärnthaler et al. for microwave cavities [34], Fano resonances are sensitive probes of decoherence: Since they result from an interference phenomenon, any small perturbation is immediately apparent as a loss of contrast and reduced phase variation across the resonance. In the case of photoionization, the interference takes place between direct ionization of an atom or molecule in its ground state and autoionization from a quasi-bound state embedded in the continuum [35]. Perturbations to this scheme such as the influence of additional levels, the interaction with a thermal bath, and/or experimental imperfections such as laser jitter [36, 37] may lead to decoherence. A high spectral resolution is generally needed to identify experimentally the modifications of the resonance profiles due to decoherence.

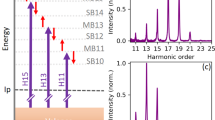
In this work, using an infrared (IR) field with a narrow spectral bandwidth, together with a deconvolution algorithm to compensate for the electron spectrometer’s response function, we perform interferometric photoelectron spectroscopy measurements, using the RABBIT technique, with unprecedented spectral resolution. We determine the amplitude and phase of EWPs created by resonant absorption of extreme ultraviolet (XUV) radiation close to the 2s2p resonance in He, plus absorption or stimulated emission of an IR photon, as shown in Fig. 1a. The high spectral resolution of our measurements allows us to investigate the degree of coherence of the emitted EWPs and to show that it depends on whether the IR photon is absorbed or emitted during the two-photon transition. The coupling of 2s2p to the 2p\(^2\) (\(^1\)S) autoionizing state, which is energetically close in the absorption case, induces a loss of purity in the measured angle-integrated wavepacket. This is verified by comparing with the two-photon wavepacket originating from emission of an IR photon from the 2s2p resonance, which does not suffer from the presence of resonances in the final state and acts as a benchmark.

Fig. 1
figure 1

Principle of the experiment. a Spectroscopic scheme of the states and transitions relevant to this study. The blue/red arrows indicate XUV/IR dipole transitions. The double-headed arrows indicate the configuration interaction between the bound states and the continuum. The reference non-resonant transitions involving H\(_{37}\) and H\(_{41}\) are not shown for simplicity. b RABBIT spectrogram after deconvolution

Full size image

2 Results

2.1 Experimental results

In our experiment, high-order harmonics are generated by focusing a 30 fs IR pulse in a cell filled with neon gas, resulting in the emission of an XUV comb of odd harmonics of the laser central frequency. The central wavelength of the IR field is chosen so that the 39th harmonic is resonant with the 2s2p resonance in He, which is located at 60.147 eV above the ground state [38] (see Fig. 1a). A 2-m-long magnetic bottle electron spectrometer (MBES), with a spectral resolution below 100 meV in the 0–5 eV spectral range, is used to detect the photoelectrons. To benefit from this resolution, a retarding voltage is applied so that electrons created by absorption of the 39th harmonic and the adjacent sidebands called SB\(_{38}\) and SB\(_{40}\) are in the 0–5 eV range. SB\(_{2q}\) originates from the interference of two quantum paths: absorption of harmonic \(2q+1\) and emission of an IR photon or absorption of harmonic \(2q-1\) and an IR photon. The spectral resolution of our measurements is further improved using a blind Lucy–Richardson deconvolution algorithm [39, 40]. In a traditional RABBIT setup, both the XUV and IR pulses have a broad bandwidth. Consequently, several combinations of XUV and IR frequencies lead to the same final energy and interfere. This finite pulse effect induces a broadening and a smoothing of resonant two-photon ionization spectra and thus a loss of spectral resolution [41]. To minimize this effect, the spectral bandwidth of the probe pulse is reduced to 10 nm (full width at half maximum) using a band-pass filter. By comparison, the bandwidth of the IR pulse used to generate the harmonics is approximately 50 nm.

The measured RABBIT spectrogram is shown in Fig. 1b. The photoelectron spectrum corresponding to the absorption of harmonic 39 and the two neighboring sidebands present a double structure, with an interference minimum, owing to the resonance. When the delay \(\tau \) between the XUV and IR pulses is varied, the sideband signal oscillates as

$$\begin{aligned} I^{(\pm )}(E,\tau )=\,{} & {} \vert A_{\textrm{R}}(E)\vert ^2+\vert A_{\textrm{NR}}(E)\vert ^2\nonumber \\{} & {} +2\vert A_{\textrm{R}}(E)\vert \vert A_{\textrm{NR}}(E)\vert \cos [2\omega \tau \mp \Delta \phi (E)],\nonumber \\ \end{aligned}$$
(1)

where \(\omega \) is the central angular frequency of the IR pulse, E is the net photon energy absorbed, \(A_{\textrm{R}}(E)\) and \(A_{\textrm{NR}}(E)\) are, respectively, the resonant and non-resonant two-photon transition amplitudes, and \(\Delta \phi (E)=\arg (A_{\textrm{R}})-\arg (A_{\textrm{NR}})\) is the phase difference between the two quantum paths. The sign ± indicates if the sideband is above \((+)\) or below \((-)\) the resonant harmonic (H\(_{39}\)). In the Rainbow version of the RABBIT method [14], the oscillations of the sidebands are fitted with Eq. (1) for each final energy E, allowing the extraction of the amplitude and phase as a function of energy, thus mapping the resonance structure.

Fig. 2
figure 2

Amplitude (a, c, e) and phase difference, \(\Delta \phi (E)\), (b, d, f) measured in sidebands SB\(_{38}\) (a, b) and SB\(_{40}\) (c–f). The experimental measurements are shown in blue, the results of the fits are shown in dashed black, and the results of the fully coherent models in red [model A in (a–d) and model B in (e, f), see main text]. The blue shaded areas correspond to the error around the measured value

Full size image
Fig. 3
figure 3

Wigner distribution calculated using the experimental complex amplitude measured in SB\(_{38}\). The observation of hyperbolic interference fringes demonstrates the high spectral resolution of our measurements

Full size image

Figure 2 shows in blue the amplitude and phase measured in SB\(_{38}\) (a,b) and in SB\(_{40}\) (c,d). In SB\(_{38}\), the amplitude exhibits a sharp interference structure which goes almost to zero at \(\sim 58.65\) eV (a) with a sharp phase jump of approximately 2 rad (b). In SB\(_{40}\), the interference contrast is reduced (c) and the phase variation is smoother, over approximately 1.5 rad (d). Compared to previous measurements reported in the literature [14, 15], the high spectral resolution of our measurements allows us to measure a significantly higher interference contrast and a larger phase jump. In addition, a clear difference between the two adjacent sidebands is observed, in contrast to previous results [14, 15].

Table 1 Values of the real and imaginary values of the q parameter retrieved from fits of the data using two different models (see main text for more details)
Full size table

Figure 3 shows the Wigner distribution for SB\(_{38}\), defined as

$$\begin{aligned} W(E,t)=\!\int \! A_\textrm{R}(E-\varepsilon /2)A_\textrm{R}^*(E+\varepsilon /2)e^{\text {i}\varepsilon t/\hbar } \textrm{d}\varepsilon , \end{aligned}$$
(2)

where \(\hbar \) is the reduced Planck constant. A spectrally broad and temporally narrow feature can be observed around \(t=0\), which corresponds to the direct ionization from the ground state to the continuum. The spectrally narrow and temporally long feature around 58.6 eV arises from the decay of the 2s2p resonance in the continuum. Finally, the large minimum at 58.65 eV and the hyperbolic fringes originate from interference between the two ionization paths. The observation of the hyperbolic interference fringes is possible thanks to the high spectral resolution achieved in this work. We note that our definition of the Wigner distribution assumes that the wavepacket, described by the complex amplitude \(A_{\textrm{R}}(E)\), is in a pure state. In the following, we investigate in detail the validity of this assumption.

2.2 Theoretical calculations

The measurements are compared to theoretical calculations based on the finite-pulse two-photon resonant model from Refs. [41, 42], in which dipole couplings between unperturbed continua are calculated using the on-shell approximation. Autoionization of the 2s2p resonance reached by absorption of a single XUV photon is formally described according to Fano’s formalism [35], with the help of a complex resonance factor defined as

$$\begin{aligned} R(\epsilon )=\frac{q+\epsilon }{\epsilon +\text {i}}. \end{aligned}$$
(3)

The quantity \(\epsilon =2(E-E_{\textrm{r}})/\Gamma \) is the reduced energy (\(E_{\textrm{r}}\) is the resonance energy and \(\Gamma \) the spectral width of the resonance), while q is a (real) asymmetry parameter depending on the relative strength between direct ionization and autoionization (see Fig. 1). Bärnthaller et al. [34], generalizing previous work on quantum dots [43], show that the influence of decoherence on a Fano lineshape can be described using Eq. (3) by allowing q to be complex. The origin of the decoherence, for example dissipation or dephasing, appears in the type of trajectory traced by the q parameter in the complex plane as the degree of coherence is varied.

As described in detail in the Supplementary Material (SM), we use the analytical formulation of [41] to describe the two-photon transitions. Although the transition amplitudes cannot be parametrized by a simple resonance factor as in Eq. (3), they can be expressed as a function of the one-photon q parameter, which is real in the absence of coupling to degrees of freedom outside the system considered in the model. We compare two analytical models (denoted A and B) to investigate decoherence in our measurements. Model A is a reduced, fully coherent model that only includes the 2s2p state and a single ionization channel. In contrast, model B includes both the 2s2p and the 2p\(^2\) states as well as two incoherent ionization channels: \(\text {s}\rightarrow \text {p}\rightarrow \text {s}\) and \(\text {s}\rightarrow \text {p}\rightarrow \text {d}\).

The results of the fit using model A are shown as dashed black curves in Fig. 2a–d, and the values of q retrieved from the fit are shown in Table 1A. In the case of SB\(_{38}\), the q parameter giving the best fit to the experimental data has a small imaginary part and a real part that is in good agreement with single-photon measurements using synchrotron radiation (\(q=-2.77\)) [44]. In contrast, for SB\(_{40}\), the fitted q parameter has an imaginary part twice as large as for SB\(_{38}\) and a real part that significantly deviates from spectroscopic data. We also show in Fig. 2a–d the results from model A using a real asymmetry parameter \(q=-2.77\) (red solid line). This calculation reproduces well the experimental measurements for SB\(_{38}\) but fails to describe the reduced contrast and phase variation in SB\(_{40}\). The good agreement obtained for SB\(_{38}\) allows us to conclude that decoherence is negligible. The small imaginary part of the fitted q parameter can be attributed to small amounts of experimental decoherence due, for example, to volume averaging over the interaction region. As a consequence, the large deviation of the fitted q parameter in SB\(_{40}\) reveals that this sideband is subjected to decoherence that cannot be explained by experimental imperfections. In both sidebands, the deviation between the experimental and theoretical amplitude at low energy can be attributed to a well-known distortion introduced by the MBES [45,46,47].

In order to understand the physical origin of the decoherence observed in SB\(_{40}\), we now use a more complete analytical model (B), which includes two ionization channels and both the 2s2p and 2p\(^2\) resonances (see SM). The latter state is accessible via two-photon absorption due to the strong dipole coupling of the 2p\(^2\) with the 2s2p state and only decays toward the \(\epsilon \)s continuum [41, 42]. The 2p\(^2\) state is also strongly coupled to the bound 1s2p state, which makes it necessary to include the non-resonant \(1\text {s}^2\rightarrow 1\text {s}2\text {p}\rightarrow 2\text {p}^2\) transition [41]. The new values of the q parameter for the 2s2p resonance retrieved from the fit of model B to the experimental data are shown in Table 1B. As expected, the results for SB\(_{38}\) are the same as those obtained with model A since including the 2p\(^2\) state, situated in the vicinity of SB\(_{40}\), should not affect the lower sideband. In contrast, the real and imaginary parts of the q parameter for SB\(_{40}\) strongly differ from that of model A and are now very similar to those measured in SB\(_{38}\). Figure 2e and f shows the experimental data for SB\(_{40}\), the fit (black dashed line) and the more complete model with \(q=-\,2.77\) (red solid line), which are all in good quantitative agreement, indicating that the origin of the decoherence observed in SB\(_{40}\) using model A is fully accounted for in model B as discussed in the following.

3 Discussion

3.1 Density matrix and entanglement

Our aim is to understand how the 2p\(^2\) state affects the coherence properties of the continuum wavepacket measured in SB\(_{40}\). In the absence of any source of decoherence outside the atomic system, the wavepacket is a pure state corresponding to a coherent superposition of s and d waves (see Fig. 1a), which can be formally expressed as

$$\begin{aligned}{} & {} \vert \Psi (t)\rangle \nonumber \\{} & {} \quad =\!\!\int \!\! \textrm{d}\epsilon \ c_{\textrm{s}}(\epsilon ,t)\vert {R_{\textrm{s}}(\epsilon )}\rangle \otimes \vert {Y_{00}}\rangle +c_{\textrm{d}}(\epsilon ,t)\vert {R_{\textrm{d}}(\epsilon )}\rangle \otimes \vert {Y_{20}}\rangle ,\nonumber \\ \end{aligned}$$
(4)

where \(\vert {R_{\ell }(\epsilon )}\rangle \) are the radial wavefunctions, \(\vert {Y_{\ell 0}}\rangle \) the spherical harmonics, \(c_\ell (\epsilon )\) the coefficients of the coherent superposition, \(\ell \) (= s or d) the electron angular momentum and \(\otimes \) the tensor product. The integral is performed over the spectral width of the wavepacket, imposed by the excitation pulses. In general, the radial or angular wavefunctions are not separable, which implies that these two degrees of freedom are entangled [48]. Note that, in this work, entanglement involves two different degrees of freedom of the same particle (see [49] for a review of single-particle entanglement), at variance with recent work on photoionization where entanglement involves two particles, the electron and the ion [27,28,29, 31]. The quantum state of the wavepacket can equivalently be represented by its density matrix

$$\begin{aligned} \begin{aligned}&{\hat{\rho }}(t)=\vert \Psi (t)\rangle \langle {\Psi (t)}\vert \\&\quad =\!\!\int \!\!\!\! \int \! \textrm{d}\epsilon \textrm{d}\epsilon 'c_{\textrm{s}}(\epsilon ,t)c_{\textrm{s}}^*(\epsilon ',t)\vert {R_{\textrm{s}}(\epsilon )}\rangle \!\otimes \!\vert {Y_{00}}\rangle \langle {R_{\textrm{s}}(\epsilon ')}\vert \!\otimes \!\langle {Y_{00}}\vert \\&\qquad +c_{\textrm{d}}(\epsilon ,t)c_{\textrm{d}}^*(\epsilon ',t)\vert {R_{\textrm{d}}(\epsilon )}\rangle \otimes \vert {Y_{20}}\rangle \langle {R_{\textrm{d}}(\epsilon ')}\vert \otimes \langle {Y_{20}}\vert \\&\qquad +c_{\textrm{s}}(\epsilon ,t)c_{\textrm{d}}^*(\epsilon ',t)\vert {R_{\textrm{s}}(\epsilon )}\rangle \otimes \vert {Y_{00}}\rangle \langle {R_{\textrm{d}}(\epsilon ')}\vert \otimes \langle {Y_{20}}\vert \\&\qquad +c_{\textrm{d}}(\epsilon ,t)c_{\textrm{s}}^*(\epsilon ',t)\vert {R_{\textrm{d}}(\epsilon )}\rangle \otimes \vert {Y_{20}}\rangle \langle {R_{\textrm{s}}(\epsilon ')}\vert \otimes \langle {Y_{00}}\vert . \end{aligned} \end{aligned}$$
(5)
Fig. 4
figure 4

Resonant wavepackets in the s and d continua calculated using model B. Relative amplitude (top) and phase (bottom) of the s (blue) and d (red) wavepackets in SB\(_{38}\) (a, c) and SB\(_{40}\) (b, d)

Full size image

The first two terms describe the reduced density matrices of the wavepackets in the s and d continua, respectively, while the last two terms describe the coherences between the two continua. In the case of angle-integrated measurements, as in this work, the angular degree of freedom of the photoelectron is not measured. As a result, the measured wavepacket is described by a reduced density matrix \({\hat{\rho }}_{\textrm{r}}\) defined as

$$\begin{aligned} \begin{aligned} \!{\hat{\rho }}_{\textrm{r}}(t)&=\textrm{Tr}_{(\theta ,\phi )}[{\hat{\rho }}(t)] \\&=\!\int \!\!\!\int \! \textrm{d}\epsilon \textrm{d}\epsilon 'c_{\textrm{s}}(\epsilon ,t)c_{\textrm{s}}^*(\epsilon ',t)\vert {R_{\textrm{s}}(\epsilon )}\rangle \langle {R_{\textrm{s}}(\epsilon ')}\vert \\&\quad +c_{\textrm{d}}(\epsilon ,t)c_{\textrm{d}}^*(\epsilon ',t)\vert {R_{\textrm{d}}(\epsilon )}\rangle \langle {R_{\textrm{d}}(\epsilon ')}\vert . \end{aligned} \end{aligned}$$
(6)

Due to the orthogonality of the spherical harmonics, the coherences between the different continua disappear and the final quantum state is a statistical mixture of the s and d wavepackets. In other words, when the radial and angular degrees of freedom are entangled, taking the partial trace over one of them leads to a mixed reduced density matrix characterized by a lower degree of coherence compared to the pure case.

In the case of SB\(_{38}\), the radial complex amplitudes for the s and d continua are almost identical, i.e., \(c_{\textrm{s}}(E)\propto c_{\textrm{d}}(E) \propto A_{\textrm{R}}(E)\) (see Fig. 4a, c). As a consequence, it is possible to factorize the radial amplitudes such that the angular integration in Eq. (4) does not lead to a loss of coherence (see SM). In contrast, in SB\(_{40}\), the 2p\(^2\) state, which has \(^1\)S\(_0\) symmetry, can only decay to the s continuum, leaving the d continuum unaffected (see Fig. 1). This results in the emission of s and d wavepackets with different amplitudes and phases as shown in Fig. 4b and d.

The amplitude of the d wavepacket is characterized by a strong destructive interference, with a maximum on the left almost twice as large as the right one. On the contrary, the amplitude of the s wavepacket shows a reduced interference contrast and the maximum on the right is slightly larger than the left one. Similarly, the phase variation of the two wavepackets is different, with the d wavepacket showing a phase variation approximately twice as large as that of the s wavepacket. The radial wavefunctions for s and d waves are different so that they cannot be factorized in Eq. (4). As a result, the radial and angular degrees of freedom are entangled. It is worth observing that neither the s nor the d channel taken individually can reproduce the measured amplitude and phase variation. Only the statistical mixture shown in red in Fig. 2e and f reproduces the experimental data. Note that in Fig. 4 we show the amplitude and phase of the resonant transition amplitude only (and not the phase difference between the non-resonant and resonant contributions as in the RABBIT scheme, see Fig. 2), so that the phases in Fig. 4c and d vary in the same way for the two sidebands.

Fig. 5
figure 5

Quantum state of the asymptotic resonant two-photon wavepacket for SB\(_{38}\) (a, b) and SB\(_{40}\) (c, d). a and c Absolute value and b and d coherence map of the density matrix. The purity in SB\(_{38}\) (a, b) is 0.998, while in SB\(_{40}\) (c, d) it is 0.898

Full size image

3.2 Decoherence

We now investigate the asymptotic quantum state of the resonant two-photon wavepacket for the two sidebands, starting with SB\(_{38}\). Figure 5a shows the absolute value of the calculated reduced density matrix \(\vert \rho _{\textrm{r}}(E,E')\vert =\lim _{t\rightarrow \infty }\vert \langle \phi _E\vert {\hat{\rho }}_{\textrm{r}}(t)\vert \phi _{E'}\rangle \vert \), where \(\vert {\phi _{E}}\rangle \) are the asymptotic radial wavefunctions of any continuum state with well-defined angular momentum and energy E. The populations, along the diagonal \(\rho _{\textrm{r}}(E,E)\), present two maxima, separated by strong destructive interference at 58.65 eV, reflecting the energy dependence of the photoelectron spectra (see Fig. 2a). The off-diagonal elements, \(\rho _{\textrm{r}}(E,E')\), which describe the coherences between the different final scattering states, are strongest when the corresponding populations \(\rho _{\textrm{r}}(E,E)\) or \(\rho _{\textrm{r}}(E',E')\) are high. To represent the degree of coherence between the scattering states at different energies, we introduce the coherence map \(C(E,E')\) defined as

$$\begin{aligned} C(E,E')=\frac{\left| \rho _{\textrm{r}}(E,E')\right| }{\sqrt{\rho _{\textrm{r}}(E,E)\rho _{\textrm{r}}(E',E')}}, \end{aligned}$$
(7)

and shown in Fig. 5b. Most of the wavepacket is fully coherent [\(C(E,E')=1\)], except for a slight decrease in the coherence in the vicinity of the destructive interference region. The purity of the wavepacket is extremely high with \(\textrm{Tr}({\hat{\rho }}_{\textrm{r}}^2)=0.998\).

Contrary to the case of SB\(_{38}\), the resonant two-photon wavepacket in SB\(_{40}\) is a statistical mixture of s and d waves with different amplitudes and phases as shown in Fig. 4b and d. Using the theoretical amplitude and phase of the two wavepackets, we fit their relative weight in the experimental data, allowing us to reconstruct the density matrix. The s wavepacket is found to be 1.15 times stronger than the d wavepacket, which agrees well with the ratio of the angular coefficients for the p \(\rightarrow \) s and p \(\rightarrow \) d transitions, which is approximately 1.12. The absolute value of the asymptotic density matrix is shown in Fig. 5c. Qualitatively, it looks similar to that obtained for SB\(_{38}\), although the destructive interference is not as pronounced. In Fig. 5d, we present the coherence map \(C(E,E')\). The degree of coherence between the low- and high-energy parts of the wavepacket and especially between the interference minimum and the rest of the wavepacket is lower than in the case of SB\(_{38}\). This originates from the difference between the s and d wavepackets in the region of the interference minimum, which are mixed in the angle-integrated measurement. Despite the clear loss of coherence between certain spectral regions of the wavepacket, the purity of the wavepacket remains high with \(\textrm{Tr}({\hat{\rho }}_{\textrm{r}}^2)=0.898\). Interestingly, our description of the effect of angular integration using the tools of quantum information shows that while, formally, the s and d waves add incoherently in both sidebands 38 and 40, only sideband 40 is subject to decoherence as a result of the stronger degree of entanglement between radial and angular degrees of freedom.

Finally, we note that the decoherence observed in this work would be suppressed by performing angle-resolved measurements. In that case, the entanglement between the radial and angular degrees of freedom is responsible for the angle dependence of the photoionization time delays [18, 50, 51]. Performing angle-resolved measurements with high spectral resolution for photoelectrons with kinetic energies around 35 eV, as is the case here, is extremely challenging. Nonetheless, such measurements have been demonstrated for slower photoelectrons close to the ionization threshold [52].

Fig. 6
figure 6

Quantum state evolution of the wavepacket in SB\(_{40}\). a Temporal evolution of the wavepacket purity. b, d, f Absolute value of the density matrix at three different times as indicated in (a). c, e, g Coherence maps corresponding to the density matrices in (b, d, f)

Full size image

3.3 Temporal evolution of the quantum state

In the case of a pure wavepacket, the temporal profile and the buildup of the wavepacket as a function of time can be reconstructed using the simple transformation, [14, 15, 19, 53]

$$\begin{aligned} A(E,t)=\int _{-\infty }^t{\tilde{A}}(t')e^{-\frac{\textrm{i}Et'}{\hbar }}\textrm{d}t', \end{aligned}$$
(8)

where \({\tilde{A}}(t)\) is the Fourier transform of the complex spectral amplitude A(E). In the case of a mixed state, it is necessary to calculate the build-up of the spectral amplitudes individually for the different angular channels in order to reconstruct the evolution of the density matrix and the coherence map during autoionization.

Figure 6a presents, for the SB\(_{40}\) case, the reconstructed evolution of the purity over time based on model B, using the experimentally retrieved relative weight of the s and d wavepackets. Snapshots of the density matrix and coherence map at three different times are shown in Fig. 6b–g. At short times, the purity is close to 1 and both the density matrix and coherence map show that all the parts of the wavepacket are fully coherent. Indeed, around \(t=0\), which corresponds to the maximum of the temporal amplitude of the wavepacket, direct ionization is the dominant ionization process so that the wavepackets in the s and d continua are almost identical, leading to a reduced density matrix corresponding to a pure state. As the 2s2p and 2p\(^2\) states decay in the continuum, with lifetimes, respectively, 18 fs and 112 fs, the amplitude and phase of the s and d wavepackets become increasingly different, resulting in a loss of purity. This appears in the density matrix and coherence map as a loss of coherence between the low and high energy parts of the wavepacket. As time progresses, the destructive interference between direct ionization and autoionization appears in the density matrix and the degree of coherence between this spectral region and the rest of the wavepacket drops. The main decrease in purity occurs during the first 20 fs, which is close to the lifetime of the 2s2p resonance, while the coherences and populations keep evolving until approximately 50 fs, after which they have converged to the asymptotic value shown in Fig. 5c and d (see movie in SM).

In conclusion, we have performed rainbow RABBIT measurements with high spectral resolution in He in the vicinity of the 2s2p Fano resonance. By fitting the measured amplitude and phase with two different models, we show that in the lower sideband, the emitted electron wavepacket is fully coherent, while, in the upper sideband, the coupling between the 2s2p and 2p\(^2\) resonances results in the emission of different wavepackets in the s and d continua, leading to an entanglement of the angular and radial degrees of freedom. Combining experiment and theory, we fully characterize the quantum state of the emitted wavepackets and show that this entanglement manifests itself as a loss of coherence in angle-integrated measurements. Finally, we reconstruct the quantum state evolution of the resonant two-photon wavepacket in SB\(_{40}\) and monitor the degree of coherence of the wavepacket during autoionization. These results pave the way toward the complete characterization of complex partially coherent electronic wavepackets, extending the range of processes that can be investigated using attosecond photoelectron interferometry.