The scattering symmetries of tetrahedral quantum structures

Abstract

The electrons associated with molecules and other small quantum structures exist in states that are bound or quasibound to the molecule. The quasibound states, which can significantly affect chemical reaction dynamics, have finite lifetimes and are associated with complex energy poles of the scattering matrix. Using Wigner–Eisenbud (R-matrix) scattering theory, we examine the symmetry properties of the quasibound states of a molecule-size tetrahedral system, and we examine the relation of quasibound states to the scattering properties. In addition, using R-matrix theory, we construct a non-Hermitian Hamiltonian whose complex energy eigenvalues coincide with the bound and quasi-bound states of the molecule. We show that each bound state and quasibound state of the tetrahedral system belongs to a distinct irreducible representation of the tetrahedral group, and that an incident electron belonging to one irreducible representation can only scatter within the same irreducible representation.

Graphic Abstract

Appendices

Appendix A: Tetrahedral group elements

Table 7 Matrix representations $D^{(\Gamma )}(R)$ of the 24 group elements R of the tetrahedral group $T_d$ in all five irreps $\Gamma$. The exact meaning of each group element symbol is discussed in Appendix A

In Sect. 2.3, we use the matrix representations of the 24 tetrahedral group elements in all five irreps to form the projection operators. These are listed in Table 7. We use symbols for each element of the tetrahedral group, which we now define in terms of the action it has on a three-dimensional object, class by class.

The first class contains only one element: the identity element. Both the element and the class have the same symbol I.

Next, we have the class $8C_3$ of eight rotations around a threefold axis. There can be rotations of either $\frac{2\pi }{3}$ or $-\frac{2\pi }{3}$. When doing such a rotation, one of the four vertices (or nuclei when considering a molecule) remains stationary. If, for example, vertex 1 remains stationary after a rotation of $\frac{2\pi }{3}$, then we have $C_{31}$. If we rotate in the other direction, we obtain $C_{31}^2$.

There are also three rotations about a twofold axis in the class $3C_2$. These rotations do not leave any vertices stationary, so the naming convention for the previous class is not useful. Instead we categorize using the axis of rotation. $C_{2x}$ is a rotation of $\pi$ around the x-axis, and similar symbols can be formed for the y- and z-axis.

The next class $6\sigma _d$ is formed by six reflections across a plane. These reflections leave two vertices unchanged, and exchange the positions of the other two. Therefore, our naming convention will specify the two vertices that have swapped locations. For example, $\sigma _{12}$ leaves vertices 3 and 4 stationary and exchanges vertices 1 and 2.

Finally, we have the class $6S_4$ of 6 rotoreflections. To apply this transformation, we first rotate by either $\frac{\pi }{2}$ or $-\frac{\pi }{2}$ around one of the Cartesian axes and then reflect across the plane normal to the same axis (that also contains the origin). If we rotate $\frac{\pi }{2}$ about the x-axis and reflect, then we have $S_{4x}$. If the rotation occurs in the opposite direction, then we have $S_{4x}^3$.

Appendix B: Wigner–Eisenbud coupling terms

As shown in Sect. 3, it is useful to split the Hamiltonian into its contribution to the reaction region and that of asymptotic region. However, the reaction- and asymptotic-region Hamiltonians, $\hat{H}_{Q}$ and $\hat{H}_{P}$, respectively, are not strictly Hermitian on their own. As shown in Eqs. 23 and 24, they need to appear alongside coupling surface terms $\hat{Q}\hat{H}\hat{P}$ and $\hat{P}\hat{H}\hat{Q}$. In this appendix, we show how to derive these coupling terms [84].

The Laplacian operator $\nabla ^2$ is Hermitian over all space. However, when considering a region of space for which the wavefunctions do not vanish at the boundaries, the Laplacian is not Hermitian. This is the case for a Laplacian in reaction region. This can be seen clearly if we start with an inner product $\langle \xi _1|\nabla ^2|\xi _2\rangle$, for arbitrary test wavefunctions $\xi _1$ and $\xi _2$, and integrate by parts. We are left with

$$\begin{aligned}&\langle \xi _1|\nabla ^2|\xi _2\rangle =\langle \xi _2|\nabla ^2|\xi _1\rangle ^*+\langle \xi _1|2\delta (r-a)\frac{\partial }{\partial r}|\xi _2\rangle \nonumber \\&\quad -\langle \xi _2|2\delta (r-a)\frac{\partial }{\partial r}|\xi _1\rangle ^*. \end{aligned}$$

(B1)

However, as evidenced by Eq. (B1), the operator $\nabla ^2-2\delta (r-a)\frac{\partial }{\partial r}$ is Hermitian in the reaction region. By a similar argument, the operator $\nabla ^2+2\delta (r-a)\frac{\partial }{\partial r}$ is Hermitian in the asymptotic region. Thus, we can maintain hermiticity while using W-E boundary conditions by accounting for the coupling term given in Eq. (27) as

$$\begin{aligned} \hat{Q}\hat{H}\hat{P}&=-\frac{\hbar ^2}{\mu }\oint _\mathbf {R}d^3r_1\oint _ \mathbf {A}d^3r_2|\mathbf {r}_1\rangle \langle \mathbf {r}_1|\mathbf {r}_2\rangle \delta (r_2-a) \frac{\partial }{\partial r_2}\langle \mathbf {r}_2|, \end{aligned}$$

(B2)

which can be further evaluated, using Eq. (22), as matrix elements of the form

$$\begin{aligned}&\langle \phi _\alpha |\hat{Q}\hat{H}\hat{P}|E\rangle =-\frac{\hbar ^2}{\mu }\int _0^a r_1^2dr_1\int _a^\infty dr_2\nonumber \\&\quad \int d\Omega _1\delta (r_1-r_2)\delta (r_2-a)\langle \phi _\alpha |r_1,\theta _1,\varphi _1\rangle \frac{\partial }{\partial r_2}\langle r_2,\theta _1,\varphi _1|\hat{P}|E\rangle , \end{aligned}$$

(B3)

where $d\Omega _1=\sin \theta _1d\theta _1d\varphi _1$ is a solid angle and is integrated over the full surface of a sphere. Plugging in the definitions of the basis states used in the reaction and the asymptotic regions—shown in Eqs. 30 and 34, respectively—we find we are left with an integral over two orthonormal angular basis states. This integral yields a Kronecker delta function $\delta _{\nu ,\nu '}$. Thus, the summation over $\nu '$ can be evaluated. Additionally, since the Dirac delta function is nonzero only on the boundary of the integration region, it will pick up a factor of $\frac{1}{2}$. This yields

$$\begin{aligned} \langle \phi _\alpha |\hat{Q}\hat{H}\hat{P}|E\rangle&=-\frac{\hbar ^2a^2}{2\mu }\sum _{\nu }\psi ^*_{\alpha ,\nu }\left[ \frac{\partial \Phi _{\nu }(kr)}{\partial r}\right] _{r=a}, \end{aligned}$$

(B4)

where $\psi _{\alpha ,\nu }$ is defined in Eq. (39).

We further note that since the coupling terms are nonzero only on the boundary $r=a$, they do not contribute to determining the energies or wavefunctions inside the reaction region. The coupling terms must be considered, however, when forming the R- and S-matrix, as they will inform how the reaction- and asymptotic-region states relate to one another.

Fig. 13

Contour plots of the differential cross sections for scattering particles with energies a $E=0.9E_0$ and b $E=1.8E_0$. c Total scattering cross section $\sigma$ as a function of the incident energy E

Appendix C: Scattering cross section

In experimental physics, scattering data are often expressed in terms of cross sections. In this appendix, we show how to compute a cross section from an S-matrix. First, we consider a plane wave incident on the tetrahedral potential propagating in the direction of $\hat{r}_\mathrm {in}=\sin \theta _\mathrm {in}\cos \varphi _\mathrm {in}\hat{x} +\sin \theta _\mathrm {in}\sin \varphi _\mathrm {in}\hat{y}+\cos \theta _\mathrm {in}\hat{z}$. We can express the outgoing scattered wavefunction as

$$\begin{aligned}&\langle \mathbf {r}|\hat{P}|E\rangle _\mathrm {out}=\sum _{\begin{array}{c} \Gamma ,\ell ,q,\\ \Gamma ',\ell ',q' \end{array}}h_\ell ^{(1)}(kr)f^{(\Gamma )}_{\ell ,q}(\theta ,\varphi )\nonumber \\&\quad \left( S_{\ell ,q; \ell ',q'}-\delta _{\ell ,\ell '}\delta _{q,q'}\right) 2\pi e^{i\pi \ell '/2}\left[ f^{(\Gamma ')}_{\ell ',q'}(\theta _\mathrm {in},\varphi _\mathrm {in})\right] ^*, \end{aligned}$$

(C.1)

where the subtraction of the Kronecker delta functions effectively omits the contributions from the incoming wave. In the limit $r\rightarrow \infty$, we have

$$\begin{aligned} h_\ell ^{(1)}(kr)\rightarrow \frac{e^{-i\pi \ell /2}e^{ikr}}{ikr}. \end{aligned}$$

(C.2)

Additionally, we define $T_{\ell ,q;\ell ',q'}=S_{\ell ,q;\ell ',q'}-\delta _{\ell ,\ell '}\delta {q,q'}$ leaving

$$\begin{aligned} \langle \mathbf {r}|\hat{P}|E\rangle _\mathrm {out}&=\frac{e^{ikr}}{r}f_\mathrm {scat}(\theta ,\varphi ), \end{aligned}$$

(C.3)

where the scattering amplitude is

$$\begin{aligned}&f_\mathrm {scat}(\theta ,\varphi )=\sum _{\begin{array}{c} \Gamma ,\ell ,q,\\ \Gamma ',\ell ',q' \end{array}}\nonumber \\&\quad \frac{2\pi }{ik}e^{-i\pi \ell /2}f^{(\Gamma )}_{\ell ,q}(\theta ,\varphi )T_{\ell ,q;\ell ',q'} e^{i\pi \ell '/2}\left[ f^{(\Gamma ')}_{\ell ',q'}(\theta _\mathrm {in},\varphi _\mathrm {in})\right] ^*. \end{aligned}$$

(C.4)

While this expression can be evaluated in any representation, it can be simplified in the spherical harmonic basis if we assume that $\hat{r}_\mathrm {in}=\hat{z}$, such that $\theta _\mathrm {in}=0$. Since $Y_{\ell '}^{m'}(0,\varphi _\mathrm {in})=\sqrt{\frac{2\ell '+1}{4\pi }}\delta _{m',0}$, we can write

$$\begin{aligned}&f_\mathrm {scat}(\theta ,\varphi )\nonumber \\&\quad =\sum _{\ell ,m,\ell '} \frac{2\pi }{ik}e^{-i\pi \ell /2}Y^m_\ell (\theta ,\varphi )T_{\ell ,m;\ell ',0} e^{i\pi \ell '/2}\sqrt{\frac{2\ell '+1}{4\pi }}.\nonumber \\ \end{aligned}$$

(C.5)

Finally, we define the differential cross section as

$$\begin{aligned} \frac{\partial \sigma }{\partial \Omega }&=\left| f_\mathrm {scat}(\theta ,\varphi )\right| ^2, \end{aligned}$$

(C.6)

where, of course, the total cross section can be obtained by integrating over all solid angles, such that

$$\begin{aligned} \sigma&=\int d\Omega \left| f_\mathrm {scat}(\theta ,\varphi )\right| ^2. \end{aligned}$$

(C.7)

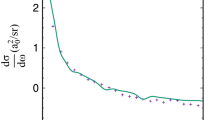
In Fig. 13a and b, we show two contour plots of the differential cross section for scattering particles with energies $E=0.9E_0$ and $E=1.8E_0$, respectively. At both of these energies, we see sharp peaks at around $\theta \approx \pi /2$. These energies also correspond with two of the S-matrix poles shown in Fig. 9. Additionally, in Fig. 13c, we plot the total cross section $\sigma$ as a function of energy E.

Fig. 14

S-matrix elements represented in the tetrahedral harmonic basis as a function of scattering energy. a $S_{35,38}$. b $S_{1,2}$

We note that for very low scattering energies, the cross section increases steeply. This is due to the quasibound state resonances at these low energies. To illustrate this more clearly, in Fig. 14, we have plotted the same S-matrix elements shown in Fig. 9. This time, we only plot over real scattering energy. Figure 14a shows the matrix element $S_{35,38}$, which we have shown has two resonances below $E=0.5E_0$. Figure 14b shows $S_{1,2}$, which we have shown does not have resonances in this low-energy region. In each of these plots, the increase in S-matrix elements is correlated with poles in the complex plane. We see that $S_{35,38}$ is significantly larger than $S_{1,2}$ for small energies due to the presence of resonances in that region. Thus, $S_{35,38}$—and similar matrix elements that show these low-energy poles—predominately contributes to total cross section in the low energy region. Similar logic can be applied to the higher energy quasibound state resonances, although it is easiest to see graphically in the lower energies.