1 Introduction

Understanding the effects induced by radiation moving through matter is of great interest in a wide variety of fields. Among them, the characterization of the damage induced by low-energy electrons (LEE), at the molecular level, has been a very active area of research in the decades since Sanche and coworkers [1, 2] showed that LEE can produce damage to DNA, even for energies below the ionization threshold. One of the main goals within this area is to achieve a modelling procedure able to describe the biological effects of the incident radiation, by considering not only the energy deposition but all the physical processes which may lead to biological damage [3]. Nowadays, one of the most successful approaches for this purpose has been the implementation of event-by-event Monte Carlo programs, which allow one to simulate all the possible scattering processes when ‘fed’ by a self-consistent data set of cross sections as the input parameters [3,4,5,6]. Therefore, electron scattering cross sections (i.e. the interaction probabilities) from biomolecules have become a necessary task, to acquire complete and comprehensive cross-section data sets, in order to provide relevant input information for the simulation of radiation tracks in matter [4, 5]. However, the study of relevant gas-phase biomolecules becomes harder or even inaccessible, either from the experimental or theoretical side, as the size of the molecules increases. Yet, those investigations have been focused on relatively simpler molecules, which can be considered as prototypes for more complex biologically relevant molecules [7].

Tetrahydrofuran (\(\mathrm{C}_{{\mathrm{4}}}\mathrm{H}_{{\mathrm{8}}}\mathrm{O})\) (THF) has a similar structure to ribose in the DNA backbone. For this reason, electron interactions with this benchmark molecule have been widely studied both in experiments and calculations at different levels of theory. As far as cross-section data are concerned, there are available results of total cross sections (TCSs) [8,9,10,11,12,13,14,15], integral elastic cross sections (ICSs) [16,17,18,19,20,21,22,23,24,25,26,27, 49], integral vibrational [23,24,25,26, 28,29,30] and electronic-state [31,32,33,34,35] excitation cross sections, total ionization cross sections [14, 36,37,38,39,40,41] and integral dissociative electron attachment (DEA) [42,43,44] cross sections. In addition, for most of the processes, differential cross sections (DCSs) [15, 26, 29, 30, 45,46,47] have been studied, including several recent studies on triple differential ionization cross sections [38, 48,49,50,51]. Furthermore, electron energy loss spectra are available for low [31, 34] and high [52] electron incident energies. This sheer volume of available data for THF, together with its role as an analogue for deoxyribose DNA constituent, makes it a perfect candidate for a careful review and compilation of the data required in Monte Carlo simulations. In recent years, and due to the relevance of this molecule, the electron swarm community has made a great effort to obtain a comprehensive “self-consistent” electron scattering data set on THF for electron transport simulations. The three most relevant papers are from Casey et al. [53], de Urquijo et al. [54], and Stokes et al. [55], although references therein should also be consulted. That work is directly relevant here, as to study the behaviour of electrons moving under the influence of an external applied electric field, a complete and comprehensive [56] cross-section database must initially be assembled. In such a situation one might think that obtaining a new set of self-consistent electron scattering data for this molecule could be redundant. However, there are new aspects that need to be considered: (i) we have recently developed an improved “state-of-the-art” magnetically confined electron beam transmission apparatus able to measure accurate total electron scattering cross section which has not been used before with THF; (ii) the elastic scattering cross-section data previously used in these compilations (see Ref. [55] for details) does not include interference effects [57] that, as demonstrated for other similar molecules [58], produce an appreciable increase in the intensity of electrons scattered in the forward direction (scattering angles \(< 1 \) deg) and therefore in the integral elastic cross sections, and (iii) the reliability of these recommended data has been checked against measured swarms parameters, such as the drift velocity, for which the angular distribution of elastically scattered electrons is not directly utilized.

The main focus of the present study is to provide accurate measurements of the total electron scattering cross sections from gaseous THF in the energy range 1 to 100 eV. From the TCSs as reference values, we can provide a self-consistent cross-section data set for electron scattering by gaseous THF in the energy range probed and also to check the reliability of our proposed data set, paying special attention to the angular distribution of the scattered electrons. We have therefore employed it as input data to simulate magnetically confined electron transport through gaseous THF at different beam energies (3, 10, and 70 eV), and gas pressures (2.5 and 5.0 mTorr), and then compared those results with the corresponding experimental data (see later). In addition, we have also compared the results obtained from our simulations with those found with the available Geant4DNA [59,60,61,62] code, using their recommended electron scattering data set.

The remainder of this paper is organized as follows. In the next section, the experimental and computational methods used are described. In Sect. 3, our experimental TCS results are presented, discussed, and compared with the available data in the literature. Additionally, the proposed data set of cross sections for THF is presented and its accuracy is evaluated, via simulations and their results being compared to independent transmission experimental data. The conclusions obtained from the present study are finally drawn in Sect. 4.

2 Experimental and computational methods

2.1 Magnetically confined electron beam experiment

The present measurements of the TCSs, as well as the transmitted electron intensity spectra, through gaseous THF, have been performed in an experimental setup described in detail elsewhere [63], but with some recent modifications. In the new configuration, the grids, where the potentials across the electrons’ path were applied, have been replaced by 1.5 mm in diameter collimators, in order to avoid the formation of secondary electrons (see ref. [63] for further details). Briefly, a pulsed electron beam, with an energy spread of about 150 meV, is obtained by thermionic emission from a hairpin filament in conjunction with a nitrogen buffer-gas trap, according to the procedure described in detail in ref. [63]. The electron beam is subsequently transported to the scattering chamber, where the target molecule is admitted via a leak valve. Finally, prior to their detection by a microchannel plate (MCP) assembly, the electrons are energy-analysed by a retarding potential analyser (RPA).

The total electron scattering cross sections, \(\sigma _{T}\), are obtained for each energy by using the well-known Beer–Lambert attenuation law and assuming an ideal gas behaviour. Note that a convenient range of gas pressures, during the attenuation measurements, was determined in order to avoid multiple scattering processes. Additionally, the transmitted electron intensity spectra have been obtained by energy-analysing the electrons after passing through a constant pressure of THF in the collision chamber.

As reported in detail elsewhere [63], due to the magnetic confinement of the electron beam, the angular resolution, \(\Delta \theta \), is dependent on both the energy resolution, \(\Delta E\), and the initial energy of the electrons, \(E_{K}\), according to Eq. (1). As a consequence, electrons scattered within \(\Delta \theta \) and \(180^\circ -\Delta \theta \) are considered by the detector to be unscattered; therefore, the measured total cross sections tend to be somewhat lower in magnitude than the ‘real’ total cross sections. However, the magnitude of this systematic error, \(\sigma (\Delta \theta )\), can be evaluated by integrating the theoretically calculated DCS over the missing angles, as shown in Eq. (2).

$$\begin{aligned} \Delta \theta ^{\circ }= & {} \sqrt{1-\frac{\Delta E}{E_{K}}} \, , \end{aligned}$$
(1)
$$\begin{aligned} \sigma \left( \Delta \theta \right)= & {} 2\pi \left( \int \limits _0^{\Delta \theta } {\frac{\mathrm{d}\left( \sigma _{el}+\sigma _{rot} \right) }{\mathrm{d}{\Omega }}\mathrm{sin}\theta \mathrm{d}\theta } \, \right. \nonumber \\&\left. +\int \limits _{180-\Delta \theta }^{180} {\frac{\mathrm{d}\left( \sigma _{\mathrm{el}}+\sigma _{\mathrm{rot}} \right) }{\mathrm{d}{\Omega }}\mathrm{sin}\theta \mathrm{d}\theta } \right) \, . \end{aligned}$$
(2)

2.2 Simulation procedure

We have simulated the transmitted intensity of magnetically confined electrons through gaseous THF, with an event-by-event Monte Carlo code developed by us for this specific application. This code has been programmed in Python, with a modular structure that allows for an easy implementation, revision and modification of each one of the physical processes incorporated into it. When simulating the tracks of charged particles, the code takes into account the different physical processes by sampling the step length between collisions, the interaction type, the energy loss and the angular deflection of the scattered particles. This sampling methodology is performed from the probability distributions derived from the total cross section, all the relevant integral cross sections, the energy loss spectra and the differential cross sections, which are fed into the code as input parameters.

The main effect of the axial magnetic field in the experiment is to confine the trajectories of the electrons to a spiral, with a radius small enough to pass through the apertures of the collimators (with a minimum diameter of 1.5 mm) (see Fig. 1). During this helical movement, the electron’s total kinetic energy and the angle that the momentum forms with respect to the axial direction remain constant. Even though the perpendicular component of the momentum, with respect to the axial direction, rotates around this axis, its magnitude does not change. Since the experimental configuration has cylindrical symmetry about the axial direction, the rotation of the perpendicular component of the momentum can thus be neglected. Therefore, in order to introduce the confinement effect of the magnetic field in the simulation, we have considered that in each step between collisions, the electrons move in the axial direction only (the perpendicular component of the velocity is neglected). Moreover, the retarding potential analyser (RPA) only discriminates against the axial component of the electron’s momentum and so the simulated transmitted intensity is obtained by measuring the kinetic energy associated with the axial component of the momentum of those electrons reaching the detector.

In the present configuration, we generated 10\(^{4\, }\) electrons, with an initial energy distribution obtained from the experimental transmission measurements in the absence of gas (0 mTorr) in the collision chamber, for each of the considered impact energies. This number of electrons was enough to assure less than a 1% variability, up to the nominal energy among simulations under the same conditions.

Fig. 1
figure 1

Schematic representation of the approximation used in the simulation for considering the confinement effect of the axial magnetic field

Full size image

3 Results and discussion

The set of results being presented and discussed here deal with the experimental TCS and their reliability, the recommended electron scattering cross sections together with a brief description of the corresponding data sources, the comparison made between the experimental and simulated transmitted electron intensities, the accuracy of the present data is also pondered, and finally we compare our results with those obtained through the Geant4DNA code.

3.1 Total electron scattering cross sections in the energy range 1 to 100 eV

The total electron scattering cross section (TCS) is a significant quantity as it represents the integral cross section sum of all scattering processes occurring at a given incident electron energy. Therefore, accurate TCS measurements provide a very useful tool to validate the self-consistency of the integral cross sections. In addition, resonant processes, due to temporary electron capture, can be experimentally characterized via TCS measurements, where these typically appear as peaks and troughs in the scattering cross-section profile. As noted earlier, the energy resolution of the present measurements is around 150 meV, and their associated uncertainties lie below 5% over the whole energy range investigated (see Table S1 which is available in the SI). Furthermore, due to the magnetic confinement of the electron beam, the angular resolution depends both on the incident energy and on the energy resolution (see Sect. 2 for further details). Note that any comparison to be relied upon other available data, either experimental or theoretical must consider the specific experimental conditions and correctly account for the so-called “missing angle” scattering effect [64].

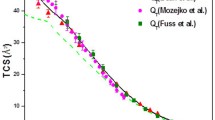
The present TCS results are shown in Fig. 2, together with other data available in the literature [8, 11, 14, 15]. In general, all of them agree well in terms of their shape, but discrepancies are noted in their magnitudes, where the TCS values obtained by Zecca et al. [8] are systematically lower. Such disagreement is likely related to the poor energy and angular resolutions, reported by Zecca et al. [8] (\(\Delta E\) \(\approx \)4–5 eV). On the other hand, even though the magnitude of our measurements is in agreement with the TCS given by Mozejko et al. [11], to within the uncertainty limits on both TCS, the present data tend to be lower in magnitude below 10 eV. As we discussed in a previous publication [18], this discrepancy is associated with the different angular acceptance of each experimental arrangement. As stated above, our angular resolution is linked to the energy resolution and the incident energy; therefore, as the collision energy decreases, our angular resolution increases, and the TCS will tend to be lower [63]. In contrast, the angular resolution in the Mozejko et al. [11] experimental conditions is fixed and given by the detector geometry (\({\Delta }\theta \sim 5^{\circ })\). A similar story applies with respect to the Baek et al.’s [15] TCS. Here, for energies below 20 eV, the angular resolution is superior (i.e. smaller) as compared to that of both Mozejko et al. [11] and the present one. Now, if Baek et al.’s data are multiplied by a constant (see Ref. [15] for details), given that the lowering of the measured TCS is due to electrons elastically scattered into the detector angle, we would expect its TCS to be somewhat higher in magnitude which is exactly what is observed in Fig. 2.

Fig. 2
figure 2

Present total electron scattering cross sections for collisions with gaseous THF together with the available experimental data in the literature (see legend in the figure)

Full size image

In order to carry out a realistic comparison, we have considered the angular resolution associated with both the present experiment and that of Mozejko et al. [11]. While the effect is not explicitly considered for the Baek et al. [15] data, the argument holds in each case. Thus, those measurements have been corrected by accounting for the elastic contribution within the acceptance angle of the detector’s “missing angles”, using our IAM-SCAR\(+\)I calculated elastic DCSs (see Sect. 3.2.2. for further details). Additionally, since THF has a relatively high permanent dipole moment (1.63 D), differential rotational excitation cross sections have also been considered and calculated via the first Born approximation [18]. Once we have included the elastic and rotational excitation cross sections over the “missing angles”, both TCS now agree quite well, as shown in Fig. 3. However, below 2 eV, our TCSs are now slightly higher than those of Mozejko, reaching a maximum difference of \(\sim 13\% \) at 1 eV.

Fig. 3
figure 3

Angular corrected total electron scattering cross sections for collisions with gaseous THF. Note that the term “corrected-R” indicates that rotational contributions are excluded from the correction (see text for further details). See also legend in figure

Full size image

This residual disagreement could be related to our treatment for the rotational excitations, as was pointed out by Fabrikant [65] and more recently by our group [66]. Therefore, we have also corrected the TCS considering only the missing elastic contribution, i.e. the rotational contribution included in the experimental values was subtracted out. Here, an excellent agreement between both corrected values for the TCSs is observed above about 2 eV. It is interesting to note that once the rotational excitations are subtracted out, up to 3 eV, the TCS is mostly given by the integral elastic cross section (IECS). As shown in Fig. 3, by comparing these latter corrected values with our recommended Schwinger multichannel (SMC) calculated integral elastic cross section (see Sect. 3.2.1 for further details), we found good agreement, which indicates that our corrected TCSs, without rotational contributions, are the most realistic values up to 2 eV. These considerations lead us to conclude that the present TCS measurements can be considered as reference values, once corrected for the missing elastic contribution due to the angular acceptance limitation of the detector. In addition, as noted earlier, our TCS values are supported by the experimental data of Mozejko et al. [11] for energies above about 2 eV, as shown in Fig. 3. The estimated uncertainty limit for our elastically corrected TCS is about 10%, at each energy considered.

We also noted earlier that resonance phenomena can be elucidated from TCS measurements. A close inspection of our TCSs at lower energies (see Fig. 2) reveals different structures, which might be related to resonant processes. Below 5 eV, we have found different features at around 1.6 eV, 3.7 eV and 4.7 eV, with the initial ones also being observed in previous measurements at around 1.9 eV and 3.5 eV [11], respectively. However, the origin of the feature at the lowest energy would be nonresonant as explained by Gauf et al. [17]. The next feature is a well-defined peak with a local maximum at 3.7 eV. In ref. [11], this maximum was indirectly explained as a resonant process leading to vibrational excitations. In contrast, we tentatively assign this feature as arising from the contribution of the maximum vibrational excitation integral cross-section value at around that energy, as discussed in Sect. 3.2.1. It is also worth mentioning that similar structures between 3 and 4 eV were experimentally observed for pyridine [67, 68], benzene [69], and nitrobenzene [66]. As far as we are aware, the feature observed at around 4.7 eV has not been reported until now, either from the experimental or theoretical points of view. In this case, its origin is not yet entirely clear, but it could be related to a core-excited Feshbach resonance. On the other hand, above 5 eV, the features observed at around 6 eV, 8 eV and 10 eV are confidently assigned to core-excited resonances according to previous experimental and theoretical results [17, 26, 46].

Fig. 4
figure 4

Proposed compilation of integral cross sections (ICSs) and the TCS for electron scattering from THF, in the energy range 1–100 eV. See also legend in figure

Full size image

3.2 Data set compilation for electron transport through gaseous THF

As we already noted in Sect. 2, where we described our simulation procedure, in order to accurately model the different physical processes that occur along the path of a charged particle moving through matter, it is necessary to sample the step length between collisions, the interaction type that takes place, as well as the associated energy loss and the scattered electron angles. Hence, the required input data sets for these Monte Carlo simulations must incorporate the total cross sections, the integral cross sections for all open channels at each energy, the energy loss spectra and the angular differential cross sections of all the relevant physical processes, if we are to achieve realistic simulations. In the following subsections, we present our compilation for all these data for electron scattering with THF in the energy range 1–100 eV.

3.2.1 Integral cross sections

The proposed integral cross-section data set for THF is shown in Fig. 4, and listed in Table 1. The elastic cross sections come from the calculated data of ref. [17], below 15 eV, and from our IAM-SCAR\(+\)I [57, 70, 71] calculation method for energies above 30 eV. In the intermediate energy region (15–30 eV), the data from both theoretical procedures have simply been interpolated. The ionization and rotational excitation cross sections are those recommended by Fuss et al. [18], and the attachment cross sections are the experimental values obtained by Janeckova et al. [44]. Deriving the recommended electronic and vibrational excitation cross section has been more challenging due to the lack of complete experimental or theoretical data for these processes. We therefore propose that the electronic and vibrational excitation cross sections are generated by subtracting the elastic and ionization cross sections from our elastically corrected TCS measurements. Subsequently, both the summed vibrational excitation and electronic excitation data sets were deconvoluted on the basis of the experimental data from references [26, 34]. Since these data have been obtained by subtracting two relatively large magnitudes, such as the TCS and the ICS, they are accompanied by relatively large error bars of about 25–30%. Nonetheless they qualitatively agree well with the summed integral cross sections for vibrational excitation compiled by Do et al. [29] and Duque et al. [72] from different experimental sources.

Table 1 Integral and total electron scattering cross sections for THF (in \(10^{-20}\mathrm{m}^2\) units), as used in the present simulations
Full size table

At this point, it is interesting to compare the present recommended TCS data, being the sum of the partial ICSs shown in Fig. 4, with those recently proposed by Stokes et al. [55] from their neural network regression procedure. These TCS values are shown in Fig. 5. As may be seen in this figure, there is very good agreement for the lower energies up to 2 eV and for energies ranging from 10 to 20 eV. Out of these energy ranges, the present cross sections are clearly higher in magnitude than those of Ref. [55]. However, in the 2–10 eV energy range, when the cited errors on the present corrected TCS are allowed for (\(\sim \) 10%), and those on the Stokes et al. [55] TCS are allowed for (also \(\sim \) 10%), then even with the y-axis log scale it is likely the two sets of data will largely overlap so that the apparent discrepancy here is not in fact significant. At higher energies (above \(\sim \) 20 eV), however, the TCS from the two groups does diverge in magnitude as the energy increases, to the point that even allowing for their cited uncertainties the data sets would not overlap. At these higher energies, the scattering is dominated by elastic scattering and ionization, so that the discrepancy here largely reflects the different preferred elastic ICSs and TICSs of the two groups. The multi-term Boltzmann equation solutions in Stokes et al. [55] do not directly rely on the elastic ICS, as it is only the momentum transfer (and higher order) cross sections that account for anisotropic scattering in their simulation. As a consequence, the simulated transport coefficients in Stokes et al. [55] are insensitive to the elastic ICSs. Stokes et al. [55] formed their elastic ICS from the momentum transfer (and higher order) cross sections using the differential cross sections which were largely based on the earlier IAM-SCAR calculations from Fuss et al. [18], which did not include interference effects [57]. But, as we have found in earlier studies, these interference terms need to be included in order to obtain TCS values in good agreement with the experimental results [58]. On the other hand, for the single electron track simulations, the elastic processes are crucial [3] since they define the track structure by sampling the scattering angles after each collision event. So that for event-by-event Monte Carlo simulations, for energies above 20 eV, the present elastic DCS and ICS values which include interference effects should be used.

Fig. 5
figure 5

Recommended total electron scattering cross sections;—, present study;- - -, Stokes et al. [55]

Full size image

3.2.2 Angular distribution functions

As explained in detail in our previous studies on the furfural [73], para-benzoquinone [74] and pyridine [75] molecules, relevant information for electron transport simulations based on event-by-event Monte Carlo procedures, include the elastic and inelastic angular distributions. This is crucial since from these distribution functions, the scattering angle is sampled after any scattering event. In this study, the elastic distributions have been obtained from the normalized elastic differential cross sections, as a function of the scattering angle, calculated up to 15 eV by McKoy and collaborators through the SMC procedure [17]. For higher energies, the cross sections calculated with the IAM-SCAR\(+\)I method [57, 70, 71] have been employed. The proposed set of angular distributions for elastic electron scattering from THF is shown in Fig. 6, with the numerical data being available in Table S2 of the SI.

Fig. 6
figure 6

Proposed elastic angular differential cross sections for electron scattering from THF in the energy range 1–100 eV. See also legend in figure

Full size image
Fig. 7
figure 7

Proposed angular differential cross sections of rotational excitations for THF in the energy range 1–100 eV. See also legend in figure

Full size image

On the other hand, for the inelastic processes, excluding rotational excitations, we have employed a semi-empirical formula (Eq. 3), which has been proven to quite accurately reproduce the inelastic angular distribution dependence for different molecules [74, 76]. Finally, the angular distributions for rotational excitations come from the dipole-Born differential cross-section calculations (see Fig. 7), the results of which can be found tabulated in the SI (Table S3).

$$\begin{aligned} {\begin{array}{l} \frac{\mathrm{d}^{2}\sigma \left( E \right) }{\mathrm{d}{\Omega }\mathrm{d}{\Delta }E}\propto \left\{ {\begin{array}{ll} \left( \frac{\mathrm{d}\sigma \left( E \right) }{\mathrm{d}{\Omega }} \right) _{\mathrm{el}}^{1-{{\Delta }E}/ E}, &{}\Delta E<30\,\mathrm{eV} \\ \left( \frac{\mathrm{d}\sigma \left( E \right) }{\mathrm{d}{\Omega }} \right) _{\mathrm{el}}^{\left( 1-{{\Delta }E} /E \right) ^{1.3}},\, \,&{} \Delta E\ge 30\,\mathrm{eV}\, \mathrm {.} \\ \end{array}} \right. \\ \end{array}} \end{aligned}$$
(3)

3.2.3 Energy loss distribution function

As far as the energy loss distribution function is concerned, in the present simulation, we have considered three different inelastic channels, i.e. electronic, vibrational discrete excitations and ionization. These functions are shown in Fig. 8, and the corresponding numerical values are presented in Table S4 of the SI. For energies up to 10 eV, we have made use of the electron energy loss spectra measured by Do et al. [34], and from 10 to 100 eV, those measured by Fuss et al. [52] were employed. Note that in previous investigations [77, 78], it was shown that the energy loss spectra do not strongly depend on the electron impact energy or the scattered electron angle. For rotational excitations, we have assumed a fixed energy loss given by the averaged rotational excitation energy of the THF molecule at 300 K (i.e. 100 meV). Kinetic energy transferred to the target via elastic processes has also been calculated, as a function of the projectile/target mass ratio and the scattering angle. In contrast, if a DEA process takes place, the trapped electron disappears from the simulation and its kinetic energy is transferred to the medium. Electrons with energies below 0.1 eV are culled from the simulation.

Fig. 8
figure 8

Proposed electron energy loss distribution function associated with each inelastic process for THF in the energy range 1–100 eV. See also legend in figure

Full size image

3.3 Experiment versus simulation

One of the main goals of this study is to provide a self-consistent data set of cross sections for electron scattering by THF, to be used for modelling purposes. A well-proven procedure to validate the accuracy of a given cross section data set is the event-by-event Monte Carlo simulation of electron transport through a gas cell. In our case, the simulation code emulates the experimental conditions of the apparatus on which the TCSs have been obtained, i.e. the intense magnetic confinement of the electron beam (in the axial direction) during the collision events. As briefly explained in Sect. 2 and in Ref. [63], under these conditions, the expected scattering angle is transformed into an energy loss in the axial direction. Therefore, the results given by the simulation are very sensitive to the differential cross sections used as input data. As we aim to provide a cross-section data set in the energy range 1–100 eV, experiments and simulations at different impact energies have been performed in order to cover the whole energy range, as far as possible. In particular, we have concentrated on three different illustrative energies, namely 70, 10 and 3 eV.

Fig. 9
figure 9

Experimental and simulated transmission intensity as a function of the axial kinetic energy for a 70 eV electron beam through pressures of 2.5 mTorr and 5 mTorr of gaseous THF. See also legend in figure

Full size image
Fig. 10
figure 10

Experimental and simulated transmission intensity as a function of the axial kinetic energy for a 10 eV electron beam through pressures of 2.5 and 5.0 mTorr of gaseous THF. See also legend in figure

Full size image
Fig. 11
figure 11

Experimental and simulated transmission intensity as a function of the axial kinetic energy for a 3 eV electron beam through a pressure of 2.5 mTorr of gaseous THF. See also legend in figure

Full size image
Table 2 Average number of interactions of each physical process per incident electron and the total energy deposited per initial electron in the simulation of each experimental condition
Full size table

In Figs. 9, 10 and 11, we present the measured electron intensity distribution of the parallel kinetic energy for incident electron energies of 70, 10 and 3 eV, respectively, together with those simulated with the present Monte Carlo code. As shown in these figures, for 10 and 70 eV the electron transmission has been measured through pressures of 2.5 mTorr and 5 mTorr of THF inside the collision chamber. However, for 3 eV, we only performed measurements for a pressure of 2.5 mTorr in order to avoid transmission difficulties that we found in our experiment at higher pressures for this incident electron energy. Also, the pressure fluctuations during the measurements, which we have estimated to be about \(\pm 10{\%}\) of the nominal value, have been taken into account. These fluctuations probably arise from the fact that THF is a very ‘sticky’ gas that adsorbs and desorbs on surfaces in the collision chamber. Thus, in order to try and quantify this effect, we have also simulated the transmitted intensity at the pressure uncertainty limits for each nominal value (i.e. 2.25 to 2.75 mTorr and 4.5 to 5.5mTorr). Note that such uncertainty ranges are depicted as a shaded region around the simulated curves, for each nominal pressure value, in Figs. 9, 10 and 11.

In general, there is good agreement between the simulated and the experimental results for all the investigated energies. However, at higher energy losses, where a tail in the spectra is visible, significant discrepancies arise and become more pronounced at 5 mTorr and especially for the highest energy beam (70 eV) that we simulated. As we mentioned in a previous study [74], this discrepancy would be related to a lower probability of the lower-energy electrons reaching the detector. Another interesting point is that the agreement found for the lower pressure case (2.5 mTorr), is significantly better than that for the higher pressure (5.0 mTorr) case (see Figs. 9 and 10). This worsening in the level of agreement between experiment and simulation, as the gas pressure increases, would be directly related to the increasing rate of multiple collisions, thus representing a major challenge for our simulation.

In order to better illustrate the differences found between our simulated and experimental results, in Table 2, we show the number of processes per incident electron, as derived from the simulation. There we can observe that the number of total interactions at 5.0 mTorr is 2.34 and 3.11 times higher than at 2.5 mTorr, for incident energies of 10 eV and 70 eV, respectively. As the number of total interactions per incident electron increases, any inaccuracy in the input data is amplified by the successive scattering processes, thereby magnifying possible discrepancies between the simulation and the experiment. At the incident energy of 70 eV, there is a substantial increase in the number of ionization processes, and, accordingly, in the number of secondary electrons produced per initial electron, when the pressure increases from 2.5 to 5.0 mTorr. In addition, the kinetic energies of such secondary electrons range from 0 to 25 eV, where the divergence between experiment and simulation is clearly appreciable (see Fig. 9). In contrast, at 10 eV incident energy, the ionization cross section is almost negligible; therefore, the ionization processes are insignificant for both pressures, thereby obtaining better agreement between the measurement and simulation even at 5 mTorr. Hence, discrepancies between the simulated and the experimental results, at the higher energies and higher pressures considered here, are likely related to the number of low-energy secondary electrons that are not appropriately transmitted by the experimental system.

As stated previously, because of the magnetic confinement conditions, the results given by the simulation are very sensitive to the DCS used as input data. In this respect, we also chose to study an electron beam energy where the main process occurring is elastic scattering, namely 3 eV. Note that even though dipole interactions are strongly enhanced at lower energies, our experiment is not able to energetically resolve them due to energy resolution limitations (\(\sim \)150 meV). As shown in Fig. 11, good agreement is found at 3 eV, thereby indicating the high precision of the angular distribution functions derived from the DCS calculated by McKoy and collaborators for the lower energies.

In general, the good level of agreement we observed between the measured and simulated electron energy distributions in all the studied cases strongly supports the reliability of the input data used in our simulations.

Fig. 12
figure 12

Comparison of the experimental transmission intensity as a function of the axial kinetic energy for a 70 eV incident electron energy, passing through 2.5 mTorr of gaseous THF, and those simulated with our code using the present cross-section data and the Geant4DNA code using the PTB interaction model (see text for details). Solid lines represent the axial component of the kinetic energy, while dashed lines represent the total kinetic energy of the electrons. See also legend in figure

Full size image
Fig. 13
figure 13

Comparison of the elastic angular differential cross sections at 70 eV used as input in the PTB model of Geant4DNA, and in our simulation code for THF. See also legend in figure

Full size image

3.4 Comparison of our simulation with Geant4DNA

Geant4DNA [61] is an open access software framework for the simulation of ionizing radiation, which is completely included in Geant4 and extends its capabilities to simulations of step-by-step physical interactions down to energies as low as about 10 eV in liquid water, DNA constituents and backbone. In particular, the simulation of the DNA constituents and backbone is achieved by implementation of the PTB models described by Bug et al. [79], for DNA-related materials including tetrahydrofuran (THF), trimethylphosphate (TMP), pyrimidine and purine. Hence, this PTB model, implemented in Geant4DNA, would be, in principle, a good candidate to compare with our simulation results of electron transmission through gaseous THF for incident electron energies above 10 eV.

In Fig. 12, we present the results obtained from both simulations, together with the experimental results at 70 eV and 2.5 mTorr of THF in the scattering chamber. In order to better focus the discussion, we have also included the simulated total kinetic energy of the electrons as it reflects possible differences in the inelastically transferred energy procedure implemented by the two simulation codes (see legend of Fig. 12).

As the lower limit of applicability of the PTB model for THF, implemented in Geant4DNA, is 10 eV, it would not be expected to reproduce accurately the low energy electron intensities. Thus, we have restricted our comparison between the two simulations to higher energies. As shown in Fig. 12, for 70 eV incident electron energy, differences in shape are found using both models. As this figure illustrates, the transmission intensity simulated by Geant4DNA is systematically lower than ours. This discrepancy might be attributed, at least in part, to the combination of two effects affecting the energy loss distributions. One is the higher magnitude of the integral inelastic cross sections, by about 3% at 70 eV, used by Geant4DNA in comparison with those recommended here, and the other is the shape of the elastic DCS at that energy, which is stronger in the backscattered region than ours (see Fig. 13). As mentioned above, differences in the lower energy range (below 10 eV) can be attributed to the low energy validity limit established by the PTB data. Additionally, however, they might also arise due to the isotropic distribution assigned in Geant4DNA to the secondary electrons produced by ionizing collisions, while our simulation calculates the angle of the ejected electrons by considering momentum conservation laws.

4 Conclusions

A complete and self-consistent data set of electron scattering cross sections, both differential and integral, for gaseous THF has been compiled for modelling purposes. In particular, it has been used in this study as input data for Monte Carlo simulations of the electron transport in gaseous THF for impact energies in the range 1–100 eV. In addition, in order to check the self-consistency of our proposed integral cross sections, we have performed accurate measurements of total electron scattering cross sections from THF, which have been used as reference values in order to validate the self-consistency of the recommended data set. Based on these data, Monte Carlo simulations were subsequently performed for different electron beam energies and THF pressures. The good agreement we typically found between the measured and simulated electron energy distributions, in all the studied cases, strongly supported the accuracy of the present data set for modelling electron transport in gaseous THF. Finally, we have also compared our simulated results, with those obtained using the PTB model implemented in Geant4DNA, for 70 eV electron impact energy. We observed appreciable differences between them in the intensity distributions of the transmitted electrons. These discrepancies were tentatively attributed to differences in the input cross sections used by each method. In particular, the integral inelastic cross sections included in the PTB model were higher in magnitude than those of the present recommended data, and the angular distribution of the elastic DCS at 70 eV, included in Geant4DNA, was more pronounced in the backscattering region than ours.