1 Introduction

The study of energetic ions traversing condensed matter has important applications in areas of nuclear medicine [1, 2], deep ion implantation [3,4,5], defect profiles [6], radiation protection [7] and atomic structure of surfaces [8, 9]. The retarding force acting on the energetic ion (projectile) due to the interaction with the irradiated material, which results in a loss of the ion kinetic energy, is referred to as stopping power S. This force can be quantitatively described as the average energy deposited per path unit length by the ion to the host (target) material. The stopping power depends on the type of ion, its kinetic energy (or its velocity relative to the host material) and also on the properties of the material it passes through. In crystalline materials, not all trajectories are equivalent; there is yet an extra dependency on its orientations with respect to crystallographic directions. This dependency is the main topic of this manuscript. Atomistic simulations are in a unique position to explore this dependency in a systematic way, beyond what models [10] and the most accurate state-of-the-art experiments can do [11].

There are two main contributions to the stopping power phenomena: (i) electronic stopping power \(S_{\mathrm{e}}\) [12,13,14,15,16] which is mainly due to electronic excitations of the target electrons and (ii) nuclear stopping power \(S_{\mathrm{n}}\) [17,18,19,20] which is due to the elastic collision of the projectile with the target nuclei, where energy is dissipated as lattice defects or vibrations. Our discussion in this paper focuses on the first category of electronic stopping and pertains to the regime in which the phenomena occur in the femtosecond time scale, with explicit simulation of electron dynamics.

Extensive experimental work on stopping of light ions on different targets at a wide range of energies has been performed over the years [21,22,23,24,25,26,27,28] (and references therein), obtaining a reasonably complete picture of the average behavior of electronic stopping power in a diversity of materials. Although there are numerous research works on stopping of ions at higher energies, there are little available data on intermediate and low energies regimes and the probing of the effects of crystalline structure of the target materials [29, 30].

As in the general case, the electronic stopping power depends on the specific target material, the elemental projectile and its velocity. Apart from this, projectile direction with respect to the crystallographic directions of the target affects the electronic stopping power as well, since the projectile tends to lose energy more effectively as more electrons are available for excitation in the nearby region. For example, a higher electronic density tends to yield higher electronic stopping. This effect is typically averaged out over directions for polycrystalline samples and most experimental setups. In fact, in Ref. [31] we proposed that a random direction can capture this average. At low energies however, an explicit discrimination of low index directions is necessary to improve averaging methods [32].

Among these crystalline systems, nickel and nickel-based alloys are known for their optimal mechanical properties, thermal stability, withstanding to swelling and radiation tolerance, therefore making them good candidates for radiation resistant structural materials for energy applications [33,34,35,36,37] and aerospace applications [38,39,40]. Given the recent interest in this family of materials, our goal is to study \(S_{\mathrm{e}}\) of proton and of helium ions in a nickel target to describe the initial stages of particle radiation in these crystalline materials. We focus on crystalline effects essentially absent in historical theories until this point [41], i.e., beyond homogeneous electron gas and/or linear response approximations. Recent advances in simulation techniques [42] and computational power [43] enable this study.

White and Mueller [44] measured the electronic stopping for H and He at energies 30–140 keV and 50–120 keV, respectively, in Cr, Mn, Fe, Co and Cu targets, and in Ni target in particular. The measurements were made utilizing a high-resolution silicon surface-barrier-detector system. Their measured average stopping values (with a reported error of \(\pm \, 3\%\)) for \(^{4}\)He (Fig. 2 in Ref. [44]) and \(^{1}\)H (Fig. 3 in Ref. [44]) were in good agreement with previous measurements in Ref. [45].

Gertner et al. [46] investigated the electronic energy loss of ions in solids in the energy range \(10^1\)–\(10^4\) keV/nucleon both experimentally and theoretically. Experimentally, they measured the \(S_{\mathrm{e}}\) on C, Cr, Cu and Ni thin targets, where the energy loss for protons and deuterons was reported. Theoretically, they used the Lindhard–Winther (LW) [47] formalism for the homogeneous electron gas to compute the \(S_{\mathrm{e}}\) of ions in a free-electron gas model (with no crystalline information). In the high-energy region (proton energies above 500 keV), they obtained relatively fair results between theory and experiment [46]. In this regime, the main contribution to \(S_{\mathrm{e}}\) is universal (linear response of the homogeneous electron gas); however, at lower energies, significant discrepancy is observed with other models where the major contribution to \(S_{\mathrm{e}}\) stems from the valence electrons only, and therefore, their lattice structure, electronic structure and directionality have to be modeled explicitly. Nonlinear response effects, which tend to be relatively stronger at low velocities, and explicit treatment of the target lattice are the main motivations to utilize ab initio simulations like the one presented here. These aforementioned historical results are now included indirectly in the SRIM database and model [10], which we include in the plots for comparison along with more recent experimental results by Roth et al. [48] (for \(\mathrm {H}^{+}\)), Mikheev et al. [49] (for He) and Tran et al. [50] (for both \(\mathrm {H}^{+}\) and He projectiles in Ni).

Regarding directionality studies, Li et al. [51] calculated, from first principles, the electronic stopping power of slow \(\mathrm {H}^{+}\) and \(\mathrm {He}^{2+}\) ions in CdTe under channeling conditions. For protons, they obtained good agreement between calculated results and experimental results up to the stopping maximum along the \(\langle 100 \rangle \) and \(\langle 111 \rangle \) directions. For the case of helium ion, the \(\langle 100\rangle \) direction results agreed well with experimental results but in the \(\langle 111\rangle \) direction, they observed a transition between two velocities regimes at \(v = 0.4\) a.u. which was attributed to extra energy loss due to charge resonance (in addition to electron-hole excitation). However, the results for \(\langle 110\rangle \) direction underestimated experimental data for \(v > 0.5\) a.u. and \(v > 1.0\) a.u. for protons and helium ions, respectively. Recently, Lee and Schleife [52] used time-dependent density functional theory to study the radiation tolerance of phosphide-based III–V semiconductor materials. To understand the high radiation tolerance of these materials, they calculated electronic stopping and proton dynamics in InP, GaP and \({\mathrm {In}}_{0.5}{\hbox {Ga}}_{0.5}{\hbox {P}}\) as an initial step in understanding collision cascades. They obtained a pronounced direction-dependence of electronic stopping along different (\(\langle 100\rangle \) and \(\langle 110\rangle \)) channels. This was attributed to the magnitude of electron density that interacts with the proton projectile in these crystalline channels.

In this paper, we present the electronic stopping power of nickel target under proton and helium irradiation, taking into account the directional dependence of the projectiles on the electronic stopping. The paper is structured as follows: We describe the simulation method, the theoretical framework and computational details in the next section; later, we present the results and their corresponding discussion, where we concentrate on the detailed analysis of the electronic stopping power and other microscopic quantities that can be extracted from postprocessing first principles simulations.

2 Method

We used time-dependent density functional theory (TDDFT) [53] for this study. TDDFT is one of the most practical frameworks used over the years to tackle the dynamics of many-body electronic systems  [16, 31, 36, 52, 54,55,56,57,58]. To obtain the electronic stopping, we solve the time-dependent Kohn–Sham (TDKS) equations. The TDKS equations describing the wavefunctions \(\varphi _i\) of effective individual electrons are (in atomic units):

$$\begin{aligned} {i} \frac{\partial }{\partial t} {\varphi }_{i}(\mathbf {r}, t) =\left\{ -\frac{\nabla ^2}{2} + V_{\mathrm{KS}}[n,\{\mathbf {R}_J(t)\}_J] (\mathbf {r}, t)\right\} \varphi _i(\mathbf {r}, t), \end{aligned}$$
(1)

where the electronic density is given by

$$\begin{aligned} n(\mathbf{r} , t) = \sum _{i}{|\varphi _i(\mathbf{r} , t)|}^2. \end{aligned}$$
(2)

The Kohn–Sham effective potential \(V_{\mathrm{KS}}\) is conceptually partitioned in three contributions:

$$\begin{aligned} V_{\mathrm{KS}}[n(t), \{\mathbf {R}_J(t)\}_J](\mathbf{r} )&= V_{\mathrm{ext}}[\{\mathbf {R}_J(t)\}_J](\mathbf {r})\nonumber \\&\quad + V_{\mathrm{H}}[n(t)](\mathbf {r})+ V_{\mathrm{xc}}[n(t)](\mathbf {r}) \end{aligned}$$
(3)

where \(V_{\mathrm{ext}}[\{\mathbf {R}(t)_J\}_J](\mathbf {r}, t)\) is the external potential due to nuclei core potential (including moving ions during the stopping process, hence the explicit t-dependence). \(V_{\mathrm{H}}[n(t)](\mathbf {r})\) is the Hartree potential which describes the classical electrostatic interaction between electrons. \(V_{\mathrm{xc}}[n(t)](\mathbf {r})\) denotes the exchange-correlation (XC) potential and it is a placeholder for common approximations to the many-body effects of the electron problem. (Time dependence is implicit in n.)

All the calculations are performed using the Qball code package [43] which contains time-dependent and other modifications over the Qbox code [59]. In this study, local density approximation (LDA) [60] XC functional was used within the adiabatic approximation. Note that the adiabatic label here refers to the fact that this XC term is taken to be an instantaneous function of the electronic density and not the density values at other (past) times; these simulations are still fully non-adiabatic with respect to ion motion.

For the current framework, a plane-wave pseudopotential scheme is used in solving the time-dependent Kohn–Sham (KS) equations. Electronic wavefunctions \(\varphi _i\) are expanded in terms of plane waves. Coulombic ionic potentials are replaced by smoother versions with approximately the same scattering properties [61] that allows to use a finite set of plane-wave terms to simulate valence electrons and ignore core, deeply bound electrons.

We use a simulation cell consisting of 108 Ni atoms (1728 explicit valence electrons) in a cubic supercell with a simulation volume of \((19.98~a_{\mathrm{B}})^3\) forming an FCC lattice. Periodic boundary conditions along with Ewald-type summation for the Coulomb energy are used throughout this study. The ions are represented by the norm-conserving Troullier–Martins pseudopotentials [62], and the KS orbitals are expanded up to a 160 Ry energy cutoff.

As any time-explicit method, a particular instance simulation needs the specification of an initial condition, both for the ion positions and the electronic state. The initial condition corresponds to a perfect FCC lattice together with the projectile (either H or He) stationary at its initial position with electrons in the corresponding ground state. The electronic ground state (i.e., \(\varphi _i(t = 0)\)) was obtained by performing a time-independent density functional theory (DFT) calculation, by solving the time-independent KS equations for the target plus projectile system. Therefore, a time-dependent DFT calculation was then carried out starting from the ground state, resulting in a time-evolving electronic wavefunction (\(\varphi _i(t >0)\)).

In each simulation, a specific velocity is given to the projectile and the electronic system is monitored for several femtoseconds. This was done to allow the moving projectiles to produce a dynamical steady state where the total energy of the electronic system increases at a well-defined rate as described in Ref. [42]. The remaining (host) ions are fixed at their perfect (unrelaxed) ion positions. This fixed-ions (host) strategy is not only a good approximation given the velocity of the projectile, but it is also a practical constrain to evaluate the electronic-only stopping (without spurious contributions from the nuclear—purely ionic—stopping).

The time propagation of Eq. 1 of the electronic system is achieved by the enforced time-reversal symmetry (ETRS) integration [63], implemented as described in Ref. [43]. A numerical integration time step of 0.024 attoseconds was used. Details of the convergence of the simulation parameters for nickel-based systems are discussed elsewhere [36, 64].

The method described here, including the approximations regarding electronic interactions, proved in the past to achieve a good balance of accuracy while treating large complicated atomistic systems. The method may still lack the accuracy of many-body approaches, for example, those based on the dielectric response including the exact dynamic exchange-correlation treatment for low velocity projectiles [65].

3 Results and discussion

3.1 Total energy increase of the target system

When the projectile is given a fixed velocity v, the total energy of the electronic system, initially at the ground state value, changes continuously as the projectile moves in the material. The total electronic energy E of the electronic system is given instantaneously by:

$$\begin{aligned} E(t)&= \sum _i\int \mathrm {d}\mathbf {r}\,\varphi _i(\mathbf {r}, t)^* \bigg [-\frac{\nabla ^2}{2} + V_{\mathrm{ext}}(\mathbf {r}, t)\bigg ] \varphi _i(\mathbf {r}, t) \nonumber \\&\quad + E_{\mathrm{H}}[n](\mathbf {r}, t) + E_{\mathrm{xc}}[n](\mathbf {r}, t) + E_{\mathrm {ion-ion}}(t), \end{aligned}$$
(4)

where the terms are: the electronic kinetic energy, the electron–ion (external) potential \(V_{\mathrm{ext}}(\mathbf {r}, t)\), the Hartree (Coulomb) interaction energy \(E_{\mathrm{H}}[n](\mathbf {r}, t)\), the XC density-functional approximation \(E_{\mathrm{xc}}[n](\mathbf {r}, t)\) and \(E_{\mathrm{ion}{-}\mathrm{ion}}(t)\) is the interaction between the nuclei (ion).

Fig. 1
figure 1

Total electronic energy as a function of proton displacement in pure Ni crystal for the \(\langle 100 \rangle \) trajectory. As proton channels through the lattice, the 108 atoms of Ni are kept at their equilibrium positions. The region below the vertical dotted lines denotes the transient phase (where the rate of change in total energy of the system with respect to projectile displacement is unsteady). The adiabatic behavior, which corresponds to the formal limit of \(v\rightarrow 0\), shows a periodic energy (with no net increase) as expected since the electrons here are constrained to remain in the ground-state

Full size image

Figure 1 shows the increase in the total electronic energy as a function of the distance traveled by the projectile, resulting from a time-dependent simulation at different velocities in a specific direction.

As the projectile starts to travel in the crystal, a steady state is achieved at some point which is roughly marked by a vertical dotted line; \(x\ge 5.0~a_0\). After this transient region, a value for the electronic stopping is then obtained as the slope fitting of the change in total energy versus projectile displacement (Eq. 5).

At finite velocities, the projectile produces electronic excitations, a non-adiabatic behavior that in turn increases the electronic energy. (In the real system, this happens at the expense of the ion kinetic energy; in the simulation, the ion kinetic energy is held constant for simplicity.) The smooth oscillations in the total energy, on top of an otherwise mostly linear increase, are correlated to the lattice periodicity of the target (host) crystal. The correlation is clear in the \(v = 0\) case, in which the simulation should not show an overall increase in the energy (adiabatic behavior), just oscillations in the energy which are natural to the periodic crystal.

For lower velocities, a linear fit coupled with oscillatory function is used to extract the \(S_{\mathrm{e}}\) with a minimal fitting error. At higher velocities, extracting the slope is more straightforward since there is relatively less oscillation amplitude in the energy versus position curve, so a simple linear fit is enough to extract electronic stopping. (For details of this fitting procedures, see Fig. 2 in Ref. [16]). The slopes are systematically extracted for different velocities and different trajectories for both the H and the He projectiles.

This rate of change in E(t) as a function of penetration depth x(t) in the material is identified as the electronic stopping power \(S_{\mathrm{e}}\) and is given by the average over a trajectory;

$$\begin{aligned} S_{\mathrm{e}}(v) = \bigg \langle \frac{\mathrm {d}E(t)}{\mathrm {d}x(t)} \bigg \rangle _v \end{aligned}$$
(5)

3.2 Directional effects

In this section, we concentrate on the behavior of \(S_{\mathrm{e}}\) for both, proton (hydrogen) and helium, in three different trajectories characterized by channeling directions. Since the projectile explores different environments and electronic densities of the lattice with respect to its direction, we expect the total electronic energy E(t), and therefore the stopping power, to change with each direction.

Fig. 2
figure 2

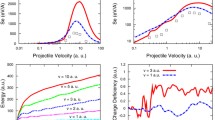
Electronic stopping power versus velocity of a \(\mathrm {H}^{+}\) (top panel) and  He (bottom panel) projectiles in bulk Ni along different crystal channel directions as obtained from TDDFT and compared with experimental measurements (SRIM database [10]; black lines). For the three directions, all the trajectories are along the centers of respective channels. The filled circles (red) with error bars, crosses (blue) and square (brown) show our calculated \(S_{\mathrm{e}}\) for \(\langle 111 \rangle \), \(\langle 110 \rangle \) and \(\langle 100 \rangle \) trajectories, respectively

Full size image
Fig. 3
figure 3

(top panel) The three directions of the projectile in the FCC nickel crystal with \(\langle 100 \rangle \), \(\langle 110 \rangle \) (most open) and \(\langle 111 \rangle \) (narrower directions). The direction of the projectile is straight inward into the viewing plane at the position of the shaded circle. (bottom panel) The electronic valence density is shown as a function of position along the \(\langle 100 \rangle \) (brown dotted lines), \(\langle 110 \rangle \) (blue dashed lines) and \(\langle 111 \rangle \) (red solid lines) directions. (Density is given in units of \(\mathrm {electrons}/a_0^3\))

Full size image

In Fig. 2, our TDDFT simulation results for protons in bulk Ni are shown for three different projectile directions. For \(\langle 100 \rangle \) and \(\langle 110 \rangle \) directions, our calculated \(S_{\mathrm{e}}\) is below the empirical SRIM data [10] for all range of velocities considered. Ullah et al. [32] obtained a similar trend, an underestimation of experimental results when they calculated electronic stopping of H in Ge for directions with open channels and therefore low electronic density (\(\langle 001 \rangle \) and \(\langle 011 \rangle \) projectile directions for \(v > 0.3\) a.u. in the diamond structure).

Our \(\langle 111\rangle \) direction result coincides with SRIM empirical data for velocities below 1.5 a.u. and for higher v, but mismatches the empirical results by more than \(25\%\) at higher velocities. No particular direction is expected to give the experimental result for experiments without directional information; in previous works, we developed an averaging method based on random directions (random high index) to compare with the bulk of these experiments.

The reason for the discrepancy between particular directions and random directions will be explained when we discuss the effective electronic density in an FCC Ni target along the three directions in the following section.

The calculated electronic stopping of He in nickel is shown in Fig. 2 for the same range of velocities and directions. As in the proton case, the \(\langle 100\rangle \) and \(\langle 110\rangle \) directions result in values below the experimental data. For the \(\langle 111 \rangle \) direction, we find it to coincide with experimental data for most of the velocity regime. Although in the \(1.5< v < 3.0\) a.u. range of our TDDFT results overshoots over SRIM data, the values still remain within \(5\%\).

For \(v < 0.5\) a.u., the \(S_{\mathrm{e}}\) results for the three different directions are converging into one curve. This means that as \(v\rightarrow 0\), the relative difference in magnitude of the electronic stopping decreases for the different directions. In previous simulations (Refs. [16, 31, 36, 54]), a similar pattern is observed, where channeling (in this case \(\langle 100\rangle \)) as well as off-channeling trajectories collapse into one curve at lower velocities, apparently showing independence of geometry on electronic stopping.

We observe that as the projectile velocity increases, there is significant difference in the electronic stopping for the different directions for both types of projectiles. For instance, in the case of helium, the difference between the \(S_{\mathrm{e}}\) for \(\langle 100\rangle \) and \(\langle 110\rangle \) directions is up to \(10\%\), and between the \(\langle 100\rangle \) and \(\langle 111\rangle \) directions it can be a factor two. To understand in detail these directional dependencies on the stopping power as depicted in Fig. 2, we plotted the ground state electronic density for the three directions (\(\langle 100\rangle \), \(\langle 110\rangle \) and \(\langle 111\rangle \)) along the z-axis as shown in Fig. 3.

The \(\langle 111 \rangle \) direction has the highest average density of \(0.098~\mathrm {electrons}/a_0^3\) compared with the other two directions. This is consistent with the high electronic stopping analyzed in Fig. 2 for both projectiles, since more valence electrons are available to be excited in this path. The average densities yield 0.040 and \(0.047~\mathrm {electrons}/a_0^3\) for \(\langle 100 \rangle \) and \(\langle 110 \rangle \), respectively. This has translated into the relatively lower \(S_{\mathrm{e}}\) observed for both directions. The relatively small difference in the average electronic density for \(\langle 100\rangle \) and \(\langle 110\rangle \) directions also corresponds to slight differences in \(S_{\mathrm{e}}\).

3.3 Channeling and off-channeling trajectories

In Fig. 4, we compare our results for the \(\langle 111 \rangle \) and off-channel directions with SRIM database and experimental works. For \(v < 2.0\) a.u., the \(\langle 111 \rangle \) and off-channel simulation results have similar stopping power values with less than \(1\%\) difference, as seen in Fig. 4a, which is an indication of fewer geometric effects on the stopping power. The two direction results compare well with recent experimental results from Roth et al. [48] and Tran et al. [50] for projectile velocities less than 1.5 a.u. The maximum \(S_{\mathrm{e}}\) occurs at similar range in v for both directions with \(\langle 111 \rangle \) direction having the lowest stopping power value. At higher projectile velocities, the off-channel results show better agreement with the SRIM database, with a gradual decrease in \(S_{\mathrm{e}}\) for \(v > 2.8\) a.u. and a faster decrease in stopping values for \(\langle 111 \rangle \) direction at the same velocities.

In Fig. 4b, there is an average of less than \(10\%\) difference between the \(\langle 111 \rangle \) and off-channel simulation results for velocities less than 1.5 a.u. At this lower v, there is a slight overestimation and underestimation of the SRIM results for the \(\langle 111 \rangle \) and off-channel directions, respectively; also, the \(\langle 111 \rangle \) results are in good agreement with Tran et al. [50] and Mikheev et al. [49]. For velocities in the range 1.5–3.0 a.u., the off-channel results agree well with SRIM results, except near \(v = 3.5\) a.u., where the \(\langle 111 \rangle \) results agree better.

Geometric effects on the stopping power are significant for the helium ions even for \(v < 1.0\) a.u., an observation which is absent in the proton case where the two direction (\(\langle 111 \rangle \) and off-channel) curves concur into a single curve at \(v<1.0\) a.u.

Fig. 4
figure 4

Electronic stopping power versus velocity of H (top panel) and He (bottom panel) projectile in bulk Ni along the \(\langle 111 \rangle \) and off-channel directions as obtained from TDDFT and compared with SRIM database [10] (black solid lines) and recent experimental results ([48] (H), [50] (H and He) and [49] (He)). The off-channel represents the average of random directions of the projectile in the nickel lattice and its data points are taken from Ref. [36]

Full size image

3.4 Charge fluctuations on projectiles

Fig. 5
figure 5

Total charge on proton (a–c in the top panel) and helium ions (d–f) in the bottom panel) at different velocities versus projectile distance along the \(\langle 100 \rangle \), \(\langle 110 \rangle \) and \(\langle 111 \rangle \) directions, calculated from the instantaneous density by the Bader method. The dotted, dashed and solid lines represent the velocities 0.5 a.u., 1.0 a.u. and 2.0 a.u., respectively. The electronic charges are extracted using the Bader Charge Analysis program [66]. In one of the extreme cases, we observe exactly zero charge for H projectile (proton) which is indicative of a total collapse of the atomic region as defined in Bader analysis (no saddle points); qualitatively, this corresponds to absence of bound charges around the projectile

Full size image

One of the advantages of using first principles atomistic methods is that it provides a lot of detailed information that can be used to contrast effective models. In particular, by using TDDFT for the stopping problem, the a priori unknown effective charge of the projectile (excited by collisions with the host) is not a simulation parameter like in model methods, but it is a natural outcome of the simulation. The main dynamical quantities in this framework are the Kohn–Sham orbitals (Eq. 1) and the total electronic density, which make the work of finding the (a posteriori) projectile charge a rather challenging task of postprocessing and physical interpretation. The challenge is that atom’s ‘charge’ (or degree of ionization) is not well defined in the general framework and a sensible determination of it has to rely in separating particular bound and free electrons in the vicinity of the ion (projectile or host atom). In place of a complicated determination, we use an approximate density-based analysis method, called Bader analysis [67,68,69,70].

In Fig. 5, we show the electronic charge transfer values for the projectiles’ trajectory as a function projectile displacement for \(v = 0.5\) a.u., 1.0 a.u. and 2.0 a.u. along the \(\langle 100 \rangle \), \(\langle 110 \rangle \) and \(\langle 111 \rangle \) directions. The top panels and the bottom panels depict the charges on proton and helium projectiles, respectively. The charges gained or lost by the projectiles in real time are extracted from the time dependent electronic density, \(n(\mathbf{r} , t)\), using the Bader Charge Analysis program [66]. The Bader analysis consists in assigning electronic charge to each atom by dividing space by surfaces defined by saddle points of the charge density. It is intuitively justified and practical in many molecular systems, although its application is extrapolated to time-dependent problems and bulk systems. For example, the assigned charge on a particular ion can be discontinuous in time even if the density changes continuously (saddle points can disappear and appear suddenly); we see instances of this artifact in the analysis of our simulations of the H projectile in narrow channels. The method is practical enough to draw conclusions about relative changes in the nominal charges.

For the proton case, the initial charge value is nominally 1.09 and there are smooth oscillations of the projectile’s charge, except in the \(\langle 111\rangle \) direction for which even at low velocities the projectile is completely depleted of its electron when the projectile passes through high density regions. High density regions can be identified in Fig. 3. In general, higher velocity implies more ionization regardless of other factors.

For the helium case, we obtained an initial electronic charge of 2.09 that approximately corresponds to the number of electrons on He. The smooth oscillation of charges and charge accumulation for \(v \le 1.0\) a.u. as seen in the H case is observed here. A partial charge depletion for \(v = 2.0\) a.u. is seen here as well. For \(v=0.5\) a.u., we have observed the projectile regaining its initial electronic charge around \(\sim 16.0~{a_0}\) for \(\langle 100 \rangle \) and \(\langle 110 \rangle \) in Fig. 5d and e, respectively. In contrast to H, the \(\langle 111 \rangle \) direction did not show complete electronic charge depletion in Fig. 5f.

For both projectiles, we observed alternate neutralization and re-ionization processes along their trajectories [51, 71]. These differences in the electronic charge of the projectiles in Fig. 5 for different velocities and direction contribute to the change in electronic stopping observed in Fig. 2. The simulations give ionization cycles that are in the scale of atomic distances in the lattice, rather than longer distances related to purely atomic (to the projectile) processes such as Auger processes, although the lack of self-interaction corrections could be biasing this particular aspect of the results. (See Ref. [58] for a study of the relation between charge oscillation in a projectile and self-interaction effects in binary atomic collisions within the same simulation framework.)

Fig. 6
figure 6

Charge deficiency of a Ni host atom neighboring the projectile trajectory (proton top panel, helium bottom panel) along the trajectory (\(x = 0\) marks the point of maximum approach). The electronic charges are extracted using the Bader Charge Analysis program [66] on the valence charge density (i.e., not including core density); therefore, only relative changes associated with valence charge are reported

Full size image

3.5 Charge deficiency on host atoms in the \(\langle 100 \rangle \) direction

In the same way as for the projectile, the charge analysis can be applied to the (stationary) host atoms (Fig. 6). Persistent charges in the host atoms lead to impulsive Coulomb-like forces that can impart radial momentum [57]. The charge deficiency (relative to its initial value) on a particular neighboring Ni atom due to the incoming projectiles (H and He) is depicted in Fig. 6. We choose an atom that is first neighbor to the trajectory channel. Initially, the projectiles are \(\sim 3.33~a_0\) from the Ni atom shown in Fig. 6a. Using the Bader analysis, the charges on the Ni atom are again extracted from the time-dependent electronic charge density, except that this time the ion center has a fixed position. As the proton and helium get closer to the neighboring Ni atom, the charges decrease gradually, indicating that the particular atom is losing charge as the projectile approaches. As the projectile passes the particular host Ni atom (after \(x > 8~a_0\)), its charge gradually stabilizes due to less interaction with the projectile. Interestingly, the cases above \(v > 1 a_0\) do not recover to the initial value for the duration of the simulation. Although outside the practical time-scales of this simulation framework, a persistent charge could lead to large momentum transfer, as discussed later.

Fig. 7
figure 7

The ratio between the calculated electronic stopping power for He and H ion as a function of the projectile ion velocity for the \(\langle 111 \rangle \) direction (red filled circle lines). Reference value of 4 (horizontal dashed line) for the linear response theory result (LRT) [47] for fully ionized projectile ions (\(Z_{\mathrm{He}} = 2\) and \(Z_{\mathrm{H}} = 1\))

Full size image

3.6 Ratio of helium/hydrogen electronic stopping

To understand our \(S_{\mathrm{e}}\) results, we compared with linear response theory (LRT) [47]. We evaluate linear response stopping \(S_{\mathrm{L}}\) based on the RPA Lindhard dielectric function for a homogeneous electron gas for effective electronic density n [72] as:

$$\begin{aligned} S_{\mathrm{L}}(n, v) = \frac{2 Z^2_1 e^2}{\pi v^2} \int _0^\infty \frac{\mathrm {d}k}{k} \int _0^{k v} \omega \mathrm {d}\omega \mathfrak {I}\left( \frac{1}{\varepsilon _{\mathrm{RPA}}(n, k, \omega )}\right) \end{aligned}$$
(6)

where \(Z_1\) is interpreted as the effective charge of the projectile, v is the velocity of the projectile and \(\varepsilon _{\mathrm{RPA}}\) is a model of the dielectric function for the linear response approximation (RPA) at frequency \(\omega \) and momentum transfer k. Regardless of the dielectric model, a characteristic of linear response is that \(S_{\mathrm{L}}\) has a quadratic dependence on the projectile ion charge \(S_{\mathrm{L}} \propto Z_1^2\), that is, an exact ratio of 4 for fully ionized hydrogen and helium. Therefore, deviations from this factor could be used as proxy of nonlinear effects in nickel (including bound charge effects).

The ratio of \(S_{\mathrm{e}}\) for helium ion to the \(S_{\mathrm{e}}\) for proton are depicted in Fig. 7 as a function of the projectile velocity, and the results are compared with linear response theory (LRT) [47] for full ionization and SRIM [10]. The TDDFT ratio surpasses 4 for \(v \ge 2.5\) a.u, which is beyond the maximum stopping for H. Their ratio should eventually approach 4 again for even higher velocities. Yost et al. [56] observed a similar trend when they utilized the same theoretical approach to study protons and \(\alpha \) particles stopping in silicon carbide.

This is an indication that an ideal factor for 4 is achieved as both the projectile becomes fully stripped and the linear response approximation becomes more accurate at large velocities. At lower velocities, for LRT to correctly predict the maximum stopping, effective ion charge models and additional higher-order Z need to be incorporated [56, 73, 74].

3.7 Radial force

Fig. 8
figure 8

Radial force exerted on host atom (Ni atom closest to the projectile’s channel \(\langle 100 \rangle \) trajectory) for a \(\mathrm {H}^{+}\) and for b He, versus projectile position for different velocities. The non-adiabatic curves have been shifted upwards for clearer view. Notice how for \(v > 0.7\) a.u. the maximum shifts relative to the position of maximum approach and, instead of going back to zero, the forces remain oscillating even for large distances

Full size image

Figure 8 shows the non-adiabatic radial forces exerted on a neighboring target atom by projectiles (\(\mathrm {H}^{+}\) and He) for a channeling trajectory, respectively. Initially, the distance of the closest Ni target atom to the projectile is about \(\sim 3.33~a_0\). For zero velocity (adiabatic limit), a maximum force on a host atom is obtained exactly when the projectile is closest. The magnitude of this adiabatic force is higher for a He projectile. This maximum value of the force is due to electronic excitation [16, 31, 54] at the closest proximity of the projectile to the target atom. As the projectile travels further away, the force decays smoothly to zero (its original value) for low velocities. (Note that the non-adiabatic curves have been shifted for clarity.)

At higher velocities \(v > 0.7\) a.u., there is persistent oscillation in the forces’ curves, as the projectile passes and the position of the maximum force with respect to their low velocity (near-adiabatic) counterparts shifts. These oscillations can be attributed to persistent plasmonic charge oscillations in the electronic system [54].

Fig. 9
figure 9

Radial momentum transferred to host atom (Ni-atom closest to projectile channel \(\langle 100 \rangle \) trajectory) vs. projectile velocity

Full size image

3.8 Radial momentum

Although eventually the radial force returns to its original value, the integral of the radial force in time does not vanish and depends on the velocity. A net force acting during a period of time produces a momentum change. For forces that depend only on the position (adiabatic forces), the momentum transfer simply decays inversely proportional to the velocity of the perturbation (as the interaction time shortens). This is the expected behavior for any classical potential for projectile–ion interaction, in particular any binary collision model [75] but deviations from it correspond here to increasing electronic non-adiabatic effects.

Figure 9 shows the lateral momentum transfer that the host atom incurs due to the non-adiabatic forces, calculated \(\varDelta {\mathbf {p}} = \int {\mathbf {F}[x(t)]}~\mathrm {d}t =\int {\mathbf {F}(x)}\mathrm {d}x/v\), by the projectile to the target atoms. This is the inverse of the projectile velocity (1/v) multiplied by the time integral of the force on the host atom over some specified projectile distance (Fig. 8). At lower velocities, the adiabatic approximation gives a good estimation of the momentum transfer up to \(v = 0.2\) a.u. and \(v = 0.15\)  a.u. for proton and alpha projectiles, respectively. At this adiabatic limit, the momentum transfer is proportional to the function k/v, where k is the integral over the adiabatic force curve as a function of projectile displacement (see Fig. 8a, b, for \(v = 0\)). For higher velocities, (\(v > 0.2\) a.u.), there is a complete deviation from their adiabatic counterparts. This is the point from which considering electronic effects would affect the results of models based purely on the molecular dynamics and interatomic potentials (in atomic time-scales).

The momentum transfers are surprisingly proportional (parallel curves in the log scale) for the proton and the He projectiles at different velocities; this proportionality extends to the non-adiabatic regime of momentum transfer. This points to a possible universal behavior to the momentum imparted by a projectile of arbitrary charge and across host materials (compare to Fig. 4 in Ref. [54]).

4 Conclusion

In summary, we presented first-principles calculations of electronic stopping power in nickel crystals for protons and helium particles in three different channel directions using a real-time electron dynamics formalism based on TDDFT. Our TDDFT results are comparable with SRIM database for most of the velocity range considered for the \(\langle 111 \rangle \) and random directions.

We have learned that the electronic stopping is sensitive to projectile direction with higher density regions yielding the highest \(S_{\mathrm{e}}\) value due to stronger electron–ion interaction. The lower density regions (most open channels) showed the lowest stopping power.

We have observed a rapid charge oscillation on the projectiles at narrower channels with a complete projectile ionization (depletion of electrons) for hydrogen in the \(\langle 111\rangle \) direction at regions during its trajectory in the crystal. Complete charge depletion for He is not achieved in any channel at any velocity studied, which is attributed to the enhanced binding of the remaining electron in the single ionized state of the projectile.

The non-adiabatic lateral momentum transfer turns to follow an approximately proportionality pattern between protons and alpha particles, both in the adiabatic limit and in the non-adiabatic limit. This scaling could help develop phenomenological models of non-adiabatic forces of swift ions in solids [76]. Very similar momentum transfer curve shapes were found for other materials, hinting to a possible universal behavior [54].

While absolute values of stopping power can be obtained by many methods, such as ab initio (this work), semianalytic methods [77] or experiments [78], it is clear that ab initio methods can access microscopic quantities such as non-adiabatic forces, specific ion charges and momentum transfer that are otherwise out of the scope of other methods.