Abstract
This roadmap article highlights recent advances, challenges and future prospects in studies of the dynamics of molecules and clusters in the gas phase. It comprises nineteen contributions by scientists with leading expertise in complementary experimental and theoretical techniques to probe the dynamics on timescales spanning twenty order of magnitudes, from attoseconds to minutes and beyond, and for systems ranging in complexity from the smallest (diatomic) molecules to clusters and nanoparticles. Combining some of these techniques opens up new avenues to unravel hitherto unexplored reaction pathways and mechanisms, and to establish their significance in, e.g. radiotherapy and radiation damage on the nanoscale, astrophysics, astrochemistry and atmospheric science.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Henning Zettergren, Alicja Domaracka, Thomas Schlathölter, Paola Bolognesi, Sergio Díaz-Tendero, Marta Łabuda, and Sanja Tosic.
Core group of the MD-GAS COST Action CA18212.
Recent experimental and theoretical advances offer unique possibilities to study the electronic and structural dynamics of molecules interacting with different forms of radiation such as photons, electrons or heavier particles (ions, atoms, molecules). These advances include: (i) preparations of neutral and chargedmolecules and clusters in well-defined quantum states and structures (isomers); (ii) cryogenic storage of ions in new time domains; (iii) pump–probe schemes using advanced light sources and table-top laser systems; (iv) new spectroscopic techniques and methods to monitor emission of fragments, electrons and photons; and (v) theoretical and computational tools to treat the dynamics from ultrafast to ultraslow timescales (attoseconds to minutes and beyond). In this roadmap article, we present nineteen contributions where a combination of early career and more experienced researchers shares their views on the advances and future challenges within their areas of expertise.
Maclot and Johnsson open up the roadmap describing how table-top high-order harmonic generation (HHG) techniques may be used to produce attosecond extreme ultraviolet (XUV) pulses with the aim to unravel ultrafast electron and nuclear dynamics in molecules and clusters in unprecedented detail. Future challenges involve, e.g. implementing pump–probe schemes with two attosecond pulses for high temporal resolution and improved control, and to combine such ultrafast techniques with cryogenic storage devices and isomer selection methods.
Steber and Tikhonov describe the development of large-scale free electron laser (FEL) facilities for production of extremely intense, ultrashort, coherent pulses, and how they, combined with theoretical advances, have revolutionized the understanding of the dynamics of molecules in the gas phase over the last decade and a half. Upgrades to existing facilities and commissioning of new ones promise improved time resolution down to the attosecond regime and higher repetition rates. This will provide access to yet unexplored details on the very first steps in molecular reactions and its consequences for applications in, e.g. astrochemical and atmospheric sciences.
Castrovilli and Avaldi show that synchrotron radiation is a versatile tool for determining inherent spectroscopic properties of (bio)molecular systems and for studying the dynamics of molecules following absorption of photons spanning from the vacuum ultraviolet (VUV) to the hard X-ray regime. Here, key challenges for future studies are to develop methods to produce biomolecular targets with sufficient densities using, e.g. electrospray ionization (ESI) techniques or cluster aggregation sources, and to improve multi-coincidence detection techniques to provide structural information (e.g. chirality).
Bari and Milosavljević focus their contribution on how ESI techniques may be used to study the structure and dynamics of complex molecular systems at advanced light sources such as synchrotrons and FELs. To exploit the full capabilities of spectroscopic techniques available at such facilities, state-of-the-art techniques need to be combined in novel ways. This involves, e.g. crossed-beam experimental setups combining high-flux ESI with isomer selection techniques under ultrahigh vacuum conditions.
Palacios and Faraji describe theoretical advances in simulating light-induced dynamics in molecules on ultrafast timescales, which are essential to interpret results and guide experiments at, e.g. advanced light sources. A particular theoretical challenge is to develop accurate methods for large molecules that include the initial electronic excitation and ionization on attosecond timescales, and the subsequent electronic-nuclear coupling occurring on femtosecond timescales and beyond. Quantum computers and computational statistical methods (e.g. machine learning) are promising tools to meet this challenge.
Ascenzi and Romanzin review important contributions and highlight recent advances in the field of low-energy ion–molecule reactions. Here, the key to a more fundamental understanding is to develop and combine state-of-the-art techniques in new ways. Future challenges involve, e.g. studies of reactions with metastable neutrals that are common in naturally occurring processes but remain largely unexplored in the laboratory, to prepare the reactants in well-defined quantum states and isomeric forms, and to study reactions under true interstellar conditions at low temperature environments.
Piekarski and Rousseau discuss collisions between keV ions and isolated complex molecules or weakly bound clusters of such molecules and show how the projectile charge, mass and velocity may be tuned to influence the ionization and fragmentation of isolated molecules or molecules in weakly bound clusters. New methods to bring fragile molecules and clusters into the gas phase, improved control of target masses, as well as pump–probe schemes combining ion and light pulses are keys to the understanding of such fundamental processes.
Erdmann and Alcamí focus on computational methods describing fragmentation dynamics on picosecond timescales. They point out that there is a need for new approaches to model delayed fragmentation processes, large molecules for which quantum chemical calculation tools are computationally too demanding and charged systems where density functional theory (DFT)-based approaches are not reliable. Another key challenge is to efficiently combine methods designed to follow the dynamics on different timescales.
Kopyra and Limão-Vieira discuss the developments of techniques to study electron interactions with gas-phase neutral molecules. These have been instrumental to advance the understanding of, e.g. radiation damage mechanisms at the single molecule level and may provide key data of targeted compounds of importance for the development of environmental (green) technologies. Future challenges involve developing new tools to monitor neutral fragments, prepare targets of increasing complexity and follow electron dynamics on ultrafast times scales.
Kočišek and Fedor present experimental techniques to produce neutral clusters for studies of interactions with low-energy electrons and highlight results showing how the dynamics induced in molecules in such interactions is affected by the cluster environment. Improved characterization of the cluster target and the reaction products will be essential to provide benchmark data for accurate theoretical descriptions and a more fundamental understanding, and to gauge the significance of such processes in nature and in man-made technical applications.
Albertini and Gatchell demonstrate that superfluid He-nanodroplets are a powerful tool for producing cold ions and clusters. The development of a new generation He-droplet devices where the droplets are highly charged promises a more efficient production and better control over the initial cluster size distributions. This has the potential to open up new avenues for, e.g. gas-phase action spectroscopy using messenger techniques.
Cederquist and Schmidt present the developments of electrostatic ion-beam storage rings. Three cryogenically cooled ion-beam storage rings have recently been commissioned and are designed for unique studies and improved control of merged beams interactions involving ions and free electrons, ions and neutrals or two different ion species in opposite charge states. A particular challenge for future studies is preparation of intense beams of isomer selected ions in single or narrow ranges of quantum states. This is key to advance the understanding of, e.g. the origin and evolution of complex molecules in space.
Gruber and Andersen focus their contribution on studies of photo-initiated dynamics of isolated molecules combining ultrafast pump–probe schemes with electrostatic ion-beam storage. Pioneering studies demonstrate the capabilities of probing the excited state decay and ground state recovery of bio-chromophores. Future challenges involve, e.g. pre-cooling the ions in cryogenic traps/rings or in superfluid He-droplets to reveal the role of excited state energy barriers, and to study the electronic couplings in chromophore complexes.
Heber and Toker discuss the advantages of using electrostatic ion beam traps (EIBTs) for studying gas-phase dynamics of molecules and outline the prospects for future studies. Combined with ingenious detection schemes, EIBTs have the potential to act as a full reaction microscope where molecular cooling processes may be followed as a function of storage time. Applying ion mobility spectroscopy techniques opens up the study of the dynamics for specific isomers. The latest addition to the EIBT family is a hybrid two-trap system allowing for low-energy merged beams interactions with stored molecular ions having the same or opposite charge states. Such studies are currently only possible at the electrostatic storage-ring facilities.
Hansen briefly reviews statistical models that have been developed to describe different types of molecular cooling processes. These models have been instrumental to successfully interpret results from studies at, e.g. electrostatic rings and traps where the dynamics is followed on microseconds timescales and beyond. Combined with the rapidly emerging development of such devices, these models are expected to significantly advance the understanding of highly excited molecules and clusters and how they cool. Of particular interest are more detailed studies of thermal emission of high-energy photons (recurrent fluorescence), which is believed to be important for the survival of, e.g. interstellar molecules.
Noble and Jouvet describe recent advances in photo-fragment and photo-detachment spectroscopy using cryogenically cooled ion traps. The most advanced techniques offer a wide range of opportunities including, e.g. high spectroscopic resolution, high mass resolution, hole-burning spectroscopies, high-resolution photoelectron spectroscopy, and studying isomer-specific dynamics and size-selected clusters. Future challenges involve unravelling the mechanisms behind (non-statistical) selective fragmentation, generation and characterization of radical species, combining different techniques to fully characterize the molecule and its fragment and study selectively excited molecules.
Kjær and Brøndsted Nielsen briefly review the new emerging field of gas-phase fluorescence spectroscopy of (complex) molecular ions. This nondestructive technique provides direct measurements of the emitted photon spectra as well as information on excited state dynamics, and it has the potential to become an important standard spectroscopic tool. Here, challenges and future prospects aim to learn how to control fluorescence by, e.g. preparing the ions cold to increase the fluorescence yield and to develop new and efficient methods to study ion–molecule complexes. Such fundamental knowledge may, for instance, aid in engineering new fluorophores.
Carrascosa and Bull present isomer-selected action spectroscopy techniques and highlight their key properties and distinct advantages. The most recent developments are based on compact designs using printed circuit boards as ion-mobility spectrometers. Major challenges involve developing techniques that are cost effective and easy to integrate into new or existing instruments, and novel approaches to improve the performance of such techniques. Examples include improved resolving power using cyclic devices with cryogenically cooled buffer gases and multiple light and/or ion mobility stages.
Candian and Petrignani describe how the synergy between astronomical observations, laboratory experiments and theoretical efforts have and will advance the understanding of the lifecycle of carbonaceous molecules in space such as, e.g. polycyclic aromatic hydrocarbons (PAHs) and fullerenes (C\(_{60}\) and C\(_{70}\)). Recent advances open up the possibility to study, e.g. excited state dynamics, anharmonic effects, isomerization and fragmentation processes of systems that are expected to be key players in astrophysical environments but so far remain largely unexplored in the laboratory and by theory. Such fundamental studies combined with the high spectral sensitivity and resolution of the James Webb Space Telescope are expected to revolutionize the way we understand the molecular universe
Covering all intriguing research activities dealing with dynamics of molecules and clusters in the gas phase is unfortunately out of the scope of this roadmap. Nevertheless, we believe that the present selection shows a rapidly moving field where new techniques and methods are constantly developed, and where future directions share common overarching challenges. These challenges include advancing:
-
Methods to fully characterize molecules and clusters with increasing complexity in terms of their internal energy states and structures before interactions with photons, electrons or heavy particles. The combination of novel approaches highlighted in this roadmap is key to successfully implement such approaches and include, e.g. coupling soft ionization techniques (e.g. ESI) with isomer selection methods, cryogenic cooling and pre-trapping of ions, and state-selective photodissociation and photo-detachment techniques.
-
Experimental techniques to monitor electronic and nuclear dynamics with improved temporal resolution and control and to follow the dynamics in unprecedented detail across ultrafast to ultraslow timescales where the final state products are fully characterized and different competing relaxation pathways are disentangled (e.g. electron emission, isomerization, fragmentation, and radiative cooling). Examples include advanced pump–probe schemes using, e.g. attosecond- (HHG and FELs), femtosecond- and ion pulses, action- and fluorescence spectroscopy techniques with internally cold ions, improving long-time storage capabilities of ions, and multi-coincidence detection schemes for use under the most demanding vacuum conditions. Combining these tools in novel ways, for instance, advanced light sources or ion-accelerator facilities with cryogenically cooled ion-beam storage devices, is fundamental to further advance the understanding of the dynamics.
-
Theoretical and computational tools treating the dynamics of molecules and clusters with increasing complexity and where the dynamics may be followed on timescales where different relaxation processes come into play. These include, e.g. coupled electron–nuclear dynamics on ultrafast timescales, delayed electron emission and fragmentation dynamics on timescales exceeding picoseconds, and radiative cooling occurring on milliseconds and beyond. Here, methods based on, e.g. machine learning and artificial intelligence are in their infancy and may play important roles to address these challenges in the future.
The combination of these new and refined approaches in the laboratory and for computations is fundamental to further advance the understanding of the dynamics of molecules and clusters in the gas phase and thus also of its consequences for a broad range of astrophysics/chemistry, astronomy, atmospheric science and radiation science. The MD-GAS COST Action CA18212 (www.mdgas.eu) acts as an interdisciplinary platform for close collaborations and knowledge exchange between researchers performing fundamental studies of the dynamics of molecules and clusters in the gas phase (experiment and theory), and with key stakeholders from applied fields of sciences and industry. Such a concerted effort is key to tackle the current and future challenges outlined in this roadmap.
Acknowledgements This article is based upon work from COST Action CA18212—Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology).
2 Probing the molecular response to ultrashort XUV pulses produced by high-order harmonic generation
Sylvain Maclot and Per Johnsson, Department of Physics, Lund University, Sweden
2.1 Status: description of the state of the art
Fundamental chemical and physical processes in molecules are governed by electron and nuclear dynamics typically occurring at a timescale from atto- to picoseconds (10\(^{-18}\)–10\(^{-12}\) s). The time-dependent electronic density is responsible for the subsequent nuclear motion taking place on a longer temporal scale. Its apprehension is thus crucial for inferring the mechanism of processes such as bond formation and bond breaking.
The emergence of coherent light pulses with femtosecond and attosecond duration provided the necessary temporal resolution to study ultrafast processes in atoms and molecules. Such pulses can be produced by high-order harmonic generation (HHG) techniques [1] and have their spectral range from the extreme ultraviolet (XUV) to the soft X-ray region. This type of source can be realized as a tabletop setup which is an advantage compared to free-electron lasers, which are costly large-scale facilities with highly competitive proposal-based access. Another asset of HHG sources lies in the availability of very high pulse repetition rates (MHz).
a Selected points of the calculated potential energy surface (PES) of adamantane (DFT level) overlapped by the experimental XUV spectrum (gray). The selected points correspond to the minima of the PES encountered during the fragmentation of the dication leading to the production of the photoion pair C\(_2\)H\(_5^+\) / C\(_8\)H\(_{11}^+\). b Mass spectrum, exhibiting a multitude of fragmentation channels with single hydrogen resolution. The correlation between the produced photo-fragments is examined through extracted TOF–TOF (time-of-flight) covariance maps, with a zoom-in around the studied photoion pair in panel (c). d, e Ion kinetic energy distributions of the two studied photoions extracted from TOF–VMI (velocity map imaging) covariance images. f Kinetic energy release distribution for the photoion pair that helped us confirming that the two-body Coulomb explosion resulted from an open cage geometry
Since the first use of ultrashort light pulses to study atoms, the progress in fundamental understandings, the emergence of new technologies as well as the support offered by theoretical quantum chemistry enabled the study of more and more complex systems, such as molecular hydrogen, molecular nitrogen, methane, acetylene, methanol, amino acids, polycyclic aromatic hydrocarbons (PAHs) and fullerenes just to name a few (see review [2] and Sect. 3 for some examples). For instance, understanding electron dynamics has been demonstrated to be key to unraveling the relaxation dynamics of ionized molecules [3]. Indeed, upon ionization, the charge/hole density evolves by moving across the different sites within the molecule on the femtosecond timescale [4].
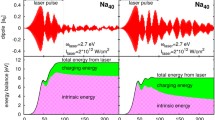
The simplest type of photoionization experiment is done using single ultrashort XUV pulses. Fundamental insight into the dynamics of complex molecular systems is available indirectly with the help of theoretical quantum chemistry calculations [5]. As an example, a result from one of our recent studies performed at the Lund Attosecond Science Center (LASC) on the diamondoid adamantane (carbon cage—C\(_{10}\)H\(_{16}\)) using an intense XUV source is summarized in Fig. 1. Combining multi-particle detection (double velocity map imaging spectrometer), covariance analysis and quantum chemistry calculations allowed us to show that the doubly charged adamantane molecule is metastable and will spontaneously dissociate [6]. Thanks to the measured ion and electron kinematics combined with theoretical calculations, we were able to discuss the internal energy distribution of the system and assess the energetic picture of the dication processes. As a result, we were able to demonstrate that, prior to dissociation, the cage structure of the dication will open and hydrogen migration(s) will occur (see Fig. 1).
A direct experimental way to precisely follow the ultrafast dynamics of complex molecular systems with temporal resolution lies in the use of pump–probe methods [7]. Within this approach, the system is ionized/excited from its initial state by an ultrashort light pulse (pump) and then probed by a second pulse arriving at a variable delay. Either of these interactions can result in photoionization/photo-excitation of molecules enabling diagnostics by time-resolved photoion–photoelectron spectroscopy.
Concerning experimental methods, the increase in complexity of systems of interest, i.e. number of degrees of freedom, number of electronic states, requires the use of multi-particle detection in coincidence (collection of all particles, ions and electrons, coming from the same molecule) coupled with high repetition rate laser sources in order to disentangle without ambiguity the dynamics of complex molecular systems. So far, the most powerful instrumental tool to tackle this challenge is the so-called reaction microscope device (ReMi or COLTRIMS [8]), which provides full kinematics of the interaction process.
It is worth mentioning that complementary spectroscopy techniques, such as high harmonic generation spectroscopy (HHGS) [9] and attosecond transient absorption spectroscopy [10], exist and largely contribute to the quest of understanding the dynamics of molecules.
2.2 Challenges and new directions
In spite of the improved understanding of the HHG process and the vast developments of related experimental technology over the last decades, the use of such sources faces various challenges in pursuit of unraveling ultrafast dynamics in molecules. For instance, the shortest available light pulses, i.e. single attosecond pulses (<100 as), have XUV spectra which span several tens of eV. When these are used for excitation, they populate a large number of excited states, which might result in complicated fragmentation dynamics. Another problem is that the most common “probe” pulses come from the laser driving the HHG process which has its spectral domain in the infrared or visual region. This poses a limitation to the temporal resolution (for example, the optical cycle of 800 nm radiation is 2.6 fs), as well as electric field strength that can be used without disturbing the studied dynamics (see pioneer work of F. Calegari for an example of XUV-IR pump–probe experiment [11]).
The latter issue can be tackled by using two XUV attosecond pulses to perform pump–probe measurements with a high temporal resolution and a weak electric field. This requires high-flux XUV sources, generally provided by very intense lasers, in order to enable sufficient signal from 2-photon absorption (one from each pulse). Some facilities, such as FORTH-IESL (Heraklion, Greece), RIKEN (Wako, Japan) and LASC (Lund, Sweden), have demonstrated the possibility to perform such experiments on atoms, but further progress needs to be made for these experiments to be fully adapted for investigations of molecular species. The challenges lie mainly in the stabilization of the HHG source, as well as in the low repetition rates characteristic of high-flux lasers (a few tens of Hz). New OPCPA-based laser technologies will be able to provide higher repetition rates alongside high pulse energies for future beamlines. An example of a very promising facility equipped with this type of source is the newly built ELI-ALPS [12] (Szeged, Hungary).
As an outlook, an interesting path beyond the state of the art would be to couple the above-mentioned ultrafast techniques with new sample environments, such as cryogenic rings (see Sect. 13). This would enable the selection of specific molecular conformations prior to interaction, helping both experimental interpretation and theoretical calculations.
2.3 Concluding remarks
The proliferation of HHG beamlines in the world and the strong interest in progressively larger polyatomic systems along with the continuous progress in theoretical quantum chemistry (see Sects. 6 and 9) foretell a bright and rich future for studies of ultrafast dynamics of molecules for the next decades. Furthermore, the technological and theoretical advances should be able to give access to the essentially unexplored dynamics occurring in molecular clusters.
3 Paving the road toward understanding molecular processes with free electron lasers
Amanda Steber and Denis Tikhonov, DESY, Germany
3.1 Status: description of the state of the art
For more than a decade, free electron lasers (FELs) have greatly advanced scientific endeavors in fields such as astrochemistry, atmospheric science, biology and energy transportation. They are intense radiation sources ranging from the THz to the hard X-ray regimes. This allows researchers to investigate the structure of systems, from atoms up to biomolecules and crystals, and their dynamics on timescales down to femto- (and recently atto-) seconds (fs). FELs, especially those operating between the vacuum ultraviolet (VUV) and hard X-ray regime, have proven to be instrumental in the field of molecular physics due to their unprecedented extremely intense (pulse energies as high as 4 mJ), ultrashort (sub-fs [13]), coherent pulses. The VUV Free-Electron Laser at Hamburg (FLASH) came online in 2005, and since then, more facilities, such as the LINAC Coherent Light Source (LCLS) in Stanford, the Japanese Spring-8 Angstrom Compact Free-Electron Laser (SACLA), the Free Electron laser Radiation for Multidisciplinary Investigations (FERMI) in Trieste, Italy and the European X-Ray Free-Electron Laser Facility (XFEL) in Hamburg, have come online operating up into the hard X-ray regime. They operate over a wide range of wavelengths and peak brilliance, as shown in Fig. 2.
These FELs have facilitated the study of phenomena such as the behavior of cold atomic and molecular systems—in particular the dynamics of excited states—and bond formation/destruction on the femto- and attosecond timescale. One gleans information on the molecular structure, chirality, isomerization effects, charge transfer, non-Born Oppenheimer effects and photo-fragmentation pathways [14,15,16]. In order to look at these phenomena induced by radiation, the FELs many times have stationary beamlines that are equipped with ion time-of-flight (TOF) mass spectrometers, velocity map imaging (VMI) spectrometers, electron spectrometers, absorption or fluorescence experiments, cold target recoil ion momentum spectrometers (COLTRIMS) and split-and-delay arrangements [14, 15].
A method used to monitor the dynamics of the molecules, which employs some of the above-mentioned techniques, is the pump–probe approach. This works in much the same way as described in Sect. 2, where two lasers, in this case the FEL and a table top laser or two FEL “beams,” can be used, or multi-photon absorption can induce indirect pump–probe effects. In these experiments, measurements are taken as the delay between the pump and probe is changed, where the pump initiates a chemical process and the probe changes the dynamical behavior of the system, allowing for new signal features from a transient species to be measured. In many cases, information from different measurements is merged together to provide details about the dynamics of the molecules. For instance, combining ionic mass spectra with electronic VMI measurements allows for the disentanglement of ionization/fragmentation channels. A very powerful set of tools in FEL-based ultrafast sciences are the covariance techniques [17]. Just recently, VMI 3D covariance imaging has progressed toward revealing information about the molecular structure and the dynamics happening through the course of the chemical reaction [18]. Direct imaging of the molecular motions by FELs is also available with more conventional diffraction techniques. They allow for the investigation of gas-phase dynamics using X-ray diffraction (XRD) due to their unprecedented intensity in the X-ray regime compared to other sources, such as X-ray tubes or synchrotrons [19]. Also, in comparison with time-resolved electron diffraction (TRED), FEL-based XRD shows better time resolution (due to the absence of electron–electron repulsion) and better shot-to-shot signal stability [20].
Theoretical work is being undertaken to investigate the dynamics of these pump–probe experiments that many times go beyond the Born–Oppenheimer approximation. The most popular methods which focus on chemical responses at the fs timescale include trajectory surface hopping molecular dynamics (TSH MD), ab initio multiple spawning (AIMS) and multi-configurational time-dependent Hartree (MCTDH) (see citations in Ref. [21]). They provide a treatment of the nuclear motions within several electronic states, but calculations of this nature are very computationally demanding (see Sect. 6 for more details).
All of these experimental and theoretical methods have culminated in state-of-the-art international collaborations aimed at carrying out investigations of the dynamics of gas-phase molecules. While many important studies have been done through these collaborations, we briefly outline just a few. One such study has been carried out on one of the most complex molecular systems studied in the gas phases with FELs thus far, the buckminsterfullerene (\(\mathrm {C_{60}}\)). In a series of works [22, 23] performed at the LCLS (Stanford) and the EXFEL (Hamburg), the authors found that upon interaction with X-ray radiation produced from FELs, C\(_{60}\) simultaneously undergoes a multitude of physical and chemical processes that are governed by the chemical bonding in this molecule [22, 23]. Upon core ionization, the Auger process was induced, which eventually led to the molecule being charged up to C\(_{60}^{8+}\) and breaking into molecular and atomic ion charge states through Coulomb explosions. They were able to accurately model this behavior through molecular dynamics simulations.
The relative ion yields of phenanthrene\(^{2+}\) (\(\mathrm {C}_{14}\mathrm {H}_{10}^{2+}\)) and the \(\mathrm {C}_2\mathrm {H}_{x}^{+}\) fragment after several time delays in the pump–probe experiments. The negative delays indicate that the IR pulse (810 nm) is the first pulse followed by the FEL pulse (30.3 nm), and for positive delays, the FEL pulse acts as the pump pulse. As can be seen, there is a slight increase in the ion yield of the dication around \(t_0\) which then depletes over time, whereas the reverse is true for the \(\mathrm {C}_2\mathrm {H}_{x}^{+}\) fragment. The step size between each point is \(\sim \)25 fs, and each point consists of approximately 1400 acquisitions. The data and theoretical treatment were first presented in Ref. [21]
Another collaborative effort has focused on the study of polycyclic aromatic hydrocarbons (PAHs). In the group of Prof. Melanie Schnell, efforts have been made to understand how harsh VUV radiation impacts the hydrogenation state, fragmentation and isomerization of PAHs with experiments done at CFEL-ASG Multi-Purpose (CAMP) end-station [24] of FLASH. Successful interpretation of the interplay between ionization and fragmentation channels in these complex system relies on the simultaneous analysis of multiple data sets, including TOF-MS and electronic and ionic VMI images. The analysis was supported by theoretical modeling [21], and it was found that phenanthrene (C\(_{14}\)H\(_{10}\)) undergoes several ionization steps as well as fragmentation. Based on covariance analysis, Coulomb explosion leads to the fragmentation of
with \(n = 2, 3, 4\) [21]. Figure 3 shows the experimental and theoretical ion yields for the dication and \(\mathrm {C}_2\mathrm {H}_{x}^{+}\) fragment. At \(t > t_0\), the IR pulse destroys the dications formed by the XUV. This is reflected by the change of behavior in the ion yield. The transient peaks at \(t \sim t_0\) are a signatures of short-lived intermediates. By modeling and experimental analysis, we attribute these intermediates to the PAH molecular/ionic excited states [21].
Molecular chirality has also been a target of study in FELs, in particular with its ultrafast manifestation, such as the work performed in Ref. [25]. The authors used photoelectron circular dichroism (PECD), which relies on forward–backward asymmetry in electron emission upon ionization with circularly polarized pulses [26]. These studies have proved challenging not only because of need in circularly polarized light from FELs, but also because of the high event statistics needed for such studies. In order to achieve the required statistics, either long beam times or high repetition rates are needed for the experiments.
3.2 Challenges and new directions
While the current state-of-the-art facilities have allowed for interesting chemical and physical processes happening in molecular systems to be scrutinized, scientists in this area are forever pushing the boundaries forward in an attempt to understand the very first steps in molecular reactions. In order to do so, it is imperative that FEL sources are able to routinely provide \(\le \)10 fs of time resolution, even as short as attoseconds, with faster repetition rates, and sequences of FEL pulses. This would at the same time require that detectors and measurement devices are able to keep up with the upgrades to efficiently collect shot-to-shot data and analysis techniques evolved to disentangle these complicated datasets. In order to provide a full picture, the new experimental setups are becoming more and more keen on combining multiple techniques for providing full insight into the systems of study. Parallel to these efforts, theoretical methods should become less computationally expensive and more accurate to provide a valid explanation of the processes observed in experiments.
Over the coming years, new FEL facilities will be coming online, and many of the older FELs will be upgraded. The European XFEL, with its superconducting linear particle accelerators, has achieved repetition rates of \(\sim \)27,000 Hz and pulse durations of \(\le \)100 fs, while FERMI has shown how using a seeded FEL in the high-gain harmonic generation configuration can improve shot-to-shot wavelength stability, transverse coherence and low-intensity fluctuations among others [27]. The LCLS-II facility is currently under construction. This instrument will implement seeding technology and superconducting linear particle accelerators, achieving repetition rates of \(\sim \)1 MHz and sub-fs pulse durations. The FLASH facility will undergo several upgrades during the FLASH2020+ project, which will see FLASH1 become a seeded FEL, pump–probe laser upgrades, and an eventual repetition rate of 1 MHz. These facilities along with the SwissFEL and the Shanghai High Repetition Rate XFEL and Extreme Light Facility (SHINE) will allow for further experimentation unraveling dynamics of the molecules in the gas phase.
3.3 Concluding remarks
The study of molecular processes in the gas phase with FELs has come a long way since FLASH first came online in 2005. With the existing facilities and their slated upgrades, as well as new facilities, this field will continue to grow and techniques will be honed to gain insight into bond formation/destruction and the interplay between electronic and nuclear motion. The increase in repetition rate will allow for the investigation of weak effects that require numerous data acquisitions that otherwise could not be studied. This will spur new understanding of elementary chemical processes in the fields of atmospheric sciences, astrochemistry, biological systems and energy transportation.
4 Biomolecules interacting with synchrotron light
Mattea Carmen Castrovilli and Lorenzo Avaldi, CNR-ISM, Monterotondo Scalo, Italy
4.1 Status: description of the state of the art
Synchrotron radiation with its tunability from the VUV to the hard X-ray regions, high flux and polarization control represents a highly valuable tool for a spectroscopic characterization of molecules of biological interest as well as to investigate the dynamical processes induced by the absorption of the radiation. The most straightforward approach to investigate the interaction of radiation with bio-matter using a tunable source is to vary the photon energy and to study photo-absorption. Below the ionization threshold, where outer electrons are promoted to empty states, direct light absorption or optical emission techniques are adopted, while above it photoionization mass spectrometry (PIMS) becomes the most suitable approach. The measurements of ionization energies and appearance energy (AE) of parent and fragment ions lead to the determination of key thermochemical quantities such as enthalpy of formation and bond dissociation energies. For example, the combined theoretical and experimental investigation of the AE of halopyrimidines and nitroimidazoles [28], with their derived compounds metronidazole and misonidazole, shed light on the radiosensitizing function of these classes of molecules, while PIMS on collagen peptides [29], the most abundant protein in the human body, showed that at low photon energy (14–20 eV), neutral molecules are lost from the amino-acid residue side-chains of both the precursor peptide and the photoionized peptide radical cation in a radical-induced process that mainly targets the Asp side-chain leading to abundant CO\(_{2}\) loss. This channel then is quenched in unfolded peptide due to the decrease in radical migration.
Photoemission and X-ray photoemission spectroscopies (PES and XPS), where the kinetic energy (KE) of the photoionized electron is measured at a fixed photon energy (\(h\nu \)), allow the reconstruction of the electronic distribution of the molecular orbitals of binding energy \(\text {BE} =h\nu -\text {KE}\). In the valence shell, the comparison of theoretical predictions and experimental photoelectron spectra in the case of antibiotics, radiosensitizers and their building blocks, but also sugars and lipids, has provided useful information on the electronic charge distribution of the outer orbitals and other properties useful to model the chemical behavior of these compounds. In the inner shell, the localized nature of the core electrons implies that each atom is affected by its surrounding chemical environment and site-selective information can be obtained. Differences among families of similar molecules (e.g. isomers, or analogues) or the effect of functionalization can be identified, assessed and discussed in terms of the measured and calculated inner-shell chemical shifts. The measurements of the N 1s spectrum of proline amino acid that allow to identify different conformers [30] can be taken as an example of the potentiality of the technique. Then, electron energy distributions measured over a broad range of kinetic energies up to several hundreds eV (including the Auger decay of core ionic states or autoionization of excited states) can be used to characterize the complete electron emission spectrum. These emission spectra at different photon energies represent the benchmark data for the Monte Carlo and Ion Tracking simulation codes [31], used to evaluate the direct and indirect radiation damage within the biological medium.
The simultaneous detection of electrons and ions in time coincidence, i.e. from the same ionization event in the photoelectron–photoion (PEPICO, Fig. 4) and photoelectron–photoion–photoion coincidence (PEPIPI-CO) experiments [32], allows for a better control over the many variables in the physical process, adding further insights into molecular fragmentation. In a series of PEPICO experiments on the building blocks of radiosensitizer compounds, it has been shown that molecular fragmentation following core excitation is strongly influenced by both the molecular site of the initial excitation and the character of the excited molecular orbital. While site/state-selective bond scission is favored when inter-site electron migration cannot occur efficiently and the chemical environment of the atomic site is very different, it becomes questionable in the case where fast electronic relaxation channels efficiently redistribute the initially localized core hole toward singly and multiply ionized states before fragmentation occurs (see Sect. 9). The selectivity and efficiency of the PEPICO technique have also allowed to find traces of minor processes like the isomerization with H transfer and dehydration of the parent ion in amino acids [33], which are relevant processes in the biological environment.
Molecular chirality is widely recognized for its relevance to the building blocks of life and its vital role for medicine and health. The advantage of synchrotron radiation, over the Xe-arc lamps of laboratory circular dichroism (CD) instruments, is the high intensity, in the VUV region below 200 nm and the broad energy range covered. Synchrotron radiation circular dichroism (SRCD) spectroscopy has been exploited to study base–base interactions in DNA/RNA, as the difference in the CD spectrum of a mononucleotide and strands of nucleotides provides evidence of interactions between neighboring bases in the electronically excited state [34] or in some cases of photo-lesion occurred on single strand. The low value (10\(^{-3}\)–10\(^{-4}\)) of the asymmetry in CD, due to the second-order perturbation level in the electric dipole/magnetic dipole and electric dipole/electric quadrupole interference terms, hampers its use for isolated molecules in the gas phase. Conversely, photoelectron circular dichroism (PECD) [35], which appears already in the electron dipole term of the transition matrix element, is characterized by asymmetries in the range of 10\(^{-1}\)–10\(^{-2}\). Thus, in the last years PECD has been exploited to study the conformational effects from isomerism and group substitution, conformer populations and clustering.
4.2 Challenges and new directions
The main challenge in studying bio-systems is their intrinsic fragility that hampers the production of beams of isolated biomolecules via thermal evaporation, which, however, has the advantage to produce beam of neutral molecules. The electrospray ionization (ESI) technique (see Sect. 5) represents the most suited tool to bring nucleotides, proteins or peptides from solution into the gaseous phase. The coupling of this versatile ion source with spectroscopic techniques implies that the mass selected ions generated in the gas phase by an ESI source are collected in an ion trap and then excited with the radiation. The combination of ESI sources with tandem mass spectrometers and ion traps has been successfully used to measure partial ion yield NEXAFS spectra of systems with sizes up to a few thousands of amu and to address, for example, photo-induced processes in molecular recognition [36]. An improvement of the throughput of the sources is the challenge to be faced to perform electron spectroscopies on these systems.
H-bonds and van der Waals interactions are ubiquitous in nature and influence the structure, stability, dynamics and function of molecules and materials and therefore play a crucial role in bio-systems. The study of these interactions in gas-phase homogeneous or hydrated clusters of increasing size (see Sect. 8) can give information on structures and mechanisms at work in both the liquid and condensed phases. Also, in this case the main challenge is the production of a controlled cluster beam with enough density. First attempts in this direction combining a gas aggregation source to produce neutral uracil clusters and XPS, where the weak, non-covalent interactions modulate the chemical shift, have been reported [37].
Metal nanoparticles are increasingly used in the biological field, due to the wide spectrum of potential applications, which include both diagnostic and therapeutic or their combination (theranostic) [38, 39]. While the possibility to exploit a wide range of materials, the established methods for the synthesis in different sizes, the easy functionalization of their surface to control the interaction with the bio-environment are making nanoparticles more and more popular, there is still a lack of understanding of the many processes that occur upon their irradiation and can explain their behavior, for example, as radiosensitizer. Synchrotron radiation with its broad tunability and fluxes and inner shell spectroscopies with their chemical selectivity can contribute to understand the electronic structure and emission spectra of metal nanoparticles and the chemistry induced by the functionalization of such complex aggregates. Studies of isolated nanoparticles are still rare. Some XPS experiments have been performed on 4-nitrothiophenolon gold nanoparticles [40], and recently, a valence study using angle resolved photoemission has been reported [41].
As for the investigation of chirality, the use of multi-coincidence technique, where up to five correlated fragment ions have been detected simultaneously [42], may pave the way to the determination of absolute configuration on the single-molecule level in the gas phase. Moreover, the recently introduced time resolved transient circular dichroism in the VUV region, which exploits the synchrotron natural polarization, allows to access timescales down to ns like in the isomer concentration changes during/after photo-isomerization [43].
4.3 Concluding remarks
The electronic structure and geometrical arrangement (conformation, isomerization, tautomerization) of molecules determine the functioning of bio-systems at the macroscale. For example, the functionality of complex molecules, like enzymes and proteins, is closely related to the details of their conformation and the macroscopic effects of radiation damage in living cells strongly depend on processes initiated at the atomic and molecular level of their constituents. Synchrotron radiation and all the armory of synchrotron-based spectroscopic tools, from the many particle coincidence experiments to the imaging techniques, represent a unique combination to unveil the radiation-induced processes in bio-systems of increasing complexity in gas phase.
Acknowledgements Work partially supported Italy–Sweden MAECI project “Novel molecular tools for the exploration of the nanoworld.”
5 Using electrospray ionization to study structure and dynamics of large biomolecules at advanced light sources
Sadia Bari, Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany
Aleksandar R. Milosavljević, Synchrotron SOLEIL, Gif-sur-Yvette Cedex, France
5.1 Status: description of the state of the art
Investigating the interaction of light with biologically relevant molecules has gained interest for a wide variety of research fields including photochemical reactions such as light harvesting as well as radiation damage in proteins and DNA related to cutting-edge cancer treatment techniques. However, in the condensed and liquid phases, disentangling direct and indirect radiation effects is often impossible. Although the investigated systems are certainly not in their natural environment, gas-phase experiments offer several advantages: The incoming projectile (photon, electron, ion) is well defined (energy, direction, charge, etc.), the target is well defined (chemical formula, structure, quantum state, temperature, mass, charge, etc.), and the interaction products are well defined (photoelectrons, ionic fragments, scattered electrons, emitted photons, etc.) and can be efficiently analyzed. In the beginning, studies on isolated biomolecules in the gas phase were limited to small molecules that are stable against thermal decomposition, because there were typically brought to the gas phase using ovens [44].
Electrospray ionization (ESI) [45] is a gentle, state-of-the-art technique to introduce intact, complex biomolecular ions from solution into the gas phase and into vacuum. The first photo-activations of electrosprayed biomolecules were performed as early as the 1980s [46], and a good overview of laser-based experiments can be found in a review by Brodbelt [47]. The advanced light sources such as synchrotrons (see Sect. 4) and free-electron lasers (FELs, see Sect. 3) have the great advantage of superior photon brilliance, a wide photon energy range (from infrared, through visible, vacuum ultra violet (VUV) up to X-rays) and, in the case of FELs, short intense pulses. More than a decade ago, the coupling of ESI tandem mass spectrometers at such light sources was introduced for a novel and unique way to investigate structure and dynamics of complex gas-phase biomolecules [29, 36, 48,49,50,51]. In all the applied setups, the light interaction with a selected ion precursor takes place in ion traps to account for the low target density due to the space charge (see also Sect. 8, 13, 14 and 17). Using ion traps, the high-resolution tandem mass spectrometry allowed the study of photon-induced fragmentation in a wide photon energy domain. Moreover, from partial and total ions yields one could determine excitation and ionization energies of the investigated systems (so-called action spectroscopy). In the soft X-ray regime, near-edge X-ray absorption fine structure (NEXAFS) spectroscopy or near-edge X ray absorption mass spectrometry (NEXAMS) probes transition between atomic core levels and orbitals of the molecular bonding states. Therefore, this action spectroscopy is a powerful site-selective, structural tool that provides information on the electronic structure, chemical environment as well as the 3D structure of the molecules. More recently, the site selectivity of this method has shown the dependence of backbone fragmentation on hydration upon X-ray absorption of water, representing a great potential for studying relaxation mechanisms in radiation damage to hydrated biomolecules in a bottom-up approach [52]. Furthermore site-selective dissociation on resonant excitation of sulfur electrons in sulfur-containing peptides was proven and paves the way for pump–probe studies of biomolecules at FELs [53].
5.2 Challenges and new directions
Although recent years have seen great progress in gas-phase investigation of complex electrosprayed systems at advanced light sources, the exploited techniques were always based solely on mass spectrometry. Therefore, the existing experimental setups do not allow exploiting a full potential of very powerful spectroscopic techniques presently accessible at advanced light sources, such as photoelectron spectroscopy (PES), including X-ray photoelectron spectroscopy (XPS), photoelectron photoion coincident (PEPICO) spectroscopy (see Sect. 4), velocity map imaging (VMI), etc. Indeed, the photoelectrons cannot be extracted from the ion traps and be analyzed in kinetic energy, both due to specific trap geometries and strong trapping fields that would significantly disturb kinetic energies of ejected electrons. Even if one overcomes later limitations (for example, by a novel trap design and short pre-detection shutdown of the trapping fields), additional difficulties arise from low-vacuum conditions in the interaction region due to the cooling gas used in the ion traps to increase their efficiency (typically He at a pressure of \(\approx 10^{-3}\) mbar). Moreover, there is a growing interest to study even more complex systems that can be produced by ESI, such as clusters, hydrated biomolecules, specific ligand complexes and functionalized nanoparticles, as well as conformer-selected biopolymers. The latter studies cannot be performed efficiently by using only RF ion traps. Technical developments toward a crossed-beams experiment, in which a focused target ion beam produced by an ESI source would be crossed by a focused photon beam inside a well-defined interaction region under high-vacuum, could allow efficient extraction and analyses of produced photoelectrons and photoions [16]. Developing such an experimental technique is rather challenging, however, as briefly elaborated below.
The essential challenge is to achieve an acceptable signal-to-noise level in the measurement, which is directly proportional to the photoionization cross section of the target and the target density in the interaction region. Whereas a high ionization cross section is expected for relatively large systems under investigation, it is experimentally non-trivial to achieve a high target density. ESI is an atmospheric pressure ionization source, and therefore, one should transfer with a minimum loss a high ion current produced by ESI to a high vacuum conditions (\(\approx 10^{-9}{-}10^{-10}\) mbar). The high vacuum is needed both to efficiently extract photoelectrons and to decrease the background contribution. To achieve such a high-current ion beam under high vacuum, one needs a complex system where the ESI source is followed by multiple deferentially pumped stages, a system of ion funnels and ion guides to collect and preserve the ions and a lens system to focus the ion beam in the interaction region. A basic principle for such a source has been laid out a few years ago for ion soft-landing applications [54]. Furthermore, in the case of a crossed-beams experiment, there should be a compromise between a well-defined small focal point and the ion acceleration that decreases both the effective ion density and the detection efficiency. Finally, due to low expected photoelectron signals a PEPICO detection scheme should be the most effective, allowing to filter out the background contribution. However, this might be an additional experimental challenge since the primary target beam is also made of charged particles that must be filtered out.
We have recently performed a proof-of-principle experiment in a collaborative project between DESY and SOLEIL synchrotron, using a high-flux ESI source developed at DESY, coupled to the MAIA branch of the PLEIADES beamline at SOLEIL (Fig. 5). The ESI source included an ion funnel stage, an ion guide stage and a quadrupole m/z filter. The target was the ubiquitin protein (10\(^+\) charge state), and the photoelectrons were acquired in coincidence with the ionized precursor detected downstream the interaction region. The measurements showed that besides a high-flux ESI source, highly focused photon and ion beams, ultrahigh vacuum conditions in the interaction region and an efficient PEPICO detection scheme are necessary to perform such studies.
5.3 Concluding remarks
In conclusion, the ESI technique combined with the last generation synchrotron light sources and FELs offers great potential to study a plethora of complex systems therefore bridging the gap between condensed/liquid phase studies and gas-phase studies of well-defined small isolated targets. So far, such studies have been performed using ion traps and newly developed state-of-the-art experiments based on tandem mass spectrometry and action spectroscopy techniques. However, further progress is necessary to exploit the full potential of both the spectroscopic methods available presently at the synchrotron and FEL sources, and variety of target systems that can be produced by ESI. One possible direction is the development of a crossed-beam experimental setup, with a high-flux ESI source, alternatively coupled to pickup gas cells, m/z and ion mobility filters [55] (see Sects. 15, 19), delivering an intensive and well-focused target ion beam into ultrahigh vacuum conditions and coupled to state-of-the-art photoelectron and coincident analyzers.
Simplified schematic figure of the ubiquitin protein photoelectron spectroscopy experiment performed at PLEIADES beamline, SOLEIL [56]
Acknowledgements The authors would like to thank all colleagues and collaborators who, in the last decade, have made it possible to study complex gas-phase biomolecules during many beam times. S.B. acknowledges funding from the Initiative and Networking Fund of the Helmholtz Association through the Young Investigators Group program. A.R.M. acknowledges support by SOLEIL synchrotron.
6 Simulating light-induced molecular dynamics in 2020: from the picosecond to the attosecond scale
Alicia Palacios, Departamento de Química, Universidad Autónoma de Madrid, Spain
Shirin Faraji, Theoretical Chemistry, University of Groningen, Netherlands
6.1 Status: description of the state of the art
Photo-induced processes lie at the heart of numerous natural phenomena, such as photosynthesis, human vitamin D production, circadian rhythm and visual response. In life sciences, optical technologies use light to visualize, detect and control biological processes in living tissues. These techniques include genetically encoded fluorescent proteins, biosensors and optogenetics. Furthermore, the world faces a rapidly increasing demand for sustainable energy, and thus, there is an enormous interest in understanding the mechanistic principles of photochemical reactions that convert sunlight into fuel. The interest in the mechanistic details of these phenomena motivated the development of sophisticated time-resolved spectroscopies, pushing further impressive advances in laser technology in the last half a century, which have enabled the real-time observation of such light-triggered processes. These techniques have rapidly evolved from the first picosecond pulse radiolysis system built in the late sixties to detect transient species in a chemical reaction, to the most recent attosecond pump–probe experiments that are able to measure time delays of a few attoseconds in the photoelectron emission from two different atomic shells [2, 3].
Time-resolved spectroscopic techniques have already given access to trace and manipulate a wide range of physical processes at different timescales. For example, the light promoted isomerization and intramolecular proton transfer between amino acids in the retinal chromophore of rhodopsin have been identified and measured in femtosecond time-resolved fluorescence experiments, while conformational changes in the chromophore environment were found to proceed in the millisecond to the picosecond timescales [57]. The most recent experiments, combining isolated attosecond and femtosecond pulses, have demonstrated the existence charge migration in amino acids in the sub-femtosecond range, indicating how preceding light-induced electron dynamics dictates the nuclear rearrangements and eventual fragmentation paths [5, 11, 58]. Even in the simplest molecular targets, the complexity of the resulting spectra can only be unraveled by means of solid theoretical input. Primary photo-induced processes occurring in both nature or clean energy devices, in general, involve inherently quantum processes such as photovoltaics effect, electron–hole migration or electron transfer phenomena [59], which need to be treated in a full-quantum mechanical manner, which is still a demanding task. Theoretical methods are thus nowadays facing new challenges that can be encompassed in the investigation of the coupled effect between electronic and nuclear motions and in the need of high-level electronic structure calculations, in particular, when higher energy photons are involved and ionization is possible. The significance of these effects or the accuracy of the methodology required strongly depends on the light frequency, timescale (as illustrated in Fig. 6) and specific phenomena under inspection.
6.2 Challenges and new directions
Photo-induced molecular dynamics at room temperature has been widely described using ground state chemistry methods, where an independent and classical picture of nuclear motion in the fundamental state already provides an accurate description of the process. However, this ultrafast dynamics often involves multiple electronic states that come into play as nuclear motion proceed, through non-adiabatic couplings between electronic and nuclear degrees of freedom (DOFs) [60, 61]. More interestingly, the advent of optical pulses in the subfemtosecond time domain opens the door to the unexplored scenario of attochemistry, where the broadband of the pulse can already create coherently an initial wave packet built of several electronic states. The theoretical strategies to time-resolve electron–nuclear dynamics then rely on two approaches, namely full-dimensional semiclassical molecular dynamics calculations and quantum wave packet propagation.
The most popular versions of the semiclassical approaches are the Ehrenfest formalism [62], where the forces felt by the nuclei are gradients of an average electronic surface, and the more accurate Tully’s fewest switches surface hopping (FSSH) [63], where transitions between electronic states are described by a stochastic algorithm. These methods have been successfully applied to retrieve dynamical information on relatively large systems; however, they fail to represent nuclear quantum effects such as tunneling, zero point energy and quantum decoherence. While zero point energy leaking and tunneling are important issues in ground-state dynamics, the geometric phase (a consequence of the existence of a conical intersection) is a multi-state quantum effect that is not taken into account in independent trajectory simulations [64]. Extended versions of FSSH pursue to overcome other important methodological limitations as describing superexchange population transfer [65], where two electronic states are coupled indirectly through an intermediate state with higher energy. FSSH also lacks the representation of transitions to high-lying states due to the missing classically forbidden transitions. This is relevant, for example, in describing electron-transfer mechanism, since electron transfer can proceed via the intermediate virtual state, which is hardly populated. Several extensions have been introduced to account for missing quantum effects in trajectory-based methods, as for the development of ab initio multiple spawning methods using Gaussian moving basis sets [66, 67], which are very promising approaches although the computational burden is considerably increased [64].
The second approach, a full quantum mechanical description of the molecular wave packet propagation, does not suffer from these drawbacks; however, it is limited by the exponential growth of computational resources as the number of DOFs increases [68]. With the current computational capabilities, a full-dimensional method that accounts for electrons and nuclei at equal footing is only possible for hydrogenic molecules [5]. A reliable alternative is the multi-configuration time-dependent Hartree method (MCTDH) method which solves the TDSE by a variational method and has been successfully applied for targets up to few tens of degrees of freedom [58, 68, 69]. In particular, its multilayer variant which enables the treatments of larger systems [70]. Although it still scales exponentially, the computational effort is greatly reduced by using time-adaptable single particle functions to construct a set of Hartree product configurations. By increasing the number of configurations, the MCTDH method converges to the numerically exact solution, while keeping the computational effort closer to a semiclassical picture. Additionally, to break the exponential scaling further and to remove the restrictions of the grid, the wave packet can be expanded over localized traveling basis functions of Gaussian shape that are variationally optimized and do not follow classical trajectories, known as variational multi-configuration Gaussian (vMCG) approach [71].
However, as for the mean-field and surface-hopping methods, its accuracy and computational efficiency remain bounded to the model potentials or the quantum chemistry method employed to describe the electronic structure. Since the introduction of Hartree–Fock theory almost a century ago, wave function-based ab initio methods have greatly evolved and a large manifold of post-Hartree–Fock methods accounting for electron correlation terms (Configuration Interaction, Coupled Cluster, Moller–Plesset perturbation theory or MCTDH) are available in most commercial (e.g., Q-Chem, Gaussian, MOLCAS, MOLPRO) and open-access (e.g., OpenMOLCAS, GAMESS, NWChem) software packages for chemistry simulations. When the exponential wall makes wave function methods impracticable, density-based methods are the only available choice. Density functional theory (DFT) methods include electron correlation through exchange-correlation functionals, still by means of a single Slater determinant that, in practice, limits its applications to describe singly excited electronic states. Even though DFT methods are known to underestimate barriers of chemical reactions, dissociation energies in ions or charge transfer excitation energies, and overestimate binding energies, they have shown to work remarkably well for structural and thermodynamics properties.
Despite the manifold of quantum chemistry packages currently available for electronic structure calculations of complex molecules isolated in the gas phase, further theoretical efforts are still required to account for photo-induced phenomena where electron correlation plays a critical role, such as core-hole states leading to Auger decay or multiple excited bound states leading to autoionization [58]. Moreover, deep insights on molecular photoionization problems can only be achieved by properly describing the electron in the continua coupled to the remaining ion, for which a scattering formalism is required [5]. These phenomena arise when molecules are exposed to highly intense field or to frequencies in the extreme ultraviolet (XUV) and X-ray range as produced in by high-order harmonic generation set ups [3, 12] and free electron lasers (FEL)[13, 24, 27], i.e., sources that are able to produce coherent light pulses with durations in the attosecond scale and wavelengths in the atomic size. The newest FEL facilities have been built with the promise of using this highly coherent ultrashort and intense light to probe matter in an unprecedented and unique way, for instance, measuring structural changes in proteins and enzymes before radiation damage occurs or resolving the structure of single biological particles prior crystallization [72]. More importantly, these sources can access fundamental processes that are still to be understood even in the simplest molecules. From the theoretical side, time-dependent scattering methods that provide an explicit evaluation of the electronic continuum wave function are nowadays under development. Above-mentioned bound-state methods have been employed the definition of the Dyson norm, resulting from a direct projection of states from the neutral molecule to the cation [73], as a very approximated value to the ionization yield. More elaborated approaches describe the continuum electron using Coulomb functions, thus accounting for the long-range part of the potential, although still are unable to reproduce the multicenter character of a molecular potential. The most sophisticated methods are based on Schwinger or complex Kohn variational principles or on close-coupling approaches as those implemented in Lippmann–Schwinger, R-matrix, Galerkin, ePolyScat, XCHEM or the most recently developed algebraic diagrammatic construction (ADC) scheme ([5, 58, 60] and references there in). These methods commonly incorporate discrete variable representation (DVR) or B-spline functions to properly represent the long-range part, combined with a representation using Gaussian or Slater-type orbitals implemented in standard quantum chemistry packages for a more efficient representation of the bound part of the wave function. These methodologies have been first applied to atoms with great success. The complexity introduced by the nuclear motion DOFs limits most of the existing applications in large molecules to calculations within the fixed nuclei approximation, although first attempts to include nuclear motion are under progress [60].
The ongoing developments of theoretical tools employed in gas-phase photochemistry come together with novel implementations to treat biological systems in their natural environment, i.e., in a solvent. These same tools can be employed to simplify the description of large-size targets as DNA or proteins, where one can concentrate on an active molecular site of the system and treat the remaining part as a solvating environment. This is the essence of the multi-scaling approaches such as hybrid quantum mechanics/molecular mechanics (QM/MM) [74]. The outcomes of QM/MM simulations depend crucially on the choice of the QM region, and one needs to carefully investigate convergence of the results with regard to the size of a QM region. Additionally, the short timescales accessible for QM/MM molecular dynamics (MD) simulations generally do not allow to investigate processes that occur on longer timescales (e.g., nanoseconds). Thus, one is restricted to performing transient dynamics along previously chosen reaction coordinates that requires some system-specific information on describing the underlying process. The identification of the relevant coordinates is not straightforward since there are many nuclear DOFs in large systems. These ambiguities may well be the origin of the many different conflicting theoretical hypotheses proposed for a given process [75].
6.3 Concluding remarks
Ab initio theoretical methods enable a rational design of novel molecules and materials. Moreover, ongoing and forthcoming applications using the newest laser technologies to explore gas-phase molecules are strongly pushing theory toward the development of full-dimensional quantum wave packet time-dependent approaches. In pursuing this goal, trajectory-based ground- and bound excited-state chemistry simulations move forward to incorporate a quantum description of the coupled electron–nuclear dynamics in processes occurring in the femtosecond to picosecond timescales, where the nuclei move significantly upon excitation involving several electronic states. On the other hand, sophisticated quantum chemistry packages using multi-reference approaches are being implemented in scattering-based approaches born in the area of atomic physics to describe XUV and X-ray-induced excitation and ionization of large molecules. These methods are only available within the fixed nuclei approximation, which can already account for the ultrafast electronic processes accessible in state-of-the-art attosecond experiments. However, the proper description of the subsequent nuclear arrangements and fragmentation paths requires of further developments.
The scalability of these methods to larger molecules, e.g. a typical chromophore has around 30 heavy atoms, is, however, limited to the current computational capabilities. New directions are being taken to overcome this limitation. Among those, it is worth to mention the long awaited availability of quantum computers, for which quantum algorithms, with scalabilities that can reach up to hundreds of DOFs, are under development for the simulation of structural and dynamical properties of molecules [76]. Alternative strategies to efficiently compute electronic structure in large molecules are based on machine learning [77] and artificial intelligence (neuromorphic computing and robotic technologies) [78]. In recent years, computational statistical learning methods (machine learning, neural networks, deep learning, unsupervised clustering, etc.) have found to provide very promising approaches to construct potential energy surfaces and have been successfully applied for both ground-state molecular dynamics simulations and (non-adiabatic) excited-state simulations [79]. Although by using those fitted potentials, the computational time for molecular dynamic simulations can be substantially reduced, the generation of the training data, which samples the important regions of the conformational space [80], still remains a big bottleneck.
Acknowledgements Shirin Faraji is thankful to Innovational Research Incentives Scheme Vidi 2017 (016.Vidi.189.044) financed by the Dutch Research Council (NWO). AP acknowledges support from the Ministerio de Ciencia e Innovación in Spain through Project PID2019-105458RB-I00 and a Ramón y Cajal contract.
7 Experimental techniques for low-energy reactions of charged species
Daniela Ascenzi, Department of Physics, University of Trento, Italy
Claire Romanzin, Institut de Chimie Physique, Université Paris-Saclay, France
7.1 Status: description of the state of the art
Low-energy ion–molecule reactions root from the very origins of mass spectrometry and positive rays’ studies, in the first years of twentieth century. It has developed in a strong field of research through the century, building from the development of advanced instrumental techniques for ion production, transport and energy definition, specific neutral sample production, optimization of their interaction region and quantitative detection methodologies, including the determination of the internal state distribution of products. The variety of ion–molecule reactive systems studied so far is vast, ranging from organic to organometallic species and biomolecular systems, but also from singly and multiply charged positive and negative ions to ionic clusters. Unravelling the role of reactions involving charged species permits to tackle fundamental questions in astrochemistry, organic and inorganic reaction mechanisms, biochemistry and catalysis. Beyond the fundamental interest on reaction dynamics, the quantitative outputs from these experiments, namely branching ratios, kinematic constants or cross sections and thermochemical information (tabulated in the form of extensive databases) are beneficial to models describing the behavior and evolution of plasmas of all sorts, from astrophysical media (e.g., [81] and refs therein), to flames or laboratory and industrial plasmas.
It is beyond the scope of this short section to provide an exhaustive review of the field, but we wish to mention here the main tools that have been developed to study the so-called low energy ion–neutral reactions, i.e., reactive collisions where collision energies range from fractions of meV to about 100 eV (for interactions at higher collision energies see Sect. 8). Indeed, it is nowadays possible to reach collision energies in the mK regime! We will describe here after aspects related to ion generation and selection, interaction region with the neutral partner, products detection and correlation.
Everything starts with the ion generation. If electron impact is a longstanding and universal ionization method, other methods are widely used for their remarkable specificities. Photoionization, via lasers or synchrotron radiation, is particularly adapted to control the energy deposition within the reactant ion, thus paving the way for state-specific reactivity. Soft ionization techniques based on chemical ionization (i.e., ion–molecule reaction) have also emerged and are now standard analytical tools. This is, for instance, the case of proton transfer reaction mass spectrometry (PTR-MS), a technique that was introduced and optimized for quantitative trace gas analysis and which is now daily used by thousands of users, with special reference to atmospheric sciences ([82], and refs therein). Yet, when one thinks about “soft ionization,” electrospray ionization (ESI) technique comes first and it is the method of choice to deliver in the gas-phase large (positively and negatively) charged molecules such as biomolecules, as detailed in Sect. 5.
Considering the interaction region between the ion and the neutral partner, the panel of experimental arrangements is large. One of the most popular and versatile is the selected ion flow tube (SIFT) technique, in which a flow of mass selected ions driven by a carrier gas reacts with a neutral target added downstream. The density of carrier gas guarantees thermal equilibrium of the target ion, thanks to multiple collisions with the non-reacting buffer gas, while the kinetic behavior of the flux allows for distance/time extraction of reaction rate coefficients and product branching ratios. The possibility to cool or heat up the buffer permits to measure rates as a function of temperature. This is illustrated in a recent work [83] where a laser vaporization ion source is coupled to a variable temperature (in the range 300–600 K) SIFT setup to generate MgO\(^+\) ions and study their reactivity with CH\(_4\), a system of potential interest in the catalytic activation of methane. The experimental results show counterintuitive behavior of reduced yield for the most exoergic channel, underlying the importance of reaction dynamics and theoretical calculations to interpret the reactivity of such “simple” systems.
A revolution in the field came with the ability to handle slow charged ions by confining them via fast oscillatory electric fields. The development of radiofrequency (RF) multipolar ion guides has led to guided ion-beam (GIB) setups where collisions with neutral targets take place in a scattering cell. This experimental arrangement permits to measure cross sections that are more informative on the reactive process than measurements of thermally averaged rate coefficients [84]. It should be noted at this point that an alternative way to trap ions for gas-phase molecular dynamics study is by electrostatic ion-beam traps, as detailed in Sect. 15.
GIB is a natural 2D ion trap, but going 3D leads to great benefits. Paul traps (such as those described in Sect. 18) or Fourier-transform ion cyclotron resonance (FT-ICR) is conventional tools to evaluate ion–molecule reactivity. Multipolar ion traps such as the 22-pole trap have become, in its cryogenically cooled version, a standard tool for the measurement of rate constants of low-temperature astrochemically relevant reactions of cations and anions [85, 86]. The quest to gain insights into fundamental aspects of chemical reactions has stimulated the development of molecular beam-based devices: Crossed-beams apparatuses remain forefront techniques to measure product differential scattering cross sections at variable collision energies that can be reduced by adopting lower crossing angles or merging supersonic beams onto a single axis (merged beams, see below). Coupling crossed-beam experiments with velocity map ion imaging techniques reveals correlation between products, thus allowing a detailed reconstruction of the reaction dynamics [87].
While this short review focuses on experiments, one should not forget that a close interplay with theory is essential. Theoretical methods can fill the gaps when experimental limitations preclude laboratory studies, and conversely, the production of high-quality experimental data is fundamental to benchmark theoretical studies and guide their development. Due to computational limitations, the vast majority of ion–neutral reaction systems comprising more than three atoms are treated by combining full quantum ab initio calculations of the potential energy hypersurface with quasi-classical trajectory methods (see, for instance, [88, 89]), while collisions involving biomolecular ions require classical trajectories and molecular mechanics [90, 91].
7.2 Challenges and new directions
In spite of the large amount of experimental technologies available to investigate low-energy ion–molecule reactions, there are three main aspects that are facing various challenges and on which researchers are concentrating their efforts: (i) extending the studies to reactions between ions and unstable neutrals (excited atoms, molecules or radicals); (ii) reaching an extreme control in quantum state selectivity of the reagents; and (iii) reaching low and ultralow collision energies and/or temperatures.
Reactions with unstable neutrals While reactivity between charged species and stable neutrals has been widely addressed, the reaction with atoms/molecules in excited states as well as with radicals is still largely unexplored, despite their relevance in natural plasmas and biological environments (free radicals and ions are highly reactive intermediates formed upon interaction of ionizing radiation with living cells). A way to prevent recombination/decay of the short lived species prior to reaction is to inject them in the buffer gas of a SIFT instrument. In this way, reactions of H, N and O atoms, O\(_2\)(\(^1\Delta _g\)), organic radicals (e.g., CH\(_3\), C\(_2\)H\(_5\)) have been studied with several cations and anions, including species of biological relevance such as deprotonated nucleobases, amino acid anions, sulfur containing anions, heterocyclic and aromatic anions (see, for instance, Ref. [92]).
Quantum state selection How chemical reactions are influenced by the electronic, vibrational and rotational excitation of the reactants is a long-standing issue in chemical reaction dynamics. Understanding how the initial quantum states of the reactants or their structures (i.e., isomers) drive the reactivity is also relevant to correctly model complex media such as plasmas or planetary ionospheres in which excited species and isomers are present. Photo-excitation with lasers or synchrotron radiation associated with various experimental setups (crossed beam, GIB or 3D trap) and ion detection techniques is a method of choice to induce specific population of reactants and to control the internal energy of either the neutral (see, for instance, [87] where vibrational excitation of the neutral partner is achieved using IR laser) or the charged species [93,94,95,96,97]. Quantum state selectivity of atomic and molecular cations can be obtained using threshold photoelectron–photoion coincidence (PEPICO) techniques, in which the time coincidence of ions with electrons having near zero kinetic energy allows to prepare vibrationally and electronically state-selected ions. Such techniques exploit the high tunability of synchrotron radiation (see Sects. 4 and 5 for synchrotron radiation tools for spectroscopic and dynamical processes) and are used, for instance, at the VUV beamline of SOLEIL synchrotron facility, to study state-selected reactivity in a GIB apparatus on which absolute reaction cross sections are measured, as a function of both the ion excitation and the collision energy [93]. Recent developments also allow to generate state selected molecular ions from beams of clusters or radicals [94], thus widening the range of possible studies, in particular to characterize the role of micro-solvation and isomer-specific reactivity [95].
Alternatively, a double quadrupole–double octopole ion–molecule reaction apparatus has been coupled with high-resolution visible–ultraviolet laser pulsed field ionization–photoion methods to study the reactivity of molecular ions (e.g., N\(_2^+\), O\(_2^+\), H\(_2^+\) and H\(_2\)O\(^+\)) in selected electronic, spin–orbit and ro–vibronic states; more recently the addition of a pulsed laser ablation ion source has extended the studies to spin–orbit state selected transition metal cations (see [96] for the vanadium case). Even more challenging than studies on the role of excited states in cation–neutral reactions are those dealing with excitation of anions, since very rarely atomic anions have bound excited state. A very recent advance is represented by a photoelectron energy spectrometer equipped with a cold octopole RF ion trap to study the reactivity of ground and excited state palladium anions with H\(_2\) [97].
Low and ultralow collision energies/reaction temperatures One of the main experimental challenges in ion–molecule studies is the possibility to reproduce in the laboratory the low temperatures (down to few tens of Kelvins) of naturally occurring cold environments such as the interstellar medium. Recently, noticeable works were presented, developing a SIFT-like injection system for a supersonic flow setup (CRESU) [98], reaching temperature as low as 49 K and opening a new field of applications of CRESU-type instruments for ion–molecule reactions. Similarly, the use of cryogenic 22-pole trap setups with buffer gas cooling has proved effective to study reactions of both cations (e.g. H\(_3 ^+\), O\(^+\), OH\(^+\), CH\(^+\), etc.) and anions (e.g., H\(^-\)/D\(^-\), O\(^-\), OH\(^-\), NH\(_2 ^-\), etc.) with simple molecules (e.g., ortho and para H\(_2\)) as well as H/D atoms from room temperature down to about 10 K (for a recent example, see [85]). By coupling 22-pole traps with IR lasers, the effect of vibrational excitation of the molecular ion on reactivity at low temperatures is possible, revealing unexpected behaviors such as the decrease in the reaction rate due to ro–vibrational excitation [86].
An emerging frontier is represented by collisions at temperatures \(<10\) K. Reaching such ultralow collision energies/temperatures with ions is particularly challenging, primarily because ions can be “heated up” by stray electric fields, thus reducing the collision energy resolution. New methodologies are in their development phase, and the interested reader is referred to two recent reviews on the chemistry at ultralow temperatures that include sections dedicated to charged systems [99, 100]. Alternative novel techniques using electrostatic ion-beam storage rings to measure reaction rates at low temperatures are discussed in Sect. 13. Two of the most promising developments employ an improved version of the merged beam technique and the phenomenon of coulomb crystallization of ions in a trap. In the first case, ultralow collision energies in the range between 0 and 30 K\(\cdot k_B\) have been obtained using highly excited Rydberg atoms or molecules in place of the ions. (The Rydberg electron shields the ionic core from stray field, but it acts as a spectator and does not affect the reactivity.) The ultralow energies are reached by merging a supersonic beam of the neutral in its ground state with a second supersonic beam of the Rydberg atom or molecule translationally cooled using a surface-electrode Rydberg–Stark decelerator and deflector. The technique has been used so far to investigate the reaction of He\(^+\) with CH\(_3\)F and, more recently, of H\(_2 ^+\) with HD [101].
The second breakthrough is the possibility to generate cold molecular ions by sympathetic cooling of charged species with laser-cooled atomic ions in Coulomb crystals. These are formed when laser-cooled, trapped atomic cations reach low enough temperatures to produce ordered structures. Studies of ion–atom interactions over a temperature range that can extend down to tens of \(\mu \)K have become feasible thanks to the development of hybrid trapping techniques, i.e., the combination of traps for ions (such as linear Paul traps) and atoms (magneto-optical traps). The co-trapping of molecular ions within the Coulomb crystal cools the ions to translational temperatures similar to the laser-cooled atomic ions [102]. Coupling cooled molecular ions with cold neutral sources (e.g. supersonically cooled molecular beams slowed down using Stark decelerators) will extend the study of state-to-state chemical reactions to more chemically complex systems, with control over all reaction parameters.
7.3 Concluding remarks
The future will see an increase in the molecular complexity of the ion–neutral reaction systems probed under controlled conditions, by developing spectroscopic methods to sensitively detect the internal energy content of product ions and by finding new ways to overcome some of the limitations with the current techniques. The big challenge will be to combine existing tools in new ways to study systems of increased complexity and broad chemical interest. Moreover, as the understanding of reaction dynamics goes together with a close interplay between theory and experiments, advanced theoretical methodologies will be essential to guide the interpretation and rationalize the experimental results.
Acknowledgements We thank Roland Thissen and Christian Alcaraz (Institut de Chimie Physique, Université Paris-Saclay) for their help during manuscript elaboration.
8 Interaction of keV ions with complex molecules and their clusters
Dariusz G. Piekarski, Institute of Physical Chemistry, Polish Academy of Sciences, Warsaw, Poland
Patrick Rousseau, Normandie Université, CIMAP, Caen, France
8.1 Status: description of the state of the art
Fundamental processes During the interaction, the projectile charge and energy determine the final charge and energy states of the molecular target (see Fig. 7a). An ion projectile with keV kinetic energy is considered as slow with respect to the velocity of the electrons in the target. Thus, the electron capture is the dominant charge transfer process in which one electron of the molecule is captured by the incoming ion after lowering of the Coulombic barrier by the projectile charge [103]. This resonant charge transfer can occur at large distance in the case of multiply charged ion collisions, and therefore, multiple electron captures are usually observed leading to the formation of “cold” multiply charged molecular cations [104]. Thus varying the charge state of the projectile, the excitation energy associated with keV ion collisions ranges from few eV [105] to few 10s of eV [106]. When the ion trajectory is penetrating the molecular system and as the projectile is a massive particle, energy can be deposited both on the electrons by friction with the electronic cloud, the so-called electronic energy loss, and on the nuclei in binary collisions, the so-called nuclear energy loss. In the latter case, the energy transfer is localized on specific bonds of the molecule and can lead to prompt and specific non-statistical fragmentation schemes [107].
Ion–molecule collisions In ion–molecule collision due to charge exchange and energy deposition from the projectile to the target, the latter undergoes ionization, excitation and eventually fragmentation processes (see Fig. 7). The quasi-symmetric fission for doubly charged species is typically known as Coulomb explosion (CE). Detailed studies of isolated positively charged biomolecules like amino acids, nucleobases and their derivatives have been recently investigated by collaborative theoretical and experimental works by means of molecular dynamics (MD), potential energy surface (PES) and coincidence mass spectrometry techniques (see Fig. 7b, c). Further details on calculations are given in Sect. 9.
Another approach that implements classical molecular dynamics simulations to study irradiation processes in particular applied to focused electron beam deposition of tungsten hexacarbonyl W(CO)\(_6\) precursor molecules on a hydroxylated SiO\(_2\) surface has also been proposed [108]. The combination of parameterized interatomic potentials with MD and reactive force fields allowed to study the dissociation processes at timescales up to hundreds of nanoseconds for few hundreds of W(CO)\(_6\) molecules. For the same system, very good agreement with the experiments was achieved by including the Monte Carlo (MC)-type simulations for the electron transport in these materials [109]. It was possible to unambiguously identify unexpected mechanisms behind the fragmentation patterns observed experimentally. Such unexpected reactivities initiated by the capture of two (or more) have been observed as a stabilization effect of the isomerization (H, OH migration and cyclization) leading to the metastable resistance against the expected CE. For instance, the ultrafast H migration competes with the CE within the first 40 femtoseconds leading to the stable dication of diol for glycine [110]. keV ion impacts on \(\alpha \)- and \(\beta \)-alanine led, respectively, to H\(_3^+\) emission [111] and hydroxyl group migration [112]. Metastable, long-lived dicationic species, including reactive nitrogen and oxygen species (RNS and ROS), were observed either due to the presence of the peptide bond for N-acetylglycine [113] or due to long chain in amino acids like \(\gamma \)-aminobutyric acid [114]. Proton transfer was also observed between sugar- and base-part of thymidine in competition with the expected glycosidic bond cleavage [105]. The above-mentioned unexpected dissociation pathways are expected to be found for many other systems, for which the reactivity is triggered by the keV ion impact [106].
Recently, Erdmann et al. [115] efficiently combined the PES, MD and MC for description of the irradiation driven chemistry. Chemical transformations induced by another sources such as (i) X-ray in the mixed water–ammonia clusters focusing on the microscopic observable [116] and (ii) electron impact showing H-migration in ethanol [117] were efficiently combined with PES and MD methodology. Interesting reactivity driven by low-energy atomic and molecular ions formed by galactic cosmic rays in the Earth’s atmosphere of highly oxygenated molecule has been studied focusing on both microscopic and molecular level understanding of nucleation, binding, evaporation, thermal effects, etc. of various clusters [118].
Ion–cluster collisions While gas-phase experiments on isolated molecules give access to the intrinsic properties of the molecular systems, weakly bound molecular clusters allow to study the effect of a simple chemical environment on those properties. On the one hand, the cluster can act as a buffer dissipating the excess of energy due to the collision by successive losses of monomer units, and thus, an overall reduced molecular dissociation is observed [104], and this reduction is even larger in the case of hydrated clusters [119]. This is due to the fact that the weak intermolecular bonds between the cluster constituents break preferably to the intramolecular covalent molecular bonds. Interestingly, the weak interaction between cluster components could also lead to additional fragmentation channels involving atoms participating in the H-bonding [119]. In the case of multiply charged clusters, the Coulomb repulsion between fragments could also be partly converted into internal energy, and therefore, a more important molecular dissociation is observed [104]. On the second hand, beside being a buffer for energy, the cluster can also act as a reservoir of matter, and thus, a reactivity inside of the cluster can be observed when a reactive fragment is produced within the cluster. In H-bound clusters, after ionization, a proton transfer occurs in several 10s of femtosecond (fs) before the cluster dissociates and protonated clusters are observed [119]. In van der Waals cluster of carbonaceous molecules such as fullerenes and polycyclic aromatic hydrocarbons (PAHs), a rich molecular growth has been observed due to the massive aspect of the projectile. In binary collision, the incoming ion can kick out a single atom from a molecule leading to prompt (fs) non-statistical dissociation channels [107] and to highly reactive species. Since the latter are surrounded by other residues in the cluster, they can further react with neighboring molecules to produce new covalently bound species as observed in clusters of PAH [120], fullerene [121] or a mixture of PAH and fullerene [122]. The very good agreement between experimental mass spectra and classical molecular dynamics simulation validates the proposed scenario. Recently, the formation of polypeptides from amino acid clusters has been reported [123]. The formation mechanism has been explored by quantum chemistry calculations. There the initial step is the protonation of the clusters after ionization which stabilized the clusters and allows further reactivity leading to the formation of peptide bonds between the cluster constituents.
8.2 Challenges and new directions
Unexpected mechanisms appear when the complexity of the molecular systems increases such as in peptides or proteins. However, bringing into the gas phase such targets is not possible by thermal evaporation. Pioneering keV ion collisions experiments have been done using electrospray ion sources to produce gas-phase peptides [124] or proteins [125]. However, the target beams produced are not dense and an ion trap is required to enhanced the target density. A step further will be to perform the usual crossed-beams experiments with more intense target and projectile beams. Considering the effects of the environment in ion–cluster collisions, so far the experiments have been performed with a size distribution of clusters. In order to get better insight into the threshold sizes associated with different mechanisms such as the molecular growth, size-selected targets are necessary. Again low-density target beams are expected and such experiments are challenging. Finally, as shown in Fig. 7, according to the molecular dynamics different timescales are associated with the different mechanisms discussed above. Thus, time-resolved ion–molecule collision experiments are very interesting as keV ion beams are a very peculiar pump compared to photons. However, due to the low density of ion beams produced by conventional ion accelerators such pump–probe experiments at least on the shortest timescales are kind of Grail quest. Nevertheless, pump–probe experiments at longer timescale (\(\upmu \)s) may be considered coupling an ion accelerator with an electrostatic storage devices such as a linear trap or a storage ring (see Sects. 13, 14 and 15).
8.3 Concluding remarks
In the last decade, the numerous combined experimental and theoretical efforts showed the roadmap to unravel the processes driven by keV ion collisions on complex molecular systems. It was possible to divide the physical processes into accessible time domains (see (a) and (b) in Fig. 7) and to cross-validate the experimental and theoretical observable by mass spectrometry and MD/PES simulations, respectively. This allows unambiguously to identify and to explain in detail the extremely fast and very slow physical events (see Sects. 6, 9). In the near future, more complex systems can be studied by means of electrospray ion source techniques as well as more efficient methodologies and accurate electronic structure methods accounting for the highly charged, large and weakly bound systems.
9 Modeling molecular fragmentation
Ewa Erdmann, Faculty of Applied Physics and Mathematics, Gdańsk University of Technology, Gdańsk, Poland
Manuel Alcamí, Departamento de Química, Facultad de Ciencias, Universidad Autónoma de Madrid, Spain
9.1 Status: description of the state of the art
Ionizing radiation interacting with molecules in the gas phase can induce numerous processes, including electronic transitions (electronic excitation, charge transfer and ionization) and nuclear excitations (rotation, vibration and fragmentation of the molecule). Understanding the fragmentation processes induced by photons, electrons and ions is crucial to many disciplines such as radiation cancer therapy, astrophysics, astrochemistry, plasma physics and atmospheric science. In this section, we highlight theoretical approaches aimed to describe molecular fragmentation processes in the gas phase and present an outlook for future studies in this field. Theoretical approaches to modeling decay processes that take place in competition with fragmentation, such as radiative cooling and delayed electron emission, are reviewed in Sect. 16. The theoretical models used to describe light-induced intramolecular electronic processes that occur in a shorter scale prior to fragmentation are reviewed in Sect. 6.
The large number of electronic and nuclear degrees of freedom involved in the study of molecular fragmentation represents the main challenge to use fully quantum mechanical methods. One of the main approximations usually needed is to consider that all electronic processes involved in the excitation of the molecule are much faster than the fragmentation and therefore the latter is treated as a post-collisional process. Fragmentation is thus considered as a relatively slow process in which excess energy is transferred to dissociative nuclear degrees of freedom. Various methodologies for studying molecular fragmentation have emerged ranging from quantum chemical, semiempirical to statistical, their applicability strongly depends on the size of the system and the timescale needed for dissociation.
The most challenging situation is when after the excitation the system is located in a highly excited electronic state. For instance, after photoemission of a core electron, Auger decay can leave the system in a doubly charged state in which electrons have been removed from inner orbitals. In this case, fragmentation dynamics starts at the same time as electronic relaxation and movement of electrons and nuclei should be considered simultaneously. Non-adiabatic molecular dynamics (see [126] and references therein) simulations are used to describe molecular fragmentation of such systems. Particularly, time-dependent density functional theory (TDDFT) molecular dynamics in the Ehrenfest formalism allows to self-consistently model both electronic and vibronic excitations. In practice, such simulations are limited to simulation times of around few hundred fs mainly due to the very small time step necessary for correct propagation of the electron dynamics. Timescale of the fragmentation process usually falls in the range of ps. However, once the system has relaxed to the ground state, further evolution can be treated with Born–Oppenheimer molecular dynamics (BOMD). With this theoretical approach, López-Tarifa et al. [61] were able to determine the effect of ionization of different molecular orbitals on the fragmentation of doubly ionized uracil molecule produced in collisions with 100 keV protons. A good agreement with the 2D time-of-flight ion coincidence spectrum was obtained, reproducing the most intense coincidence islands and their shapes.
Another approach is to assume that fragmentation occurs in the ground electronic state and the system follows the lowest energy pathway. This has been adopted in many theoretical studies employing different methodologies. One successful theoretical approach relies on the combination of ab initio molecular dynamics (AIMD) simulations in the ground state and exploration of the potential energy surface (PES) with density functional theory (DFT). Such methodology works under the assumption of efficient redistribution of the excitation energy across all vibrational degrees of freedom, so that excess excitation energy can be introduced as internal vibrational temperature in a molecule in an electronic ground state. In order to mimic the sudden ionization, the simulations consider vertical transition. The computational cost of the simulations mainly depends on the particular AIMD methodology used. For instance, efficient implementations, as the atom-centered density matrix propagation method (ADMP), allow to run hundreds of trajectories with simulations times of the order of few hundred fs in systems of the order of a dozen atoms. These dynamics allow to evaluate, for different internal energies, the relative importance of different channels as Coulomb explosions, isomerization or combined isomerization + fragmentation, and to identify intermediates that many times would not be envisaged following chemical intuition. Once the most relevant intermediates have been identified, they can be studied in detail using DFT methods to obtain their energetics and structural properties. Also transition states connecting different intermediates can be located, providing a general view of the PES, the lowest energy pathways and the corresponding energy barriers. All this information is extremely valuable for a correct interpretation of experiments. Combination of ADMP simulations and PES exploration has been successfully applied, e.g. to predict unusual hydroxyl migration induced by 48 keV O\(^{6+}\) collisions with \(\beta \)-alanine [112].
For larger systems and/or longer simulation times, AIMD can be replaced by the self-consistent charge density functional tight binding (SCC-DFTB) method [127]. As previously mentioned, maximum simulation times available for quantum chemistry molecular dynamics are of the order of few ps; however, those can be extended until a nanosecond with SCC-DFTB methodology and still provide reliable results [128]. Purely classical molecular dynamics simulations are suitable for modeling fragmentation of more complex molecular systems and at longer time scales (ns) if adequate many-body force fields are included. Investigation of chemical bonding without expensive quantum mechanical calculations is attainable, e.g., with the Adaptive Intermolecular Reactive Empirical Bond Order (AIREBO) potential [129] implemented in the LAMMPS software package [130]. In addition to LAMMPS, several molecular dynamics codes are available, one of them being NAMD [131]—an open-source software designed for high-performance simulations of large biomolecular systems.
It has been shown that under certain experimental conditions, ion impact can induce bottom-up processes of molecular growth by species produced in a cluster fragmentation covalently bonding with other molecular fragments or intact monomers. Such reactions are of great importance among others in the fields of astrophysics and the atmospheric sciences because they constitute possible ways of formation of PAHs and fullerenes in space or formation of aerosols in the atmosphere. From a theoretical point of view, ion–cluster collisions have been typically modeled with classical molecular dynamics simulations due to high complexity of those systems (as many as few hundred atoms). Importantly, such theoretical approaches are only able to model neutral systems. For large molecules with many delocalized electrons (e.g., fullerenes), exclusion of charges is thought to have minor effect on the MD results. However, for clusters of smaller molecules inclusion of charges, e.g., with SCC-DFTB method, might improve the predictions of molecular properties. In the case of 12 keV Ar collision with pyrene clusters [120], this method has been applied in a simplified manner (only for trajectories that resulted in molecular growth and included only the reacting fragments identified in the classical calculations). DFTB simulations reproduced the classical simulations results quite well, but at higher temperatures DFTB molecular dynamics simulations predicted easier bond cleavages than simulations of classical molecular dynamics.
One interesting modification of classical molecular dynamics simulations adequate to study complex molecular systems over nanosecond timescales consists in the introduction of random and local modifications of the classical force fields to account for chemical transformations, i.e., bond cleavages/formations, dangling bonds and changes in molecular topology of the system. Such approach allows to study irradiation driven chemistry—a family of chemical modifications induced by irradiation with external fields. This methodology called Irradiated Driven Molecular Dynamics (IDMD) [108] has been implemented into the MBN Explorer software package [132] and applied to the study of focused electron beam deposition of tungsten hexacarbonyl W(CO)\(_6\) precursor molecules on a hydroxylated SiO\(_2\) surface demonstrating its potential to describe complex dynamics and nanostructure formation and growth [109].
Statistical methodologies such as Weisskopf theory, the RRKM Theory of Unimolecular Reactions and Microcanonical Metropolis Monte Carlo method also play a key role in the investigation of fragmentation processes due to significantly reduced computational cost with respect to molecular dynamics. In the study of C\(^{6+}\) collisions with C\(_{60}\) [133], the rate constants for C\(_{2}\) and C\(_{2}^{+}\) emission from the excited and charged fullerene were calculated within the Weisskopf formalism and subsequently used to evaluate the fragmentation dynamics. The fundamental RRKM theory is widely applied in photodissociation or thermal decomposition studies to predict molecular fragmentation rate constants. In order to produce a breakdown diagram, one needs to locate all rate-limiting transition states, which is generally a formidable task in systems with large number of nuclear degrees of freedom. However, a recently developed transition state search using chemical dynamics simulations (TSSCDS) methodology [134] shows promising results for global and automatic location of stationary points of a PES with semiempirical accelerated dynamics simulations and is now implemented in the AutoMeKin code [135]. Combination of TSSCDS with chemical dynamics simulations (implemented in the VENUS package) has recently allowed for correct prediction of fragmentation patterns involved in the Collision-Induced Dissociation of deprotonated cysteine-S-sulfate [90]. Another recent implementation, named M\(_3\)C [136], introduces entropy maximization as a procedure equivalent to an MD simulation in the infinite integration time limit. This approach has proven to be a successful tool for obtaining fragmentation breakdown curves of, e.g. adamantane dication [6].
Finally, different methodologies aim to compute mass spectra from first principles. Quantum chemical electron ionization mass spectrometry (QCEIMS) has been developed by combining elements of statistical theory (used for the assignment of a statistical charge to a fragment) with BOMD and has been shown to correctly reproduce experimental mass spectra of organic compounds [137]. Other approaches based in Chemical Dynamics Simulations have been recently reviewed [91].
9.2 Challenges and new directions
Delayed fragmentation Interaction of ionizing radiation with complex molecules may lead to time delayed processes due to their energy storing capabilities connected with large number of nuclear degrees of freedom. Such systems can remain internally “hot” and with that hinder the observation of fragmentation channels at threshold energies. Experimental observations have indicated production of metastable species surviving on the microsecond timescale before the fragmentation, e.g. in C\(^{6+}\)–C\(_{60}\) collisions [133]. Hence, from a theoretical perspective, there is a need of new, reliable statistical methodologies that could explain such processes on an appropriate timescale.
Large molecules The drawback of employing AIMD-based approaches for elucidation of fragmentation patterns is the need to run a large number of long calculations, which is unfeasible for larger systems. Depending on the underlying quantum chemical method, molecular dynamics simulations quickly become very expensive, so efficient code parallelization of AIMD approaches is crucial for the technical feasibility of such calculations.
Charge distribution Most of the previously discussed methodologies employ DFT as the underlying quantum chemical method. It is well known that this level of theory can lead to unphysical fractional charges; thus, DFT-calculated charge distributions must always be approached with caution. When obtained fractional charges are close to +0.5, dissociation on various PESs with charge asymmetrically and alternatively distributed might occur. Moreover, fractional charges are also expected within Ehrenfest–TDDFT as Ehrenfest dynamics evolves the electronic and nuclear degrees of freedom on an average potential. Explicitly considering the transitions between various electronic states would remove such discrepancies.
9.3 Concluding remarks
Studies of molecular fragmentation are essential to various branches of science. MD-based approaches described in the present review are able to explore energetically available regions of phase space in an automatic manner and thus identify fragmentation pathways that sometimes do not follow the “chemical intuition.” On the other hand, statistical methodologies proved to be powerful tools in extending the simulation times close to the experimental timescale. Efficient combination of these different techniques is necessary to explore fragmentation at long times. Proceeding beyond the state of the art will require accompanying experimental data that could aid with testing and benchmarking of the newly developed theoretical procedures.
Acknowledgements This work was supported by the MINECO project CTQ2016-76061-P and MICINN project PID2019-110091GB-I00.
10 Electron interactions with gas-phase molecules
Janina Kopyra, Faculty of Exact and Natural Sciences, Siedlce University of Natural Sciences and Humanities, Siedlce, Poland
Paulo Limão-Vieira, Atomic and Molecular Collisions Laboratory, CEFITEC, Department of Physics, Universidade NOVA de Lisboa, Portugal
10.1 Status: description of the state of the art
Electron scattering on atoms and/or neutral molecules is one of the most essential classes of chemical reactions and has been studied extensively in gas phase over a long period of time. These processes are of high importance for understanding and developing of many naturally and technologically occurring processes [138]. Among them, the attachment of low-energy electrons to molecules is an important process considering multiple perspectives, including atmospheric, environmental, (nano)technological (e.g., gaseous dielectrics, gas discharge lasers, plasma etching industry, electronic industry, nanofabrication, modification and functionalization of the surfaces) applications. In addition to the aforementioned, this process and its specificity are relevant for radiation chemistry. Therefore, a detailed knowledge of dissociative attachment is important for understanding and modeling electron driven processes.
Over the past decades, a vast time was dedicated to study interaction of low-energy electrons with biomolecules. Such interaction is considered to play a pivotal role in the description of radiation damage to living cells on a molecular level. This stems from the fact that high-energy radiation generates an exceeding amount of secondary electrons having initial energies in the range of a few tens of eV. Within picoseconds, these secondary electrons are slowed down; however, prior being solvated they may still induce reactions. Twenty years ago, it has been shown that single and double strand breaks can be caused by low-energy electron (LEE) impact to plasmid DNA [139]. As a result, strong activities emerged to understand the fundamental damage mechanisms. Initially, mainly small organic compounds, which represent the building blocks of biomacromolecules, have been studied. These included dissociative electron attachment (DEA) to the building blocks of DNA, namely the nucleobases, the phosphate and the sugar units. This stems from the fact that they are relatively easy to evaporate to be studied directly in the gas phase or deposited as thin films in the condensed phase [140]. In this way, interaction cross sections and fragmentation patterns are accessible. On this line of research activities, a peculiarity has been demonstrated namely site and bond selectivity in the loss of a neutral hydrogen atom from nucleobases at sub-excitation energies, < 3 eV [141]. More recently, DEA and electron transfer studies have been extended to nucleosides showing a particular fragility of the glycosidic bond. Up to now, there is only one experimental gas-phase study on the entire nucleotide, \(2'\)-deoxycytidine \(5'\)-monophosphate (dCMP) [142]. The results indicated that in dCMP electron attachment can induce bond breakage between the phosphate group and the sugar not only by direct electron localization on the phosphate unit but also indirectly by initial electron localization on the nucleobase and subsequent transfer of the excess electron to the sugar–phosphate backbone. However, as was shown the majority of bond ruptures within dCMP nucleotide results from direct electron attachment to the sugar–phosphate backbone.
Recent advances in electron–molecule interactions and the associated instrumentation have led to the development of a softer method for bringing non-volatile/fragile samples into the gas phase. As such, LIAD (laser-induced acoustic desorption) is a promising technique not yet fully explored in the field of electron-induced damage to more complex molecules. The first results obtained from ribose-5’-phosphate unit [143] did demonstrate that it can be successfully used for the fragile systems which otherwise could be easily thermally destroyed. The challenges in studying complex biomolecules can also be overcome using a DNA origami technique [144]. This method is successfully applied to study electron-induced decomposition of biotinylated target sequences (oligonucleotides of specific sequence) attached to the DNA origami platforms that are immobilized on Si/SiO\(_2\) substrates. After electron irradiation, the remaining intact oligonucleotides are visualized by atomic force microscopy with streptavidin, which allows a quantitative analysis of the electron-induced damage.
Given the growing application of radiotherapy employed in anticancer treatment, there is still a need to develop more effective methods of sensitizing cancer cells to radiation, thereby lowering the lethal dose of ionizing radiation. Most of the therapeutics used are derivatives of nucleosides substituted with electroaffinic substituents and are relatively easy incorporated into the DNA structure. These so-called radiosensitizers are promising chemical agents that modify radiation response of tumor tissue by increasing DNA damage and producing highly reactive species or by reduction of the targeted molecule (as the case of nimorazole [145]). These chemicals, as shown by recent studies, are prone to dissociative electron attachment that is at least in part responsible for the final biological effect. More recently, metal-based nanoparticles have been suggested as effective radiosensitizers. The possible mode of action of these metallic nanoparticles includes the radiation-induced release of an avalanche of low-energy secondary electrons that are responsible for further damage of DNA.
10.2 Challenges and new directions
Significant developments have been made during the last decades in exploring electron-induced processes in molecules as a function of phase and stage of aggregation. Such has been attained by combining high-resolution beams with state-of-the art spectroscopic (and spectrometric) tools capable of unraveling key features relevant to assess the nature of transient molecular states. In most of the environments noted before, where electrons play relevant roles in the local chemistry, one key aspect is still related to neutral dissociation (ND) which is central to electronically excited precursors yielding neutral fragmentation, although the products of ND appear to be more difficult to monitor than charged products. Thus, detailed knowledge of the nature of the electronically excited states by experimental and theoretical methods is also demanded to assess the nature of the excited states from which estimates of ND cross sections can be obtained.
The international scientific community has long ago identified the need to increase the complexity of molecular targets in the gas phase, where different experimental techniques have been put forward to allow more complex molecular structures to be probed (e.g. electrospray—see Sect. 5, LIAD), not only at room temperatures but in the case of clusters and complexes (Sect. 11) at particular cold temperatures [146] (Sect. 12). The recent advances in the physical–chemistry of gas–liquid interface (e.g. atmospheric chemistry) are still in its early days as to the majority of different environments where they prevail, but still posing an enormous challenge from the experimental and theoretical point of views to larger macromolecular systems.
The reaction microscope developed to obtain relevant information on the vector momenta of several ions and electrons resulting from atomic or molecular fragmentation is still a powerful electron momentum spectroscopy technique, which has been evolving into different fields with special attention to the investigation of high-intensity short-pulse laser-induced fragmentation of atoms and molecules [8]. This technique coupled with state-of-the-art methodologies involving tunable high-intensity short-pulse VUV, or even X-ray self-amplifying (SASE) free-electron lasers (FELs, see Sect. 3), yields an important opportunity to explore and monitor the time evolution of correlated atomic and molecular electronic processes on attosecond timescales.
Finally, from the theoretical point of view, quantum chemical tools capable of providing fast and complex electron dynamics data on attosecond timescale processes (e.g., HHG, FEL and photo-induced dynamics of molecular systems, see Sects. 2, 3, 6) will demand a considerable joint effort seeking for efficient and reliable supercomputer facilities, notwithstanding the considerable challenge as to the breakdown in the Born–Oppenheimer approximation.
10.3 Concluding remarks
Electron interactions with gas-phase atoms and/or molecules are still necessary to provide important data to assess the role of such target compounds under isolated conditions where key spectroscopic features will be hided or even quenched as a function of the environment. Here, we have decided to focus on the current global political decisions regarding the long-term strategies under the Paris 2019 agreement. These are mainly related to the environmental impact and the urgent need to keep finding replacement feedstock gases for the semiconductor manufacturing industry, given that the majority of the traditionally used, and most efficient chemical compounds have been banned due to their strong contribution to global warming and ozone depletion. This is a result of an international effort that we have embraced as part of a larger programs aimed at understanding the underlying molecular mechanism of targeted compounds, and the role of these trace gases in the Earth’s chemical and physical environments, and investigate alternative compounds for the development of a so-called green technology. The experimental techniques in electron and photon interactions with molecules allow a comprehensive and unique methodology to probe the role of such compounds in different environments where they determine the local chemistry, thus with considerable societal impacts. The current rising need for improved technologies capable of delivering faster and larger amounts of data, as well as a growing demand on efficient and reliable communications in the different sectors of the global economy, demands a rapid response from the micro- and nanotechnological industries exerting an enormous pressure on the processing capabilities of such semiconductor plants.
Acknowledgements JK acknowledges the support from a statutory activity subsidy (No. 25/20/B) from the Polish Ministry of Science and Higher Education. PLV acknowledges the Portuguese National Funding Agency FCT through Research Grants CEFITEC (UIDB/00068/2020) and PTDC/FIS-AQM/31281/2017.
11 Interactions of low-energy electrons with clusters
Jaroslav Kočišek and Juraj Fedor, J. Heyrovský Institute of Physical Chemistry, Czech Republic
11.1 Status: description of the state of the art
In this section, low-energy electrons (LEE) are considered those having a kinetic energy below the ionization threshold. Their collisions with molecules can lead to the formation of transient anion states—resonances. This can be followed by dissociative electron attachment (DEA). DEA has several peculiarities, e.g., it is the only fragmentation process operative at sub-excitation energies, and the fragmentation pattern is often strongly dependent on the electron energy (bond selectivity). DEA often occurs in complex environments where LEE is formed as secondary species after passage of high-energy radiation through matter. Examples include radiation damage to living tissue, chemoradiation therapy of cancer, focused electron beam-induced deposition (FEBID) and processes on atmospheric and astrophysical ices. In all these cases, the interaction of the target molecules with LEE will be influenced by the surrounding environment.
Experimental studies of environmental effects on DEA are complicated by the fact that the mean free path of LEE in a dense bulk environment is short, on the order of nm. Tracing the LEE before their solvation in liquids therefore requires ultrafast spectroscopy [147]. Another experimental approach, which is a subject of the present contribution, is to study interactions of free electrons with clusters—nm sized models of bulk. The correct modeling of the environmental conditions is then reduced to preparation of neutral cluster target of specific composition or thermodynamic state. Current state-of-the-art techniques used to prepare neutral clusters for LEE studies are outlined in Fig. 8.
Various approaches to study interaction of free LEE with clusters such as electron attachment spectroscopy (EAS), mass spectrometry (MS), photoelectron spectroscopy (PES) or optical spectroscopy (OS) and methods to prepare molecular beams of neutral clusters: a clusters of rare gas or selected molecule such as water pick up sample molecules, which aggregate to form clusters; this method is useful for studies of processes on surfaces and interfaces. b He droplets reach sizes of micrometers; the size allows for pickup of molecules with very low vapor pressures and studies of interactions at liquid He temperature. c Co-expansion enables studies of heterogeneous clusters of many components. d Use of humidified gas as one of the components of the co-expansion enables studies of single hydrated molecules. e Aerosol transport into vacuum enables studies of fragile molecules that cannot be sublimed
The most important environmental effects on the interaction of LEE which were identified so far include:
(i) Suppression of molecular fragmentation induced by LEE [148, 149]. Several mechanisms were proposed for the stabilization of transient negative anions and closing of dissociation channels by the environment. These include caging of dissociation products, energy transfer to the solvent or changing the molecular dipole moment [150,151,152,153]. Recently, another mechanism was proposed, based on a strong coupling of the inter- and intra-molecular vibrational motion [154].
(ii) Molecules of the environment can allow for additional reaction pathways. A well-explored example is the mechanism of proton transfer after electron attachment, e.g., in the formic acid dimer [155]. This mechanism will be particularly important in complex molecules with several electron-affinic moieties. For example, in deoxycytidine monophosphate (dCMP), the electron attachment primary occurs on the cytidine base. In a water environment, the base is neutralized by proton transfer from the neighboring molecules and the electron is transferred to a sugar moiety [156]. As a result, the dissociation of a glycosidic bond is the primary fragmentation channel in water [157], in contrast to the dissociation of a sugar–phosphate bond in isolated dCMP [142].
(iii) An important process is self-scavenging (autoscavenging in heterogeneous clusters) caused by inelastic scattering of an electron on one molecule, which becomes electronically excited, and subsequent DEA of the decelerated electron to another molecule [158, 159]. Energy transfer to the solvent (i) causes stabilization of TNI up to high energies and enhancement of parent ion signal. Contrary to that, self-scavenging enhances dissociation at these energies. Simply, electronic excitation in one of the cluster molecules can result in dissociation of another cluster molecule. This means that with a rising number of different molecules in the local environment, DEA can occur in a wide interval of energies of the impinging electrons in contrast to narrow resonances typical for isolated molecules. The probability of LEE-induced dissociation in real environments may be therefore much higher than estimated from cross sections known for isolated molecules.
11.2 Challenges and new directions
One advantage of clusters is that they are sufficiently small to be described theoretically. For direct comparison with experiment, however, it is important to work with well-defined and controlled target clusters. The main drawbacks of the present state-of-the-art experiments, as shown in Fig. 8, are that (i) all the techniques work with size distributions of clusters, (ii) we do not know the thermodynamic state of the clusters and (iii) often we cannot distinguish the pre- and post-interaction effects of the solvent.
Better defined clusters can be produced by improved control of expansion conditions (e.g. Fig. 8d) [160]. It may be also advantageous to use approaches toward controlled chemical dynamics such as electrostatic deflectors selecting the neutral cluster species according to their effective-dipole-moment-to-mass ratio [161]. Another approach to better define the target state is the technique of He droplets (Fig. 8b), where the clusters cool down to 0.37 K. However, at the same time here the He matrix prevents the direct interaction of LEE with embedded clusters [146].
The techniques used so far to prepare target clusters are based on expansion or pickup of the studied molecules in the form of gas or vapor. This limits the studies to thermally stable molecules, which can be evaporated or sublimed. A possible approach to study clusters of thermally sensitive molecules is by forming an aerosol of studied molecules and solvent (Fig. 8d). The aerosols can be transported into vacuum directly [162] or after drying the solvent [163]. Another possible approach may be to select neutral species from an electrospray ion source.
It is also challenging to detect neutral reaction by-products. Theoretical modeling often predicts complex rearrangement reactions in neutral dissociation products. While there have been initial attempts to characterize neutrals in electron interactions with isolated molecules in the gas phase [164], there are no such studies for clusters. The cross sections for interaction with LEE are generally small, and therefore, even the use of sensitive techniques of neutral detection such as laser-induced fluorescence, resonance-enhanced multi-photon ionization or single-photon ionization may be challenging.
Reaction of LEE in clusters may result in polymerization or isomerization, which cannot be experimentally proved in the current state-of-the-art experiments. Polymerization reactions may be traced by conceptually simple techniques such as collision-induced dissociation. Unambiguous identification of novel bonding motifs or isomerization reactions will then require the analysis of reaction products by advanced optical spectroscopy techniques.
As mentioned above, intermolecular charge transfer may play an important role after LEE interaction in complex environments, but their experimental studies are scarce. Theoretically proposed processes such as interatomic Coulombic electron capture have not been experimentally observed at all [165]. Identification of these processes will require a combination of cluster molecular beams with advanced coincidence techniques [8].
11.3 Concluding remarks
Electron collisions with free clusters represent a powerful tool for probing the environmental effects on reaction dynamics. It is worth noting that in cluster physics, the main focus has been historically on photo-induced processes. The apparent importance of LEE-induced reactions in natural and technological processes offers new directions which may be interesting to explore in the future.
Acknowledgements We acknowledge the support of the Czech Science Foundation via grants no 19-01159S and 20-11460S, and Czech Ministry of Youth, Education and Sports via grant no LTC20067.
12 Helium nanodroplets: a versatile medium for producing cold ions
Simon Albertini and Michael Gatchell, Institute for Ion Physics and Applied Physics, University of Innsbruck, Austria
12.1 Status: description of the state of the art
Droplets of helium (\(^4\)He specifically will be discussed here) have been used for decades to produce and study cold atoms, molecules and clusters—both as neutrals and ions [146, 166]. Ranging in sizes from thousands to billions of atoms or more, He droplets are able to capture essentially any gas-phase atom or molecules they interact with. Due to the superfluid nature of the droplets, they possess an exceptionally high thermal conductivity and cooling power that allows captured dopants to rapidly cool to the 0.37 K equilibrium temperature of the droplets. This allows a wide range of clusters consisting of one or more species to be grown within the cold liquid that can be extracted to the gas phase for further studies [146, 166]. In addition to producing cold clusters for experiments using mass spectrometry, the weak interactions between He atoms and the solvated species make helium nanodroplets an ideal matrix for spectroscopic studies of cold, complex molecules and ions [146, 166, 167].
The intrinsic properties of pristine helium clusters and droplets have been the focus of numerous studies over the years. These have revealed remarkable structures such as Atkins snowballs [146, 168] and quantum vortices [146, 169]. The term Atkins snowballs describes a class of cationic helium clusters for which electrostriction effects cause the surrounding atoms to bind strongly to the ionic core. The resulting clusters are essentially in a solid state, commonly referred to as snowballs, and have a density that surpasses that of solid He [168]. Similar snowballs have later been found when other ionic species are solvated in He and can often be identified from magic numbers (corresponding to solvation shells) in mass spectra [146, 170, 171]. Quantum vortices carry quantized angular momentum in quantum fluids, e.g. superfluid He, and were first identified in large (\(>300\) nm diameter) helium droplets doped with Ag atoms where the vortices facilitated the growth of nanowires [169].
A recent development in our understanding of He-nanodroplets and their potential applications was the discovery of stable, highly charged droplets [172]. The cohesive forces in liquid helium are extremely weak, only 0.6 meV per atom [146], and there was some uncertainty regarding the stability of multiple charge centers in a single droplet. Strongly ionizing helium droplets, e.g. with high currents of energetic electrons, will generally reduce the average mass-per-charge ratio of a population. Possible explanations were either fragmentation of droplets after accumulation of charges, e.g. by Coulomb explosions, or a charge buildup in the droplet.
Mass-per-charge selected cationic helium droplets (\(3.8\times 10^6\) He atoms per charge) have been impacted a second time with energetic electrons and measured using an electrostatic analyzer. Low-energy electrons (red) reduce the net charge of the precursor droplets, increasing their mass-per-charge ratio, and high energy electrons (blue) increase the net charge, decreasing the mass-per-charge ratios. Adapted from Laimer et al. [172]
Figure 9 shows results from measurements of cationic droplets with a selected size of 3.8 million He atoms per charge (produced by electron impact ionization on neutral droplets) that were impacted a second time with electrons at two different energies [172]. At 80 eV (in blue), above the 24.6 eV ionization energy of He, the net charges of the droplets are increased leading to a series of narrow peaks with mass-per-charge ratios lower than that of the size-selected precursors. The positions of the product peaks are exclusively at rational fractions of the precursors that are determined by the ratios between the precursor and product charge states. The evidence that these products are the result of charge buildup and not fragmentation comes from the red curve in Fig. 9. With electron energies below the ionization energy of He, here 22 eV, the net charge of the droplets is decreased, increasing their mass-per-charge ratios. Again, the positions of the product peaks are at rational fractions of that of the precursors. Since the droplets cannot gain mass after they are formed, these peaks must arise from multiply charged droplets that are partially neutralized [172]. In this study, net charge states of up 55+ were directly identified and their critical sizes were determined, with higher charge states being inferred indirectly.
12.2 Challenges and new directions
Even with the recent advances in our understanding of the characteristics of He droplets, our main motivation is still driven by their use in ion- and cluster physics. Helium nanodroplets are a versatile medium for producing cold ions and complexes of practically any atomic or molecular species. In light of this, we have begun developing a new generation of devices that utilize highly charged droplets of liquid He [173]. What sets this new type of setup apart from previous ones is that dopants are deposited into charged droplets instead of neutral ones. Dopants captured by neutral droplets tend to coalesce into a single cluster near the center of droplets, which are then ejected into the gas phase upon ionization of the droplets [146, 166]. In contrast, pickup into multiply charged droplets leads to multicenter growth of clusters where each charge center acts as an individual nucleation site. The simultaneous growth of many clusters in a single droplet leads to a higher number of smaller clusters with a narrower size distribution compared to clusters grown in neutral droplets [173].
One area of broad interest where these techniques are expected to play an important role is in spectroscopic studies of complex ions. For many complex molecular species, direct measurements of gas-phase spectra under optimal conditions, e.g. at low temperatures, present severe technical difficulties. A widely used alternative has long been matrix isolation spectroscopy, but even with cold rare gas matrices the spectra are often perturbed in a way that makes direct comparisons with, e.g., accurate astronomical data difficult. Another approach is messenger spectroscopy where the loss of loosely bound atomic or molecular tags from an ion complex is measured as a function of wavelength with a mass spectrometer [174]. If the tagged ion absorbs light, the excitation energy will cause the complex to fragment and the measured ion yield spectrum will thus be an approximation of its absorption spectrum.
In messenger spectroscopy, the chemical shift in the band positions induced by the messenger species can be minimized by using tags with as weak interactions as possible [175]. For this, He is ideal. However, the low binding energy of He to other species means that temperatures on the order of a few kelvin are required to form He-tagged ions. This has been achieved in, e.g., cryogenic ion traps, and the method was particularly well demonstrated when the C\(_{60}^+\) ion became the first identified carrier of diffuse interstellar bands [167, 176].
Measured yields of C\(_{60}^+\) ions solvated in different numbers of He atoms as a function of the wavelength of the probing laser [167, 177]. Absorption of photons by the fullerene ion triggers the loss of He, depleting the yield of clusters that are in resonance. Shifts in the band position are visible between different numbers of solvating He atoms
Helium-tagged ions are readily produced from doped He droplets, and this method was successfully used to confirm the spectrum of C\(_{60}^+\) [167, 177]. With He droplets, it is possible to form ions solvated in essentially any number of He atoms, which allows the action spectrum of ions to be studied as a function of the degree of solvation (see Fig. 10) more efficiently than in traps. A benefit of this is that the gas-phase spectrum can be more accurately estimated from the action spectra and it also provides information on the structures of solvation layers, which in turn can be used to gain information of the structures of the ions themselves [178]. Here, a close cooperation between experimentalists and theorists is important for the interpretation of results and to identify details on the solvation structures. The theoretical studies of ions solvated in He present a number of technical challenges due to the low binding energies involved as well as the low mass of the He atoms. Because of this, quantum descriptions of nuclear motion are generally required to properly sample the dynamics of He solvation layers [170, 179]. The advancement of experimental methods using highly charged droplets has started to show improvements relevant to these types of studies as well, in particular with regard to controlling the number of tagged species formed and in forming more challenging complexes such as tagged anions.
12.3 Concluding remarks
Helium droplets have proven to be a very powerful tool for producing cold ions and clusters. The development of new techniques using charged droplets is enabling a new generation experiments, the first of which having recently been commissioned. Other applications being investigated are the use of charged He droplets in producing well-defined beams of nanoparticles for technical applications such as surface deposition.
Acknowledgements We thank Paul Scheier for his invaluable support and input. This work was supported by the EU commission, EFRE K-Regio FAENOMENAL EFRE 2016-4, the Austrian Science Fund FWF (P31149 and I4130) and the Swedish Research Council (Contract No. 2016-06625).
13 Electrostatic ion-beam storage rings
Henrik Cederquist and Henning T. Schmidt, Department of Physics, Stockholm University, Sweden
13.1 Status: description of the state of the art
Worldwide, about ten electrostatic ion-beam storage rings are in operation [180]. At DESIREE, the Double ElectroStatic Ion Ring ExpEriment, at Stockholm university, it is possible to store two keV ion beams—one with negatively and one with positively charged ions—on 8.7 m circumference trajectories. These two beams may be merged for studies of charge-, mass- and energy-transfer processes down to sub-eV collision energies [181, 182]. The CSR, the Cryogenic Storage Ring, at the Max Planck Institute in Heidelberg is larger, has a circumference of 35 m, and is equipped with a free-electron target, a neutral-beam target and in the future it will be equipped with a gas-jet target for kinematically complete studies of ion–neutral reactions at keV–MeV energies [183]. By using the merged-beams technique, reactions between the stored ions and free electrons or neutral species can be studied down to micro- and millielectronvolts in CSR. RICE, RIken Cryogenic Electrostatic Ring, at the RIKEN laboratory in Japan [184], has, like the CSR, a beam target for merging the stored ion beam with neutral atoms or molecules. RICE is smaller with a circumference of 2.9 m. DESIREE, CSR and RICE are operated at cryogenic temperatures between about 5 K (RICE) and 13 K (DESIREE). Thus, most stored ions relax spontaneously toward thermal equilibrium at these low temperatures such that rotational, vibrational, and electronic excitations are strongly limited after some time. Ideally, and in practice for favorable cases, molecular-ion beams with all their molecules in a single rovibrational quantum state may thus be formed. The cryogenic cooling of DESIREE, CSR and RICE also leads to very low residual gas densities (10\(^2\)–10\(^4\) H\(_2\) molecules per cm\(^3\)) and thus possibilities for very long ion-beam storage lifetimes. The very low temperatures and pressures are similar to those in interstellar space and action spectroscopy on internally cold ions is a common highly attractive option at these three storage rings. Furthermore, measurements of reaction rates at low temperatures can be directly related to astronomical observations of cold interstellar regions.
The era of electrostatic ion-beam storage rings began with the construction and commissioning of ELISA at Aarhus University in the 1990s [185]. The development of electrostatic—rather than magnetic—devices was to a large extent motivated by the possibility to store beams of different types of heavy ions. This is a common advantage of all purely electrostatic ion-beam storage rings, and also of the conceptually related ion-beam traps [186, 187] (see Sect. 15). For all the electrostatic storage devices, the settings on beam deflectors and lenses for ion-beam storage only depend on the kinetic energy per charge of the ions and not on the mass. ELISA paved the way for other electrostatic ion-beam storage devices through a range of highly successful studies of properties of isolated biomolecules, biomolecules in solution, clusters, and other molecules and in particular fullerenes such as C\(_{60}\). In these studies, the action spectroscopy method, in which the photo-absorption spectrum is recorded by measuring the probability for photo-induced fragmentation or electron detachment as a function of the wavelength of the photon, was often used [188] (see Sect. 14). ELISA has a circumference of 7.1 m and is normally operated at room temperature, as is the smaller electrostatic ion-beam ring, SAPHIRA, which was commissioned at Aarhus University in 2015 [189]. SAPHIRA is used for photo-fragmentation studies by the action spectroscopy method and it has a square-shaped structure with a side length of 1.0 m. The World’s second and third electrostatic ion-beam storage rings were, however, built much earlier in Japan at KEK, Tsukuba [190] and at the Tokyo Metropolitan University, TMU [191].
The TMU ring is similar to ELISA and mainly used for photo-fragmentation and photo-detachment studies. A prominent example is the direct observation of recurrent fluorescence [192], which is a very fast molecular relaxation process driven by couplings between vibrationally hot ions in the electronic ground state and electronically excited states with less vibrational excitations. This type of process has also been studied at Mini-ring, a 75 cm circumference ion-beam storage ring, at Université Lyon 1 in Lyon [193]. The Mini-ring has conical electrostatic ion-beam mirrors inspired by the ion-beam trap, CONEtrap in Stockholm [187], and its small size makes it easy to handle and operate at a reasonably low cost. At TMU in Tokyo, the \(\mu \)-ring with an 88 cm circumference was recently commissioned and its usefulness for measurements of absolute charge exchange cross sections was demonstrated [194]. The smaller rings, Mini- and \(\mu \)-ring, are well suited for studies of decay processes on \(\upmu \)s and ms timescales whereas the larger rings are used for measurements of slower or much slower decay processes up to minutes or hours.
13.2 Challenges and new directions
Common challenges for the electrostatic ion-beam storage rings are the preparation and loading of positively and negatively charged ions for in-ring experiments. Here, the ongoing development aims for a broad selection of atomic, molecular, cluster, fullerene, and biomolecular ion-beams, as well as for methods to handle micro-solvated ions and ions in He-nanodroplets. A range of plasma-, sputter-, electron-cyclotron-resonance- (ECR), cluster-, electrospray- and nanodroplet sources are needed to fulfill these goals. In addition, ion-mass selection devices with sufficient resolution to separate ions, in particular heavy ions, of nearby masses should be combined with accumulation and pre-cooling traps in order to form ion bunches of sufficient intensities and suitable duration for cyclic injection in the storage rings. The latter is to be able to inject sufficiently intense ion bunches—ideally with all ions having the same mass, charge, internal energy, and conformation—and to store them long enough for further manipulation (e.g. with lasers) for experiments. The preparation of beams of small molecular ions with nearly all of them in a single ro-vibrational quantum state has been demonstrated for OH\(^-\) at both CSR and DESIREE [195, 196]. Diatomic molecules, such as OH\(^-\), have only one possible conformation, while larger molecules may have many different forms. Ways to select specific molecular isomers for injection and in-ring storage have to be developed.
For the three cryogenic ion-beam storage rings [181,182,183,184], the key aim is to be able to prepare ions—in particular molecular ions—in a single well-defined quantum state. Having ions in well-defined states is a clear advantage as this strongly limits the number of calculations needed for comparisons with results of newly developed quantum-state-specific models. A very broad distribution of initial states in the experiment could conceal distinct state-sensitive phenomena through the need to average over many initial quantum states when evaluating the model. The importance of experiments on internally cold ions was recently demonstrated through measurements of dissociative-recombination rates as functions of the rotational state in HeH\(^+\) + e\(^-\) reactions (all HeH\(^+\) ions in the vibrational ground state v=0) at CSR [197]. It was then found that the rate is a strong function of the rotational excitation, which is in stark contrast to what has been assumed in earlier astrophysical models. At DESIREE, the branching fraction for the population of the Li (3s) state—important for gauging the Li abundance in stars—was measured in Li\(^+\) + D\(^-\) mutual neutralization reactions [198] at meV energies. In the next step, reactions between small internally cold molecular anions and atomic cations present in the interstellar medium will be performed with improved methods to control the overlap between the merged beams in DESIREE. Additional trends in the field are studies of stabilities of astrophysical reaction products. It is of particular interest to study knockout fragments of polycyclic aromatic hydrocarbon (PAH) molecules and fullerenes, as these fragments of interstellar molecules are highly reactive. Likewise, stabilities of molecular fusion products, in particular fusions between fullerenes or between PAH molecules, will also be studied for comparisons with astronomical observations using the action spectroscopy method.
Further challenges include studies of inherent properties of multiply charged anions, where stability issues are of large interest for, for example, C\(_{60}^{2-}\). Inherent stabilities of metal clusters and reactions with biomolecular ions in vacuum will also be important fields of study. Recent experiments unexpectedly revealed that slow electron emission, rather than fragmentation, dominates the decay of Ag\(_{2}^{-}\) clusters of certain internal excitations [199]. Molecules and atoms in charged nanodroplets of helium will be used for highly sensitive action spectroscopy measurements using the so-called tagging technique.
13.3 Concluding remarks
A key feature of electrostatic ion-beam storage rings and traps is that ions of any mass can be conveniently stored. Further key features of cryogenic, electrostatic ion-beam rings are the possibilities to produce beams of (light or heavy) ions in narrow ranges of, or in single, quantum states. There are three cryogenic storage rings in operation where it is possible to merge stored ion beams with (i) stored beams of ions in the opposite charge state (DESIREE); (ii) free electrons (CSR); (iii) beams of neutral atoms or molecules (RICE and CSR); and (iv) laser beams (RICE, CSR and DESIREE). Major challenges involve beam preparation with isomer selection and in-ring separations of molecular and cluster reaction products with high mass resolution.
Acknowledgements We want to thank all colleagues of the electrostatic ion-storage ring community for many interesting and pioneering experiments of which only a small fraction are presented in this brief report. DESIREE is a Swedish National Infrastructure (Swedish Research Council contract No. 2017-00621). The authors further acknowledge individual Swedish Research Council grants (2019-04379 and 2018-04092) and the support from the Knut and Alice Wallenberg Foundation for the project “Probing charge- and mass–transfer reactions on the atomic level” (2018.0028).
14 Studies of photo-induced dynamics in bio-chromophores using electrostatic ion-storage rings
Elisabeth Gruber and Lars H. Andersen, Department of Physics and Astronomy, Aarhus University, Denmark
14.1 Status: description of the state of the art
Many important processes in nature and in man-made devices are light-driven and proceed with remarkably high efficiency upon molecular photo-excitation. In conventional spectroscopy, the absorption of light in a sample of molecules is normally determined from the intensity of incident and transmitted light according to the Lambert–Beer law. To study the photo-physics of (bio)molecules under vacuum conditions, free from perturbation by nearby molecules, or in a well-defined and controllable environment with known perturbations, gas-phase action spectroscopy has been established as the first-choice method (see also Sects. 18, 19). Here, a detectable “action” induced by photo-absorption, i.e. dissociation, electron detachment or fluorescence, is used to register absorption events with high efficiency, hence determining absorption spectra, and provide benchmark data for quantum-chemical calculations.
In the last decades, several devices have been developed for action spectroscopy, including electrostatic ion-storage devices, accelerator mass spectrometers, reflectron time-of-flight mass spectrometers, ion traps and photoelectron spectrometers. Here, we focus on electrostatic ion storage rings [200]. The first electrostatic storage-ring ELISA was developed at Aarhus University in 1997 [185] and was initially used for lifetime studies, including research on thermalization of hot metal-cluster ions [201]. Later, other electrostatic rings were constructed to study processes induced by interactions with photons, ions or electrons [180]. The general advantage of these electrostatic storage devices is that they allow some relaxation of vibrationally excited states, which is particularly relevant when a hot ion source is used, as well as an efficient detection of reaction products. Moreover, they are, in principle, free from mass restrictions and therefore ideal tools for studies on dilute targets of heavy molecular systems.
By combining an electrospray-ionization source with an ion trap prior to ion injection into the ELISA storage ring, the electronic absorption spectra of closed-shell biomolecular ions were measured in groundbreaking experiments [188, 202]. The yield of neutral products following either photo-detachment or photo-fragmentation was taken to represent the gas-phase absorption spectrum.
Studies on molecular chromophores, the photo-active part of photo-active proteins, have attracted immense attention not only because of their crucial role for the functioning of living organisms and applications, but also because they are excellent systems for studying elementary processes, such as photo-isomerization, light-driven energy transfer and charge separation. These processes proceed typically on a femto-to-picosecond timescale, and hence ultrafast, optical techniques are required to follow such reactions together with detection schemes to reveal the status of the molecular system in real time.
14.2 Challenges and new directions
The development of laser pulses with short time duration has opened a new era of molecular research, primarily for probing the nuclear dynamics in the molecules. Zewail was awarded the Nobel prize for his contributions in this field [7]. This type of work has later been followed in many other groups, primarily working with negative ions, where photoelectrons conveniently may be detected [203,204,205,206,207].
The combination of ultrafast pump–probe schemes with an electrostatic ion-storage ring technique gives a new approach to resolve ultrafast photo-initiated dynamics of molecular ions in vacuum (see also contributions on other gas-phase techniques in Sects. 2 and 3). It was recently successfully engineered and implemented at the electrostatic ion-storage ring SAPHIRA at Aarhus University, for details see Ref. [189].
At SAPHIRA (Fig. 11), a tunable femtosecond laser system is used for fs-pump–probe spectroscopy on stored molecular ions. The method combines the pump–probe time delay with the action-response time registered in the ring, and is hence based on time in two dimensions. In short, we register when a given molecular system is capable of absorbing a (second) probe photon upon initial pump excitation, by registering the fast/prompt action in the ring, associated with the extra energy gain provided by the absorption of two photons (instead of one). The prompt molecular photo-response is typically on the sub \(\upmu \)s–ms timescale and hence detected by a detector located immediately after the interaction region. The method is highly advantageous for mapping out the excited-state decay as well as the ground-state recovery, and is applicable for negative as well as positive ions. First results with this new technique have demonstrated the superiority of using fs-laser pulses [208] and the applicability to study dynamical processes of bio-chromophores [209, 210].
The SAPHIRA ion-storage ring, equipped with an ESI source and an ion trap that optionally may be cooled with liquid nitrogen. In the ring, stored ions may be studied by time-resolved action spectroscopy upon excitation by tunable fs laser pulses. Figure adapted from [210]
Excited-state decay (upper figure) and ground-state recovery (lower figure) of GFP chromophore anions, pumped at 480 nm, and probed at 800 nm (for the excited state lifetime) or 480 nm (for the ground state recovery). The data were recorded at 300 K (room temperature) and at 100 K by pre-cooling them in an ion trap. The cooled ions show a much longer decay due to trapping behind a potential energy barrier in the first excited state. Data are taken from [209]
Measurements have been performed with molecules at room temperature or pre-cooled to 100 K in the present ion trap. A significant temperature dependence on the excited state lifetime reveals the role of energy barriers in the electronically excited states [209, 210]. It was shown that the isolated deprotonated GFP chromophore is trapped for 1.2 ns in the first excited state when cooled to 100 K, establishing conditions for fluorescence in the gas phase (see Fig. 12). Direct detection of fluorescence from the gas-phase chromophore is, however, still lacking. Our next step is to pre-cool the ions in a cryogenic multi-pole trap (liquid helium temperature) before injection into the storage ring to further investigate rate-limiting excited-state energy barriers and for improved spectroscopy (less in-homogeneous broadening). Other cooling schemes are discussed in Sects. 11 and 12.
Another approach to obtain cold molecular ions is to use cryogenically cooled storage rings. Recently, the facility at DESIREE at Stockholm University [182], at CSR at the Max-Planck Institute for Nuclear Physics in Heidelberg [183], and at RICE at RIKEN, Japan [184] have become operational (see also Sects. 13, 15). Here, the whole ring is cooled down to 10 K, which, in addition to cold ions, ensures very high vacuum conditions and long storage lifetimes (up to an hour) which also provides rotational cooling. Another exciting method is to embed chromophores into superfluid helium nanodroplets [211, 212]. With an equilibrium temperature of \(\sim \)0.4 K, superfluid helium droplets can serve as gentle matrices to provide an isothermal environment at cryogenic temperature. The low temperature reduces the number of populated quantum states and freezes out structural fluctuations. Further, liquid helium is optical transparent from the deep UV to the far IR.
Another challenge is to move from single isolated molecules to larger molecular complexes to study the electronic coupling between multiple chromophores, energy and charge transfer processes and the role of interactions with a host medium. Such experimental data provide benchmark values for quantum calculations, making theoretical progress possible and hopefully reliable for large-scale applications.
14.3 Concluding remarks
Action spectroscopy is a very powerful method to explore spectroscopy and dynamics of gas-phase molecules. We have demonstrated how pump–probe schemes may be combined with detection of time-resolved action in ion-storage rings to reveal internal dynamics of molecules. We have also shown that temperature matters for the dynamics, and we foresee that with new cooling schemes, exciting new photo-physics will be revealed at the many ion-storage rings.
15 Electrostatic ion-beam traps
Oded Heber, Department of Particle Physics and Astrophysics, Weizmann Institute of Science, Israel
Yoni Toker, Department of Physics and Institute for Nanotechnology and Advanced Materials, Bar-Ilan University, Israel
15.1 Status: description of the state of the art
Electrostatic ion-beam traps (EIBTs) have been used for studying the gas-phase internal dynamics of molecules for many years [200]. Many EIBTs exist worldwide for various usages including, for example, high-resolution charge detection mass spectroscopy of large molecules [213] and isotope separation [214]. EIBTs have an advantage as a tool for studying gas-phase internal dynamics of molecules due to their compact size which can fit into a university-size laboratory. EIBTs are efficient tools for studying photon absorption bands and photon emission of isolated ions as well as controlling the molecular environmental temperature. Also, as will be described below, they are efficient tools for studying collisions including intra-beam collision, collisions with electrons, gas targets and other beams.
The dynamics of molecules is strongly dependent on the internal energy distribution (IED) of the molecules. Therefore, control over the ions’ IED is important. Generally there are two ways to control the IED: (1) Conditioning of the molecules before injection into the EIBT, e.g., by buffer-gas cooling; (2) Manipulation of the ions’ IED inside the trap. For the former option care must be taken that following conditioning and prior to injection the ions’ IED does not change, for example, due to collisional heating during acceleration. For the latter case, one process which occurs spontaneously is radiative cooling which eventually results in the equilibration of the ions with the EIBT’s temperature. For this goal it is desirable to have the ability to control the EIBT’s temperature and to be able to cool it down to cryogenic temperatures. Indeed, recent years have seen the advent of cryogenic electrostatic storage rings and EIBTs, with EIBTs being simpler to cool due to their compact size.
It is also desirable to be able to cool the kinetic degrees of freedom of the trapped ions. One promising avenue for achieving cooling is through autoresonance, where ions within the EIBT are accelerated by chirping a small oscillation frequency, which causes an enhancement of the coldest population by ion–ion interactions. Recently, the ability to cool the kinetic degrees of freedom using autoresonance was demonstrated [215]. It remains to be seen whether the external kinetic temperature and IED are coupled, and if autoresonance can also be used to cool the IED.
15.2 Challenges and new directions
One of the challenges in studying the internal dynamics of molecules is to characterize all the different reaction products following an excitation or collision and do so as a function of the ions internal energy distribution and as a function of time. The EIBT can potentially meet this challenge with a full reaction microscope: with simultaneous detection of photons, electrons, neutral and charged fragments. Detection of each of these products has been implemented separately in EIBTs. However, the full combination of all of them simultaneously is still a challenge. For example, in a few groups a velocity map imaging (VMI) electron spectrometer has been combined with an EIBT, such that upon photo-excitation one can detect the emitted electrons and deduce their kinetic energy, and simultaneously also measure the neutral products [216]. Figure 13 shows a VMI image of electrons from OH\(^-\), measured in coincidence with the neutral OH after laser interaction for two different trapping time regimes [217]. The image clearly shows the rotational cooling of OH\(^-\).
Following excitation by a short laser pulse or by collisions, ions often dissociate (by emitting an electron or fragmenting) on very long timescales ranging up to milliseconds. This fascinating phenomena has been the subject of a great deal of research in its own right, and is important to account for in deducing the correct shape of an absorption band due to kinetic shifts. Statistical dissociation has been used as a tool for studying statistical properties of ions, for example, for radiative cooling measurements [218], for calorimetry [219]. In a recent work, it was shown that one can describe simultaneously the isomerization, the delayed electron emission and internal cooling for C\(_{10}^-\) molecules [220]. Even though statistical dissociation has been known for over 30 years, the proper methodology for modeling it is still an ongoing research topic and currently depends on the simultaneous deduction of many molecular parameters such as the ions activation energy, IED, polarizability, etc. We expect that the study of statistical dissociation of ions photoexcited from their vibrational ground state will provide a stringent test of theory and a significant step forward. Moreover, we expect this goal to be achieved in the near future thanks to cryogenically cooled electrostatic storage devices.
As EIBTs, are purely electrostatic devices, they can trap any molecular ion (positive, negative and multiply charged) using the same electrode settings, as long as the kinetic energy to charge ratio is the same. This allows to trap many different molecules simultaneously, and to study the interactions between them. For studying collision dynamics, it is essential to control the relative velocities of the different ions. Recently, an EIBT called hybrid EIBT (HEIBT) was designed with this goal in mind [221]. The device, shown in Fig. 14, is composed of two EIBTs: The inner EIBT traps ions with lower kinetic energy and the outer for higher kinetic energy ions. The relative energy can be tuned to match the velocities. Moreover the HEIBT can trap simultaneously two different species with the same charge or with opposite charges. It is expected that such a device will be a new compact tool for time dependent studies of molecular ion reactions at very low collision energies.
One complication that arises in studying molecules composed of more than three atoms is that they may have different stable conformations, different isomers, which may possess very different dynamical properties. For example, studies of the retinal protonated Schiff base (RPSB), have shown that even when sprayed from an all-trans solution the isomer distribution in the gas-phase consists of many isomers, which have different photon-absorption bands [222]. Notably, different isomers have the same charge over mass ratio and cannot be separated with conventional mass spectrometric techniques. It is therefore highly desirable to have an isomer selection stage prior to injection into the EIBT. The most promising approach for achieving this goal is through ion mobility spectroscopy (IMS). IMS enables separation of isomers according to the differences in their collisional cross section with a buffer gas. Conventional drift tube IMS relies on long drift tubes. However, novel developments such as trapped ion mobility spectroscopy (TIMS) and structures for lossless ion manipulation (SLIM) offer compact methods for achieving high-resolution IMS separation which potentially can be mounted on ion source platforms and combined with EIBTs. We expect in the coming years that the combination of EIBTs with IMS will permit isomer dependent studies of the dynamics in molecular systems.
15.3 Concluding remarks
EIBTs are a versatile tool for studying time dependent dynamics of molecules in the gas phase. New techniques such as cryogenically cooled EIBTs, combination of EIBTs with VMI photoelectron spectrometers, use of sophisticated ion sources which include IMS separation, sophisticated cooling techniques such as autoresonance cooling and the hybrid trap for ion–ion collisions promise to open new exciting new prospects and possibilities.
Acknowledgements We would like to thank Michael Rappaport for his help in writing this paper.
16 Cooling dynamics of molecules and clusters
Klavs Hansen, Center for Joint Quantum Studies, Tianjin University, Tianjin, P.R.China
16.1 Status: description of the state of the art
Molecules and clusters containing sufficient randomized (thermal) excitation energy can potentially decay through a number of channels. These can often be modeled in terms of an activation energy and a frequency factor which multiplies what can be imagined as an effective Boltzmann factor.
The most frequently encountered decays are the fragmentation processes that are known as unimolecular reactions. These include loss of a single atom or larger moieties. The most commonly used description is RRKM, which was suggested as a model for traversal of a saddle point in the potential energy curve in a one dimensional trajectory. This has been elaborated with the addition of angular momentum to the channel in the so-called phase space theory [223].
A third theory is based on detailed balance, originally derived to describe thermal decay in nuclei. It is particularly useful for clusters as these very rarely have any saddle point but absorb and emits monomers without any reverse process activation barrier. Saddle point transition states seem also to be much less frequent occurrences for molecules than a naive consideration of dynamics on Born–Oppenheimer surfaces would suggest, as judged by measured kinetic energy release distributions.
The kinetic energy resolved detailed balance rate constant for evaporation of a single atom is [224]
(ignoring angular momentum quantization and constraints imposed by its conservation). g is the atomic electronic degeneracy, m the reduced mass of the channel, \(\sigma \) the inverse reaction capture cross section, \(\varepsilon \) the kinetic energy release, the \(\rho \)’s the level densities of the species indicated by the subscripts (p for product, r for reactant), and \(E_a\) the evaporative activation energy.
Another potential channel is thermal electron emission, the molecular analogue of macroscopic thermionic emission. In neutral systems it tends to be present in clusters of highly refractory elements, because the activation energy for this channel is the ionization energy versus the competing unimolecular dissociation energy, and only for refractory elements will the difference in these two values be in favor of electron emission. The rate constant for this process is also derived by application of detailed balance, and Eq. (1) only needs to be modified for the mass, the level densities and the degeneracy g [225]. As the process depends on thermally excited electronic degrees of freedom, it may for consistency be relevant to include these degrees of freedom into the level densities.
The third channel, thermal radiation, can also be derived with detailed balance. It differs from the two other channels both by having a lower activation energy, which is simply the emitted photon energy, and by a much smaller frequency factor. The latter is related to the much smaller density of states of the emitted photons compared to that of free atoms or electrons. Combined, these two facts make the channel the dominant one at low energies, and it is therefore of special interest for experiments on long timescales, in particular but not restricted to storage-ring experiments [182, 183, 185, 192, 226]. In addition, the quantum nature of the photon modifies its emission rate constant with the contribution from stimulated emission. The resulting photon emission rate constant is [225]
Figure 15 illustrates the typical behavior of the observable emission rate constants for C\(_4^-\).
Calculated emission rate constants for C\(_4^-\) for the processes indicated in the frame, published in [226]. The rate constant for fragmentation has a form similar to that of electron emission. It is only appreciable at much higher energy due to its high activation energy and does not compete with electron emission for the anion. The slow variation of both photon rates with energy is a common feature for these channels
This equation describes both the radiation from vibrational transitions and the radiation that originates in thermally excited electronic states, a phenomenon that has received some attention recently. The high oscillator strength of electronic transitions can more than compensate for the relatively low population of these states, and the time constants of these processes, for historical reasons called recurrent fluorescence, can have time constants on the order of \(\upmu \)s, versus the typically ms values for vibrational transitions. The energy of the excited state plays the role of activation energy for the process, and the emission rate constants can therefore vary dramatically between molecules of similar kind but with an even very small difference in chemical composition.
Decays of molecular beams come with a special feature when internal energy distributions have a width that exceeds the relatively small value \(\delta E\) determined by
where \(\omega \) is the frequency factor of the dominant decay, t is the time after production of the beam in the source, and E is the energy of the decaying molecules. The right hand side is around 0.05 for the microsecond timescales of single pass devices and smaller for the long times realized in ion traps and storage rings [182,183,184,185, 189]. The range of rate constants across such distributions produces a decay rate, R, which varies with time as a power law [201]:

where C is the heat capacity of the decaying system. The power of \(-1\) on time will acquire corrections from a finite heat capacity and the slow variation of the width of the distribution, and the experimentally observed power is often slightly below \(-1\).
The power law decay can be derived independently of the precise dependence of the rate constants on the excitation energy. The only requirement is that it varies rapidly with energy. This is the case for both thermionic emission and the usual unimolecular decay rate constants, and both types of decays have a propensity to show power law decay rates. Photon emission rate constants, in contrast, usually have a much slower energy dependence and can in general not be expected to follow this simple behavior.
The power law decay also provides the expressions for the amount of the metastable decay that is often seen in time-of-flight mass spectrometers as a delayed decay between mass selection and detection. The relative amount of this component of the beam is simply the integrated and normalized decay rate. It contains information about the relative dissociation energies of the decaying cluster and it precursor, in addition to their heat capacities. Some results on this were derived by Klots [227], remarkably without the knowledge of the power law decay which simplifies derivations.
The power law decay has likewise been extremely useful as a tool to measure the presence and magnitude of dark channels. A dark (non-observed) channels can influence the power law decay in several different way, depending on its nature. The first observation of this kind was the thermionic emission rate of C\(_{60}\) which showed the expected power law nature, but with a power around 0.65 [228]. The explanation was found in the loss of C\(_2\) from the neutral molecule. The observed power provided a value for the activation energy of this channel, a value which is significant higher than the number commonly accepted at the time, but which is close to the currently accepted value.
Another channel for which the power law has provided a very powerful diagnostic tool is the thermal photon emission [229, 230]. Radiative cooling will modify the power law decay by suppressing it at long times with an exponential factor. The precise form of the factor depends on the magnitude of the emitted photons. In the small photon energy limit the emission will cause a practically continuous energy loss. The time constant for the exponential suppression in this limit involves several quantities, such as the emitted power, the molecular heat capacity, and the dissociation energy. It should be emphasized that the measured time constants for these cases are not the photon emission time constants. In the other limit, of large photon energies, emission of a single high-energy photon will quench any further unimolecular decay, and in this limit is the measured quenching time constant equal to the photon emission time constant. The quenched power law curves that result from these two limits are slightly different, but similar enough to prevent an experimental identification of the type of photon emission from the shape of the quenched curves alone.
Although the two types of quenching have very similar temporal behavior, the origins of the exponential suppression are different. Emission of large energy photons will deplete the decaying part of the energy distribution and is therefore similar to a normal exponential decay, e.g., a radioactive decay of a nucleus. The small photon energy cooling, in contrast, suppresses the decay by introducing an exponential decay of the value of the time constant.
16.2 Challenges and new directions
The phenomenon of thermal high-energy photon emission results from a finite thermal population of the emitting state, without any major restrictions on its presence. The only important requirement is that radiationless transitions after photo-excitation occur. This ensures that the inverse process can happen by time reversal. Radiationless transitions are indeed a very common phenomenon and the thermal emission of visible and near-IR photons is therefore much more common for highly excited species than apparent from the literature. At present the direct detection of photons emitted in such processes have only been accomplished for C\(_4^-\) and C\(_6^-\) [192]. In both cases an optical filter was used to select the emitted photon wavelength to correspond to the absorbing value. This background elimination greatly supported the identification of the measured photons, but is an unnecessary limitation once the assignment of the origin of the emitted photon has been established. Future measurements of emission spectra in the visible and near-infrared sectors will provide much more detailed information about the emitting molecules, as will time resolved measurements. This development will take place at traps and storage rings [185, 226, 231]. Although photon detection efficiencies will remain below those of massive particles for some time, the technique promises ultimately nondestructive information on a par with or surpassing the one obtained by measurements of unimolecular fragmentation.
In parallel with such experimental activity, developments of unimolecular reaction rate theories will be both necessary and fruitful. Although the subject is more than a century old, it still harbors open questions. Some of these are posed particularly acutely for decays of clusters. One question is the role of the traditional saddle point transition state which seems to be absent in clusters and certainly is so in the bulk limit for virtually all materials. (For the elements, only zinc is known to be an exception to this rule.) Another question is the role of angular momentum in the description of the particles. As a conserved quantity, angular momentum must obviously enter a description of thermal reactions in vacuum. Nevertheless, it is well known that vibrational motion can carry angular momentum, both on general grounds [232] and as described, e.g., for helium droplets [233]. Although rotational motion in the transition state has attracted attention in the past, this aspect of angular momentum in the description of reactivity is fairly unexplored.
Molecular beam studies share a good vacuum with the interstellar and star-forming regions of space, and the dynamics studied in the laboratory provides important information for the quantitative description of the interstellar molecular dynamics [234]. Molecules formed by collisions in space are guaranteed to be born with enough excess energy to fragment, and also to dissipate energy through emission of photons and potentially also electrons or atoms in channels that differ from that of the formation process. As a competing channel to fragmentation, radiative cooling therefore plays an essential role for the survival rate of the collision complexes. The possibility to form surviving larger molecules in a second collision step will then obviously also benefit from radiative stabilization. The formation of large molecules, including those of biological nature, will thus be characterized by survival of the fittest on the fundamental molecular level.
16.3 Concluding remarks
The development of ion traps and storage rings, in particular of the cryogenic variety, has greatly extended the time range for which it is possible to observe the decay dynamics of mass selected gas-phase molecules and clusters. In such studies, the non-exponential decays have appeared as an important diagnostic tool. Combined with the emerging field of spectroscopy of thermally emitted photons, it promises to open new venues for studies of highly excited molecules and clusters.
17 Photo-fragment and photo-detachment spectroscopy in cryogenically cooled ion traps
Jennifer A. Noble and Christophe Jouvet, PIIM Laboratory, CNRS/Aix-Marseille Université, France
17.1 Status: description of the state of the art
The general principle of photo-fragment or photo-detachment spectroscopy is as follows: ions generated in different charge states (radical cation, protonated, deprotonated, etc.) and different structures (isomeric or tautomeric) using a source such as a discharge or an electrospray ionization (ESI) source are guided into a cryogenically cooled ion trap where they are cooled to temperatures of a few Kelvin by collisions with a buffer gas. Laser excitation induces fragmentation and/or photodissociation, and the products are extracted into a mass spectrometer for analysis. The photo-fragment or photo-detachment process is monitored as a function of the laser wavelength to generate the spectrum.
Major advances in the experimental technique have been made over the past 15 years, beginning with the cooling of ions via cryogenic technology [235]. Compared to room temperature, at a few tens of Kelvin, molecules present restricted isomers and discrete vibrational/rotational levels can be distinguished in their spectra. Contemporary cryogenic ion spectroscopic results are analogous to those achieved from around 40 years ago onwards for neutrals in supersonic jets, as is evident from the examples provided in multiple sections of this roadmap.
Using a cold ion trap, one can follow the molecular relaxation dynamics over more than 12 orders of magnitude: The ultrafast fs excited state lifetime prior to charge transfer (CT) is obtained from line broadening; the ps, ns and \(\upmu \)s evolutions of CT, internal conversion (IC) and intersystem crossing (ISC) by pump probe methods using ps and ns lasers; and the longer ms to s dynamics of ISC and ground state (S0)/secondary fragmentation by delayed extraction of the fragment(s) from the trap. The schematic is inspired by the complicated time evolution of the dynamics of protonated cytosine, adapted from Ref. [242]
Advances in mass resolution—before and after trapping—have allowed more precise selection or measurement of individual masses. Ion mobility techniques (see Sect. 19) allow the selection of a single isomer or tautomer of a given mass, and thus the study, for example, of its specific dynamics [236]. Most recently, the coupling of a cold trap with orbitrap technology has allowed the development of a combination of high spectroscopic resolution with a high resolution in mass [237].
Throughout the community, a multitude of photo-fragment and photo-detachment spectroscopies are applied to cold, trapped ions, from single laser UV–visible photo-fragmentation to pump–probe depletion/gain spectroscopies. The coupling of ESI with advanced light sources for the study of biomolecules over a wide photon energy domain is reviewed in Sect. 5. Of particular note has been the development of hole-burning spectroscopies, which allow the differentiation of bands belonging to different species by comparing the spectral response of different channels to bleaching of a selected transition. The latest variant to be adopted was UV/UV hole-burning spectroscopy, due to the complications arising from the pump and probe pulses both generating the same product [238]. In this section we concentrate on action spectroscopy methods, but the nondestructive technique of fluorescence spectroscopy can also provide complementary information on excited state dynamics for certain (fluorescent!) ions, as discussed in the following section (Sect. 18).
In the case of negative ions, the cooling of the parent coupled with the development of the high-resolution photoelectron spectrometer has shed new light on the photo-detachment process as well as allowing the characterization of deprotonated ions and their photo-detachments products—i.e. dehydrogenated radicals—which are often the intermediates in reactions [239]. Following photo-detachment of the deprotonated ion, the resulting dehydrogenated radical is not necessarily stable. If the photo-detachment is performed after the extraction of the deprotonated ion from the cold trap, the detection of the fast neutrals formed upon fragmentation of the dehydrogenated radical allows measurement of the kinetic energy released by the fragmentation process [240].
The generation of size-selected clusters or larger aggregates can be achieved by the addition of a second cold trap between the ion source and the photo-fragmentation trap. The systematic study of size-selected clusters consisting of an ion surrounded by increasing numbers of solvent molecules allows the investigation of the influence of the solvent molecule on the dynamics of the system [241]. This approach can, to a first order, be considered analogous to a study of the first solvation shell of the ion in a liquid solvent, allowing parallels to be drawn between gas-phase and solution-phase experiments.
One of the most remarkable outcomes of the work produced by the community in recent years is the revelation that the temporal range over which dynamics in molecular ions and their clusters can be experimentally observed extends more than 15 orders of magnitude. Indeed, it has been observed that the dynamics of photo-fragmentation extend over this entire temporal range—even for a molecule of a well-defined energy—with excited state relaxation occurring on the femtosecond timescale, ground state fragmentation of the parent ions in the nanosecond to millisecond range, and secondary fragmentation occurring over seconds, as illustrated in Fig. 16.
17.2 Challenges and new directions
The wealth of spectroscopic studies performed to date using cryogenic ion traps have revealed and characterized photon-driven processes in molecular systems of varying charge states. The interpretation of these data represents a major challenge for ab initio calculation methods. Consider, for example, the experimental evidence that different, highly selective, fragmentation channels can be accessed upon the excitation of extremely closely-spaced excited states, with selective fragmentation being observed not only between two electronic states, but even between vibrational levels within the same electronic excited state differing in energy by less than 1 %. The assumption made in the statistical fragmentation argument is that once in the ground state, the whole potential surface can be explored by the molecule. In this case, the selective fragmentation cannot be attributed to overcoming certain barriers to fragmentation routes. Can the on-the-fly method be applied to these molecular systems in order to pinpoint the origin of the new fragmentation channels opened up by the tiny change in energy? While excited states of closed-shell molecules are typically very well simulated in calculations, open-shell structures still offer an interesting conundrum. The development of additional, more specialized, experimental setups dedicated to the generation and characterization of charged and/or neutral radical species is required to provide a thorough benchmark for theoretical efforts in this area.
Other experimental developments which promise to revolutionize the field include the new analytical methods of mass spectrometry which combine mass with the spectral fingerprint for a full diagnostic of the molecule and its fragments. It has previously been demonstrated that the development of a multi-step (UV/ms)\(^n\) process, where the parent ion and fragment(s) are successively excited then mass characterized, could go a long way to resolving some of the outstanding issues of molecular characterization in pharmaceutical research and development [243]. Finally, the laser-induced inhibition of complex growth (LIICG) method [244], in which the internal energy introduced into the molecule by the laser prevents it forming clusters with atoms such as helium in the trap, is a technique which is potentially universally-available but has not yet been extensively applied. It is a very promising method for the study of selectively excited molecules, although the distribution of the injected energy across a large number of states means that, for certain larger molecular systems, the experiment requires careful calibration in order to extract an exploitable signal.
17.3 Concluding remarks
Since the pioneering work of the EPLF team [235], photo-fragment and photo-detachment spectroscopy in cryogenically cooled ion traps has flourished [175, 245]. This method has opened the door to the high precision study of very big and “floppy” molecular systems; the characterization, for example, of decapeptide [246]—a polypeptide consisting of a chain of ten amino acids—would previously have been inconceivable. The technique has also allowed the study of molecular species in different charge states which were hitherto totally unexplored (protonated, deprotonated, dehydrogenated, etc.), providing information on ions and radicals which represent reaction intermediates in domains as diverse as biology and astrophysics.
Acknowledgements We thank Claude Dedonder for her invaluable input.
18 Gas-phase fluorescence spectroscopy of complex molecular ions
Christina Kjær and Steen Brøndsted Nielsen, Department of Physics and Astronomy, Aarhus University, Denmark
18.1 Status: description of the state of the art
Action spectroscopy has for many years provided significant information on electronic transition energies of isolated molecular ions in vacuo. It is an indirect technique based on either photodissociation, electron detachment, or photoisomerization (see Sects. 14.1, 17.1, 19.1) to identify photon absorption, which is necessary as the ion density is too low for traditional light-transmission experiments. However, the requirement of “action” is an inherent problem, in particular, in the case of complex ions with many degrees of freedom or strongly bound ones as there is limited dissociation within the time frame of the mass spectrometer, typical a few microseconds to tens of milliseconds dependent on the setup [247]. The result is no “action” or spectra skewed toward the blue. A nondestructive technique is therefore advantageous such as fluorescence spectroscopy where emitted photons are detected.
While there is no molecular size limitation in fluorescence spectroscopy, it is still challenging to measure fluorescence from a thin cloud of ions, say 1 million ions in a volume of 1 mm\(^3\). To put things in perspective, compare with the \(6\times 10^{13}\) ions in the same volume of a 0.1-mM solution, a difference of seven orders of magnitude! Clearly, the background counts of scattered photons and the noise level have to be kept as low as possible in the gas-phase experiment. Nevertheless, beautiful work has been done by several groups to establish the intrinsic photophysics of many fluorescent molecular ions and the impact of a microenvironment, including transition energies determined from dispersed fluorescence spectra and excited-state lifetimes (see, e.g. [248] and PIs listed in Table 1). Also gas-phase Förster resonance energy transfer (FRET) experiments on macromolecular ions labeled with two fluorescent dyes have revealed important information on folding motifs of peptides, proteins, and nucleic acids [249, 250], information that traditionally is established in ion-mobility experiments.
One large advantage of the gas-phase experiment is that the impact of individual perturbations can be disentangled one at a time, e.g., how much a nearby charge affects the spectroscopic properties as previously done for rhodamine dyes [251]. Also noteworthy, even though the ion density is much lower than in solution, the gas-phase experiment is in itself much cleaner as only mass-selected ions contribute to the fluorescence; there are no impurities.
In a typical experiment, complex ions are formed in the gas phase by electrospray ionization (ESI) and transferred to an ion trap where they are stored, and those of interest are mass selected. Often a Paul trap is used as here the ions are located in the center after collisional cooling and act as a point source for light emission. Still, it is non-trivial to extract the emitted photons after photo-excitation, and collection efficiencies are often less than half a percent. In our luminescence setup (denoted LUNA [231]) we use a cylindrical Paul trap where the exit electrode is a mesh grid to allow as many photons as possible to exit the “fluorescence cell.” This approach increases the collection efficiency to about 5%.
A summary of laboratories that have reported fluorescence from ions produced by ESI or MALDI (matrix-assisted laser desorption/ionization) is given in Table 1 including the year of the first publication and the type of trap (Paul, linear quadrupole trap (LQT), or Penning). Different lasers have been used in combination with the mass spectrometers, both CW and pulsed ones with low repetition rates (10–20 Hz) and very high rates (80 MHz). A high repetition rate has obvious advantages but does not allow for mass selection in between each laser irradiation event, and collisional cooling can also be an issue when the time between two laser pulses is only 12.5 ns (cf., 80 MHz).
Most experiments are done at room temperature but it is worth to mention two unique setups built by Kappes, Schooss and their co-workers [252] and Ferzoco and co-workers [253] where ions are cooled to low temperatures. The former operates close to 77 K (liquid nitrogen temperature) while in the latter, ions are stored in a LQT at ambient to cryogenic temperatures. Indeed, the almost open geometry of the linear ion trap and the collection optics gives an excellent signal; about 10\(^7\) photons per second are collected from between the trapping rods.
18.2 Challenges and new directions
A fluorescence experiment obviously only makes sense if the ions are fluorescent! This is an obstacle in many cases, in particular as it is hard to detect fluorescence if the quantum yield is too low (lower limit is about 0.1% in our experiments). Fluorescence can be quenched because of out-of-plane deformations of the chromophore or twist motions, and freezing out this motion as much as possible often increases the fluorescence. One prime example is the green fluorescent protein (GFP) chromophore anion that is non-fluorescent in solution and in vacuo while fluorescence in solutions is established at liquid nitrogen temperatures (see discussion in [254] with references). According to pump–probe experiments, the excited-state lifetime of the isolated chromophore anion is long (about 1 ns) at 100 K [209], and a relevant experiment would be to establish if the isolated anion is fluorescent at low temperatures. It is in this regard important to reduce RF heating in the trap, which is most easily done by mass selection at a prior stage and not in the trap itself. Oxyluciferin is another non-fluorescent ion at room temperature that may become fluorescent upon cooling; this ion accounts for the bioluminescence seen from many light-emitting insects such as fireflies.
Another interesting aspect is how a single solvent molecule (e.g., water) or a molecular dipole (e.g., betaine that has a dipole moment of 12 D) affects the fluorescence, both the quantum yield and the spectrum itself. Clearly, amino acid residues in a protein cavity are crucial to suppress the intramolecular twist motions that quickly brings the chromophore from the excited state back to the ground state, either due to space restrictions inside the cavity (steric crowding) or by providing high local electric fields at relevant chromophore sites (for example, a protonated arginine residue close to the phenolate oxygen in case of the GFP chromophore anion). Experiments on ion–molecule complexes are, however, non-trivial as unwanted reactions such as photodissociation would quickly reduce the number of ions in the trap to zero. One way could be to seed the helium buffer gas with water vapor to constantly reform the complexes. These experiments would require a low frequency laser (e.g., 20 Hz) to have enough time to remove bare ions between irradiation events.
Finally, it is worth to emphasize that fluorescence experiments can provide significant information on the excited-state dynamics as structural changes are evidenced from large Stokes shifts, one example being the fluorescein anion. Indeed, being able to measure dispersed fluorescence spectra on a picosecond timescale would provide unprecedented information on the dynamics and associated microenvironmental changes.
18.3 Concluding remarks
How to turn on fluorescence (or how to slow down excited-state dynamics) is in our view an interesting prospect for the future. Such fundamental understanding is to be obtained from experiments done at low temperatures and on cleverly designed ion–molecule complexes and could be beneficial for the engineering of new fluorophores, in particular in the red region of the visible spectrum where light penetration through tissue is high. In our laboratory, we are currently developing LUNA2 that operates at 77-K temperature, and where mass selection is done before the ions enter the cold Paul trap (Fig. 17).
Gas-phase fluorescence spectroscopy of complex ions is still in its infancy, involving a limited number of groups worldwide. However, new instrumental developments could very well boost this area of research, and in a few years, fluorescence detection may become a standard method in the ever increasing toolkit of mass spectrometry. We believe the future is bright.
LUNA2 is a new setup to measure luminescence from cold, photoexcited molecular ions that is under construction in our laboratory. It contains two traps: Trap1 is used as a pretrap and to filter off unwanted ions. Ions of interest are transferred to Trap2, placed in a copper block cooled to lq-N\(_2\) temperature. In Trap2, photo-excitation is done, and emitted photons are collected and detected
19 Action spectroscopy of isomer-selected molecules
Eduardo Carrascosa, Laboratoire de Chimie Physique Moléculaire, École Polytechnique Fédérale de Lausanne, Switzerland
James Bull, School of Chemistry, University of East Anglia, United Kingdom
19.1 Status: description of the state of the art
Many gas-phase ions can exist in more than one isomeric form, each of which may have distinct absorption properties and excited-state dynamics. Examples include carbon clusters, which have 1D linear chains, 2D rings, and 3D structures, polycyclic aromatic hydrocarbons (Sect. 20) with structural isomers, and photo-active protein chromophores or biomolecules (Sects. 4, 5, 14, 17), which often have several geometric isomers, tautomeric and (de)protomeric forms. Biomolecular ions typically have a high degree of conformational fluxionality, ideally requiring action spectroscopy techniques to sample this complexity in a sensitive manner. However, the gas-phase abundance of each isomer usually depends on many factors including the precursor form and any solvation environment, the ion source (e.g. electrospray ionization (Sects. 5, 14, 17, 18), laser ablation, thermal evaporation), and the collisional treatment of the ions as they are introduced into vacuum. For example, energetic collisions between the target ions and background gas by extraction, acceleration or RF fields before spectroscopic investigation can increase the target ion’s internal vibrational energy (temperature), inducing interconversion between the isomers. On the other hand, if there are substantial isomerization barriers, an ion source may generate kinetically-trapped species. Although many implementations of gas-phase action spectroscopy select target ions based on their mass-to-charge (m/z) ratio, e.g. time-of-flight, quadrupole, or sector mass spectrometers, these approaches are unable to distinguish isomers.
Action spectroscopy with SLIM-IMS and cryogenic ion trapping: a schematic illustration of the instrumentation, b arrival time distribution of two electrosprayed anomers (A and B), c IR spectra of mobility-selected and cryocooled anomer ions A and B. Molecular structures of A and B are shown with the arrows indicating the important equatorial (red) and axial (blue) hydroxide groups. Key: ESI—electrospray ionization, TOF-MS—time-of-flight mass spectrometry, quad MS—quadrupole mass filter, MCP—multi-channel plate detector, OPO—optical parametric oscillator. Figure adapted from Ref. [274]
The most common strategy for separating isomers in the gas-phase is through ion mobility spectrometry (IMS) [261]. In IMS, charged isomers propelled through a buffer gas (e.g. He, N\(_{2}\) or CO\(_{2}\)) under the influence of an electric field are separated according to their collision cross sections (\(\Omega \)). \(\Omega \), which represents the effective collisional surface area presented by an ion, typically has two contributions: a small impact parameter (hard-sphere collision) component, and a large impact parameter (glancing collision) component. Whereas He buffer gas is best suited for distinguishing isomers with substantially different shapes defined by the first contribution, buffer gases such as N\(_{2}\), CO\(_{2}\), or those seeded with organic dopants are suited for distinguishing isomers with differing long-range intermolecular interactions, including dipole-quadrupole and hydrogen bonding.
There are four primary IMS techniques: drift-time (or drift-tube) ion mobility spectrometry (DTIMS), traveling-wave ion mobility spectrometry (TWIMS), field-asymmetric ion mobility spectrometry (FAIMS), and trapped ion mobility spectrometry (TIMS), with each having certain advantages [261,262,263]. Selected key properties are summarized in Table 2. SLIM-IMS (structures for lossless ion manipulations ion mobility spectrometry) is a promising development, which involves isomer separation using printed circuit boards [264].
Several research groups have coupled IMS techniques with tunable light sources to enable isomer-selected action spectroscopy. Implementations include IMS coupled with photoelectron spectroscopy [265, 266], photodissociation spectroscopy [267,268,269,270,271,272], and photoisomerization spectroscopy [273]. A recent example of isomer-specific IR action spectroscopy is shown in Fig. 18 [274]. In this example, a SLIM-IMS device has been coupled with a quadrupole mass filter, cryogenic ion trap and time-of-flight (reflectron) mass spectrometer. The study was able to separate and identify two glycan anomers from the ion’s arrival time distribution (ATD, Fig. 18b). Glycan anomers are difficult to distinguish using other ion mobility techniques because \(\Omega \) values for different anomers usually differ by less than 1%. Cryogenic cooling of each isomer in the trap and messenger tagging allowed acquisition of distinct isomer-specific IR spectra in the hydroxide stretching region (Fig. 18c). Supporting experiments on labelled and methylated analogues gave unambiguous assignment of each ATD peak to an anomer structure.
19.2 Challenges and new directions
Current challenges in this field can be divided into two categories: (1) development of universal and cost effective isomer-selection instrumentation that can be easily coupled with existing action spectroscopy experiments, (2) new strategies for improving information content during spectral acquisition.
Currently, isomer-specific action spectroscopy instrumentation is either built by specialist research groups [265, 266, 273], or is based on modified commercial mass spectrometers [268, 271, 272]. General availability of a well-characterized IMS device, such as SLIM-IMS with ion trapping capacity, which could be easily integrated into new or existing instrument, would be a decisive step in setting isomer-selected action spectroscopy as the standard. Cryocooling potential is highly desirable.
The second major challenge is improving the key performance characteristics of IMS techniques (Table 2) and the development of methodology to provide enhanced information content. In the first instance, this could be through improving resolving power (e.g. cyclic devices) combined with cryocooled buffer gas. While a lower temperature of buffer gas improves isomer separation, it also allows separation and isolation of isomers with low barriers to interconversion (e.g. rotamers), which rapidly interconvert at elevated temperatures. This can be particularly important for resolving specific biomolecule interactions and photochemistry, for example, open versus \(\pi \)-stacked structures of DNA polynucleotides [275]. Enhancing information content might involve the use of several light sources to photogenerate and probe isomeric intermediates, or incorporation of additional orthogonal analysis techniques (e.g. multi-dimensional action spectroscopy). A significant development by the Bieske group involved coupling of two ion mobility stages with laser spectroscopy, allowing isomer-selection of a target ion [273]. This strategy has enabled simultaneous monitoring of photoisomerization, photodissociation, and photo-detachment (for anions). Furthermore, the methodology can be adapted to numerous IMS and photo stages, allowing the study of multi-step photoreactions in the gas phase.
19.3 Concluding remarks
Isomer-resolved action spectroscopy is a rapidly evolving field, offering the capacity to study the photochemistry and photophysics of individual isomers. The possibility that an ion source could generate more than one gas-phase isomer is an important, possibly crucial, factor to consider for gas-phase systems such as biomolecules due to the range of potential isomers. There is an increasing expectation that robust action spectroscopy investigations should include some degree of isomer selectivity.
20 Deciphering the lifecycle of carbon macromolecules in space
Alessandra Candian and Annemieke Petrignani, van ’t Hoff Institute for Molecular Sciences, University of Amsterdam, The Netherlands
20.1 Status: description of the state of the art
Carbon is one of the most abundant elements in the Universe, produced by nucleosynthesis in dying low-mass stars; this together with its unique ability to form multiple stable bonds with itself and other elements, makes carbon one of the building blocks of life. Understanding carbon chemistry, i.e., the path of carbon species from their synthesis to their transformation and destruction down to their delivery in exosolar system is of paramount importance. Key organic species are polycyclic aromatic hydrocarbon (PAH) molecules, in which 10% of all cosmic carbon could be locked. PAHs are detected in space through the aromatic infrared bands (AIBs), a family of emission features in the mid-infrared (3–20 \(\upmu \)m or 3100 to 500 cm\(^{-1}\)) seen toward different astronomical environments in our Galaxy and beyond (see [276] for a recent review). Since their discovery in the previous century, much effort had gone into their spectroscopy and the development of astronomical PAH models. As our understanding advances, the importance of the underlying mechanisms driving and affecting the spectral signatures, evolution, and the role these large hydrocarbons play in the production of other (organic) species, has become increasingly apparent.
PAHs are efficient energy converters that absorb UV/Vis photons coming from young stars and re-emit them in the infrared, producing the AIBs. The high spectral resolution achieved by past space observatories (ISO and Spitzer) has allowed astronomers to have a better grasp of the composition of the astronomical PAH population. Astro-PAHs have a size between roughly 40 and 120 carbon atoms [277] and their charge varies from − 1 to \(+\) 2 depending on a fine-tuned balance between the hardness of the radiation impinging on PAHs and the density of the gas where they reside. There is evidence that in astronomical environments PAHs can have heteroatom substitutions and side groups [276]. The variations in the appearance of the astronomical spectra hint to an active chemistry molding the populations of astro-PAH (Fig. 19), originating from the photoevaporation of very small (nanometer size) carbonaceous grains. The state-of-the-art model of the photophysical evolution of astro-PAHs (e.g. [278]) considers mostly charge and H-coverage. The latter has implications for the formation of H\(_2\), the most abundant molecule in space. PAHs can also act as source of smaller hydrocarbons, which importance has recently also been assessed [279]. Not included in astronomical modeling (yet), is the role of isomerization, which has now also been shown to play a role in the dynamics of photodissociation of astro-PAHs [280,281,282].
In 2010, the Buckminsterfullerene C\(_{60}\) was detected through its vibrational modes in the planetary nebula TC 1 [283]; since then C\(_{60}\) have been discovered in many other environments, including the diffuse interstellar medium. Indeed, thanks to a state-of-the-art experiment, the electronic transitions of the radical cation of fullerene, C\(_{60}^+\), have been matched to four diffuse interstellar bands (or DIBs) [176] a set of more than 200 unidentified absorption bands in the UV–visible that have been named “the longest standing puzzle in astronomical spectroscopy.” The discovery of C\(_{60}\) in regions where also PAHs are present has pushed forward the idea that the lifecycle of these carbon macromolecules is intertwined; the top-down formation of C\(_{60}\) from the photoprocessing of large PAHs has been proved experimentally [284] but the details of the process and the intermediates have yet to be characterized.
Evolution of carbonaceous material across a star forming region, adapted from Ref. [285]. The dominant charge/type of material and the processes at play are indicated in the bottom of the figure. Carbonaceous very small grains, residing in the dense molecular cloud, are converted to free flying PAHs in the photodissociation region (PDR) that is created by photons below 13.6 eV illuminating the outer layers of the cloud. Closer to star, in the so-called cavity, the density and strength of photons change the PAH populations and led to the formation of C\(_{60}\)
20.2 Challenges and new directions
To model the processes driving PAHs evolution requires detailed studies of these processes and corresponding spectral behavior of the species involved. This includes studies of vibrational normal modes, UV photo-absorption cross sections and ionization yields, electron attachment, recombination, reactivity to atomic hydrogen, and photodissociation rates [279], to name a few. In many cases, these processes have been necessarily studied for only a handful of relatively small PAHs, either neutral or positively charged, sometimes with additional hydrogen atoms or substitutions, and the results are applied to larger PAHs without further adjustment. For fullerenes and carbon cages experimental studies are limited to C\(_{60}\) and C\(_{70}\). Theoretical chemistry methods can be used to study molecular systems of astrochemical interest with less limits in shape and charge. Statistical rate theory applications are often used in kinetic studies for small molecules. Such studies typically employ Density Functional Theory (DFT) for most properties (geometries, vibrational frequencies) and, when the size of the system allows, higher accuracy calculations, such as ab-initio or composite methods, for, e.g., relative energies [286, 287]. For large carbonaceous molecules, thorough investigation of dissociation channels using static DFT quickly becomes unfeasible. In this situation, molecular dynamics (MD) simulations provide a powerful tool, not only to complement statistical theories, but also to tackle other questions, for example, overlooked reactions pathways. The accuracy of MD simulations in predicting the dynamics of a system depends on the method used to compute the force. The reactive empirical bond order (REBO) models and the adaptive interatomic reactive empirical bond order (AIREBO) are natural choices when studying clustering and dimerization of large carbon and hydrocarbon structures, because these models enable bond formation or bond breaking at relatively small computational cost [288]. Molecular dynamics (MD) based on density functional tight binding (DFTB) (see Sect. 9) provides a computationally-efficient tool to investigate photo-induces fragmentation and isomerization; not only does it compare successfully with experimental results, it also gives energetics comparable to standard DFT [280]. Alternatively, isomerization pathways and equilibrium properties at fixed total energy in the canonical or microcanonical ensembles can be described using biased Monte-Carlo methods [289]. Potential energy of specific molecular configurations are determined using a reactive force field, such as AIREBO, which includes also the effects of anharmonicity, and the thermodynamical properties are evaluated through the Wang-Landau approach; this approach consists in random walk around the configurations that is quickly able to visit all the available states and build an estimate of the density of configurational states.
To avoid the limitation of remaining trapped into local free-energy-minimum conformations when exploring the energy surface—a realistic problem for large hydrocarbons—replica exchange MD simulations or metadynamics should be considered [290]. MD calculations create a large amount of data that need to be analyzed and processed in order to obtain results such as reaction barriers that are ingredients for photophysical models. Automated software that uses graph theory to extract reactive pathways from MD simulations and then simulates the fragmentation dynamics through kinetic approaches can thus be used to great advantage.
Experiments on the fragmentation of large, non-standard PAHs with different charge states and fullerenes are fundamental to benchmark the results of the simulations. Advances in experimental technique have opened up new possibilities to study these species and learn more about their isomerization and radiative lifetimes. Ion mobility spectrometry (IMS) has undergone major developments (see Sect. 19) that allow for increasingly improved separation and identification of isomeric species. Combining IMS with the current state-of-the-art mass spectrometric and spectroscopic techniques offers much potential to study photo-induced isomerization and fragmentation.
The anharmonic behavior of molecules strongly affect the reaction rates through density of states and energy barriers. Understanding the anharmonic behavior of PAHs, which is now possible at least for small sizes [291] thanks to synergy between state-of-the-art calculations and experiments, will allow an accurate modeling of reaction rates with the exciting possibility to implement machine learning techniques to extended the knowledge to larger molecules [292] such as fullerene. IR inactive normal modes are essential in the calculations of density of states. Here, techniques such as zero-electron kinetic energy (ZEKE) spectroscopy could provide important information on not only IR-, but also Raman-active modes.
Finally, a deeper understanding of the ultrafast radiative and non-radiative processes occurring after photo-excitation is fundamental to assess the stability of molecules and correctly model their behavior. With the emergence of electrostatic storage rings (see Sect. 13) that allow for long storage times under ultrahigh vacuum conditions, experimental investigations on radiative cooling of increasingly larger species are becoming possible. At the same time, the field of excited state quantum dynamics is rapidly evolving with the promise of being applied to carbon macromolecules in the very near future.
20.3 Concluding remarks
The James Webb Space Telescope (JWST), the next infrared space telescope a joint European-Northern American venture, is now scheduled to be launched in Fall 2021. Thanks to its superior spectral sensitivity and resolution, JWST is expected to deliver incredible spectra, opening up a new window on the evolution of carbonaceous material in space. A timely and concerted effort on both experimental and theoretical sides is fundamental to exploit JWST capabilities and its promise to revolutionize our view of the carbonaceous universe.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: No new data is being presented in this review article.]
References
M. Ferray, A. L’Huillier, X.F. Li, L.A. Lompre, G. Mainfray, C. Manus, J. Phys. B: At. Mol. Opt. Phys. 21(3), L31 (1988). https://doi.org/10.1088/0953-4075/21/3/001
F. Lépine, M.Y. Ivanov, M.J.J. Vrakking, Nat. Photonics 8(3), 195 (2014). https://doi.org/10.1038/nphoton.2014.25
M. Nisoli, P. Decleva, F. Calegari, A. Palacios, F. Martín, Chem. Rev. 117(16), 10760 (2017). https://doi.org/10.1021/acs.chemrev.6b00453
H.J. Wörner, C.A. Arrell, N. Banerji, A. Cannizzo, M. Chergui, A.K. Das, P. Hamm, U. Keller, P.M. Kraus, E. Liberatore, P. Lopez-Tarifa, M. Lucchini, M. Meuwly, C. Milne, J.E. Moser, U. Rothlisberger, G. Smolentsev, J. Teuscher, J.A. van Bokhoven, O. Wenger, Struct. Dyn. 4(6), 061508 (2017). https://doi.org/10.1063/1.4996505
A. Palacios, F. Martín, WIREs Comput. Mol. Sci. 10(1), 1 (2020). https://doi.org/10.1002/wcms.1430
S. Maclot, J. Lahl, J. Peschel, H. Wikmark, P. Rudawski, F. Brunner, H. Coudert-Alteirac, S. Indrajith, B.A. Huber, S. Díaz-Tendero, N.F. Aguirre, P. Rousseau, P. Johnsson, Sci. Rep. 10, 2884 (2020). https://doi.org/10.1038/s41598-020-59649-1
A.H. Zewail, J. Phys. Chem. A 104(24), 5660 (2000). https://doi.org/10.1021/jp001460h
J. Ullrich, R. Moshammer, A. Dorn, R. Dörner, L.P.H. Schmidt, H. Schmidt-Böcking, Rep. Prog. Phys. 66(9), 1463 (2003). https://doi.org/10.1088/0034-4885/66/9/203
J.P. Marangos, J. Phys. B: At. Mol. Opt. Phys. 49(13), 132001 (2016). https://doi.org/10.1088/0953-4075/49/13/132001
R. Geneaux, H.J.B. Marroux, A. Guggenmos, D.M. Neumark, S.R. Leone, Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 377(2145), 20170463 (2019). https://doi.org/10.1098/rsta.2017.0463
F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J.B. Greenwood, F. Martín, M. Nisoli, Science 346(6207), 336 (2014). https://doi.org/10.1126/science.1254061
S. Kühn, M. Dumergue, S. Kahaly, S. Mondal, M. Füle, T. Csizmadia, B. Farkas, B. Major, Z. Várallyay, E. Cormier, M. Kalashnikov, F. Calegari, M. Devetta, F. Frassetto, E. Månsson, L. Poletto, S. Stagira, C. Vozzi, M. Nisoli, P. Rudawski, S. Maclot, F. Campi, H. Wikmark, C.L. Arnold, C.M. Heyl, P. Johnsson, A. L’Huillier, R. Lopez-Martens, S. Haessler, M. Bocoum, F. Boehle, A. Vernier, G. Iaquaniello, E. Skantzakis, N. Papadakis, C. Kalpouzos, P. Tzallas, F. Lépine, D. Charalambidis, K. Varjú, K. Osvay, G. Sansone, J. Phys. B: At. Mol. Opt. Phys. 50(13), 132002 (2017). https://doi.org/10.1088/1361-6455/aa6ee8
J. Duris, S. Li, T. Driver, E.G. Champenois, J.P. MacArthur, A.A. Lutman, Z. Zhang, P. Rosenberger, J.W. Aldrich, R. Coffee, G. Coslovich, F.J. Decker, J.M. Glownia, G. Hartmann, W. Helml, A. Kamalov, J. Knurr, J. Krzywinski, M.F. Lin, J.P. Marangos, M. Nantel, A. Natan, J.T. O’Neal, N. Shivaram, P. Walter, A.L. Wang, J.J. Welch, T.J.A. Wolf, J.Z. Xu, M.F. Kling, P.H. Bucksbaum, A. Zholents, Z. Huang, J.P. Cryan, A. Marinelli, Nat. Photonics 14(1), 30 (2020). https://doi.org/10.1038/s41566-019-0549-5
J. Ullrich, A. Rudenko, R. Moshammer, Annu. Rev. Phys. Chem. 63(1), 635 (2012). https://doi.org/10.1146/annurev-physchem-032511-143720
R. Moshammer, K. Schnorr, in Synchrotron Light Sources and Free-Electron Lasers: Accelerator Physics, Instrumentation and Science Applications, ed. by E.J. Jaeschke, S. Khan, J.R. Schneider, J.B. Hastings (Springer International Publishing, Cham, 2020), pp. 1493–1524. https://doi.org/10.1007/978-3-030-23201-6_26
K. Ueda, E. Sokell, S. Schippers, F. Aumayr, H. Sadeghpour, J. Burgdörfer, C. Lemell, X.M. Tong, T. Pfeifer, F. Calegari, A. Palacios, F. Martin, P. Corkum, G. Sansone, E.V. Gryzlova, A.N. Grum-Grzhimailo, M.N. Piancastelli, P.M. Weber, T. Steinle, K. Amini, J. Biegert, N. Berrah, E. Kukk, R. Santra, A. Müller, D. Dowek, R.R. Lucchese, C.W. McCurdy, P. Bolognesi, L. Avaldi, T. Jahnke, M.S. Schöffler, R. Dörner, Y. Mairesse, L. Nahon, O. Smirnova, T. Schlathölter, E.E.B. Campbell, J.M. Rost, M. Meyer, K.A. Tanaka, J. Phys. B: At. Mol. Opt. Phys. 52(17), 171001 (2019). https://doi.org/10.1088/1361-6455/ab26d7
L.J. Frasinski, J. Phys. B: At. Mol. Opt. Phys. 49(15), 152004 (2016). https://doi.org/10.1088/0953-4075/49/15/152004
J.W.L. Lee, H. Köckert, D. Heathcote, D. Popat, R.T. Chapman, G. Karras, P. Majchrzak, E. Springate, C. Vallance, Commun. Chem. 3(1), 72 (2020). https://doi.org/10.1038/s42004-020-0320-3
M.P. Minitti, J.M. Budarz, A. Kirrander, J.S. Robinson, D. Ratner, T.J. Lane, D. Zhu, J.M. Glownia, M. Kozina, H.T. Lemke, M. Sikorski, Y. Feng, S. Nelson, K. Saita, B. Stankus, T. Northey, J.B. Hastings, P.M. Weber, Phys. Rev. Lett. 114, 255501 (2015). https://doi.org/10.1103/PhysRevLett.114.255501
L. Ma, H. Yong, J.D. Geiser, A. Moreno Carrascosa, N. Goff, P.M. Weber, Struct. Dyn. 7(3), 034102 (2020). https://doi.org/10.1063/4.0000010
D.S. Tikhonov, A. Datta, P. Chopra, A.L. Steber, B. Manschwetus, M. Schnell, Z. Phys. Chem. 234(7–9), 1507 (2020). https://doi.org/10.1515/zpch-2020-0009
B.F. Murphy, T. Osipov, Z. Jurek, L. Fang, S.K. Son, M. Mucke, J.H.D. Eland, V. Zhaunerchyk, R. Feifel, L. Avaldi, P. Bolognesi, C. Bostedt, J.D. Bozek, J. Grilj, M. Guehr, L.J. Frasinski, J. Glownia, D.T. Ha, K. Hoffmann, E. Kukk, B.K. McFarland, C. Miron, E. Sistrunk, R.J. Squibb, K. Ueda, R. Santra, N. Berrah, Nat. Commun. 5(1), 4281 (2014). https://doi.org/10.1038/ncomms5281
N. Berrah, A. Sanchez-Gonzalez, Z. Jurek, R. Obaid, H. Xiong, R.J. Squibb, T. Osipov, A. Lutman, L. Fang, T. Barillot, J.D. Bozek, J. Cryan, T.J.A. Wolf, D. Rolles, R. Coffee, K. Schnorr, S. Augustin, H. Fukuzawa, K. Motomura, N. Niebuhr, L.J. Frasinski, R. Feifel, C.P. Schulz, K. Toyota, S.K. Son, K. Ueda, T. Pfeifer, J.P. Marangos, R. Santra, Nat. Phys. 15(12), 1279 (2019). https://doi.org/10.1038/s41567-019-0665-7
B. Erk, J.P. Müller, C. Bomme, R. Boll, G. Brenner, H.N. Chapman, J. Correa, S. Düsterer, S. Dziarzhytski, S. Eisebitt, H. Graafsma, S. Grunewald, L. Gumprecht, R. Hartmann, G. Hauser, B. Keitel, C. von Korff Schmising, M. Kuhlmann, B. Manschwetus, L. Mercadier, E. Müller, C. Passow, E. Plönjes, D. Ramm, D. Rompotis, A. Rudenko, D. Rupp, M. Sauppe, F. Siewert, D. Schlosser, L. Strüder, A. Swiderski, S. Techert, K. Tiedtke, T. Tilp, R. Treusch, I. Schlichting, J. Ullrich, R. Moshammer, T. Möller, D. Rolles, J. Synchrotron Radiat. 25(5), 1529 (2018). https://doi.org/10.1107/S1600577518008585
P. Schmidt, V. Music, G. Hartmann, R. Boll, B. Erk, S. Bari, F. Allum, T.M. Baumann, G. Brenner, M. Brouard, M. Burt, R. Coffee, S. Dörner, A. Galler, P. Grychtol, D. Heathcote, L. Inhester, M. Kazemi, M. Larsson, J. Lee, Z. Li, A. Lutmann, B. Manschwetus, L. Marder, R. Mason, S. Moeller, T. Osipov, H. Otto, C. Passow, D. Rolles, P. Rupprecht, K. Schubert, L. Schwob, R. Thomas, C. Vallance, C. von Korff Schmising, R. Wagner, P. Walter, T.J.A. Wolf, V. Zhaunerchyk, M. Meyer, A. Ehresmann, A. Knie, P.V. Demekhin, M. Ilchen, J. Phys: Conf. Ser. 1412, 112009 (2020). https://doi.org/10.1088/1742-6596/1412/11/112009
M.H.M. Janssen, I. Powis, Phys. Chem. Chem. Phys. 16, 856 (2014). https://doi.org/10.1039/C3CP53741B
E. Allaria, R. Appio, L. Badano, W.A. Barletta, S. Bassanese, S.G. Biedron, A. Borga, E. Busetto, D. Castronovo, P. Cinquegrana, S. Cleva, D. Cocco, M. Cornacchia, P. Craievich, I. Cudin, G. D’Auria, M. Dal Forno, M.B. Danailov, R. De Monte, G. De Ninno, P. Delgiusto, A. Demidovich, S. Di Mitri, B. Diviacco, A. Fabris, R. Fabris, W. Fawley, M. Ferianis, E. Ferrari, S. Ferry, L. Froehlich, P. Furlan, G. Gaio, F. Gelmetti, L. Giannessi, M. Giannini, R. Gobessi, R. Ivanov, E. Karantzoulis, M. Lonza, A. Lutman, B. Mahieu, M. Milloch, S.V. Milton, M. Musardo, I. Nikolov, S. Noe, F. Parmigiani, G. Penco, M. Petronio, L. Pivetta, M. Predonzani, F. Rossi, L. Rumiz, A. Salom, C. Scafuri, C. Serpico, P. Sigalotti, S. Spampinati, C. Spezzani, M. Svandrlik, C. Svetina, S. Tazzari, M. Trovo, R. Umer, A. Vascotto, M. Veronese, R. Visintini, M. Zaccaria, D. Zangrando, M. Zangrando, Nat. Photonics 6(10), 699 (2012). https://doi.org/10.1038/nphoton.2012.233
A. Cartoni, A.R. Casavola, P. Bolognesi, M.C. Castrovilli, D. Catone, J. Chiarinelli, R. Richter, L. Avaldi, J. Phys. Chem. A 122(16), 4031 (2018). https://doi.org/10.1021/acs.jpca.8b01144
L. Schwob, M. Lalande, D. Egorov, J. Rangama, R. Hoekstra, V. Vizcaino, T. Schlathölter, J.C. Poully, Phys. Chem. Chem. Phys. 19, 22895 (2017). https://doi.org/10.1039/C7CP03376A
O. Plekan, V. Feyer, R. Richter, M. Coreno, M. de Simone, K.C. Prince, V. Carravetta, Chem. Phys. Lett. 442(4), 429 (2007). https://doi.org/10.1016/j.cplett.2007.05.110
A. Verkhovtsev, A. Traore, A. Muñoz, F. Blanco, G. García, Radiat. Phys. Chem. 130, 371 (2017). https://doi.org/10.1016/j.radphyschem.2016.09.021
T. Arion, U. Hergenhahn, J. Electron Spectrosc. Relat. Phenom. 200, 222 (2015). https://doi.org/10.1016/j.elspec.2015.06.004
J. Chiarinelli, P. Bolognesi, A. Domaracka, P. Rousseau, M.C. Castrovilli, R. Richter, S. Chatterjee, F. Wang, L. Avaldi, Phys. Chem. Chem. Phys. 20, 22841 (2018). https://doi.org/10.1039/C8CP03473G
N.C. Jones, S.B. Nielsen, S.V. Hoffmann, Phys. Chem. Chem. Phys. 22, 2188 (2020). https://doi.org/10.1039/C9CP05292E
I. Powis, in Advances in Chemical Physics, ed. by S.A. Rice (John Wiley & Sons, Ltd, 2008), chap. 5, pp. 267–329. https://doi.org/10.1002/9780470259474.ch5
M. Abdelmouleh, M. Lalande, V. Vizcaino, T. Schlathölter, J.C. Poully, Chem. A Eur. J. 26(10), 2243 (2020). https://doi.org/10.1002/chem.201904786
G. Mattioli, L. Avaldi, P. Bolognesi, J.D. Bozek, M.C. Castrovilli, J. Chiarinelli, A. Domaracka, S. Indrajith, S. Maclot, A.R. Milosavljević, C. Nicolafrancesco, C. Nicolas, P. Rousseau, Sci. Rep. 10, 10381 (2020). https://doi.org/10.1038/s41598-020-69947-3
J. Schuemann, A.F. Bagley, R. Berbeco, K. Bromma, K.T. Butterworth, H.L. Byrne, B.D. Chithrani, S.H. Cho, J.R. Cook, V. Favaudon, Y.H. Gholami, E. Gargioni, J.F. Hainfeld, F. Hespeels, A.C. Heuskin, U.M. Ibeh, Z. Kuncic, S. Kunjachan, S. Lacombe, S. Lucas, F. Lux, S. McMahon, D. Nevozhay, W. Ngwa, J.D. Payne, S. Penninckx, E. Porcel, K.M. Prise, H. Rabus, S.M. Ridwan, B. Rudek, L. Sanche, B. Singh, H.M. Smilowitz, K.V. Sokolov, S. Sridhar, Y. Stanishevskiy, W. Sung, O. Tillement, N. Virani, W. Yantasee, S. Krishnan, Phys. Med. Biol. 65(21), 21RM02 (2020). https://doi.org/10.1088/1361-6560/ab9159
M. Yamada, M. Foote, T.W. Prow, WIREs Nanomed. Nanobiotechnol. 7(3), 428 (2015). https://doi.org/10.1002/wnan.1322
R. Schürmann, K. Ebel, C. Nicolas, A.R. Milosavljević, I. Bald, J. Phys. Chem. Lett. 10(11), 3153 (2019). https://doi.org/10.1021/acs.jpclett.9b00848
D.K. Božanić, G.A. Garcia, O. Sublemontier, J. Pajović, V. Djoković, L. Nahon, J. Phys. Chem. C 124(44), 24500 (2020). https://doi.org/10.1021/acs.jpcc.0c08152
M. Pitzer, M. Kunitski, A.S. Johnson, T. Jahnke, H. Sann, F. Sturm, L.P.H. Schmidt, H. Schmidt-Böcking, R. Dörner, J. Stohner, J. Kiedrowski, M. Reggelin, S. Marquardt, A. Schießer, R. Berger, M.S. Schöffler, Science 341(6150), 1096 (2013). https://doi.org/10.1126/science.1240362
F. Auvray, D. Dennetiere, A. Giuliani, F. Jamme, F. Wien, B. Nay, S. Zirah, F. Polack, C. Menneglier, B. Lagarde, J.D. Hirst, M. Réfrégiers, Struct. Dyn. 6(5), 054307 (2019). https://doi.org/10.1063/1.5120346
A.R. Milosavljević, A. Giuliani, C. Nicolas, in X-ray and Neutron Techniques for Nanomaterials Characterization, ed. by C.S.S.R. Kumar (Springer, Berlin, 2016), pp. 451–505. https://doi.org/10.1007/978-3-662-48606-1_8
J.B. Fenn, Angew. Chem. Int. Ed. 42(33), 3871 (2003). https://doi.org/10.1002/anie.200300605
W.D. Bowers, S.S. Delbert, R.L. Hunter, R.T. McIver, J. Am. Chem. Soc. 106(23), 7288 (1984). https://doi.org/10.1021/ja00335a094
J.S. Brodbelt, Chem. Soc. Rev. 43(8), 2757 (2014). https://doi.org/10.1039/C3CS60444F
N.C. Polfer, J. Oomens, Mass Spectrom. Rev. 28(3), 468 (2009). https://doi.org/10.1002/mas.20215
S. Bari, O. Gonzalez-Magaña, G. Reitsma, J. Werner, S. Schippers, R. Hoekstra, T. Schlathölter, J. Chem. Phys. 134(2), 024314 (2011). https://doi.org/10.1063/1.3515301
A.R. Milosavljević, C. Nicolas, J. Lemaire, C. Dehon, R. Thissen, J.M. Bizau, M. Réfrégiers, L. Nahon, A. Giuliani, Phys. Chem. Chem. Phys. 13, 15432 (2011). https://doi.org/10.1039/C1CP21211G
T. Schlathölter, G. Reitsma, D. Egorov, O. Gonzalez-Magaña, S. Bari, L. Boschman, E. Bodewits, K. Schnorr, G. Schmid, C.D. Schröter, R. Moshammer, R. Hoekstra, Angew. Chem. Int. Ed. 55(36), 10741 (2016). https://doi.org/10.1002/anie.201605335
A.R. Milosavljević, K. Jänkälä, M.L. Ranković, F. Canon, J. Bozek, C. Nicolas, A. Giuliani, Phys. Chem. Chem. Phys. 22, 12909 (2020). https://doi.org/10.1039/D0CP00994F
L. Schwob, S. Dörner, K. Atak, K. Schubert, M. Timm, C. Bülow, V. Zamudio-Bayer, B. von Issendorff, J.T. Lau, S. Techert, S. Bari, J. Phys. Chem. Lett. 11(4), 1215 (2020). https://doi.org/10.1021/acs.jpclett.0c00041
K.D.D. Gunaratne, V. Prabhakaran, Y.M. Ibrahim, R.V. Norheim, G.E. Johnson, J. Laskin, Analyst 140, 2957 (2015). https://doi.org/10.1039/C5AN00220F
I. Aloui, V. Legros, A. Giuliani, W. Buchmann, Rapid Commun. Mass Spectrom. 34(S2), e8773 (2020). https://doi.org/10.1002/rcm.8773
S. Bari, J.M. Bizau, K. Schubert, L. Schwob, S. Dörner, J. Bozek, C. Nicolas, D. Cubaynes, A. Milosavljević, (2021). In preparation
J.M. Sullivan, P. Shukla, Biophys. J. 77(3), 1333 (1999). https://doi.org/10.1016/S0006-3495(99)76983-3
A.I. Kuleff, L.S. Cederbaum, J. Phys. B: At. Mol. Opt. Phys. 47(12), 124002 (2014). https://doi.org/10.1088/0953-4075/47/12/124002
S. Faraji, D. Zhong, A. Dreuw, Angew. Chem. Int. Ed. 55(17), 5175 (2016). https://doi.org/10.1002/anie.201511950
F. Agostini, B.F.E. Curchod, Wiley Interdiscipl. Rev. Comput. Mol. Sci. 9, e1417 (2019). https://doi.org/10.1002/wcms.1417
P. López-Tarifa, M.A. Hervé du Penhoat, R. Vuilleumier, M.P. Gaigeot, I. Tavernelli, A. Le Padellec, J.P. Champeaux, M. Alcamí, P. Moretto-Capelle, F. Martín, M.F. Politis, Phys. Rev. Lett. 107, 023202 (2011). https://doi.org/10.1103/PhysRevLett.107.023202
C.A. Rozzi, F. Troiani, I. Tavernelli, J. Phys.: Condens. Matter 30(1), 013002 (2018). https://doi.org/10.1088/1361-648X/aa948a
J.C. Tully, J. Chem. Phys. 93(2), 1061 (1990). https://doi.org/10.1063/1.459170
M. Persico, G. Granucci, Theoret. Chem. Acc. 133(9), 1526 (2014). https://doi.org/10.1007/s00214-014-1526-1
L. Wang, D. Trivedi, O.V. Prezhdo, J. Chem. Theory Comput. 10(9), 3598 (2014). https://doi.org/10.1021/ct5003835
D.V. Makhov, W.J. Glover, T.J. Martinez, D.V. Shalashilin, J. Chem. Phys. 141(5), 054110 (2014). https://doi.org/10.1063/1.4891530
M. Ben-Nun, J. Quenneville, T.J. Martínez, J. Phys. Chem. A 104(22), 5161 (2000). https://doi.org/10.1021/jp994174i
M.H. Beck, A. Jäckle, G.A. Worth, H.D. Meyer, Phys. Rep. 324(1), 1 (2000). https://doi.org/10.1016/S0370-1573(99)00047-2
S. Faraji, S. Gomez-Carrasco, H. Köppel, Conical Intersection: Theory, Computation and Experiment (World Scientific, Singapore, 2011)
U. Manthe, J. Chem. Phys. 128(16), 164116 (2008). https://doi.org/10.1063/1.2902982
G. Richings, I. Polyak, K. Spinlove, G. Worth, I. Burghardt, B. Lasorne, Int. Rev. Phys. Chem. 34(2), 269 (2015). https://doi.org/10.1080/0144235X.2015.1051354
G. Geloni, Z. Huang, C. Pellegrini, in X-Ray Free Electron Lasers: Applications in Materials, Chemistry and Biology, ed. by U. Bergmann, V. Yachandra, J. Yano (The Royal Society of Chemistry, 2017), chap. 1, pp. 1–44. https://doi.org/10.1039/9781782624097-00001
Y. Öhrn, G. Born, P.O. Löwdin, in Advances in Quantum Chemistry, vol. 13 (Academic Press, 1981), pp. 1–88. https://doi.org/10.1016/S0065-3276(08)60291-9
H. Martin Senn, W. Thiel, Angew. Chem. Int. Ed. 48, 1198 (2009). https://doi.org/10.1002/anie.200802019
S. Faraji, A. Dreuw, Photochem. Photobiol. 93(1), 37 (2017). https://doi.org/10.1111/php.12679
Y. Cao, J. Romero, J.P. Olson, M. Degroote, P.D. Johnson, M. Kieferová, I.D. Kivlichan, T. Menke, B. Peropadre, N.P.D. Sawaya, S. Sim, L. Veis, A. Aspuru-Guzik, Chem. Rev. 119(19), 10856 (2019). https://doi.org/10.1021/acs.chemrev.8b00803
M. Gastegger, J. Behler, P. Marquetand, Chem. Sci. 8, 6924 (2017). https://doi.org/10.1039/C7SC02267K
J. Hermann, Z. Schätzle, F. Noé, Nat. Chem. 12(10), 891 (2020). https://doi.org/10.1038/s41557-020-0544-y
J. Westermayr, P. Marquetand, Mach. Learn. Sci. Technol. 1(4), 043001 (2020). https://doi.org/10.1088/2632-2153/ab9c3e
J. Westermayr, M. Gastegger, M.F.S.J. Menger, S. Mai, L. González, P. Marquetand, Chem. Sci. 10(35), 8100 (2019). https://doi.org/10.1039/C9SC01742A
V. Vuitton, R.V. Yelle, S.J. Klippenstein, S.M. Hörst, P. Lavvas, Icarus 324, 120 (2019). https://doi.org/10.1016/j.icarus.2018.06.013
B. Yuan, A.R. Koss, C. Warneke, M. Coggon, K. Sekimoto, J.A. de Gouw, Chem. Rev. 117(21), 13187 (2017). https://doi.org/10.1021/acs.chemrev.7b00325
B.C. Sweeny, H. Pan, A. Kassem, J.C. Sawyer, S.G. Ard, N.S. Shuman, A.A. Viggiano, S. Brickel, O.T. Unke, M. Upadhyay, M. Meuwly, Phys. Chem. Chem. Phys. 22, 8913 (2020). https://doi.org/10.1039/D0CP00668H
I. Savic, S. Schlemmer, D. Gerlich, ChemPhysChem. 21(13), 1429 (2020). https://doi.org/10.1002/cphc.202000258
Š. Roučka, S. Rednyk, A. Kovalenko, T.D. Tran, R. Plašil, Á. Kálosi, P. Dohnal, D. Gerlich, J. Glosík, Astron. Astrophys. 615, L6 (2018). https://doi.org/10.1051/0004-6361/201833264
C.R. Markus, O. Asvany, T. Salomon, P.C. Schmid, S. Brünken, F. Lipparini, J. Gauss, S. Schlemmer, Phys. Rev. Lett. 124, 233401 (2020). https://doi.org/10.1103/PhysRevLett.124.233401
T. Michaelsen, B. Bastian, A. Ayasli, P. Strübin, J. Meyer, R. Wester, J. Phys. Chem. Lett. 11(11), 4331 (2020). https://doi.org/10.1021/acs.jpclett.0c01095
G. Czakó, T. Győri, B. Olasz, D. Papp, I. Szabó, V. Tajti, D.A. Tasi, Phys. Chem. Chem. Phys. 22, 4298 (2020). https://doi.org/10.1039/C9CP04944D
N. Bulut, A. Aguado, C. Sanz-Sanz, O. Roncero, J. Phys. Chem. A 123(41), 8766 (2019). https://doi.org/10.1021/acs.jpca.9b06081
V. Macaluso, D. Scuderi, M.E. Crestoni, S. Fornarini, D. Corinti, E. Dalloz, E. Martínez-Núñez, W.L. Hase, R. Spezia, J. Phys. Chem. A 123(17), 3685 (2019). https://doi.org/10.1021/acs.jpca.9b01779
A. Martin Somer, V. Macaluso, G.L. Barnes, L. Yang, S. Pratihar, K. Song, W.L. Hase, R. Spezia, J. Am. Soc. Mass Spectrometry 31(1), 2 (2020). https://doi.org/10.1021/jasms.9b00062
C.M. Nichols, Z.C. Wang, W.C. Lineberger, V.M. Bierbaum, J. Phys. Chem. Lett. 10(17), 4863 (2019). https://doi.org/10.1021/acs.jpclett.9b01997
B. Cunha de Miranda, C. Romanzin, S. Chefdeville, V. Vuitton, J. Žabka, M. Polášek, C. Alcaraz, J. Phys. Chem. A 119(23), 6082 (2015). https://doi.org/10.1021/jp512846v
A. Cernuto, A. Lopes, C. Romanzin, B. Cunha de Miranda, D. Ascenzi, P. Tosi, G. Tonachini, A. Maranzana, M. Polášek, J. Žabka, C. Alcaraz, J. Chem. Phys. 147(15), 154302 (2017). https://doi.org/10.1063/1.4990514
M. Polášek, E.L. Zins, C. Alcaraz, J. Žabka, V. Křížová, L. Giacomozzi, P. Tosi, D. Ascenzi, J. Phys. Chem. A 120(27), 5041 (2016). https://doi.org/10.1021/acs.jpca.5b12757
C.Y. Ng, Y. Xu, Y.C. Chang, A. Wannenmacher, M. Parziale, P.B. Armentrout, Phys. Chem. Chem. Phys. 23, 273 (2021). https://doi.org/10.1039/D0CP04333H
R. Tang, X. Fu, Y. Lu, C. Ning, J. Phys. Chem. Lett. 10(4), 702 (2019). https://doi.org/10.1021/acs.jpclett.8b03859
B. Joalland, N. Jamal-Eddine, D. Papanastasiou, A. Lekkas, S. Carles, L. Biennier, J. Chem. Phys. 150(16), 164201 (2019). https://doi.org/10.1063/1.5086386
J. Toscano, H.J. Lewandowski, B.R. Heazlewood, Phys. Chem. Chem. Phys. 22, 9180 (2020). https://doi.org/10.1039/D0CP00931H
B.R. Heazlewood, T.P. Softley, Nat. Rev. Chem. 5(2), 125 (2021). https://doi.org/10.1038/s41570-020-00239-0
K. Höveler, J. Deiglmayr, J.A. Agner, H. Schmutz, F. Merkt, Phys. Chem. Chem. Phys. 23, 2676 (2021). https://doi.org/10.1039/D0CP06107G
A.D. Dörfler, P. Eberle, D. Koner, M. Tomza, M. Meuwly, S. Willitsch, Nat. Commun. 10(1), 5429 (2019). https://doi.org/10.1038/s41467-019-13218-x
P. Rousseau, B.A. Huber, in Nanoscale Insights into Ion-Beam Cancer Therapy, ed. by A.V. Solov’yov (Springer International Publishing, 2017), chap. 4, pp. 121–157
P. Rousseau, A. Ławicki, A. Holm, M. Capron, R. Maisonny, S. Maclot, E. Lattouf, H. Johansson, F. Seitz, A. Méry, J. Rangama, H. Zettergren, S. Rosén, H. Schmidt, J.Y. Chesnel, A. Domaracka, B. Manil, L. Adoui, H. Cederquist, B. Huber, Nucl. Instrum. Methods Phys. Res. Sect. B 279, 140 (2012). https://doi.org/10.1016/j.nimb.2011.10.050
S. Maclot, R. Delaunay, D.G. Piekarski, A. Domaracka, B.A. Huber, L. Adoui, F. Martín, M. Alcamí, L. Avaldi, P. Bolognesi, S. Díaz-Tendero, P. Rousseau, Phys. Rev. Lett. 117, 073201 (2016). https://doi.org/10.1103/PhysRevLett.117.073201
B. Li, A.R. Allouche, J. Bernard, R. Brédy, D.B. Qian, X. Ma, S. Martin, L. Chen, J. Chem. Phys. 146(12), 124302 (2017). https://doi.org/10.1063/1.4978626
M.H. Stockett, H. Zettergren, L. Adoui, J.D. Alexander, U. Bērziņš, T. Chen, M. Gatchell, N. Haag, B.A. Huber, P. Hvelplund, A. Johansson, H.A.B. Johansson, K. Kulyk, S. Rosén, P. Rousseau, K. Støchkel, H.T. Schmidt, H. Cederquist, Phys. Rev. A 89, 032701 (2014). https://doi.org/10.1103/PhysRevA.89.032701
G.B. Sushko, I.A. Solov’yov, A.V. Solov’yov, Eur. Phys. J. D 70, 217 (2016). https://doi.org/10.1140/epjd/e2016-70283-5
P. de Vera, M. Azzolini, G. Sushko, I. Abril, R. Garcia-Molina, M. Dapor, I.A. Solov’yov, A.V. Solov’yov, Sci. Rep. 10(1), 20827 (2020). https://doi.org/10.1038/s41598-020-77120-z
S. Maclot, D.G. Piekarski, A. Domaracka, A. Méry, V. Vizcaino, L. Adoui, F. Martín, M. Alcamí, B.A. Huber, P. Rousseau, S. Díaz-Tendero, J. Phys. Chem. Lett. 4(22), 3903 (2013). https://doi.org/10.1021/jz4020234
S. Bari, P. Sobocinski, J. Postma, F. Alvarado, R. Hoekstra, V. Bernigaud, B. Manil, J. Rangama, B. Huber, T. Schlathölter, J. Chem. Phys. 128(7), 074306 (2008). https://doi.org/10.1063/1.2830032
D.G. Piekarski, R. Delaunay, S. Maclot, L. Adoui, F. Martín, M. Alcamí, B.A. Huber, P. Rousseau, A. Domaracka, S. Díaz-Tendero, Phys. Chem. Chem. Phys. 17, 16767 (2015). https://doi.org/10.1039/C5CP01628B
J. Kocisek, D.G. Piekarski, R. Delaunay, B.A. Huber, L. Adoui, F. Martín, M. Alcamí, P. Rousseau, A. Domaracka, J. Kopyra, S. Díaz-Tendero, J. Phys. Chem. A 119(37), 9581 (2015). https://doi.org/10.1021/acs.jpca.5b06009
D.G. Piekarski, R. Delaunay, A. Mika, S. Maclot, L. Adoui, F. Martín, M. Alcamí, B.A. Huber, P. Rousseau, S. Díaz-Tendero, A. Domaracka, Phys. Chem. Chem. Phys. 19, 19609 (2017). https://doi.org/10.1039/C7CP00903H
E. Erdmann, N.F. Aguirre, S. Indrajith, J. Chiarinelli, A. Domaracka, P. Rousseau, B.A. Huber, P. Bolognesi, R. Richter, L. Avaldi, S. Díaz-Tendero, M. Alcamí, M. Łabuda, Phys. Chem. Chem. Phys. 23, 1859 (2021). https://doi.org/10.1039/D0CP04890A
B. Oostenrijk, D. Barreiro, N. Walsh, A. Sankari, E.P. Månsson, S. Maclot, S.L. Sorensen, S. Díaz-Tendero, M. Gisselbrecht, Phys. Chem. Chem. Phys. 21, 25749 (2019). https://doi.org/10.1039/C9CP04221K
E. Wang, X. Shan, L. Chen, T. Pfeifer, X. Chen, X. Ren, A. Dorn, J. Phys. Chem. A 124(14), 2785 (2020). https://doi.org/10.1021/acs.jpca.0c02074
C. Frege, I.K. Ortega, M.P. Rissanen, A.P. Praplan, G. Steiner, M. Heinritzi, L. Ahonen, A. Amorim, A.K. Bernhammer, F. Bianchi, S. Brilke, M. Breitenlechner, L. Dada, A. Dias, J. Duplissy, S. Ehrhart, I. El-Haddad, L. Fischer, C. Fuchs, O. Garmash, M. Gonin, A. Hansel, C.R. Hoyle, T. Jokinen, H. Junninen, J. Kirkby, A. Kürten, K. Lehtipalo, M. Leiminger, R.L. Mauldin, U. Molteni, L. Nichman, T. Petäjä, N. Sarnela, S. Schobesberger, M. Simon, M. Sipilä, D. Stolzenburg, A. Tomé, A.L. Vogel, A.C. Wagner, R. Wagner, M. Xiao, C. Yan, P. Ye, J. Curtius, N.M. Donahue, R.C. Flagan, M. Kulmala, D.R. Worsnop, P.M. Winkler, J. Dommen, U. Baltensperger, Atmos. Chem. Phys. 18, 65 (2018). https://doi.org/10.5194/acp-18-65-2018
P. Markush, P. Bolognesi, A. Cartoni, P. Rousseau, S. Maclot, R. Delaunay, A. Domaracka, J. Kocisek, M.C. Castrovilli, B.A. Huber, L. Avaldi, Phys. Chem. Chem. Phys. 18, 16721 (2016). https://doi.org/10.1039/C6CP01940D
R. Delaunay, M. Gatchell, P. Rousseau, A. Domaracka, S. Maclot, Y. Wang, M.H. Stockett, T. Chen, L. Adoui, M. Alcamí, F. Martín, H. Zettergren, H. Cederquist, B.A. Huber, J. Phys. Chem. Lett. 6(9), 1536 (2015). https://doi.org/10.1021/acs.jpclett.5b00405
R. Delaunay, M. Gatchell, A. Mika, A. Domaracka, L. Adoui, H. Zettergren, H. Cederquist, P. Rousseau, B. Huber, Carbon 129, 766 (2018). https://doi.org/10.1016/j.carbon.2017.12.079
A. Domaracka, R. Delaunay, A. Mika, M. Gatchell, H. Zettergren, H. Cederquist, P. Rousseau, B.A. Huber, Phys. Chem. Chem. Phys. 20, 15052 (2018). https://doi.org/10.1039/C8CP01179F
P. Rousseau, D.G. Piekarski, M. Capron, A. Domaracka, L. Adoui, F. Martín, M. Alcamí, S. Díaz-Tendero, B.A. Huber, Nat. Commun. 11, 3818 (2020). https://doi.org/10.1038/s41467-020-17653-z
S. Bari, R. Hoekstra, T. Schlathölter, Phys. Chem. Chem. Phys. 12, 3376 (2010). https://doi.org/10.1039/B924145K
A.R. Milosavljević, P. Rousseau, A. Domaracka, B.A. Huber, A. Giuliani, Phys. Chem. Chem. Phys. 19, 19691 (2017). https://doi.org/10.1039/C7CP02075A
I. Tavernelli, Acc. Chem. Res. 48, 792 (2015). https://doi.org/10.1021/ar500357y
F. Spiegelmamn, N. Tarrat, J. Cuny, L. Dontot, E. Posenitskiy, C. Martí, A. Simon, M. Rapacioli, Adv. Phys. X 5(1), 1710252 (2019). https://doi.org/10.1080/23746149.2019.1710252
M. Gatchell, M.H. Stockett, N. de Ruette, T. Chen, L. Giacomozzi, R.F. Nascimento, M. Wolf, E.K. Anderson, R. Delaunay, V. Vizcaino, P. Rousseau, L. Adoui, B.A. Huber, H.T. Schmidt, H. Zettergren, H. Cederquist, Phys. Rev. A 92, 050702 (2015). https://doi.org/10.1103/PhysRevA.92.050702
S.J. Stuart, A.B. Tutein, J.A. Harrison, J. Chem. Phys. 112(14), 6472 (2000). https://doi.org/10.1063/1.481208
S. Plimpton, J. Comput. Phys. 117(1), 1 (1995). https://doi.org/10.1006/jcph.1995.1039
J.C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R.D. Skeel, L. Kalé, K. Schulten, J. Comput. Chem. 26(16), 1781 (2005). https://doi.org/10.1002/jcc.20289
I.A. Solov’yov, A.V. Yakubovich, P.V. Nikolaev, I. Volkovets, A.V. Solov’yov, J. Comput. Chem. 33(30), 2412 (2012). https://doi.org/10.1002/jcc.23086
H. da Silva, J. Oller, M. Gatchell, M.H. Stockett, P.A. Hervieux, L. Adoui, M. Alcamí, B.A. Huber, F. Martín, H. Cederquist, H. Zettergren, P. Rousseau, S. Díaz-Tendero, Phys. Rev. A 90, 032701 (2014). https://doi.org/10.1103/PhysRevA.90.032701
E. Martínez-Núñez, Phys. Chem. Chem. Phys. 17, 14912 (2015). https://doi.org/10.1039/C5CP02175H
A. Rodríguez, R. Rodríguez-Fernández, S.A. Vázquez, G.L. Barnes, J.J.P. Stewart, E. Martínez-Núñez, J. Comput. Chem. 39(23), 1922 (2018). https://doi.org/10.1002/jcc.25370
N.F. Aguirre, S. Díaz-Tendero, P.A. Hervieux, M. Alcamí, F. Martín, J. Chem. Theory Comput. 13, 992 (2017). https://doi.org/10.1021/acs.jctc.6b00984
C.A. Bauer, S. Grimme, J. Phys. Chem. A 120(21), 3755 (2016). https://doi.org/10.1021/acs.jpca.6b02907
L.G. Christophorou, D.L. McCorkle, A.A. Christodoulides, Electron Molecule Interactions and their Applications, vol. 1 & 2 (Academic Press, New York, 1984)
B. Boudaïffa, P. Cloutier, D. Hunting, M.A. Huels, L. Sanche, Science 287(5458), 1658 (2000). https://doi.org/10.1126/science.287.5458.1658
I. Baccarelli, I. Bald, F.A. Gianturco, E. Illenberger, J. Kopyra, Phys. Rep. 508(1), 1 (2011). https://doi.org/10.1016/j.physrep.2011.06.004
S. Ptasinska, S. Denifl, P. Scheier, E. Illenberger, T.D. Märk, Angew. Chem. Int. Ed. 44(42), 6941 (2005). https://doi.org/10.1002/anie.200502040
J. Kopyra, Phys. Chem. Chem. Phys. 14, 8287 (2012). https://doi.org/10.1039/C2CP40847C
I. Bald, I. Da̧bkowska, E. Illenberger, Angew. Chem. Int. Ed. 47(44), 8518 (2008). https://doi.org/10.1002/anie.200803382
A. Keller, I. Bald, A. Rotaru, E. Cauët, K.V. Gothelf, F. Besenbacher, ACS Nano 6(5), 4392 (2012). https://doi.org/10.1021/nn3010747
R. Meißner, J. Kočišek, L. Feketeová, J. Fedor, M. Fárník, P. Limão-Vieira, E. Illenberger, S. Denifl, Nat. Commun. 10(1), 2388 (2019). https://doi.org/10.1038/s41467-019-10340-8
A. Mauracher, O. Echt, A.M. Ellis, S. Yang, D.K. Bohme, J. Postler, A. Kaiser, S. Denifl, P. Scheier, Phys. Rep. 751, 1 (2018). https://doi.org/10.1016/j.physrep.2018.05.001
J. Ma, F. Wang, S.A. Denisov, A. Adhikary, M. Mostafavi, Sci. Adv. 3, 12 (2017). https://doi.org/10.1126/sciadv.1701669
M. Neustetter, J. Aysina, F.F. da Silva, S. Denifl, Angew. Chem. Int. Ed. 54(31), 9124 (2015). https://doi.org/10.1002/anie.201503733
J. Kočišek, A. Pysanenko, M. Fárník, J. Fedor, J. Phys. Chem. Lett. 7(17), 3401 (2016). https://doi.org/10.1021/acs.jpclett.6b01601
H. Hotop, M.W. Ruf, M. Allan, I.I. Fabrikant, B. Bederson, H. Walther, in Advances In Atomic, Molecular, and Optical Physics, vol. 49 (Academic Press, 2003), pp. 85–216. https://doi.org/10.1016/S1049-250X(03)80004-6
J.D. Gorfinkiel, Eur. Phys. J. D 74(3), 51 (2020). https://doi.org/10.1140/epjd/e2020-100550-7
R.F. da Costa, M.T.d.N. Varella, M.H.F. Bettega, M.A.P. Lima, Eur. Phys. J. D 69(6), 159 (2015). https://doi.org/10.1140/epjd/e2015-60192-6
I.I. Fabrikant, Eur. Phys. J. D 72(6), 96 (2018). https://doi.org/10.1140/epjd/e2018-90082-2
J. Med, Š. Sršeň, P. Slavíček, A. Domaracka, S. Indrajith, P. Rousseau, M. Fárník, J. Fedor, J. Kočišek, J. Phys. Chem. Lett. 11(7), 2482 (2020). https://doi.org/10.1021/acs.jpclett.0c00278
M. Allan, Phys. Rev. Lett. 98, 123201 (2007). https://doi.org/10.1103/PhysRevLett.98.123201
M. McAllister, M. Smyth, B. Gu, G.A. Tribello, J. Kohanoff, J. Phys. Chem. Lett. 6(15), 3091 (2015). https://doi.org/10.1021/acs.jpclett.5b01011
J. Kočišek, B. Sedmidubská, S. Indrajith, M. Fárník, J. Fedor, J. Phys. Chem. B 122(20), 5212 (2018). https://doi.org/10.1021/acs.jpcb.8b03033
O. Ingólfsson, F. Weik, E. Illenberger, Int. J. Mass Spectrom. Ion Process. 155(1), 1 (1996). https://doi.org/10.1016/S0168-1176(96)04392-3
J. Lengyel, J. Kočišek, M. Fárník, J. Fedor, J. Phys. Chem. C 120(13), 7397 (2016). https://doi.org/10.1021/acs.jpcc.6b00901
J. Poštulka, P. Slavíček, J. Fedor, M. Fárník, J. Kočišek, J. Phys. Chem. B 121(38), 8965 (2017). https://doi.org/10.1021/acs.jpcb.7b07390
M. Johny, J. Onvlee, T. Kierspel, H. Bieker, S. Trippel, J. Küpper, Chem. Phys. Lett. 721, 149 (2019). https://doi.org/10.1016/j.cplett.2019.01.052
K. Kitajima, H. Tsuchida, T. Majima, M. Saito, J. Chem. Phys. 150(9), 095102 (2019). https://doi.org/10.1063/1.5081883
B.W. LaFranchi, G.A. Petrucci, Int. J. Mass Spectrom. 258(1), 120 (2006). https://doi.org/10.1016/j.ijms.2006.06.013
Z. Li, A.R. Milosavljević, I. Carmichael, S. Ptasinska, Phys. Rev. Lett. 119, 053402 (2017). https://doi.org/10.1103/PhysRevLett.119.053402
T. Jahnke, U. Hergenhahn, B. Winter, R. Dörner, U. Frühling, P.V. Demekhin, K. Gokhberg, L.S. Cederbaum, A. Ehresmann, A. Knie, A. Dreuw, Chem. Rev. 120(20), 11295 (2020). https://doi.org/10.1021/acs.chemrev.0c00106
J.P. Toennies, A.F. Vilesov, Angew. Chem. Int. Ed. 43(20), 2622 (2004). https://doi.org/10.1002/anie.200300611
H. Linnartz, J. Cami, M. Cordiner, N.L.J. Cox, P. Ehrenfreund, B. Foing, M. Gatchell, P. Scheier, J. Mol. Spectrosc. 367, 111243 (2020). https://doi.org/10.1016/j.jms.2019.111243
K.R. Atkins, Phys. Rev. 116, 1339 (1959). https://doi.org/10.1103/PhysRev.116.1339
L.F. Gomez, E. Loginov, A.F. Vilesov, Phys. Rev. Lett. 108, 155302 (2012). https://doi.org/10.1103/PhysRevLett.108.155302
R. Rodríguez-Cantano, T. González-Lezana, P. Villarreal, Int. Rev. Phys. Chem. 35(1), 37 (2016). https://doi.org/10.1080/0144235X.2015.1132595
F. Calvo, J. Phys. Chem. A 119(23), 5959 (2015). https://doi.org/10.1021/jp510799h
F. Laimer, L. Kranabetter, L. Tiefenthaler, S. Albertini, F. Zappa, A.M. Ellis, M. Gatchell, P. Scheier, Phys. Rev. Lett. 123(16), 165301 (2019). https://doi.org/10.1103/PhysRevLett.123.165301
L. Tiefenthaler, J. Ameixa, P. Martini, S. Albertini, L. Ballauf, M. Zankl, M. Goulart, F. Laimer, K. von Haeften, F. Zappa, P. Scheier, Rev. Sci. Instrum. 91(3), 033315 (2020). https://doi.org/10.1063/1.5133112
M. Okumura, L.I. Yeh, Y.T. Lee, J. Chem. Phys. 83(7), 3705 (1985). https://doi.org/10.1063/1.449127
H.J. Zeng, N. Yang, M.A. Johnson, Faraday Discuss. 217, 8 (2019). https://doi.org/10.1039/C9FD00030E
E.K. Campbell, M. Holz, D. Gerlich, J.P. Maier, Nature 523(7560), 322 (2015). https://doi.org/10.1038/nature14566
M. Kuhn, M. Renzler, J. Postler, S. Ralser, S. Spieler, M. Simpson, H. Linnartz, A.G.G.M. Tielens, J. Cami, A. Mauracher, Y. Wang, M. Alcamí, F. Martín, M.K. Beyer, R. Wester, A. Lindinger, P. Scheier, Nat. Commun. 7, 13550 (2016). https://doi.org/10.1038/ncomms13550
M. Gatchell, P. Martini, F. Laimer, M. Goulart, F. Calvo, P. Scheier, Faraday Discuss. 217, 276 (2019). https://doi.org/10.1039/C8FD00178B
T. González-Lezana, O. Echt, M. Gatchell, M. Bartolomei, J. Campos-Martínez, P. Scheier, Int. Rev. Phys. Chem. 39(4), 465 (2020). https://doi.org/10.1080/0144235X.2020.1794585
H.T. Schmidt, Phys. Scr. T166, 014063 (2015). https://doi.org/10.1088/0031-8949/2015/t166/014063
R.D. Thomas, H.T. Schmidt, G. Andler, M. Björkhage, M. Blom, L. Brännholm, E. Bäckström, H. Danared, S. Das, N. Haag, P. Halldén, F. Hellberg, A.I.S. Holm, H.A.B. Johansson, A. Källberg, G. Källersjö, M. Larsson, S. Leontein, L. Liljeby, P. Löfgren, B. Malm, S. Mannervik, M. Masuda, D. Misra, A. Orbán, A. Paál, P. Reinhed, K.G. Rensfelt, S. Rosén, K. Schmidt, F. Seitz, A. Simonsson, J. Weimer, H. Zettergren, H. Cederquist, Rev. Sci. Instrum. 82(6), 065112 (2011). https://doi.org/10.1063/1.3602928
H.T. Schmidt, R.D. Thomas, M. Gatchell, S. Rosén, P. Reinhed, P. Löfgren, L. Brännholm, M. Blom, M. Björkhage, E. Bäckström, J.D. Alexander, S. Leontein, D. Hanstorp, H. Zettergren, L. Liljeby, A. Källberg, A. Simonsson, F. Hellberg, S. Mannervik, M. Larsson, W.D. Geppert, K.G. Rensfelt, H. Danared, A. Paál, M. Masuda, P. Halldén, G. Andler, M.H. Stockett, T. Chen, G. Källersjö, J. Weimer, K. Hansen, H. Hartman, H. Cederquist, Rev. Sci. Instrum. 84(5), 055115 (2013). https://doi.org/10.1063/1.4807702
R. von Hahn, A. Becker, F. Berg, K. Blaum, C. Breitenfeldt, H. Fadil, F. Fellenberger, M. Froese, S. George, J. Göck, M. Grieser, F. Grussie, E.A. Guerin, O. Heber, P. Herwig, J. Karthein, C. Krantz, H. Kreckel, M. Lange, F. Laux, S. Lohmann, S. Menk, C. Meyer, P.M. Mishra, O. Novotný, A.P. O’Connor, D.A. Orlov, M.L. Rappaport, R. Repnow, S. Saurabh, S. Schippers, C.D. Schröter, D. Schwalm, L. Schweikhard, T. Sieber, A. Shornikov, K. Spruck, S. Sunil Kumar, J. Ullrich, X. Urbain, S. Vogel, P. Wilhelm, A. Wolf, D. Zajfman, Review of Scientific Instruments 87(6), 063115 (2016). https://doi.org/10.1063/1.4953888
Y. Nakano, Y. Enomoto, T. Masunaga, S. Menk, P. Bertier, T. Azuma, Rev. Sci. Instrum. 88(3), 033110 (2017). https://doi.org/10.1063/1.4978454
S.P. Møller, Nucl. Instrum. Methods Phys. Res. Sect. A 394(3), 281 (1997). https://doi.org/10.1016/S0168-9002(97)00673-6
D. Zajfman, O. Heber, L. Vejby-Christensen, I. Ben-Itzhak, M. Rappaport, R. Fishman, M. Dahan, Phys. Rev. A 55, R1577 (1997). https://doi.org/10.1103/PhysRevA.55.R1577
H.T. Schmidt, H. Cederquist, J. Jensen, A. Fardi, Nucl. Instrum. Methods Phys. Res. Sect. B 173(4), 523 (2001). https://doi.org/10.1016/S0168-583X(00)00415-8
S.B. Nielsen, A. Lapierre, J.U. Andersen, U.V. Pedersen, S. Tomita, L.H. Andersen, Phys. Rev. Lett. 87, 228102 (2001). https://doi.org/10.1103/PhysRevLett.87.228102
H.B. Pedersen, A. Svendsen, L.S. Harbo, H.V. Kiefer, H. Kjeldsen, L. Lammich, Y. Toker, L.H. Andersen, Rev. Sci. Instrum. 86(6), 063107 (2015). https://doi.org/10.1063/1.4922826
T. Tanabe, K. Noda, M. Saito, S. Lee, Y. Ito, H. Takagi, Phys. Rev. Lett. 90, 193201 (2003). https://doi.org/10.1103/PhysRevLett.90.193201
S. Jinno, T. Takao, Y. Omata, A. Satou, H. Tanuma, T. Azuma, H. Shiromaru, K. Okuno, N. Kobayashi, I. Watanabe, Nucl. Instrum. Methods Phys. Res. Sect. A 532(1), 477 (2004). https://doi.org/10.1016/j.nima.2004.06.070
Y. Ebara, T. Furukawa, J. Matsumoto, H. Tanuma, T. Azuma, H. Shiromaru, K. Hansen, Phys. Rev. Lett. 117, 133004 (2016). https://doi.org/10.1103/PhysRevLett.117.133004
J. Bernard, G. Montagne, R. Brédy, B. Terpend-Ordacière, A. Bourgey, M. Kerleroux, L. Chen, H.T. Schmidt, H. Cederquist, S. Martin, Rev. Sci. Instrum. 79(7), 075109 (2008). https://doi.org/10.1063/1.2957609
J. Matsumoto, R. Saiba, K. Gouda, E. Makino, K. Hashimoto, K. Fueta, N. Kondo, H. Shiromaru, Nucl. Instrum. Methods Phys. Res. Sect. B 454, 23 (2019). https://doi.org/10.1016/j.nimb.2019.05.002
C. Meyer, A. Becker, K. Blaum, C. Breitenfeldt, S. George, J. Göck, M. Grieser, F. Grussie, E.A. Guerin, R. von Hahn, P. Herwig, C. Krantz, H. Kreckel, J. Lion, S. Lohmann, P.M. Mishra, O. Novotný, A.P. O’Connor, R. Repnow, S. Saurabh, D. Schwalm, L. Schweikhard, K. Spruck, S. Sunil Kumar, S. Vogel, A. Wolf, Phys. Rev. Lett. 119, 023202 (2017). https://doi.org/10.1103/PhysRevLett.119.023202
H.T. Schmidt, G. Eklund, K.C. Chartkunchand, E.K. Anderson, M. Kamińska, N. de Ruette, R.D. Thomas, M.K. Kristiansson, M. Gatchell, P. Reinhed, S. Rosén, A. Simonsson, A. Källberg, P. Löfgren, S. Mannervik, H. Zettergren, H. Cederquist, Phys. Rev. Lett. 119, 073001 (2017). https://doi.org/10.1103/PhysRevLett.119.073001
O. Novotný, P. Wilhelm, D. Paul, Á. Kálosi, S. Saurabh, A. Becker, K. Blaum, S. George, J. Göck, M. Grieser, F. Grussie, R. von Hahn, C. Krantz, H. Kreckel, C. Meyer, P.M. Mishra, D. Muell, F. Nuesslein, D.A. Orlov, M. Rimmler, V.C. Schmidt, A. Shornikov, A.S. Terekhov, S. Vogel, D. Zajfman, A. Wolf, Science 365(6454), 676 (2019). https://doi.org/10.1126/science.aax5921
G. Eklund, J. Grumer, S. Rosén, M. Ji, N. Punnakayathil, A. Källberg, A. Simonsson, R.D. Thomas, M.H. Stockett, P. Reinhed, P. Löfgren, M. Björkhage, M. Blom, P.S. Barklem, H. Cederquist, H. Zettergren, H.T. Schmidt, Phys. Rev. A 102, 012823 (2020). https://doi.org/10.1103/PhysRevA.102.012823
E.K. Anderson, A.F. Schmidt-May, P.K. Najeeb, G. Eklund, K.C. Chartkunchand, S. Rosén, Å Larson, K. Hansen, H. Cederquist, H. Zettergren, H.T. Schmidt, Phys. Rev. Lett. 124, 173001 (2020). https://doi.org/10.1103/PhysRevLett.124.173001
L.H. Andersen, O. Heber, D. Zajfman, J. Phys. B: At. Mol. Opt. Phys. 37(11), R57 (2004). https://doi.org/10.1088/0953-4075/37/11/r01
K. Hansen, J.U. Andersen, P. Hvelplund, S.P. Møller, U.V. Pedersen, V.V. Petrunin, Phys. Rev. Lett. 87, 123401 (2001). https://doi.org/10.1103/PhysRevLett.87.123401
L.H. Andersen, I.B. Nielsen, M.B. Kristensen, M.O.A. El Ghazaly, S. Haacke, M.B. Nielsen, M.Å. Petersen, J. Am. Chem. Soc. 127(35), 12347 (2005). https://doi.org/10.1021/ja051638j
D.W. Boo, Y. Ozaki, L.H. Andersen, W. Lineberger, J. Phys. Chem. A 101(36), 6688 (1997). https://doi.org/10.1021/jp9711353
A. Stolow, Annu. Rev. Phys. Chem. 54(1), 89 (2003). https://doi.org/10.1146/annurev.physchem.54.011002.103809
D.M. Neumark, Annu. Rev. Phys. Chem. 52(1), 255 (2001). https://doi.org/10.1146/annurev.physchem.52.1.255
J.R. Verlet, Chem. Soc. Rev. 37(3), 505 (2008). https://doi.org/10.1039/B700528H
D. Parker, R. Minns, T. Penfold, G. Worth, H. Fielding, Chem. Phys. Lett. 469(1–3), 43 (2009). https://doi.org/10.1016/j.cplett.2008.12.069
H.V. Kiefer, H.B. Pedersen, A.V. Bochenkova, L.H. Andersen, Phys. Rev. Lett. 117, 243004 (2016). https://doi.org/10.1103/PhysRevLett.117.243004
A. Svendsen, H.V. Kiefer, H.B. Pedersen, A.V. Bochenkova, L.H. Andersen, J. Am. Chem. Soc. 139(25), 8766 (2017). https://doi.org/10.1021/jacs.7b04987
H.V. Kiefer, E. Gruber, J. Langeland, P.A. Kusochek, A.V. Bochenkova, L.H. Andersen, Nat. Commun. 10(1), 1210 (2019). https://doi.org/10.1038/s41467-019-09225-7
F. Bierau, P. Kupser, G. Meijer, G. von Helden, Phys. Rev. Lett. 105(13), 133402 (2010). https://doi.org/10.1103/PhysRevLett.105.133402
M. Alghamdi, J. Zhang, A. Oswalt, J.J. Porter, R.A. Mehl, W. Kong, J. Phys. Chem. A 121(36), 6671 (2017). https://doi.org/10.1021/acs.jpca.7b05718
J.A. Hogan, M.F. Jarrold, J. Am. Soc. Mass Spectrom. 29(10), 2086 (2018). https://doi.org/10.1021/jasms.8b05683
R.N. Wolf, M. Eritt, G. Marx, L. Schweikhard, Hyperfine Interact. 199(1), 115 (2011). https://doi.org/10.1007/s10751-011-0306-8
R.K. Gangwar, K. Saha, O. Heber, M.L. Rappaport, D. Zajfman, Phys. Rev. Lett. 119, 103202 (2017). https://doi.org/10.1103/PhysRevLett.119.103202
K. Saha, A. Prabhakaran, V. Chandrasekaran, M.L. Rappaport, O. Heber, D. Zajfman, Rev. Sci. Instrum. 88(5), 053101 (2017). https://doi.org/10.1063/1.4982034
C.J. Johnson, B.B. Shen, B.L.J. Poad, R.E. Continetti, Rev. Sci. Instrum. 82(10), 105105 (2011). https://doi.org/10.1063/1.3641875
Y. Toker, O. Aviv, M. Eritt, M.L. Rappaport, O. Heber, D. Schwalm, D. Zajfman, Phys. Rev. A 76, 053201 (2007). https://doi.org/10.1103/PhysRevA.76.053201
Y. Toker, A. Svendsen, A.V. Bochenkova, L.H. Andersen, Angew. Chem. Int. Ed. 51(35), 8757 (2012). https://doi.org/10.1002/anie.201203746
K. Saha, V. Chandrasekaran, O. Heber, M.A. Iron, M.L. Rappaport, D. Zajfman, Nat. Commun. 9(1), 912 (2018). https://doi.org/10.1038/s41467-018-03197-w
A. Shahi, R. Singh, Y. Ossia, D. Zajfman, O. Heber, D. Strasser, Rev. Sci. Instrum. 90(11), 113308 (2019). https://doi.org/10.1063/1.5114908
N.J.A. Coughlan, B.D. Adamson, L. Gamon, K. Catani, E.J. Bieske, Phys. Chem. Chem. Phys. 17, 22623 (2015). https://doi.org/10.1039/C5CP03611A
W. Forst, Theory of unimolecular reactions (Academic Press (New York and London), 1973)
P.A. Hervieux, D.H.E. Gross, Z. Phys. D Atoms Mol. Clust. 33(4), 295 (1995). https://doi.org/10.1007/BF01437510
J.U. Andersen, E. Bonderup, K. Hansen, J. Phys. B: At. Mol. Opt. Phys. 35(5), R1 (2002). https://doi.org/10.1088/0953-4075/35/5/201
N. Kono, T. Furukawa, H. Tanuma, J. Matsumoto, H. Shiromaru, T. Azuma, K. Najafian, M.S. Pettersson, B. Dynefors, K. Hansen, Phys. Chem. Chem. Phys. 17, 24732 (2015). https://doi.org/10.1039/C5CP02549D
C.E. Klots, Z. Phys. D 21, 335 (1991)
K. Hansen, O. Echt, Phys. Rev. Lett. 78, 2337 (1997)
J.U. Andersen, C. Brink, P. Hvelplund, M.O. Larsson, B.B. Nielsen, H. Shen, Phys. Rev. Lett. 77, 3991 (1996). https://doi.org/10.1103/PhysRevLett.77.3991
P. Ferrari, E. Janssens, P. Lievens, K. Hansen, Int. Rev. Phys. Chem. 38(3–4), 405 (2019). https://doi.org/10.1080/0144235X.2019.1678929
M.H. Stockett, J. Houmøller, K. Støchkel, A. Svendsen, S. Brøndsted Nielsen, Rev. Sci. Instrum. 87(5), 053103 (2016). https://doi.org/10.1063/1.4948316
L.D. Landau, E.M. Lifshitz, Quantum Mechanics (Pergamon Press, London, 1959)
D.M. Brink, S. Stringari, Z. Phys. D 15, 257 (1990)
L. Bizzocchi, D. Prudenzano, V.M. Rivilla, A. Pietropolli-Charmet, B.M. Giuliano, P. Caselli, J. Martín-Pintado, I. Jiménez-Serra, S. Martín, M.A. Requena-Torres, F. Rico-Villas, S. Zeng, J.C. Guillemin, A&A 640, A98 (2020). https://doi.org/10.1051/0004-6361/202038083
J.A. Stearns, S. Mercier, C. Seaiby, M. Guidi, O.V. Boyarkin, T.R. Rizzo, J. Am. Chem. Soc. 129(38), 11814 (2007). https://doi.org/10.1021/ja0736010
G. Papadopoulos, A. Svendsen, O.V. Boyarkin, T.R. Rizzo, J. Am. Soc. Mass Spectrom. 23(7), 1173 (2012). https://doi.org/10.1021/jasms.8b04319
V. Kopysov, A. Makarov, O.V. Boyarkin, Anal. Chem. 87(9), 4607 (2015). https://doi.org/10.1021/acs.analchem.5b00822
H. Kang, G. Féraud, C. Dedonder-Lardeux, C. Jouvet, J. Phys. Chem. Lett. 5(15), 2760 (2014). https://doi.org/10.1021/jz5012466
L.S. Wang, J. Chem. Phys. 143(4), 040901 (2015). https://doi.org/10.1063/1.4927086
J.A. Noble, J.P. Aranguren-Abate, C. Dedonder, C. Jouvet, G.A. Pino, Phys. Chem. Chem. Phys. 21, 23346 (2019). https://doi.org/10.1039/C9CP04302K
B.M. Marsh, J.M. Voss, E. Garand, J. Chem. Phys. 143(20), 204201 (2015). https://doi.org/10.1063/1.4936360
M. Broquier, S. Soorkia, G. Pino, C. Dedonder-Lardeux, C. Jouvet, G. Grégoire, J. Phys. Chem. A 121(34), 6429 (2017). https://doi.org/10.1021/acs.jpca.7b06423
C. Dedonder, G. Féraud, C. Jouvet, J. Chem. Phys. 141(13), 131101 (2014). https://doi.org/10.1063/1.4896981
S. Chakrabarty, M. Holz, E.K. Campbell, A. Banerjee, D. Gerlich, J.P. Maier, J. Phys. Chem. Lett. 4(23), 4051 (2013). https://doi.org/10.1021/jz402264n
O.V. Boyarkin, Int. Rev. Phys. Chem. 37(3–4), 559 (2018). https://doi.org/10.1080/0144235X.2018.1547453
N.S. Nagornova, T.R. Rizzo, O.V. Boyarkin, Angew. Chem. Int. Ed. 52(23), 6002 (2013). https://doi.org/10.1002/anie.201301656
J.A. Wyer, (Springer Berlin Heidelberg, Berlin, Heidelberg, 2013), chap. 3, pp. 21–44. https://doi.org/10.1007/978-3-642-40190-9_3
A.M. Nagy, F.O. Talbot, M.F. Czar, R.A. Jockusch, J. Photochem. Photobiol. A 244, 47 (2012). https://doi.org/10.1016/j.jphotochem.2012.06.017
A.S. Danell, J.H. Parks, Int. J. Mass Spectrom. 229(1), 35 (2003). https://doi.org/10.1016/S1387-3806(03)00253-7
F.O. Talbot, A. Rullo, H. Yao, R.A. Jockusch, J. Am. Chem. Soc. 132(45), 16156 (2010). https://doi.org/10.1021/ja1067405
C. Kjær, H. Lissau, N.K. Gravesen Salinas, A. Østergaard Madsen, M.H. Stockett, F.E. Storm, T. Holm Hansen, J.U. Andersen, B.W. Laursen, K.V. Mikkelsen, M. Brøndsted Nielsen, S. Brøndsted Nielsen, ChemPhysChem 20(4), 533 (2019). https://doi.org/10.1002/cphc.201800933
M. Kordel, D. Schooss, C. Neiss, L. Walter, M.M. Kappes, J. Phys. Chem. A 114(17), 5509 (2010). https://doi.org/10.1021/jp100636x
V. Rajagopal, C. Stokes, A. Ferzoco, J. Am. Soc. Mass Spectrom. 29(2), 260 (2018). https://doi.org/10.1021/jasms.8b05741
J. Langeland, C. Kjær, L.H. Andersen, S. Brøndsted Nielsen, ChemPhysChem 19(14), 1686 (2018). https://doi.org/10.1002/cphc.201800225
J.T. Khoury, S.E. Rodriguez-Cruz, J.H. Parks, J. Am. Soc. Mass Spectrom. 13(6), 696 (2002). https://doi.org/10.1021/jasms.8b01800
J. Friedrich, J. Fu, C.L. Hendrickson, A.G. Marshall, Y.S. Wang, Rev. Sci. Instrum. 75(11), 4511 (2004). https://doi.org/10.1063/1.1795111
V. Frankevich, X. Guan, M. Dashtiev, R. Zenobi, Eur. J. Mass Spectrom. 11(5), 475 (2005). https://doi.org/10.1255/ejms.720
N.A. Sassin, S.C. Everhart, B.B. Dangi, K.M. Ervin, J.I. Cline, J. Am. Soc. Mass Spectrom. 20(1), 96 (2009). https://doi.org/10.1021/jasms.8b03299
K. Honma, Phys. Chem. Chem. Phys. 20(42), 26859 (2018). https://doi.org/10.1039/C8CP04067B
P. Tiwari, J.B. Metternich, M.F. Czar, R. Zenobi, J. Am. Soc. Mass Spectrom. 32(1), 187 (2021). https://doi.org/10.1021/jasms.0c00264
G.A. Eiceman, Z. Karpas, H.H. Hill Jr., Ion Mobility Spectrometry, 3rd edn. (CRC Press, London, 2013)
F. Lanucara, S.W. Holman, C.J. Gray, C.E. Eyers, Nat. Chem. 6(4), 281 (2014). https://doi.org/10.1038/nchem.1889
M.E. Ridgeway, M. Lubeck, J. Jordens, M. Mann, M.A. Park, Int. J. Mass Spectrom. 425, 22 (2018). https://doi.org/10.1016/j.ijms.2018.01.006
L. Deng, Y.M. Ibrahim, A.M. Hamid, S.V.B. Garimella, I.K. Webb, X. Zheng, S.A. Prost, J.A. Sandoval, R.V. Norheim, G.A. Anderson, A.V. Tolmachev, E.S. Baker, R.D. Smith, Anal. Chem. 88(18), 8957 (2016). https://doi.org/10.1021/acs.analchem.6b01915
R. Fromherz, G. Ganteför, A.A. Shvartsburg, Phys. Rev. Lett. 89, 083001 (2002). https://doi.org/10.1103/PhysRevLett.89.083001
M. Vonderach, O.T. Ehrler, P. Weis, M.M. Kappes, Anal. Chem. 83(3), 1108 (2011). https://doi.org/10.1021/ac1029677
G. Papadopoulos, A. Svendsen, O.V. Boyarkin, T.R. Rizzo, Faraday Discuss. 150, 243 (2011). https://doi.org/10.1039/C0FD00004C
B. Bellina, J.M. Brown, J. Ujma, P. Murray, K. Giles, M. Morris, I. Compagnon, P.E. Barran, Analyst 139, 6348 (2014). https://doi.org/10.1039/C4AN01656D
A.L. Simon, F. Chirot, C.M. Choi, C. Clavier, M. Barbaire, J. Maurelli, X. Dagany, L. MacAleese, P. Dugourd, Rev. Sci. Instrum. 86(9), 094101 (2015). https://doi.org/10.1063/1.4930604
O. Hernandez, S. Isenberg, V. Steinmetz, G.L. Glish, P. Maitre, J. Phys. Chem. A 119(23), 6057 (2015). https://doi.org/10.1021/jp511975f
S.J.P. Marlton, B.I. McKinnon, B. Ucur, A.T. Maccarone, W.A. Donald, S.J. Blanksby, A.J. Trevitt, Faraday Discuss. 217, 453 (2019). https://doi.org/10.1039/C8FD00212F
N.J.A. Coughlan, P.J.J. Carr, S.C. Walker, C. Zhou, M. Guna, J.L. Campbell, W.S. Hopkins, J. Am. Soc. Mass Spectrom. 31(2), 405 (2020). https://doi.org/10.1021/jasms.9b00039
B.D. Adamson, N.J.A. Coughlan, P.B. Markworth, R.E. Continetti, E.J. Bieske, Rev. Sci. Instrum. 85(12), 123109 (2014). https://doi.org/10.1063/1.4903753
S. Warnke, A. Ben Faleh, V. Scutelnic, T.R. Rizzo, J. Am. Soc. Mass Spectrom. 30(11), 2204 (2019). https://doi.org/10.1021/jasms.8b06266
J. Gidden, M.T. Bowers, J. Am. Soc. Mass Spectrom. 14, 161 (2003). https://doi.org/10.1021/jasms.8b01923
A.G.G.M. Tielens, Rev. Mod. Phys. 85(3), 1021 (2013). https://doi.org/10.1103/RevModPhys.85.1021
B.A. Croiset, A. Candian, O. Berné, A.G.G.M. Tielens, Astron. Astrophys. 590, A26 (2016). https://doi.org/10.1051/0004-6361/201527714
H. Andrews, A. Candian, A.G.G.M. Tielens, Astron. Astrophys. 595, A23 (2016). https://doi.org/10.1051/0004-6361/201628819
M.S. Murga, M.S. Kirsanova, A.I. Vasyunin, Y.N. Pavlyuchenkov, Mon. Not. R. Astron. Soc. 497(2), 2327 (2020). https://doi.org/10.1093/mnras/staa2026
A. Simon, M. Rapacioli, G. Rouaut, G. Trinquier, F.X. Gadea, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 375(2092), 20160195 (2017). https://doi.org/10.1098/rsta.2016.0195
P. Castellanos, A. Candian, J. Zhen, H. Linnartz, A.G.G.M. Tielens, Astron. Astrophys. 616, A166 (2018). https://doi.org/10.1051/0004-6361/201833220
Wiersma, Sandra D., Candian, Alessandra, Bakker, Joost M., Martens, Jonathan, Berden, Giel, Oomens, Jos, Buma, Wybren Jan, Petrignani, Annemieke, A&A 635, A9 (2020). https://doi.org/10.1051/0004-6361/201936982
J. Cami, J. Bernard-Salas, E. Peeters, S.E. Malek, Science 329, 1180 (2010). https://doi.org/10.1126/science.1192035
J. Zhen, P. Castellanos, D.M. Paardekooper, H. Linnartz, A.G.G.M. Tielens, Astrophys. J. 797(2), L30 (2014). https://doi.org/10.1088/2041-8205/797/2/L30
H. Andrews, C. Boersma, M.W. Werner, J. Livingston, L.J. Allamandola, A.G.G.M. Tielens, Astrophys. J. 807(1), 99 (2015). https://doi.org/10.1088/0004-637X/807/1/99
Y.A. Dyakov, C.K. Ni, S.H. Lin, Y.T. Lee, A.M. Mebel, Phys. Chem. Chem. Phys. 8, 1404 (2006). https://doi.org/10.1039/B516437K
E.A. Solano, P.M. Mayer, J. Chem. Phys. 143(10), 104305 (2015). https://doi.org/10.1063/1.4930000
M. Hanine, Z. Meng, S. Lu, P. Xie, S. Picaud, M. Devel, Z. Wang, Astrophys. J. 900(2), 188 (2020). https://doi.org/10.3847/1538-4357/abab06
P. Parneix, A. Gamboa, C. Falvo, M. Bonnin, T. Pino, F. Calvo, Mol. Astrophys. 7, 9 (2017). https://doi.org/10.1016/j.molap.2017.05.001
M. Rapacioli, A. Simon, C.C.M. Marshall, J. Cuny, D. Kokkin, F. Spiegelman, C. Joblin, J. Phys. Chem. A 119(51), 12845 (2015). https://doi.org/10.1021/acs.jpca.5b09494
C.J. Mackie, A. Candian, X. Huang, E. Maltseva, A. Petrignani, J. Oomens, W.J. Buma, T.J. Lee, A.G.G.M. Tielens, Phys. Chem. Chem. Phys. 20, 1189 (2018). https://doi.org/10.1039/C7CP06546A
J. Lam, S. Abdul-Al, A.R. Allouche, J. Chem. Theory Comput. 16(3), 1681 (2020). https://doi.org/10.1021/acs.jctc.9b00964
Acknowledgements
The authors are supported by a VIDI grant (723.014.007) of A.P. from The Netherlands Organisation for Scientific Research (NWO).
Funding
Open access funding provided by Stockholm University.
Author information
Authors and Affiliations
Contributions
All authors contributed equally through the writing of the individual sections in the manuscript. All authors have read and approved the final manuscript.
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zettergren, H., Domaracka, A., Schlathölter, T. et al. Roadmap on dynamics of molecules and clusters in the gas phase. Eur. Phys. J. D 75, 152 (2021). https://doi.org/10.1140/epjd/s10053-021-00155-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-021-00155-y