1 Introduction

Electron scattering on molecules of biological importance has become a frequently discussed topic since the publication of the results of Boudaïffa and coworkers in 2000 [1]. They showed that electrons below the ionization threshold can induce single- and double-strand breaks in DNA, which echoed widely in radiation chemistry. Although this manifestation of electron–matter interaction is of great importance, there are many other fields that benefit from the studies of scattering phenomena, in particular astrochemistry [2, 3], atmospheric physics [3], astrophysics [4], or technologies of thin film deposition, such as FEBID [5]. Further discussion on the applications of electron–molecule interactions in nature and technologies can be found, for example, in [6, 7]. One of the most interesting processes, from both applicational and fundamental points of view, is dissociative electron attachment (DEA), a possible route of decay after forming the temporary negative ion (TNI). TNI is an object consisting of an impinging electron and a molecule with negative electron affinity (EA), that is whose energy is below that of an anion. Such a system, with a lifetime significantly longer than the time needed for an electron to pass through the molecule, can arise through a resonant process, of which there are several types, divided historically into two main groups of shape and Feshbach resonances [8, 9].

Theoretical studies on electron–molecule interactions are particularly difficult when it comes to considerations about unstable states, like TNI. Certainly, the most formally correct methods are those applied in scattering calculations, such as the multichannel Schwinger method [10], or R-matrix approach [11], providing resonance parameters, but relatively computationally demanding and sophisticated. Other approaches, applied to determine the electron affinity for transient states, consist of, e.g., stabilization [12] or scaling method [13]. EA is defined as the energy difference between the ground neutral and anion state:

$$\begin{aligned} \text {EA} = \text {E(neutral)} - \text {E(anion)} \end{aligned}$$
(1)

If adiabatic EA is negative, in standard quantum chemical methods the extra electron should tend to escape from the molecule’s surroundings, since this minimizes the energy. Methods relying on obtaining the electron affinity from the energy difference with common methods like Hartree–Fock (HF) or density functional theory (DFT) are therefore formally incorrect. However, there are numerous works on the determination of electron affinity using the DFT method, with reasonable results [14,15,16] and in good agreement with the experimental data. This is explained, in short, by basis set finiteness and mutual error cancellation [14]. As for the DFT method, it should be noted that it suffers from a disadvantages even for some stable anions due to an incorrect self-repulsion cancellation [17]. This effect is manifested by the positive energy of the singly occupied molecular orbital (SOMO) and sometimes mitigated if a nonlocal potential is incorporated, as, for example, in hybrid functionals. Pyridine ring is present, for instance, in niacin and pyridoxine (B vitamins), as well as in nicotine and anabasine, agrochemicals and pharmaceuticals. Niacin and its derivatives have been found in Murchison [18, 19] and Tagish Lake [20] chondrites, which is one of the reasons why pyridine is of interest in astrochemical experiments [21]. Pyrazine derivatives occur in riboflavin and folacin, a variety of pharmaceuticals and flavor compounds. Pyrazine-based nucleic acid has also been considered as a prebiotic RNA precursor [22].

Pyridine [23,24,25,26,27,28,29,30,31] and pyrazine [27, 28, 32,33,34] are fairly well studied for its interaction with electrons, both experimentally and theoretically. Pyridine has negative electron affinity and displays three \(\pi ^*\) resonances in the low-energy regime, which has B\(_1\), A\(_2\) (shape resonances) and B\(_1\) (mixed-type resonance) symmetry, from the lowest to highest energy. In pyrazine, also three low-lying \(\pi ^*\) resonant structures: \(^2\)B\(_{3u}\), \(^2\)A\(_u\) (shape) and \(^2\)B\(_{2g}\) (mixed), have been found both in calculations and experiment, although there are indications that the \(^2\)B\(_{3u}\) state is stable.

Halogenated derivatives of pyridine and pyrazine are crucial intermediates for pharmaceuticals and agrochemicals [35,36,37]. Forming of pyridyl radicals from halopyridines is important in, e.g., astrochemical [38], environmental [39] or corrosion [40] experimental studies. The effect of the substituent on the orbitals in pyridine has been studied extensively (e.g., [41, 42] and references therein). However, to the author’s knowledge, there are no experimental or theoretical data on the interaction of electrons with halopyrazines and the only existing data concerning halo derivatives of pyridine, determined with electron transmission spectrometer (ETS), can be found in [31, 43]. Electron affinities in their work were obtained as the vertical midpoint of the overall band in the derivative of the transmitted current spectra. This quantity is proportional to the total cross section on electron scattering, and the midpoint is assumed to be approximately the vertical attachment energy (vertical electron affinity with the opposite sign).

In this work, we employ the DFT with B3LYP functional on pyridine, pyrazine and their chloro and bromo derivatives to determine the electron affinities and potential energy curves along the path of the anion dissociation into the atom X\(=\)H, Cl, Br (this designation will be used throughout the text) and the remaining fragment. Electron affinities and dissociation enthalpies were also calculated using Møller–Plesset second-order perturbation theory (MP2) [44].

2 Methods

All calculations were performed with Gaussian 16 suite [45]. Vertical electron affinities (VEAs) were obtained according to Eq. (1), with both species in optimized neutral geometry. For the pyrazines, whose anions in \(\pi ^*\) state may be stable, an optimization of anions has been performed and adiabatic electron affinities (AEAs) are also given. Various basis sets were selected to assess their impact on the quality of the results: 6-31G*, 6-311G**, 6-31+G*, 6-311++G** and aug-cc-pVTZ were applied in B3LYP and MP2 methods. The optimization of neutrals and anions was performed together with frequencies calculation, under no symmetry constraints. A series of VEAs calculations were performed in each diffuse basis to ensure that the obtained SOMO is the lowest possible, taking into account that in calculations with basis sets extended by diffuse functions SOMO could have a different symmetry. Configurations with reversed order of \(\pi \)* and \(\sigma \)* orbitals were tested as well as forcing the symmetry. Only the results where the lowest SOMO is found to be of a different type than \(\pi \)* are shown. For all investigated molecules, four other functionals were also applied (namely \(\omega \)B97XD [46], CAM-B3LYP [47], PBE0 [48] and PBE0DH [49]) with diffuse basis sets (6-31+G*, 6-311++G** and aug-cc-pVTZ) and the results are shown in Table 1 and 2 in the supplementary material. All potential energy curves (PECs) along the C\(_{\text {n}}\)-X bond were obtained at B3LYP/6-31+G* level of theory, since increasing the basis set does not change the electron affinity significantly and MP2 considerably underestimates VEAs of examined molecules, as discussed in Sec. 3.1. The keywords opt=ModRedundant allowing the modification of a redundant coordinate (C\(_{\text {n}}\)-X bond in this case) and pop=always for Mulliken population analysis at every step were used for the initial scan. For each molecule, four potential energy curves were determined, one of the neutral compounds (the reference curve) with unrestricted B3LYP and guess=mix keyword for the HOMO and LUMO mixing, and three curves of anion dissociation: of \(\pi ^*\) state, \(\sigma ^*\) state and with no symmetry constraints, that is a \(\pi ^*\)/\(\sigma ^*\) mixed curve, see Sect. 3.2. All PECs are relaxed, i.e., optimized with respect to all the geometric parameters except the C\(_{\text {n}}\)-X bond length. The numbering of atoms in pyridine and pyrazine rings, labeled in the following tables and figures as Py and Pz, respectively, is shown in Fig. 1.

3 Results and conclusions

3.1 Vertical and adiabatic electron affinities

Table 1 Calculated VEAs (eV) obtained at various levels of theory
Full size table
Fig. 1
figure 1

Designations of individual atoms comprising pyridine (Py) and pyrazine (Pz) used for description of PECs and dihedral angles. For halo derivatives, one of the H atoms is replaced by Cl or Br and the numbering does not change

Full size image

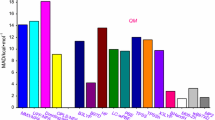
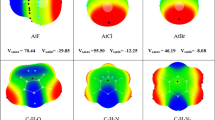
Table 1 and Fig. 2 present the results of vertical electron affinity calculations. Other available experimental and theoretical data are summarized in Table 2. The following conclusions can be drawn for pyridines: (1) Inclusion of the diffuse functions causes augmentation and reordering of LUMO orbitals. This can be seen in Table 1 where in boxes with two values the lower corresponds to the diffuse type of SOMO orbital. Computing sets particularly sensitive to this effect are MP2/6-311++G** and MP2/aug-cc-pVTZ. Of course, the molecule itself and its permanent dipole moment are crucial. The lowest anion \(\pi ^*\) resonant orbital and the diffuse state are depicted in Fig. 3a and b, respectively.

Fig. 2
figure 2

Calculated VEAs to the lowest \(\pi ^*\) orbital, obtained at various levels of theory

Full size image

(2) VEAs obtained with B3LYP functional generally converge to certain values as the basis set increases (ignoring the effect of changing the symmetry of the SOMO orbital), faster than in MP2 calculations. The accordance of these values with available experimental data is mediocre. As shown in Fig. 4, the greatest discrepancy is found for the 4-substituted pyridines. All of the applied methods and basis sets, including functionals other than B3LYP (see the supplementary material), predict similar VEAs for the 2-, 3- and 4-chloropyridine, whereas the experimental VEAs for 4-chloropyridine are higher than for the other two molecules. The reasons may be the following: (1) The VEA obtained by Modelli et al. for 4-chloropyridine is marked to be the upper limit value and is obtained from the differential cross section at high angles, unlike for the rest of halopyridines; (2) the potential energy curves of 4-substituted pyridines are repulsive in the equilibrium range of r\(_{\text {C}_n-\text {X}}\) and neutral and anionic curve cross near the equilibrium, whereas the theory applied does not include the vibrational states into account and this might cause discrepancies. Unfortunately, there are no data for 2- and 3-bromopyridine, so this explanation can only be proposed for further investigation.

Table 2 Experimental (Refs. [26,27,28, 31, 43]) and theoretical (Refs. [23, 24, 32]) positions of the first resonances in electron scattering
Full size table

Table 3 contains equilibrium distances and adiabatic electron affinities with and without zero-point correction for pyrazines. Pyrazine anion in terms of the density functional theory changes character from unstable to stable if the diffuse functions and zero-point corrections are included, but the electron affinity stays near zero. In MP2, however, it remains unstable. For pyrazine derivatives, it is difficult to determine the correctness of computed data as experimental data are lacking. Based on the results for the rest of molecules, that B3LYP underestimates VEAs, it can be concluded that the VEAs of halo pyrazines are positive. This is in accordance with intuition, since pyrazine has a near-zero affinity and the replacement of hydrogen with a halogen atom stabilizes the anion.

3.2 Potential energy curves

All neutral optimized molecules are of planar geometry.

Fig. 3
figure 3

a \(\pi ^*\) orbital representing the first resonance in pyridine, obtained with B3LYP/6-31+G*. b SOMO diffuse \(\sigma ^*\) pyridine orbital obtained with MP2/6-31+G*. c 2-chloropyrazine SOMO orbital at the distance r\(_{\text {C}_{\text {n}}\text {-Cl}}\) = 2.27 Å, obtained with B3LYP/6-31+G*

Full size image
Fig. 4
figure 4

Comparison of calculated VEAs with available experimental data for halopyridines

Full size image
Table 3 Adiabatic electron affinities (eV) with and without zero-point correction (ZPC) for pyrazines. r\(_{\text {C}_{\text {n}}\text {-X}}\) (Å) is the equilibrium distance in optimized anions, obtained at B3LYP/6-31+G* level of theory
Full size table

For pyridine, only the PEC of C\(_4\)-H\(_{10}\) is shown (Fig. 5), since the PECs of the C\(_3\)-H\(_9\) and C\(_5\)-H\(_11\) bonds are qualitatively very similar. PECs for pyrazines are depicted in Fig. 6 and for 2-,3- and 4-halopyridines in Fig. 7. Parameters of the curves, i.e., equilibrium C\(_{\text {n}}\)-X distance for neutral molecules, activation energies and enthalpies of the following reactions:

$$\begin{aligned}&\text {R}-\text {H} + e^-_{0} \rightarrow \text {R}^- + \text {H}^{\bullet } \end{aligned}$$
(2)
$$\begin{aligned}&\text {R}-\text {Y} + e^-_{0} \rightarrow \text {R}^{\bullet } + \text {Y}^- \end{aligned}$$
(3)

are indicated in Table 4, where \(e_0^-\) is the thermal (near-zero eV) electron, Y here is chlorine or bromine, R\(^{\bullet }\)/R\(^-\) is the pyridyne or pyrazine radical/anion, and all species are in their ground state. The typical behavior of investigated molecules during bond stretching is the change of the dihedral angle (‘wagging angle,’ see, e.g., [50] and references therein) containing the ring plane and the X atom to about \(40^{\circ }\). This happens at the distance of the intersection of pure \(\pi ^*\) and dissociative \(\sigma ^*\) state, where the adiabatic curve deviates from the \(\pi ^*\) curve and avoided crossing occurs (Fig. 3c). At larger distances, initially the molecule becomes planar again, but then the \(\sigma ^*\) state is the SOMO and eventually the X atom detaches. The analysis of C-X bond dissociation in anions of 5-halouracils performed by Li et al. [51] with B3LYP functional showed a trend very similar to that described above. As can be seen from the PECs, for all molecules the dissociation to the excited radical (without symmetry change) is highly endothermic. Pyridine and pyrazine PECs are quite similar, but pyrazine anion \(\pi ^*\) curve is very close to the neutral at short distances. It should be noted here that the \(\sigma ^*\) state for all molecules is deformed below the \(\pi ^*\)-\(\sigma ^*\) intersection distance, due to the diffuse functions inclusion. According to calculations with B3LYP/6-31+G*, B3LYP/aug-cc-pVTZ and MP2/6-31+G*, separation of one of the hydrogens from pyridine requires around 3.30 - 3.75 eV, depending on the position (see Table 4), which is in a good agreement with the results of Ryszka et al. [29], obtained with cbs-qb3 method. However, they observed a weak signal for the formation of [Py-H]\(^-\) anion by DEA at 2.5, 5.3, 7.0 and 9.0 eV, so the first peak is much below the reaction threshold.

Fig. 5
figure 5

Potential energy curve of one of the C-H bonds in pyridine obtained at B3LYP/6-31+G* level

Full size image
Fig. 6
figure 6

Potential energy curves of pyrazines obtained with B3LYP/6-31+G*. For the numbering of atoms, the reader is referred to Fig. 1

Full size image

The adiabatic curves of halopyridine anions do not show a minimum in the region of neutral molecule equilibrium, or the minimum is very shallow. (The activation energy is close to zero.) It is also manifested in the attempts of optimization to the \(\pi ^*\) state, in the form of imaginary frequency indicating the wagging angle. The PECs of 3- and 4-substituted halopyridines reveal another minimum at larger distance that corresponds to the \(\sigma ^*\) dissociative state, stable with respect to the neutral, and with all real frequencies. The halopyrazines curves have a minimum in \(\pi ^*\) state slightly shifted from the neutral curve toward longer distance, as well as shallow \(\sigma ^*\) minimum.

According to B3LYP calculations, the enthalpy of LEE-induced dissociation (Eq. (3)) for 2-substituted pyridines and pyrazines is a low-energy reaction or even exothermic in both 6-31+G* and aug-cc-pVTZ basis set. For all halopyridines, the enthalpy of the reaction from Eq. (3) is close to zero and fulfills the equation:

$$\begin{aligned} \Delta H + \text {VEA} < 0, \end{aligned}$$
(4)

so in fact the VEA determines the energy required for dissociation. (The dissociation products are stable with respect to the anion energy.) This is consistent with the halogen anion formation from 4-ClPy and 4-BrPy at 0.26 eV and 0.10 eV, respectively, observed by Modelli et al. [43]. The agreement between enthalpies obtained with the B3LYP functional and MP2 method in 6-31+G* basis is excellent for pyridine and pyrazine, but rather poor for halo derivatives. Similarly to B3LYP, enthalpies of halopyridines calculated with MP2/6-31+G* satisfy Eq. (4) and dissociation of halopyrazines is energetically unfavorable after electron attachment. To determine the most likely products of dissociation of the studied molecules, the Mulliken charge and spin analysis were performed on the B3LYP/6-31+G* level of theory for every point on the adiabatic potential energy curves of anions (Fig. 8). At large distances in halo derivatives, almost all of the charge (around −0.9) is deposited on the halogen atom with spin density dropping to around 0, the slowest in 4-substituted pyridines. In pyridine and pyrazine, most of the charge is localized on the ring, whereas about −0.2 charge and 0.8 spin are carried by the hydrogen atom. The transition from \(\pi ^*\) to \(\sigma ^*\) state is clearly visible in the sharp changes of spin density. It should be noted that in Hartree–Fock calculations in the \(r\rightarrow \infty \) limit, the charge and spin should go to integer values, which is not the case in DFT. This is a well-known problem [52,53,54] related to the use of DFT method for the determination of the potential energy curves, another consequence of the self-interaction error. Roughly speaking, in certain conditions there is a solution in which part of the charge is accumulated on the electronegative fragment and part on the electropositive one. Anions affected the most by this method are pyridine and pyrazine, which can be concluded from Fig. 8. Charge distributions on the dissociating neutral molecules are also seriously flawed (see Fig. 9a) but neutrals are not the subject of study in this work. Charge in the anions of halo derivatives according to DFT and HF is similar (Fig. 9b).

Table 4 Selected parameters of PECs for investigated compounds. Equilibrium distances (Å) were obtained with 6-31+G* basis set. Activation energies and enthalpies of reactions described by Eq. (2) and Eq. (3) are given in kcal/mol (eV)
Full size table
Fig. 7
figure 7

Potential energy curves obtained with B3LYP/6-31+G*. For the numbering of atoms, the reader is referred to Fig. 1

Full size image
Fig. 8
figure 8

Mulliken charges (upper) and spin densities (lower) on the X atom along the adiabatic potential energy curve of anion molecules

Full size image
Fig. 9
figure 9

B3LYP and Hartree–Fock charges on Cl on the points of potential energy curve along C-Cl bond in 4-chloropyridine for the neutral molecule (upper) and anion (lower)

Full size image

4 Final remarks

Vertical electron affinities of pyridine and 2- and 3-chloropyridine are in satisfactory agreement with the experimental data if the diffuse functions are included, whereas the theoretical VEAs of 4-substituted pyridines are significantly lower, which may originate from the lack of the treatment of the vibrational motion in the applied approach. If the B3LYP functional is used with diffuse basis sets (6-31+G*, 6-311++G** and aug-cc-pVTZ), the position of the substituent affects the VEA (in general, the farther the position from nitrogen atom, the greater the affinity), but less than the type of substituent. (Bromo-substituted molecules have greater VEAs than chloro substituted.) There is no significant improvement when increasing the basis set from 6-31+G* to aug-cc-pVTZ. SOMOs obtained with MP2 are more sensitive to inclusion of diffuse functions than those calculated with the B3LYP functional, and values of VEAs within this method are generally more sensitive to enlargement of basis set. This method also considerably underestimates vertical electron affinities and presumably enthalpies of anion dissociation. Obtained potential energy curves indicate that the SOMO of all anion molecules undergoes a symmetry change from \(\pi ^*\) first resonant state to \(\sigma ^*\) when the bond C\(_\text {n}\)-X is stretched. The extra electron stays at the ring in pyrazine and pyridine or at halogen atom in case of halo derivatives. Curves of 2-substituted halopyridines have no minimum, or the minimum is very shallow, whereas 3- and 4-substituted have quite clearly marked, although still rather flat minimum at larger C\(_\text {n}\)-X distance, corresponding to the \(\sigma ^*\) dissociative state. The detachment of chlorine or bromine atom should be achievable at VEA energy, which is the confirmation of previous results of Modelli et al. for 4-substituted pyridines [43]. Anions of halopyrazines according to DFT are stable, and the activation energy to pass to the \(\sigma ^*\) state is 3.79 kcal/mol and 5.78 kcal/mol for 2-bromo- and 2-chloropyrazine, respectively. Although PECs obtained with DFT functionals are quite problematic and require special care, in case of investigated anions B3LYP gives reasonable results.