1 Introduction

One of the most critical industries that secure the future of human energy is the nuclear industry. Fusion reactors such as the International Thermonuclear Experimental Reactor (ITER) have been developed to produce and confine the plasma [1]. The choice of beryllium as the first wall of the fusion reactor is due to the fact that it is a light element with unique properties. So one of the elemental impurities in the reactor chamber can be the beryllium ions, which can enter the plasma due to wall erosion. Avoiding the dangerous and disadvantageous consequences of impurities, it is a critical point how they can be detected and eliminated from the plasma. Beryllium ions can collide with the ground and excited state of the hydrogen atoms; therefore, the accurate knowledge of these reaction cross sections are essential in fusion research. The accurate state-selective charge exchange cross sections are also extremely important in the charge exchange recombination spectroscopy (CXRS) [2].

The total and partial cross sections for the charge exchange in collisions between \(\hbox {Be}^{\mathrm {4+}}\) and ground state hydrogen atoms were already studied using classical and different quantum-mechanical models [3,4,5,6,7,8,9,10,11,12]. Cornelius et al. [13] and Hoekstra et al. [14] have calculated the charge exchange cross sections into the final states n, in collisions of \(\hbox {Be}^{\mathrm {4+}}\) with an excited hydrogen atom (\(\hbox {H}(n = 2\))) by the classical trajectory Monte Carlo method (CTMC). Igenbergs et al. [15] and Shimakura et al. [16] have studied the charge exchange cross sections in \(\hbox {Be}^{\mathrm {4+}}\)–\(\hbox {H}(n = 2)\) collision system in the framework of atomic-orbital close-coupling (AOCC) and molecular orbital close-coupling (MOCC) methods, respectively. Errea et al. [5] have computed the total and n-partial cross sections at low impact energies for charge exchange in \(\hbox {Be}^{{4+}}+ \hbox {H}(1s, 2s)\) collisions using quantum-mechanical and semiclassical approaches.

The success of different approaches strongly depends on their ability to describe the many-body character of the collisions. The CTMC method is a well-known method to describe atomic collision cross sections. The CTMC method is a non-perturbative method where classical equations of motions are solved numerically, and the initial conditions are chosen randomly [3, 12, 15]. The classical trajectory Monte Carlo method has succeeded in dealing with the charge exchange processes in ion atom collisions [3, 12]. One of the advantages of this method is that many-body interactions are taken into account during the collisions on a classical level.

In the present work, we focus on the charge exchange cross sections in collisions between \(\hbox {Be}^{\mathrm {4+}}\) and excited state hydrogen atoms, H(n,l,m). We calculate the state-selective cross sections from \(\hbox {H}(2{s}, 2{p}m)\) to \(\hbox {Be}^{{3+}}(2l, 3l, 4l)\) states as a function of the projectile energy. Calculations are made using the three-body classical trajectory Monte Carlo method for impact energies between 10 and 200 keV/amu. Since there is no experimental data in \(\hbox {Be}^{{4+}}\) and H(2lm) collision system, we compare our results with the previous theoretical results.

2 Theory

In the three-body configuration, a projectile, an electron, and a target nucleus interact with each other according to net Coulomb potential.

The Hamiltonian equation for the three particles is defined as:

$$\begin{aligned} H=T+V_{\mathrm{coul}}, \end{aligned}$$
(1)

where

$$\begin{aligned} T=\frac{\mathbf {P}_{p}^{2}}{2m_{p}}+\frac{{\mathbf {P}}_{\mathrm{e}}^{2}}{2m_{\mathrm{e}}}+\frac{{\mathbf {P}}_{T}^{2}}{2m_{T}} , \end{aligned}$$
(2)

and

$$\begin{aligned} V_{\mathrm{coul}}=\frac{Z_{p}Z_{\mathrm{e}}}{\left| {\mathbf {r}}_{p}-{\mathbf {r}}_{\mathrm{e}} \right| }+\frac{Z_{\mathrm{e}}Z_{T}}{\left| {\mathbf {r}}_{\mathrm{e}}-{\mathbf {r}}_{T} \right| }+\frac{Z_{p}Z_{T}}{\left| {\mathbf {r}}_{p}-{\mathbf {r}}_{T} \right| }, \end{aligned}$$
(3)

are the total kinetic energy and potential energy of the interaction system, \({\mathbf {r}}\), \({\mathbf {p}}\), Z and m are the position vector, momentum vector, the charge and the mass of the given particles (p; projectile, e; electron, T; target), respectively.

The equations of motion arising from the Hamiltonian mechanics according to relative position \({\mathbf {A}}={\mathbf {r}}_{\mathrm{e}}-{\mathbf {r}}_{T}\mathrm {,} {\mathbf {B}}={\mathbf {r}}_{T}-{\mathbf {r}}_{p}\) and \({\mathbf {C}}={\mathbf {r}}_{p}-{\mathbf {r}}_{\mathrm{e}}\), are given as follows:

$$\begin{aligned} \ddot{{\mathbf {A}}}= & {} \left\{ \frac{N_{\mathrm{e}}Z_{p}Z_{\mathrm{e}}}{\left| {\mathbf {A}}+{\mathbf {B}} \right| ^{3}}+\frac{\left( N_{\mathrm{e}}+N_{T} \right) Z_{\mathrm{e}}Z_{T}}{\left| {\mathbf {A}} \right| ^{3}} \right\} {\mathbf {A}}\nonumber \\&+\left\{ \frac{N_{\mathrm{e}}Z_{p}Z_{\mathrm{e}}}{\left| {\mathbf {A}}+{\mathbf {B}} \right| ^{3}}-\frac{N_{T}Z_{p}Z_{T}}{\left| {\mathbf {B}} \right| ^{3}} \right\} {\mathbf {B}} \end{aligned}$$
(4)
$$\begin{aligned} \ddot{{\mathbf {B}}}= & {} \left\{ \frac{N_{p}Z_{p}Z_{\mathrm{e}}}{\left| {\mathbf {A}}+{\mathbf {B}} \right| ^{3}}-\frac{N_{T}Z_{\mathrm{e}}Z_{T}}{\left| {\mathbf {A}} \right| ^{3}} \right\} {\mathbf {A}}\nonumber \\&+\left\{ \frac{\left( N_{T}+N_{p} \right) Z_{p}Z_{T}}{\left| {\mathbf {B}} \right| ^{3}}+\frac{N_{p}Z_{p}Z_{\mathrm{e}}}{\left| {\mathbf {A}}+{\mathbf {B}} \right| ^{3}} \right\} {\mathbf {B}}, \end{aligned}$$
(5)

where \(N_{i}=\frac{1}{m_{i}}\). The total cross sections and the statistical uncertainty are given by:

$$\begin{aligned} \sigma= & {} \frac{2\pi b_{\mathrm{max}}}{T_{N}}\sum \nolimits _j b_{j}^{(i)} \end{aligned}$$
(6)
$$\begin{aligned} \Delta \sigma= & {} \sigma \left( \frac{T_{N}-T_{N}^{(i)}}{T_{N}T_{N}^{(i)}} \right) ^{1\big /2}, \end{aligned}$$
(7)

where \(T_{N}\) is the total number of trajectories calculated for impact parameters less than \(b_{\mathrm{max}}\), \(T_{N}^{(i)}\) and \(b_{j}^{(i)}\) are the number of trajectories and the actual impact parameter for the trajectory corresponding to the charge exchange processes.

Fig. 1
figure 1

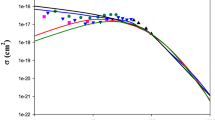
Total cross sections for charge exchange in \(\hbox {Be}^{{4+}}+ \hbox {H}(2s)\) collision as a function of the impact energy. Solid red line presents CTMC results, (

figure b
) semi-classical results of Errea et al. for H(2s) target [5], (
figure c
) AOCC results of Igenbergs et al. for H(2s) target [15], (
figure d
) AOCC results of Igenbergs et al. for \(\hbox {H}(n= 2)\) target [15], (
figure e
) CTMC results of Hoekstra et al. for \(\hbox {H}(n = 2)\) target [14]

Full size image
Fig. 2
figure 2

Total cross sections for charge exchange in \(\hbox {Be}^{{4+}}+ \hbox {H}(2{p}m)\) collision as a function of the impact energy. Solid red line presents CTMC results for H(2p0) target, Solid green line presents CTMC results for \(\hbox {H}(2{p}+1)\) target, Solid black dash line presents CTMC results for H\((2p-1)\) target, (

figure f
) AOCC results of Igenbergs et al. for H(2p) target [15], (
figure g
) AOCC results of Igenbergs et al. for \(\hbox {H}(n = 2)\) target [15], (
figure h
) CTMC results of Hoekstra et al. for \(\hbox {H}(n = 2)\) target [14]

Full size image
Table 1 nl state-selective cross sections (in \(\hbox {cm}^{{2}})\) for \(\hbox {Be}^{{4+}}+\hbox {H(2s)}\)
Full size table
Table 2 nl state-selective cross sections (in \(\hbox {cm}^{{2}})\) for \(\hbox {Be}^{{4+}}+\hbox {H(2p0)}\)
Full size table

In the CTMC calculations, the energy level E of an electron after the excitation is determined simply by calculating its binding energy \(U = -E\). A classical principal quantum number is assigned according to:

$$\begin{aligned} n_{\mathrm{c}}=Z_{T}Z_{\mathrm{e}}\sqrt{ \left( \frac{\mu _{Te}}{2U} \right) }, \end{aligned}$$
(8)

where \(\mu _{Te}\) is the reduced mass of the target nucleus and the target electron. The classical orbital angular momentum is defined by

$$\begin{aligned} l_{\mathrm{c}}=\sqrt{m_{\mathrm{e}}\left[ \left( x\dot{y}-y\dot{x} \right) ^{2}+\left( x\dot{z}-z\dot{x} \right) ^{2}+\left( y\dot{z}-z\dot{y} \right) ^{2} \right] } ,\nonumber \\ \end{aligned}$$
(9)

where x, y, and z are the Cartesian coordinates of the electron relative to the nucleus. The magnetic quantum number m is determined via uniform binning of the classical ratio of the z-component of the angular momentum \(m_{\mathrm{c}}\) to the total angular momentum \(l_{\mathrm{c}}\) [17]

$$\begin{aligned} m_{\mathrm{c}}=\frac{\left( l+1\big /2 \right) }{l_{\mathrm{c}}}, \end{aligned}$$
(10)

where l is the orbital quantum number. The classical values of \(n_{\mathrm{c}}\), \(l_{\mathrm{c}}\), and \(m_{\mathrm{c}}\) are quantized to a specific levels n, l, and m if they satisfy the relations [17,18,19]:

$$\begin{aligned}&\left[ \left( n-1 \right) \left( n-1/2 \right) n \right] ^{1/3}\le n_{\mathrm{c}}\le \left[ \left( n+1 \right) \left( n+1/2 \right) n \right] ^{1/3}\nonumber \\ \end{aligned}$$
(11)
$$\begin{aligned}&l\le \frac{n}{n_{\mathrm{c}}}l_{\mathrm{c}}\le l+1 \end{aligned}$$
(12)
$$\begin{aligned}&\frac{2m-1}{2l+1} \le \frac{m_{\mathrm{c}}}{l_{\mathrm{c}}} <\frac{2m+1}{2l+1}. \end{aligned}$$
(13)

3 Results

In our case, the charge exchange process is defined by equation:

$$\begin{aligned} \hbox {Be}^{{4+}}+ \hbox {H}(2{\textit{lm}}) \rightarrow \hbox {Be}^{{3+}}({\textit{nl}})+ \hbox {H}^{{+}}. \end{aligned}$$
(14)

For the determination of the state-selective charge exchange cross sections, we calculated \(5\times 10^{{6}}\) individual trajectories for each collision energies. Figure 1 shows our results of the total charge exchange cross sections in \(\hbox {Be}^{{4+}}+\hbox {H(2s)}\). The comparison was made with the quantum-mechanical results based on the AOCC method [15] and the semi-classical approach [5] for H(2s). We also show the results for \(\hbox {H}(n = 2)\) target based on the classical simulation [14] and on the AOCC models[15].

At low energies, our CTMC cross sections from H(2s) state into the Be bound states are in good agreement with the results of Igenbergs et al. [15]. At the same time at higher energies, our CTMC cross-section data are significantly smaller than the data of Igenbergs et al. [15] and closer to the cross sections calculated from \(\hbox {H}(n=2)\) state by Hoekstra et al. [14] and Igenbergs et al. [15]. We note that all cross sections calculated using the semiclassical approach [5] are higher than any other results.

Table 3 nl state-selective cross sections (in \(\hbox {cm}^{\mathrm {2}}\)) for \(\hbox {Be}^{\mathrm {4+}}+\hbox {H}(2\hbox {p}+1)\)
Full size table
Table 4 nl state-selective cross sections (in \(\hbox {cm}^{{2}}\)) for \(\hbox {Be}^{{4+}}+\hbox {H}(2p-1)\)
Full size table

Figure 2 shows the total charge exchange cross sections from H(2lm) corresponding to orbital quantum numbers \(l = 1\) and magnetic quantum numbers m (\({-}\) 1, 0, 1), respectively. Our results compared to different theoretical approach, namely an atomic orbital close coupling for H(2p) and \(\hbox {H}(n= 2)\) as the target [15] and CTMC for \(\hbox {H}(n = 2)\) [14]. The cross sections from \(\hbox {H}(n = 2)\) are matched to present cross sections from H(2lm) below 100 keV/amu impact energies. Also, at low impact energies, the AOCC results of Igenbergs et al. [15] for H(2p) target are in good agreement with our H(2lm) results. Our results show that the cross sections corresponding from the \(\hbox {H}(2p0)\), \(\hbox {H}(2\hbox {p}+1)\), and \(\hbox {H}(2p-1)\) states almost coincide with each other, and the differences are hardly visible. Our CTMC results for nl state-selective charge exchange cross section in \(\hbox {Be}^{{4+}}+ \hbox {H}(2s, 2p0, 2\hbox {p}+1, 2p-1\)) collisions for different subshells of Be are given in Tables 1, 2, 3 and 4.

4 Conclusion

A three-body classical trajectory Monte Carlo method was preformed to calculate the nl state-selective charge exchange cross sections in \(\hbox {Be}^{{4+}}+\) H(2lm) collisions in the energy range between 10 and 200 keV/amu. \(5\times 10^{{6}}\) individual trajectories for each collision energies have been calculated. The state-selective cross sections for charge exchange into \(\hbox {Be}^{{3+}}\)(nl) (\(\textit{nl} = 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f)\) states as a function of impact energy were presented. As a result of the large number of classical trajectories the uncertainty of the cross sections are less than 1%. Due to the lack of experimental data for the investigated collision system, we compared our results with the theoretical approaches. We found that the CTMC method can able to describe reasonably the cross sections of the charge exchange channel from the excited states of H atom.