Precursor state of chemi-ionization reactions and confinement of valence electrons by anisotropic intermolecular forces

Abstract

Modifications in atomic alignment and in molecular alignment/orientation determine a different structure of the adduct, formed by collisions of reagents, which represents the precursor state of many elementary chemical–physical processes. The following evolution of the system is directly controlled by the confinement of interacting partners in such a precursor state. However, a deep characterization of these phenomena is still today not fully available, especially when weak intermolecular forces are operative, although the inquiry is of general relevance for the control of the stereodynamics of processes, occurring under a variety of conditions both in gas phase and at surface. In this paper recent advances in the knowledge of the selective role of atomic alignment and molecular orientation effects on the stereodynamics of chemi-ionization reactions will be presented and discussed. These advances represent a basic step along a path whose final target is the complete and internally consistent rationalization and revaluation of the experimental findings already obtained, and published, in our and in other laboratories on chemi-ionization reactions involving as reagent molecules which are of great relevance in several fields. The basic idea is to export important guidelines provided by a recent detailed study of chemi-ionization of noble gas atoms to more complex reactions involving molecules. The main focus of the present paper is on the quantum confinement effects of valence electrons within the reaction transition state.

Graphic abstract

1 Introduction

Understanding the mode-specificity in reaction dynamics of open-shell atoms, free radicals, molecules, atomic and molecular ions, under hyper-thermal, thermal and sub-thermal conditions is a general topic of fundamental importance for catalysis, plasmas, photo-dynamics as well as interstellar and low-temperature chemistry. However, a pivotal target to assess the selectivity of the molecular dynamics under a variety of conditions is the knowledge of strength, anisotropy and radial dependence of the leading intermolecular interaction components which drive two-body collisions. A basic component of the intermolecular interaction is the charge transfer (CT). Despite CT affects a relevant variety of phenomena [1], its role is not fully understood, being difficult to characterize at the high level of detail often required. They include harpooning, coulomb explosion, proton transfer and the formation of intermolecular halogen and hydrogen bonds. CT can also affect structure and stability of the precursor state of several elementary chemical reactions, determining their following evolution towards the final products.

Chemi-ionization processes, also known as Penning or auto-ionization phenomena [2,3,4], represent barrier-less reactions promoted by collisions of a neutral reagent, exhibiting a sufficiently high internal energy content, with an atomic/molecular partner leading to the formation of ionic products. Such processes are driven by an anisotropic optical potential, whose real part controls approach of reactants and removing of products, while the imaginary part triggers the passage from neutral reactants to ionic products through a selective electronic rearrangement. The investigation at microscopic level of these reactions is important for fundamental research, to assess the coherent control of reactive events at low temperature and then to explore the quantum nature of matter [5], and also for the applied research, to exploit the soft ionization in the development of mass spectrometry technique [6] and to prepare particular ionic clusters [7]. However, detailed information on radial and angular dependences of the optical potential is rather limited since the quantitative relations between real and imaginary part of the optical potential and basic components of the intermolecular forces involved are still lacking. In particular, their strength is often smaller than few meV (a fraction of kJ/mol) and then they are very difficult to obtain by ab initio methods.

Main focus of this paper is on the selective role of anisotropic CT, a fundamental component of the intermolecular interaction affecting both real and imaginary parts of the optical potential, on the stereo-dynamics of chemi-ionization processes promoted by collisions of an open shell atom, electronically excited in a high energetic metastable state, with another atomic/molecular partner. The reactions give rise to the spontaneous emission of electrons accompanied by the formation of parent ions, aggregate ions and fragmentation ions as final products. Particular attention is addressed to structure and stability of the adduct formed by collisions of reagents which represents the confined environment where all basic electronic rearrangements triggering the reactions occur. In particular, the measure of the energy dependence of electrons, emitted by single collision events and known as Penning Ionization Electron Spectra (PIES), represents a sort of spectroscopic investigation of the collision complex [8,9,10]: it provides direct information on the occurring electronic rearrangements, which directly correlates with structure and stability the precursor transition state of involved reactions. According to the different structure of the adduct, molecular ionization probability and emitted PIES are strongly dependent on symmetry and energy of the atomic or molecular orbital from which the electron is extracted and ends, and then on their spatial orientation within the collision complex [11,12,13].

Recent advances obtained in our laboratory and concerning the characterization of the selectivity of the electronic rearrangements which drive the stereo-dynamics of chemi-ionization reactions will be presented and discussed in the next sections. In particular, in the following we summarize basic details of the chemi-ionization stereo-dynamics, obtained in our laboratory on two prototype processes [11, 12, 14,15,16,17,18], in order to emphasize better the focus of our present research, indicating also important perspectives.

2 Structure of the collision complex and observables

Figure 1 shows a metastable $\hbox {Ne}^{*}$atom, whose external electron is excited in the 3s orbital and its ionic core exhibits the same electronic configuration of the fluorine (a high electron affinity species), that approaches to a krypton atom or to a water molecule. The adducts formed by the collision events are depicted in the same figure and their structure emphasizes the different environments where the valence electrons are confined. The selectivity of the electronic rearrangements, which drive the reactions stereo-dynamics, is directly controlled by the features of quantum states populated by valence electrons in such environments.

It is of relevance to note that in both cases at large separation distance $\hbox {Ne}^{*}$, whose external electronic configuration is $2s^{2}2p^{5}3s^{1}$, exhibits the same chemical-physical properties of a sodium atom, while at short distances the properties of its ionic core $\hbox {Ne}^{+}$, an open shell fluorine-like atom, emerge. In particular, decreasing the intermolecular distance, a pronounced polarization of the “floppy” external electronic cloud of $\hbox {Ne}^{*}$ becomes effective, which promotes in the case of collision with Kr the formation a potential box where an ionic core [Ne–Kr]$^{+}$ is surrounded by a Rydberg electron (See upper panel of Fig. 1). However, in the case of water, its high permanent electric dipole leads to the formation of an adduct exhibiting a different polarization of the external electronic cloud (See intermediate and lower panels in Fig. 1). In particular, the approach towards the hydrogen atom of water favors, at intermediate distances, the formation of a weak intermolecular hydrogen bond which hinders the reactivity. On the other hand, the approach on the oxygen side promotes a different polarization, with the disclosure of the open shell $\hbox {Ne}^{+}$ ionic core, a halogen-like species, that favors the reactivity stimulated by CT. Therefore, in $\hbox {Ne}^{*}$-Kr and $\hbox {Ne}^{*}$-$H_{2}\hbox {O}$ systems, the confined environment changes and, as a consequence, stability and structure of the reaction precursor state are different.

The spontaneous jump of the electron from one valence atomic orbitals of Kr, or from one of HOMO orbitals of water, to the ionic core of $\hbox {Ne}^{*}$ releases enough energy to eject the 3s electron with a defined kinetic energy. Therefore, the measure of the energy dependence of emitted electrons, also known as Penning Ionization Electron Spectra (PIES), provides direct information on the electronic rearrangements occurring within the collision complex, which directly correlates with basic selectivity of the reactions. In particular, ionization probability and emitted PIES are strongly dependent on symmetry and energy of the atomic/molecular orbital from which the electron is extracted and ends, and consequently on their spatial orbital orientation within the collision complex [11,12,13].

In the case of Kr, we have been able to resolve in PIES shown in Fig. 2, measured with the experimental apparatus presented in the next section, the contribution of the different spin orbit states of reagents and products [14, 15]. Moreover, for important hydrogenated molecules, as water, ammonia and hydrogen sulfide, we characterized in detail the selectivity of the molecular orbital orientation promoting the formation of molecular ion in the ground and in the excited electronic state. The PIES measured for water with the same apparatus is also given in Fig. 2, while results obtained for other systems have been reported and discussed in detail elsewhere [10, 11]. It has been also demonstrated [10, 11, 14,15,16,17,18,19] that position, relative height and area of peaks in PIES depend on the critical balance of the intermolecular forces driving the collision dynamics along specific reaction channels.

However, the dependence of the reaction probability on the half-filled valence orbital alignment of open-shell atoms still represents a basic open question. Recently, our investigation focused on atom–atom $\hbox {Ne}^{*}$-Ng ($\hbox {Ng} = \hbox {Ar}$, Kr, Xe), in order to obtain information on this basic target [14,15,16,17,18,19]. These are prototype cases for which the achievement of the target has been facilitated, since molecular ion fragmentation is absent. Some of the new insights, obtained on the stereo-dynamics of elementary processes involved in the specific case of Kr, are summarized in the next sections, where implications of general relevance for many other processes are presented and discussed.

Fig. 1

Upper panel The approach of the metastable $\hbox {Ne}^{*}(^{3}\hbox {P}_{\mathrm{J}})$ atom to Kr with the formation of [Ne–Kr]$^{+}$ ionic core surrounded by a Rydberg electron. Middle panel The approach of the metastable $\hbox {Ne}^{*}(^{3}\hbox {P}_{\mathrm{J}})$ atom to water on the oxygen side where the propensity to form a weak intermolecular halogen bond is emphasized. Lower panel The approach of the metastable $\hbox {Ne}^{*}(^{3}\hbox {P}_{\mathrm{J}})$ atom to water on the hydrogen side where the propensity to form a weak intermolecular hydrogen bond is emphasized

Fig. 2

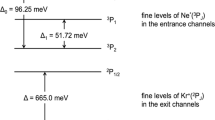
Upper panel The PIES spectra of $\hbox {Ne}^{*}$-Kr system measured at a collision energy of 50 meV: the contributions of the reaction channels, related to the two different spin-orbit J states of $\hbox {Ne}^{*}$ ($J_{i} = 2$,0) and to the $\hbox {Kr}^{+}$ ionic products ($J_{f} = 3/2$, 1/2), have been resolved. The relative reaction yields of the four investigated channels have been determined by evaluation of the peak area ratios, via an analysis using four independent Gaussian functions with the same width [15, 16]. Lower panel The $\hbox {Ne}^{*}$-$\hbox {H}_{2}\hbox {O}$ PIES measured at low collision energy (40 meV), where the contributions of reactions leading to the formation of the water ion in the ground X and in the first excited electronic state A are resolved [11] and reported for a comparison

3 Experimental apparatus and theoretical framework

The experimental device, used to investigate the dynamics of chemi-ionization reactions involving as reagents $\hbox {Ne}^{*}$ and Kr or $\hbox {Ne}^{*}$ and a hydrogenated molecule, has been presented in detail in refs. [11, 16] and a schematic view is given in Fig. 3.

Fig. 3

The scheme of the experimental apparatus: a beam of $\hbox {Ne}^{*}(^{3}\hbox {P}_{2,0})$ atoms emerges from an electron bombardment supersonic source and crosses at right angles a beam of the target reagent (atomic or molecular) species. PIES spectra have been recorded by a hemispherical electron energy analyzer and the product ions are detected by a quadrupole mass filter

Shortly, it is a molecular beam (MB) apparatus, formed by a noble gas beam source from which the emerging Ne atoms are electronically excited by collisions with energetic electrons. The $\hbox {Ne}^{*}$ MB crosses at right angles the MB of target species. PIES are measured by exploiting a hemispherical electron energy analyzer, while total, partial ionization cross sections Q and branching ratios (BRs), with their collision energy dependence, are obtained adopting the mass spectrometry technique coupled with time-of-flight measurement. In the present case, BRs of relevance are also those associated to the relative formation probability of the parent ion $\hbox {Kr}^{+}$ and of the ionic adduct $\hbox {Kr}^{+}$–Ne, also indicated as associated ion.

The real V and imaginary part $\varGamma$ of the optical potential have been obtained in analytical form, adopting few parameters having a proper physical meaning, exploiting the ample phenomenology of the interaction of open shell species. This phenomenology has been characterized by using the scattering of state selected atomic beams and suitable theoretical schemes for the analysis of measured scattering observables [20]. An extended analysis of interaction potentials so characterized permitted to correlated strength and range of the leading interaction components to the fundamental physical properties of involved partners and then to develop empirical and semi-empirical methods useful for their representation [20]. Total, partial and associative ionization cross section, of great interest in our study, have been calculated within the semiclassical method [2, 3].

4 Results, discussion and perspectives

Results of recent experiments [15, 16], performed at low collision energy and under high resolution conditions, as stressed above, permitted us to separate in measured PIES the contributions of entrance and exit channels referred to specific spin-orbit levels J of $\hbox {Ne}^{*}$ reagent and of $\hbox {Kr}^{+}$ product, which are both open shell species. In Fig. 2 is reported the comparison of PIES measured for the ionization of Kr and $\hbox {H}_{2}\hbox {O}$ under very similar collision energy conditions. Moreover, PIES for Kr and Xe have been also measured as a function of the collision energy and obtained results and their analysis provided the dependences on the collision energy of the peak positions, related to the change of the precursor (transition) state stability, and of the peak area ratios, determined by the change of relative reaction yields [15, 16].

These experimental findings, coupled with the ample phenomenology achieved in our laboratory on the anisotropic dynamical behavior of open-shell atoms [20], suggested us that electronic rearrangements driving the reaction directly arise from polarization of external-floppy cloud of the 3s electron, charge transfer and modifications of angular momentum couplings of other valence electrons within the collision complex, which defines all properties of the reaction precursor state. The adopted interaction potential formulation, recently discussed in detail elsewhere [18, 19], suggests that entrance and exit channels must be considered as belonging to a manifold of coupled states of the same system, confined in the same environment. All rearrangements are also accompanied by adiabatic and non-adiabatic effects, which play a crucial role in the control of the collision dynamics [14,15,16,17,18,19].

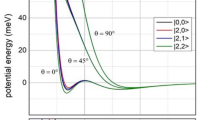
In particular, adiabatic effects mostly arise from strength and selectivity of configuration interaction which couples entrance and exit channels, having the same molecular symmetry and differing for one electron exchange (see left panel of Fig. 4, where it is shown that in entrance channels most part of the anisotropy arises from the open shell nature of $\hbox {Ne}^{+}$ ion). They affect the anisotropic behavior of the real part of the optical potential and account for the adiabatic conversion of atomic states, defined in terms of J, $\varOmega$ quantum numbers, where J represents the total electronic angular momentum of open shell species and $\varOmega$ describes its absolute projection along the inter-atomic electric field direction, into molecular states of $\Sigma$ and $\Pi$ symmetry. The latter are emerging only at short separation distances, where the increased inter-atomic electric field destroys the atomic spin-orbit levels J forming molecular states identified by the quantum number $\Lambda$ (the absolute projection of the orbital electronic angular momentum along the inter-atomic distance). While the atomic states are representative of the system at large distances, at short distances, $\Sigma$ and $\Pi$ denote molecular states having $\Lambda =0$ and $\Lambda =1$, respectively. Moreover, the state conversion involves both entrance and exit channels and the effective interaction components, defining the real part V of the optical potential, obtained following guidelines reported in refs. [18, 19], are plotted in the right panel of Fig. 4.

Fig. 4

Left panel Representation of the configuration interaction, between states of entrance and exit channels differing for one electron exchange, which defines the CT contribution for $\Sigma$ states. The corresponding component for $\Pi$ states is much smaller ($\sim$ 1/5) [15, 16] because of the reduced overlap integral between atomic half-filled orbital exchanging the electron and aligned orthogonal to R. Right panels The real part V of the optical potential represented by adiabatic potential energy curves that are formulated in an internally consistent way for both entrance and exit channels and indicated as $V_{|J, \Omega \rangle }$. The interaction anisotropy at long range depends on the polarizability anisotropy of $\hbox {Ne}^{*}$atom and of $\hbox {Kr}^{+}$ ion, while, at intermediate and short range, it arises from anisotropic charge transfer (CT) contributions associated to configuration interaction between states differing for one electron exchange

The imaginary $\varGamma$ components, defined in terms of quantum numbers proper of entrance and exit channels, are controlled by strength and radial dependence of non-adiabatic effects. They arise again from polarization, selective configuration interactions, changes in electron angular momentum couplings, spin-orbit and Coriolis contributions. Such components obtained according to the criteria discussed in refs. [18, 19], are plotted in the left panels of Fig. 5. An important point to be stressed is that the nature of the interaction components, determining both real and imaginary parts of the optical potential, clearly indicates that the two parts must be interdependent. As indicated in the previous section, we have provided their formulation in terms of fundamental physical properties of the interacting partners, and this is a crucial aspect for its generalization to more complex systems. From Figs. 4 and 5, that provide a summary of main results reported in ref. [18], it appears that in the internuclear distance range of 3–5 Å, mainly probed under thermal collision conditions, both V and $\Gamma$ parts of the optical potential are rather weak ($\Gamma$ varies from 1 to 0.1 meV, i.e. 0.1–0.01 kJ/mol). It has been also demonstrated [18, 19] that their strength and anisotropy directly control the stereo-dynamics selectivity, as shortly reported below.

Fig. 5

Left panel The state-to-state imaginary components $\varGamma$ of the optical potential, defined in terms of J and $\varOmega$ quantum numbers, as $|J,\Omega \rangle$, of $\hbox {Ne}^{*}$ ($^{3}\hbox {P}_{\mathrm{J}}$) reagent , with $J=2$ and $J=0$, and of $\hbox {Kr}^{+}(^{2}\hbox {P}_{\mathrm{J}})$ product, with $\hbox {J}=3/2$ and $J= 1/2$. Right panel The radial dependence of the $\Sigma$ character in entrance ($C_{x}$) and exit ($C_{y}$) channels, the $\Pi$ character is defined as complement to 1 of the $\Sigma$ one. All states accessible to the system are indicated in terms of J and $\varOmega$ quantum numbers as $|J,\Omega \rangle$. The $|3/2,3/2\rangle$ states are not included in the figure since they exhibit a pure $\Pi$ character at all interatomic distances

The nature of the non-adiabatic effects suggests that an atom–atom chemi-ionization reaction occurs through two complementary microscopic mechanisms, discussed in detail in refs [15,16,17,18,19]. They can be classified as:

• (i) Direct mechanism it is triggered by an homogeneous electron exchange, with coupling terms, between entrance and exit channels, called $\hbox {A}_{\Sigma \text {-}\Sigma }$ and $\hbox {A}_{\Pi \text {-}\Pi }$ on the basis of molecular character ($\Sigma$ or $\Pi$) of initial and final state. The molecular character degrees of interest are given in upper right panel of Fig. 4 and they refer to the manifold of states effectively coupled by CT within the [Ne–Kr]$^{+}$ molecular ionic. This mechanism, dominant at high collision energy (that is when short intermolecular distances are probed), drives a true chemical reaction:

• (ii) Indirect mechanism it is stimulated by a heterogeneous electron exchange and it is accompanied by mixing/exchange between initial and final states of different symmetry [15, 16]. This mechanism, driven by $\hbox {A}_{\Sigma \text {-}\Pi }$ and $\hbox {A}_{\Pi \text {-}\Sigma }$ couplings, is basically promoted by spin-orbit, Coriolis electron polarization effects. The latter interaction contributions, emerging, as anticipated before, at large separation distances, tend to break the validity of the optical selection rules, allowing ionization to occur also by a concerted emission-absorption of a “virtual” photon [18, 19]. That is a photo-ionization process that tends to replace the chemical mechanism.

It is important to note that the two mechanisms show a different radial dependence and therefore their relative role varies with the collision energy. In particular, the indirect mechanism emerging at inter-nuclear distances R sufficiently large, that is when the interaction components, effectively promoting this mechanism, become relatively more effective because of their less pronounced radial dependence (see left panels of Fig. 5).

Fig. 6

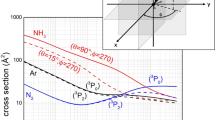
Total ionization cross sections, determined for all allowed state-resolved entrance reaction channels, plotted as a function of the collision energy. The comparison with early results by Greogor and Siska [21], reported as black points and referred to state averaged conditions, permits to emphasize differences in value and in energy dependence of state-resolved results, while their statistical average is consistent with the experimental determination

The interaction components, formulated as summarized above and plotted in Figs. 4 and 5, permitted us to calculate within a semiclassical method [2, 3] the state-to-state ionization cross sections in a wide collision energy range. In order to emphasize the selective contributions of the different entrance channels, obtained results, averaged over all exit channels, are plotted in Fig. 6 where it appears that such contributions exhibit rather different values and energy dependences. From these data, also BRs, defining the relative probability of selected channels, are here easily evaluable. This treatment provided, for the first time, an internally consistent rationalization of most relevant experimental findings, characterized with different techniques in various laboratories, that includes total and partial ionization cross sections, BRs and PIES [18, 19].

Fig. 7

Upper panel Branching ratio $R_{i}$ defined in terms cross section components $Q_{J_{i},J_{f}}$ referred to selected entrance and exit channels, identified by $J_{i}$ and $J_{f}^{.}$. Left lower panel $R_{i}$ values, representative of the cross-section ratios of different channels $|J_{i}\rightarrow J_{f}\rangle$ respect to a reference one, as defined in the upper part of the figure. The continuous lines are the results of the present treatment carried out assuming a $^{3}\hbox {P}_{2}/^{3}\hbox {P}_{0}$ population ratio of about 3, as found for a $\hbox {Ne}^{*}$ beam generated by electron impact [2, 3]. Points represent peak area ratios extracted from the analysis of PIES as depicted in the right panel

Important observables are total ionization cross sections, reported some years ago by Gregor and Siska [21] and obtained, without any type of state selection, in a wide collision energy range. Some representative results are reported in Fig. 6 as black points. A very good agreement between theoretical predictions and experimental data is obtained if present state-resolved results are averaged over the statistical distribution of quantum states accessible in the Gregor and Siska experiment [21].

The energy dependence of BRs between selected reaction channels must also relate with the PIES measured in our laboratory and reported in Fig. 2. BRs of interest for such a purpose are indicated in the upper part of Fig. 7.

Results of state selected Associative/Penning ratios, predicted as a function of the collision energy, are plotted in Fig. 8 together with some experimental data (black points), measured some years ago in our laboratory without state selection [22]. Again, the experimental data compare well with the statistical average of present results. However, the most important and cogent comparison can be performed with recent data measured in the Losanna laboratory by Osterwalder group [23, 24]. In such experiments the $\hbox {Ne}^{*}$ beam has been state selected in $J=2$ and $\varOmega =2$, 1, 0 sublevels and important anisotropies in the reaction probability have been characterized, as shown by some representative data (open circles) reported in Fig. 8: they appear to be consistent with the selectivity of state-resolved entrance channels predicted by the present treatment.

Fig. 8

Associative/Penning ratios predicted for all entrance reaction channels as a function of the collision energy. The comparison involves some old experimental results [22], reported as black points and referred to state averaged conditions. Recent data [23, 24], measured with $\hbox {Ne}^{*}(^{3}\hbox {P}_{2})$ beams state selected in $\Omega =2$, 1, 0 quantum states, are also reported (open circles) for a further important comparison since they represent the only data obtained under initial state-selected conditions

Our recent investigation provides therefore unique information on the stereo-dynamics of state-to-state chemi-ionization reactions. For prototype atom–atom systems, our approach allows to rationalize in a unifying picture most of the available experimental findings from our and other laboratories [18, 19]. The possibility to obtain state-to-state cross sections is of great interest for the investigation of quantum effects in the coherent control of collision processes, promoting Penning and associative ionization, from ultra-cold up to thermal reactive collisions [5]. Moreover, being an atom–atom collision the equivalent of a half rotation of a diatom, obtained results can also provide additional microscopic details on the electronic rearrangements controlling the reaction path. Specifically, the collision dynamics can be confined in different Hund’s cases, which represent quantum effects of angular momentum couplings in selected environments, whose dimensions are controlled by the different strength and anisotropy of the intermolecular forces involved. This is a “hot” topic of our present interest. In particular, for chemi-ionization reactions involving $\hbox {Ne}^{*}+$Ar, Kr and Xe as reagents we have recently demonstrated [25] that the direct mechanism emerges when the collision complex is confined in Hund’s case (a) or in the transition between Hund’s case (c) and Hund’s case (a): it is important to stress that in both these cases the “internal” electronic angular momentum couplings dominate over their “external” coupling with the orbital angular momentum component of the collision complex. On the other hand, the indirect mechanism becomes relevant in the passage from Hunds case (c) to Hund’s case (e), that is when the orbital angular momentum directly controls the reduced selectivity of collision stereo-dynamics. Moreover, for atom–atom reactions we have found that the critical balance between interaction potential and centrifugal components determines a well-defined range of turning points, where the reaction mainly occurs, that shifts with continuity as a function of the collision energy [19]. This feature controls the gradual variation of the relative role of two mechanisms when the collision energy increases from sub-thermal up to hyper-thermal conditions [19].

As stressed above, an important target of our present activity is the extension of the methodology to chemi-ionization reactions involving molecules [11, 12, 26] for their great interest in several fields, including the balance of phenomena occurring in interstellar environments and planetary atmospheres [27, 28]. In the following we report some highlights of our recent research. For such reactions the relative role of direct and indirect mechanisms is expected to vary with respect to the atom–atom case since depending on the different structure of the confined environment where the electronic rearrangements occur, as shown in Fig. 1 for water. Moreover, with respect to the prototype $\hbox {Ne}^{*}+$Ar, Kr and Xe systems, for the case of polar molecules, as water and ammonia, the trapping effect of the stronger attraction component in the real part of the optical potential promotes an increased role of the orbital angular momentum. Such an increase provides a centrifugal barrier in the entrance channels whose height modulates strongly the values of orbital angular momentum effective for reaction. In particular, especially under thermal and sub-thermal collision energy conditions, the range of separation distances where the reaction mainly occurs splits into two well separated intervals, on both sides of the centrifugal barrier, where the two different mechanisms dominate, respectively. Therefore, the orbital angular momentum value represents a sort of a “selector” of the reaction mechanism [29]. Finally, the selectivity of intermolecular forces involved, determines, in the case of chemi-ionization reactions of $\hbox {N}_{2}$ and $\hbox {O}_{2}$, a different confinement of the more external electrons to which can be associated the formation of reaction transition states exhibiting well evident changes in their structure [30]. This finding, suggested by the change in the critical balance of the intermolecular forces involved, is consistent with the completely different energy dependence of measured total ionization cross section.

It is interesting to note also that the dynamics of electron-molecule impacts, which can be considered as the inverse of chemi-ionization processes, is of crucial relevance in many applications of molecular plasmas [31]. It is of interest to emphasize that the microscopic dynamics of promoted dissociative electron attachment and resonant vibrational excitations [31, 32], driven by a local complex potential, must be considered complementary to that of autoionization reactions.

In conclusion, the microscopic mechanisms, recently proposed and properly generalized, driven by valence electron polarization, by changes in electron angular momentum couplings and by selective charge transfer effects, all operative within the collision complex, are also of great relevance from a point of view of fundamental science [33, 34]. Specifically, they help to identify the role of electronic rearrangements determining the fate of the precursor state of many other types of more complex chemical processes.