Abstract
Antihydrogen atoms are produced at CERN in highly excited Rydberg states. However, precision measurements require anti-atoms in ground state. Whereas experiments currently rely on spontaneous emission only, simulations have shown that THz light can be used to stimulate the decay towards ground state and thus increase the number of anti-atoms available for measurements. We review different possibilities at hand to generate light in the THz range required for the purpose of stimulated deexcitation. We demonstrate the effect of a blackbody type light source, which however presents drawbacks for this application including strong photoionization. Further, we report on the first THz transitions in a beam of Rydberg caesium atoms induced by photomixers and conclude with the implications of the results for the antihydrogen case.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
After years of technical developments, antihydrogen (\({\bar{\hbox {H}}}\)) atoms can be regularly produced at CERN’s Antiproton Decelerator complex [1,2,3]. This anti-atom is used for stringent tests of the Charge-Parity-Time (CPT) symmetry as well as for the direct measurements of the effect of the Earth’s gravitational acceleration on antimatter. For precision measurements towards both of these goals ground-state antihydrogen atoms are needed.
The atoms are mostly synthesized using either a charge exchange (CE) reaction where an excited positronium (Ps) atom (bound state of an electron and a positron) releases its positron to an antiproton or a so-called three-body recombination reaction (3BR) where a large number of positrons and antiprotons are brought together to form antihydrogen.
Both formation mechanisms produce antihydrogen atoms in highly excited Rydberg states with so-far best achieved temperatures of \(\sim 40\hbox { K}\) [1] (corresponding to a mean velocity of \(\sim 1000\hbox { m/s}\)) and in the presence of relatively strong magnetic fields (\(\mathcal {O}(1\hbox { T})\)) to confine the charged particles and, in some cases, trap the antihydrogen atoms. Although experimentally not well studied, the antihydrogen atoms formed via 3BR are expected to cover a broad range of principle quantum numbers up to \(n \sim 100\) [4,5,6,7,8]. Highly excited states will be ionized by the electric field present at the edges of the charged clouds so that in general only antihydrogen with \(n<50\) can escape the formation region. Via the CE reaction, specific \(n \sim 30\) values can be targeted resulting in a narrower spread in n that is mainly determined by the velocity and velocity distribution of the impinging Ps [9,10,11]. In either case, all (k, m) substates are populated where m is the magnetic quantum number and k a labeling index according to the strength of the substate’s diamagnetic interaction that becomes in a field-free environment the angular momentum quantum number l. The field-free lifetime \(\tau _{n,l}\) of the Rydberg states produced
is of the order of several milliseconds [12] and can be considered a good approximation in the presence of a magnetic field \(B \sim 1\hbox { T}\) [13]. Given the currently achieved formation temperatures, this results, for experiments that rely on an antihydrogen beam, in a large fraction of atoms remaining in excited states before escaping the formation region which complicates beam formation and hinders in-situ measurements.
In a previous publication [14] the stimulation of atomic transitions in (anti-)hydrogen using appropriate light in order to couple the initial population to fast spontaneously decaying levels was studied. Indeed, such techniques allow to increase the ground state fraction within a few microseconds which corresponds to an average flight path of the atoms on the order of centimeters. Different deexcitation schemes, making use of THz light, microwaves and visible lasers were investigated. Microwave sources and lasers at the wavelengths and intensities identified in [14] are commercially available and measurements of single Rydberg-Rydberg transitions have been reported [15]. The simultaneous generation of multiple powerful light frequencies in the high GHz to THz regime however still remains a technical challenge. After providing some insights into the antihydrogen deexcitation schemes dealt with and clarifying which light intensities and wavelengths are required in Sect. 2, we analyse in Sect. 3 the suitability of different THz light sources for this purpose. We report in Sect. 4 on the effect of a broadband lamp and on the first observation of highly selective THz light stimulated population transfer between Rydberg states with a photomixer in a proof-of-principle experiment with a beam of excited caesium atoms.
2 THz-induced antihydrogen deexcitation and state mixing
For both production schemes, CE and 3BR, the idea of stimulated deexcitation of antihydrogen comes down to mixing many initially populated long-lived states and simultaneously driving transitions to fewer short-lived levels from where the spontaneous cascade decay towards the ground state is fast. Relying on a pulsed CE production scheme the initially populated states can be mixed by applying an additional electric field to the already present magnetic one [16]. A deexcitation/mixing scheme based on the stimulation of atomic transitions via light in the THz frequency range is thoroughly discussed in [14] for the 3BR case. This latter scheme is equally applicable to a pulsed CE production.
When coupling a distribution of N long-lived levels with an average lifetime of \(\tau _\mathrm{{N}}\) to \(N'\) levels with an average deexcitation time to ground state of \(\tau _\mathrm{{N'}}^\mathrm{{GS}} \ll \tau _\mathrm{{N}}\), the minimum achievable time \(t_\mathrm{{deex}}\) for the entire system to decay to ground state can be approximated by
In (anti)hydrogen, the average decay time of a \(n'\)-manifold with \(N'\) fully mixed states to ground state can be approximated, for low \(n'\), by the average lifetime of the manifold: \(\tau _{N'}^\mathrm{{GS}} \sim 2\,{\upmu }\hbox {s} \times \left( n'/10 \right) ^{4.5}\) [16]. Consequently, when coupling some thousands of initially populated Rydberg antihydrogen levels (\(n\sim 30\)) to a low lying manifold this intrinsic limit would lead to a best deexcitation time towards ground state of roughly a few tens of \(\upmu \hbox {s}\). Within such a time interval the atoms move only by a few tens of millimeters and thus stay close to the formation region from where, once deexcited, a beam can be efficiently formed.
Binding energy of (anti-)hydrogen Rydberg states in a \(1\hbox { T}\) magnetic field as a function of the magnetic quantum number m. Inter-n manifold transitions in the THz region are indicated by continuous errors. Dashed arrows illustrate some examples of spontaneous transitions. The figure is adapted from Ref. [14].
Figure 1 shows the binding energy diagram of antihydrogen states in a \(1\hbox { T}\) magnetic field. Recalling the \(|\varDelta m|=1\) selection rule, it becomes apparent that, especially to address high angular momentum states that are incidentally the longest lived ones, all \(\varDelta n= -1\) THz-transitions need to be driven to achieve an efficient mixing. In Ref. [14] the efficiency of stimulating simultaneously all \(\varDelta n = -1\) inter-n manifold transitions from Rydberg levels (n, k, m) down towards a manifold \(n'\) that is rapidly depopulated to ground state by spontaneous emission (in the following referred to as THz deexcitation) is studied.
For \(n=30\) and \(n'=5\) it is found that the total (summed over all driven transitions) light intensity necessary is of \(> 10\hbox { mW/cm}^{2}\) covering a frequency range from \(\sim 200\hbox { GHz}\) to well within the few \(\hbox {THz}\) region (the frequencies range from over 40 THz for \(n=6\rightarrow 5\) to 0.26 THz for \(n=30 \rightarrow 29\)).
As an alternative scheme (in the following referred to as THz mixing), it was proposed to restrict the THz light to a certain fraction of the initially populated levels in order to mix all (k, m) sublevels within, for example, \(25 \le n \le 35\). Retaining the levels equipopulated allows for a narrowband deexcitation laser to couple the Rydberg state distribution directly to the \(n=3\) manifold which decays on a nanosecond timescale. This results in a reduction of the total THz light intensity required by more than an order of magnitude to \(1\hbox { mW/cm}^{2}\).
In summary, THz mixing or deexcitation requires the simultaneous generation of multiple light frequencies in the mW power regime. As derived in Ref. [14], optimal conditions to transfer population are given when sending equally intense light to stimulate the desired individual \(n \rightarrow n-1\) transitions.
3 THz sources
The spectral range in the THz region—also called far-infrared or sub-mm region, depending on the community (1 THz corresponds to 33 \(\hbox {cm}^{-1}\), to \(\sim 4\) meV, and to a wavelength of 0.3 mm) – is situated at frequencies at which powerful sources are not easily available and mW power is roughly the bottleneck even if THz technology is a fast moving field (see for instance the reviews given in [17,18,19,20,21]). The multiple frequencies light necessary for deexcitation or state mixing in antihydrogen can be generated via two techniques: either via several narrowband sources that emit a sharp spectrum at the wavelengths required to drive single or few transitions, or via a single broadband source that covers the frequency range of all required transitions. In the following, we will give a general overview of the constraints and limitations of either solution.
A first general constrain, whatever the source is, is linked to the fact that all transitions should be driven simultaneously (and not sequentially) in order to avoid a mere population exchange between the levels. In the following, we will thus restrain ourselves to fixed frequency sources. We first study the possible narrowband sources and then the broadband ones.
3.1 Narrowband THz sources
In the case of narrowband sources, particular atomic transitions can be targeted and therefore the power provided by the source at those wavelengths is entirely used to drive the transition. Thus, ionization due to off-resonant wavelengths can be minimized. The usage of multiple sources allows to implement the correct power scaling as a function of output frequency increasing the efficiency of the deexcitation. However, when stimulating all \(\varDelta n = -1\) transitions from \(n=30\) down to \(n'=5\) a totality of 25 wavelengths is required. In the presence of a magnetic field which leads to significant degeneracy lifting of the levels, the necessary number of (very) narrowband sources can even increase further due to the spectral broadening of the atomic transitions. In view of the high number of desired wavelengths that need to be produced the usage of expensive direct synthesis such as quantum cascade or molecular lasers is not an option. Furthermore, as mentioned earlier, the exact distribution of quantum states populated during antihydrogen synthesis is not well known and thus a versatile apparatus is needed to adapt the frequencies generated and used for mixing. Given this point, CMOS-based terahertz sources or powerful diodes (\(>1\hbox { mW}\)) are not versatile enough solutions, due to the requirement of several frequency multiplications and the necessity of many waveguides given their cut-off frequencies.
In contrast, photomixing or optical rectification [22] seems to be an attractive option. Given \(n_0\) different laser frequencies \(\nu _i\) input signals, the photomixer optical beatnote produces, in the ultra-fast semiconductor material, THz waves at all \(\nu _i-\nu _j\) frequencies; the number of which being \(n_0(n_0-1)/2\). Photomixing can nowadays reach the mW level, shared by all generated frequencies [23]. The \(n_0\) laser inputs can be produced using pulse shaping from a single broadband laser source [24,25,26,27]. Given the limitation of a photomixer’s total output power, the device is an especially attractive solution for THz mixing purposes (and not necessarily deexcitation towards low \(n'\)) where the total power is divided up into less frequencies. As mentioned in Sect. 2, this is the case for schemes relying on deexcitation lasers. Additionally, the maximum achievable output power rapidly decreases towards the few THz frequency region rendering the device unfit for the deexcitation purpose below \(n<15\). We conclude that, in particular for the THz mixing scheme, photomixers exhibit very attractive characteristics. Furthermore the photomixer simply reproduces the beating in the laser spectrum and can thus also be used as a broadband source.
3.2 Broadband THz sources
Using a broadband source has the main advantage that a single device might be able to drive many transitions significantly facilitating the experimental implementation. The obvious drawback, however, is that most of the power will not be emitted at resonant frequencies and thus much higher total power would be required to drive the needed transitions. This might lead to significant losses due to ionization [28, 29] even if filters can be used to reduce this effect. As pointed out earlier, the source output power should ideally be constant over the exploited range of emitted wavelengths which is more difficult to implement with a single broadband source.
Portable synchrotron [30] or table-top Free Electron Laser sources [31,32,33,34] would be ideal broadband sources with intense radiance in the far-infrared region, but the costs of such apparatus are still prohibitive. A possible alternative is the use of femtosecond mode-locked lasers to generate very short THz pulses using optical rectification, surface emitters or photoconductive (Auston) switches. However, we can only use sources with fast repetition rates in order for the spontaneous emission to depopulate all levels. Unfortunately, even though photoconductive switches with mW THz average output power exist [35], and THz bandwidth in excess of 4 THz with power up to \(64\,\upmu \hbox {W}\) as well as optical-power-to-THz-power conversion efficiencies of \(\sim 10^{-3}\) have been demonstrated [36], the efficiency drops to \(\sim 10^{-5}\) for fast repetition rates low femtosecond pulse energies. Thus, if using a standard oscillator providing for instance 1 W average power, no more than \(10\,\upmu \hbox {W}\) total output power is expected [18]. Such sources have been tested to drive transitions between Rydberg atoms, but with only \(10\%\) of the population transfer from the \(n=50\) initial states down to \(n<40\) [37,38,39].
A simple solution would consist of a blackbody emitter which efficiently radiates in the THz range [40]. A 1000 K blackbody emits in the far infrared region of 0.1–5 THz, with a band radiance of \(4\hbox { mW/cm}^{2}\) which seems perfectly compatible with the requirements found for the antihydrogen deexcitation purpose. Such a radiation source has been proposed in order to cool internal degrees of freedom of \(\hbox {MgH}^+\) molecular ions [41]. Between about 400 and \(100\hbox { cm}^{-1}\), the radiant power emitted by a silicon carbide (Globar) source is as high as any conventional infrared source, but below \(100\hbox { cm}^{-1}\), as for Nernst lamps or glowers that become transparent below about \(200\hbox { cm}^{-1}\), the emissivity is low. In the region between \(\sim \) 50 and 10\(\hbox { cm}^{-1}\) it is thus customary to use a high-pressure mercury lamp with a spectrum close to a blackbody one of effective temperature of 1000–5000 K [30, 40, 42,43,44,45,46].
4 Experimental caesium test setup
In order to experimentally assess the potential of the discussed source types, to evaluate realistic power outputs, and to study the suitability of the sources for application to antihydrogen state mixing and deexcitation, we have tested, on a beam of excited Rydberg caesium atoms, the narrow- and broadband solution which seemed most optimal. The reason to use caesium and not directly hydrogen atoms is mainly due to the fact that, compared to hydrogen, light to manipulate caesium atoms is much easier to generate and off-the-shelf solutions readily exist. However, alkaline Rydberg atoms, such as caesium, have a behavior close to that of hydrogen.
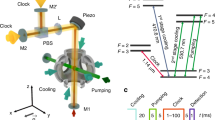
In our experimental setup, illustrated in Fig. 2, a caesium effusive beam emitted out of an oven enters a vacuum chamber. The atoms are excited by a cw diode at 852 nm from the \(6\mathrm{S}_{1/2}\) to the \(6\mathrm{P}_{3/2}\) level. A second tunable pulsed laser (OPO pumped by a Nd:YAG) then addresses the \(n\hbox {S}\) or \(n\hbox {D}\) Rydberg level. The excitation lasers are sent perpendicular to the beam direction. Two grids opposing each other perpendicular to the beam direction introduce an electric field to field ionize the atoms and study the population of each (n, l) state. The THz radiation emitted by a narrowband photomixer outside the chamber can be sent through a THz transparent viewport towards the excited Cs atoms. Alternatively, a broadband lamp is mounted inside the chamber in proximity to the measurement region to stimulate a population transfer.
The caesium state population was studied by applying a high voltage pulse to the lower grid (cf. Fig. 2, the other grid was grounded) of the field ionizer surrounding the atomic beam at a given delay time \(t_D\) with respect to the laser excitation pulse. The ionizing field was ramped making use of an RC circuit with a rise time of \(4\,\upmu \hbox {s}\). Since each state ionizes at a given electric field strength, the state distribution can be probed by collecting either the ions or electrons from the ionization on a Chevron stack micro-channel plate (MCP) charge detector [47, 48].
We tested a commercial (GaAs Toptica) photomixer acting as a THz source stimulating the \(97\hbox { GHz}\) transition between the initially excited \(36 \mathrm{S}_{1/2}\) state towards the \(36 \mathrm{P}_{3/2}\) Rydberg state. This transition was chosen due to a strong dipole transition, easy laser excitation and a well defined field ionization signal. Undoubtedly, much more cost-effective, convenient and efficient ways to induce a \(97\hbox { GHz}\) transition would have been to use a voltage-controlled oscillator (VCO), semi-conductor (Gunn or IMPATT diode), backward-wave oscillator or a submillimeter-wave source based on harmonic generation of microwave radiation. However, our goal was not to drive specifically this transition, but to demonstrate the use of a photomixer to drive Rydberg transitions. This technology allows to create a spectrum of multiple sharp frequencies to simultaneously drive many transitions in antihydrogen which ultimately results in a deexcitation of the atoms. In the context of this proof-of-principle experiment, mixing of near \(852\hbox { nm}\) laser lines from a Ti:Sa laser and a diode laser was used to produce \(\sim 1\,\upmu \hbox {W}\) THz output power at \(97\hbox { GHz}\) with a spectral linewidth which reproduces the one of the input lasers (\(<5\hbox { MHz}\)). The THz light was sent through a TPX viewport (transparent to THz radiation) and illuminated the sample for \(\sim 10\,\upmu \hbox {s}\). A population transfer is clearly visible in Fig. 3 and amounts to \(\sim 15\%\) corresponding to a stimulated transition rate of the order of \(10^{4}\hbox {s}^{-1}\). In theory, the large Cs dipole matrix element (\(554.4 e a_0\) for the \(36\mathrm{S}_{1/2} \rightarrow 36\mathrm{P}_{3/2}\) transition [49]) should lead to a much faster transition rate of \(\varOmega \sim 10^{8}\hbox {s}^{-1}\) when assuming a light intensity of \(\sim 1\,\upmu \hbox {W/cm}^{2}\). The experimentally observed lower rate is mainly explained by a transition broadening due to large field inhomogeneities in the region traversed by the Cs beam. Indeed, in our geometry, the MCP produces a fringe field between the two field-ionizer plates that can reach tens of V/cm leading to a broadening of tens of GHz for the transition addressed [49]. This measurement demonstrates the first, to our knowledge, use of a photomixer to stimulate Rydberg transitions in caesium atoms.
Caesium population transfer from the \(36\mathrm{S}_{1/2}\) to the \(36\mathrm{P}_{3/2}\) level. The obtained MCP signal is plotted for case (1) where the photomixer is switched on (triangle) and case (2) where the photomixer is turned off (square). We indicate on the x-axis the time reference of the signal to the high voltage ramp that is applied to the field ionizer grids. The Cs atoms ionize at a given electric field strength and accelerate towards the MCP. The ionization rate of the \(36\mathrm{P}_{3/2}\) level peaks around \(\sim 3.15\,\upmu \hbox {s}\) after the high voltage ramp is started. The detection rate of ions originating from the ionization of the \(36\mathrm{S}_{1/2}\) level reaches its maximum approximately \(250\hbox { ns}\) later. To improve the readability, the signals are averaged over \(0.4\,\upmu \hbox {s}\).
Figure 4 shows results obtained using a globar type (ASB-IR-12K from Spectral Products) lamp which is a silicon nitride emitter mounted in a \(1\hbox { inch}\) parabolic reflector that is small enough to be placed inside the vacuum chamber \(\sim 2\hbox { cm}\) away from where the caesium atoms are excited and ionized. Here, the delay time \(t_D\) of the applied ionizing field ramp with respect to the excitation laser was varied to study the population of a given state (that ionizes at a given field strength) as a function of time. To probe the population of these states we integrate the signal in a \(\sim 200\hbox { ns}\) time window around the mean arrival time of the field ionization signal. The desired signal can thus be slightly contaminated by the ionization signal from nearby states. We compare the lifetimes of the state for stimulated population transfer (lamp on) and sole spontaneous emission (lamp off). Figure 4 shows the results obtained for the \(40\mathrm{D}_{5/2}\) level. This level was chosen because \(n\sim 40\) is close to the highest level that we would hope to transfer in the case of antihydrogen [14]. Although the decay curves are non-exponential, we indicate the 1/e depopulation time that decreases from 11 to \(3.5\,\upmu \hbox {s}\) using the lamp. To interpret this result, we simulate the spontaneous and light induced depopulation of the \(40\mathrm{D}_{5/2}\) state within the caesium atomic system. Dealing with non-coherent light sources we place ourselves in the low saturation limit and reduce the optical Bloch equations to a much simpler set of rate equations. The resulting matrix system is numerically solved for a few hundred atoms as detailed in [50]. The simulations indicate that the enhancement of the decay achieved experimentally is comparable to the simulation result obtained by implementing a light source that emits an isotropic blackbody spectrum of \(\sim 1100\hbox { K}\). This is close, and even slightly higher than the temperature emitted by the collimated lamp. Since the device is mounted in close proximity to the caesium beam, it is possible that the radiative spectrum is indeed focused on the atoms. In addition, we observed that \(\sim 50 \%\) of the atoms are either excited to higher levels or photoionized [51]. However, we note that filters, such as TPX, PTFE or Teflon [40], can be used to cut out the low (to avoid \(n \rightarrow n+1\) transitions) and high (to avoid direct photoionization) frequency parts of the spectrum that lead to these effects [51].
We note that in the cryogenic environment of an antihydrogen experiment the installation of such a high temperature lamp in the vicinity of the atoms remains hypothetical. However, using transport of THz radiation by, for example, a metallic light pipe is simple and efficient [40]. We investigated the transmission efficiency of the lamp’s broadband spectrum with a \(30\hbox { cm}\) long copper tube (diameter: \(\sim 1\hbox { cm}\)) and could transfer \(\ge 94.5 \%\) [51] of the radiation.
Experimentally measured lifetimes of the caesium \(40\mathrm{D}_{5/2}\) level with and without a lamp (globar type). The time \(t_D\), given on the x-axis, indicates the time delay of the field ionization ramp with respect to the excitation laser. We include simulation results for a 1100 K blackbody spectrum (gray). To improve the readability the experimental signals are averaged over \(0.1\,\upmu \hbox {s}\).
5 Conclusions
This work reviewed different methods of generating light in the THz region to stimulate the decay of Rydberg antihydrogen atoms towards ground state.
We commissioned a beamline to study Rydberg population transfer in alkaline atoms. Cesium atoms are much easier to produce than (anti-)hydrogen and are thus ideal for proof-of-principle studies. A \(\sim 15\%\) population transfer within the \(n=36\) manifold was demonstrated using photomixing at \(\sim 0.1\hbox { THz}\). Such THz transitions between Rydberg states can be used to mix the states of antihydrogen atoms while a laser deexcites the Rydberg state distribution towards low n-manifolds [14]. Because antihydrogen is formed (by collisions) in many Rydberg levels this mixing and deexcitation requires several frequencies. The photomixer frequency range of \(\sim \) 0–2 THz is especially adapted to this purpose. An attractive solution to generate a continuum around the few hundred GHz region (needed for Rydberg states around \(25 \le n \le 30\)) could be the use of tapered amplifiers, i.e. semiconductor optical amplifiers, or the amplified spontaneous emission output of an optical amplifier, as radiation inputs towards the photomixer.
A deexcitation of the Cs \(40\mathrm{D}_{5/2}\) level was observed using a blackbody type light source. However, the ionization fraction for a broadband source lies around \(\sim 50 \%\) and is significantly elevated compared to the use of narrowband light sources that emit sharp frequencies targeted towards single \(n \rightarrow n-1\) transitions. In combination with the lack of flexibility in the source output power distribution as a function of the emitted wavelength, broadband sources seem consequently rather unfit for the antimatter application. In particular the high ionization potential must be pointed out as a very harmful effect in the context of antihydrogen experiments where atoms are only available in the few hundreds at a time following a complicated synthesis procedure at CERN’s Antiproton Decelerator.
We conclude that in particular photomixing has potential for an application in experiments aiming for a deexcitation of antihydrogen atoms. As pointed out, the field of THz light sources is rapidly evolving and output powers in the mW range have been demonstrated. In view of the theoretical studies published in [14] and the complementary experimental conclusions drawn in this manuscript, we aim to next demonstrate the first experimental deexcitation of Rydberg hydrogen atoms to ground state in a few tens of microsecond time scales. Addressing this long standing issue in the antihydrogen community has the potential to pave the way for further antimatter precision measurements at CERN.
Data Availibility Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.]
References
M. Ahmadi, B.X.R. Alves, C.J. Baker, W. Bertsche et al., Antihydrogen accumulation for fundamental symmetry tests. Nat. Commun. 8, 681 (2017)
N. Kuroda, S. Ulmer, D.J. Murtagh, S. Van Gorp et al., A source of antihydrogen for in-flight hyperfine spectroscopy. Nat. Commun. 5, 3089 (2014)
G. Gabrielse, R. Kalra, W.S. Kolthammer, R. McConnell et al., Trapped antihydrogen in its ground state. Phys. Rev. Lett. 108, 113002 (2012)
G. Gabrielse, N.S. Bowden, P. Oxley, A. Speck et al., Background-free observation of cold antihydrogen with field-ionization analysis of its states. Phys. Rev. Lett. 89(21), 213401 (2002)
C. Malbrunot, C. Amsler, S. Arguedas Cuendis, H. Breuker et al., The ASACUSA antihydrogen and hydrogen program: results and prospects. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 376(2116), 20170273 (2018)
F. Robicheaux, Atomic processes in antihydrogen experiments: a theoretical and computational perspective. J. Phys. B Atomic Mol. Opt. Phys. 41(19), 192001 (2008)
B. Radics, D.J. Murtagh, Y. Yamazaki, F. Robicheaux, Scaling behavior of the ground-state antihydrogen yield as a function of positron density and temperature from classical-trajectory monte carlo simulations. Phys. Rev. A 90, 032704 (2014)
S. Jonsell, M. Charlton, Formation of antihydrogen beams from positron–antiproton interactions. New J. Phys. 21(7), 073020 (2019)
D. Krasnický, G. Testera, N. Zurlo, Comparison of classical and quantum models of anti-hydrogen formation through charge exchange. J. Phys. B Atomic Mol. Opt. Phys. 52(11), 115202 (2019)
D. Krasnický, R. Caravita, C. Canali, G. Testera, Cross section for Rydberg antihydrogen production via charge exchange between Rydberg positroniums and antiprotons in a magnetic field. Phys. Rev. A 94(2), 022714 (2016)
M. Doser, C. Amsler, A. Belov, G. Bonomi et al., Exploring the WEP with a pulsed cold beam of antihydrogen. Class. Quantum Gravity 29(18), 184009 (2012)
Edward S. Chang, Radiative lifetime of hydrogenic and quasihydrogenic atoms. Phys. Rev. A 31, 495–498 (1985)
T. Topçu, F. Robicheaux, Radiative cascade of highly excited hydrogen atoms in strong magnetic fields. Phys. Rev. A 73(4), 043405 (2006)
T. Wolz, C. Malbrunot, M. Vieille-Grosjean, D. Comparat, Stimulated decay and formation of antihydrogen atoms. Phys. Rev. A 101, 043412 (2020)
T.F. Gallagher, Rydberg Atoms, Cambridge Monographs on Atomic, Molecular and Chemical Physics (Cambridge University Press, Cambridge, 1994)
D. Comparat, C. Malbrunot, Laser stimulated deexcitation of Rydberg antihydrogen atoms. Phys. Rev. A 99, 013418 (2019)
P. Latzel, F. Pavanello, S. Bretin, M. Billet, et al., High efficiency UTC photodiode for high spectral efficiency THz links, in 2017 42nd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz) (2017), pp. 1–2
M. Hangyo, Development and future prospects of terahertz technology. Jpn. J. Appl. Phys. 54(12), 120101 (2015)
S.S. Dhillon, M.S. Vitiello, E.H. Linfield, A.G. Davies et al., The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 50(4), 043001 (2017)
K. Zhong, W. Shi, D. Xu, P. Liu et al., Optically pumped terahertz sources. Sci. China Technol. Sci. 60(12), 1801–1818 (2017)
T. Elsässer, K. Reimann, M. Woerner, Concepts and Applications of Nonlinear Terahertz Spectroscopy (Morgan & Claypool Publishers, San Rafael, 2019)
J. Ahn, A.V. Efimov, R.D. Averitt, A.T. Taylor, Terahertz waveform synthesis via optical rectification of shaped ultrafast laser pulses. Opt. Express 11, 2486 (2003)
S. Preu, G.H. Döhler, S. Malzer, L.J. Wang et al., Tunable, continuous-wave Terahertz photomixer sources and applications. J. Appl. Phys. 109(6), 061301–061301 (2011)
Y. Liu, S. Park, A.M. Weiner, Terahertz waveform synthesis via optical pulse shaping. IEEE J. Sel. Topics Quantum Electron. 2(3), 709–719 (1996)
A.J. Metcalf, V.R. Supradeepa, D.E. Leaird, A.M. Weiner et al., Fully programmable two-dimensional pulse shaper for broadband line-by-line amplitude and phase control. Opt. express 21(23), 28029–28039 (2013)
M. Hamamda, P. Pillet, H. Lignier, D. Comparat, Ro-vibrational cooling of molecules and prospects. J. Phys. B Atomic Mol. Opt. Phys. 48(18), 182001 (2015)
A.I. Finneran, J.T. Good, D.B. Holland, P.B. Carroll et al., Decade-spanning high-precision terahertz frequency comb. Phys. Rev. Lett. 114(16), 163902 (2015)
I.L. Glukhov, E.A. Nekipelov, V.D. Ovsiannikov, Blackbody-induced decay, excitation and ionization rates for rydberg states in hydrogen and helium atoms. J. Phys. B Atomic Mol. Opt. Phys. 43(12), 125002 (2010)
C. Seiler, J.A. Agner, P. Pillet, F. Merkt, Radiative and collisional processes in translationally cold samples of hydrogen rydberg atoms studied in an electrostatic trap. J. Phys. B Atomic Mol. Opt. Phys. 49(9), 094006 (2016)
P.R. Griffiths, C.C. Homes, Instrumentation for Far-Infrared Spectroscopy (Wiley, New York, 2006)
S.M. Hooker, Developments in laser-driven plasma accelerators. Nat. Photonics 7(10), 775–782 (2013)
Y. Shibata, K. Ishi, S. Ono, Y. Inoue et al., Broadband free electron laser by the use of prebunched electron beam. Phys. Rev. Lett. 78(14), 2740 (1997)
K. Nakajima, Laser-driven electron beam and radiation sources for basic, medical and industrial sciences. Proc. Jpn. Acad. Ser. B 91, 223–245 (2015)
A. Wetzels, A. Gürtler, L.D. Noordam, F. Robicheaux, Far-infrared Rydberg–Rydberg transitions in a magnetic field: Deexcitation of antihydrogen atoms. Phys. Rev. A 73(6), 062507 (2006)
E.R. Brown, Milliwatt Thz average output power from a photoconductive switch, in 33rd International Conference on Infrared, Millimeter and Terahertz Waves, 2008. IRMMW-THz 2008, (IEEE, 2008), pp. 1–2
R.J.B. Dietz, B. Globisch, M. Gerhard, A. Velauthapillai et al., 64 \(\mu \)W pulsed terahertz emission from growth optimized InGaAs/InAlAs heterostructures with separated photoconductive and trapping regions. Appl. Phys. Lett. 103(6), 061103 (2013)
P.K. Mandal, A. Speck, Half-cycle-pulse-train induced state redistribution of Rydberg atoms. Phys. Rev. A 81(1), 013401 (2010)
T. Kopyciuk, Deexcitation of one-dimensional Rydberg atoms with a chirped train of half-cycle pulses. Phys. Lett. A 374(34), 3464–3467 (2010)
A. Takamine, R. Shiozuka, H. Maeda, Population redistribution of cold rydberg atoms, in Proceedings of the 12th International Conference on Low Energy Antiproton Physics (LEAP2016) (2017), p. 011025
E. Bründermann, H. Hübers, M.F. Kimmitt, Terahertz Techniques, vol. 151 (Springer, Berlin, 2012)
I.S. Vogelius, L.B. Madsen, M. Drewsen, Rotational cooling of molecules using lamps. J. Phys. B 37, 4571–4574 (2004)
M.W.P. Cann, Light sources in the 0.15–20-\(\mu \) spectral range. Appl. Opt. 8(8), 1645–1661 (1969)
W.L. Wolfe, G.J. Zissis, The Infrared Handbook, vol. 1 (Spie Press, Bellingham, 1978)
M.F. Kimmitt, J.E. Walsh, C.L. Platt, K. Miller et al., Infrared output from a compact high pressure arc source. Infrared Phys. Technol. 37, 471–477 (1996)
H. Buijs, Incandescent Sources for Mid-and Far-Infrared Spectrometry (Wiley, New York, 2002)
M. Abo-Bakr, J. Feikes, K. Holldack, P. Kuske, et al., Brilliant, coherent far-infrared (THz) synchrotron radiation. Phys. Rev. Lett., 90(9):094801–+ (2003)
T.W. Ducas, W.P. Spencer, A.G. Vaidyanathan, W.H. Hamilton et al., Detection of far-infrared radiation using Rydberg atoms. Appl. Phys. Lett. 35(5), 382–384 (1979)
L. Hollberg, J.L. Hall, Measurement of the shift of Rydberg energy levels induced by blackbody radiation. Phys. Rev. Lett. 53(3), 230 (1984)
N. Sibalić, J.D. Pritchard, C.S. Adams, K.J. Weatherill, ARC: an open-source library for calculating properties of alkali Rydberg atoms. Comput. Phys. Commun. 220, 319–331 (2017)
D. Comparat, Molecular cooling via Sisyphus processes. Phys. Rev. A 89(4), 43410 (2014)
M. Vieille Grosjean, Atomes de Rydberg : Etude pour la production d’une source d’électrons monocinétique. Désexcitation par radiation THz pour l’antihydrogène. PhD thesis, Laboratoire Aimé Cotton, Orsay (2018)
Acknowledgements
We dedicate this work to the memory of our co-author Emiliya Dimova who passed away at the age of 50. This work has been sponsored by the Wolfgang Gentner CERN Doctoral Student Program of the German Federal Ministry of Education and Research (Grant No. 05E15CHA, university supervision by Norbert Pietralla). It was supported by the Studienstiftung des Deutschen Volkes and the Bulgarian Science Fund Grant DN 18/14.
Funding
Open access funding provided by CERN (European Organization for Nuclear Research)
Author information
Authors and Affiliations
Contributions
All authors contributed to the work reported in this manuscript.
Corresponding author
Additional information
E. Dimova: Deceased September 08, 2020
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vieille-Grosjean, M., Dimova, E., Mazzotta, Z. et al. Induced THz transitions in Rydberg caesium atoms for application in antihydrogen experiments. Eur. Phys. J. D 75, 27 (2021). https://doi.org/10.1140/epjd/s10053-020-00013-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjd/s10053-020-00013-3