Conditional quasi-exact solvability of the quantum planar pendulum and of its anti-isospectral hyperbolic counterpart

Abstract

We have subjected the planar pendulum eigenproblem to a symmetry analysis with the goal of explaining the relationship between its conditional quasi-exact solvability (C-QES) and the topology of its eigenenergy surfaces, established in our earlier work [Front. Phys. Chem. Chem. Phys. 2, 1 (2014)]. The present analysis revealed that this relationship can be traced to the structure of the tridiagonal matrices representing the symmetry-adapted pendular Hamiltonian, as well as enabled us to identify many more – 40 in total to be exact – analytic solutions. Furthermore, an analogous analysis of the hyperbolic counterpart of the planar pendulum, the Razavy problem, which was shown to be also C-QES [Am. J. Phys. 48, 285 (1980)], confirmed that it is anti-isospectral with the pendular eigenproblem. Of key importance for both eigenproblems proved to be the topological index κ, as it determines the loci of the intersections (genuine and avoided) of the eigenenergy surfaces spanned by the dimensionless interaction parameters η and ζ. It also encapsulates the conditions under which analytic solutions to the two eigenproblems obtain and provides the number of analytic solutions. At a given κ, the anti-isospectrality occurs for single states only (i.e., not for doublets), like C-QES holds solely for integer values of κ, and only occurs for the lowest eigenvalues of the pendular and Razavy Hamiltonians, with the order of the eigenvalues reversed for the latter. For all other states, the pendular and Razavy spectra become in fact qualitatively different, as higher pendular states appear as doublets whereas all higher Razavy states are singlets.

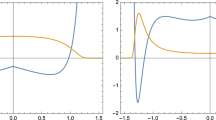
Graphical abstract