Estimation of the Hubble constant using Gaussian process regression and viable alternatives

Abstract

A well-known problem in cosmology is the ‘Hubble tension’ problem, i.e. different estimates for the Hubble constant $H_0$ are not concordant with each other. This work investigates different statistical methods for estimating this value using cosmic chronometer, type Ia supernova and baryonic acoustic data. We start by making use of methods already established in the literature for this purpose, namely Gaussian process regression and Markov chain Monte Carlo (MCMC) methods based on the concordance $\varLambda$CDM model. We also consider two novel approaches; the first makes use of non-parametric MCMC inference on the hyperparameters of a Gaussian process kernel, independently of any cosmological model. The second approach is Student’s t-process regression, which is a generalised version of Gaussian process regression that makes use of the multivariate Student’s t-distribution instead of the multivariate Gaussian distribution. We also consider variants of these two methods which account for heteroscedasticity within the data. A comparison of the different approaches is made. In particular, the model-independent techniques investigated mostly agree with predictions based on the $\varLambda$CDM model. Moreover, Gaussian process regression is highly sensitive to the prior specification, while Student’s t-process regression and the heteroscedastic variants of both methods are more robust to this. Student’s t-process regression and both heteroscedastic models suggest a lower value of the Hubble constant. Across all the estimates obtained for the Hubble constant within this work, the median value is $\hat{H}_0^{med} = 68.85 \pm 1.67$ km s$^{-1}$ Mpc$^{-1}$.

1 Introduction

The Hubble constant $H_0$ is one of the fundamental constants within cosmology and is sourced originally by the direct proportionality relationship between the recessional velocity of distant objects together with their radial distance. However, whereas the linear relationship, initially made famous in [1], has been widely accepted within the astrophysics community, the exact value of $H_0$ is still a matter of great debate, with different techniques for estimating this parameter producing different results that do not agree with each other. This problem is known as the ‘$H_0$ tension’ [2, 3].

In recent years, there has been a marked increase in the reported divergence of the Hubble constant. The discrepancy originates in the measurement of the $H_0$ parameter using direct and indirect techniques and has now reached a critical statistical threshold [4,5,6]. The early Universe results in a low estimation of the Hubble constant [4, 7], when the concordance model is used to interpret observations. On the other end of the spectrum, direct measurements in the late Universe produce higher corresponding estimates of $H_0$ [8, 9]. Internally, each survey shows a high level of internal consistency making this a tension between surveys, and is particularly relevant when the concordance model is used against direct astrophysical data sets [10].

There has been a wide range of nonparametric approaches in the literature where the evolution profile of the Hubble parameter is reconstructed from observational data using statistical techniques. Gaussian process regression (GPR) is the most applied of these techniques [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], where a nonphysical kernel is used to characterize the covariance relationships between within a data set. This naturally leads to the ability to broaden the Hubble reconstruction interval of a wider evolution profile. However, GPR suffers from some disadvantages such as having to select a kernel function as well as possible overfitting [26] at low-redshift values. Student’s t-process regression (TPR) offers a generalisation of GPR which has several advantages including needing low amounts of data to reconstruct underlying behaviour, as well as its better handling of outliers [27,28,29].

In this work, we explore different statistical methods for obtaining estimates for $H_0$. We consider methods already present in the astrophysical literature, such as GPR [16] and Markov chain Monte Carlo (MCMC) methods based on the ‘concordance’ Lambda cold dark matter ($\varLambda$CDM) cosmological model [30]. We also consider some novel approaches to estimating $H_0$. In particular, these include model-independent MCMC methods based on the kernel hyperparameters of GPR, TPR, and variants of GPR and TPR that allow for heteroscedasticity in the underlying data. Other interesting approaches exist in the literature (such as the “move” method where the iterations of the walkers in the MCMC are updated in a novel way [31]), but the fast and low uncertainty convergence of the hyperparameter MCMC implies that this approach is competitive with other fitting methods. All these novel methods have the advantage of being independent from any pre-supposed cosmological model such as $\varLambda$CDM, since they rely only on the data supplied.

This paper is structured as follows. Firstly, in Sect. 2, we introduce the datasets used throughout our analysis. Then, in Sect. 3, we go into some detail on the statistical methods used. This is followed by Sect. 4, where we summarise the results and different estimates which we obtained for $H_0$. Lastly, in Sect. 5, we discuss our findings in relation to the present literature on the $H_0$ tension and suggest areas for further research.

2 Observational datasets and $H_0$ priors

Throughout this work, we shall be concerned with three main data sources for H(z). These are cosmic chronometers (CC), type Ia supernovae (SN), and baryonic acoustic oscillations (BAO).

CC are used to obtain measurements for H(z) using red-envelope galaxies [32]. These measurements are based on the observed 4000Å break in the passively evolving galaxy spectra, caused by the absorption of high-energy radiation from metals and by a scarcity of hot blue stars [33]. According to the CC approach, the expansion rate H(z) may be measured by using the redshift-time derivative $\frac{\textrm{d}z}{\textrm{d}t}$ between these galaxies [34], i.e.

$$\begin{aligned} H(z) = - \frac{1}{1+z} \frac{\textrm{d}z}{\textrm{d}t} \approx -\frac{1}{1+z} \frac{\varDelta z}{\varDelta t}. \end{aligned}$$

(1)

The CC approach has the advantage of not relying on any cosmological models, since one is measuring only the redshift difference between ‘local’ galaxies. Moreover, it is ideal for obtaining H(z) data at redshifts of $z \le 2$ [35]. For CC, the data in Table 4 of the study by [36] is used. To avoid the effects of cosmological model dependence and therefore retain independence from any cosmological models, only those points that are independent of BAO observations are considered.

For the SN data, the compressed Pantheon compilation data (SN) [37] is used throughout most of this work. While the compressed dataset consists of only six points, these data points are effectively a compressed version of a set of around 1048 SN data points at $z < 1.5$ of the Pantheon compilation [38] together with the 15 data points obtained by the HST at $z > 1.5$ as part of the CANDELS and CLASH Multi-Cycle Treasury programs [37]. The values given in [37] are values for $E(z) = H(z)/H_0$ instead of H(z), but these values are still proportional to H(z), since $H_0$ is a constant. The compressed data point for $z=1.5$ in Table 6 of [37] is excluded, since the error is non-Gaussian. Moreover, the full set of 1048 SN data points, which we will denote as SN_*, is used in conjunction with the $\varLambda$CDM cosmological model within Sect. 3.1.2 of this work. A more recent development in this field is the release of the ‘Pantheon+’ dataset [39], which combines the SN_* dataset with other cosmological surveys.

The 1048 observations of the full Pantheon dataset [38] are given in terms of the distance modulus $\mu (z)$, so the use of SN_* requires the distance modulus values to be converted to H(z) values, which can only be done given a cosmological model. Therefore, model-independent statistical methods, such as GPR and TPR, cannot be carried out using the full Pantheon dataset. Converting the $\mu (z)$ values to H(z) is quite an involved process that requires numerical integration. In particular, defining the luminosity distance $d_L(z)$ by

$$\begin{aligned} d_L(z) = c \ (1 + z) \int _0^{z} \frac{1}{H(z')} \ \textrm{d}z', \end{aligned}$$

where c is the speed of light and $z'$ is a variable of integration, then

$$\begin{aligned} \mu (z) = 5 \log _{10} \left( d_L(z) \right) + M, \end{aligned}$$

for some arbitrary fiducial absolute magnitude M [30].

The BAO data points included are from the SDSS compilation [40, 41]. BAO observations are mainly constructed from high resolution images of the distribution of galaxies at different redshifts across the Universe. In this way, a map of the evolution of the large scale structure of the Universe can be built which can then be used to infer the expansion velocity at different redshifts. At lower redshifts, BAO readings may be obtained by observing galaxy clusters [42]. Another source of BAO measurements is from the Lyman-alpha (Ly-$\alpha$) forest [43]; however, a significant tension of $2.5\sigma$ exists between galaxy BAO and Ly-$\alpha$ BAO. A similar tension exists between Ly-$\alpha$ BAO and predictions based on the widely accepted $\varLambda$CDM cosmological model, while galaxy BAO measurements are consistent with $\varLambda$CDM predictions. The mechanism behind obtaining BAO observations is more complicated than for both CC and SN. Essentially, BAO are fluctuations in the density of matter of the Universe and provide a ‘standard ruler’ for measuring large distances within the Universe in the same way that SN of known brightness provides a ‘standard candle’ [44, 45].

For each of the statistical approaches discussed in this work, the different data sources will often be amalgamated. In particular, we shall consider the datasets CC, CC+SN, and CC+SN+BAO, where + denotes the concatenation of datasets. Moreover, for the MCMC $\varLambda$CDM approach, we also consider the datasets CC+SN_* and CC+SN_*+BAO. The datasets are also combined with pre-established estimates for $H_0$ present in the literature, which we shall refer to as ‘priors’. The priors used are summarised in Table 1. Each of the priors is presented in the form $x \pm y$km s$^{-1}$ Mpc$^{-1}$, where x is the point estimate and y represents the uncertainty of this estimate. For each combination of dataset and statistical method, we will consider each ‘prior’ $H_0$ value separately and also the priorless case.

Table 1 Values of different estimates for $H_0$ to be used as ‘priors’

3 Statistical methods

As mentioned towards the end of Sect. 1, we shall be considering a number of statistical methods for the purpose of estimating the Hubble constant $H_0$. Each of the methods obtains an estimate for $H_0$ by using the data available to reconstruct the relationship between z and H(z) and extrapolating the resulting reconstruction function to $z=0$. These statistical methods can be broadly divided into two classes, namely methods already established in the literature and novel methods.

The established methods include GPR [13, 22] and MCMC inference based on the $\varLambda$CDM model [30, 51], using the ensemble sampler [52, 53]. Of these, the first method is said to be model-independent, since it does not assume any cosmological model but is instead dependent only on the observational data. Oppositely, the latter method necessarily assumes the $\varLambda$CDM concordance model. The remaining methods are said to be ‘novel’ methods since, to our knowledge, they have not yet been used within the astrophysical literature to obtain estimates for $H_0$. The novel methods to be discussed within this paper include model-independent MCMC-based inference, TPR, and variants of both GPR and TPR that allow for heteroscedasticity in the data reconstructions.

3.1 Established methods

3.1.1 Gaussian process regression

A GP is a stochastic process that is effectively a generalisation of the multivariate Gaussian distribution, in the sense that any finite sample of random variables from such a process has the multivariate Gaussian distribution as its joint distribution. In the same way that a multivariate Gaussian distribution can be characterised by its mean vector and variance-covariance matrix, a GP can be completely characterised by its mean and kernel functions. If f is a GP with mean function m and kernel function k, this is denoted by $f \sim GP(m,k)$ for notational convenience. Since there is a one-to-one correspondence between f and pairs (m, k) of mean and kernel functions, then specifying m and k implicitly corresponds to a ‘unique’ GP(m, k).

GPR, which has been extensively covered within the statistical literature [54], is a model-independent supervised learning approach based on constraining a kernel function [55], which can then be used to ‘reconstruct’ data, that is, to smoothen out observed data and simulate unobserved data points using interpolation and extrapolation. An example of an admissible kernel function is the square exponential kernel

$$\begin{aligned} k(\textbf{x}, \textbf{x}'; \sigma _f, l) = \sigma _f^2 \exp \left[ - \frac{\Vert \textbf{x}-\textbf{x}'\Vert ^2}{2l^2} \right] . \end{aligned}$$

(2)

For this kernel, the quantities $\sigma _f$ and l are the hyperparameters, which allow for flexibility in the kernel specification. For example, a larger value for the length scale l means that the function values change more slowly and is therefore suitable for capturing a long-term trend. On the other hand, $\sigma _f$ is a scale factor that determines the average distance of the function from its mean [55].

GPR has been used extensively within the field of astrophysics, for example in the analysis of light curves of stars and active galactic nuclei [56, 57]. GPs have also more recently found use in the estimation of core cosmological parameters, such as $H_0$ and $f \sigma _8$, with the goal of understanding better the tension between the different estimates for these parameters. In particular, GPR has been widely used in the literature for smoothing Hubble data [16, 35].

GPR may be viewed as a Bayesian inference problem. The GP prior $f \sim GP(m, k)$ is combined with a Gaussian likelihood function for each of the observed vectors. The mean function m is usually taken to be zero throughout, since GPs are able to model the mean arbitrarily well [54]. The combination of GP prior and Gaussian likelihood results in a Gaussian posterior distribution of f. The hyperparameters present in the mean and covariance structure of the GP, as well as the posterior mean and covariance, are unknown a priori; instead, they are inferred from the data.

In GPR, we are given the observations $(\textbf{x}_i, y_i), i \in \{1, 2, \dots , n\}$. We use a regression model, i.e.

$$\begin{aligned} y_i = f(\textbf{x}_i) + \epsilon , \end{aligned}$$

(3)

where $\epsilon$ corresponds to random noise which is assumed to follow a Gaussian distribution with mean zero and variance $\sigma _{\epsilon }^2$. The $\textbf{x}_i$s can be rearranged as a data matrix $\mathbb {X}$, and the values $y_i$ can be joined into a vector $\textbf{y}$. Then, the log-marginal likelihood can be derived [54] and is given by:

$$\begin{aligned} \log \mathbb {P}(\textbf{y} \vert \mathbb {X}) = -\frac{1}{2} \textbf{y}^T \mathbb {K}_y^{-1} \textbf{y} - \frac{1}{2} \log \vert \mathbb {K}_y\vert - \frac{n}{2} \log 2\pi , \end{aligned}$$

(4)

where $\mathbb {K}_y = \textrm{Cov}(Y \vert \mathbb {X}) = \mathbb {K} + \sigma _{\epsilon }^2 \mathbb {I}_N$ is known as the kernel matrix.

In the right-hand side, the first two terms represent the data fit and model complexity respectively, while the last term is simply a constant. Moreover, for GPR, the posterior predictive mean is $\mathbb {K}_*^T \mathbb {K}_y^{-1}\textbf{y}$.

We obtain a reconstruction of the relationship between H(z) and z that is independent of any physical or cosmological models through the minimisation of a Chi-squared statistic that measures the discrepancies between the observed points at redshifts $z_1, z_2,\ldots , z_N$ [22], as in Eq. (5):

$$\begin{aligned} \chi ^2_{\hat{H}} = \sum _{i=1}^N \frac{\left[ \hat{H}_{pred}(z_i) - H_{obs}(z_i)\right] ^2}{\hat{\sigma }_H^2(z_i)}, \end{aligned}$$

(5)

where $\hat{H}_{pred}(z_i)$ and $H_{obs}(z_i)$ are the reconstructed and observed values of H at redshift $z_i$, and $\hat{\sigma }_H^2(z_i)$ is the estimated variance of the observation $H_{obs}(z_i)$. This Chi-squared statistic reaches a minimum value of 0 when the observed and reconstructed $H(z_i)$ values are equal for each redshift value $z_i$. Minimisation of this statistic is equivalent to estimating H(z) using maximum likelihood estimation [58].

3.1.2 Markov chain Monte Carlo based on $\varLambda$CDM

In this work, we consider a family of MCMC methods known as ensemble samplers. The term ‘ensemble’ relates to multiple samplers, or ‘walkers’, of the standard MCMC algorithms (such as the Metropolis–Hastings algorithm or Gibbs sampler) being run in parallel. Ensemble samplers that are invariant under affine transformations of the coordinate space have been proposed by [52]. These samplers have been used extensively within cosmology, particularly for Bayesian inference of the parameters of some pre-defined cosmological model given a set of data [59]. In this paper, we consider the ‘concordance’ $\varLambda$CDM model, the parameters of which are the Hubble constant $H_0$ and the matter density parameter $\varOmega _{M0}$.

MCMC algorithms aim to sample from some desired joint distribution $f(\textbf{a}) = f(a_1, a_2, \dots , a_p)$ in cases where sampling directly from such a distribution is not possible or feasible. MCMC algorithms achieve this by starting from some initial state $\textbf{a}^{(0)}$ and iteratively sampling $\textbf{a}^{(t)}$ given the value of $\textbf{a}^{(t-1)}$ for $t = 1, 2, \dots$ until some stopping criterion is achieved.

An ensemble $\overrightarrow{\textbf{A}}$ consists of L random vectors known as ‘walkers’ $\{\textbf{A}_1, \textbf{A}_2,\ldots , \textbf{A}_L\}$, each of which is in $\mathbb {R}^p$. Hence, the ensemble can be thought of as being in $\mathbb {R}^p \times \mathbb {R}^L$. The idea behind the ensemble sampler is to independently sample each walker from f.

The term ‘ensemble MCMC algorithm’ arises from the fact that the sampler is made up of a Markov chain on the state space of ensembles. The ensemble algorithm generates $\overrightarrow{\textbf{A}}^{(0)}, \overrightarrow{\textbf{A}}^{(1)}, \dots , \overrightarrow{\textbf{A}}^{(T)}$ iteratively starting from the initial point $\overrightarrow{\textbf{A}}^{(0)}$.

The ensemble algorithm obtains $\overrightarrow{\textbf{A}}^{(t)}$ from $\overrightarrow{\textbf{A}}^{(t-1)}$ by updating one walker at a time, i.e. by cycling through each of the L walkers in the ensemble. Each walker is typically implemented as a Metropolis–Hastings Markov chain, although in theory any MCMC algorithm can be used [53]. For each $i \in \{1, 2, \dots , L\}$, the walker $\textbf{A}_i$ is updated based on the current positions of the other walkers, i.e. the walkers making up the complementary ensemble $\overrightarrow{\textbf{A}}_{[i]}:= \{\textbf{A}_j: j \ne i \}$. If, for each i, the single-walker move from $\textbf{A}_i^{(t-1)}$ to $\textbf{A}_i^{(t)}$ preserves the conditional distribution of $\textbf{A}_i \vert \overrightarrow{\textbf{A}}_{[i]}^{(t)}$, then the overall ensemble update from $\overrightarrow{\textbf{A}}^{(t-1)}$ to $\overrightarrow{\textbf{A}}^{(t)}$ preserves the product density [52].

Three different types of moves which one may wish to carry out on the individual walkers have been proposed by [52]. The type of move most recommended by the authors is the ‘stretch move’, where the walker $\textbf{A}_i$ is updated using one complementary walker, that is, using $\textbf{A}_j$ for some $i \ne j$. Starting from $\textbf{A}_i^{(t-1)}$, a new value $\textbf{A}_i^{(t)*}$ is proposed as follows:

$$\begin{aligned} \textbf{A}_i^{(t)*} := \textbf{A}_j^{(t-1)} + Y \left( \textbf{A}_i^{(t-1)} - \textbf{A}_j^{(t-1)} \right) , \end{aligned}$$

(6)

where Y is a scaling variable. This proposed value is then accepted or rejected through the ‘usual’ Metropolis–Hastings rule.

In this work, we consider the use of the ensemble sampler as implemented in the Python package +emcee+ [53] with the aforementioned stretch move in order to obtain estimates for $H_0$ based on the $\varLambda$CDM cosmological model. The density of the Universe at current time is expressed as a parameter $\varOmega _0$ that is made up of three sub-quantities. The first is the mass density of matter – including both baryonic matter as well as dark matter – and is denoted by $\varOmega _{M0}$. The second density parameter, denoted by $\varOmega _{R0}$, is the effective mass density of the relativistic particles, i.e. light and neutrinos, while the final density parameter $\varOmega _{\varLambda 0}$ is the effective mass density of the dark energy:

$$\begin{aligned} \varOmega _0 = \varOmega _{M0} + \varOmega _{R0} + \varOmega _{\varLambda 0}. \end{aligned}$$

(7)

Using observations from the Wilkinson Microwave Anisotropy Probe (WMAP) and assuming the $\varLambda$CDM model, it was found that $\varOmega _{M0}$ is around 0.3, while $\varOmega _{R0}$ is very close to zero and $\varOmega _{\varLambda 0}$ is around 0.7 [60, p. 129]. Therefore, the total mass density as defined in Eq. (7) is close to 1, suggesting a Euclidean or ‘flat’ Universe. The dominance of the mass and dark energy densities compared to that of the relativistic particles at current time is contrasted with that at early times in the Universe. In fact, radiation was then dominant over both mass and dark energy [61]. The true values of the density parameters determine the shape and ultimate fate of the Universe, with current research mostly in favour of accelerating expansion [62].

According to [63], the first Friedmann equation relates the different density parameters to the Hubble parameter and Hubble constant, namely:

$$\begin{aligned} \frac{H(z)^2}{H_0^2} = \varOmega _{R0} (1+z)^4 + \varOmega _{M0} (1+z)^3 + \varOmega _{K0} (1+z)^2 + \varOmega _{\varLambda 0}, \end{aligned}$$

where $\varOmega _{K0} \approx 0$ so the third term may therefore be eliminated. Similarly, the term containing $\varOmega _{R0}$ can also be eliminated, and $\varOmega _{\varLambda 0}$ may alternatively be expressed as $1 - \varOmega _{M0}$ from Eq. (7). Therefore, the model under consideration becomes:

$$\begin{aligned} H(z) = H_0 \ \sqrt{\varOmega _{M0} (1+z)^3 + (1 - \varOmega _{M0})}. \end{aligned}$$

Virtually all modern estimates of $H_0$ lie in the range of $65-80$ km s$^{-1}$ Mpc$^{-1}$, and $\varOmega _{M0}$ is known to be very close to 0.3 [64]. Therefore, we conservatively set a mostly uninformative prior on the parameters, defined by:

$$\begin{aligned} \log \mathbb {P}(\varvec{\theta }) = {\left\{ \begin{array}{ll} 0 \phantom {-\infty } H_0 \in [50, 100] \text { and } \varOmega _{M0} \in [0.1, 0.5] \\ -\infty \phantom {0} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(8)

where $\varvec{\theta }$ is the vector of parameters $(H_0, \varOmega _{M0})^T$. As initial points, we use $\hat{H}_0^{(0)} = 75$ km s$^{-1}$ Mpc$^{-1}$and $\hat{\varOmega }_{M0}^{(0)} = 0.3$.

As was done with GPR, we fit the H(z)-against-z curve by comparing the predicted and observed values of H(z). In particular, for CC and BAO, our objective is analogous to weighted least squares estimation. Therefore, the objective function is proportional to

$$\begin{aligned} - \sum _{i=1}^{n} \frac{\left[ \hat{H}_{pred}(z_i) - H_{obs}(z_i)\right] ^2}{\hat{\sigma }_H^2(z_i)}, \end{aligned}$$

(9)

where $\hat{H}_{pred}(z_i)$ and $H_{obs}(z_i)$ are the predicted and observed values of H at redshift $z_i$ and $\hat{\sigma }_H^2(z_i)$ is the variance of the observation $H_{obs}(z_i)$. The idea behind such a function is to minimise the distance between the predicted and observed values for H at each of the redshifts $z_i$ present in the CC dataset. This quantity reaches a maximum of 0 when the predicted and observed values of H for each $z_i$ are equal.

For the SN data, the objective function is similar but it differs in that we use $E(z) = H(z)/H_0$ values instead of using H values directly, and additionally we need to incorporate the $5 \times 5$ covariance matrix of these readings [30].

Therefore, suppose that the five values of z form a vector $\textbf{z} = (z_1, z_2,\ldots , z_5)^T$, and let the corresponding observed values of ${\textbf {E}}$ at these z-values form a vector ${\textbf {E}}_{obs}(\textbf{z})$, and similarly for the predicted values. In this case, we have that the objective function is proportional to

(10)

For all three data sources, since we are assuming a regression structure with independent Gaussian errors, estimation using the CC and BAO cases is analogous to ordinary least squares regression, while the SN data takes a weighted least squares structure since the SN error terms are correlated.

This is similar to the statistical technique of maximum likelihood estimation; in fact, we inherit asymptotic consistency and efficiency [58] for our estimates. Moreover, the objective functions are often directly referred to as ‘likelihood functions’ within the astrophysics literature [30]. We denote the likelihood relating to each dataset as $\varLambda _{CC}$, $\varLambda _{SN}$, and $\varLambda _{BAO}$ respectively. The overall log-likelihood when all the datasets are considered altogether is then given by the summation of the component log-likelihoods, i.e.:

$$\begin{aligned} \log \varLambda _{tot}(f | \varvec{\theta })= & \log \varLambda _{CC}(f | \varvec{\theta })+ \log \varLambda _{SN}(f | \varvec{\theta })\nonumber \\ & + \log \varLambda _{BAO}(f | \varvec{\theta }). \end{aligned}$$

(11)

Using Bayes’ rule, the posterior log-probability is proportional to the summation of the log-prior and log-likelihood, i.e.:

$$\begin{aligned} \begin{aligned} \mathbb {P}(\varvec{\theta }| f) \propto&\ \mathbb {P}(\varvec{\theta }) \varLambda _{tot}(f | \varvec{\theta }) \\ \implies&\ \log \mathbb {P}(\varvec{\theta }| f) \propto \log \mathbb {P}(\varvec{\theta }) + \log \varLambda _{tot}(f | \varvec{\theta }). \end{aligned} \end{aligned}$$

In order to obtain the parameter estimates $\hat{H}_0$ and $\hat{\varOmega }_{M0}$ for each combination of dataset and ‘prior’, we use the affine ensemble sampler as implemented in +emcee+ with 5000 iterations and 200 walkers. Each walker is initialised close to the point $\varvec{\theta }^{(0)}:= \big ( \hat{H}_0^{(0)}, \hat{\varOmega }_{M0}^{(0)} \big )^T = (75, 0.3)^T$, and the parameter values are updated iteratively using the parallelised version of the stretch move such that the log-likelihood function of Eq. (11) is maximised with respect to $\varvec{\theta }$.

3.2 Novel methods

3.2.1 Markov chain Monte Carlo based on kernel hyperparameters

The first novel method investigated is a non-parametric implementation of the ensemble MCMC sampler. In particular, we consider a GPR structure and use an ensemble sampler to obtain estimates for the hyperparameters of the kernel functions involved. These hyperparameter values are then used to obtain estimates for the Hubble constant. When compared to the approach of Sect. 3.1.2, this novel approach has the advantage of being independent from any cosmological model.

The module +mcmcdgp+ within the Python package +GaPP+ [13] allows for a non-parametric reconstruction of the H(z)-against-z function through MCMC inference on the hyperparameters of the kernel function. This reconstruction is carried out in exactly the same way as in Sect. 3.1.1. In particular, we minimise the Chi-squared statistic between the reconstructed/estimated and observed value of H(z) in each case, as in Eq. (5). The only difference between the theoretical setup used here when compared to GPR is that the values for the kernel hyperparameters are obtained using the affine ensemble sampler described in Sect. 3.2.1 and as implemented in +emcee+ instead of the usual minimisation of derivatives.

3.2.2 Student’s t-process regression

While GPR has been extensively used within the astrophysical literature, including obtaining estimates for $H_0$ [10, 30], this work also explores the use of TPR to obtain estimates for this constant. As the name implies, TPs are highly similar to GPs, but with the multivariate Student’s t-distribution replacing the multivariate Gaussian distribution. A TP is therefore characterised by its mean and kernel functions, as well as an additional degrees of freedom parameter.

The main drawbacks of GPR include the normality assumption taken on the observations, as well as the poor performance of GPR when outliers are present in the data and the tendency to overfit. The Student’s t-distribution has comparatively heavier tails than the Gaussian distribution [65, p. 2], so TPR can address these disadvantages [66, 67]. In this work, we consider a form of TPR that introduces dependent Student’s t-noise, in that the variance of the noise is dependent on how well the corresponding noise-free model fits the data [68]. This is referred to as the Student’s t-process regression with dependent Student’s t noise (TPRD) model. Analogously to the Gaussian case, in TPR we let the latent function f be a TP and assign a multivariate Student’s t-distributed likelihood function, leading to a TP posterior.

The p-variate Student’s t-distribution [68] with mean function $\textbf{m}$, $(p \times p)$ scale matrix $\mathbb {K}$, and degrees of freedom parameter $\nu > 2$ has joint probability density function

$$\begin{aligned} \mathbb {P}(\textbf{x})= & \frac{\varGamma (\frac{\nu +p}{2})}{(\nu \pi )^{\frac{p}{2}} \varGamma \left( \frac{\nu }{2} \right) } |\mathbb {K}|^{-\frac{1}{2}} \nonumber \\ & \times \left[ 1 + \frac{(\textbf{x} - \textbf{m})^T \mathbb {K}^{-1} (\textbf{x} - \textbf{m})}{\nu } \right] ^{-\frac{\nu +p}{2}}, \end{aligned}$$

(12)

We denote this as $\textbf{X} \sim MVT_p(\textbf{m}, \mathbb {K}, \nu )$.

Then, we define a TP in a similar manner to a GP, except that the multivariate Gaussian distribution is replaced with the multivariate Student’s t-distribution. In other words, any finite sample of random variables from a TP is jointly multivariate Student’s t-distributed. Similar to the notation for Gaussian processes, we denote a TP using $f \sim TP(m, k, \nu )$.

Many of the properties of TPs follow from those of GPs, since the Student’s t-distribution is closely related to the Gaussian distribution. In particular, given some fixed $\textbf{m}$ and $\mathbb {K}$, then a TP becomes equivalent to the corresponding GP at the limit $\nu \rightarrow \infty$. This follows immediately from the fact that the multivariate Student’s t-distribution converges to the multivariate Gaussian distribution at this limit [69], and from the definitions of GPs and TPs.

Moreover, the additional ‘degrees of freedom’ parameter $\nu$ within the TP controls the degree of dependence between jointly t-distributed variables [67] as well as the heaviness of the tails, with smaller values of $\nu$ corresponding to heavier tails. However, the behaviour of a TP becomes closer to that of a GP as we increase $\nu$. Additionally, the conditional distribution for the multivariate Student’s t-distribution can be worked out analytically, and it then follows that the posterior predictive distribution of a TP converges to that of a GP as $\nu \rightarrow \infty$. Therefore, assuming that the same kernel with the same hyperparameters is used, the posterior predictive mean of a TP has the same form as in a GP. However, the same cannot be said for the predictive covariance. In fact, the predictive covariance for a TP depends on the observed values. This allows for increased flexibility in using a TP when compared with GPs, as in the latter case the predictive covariance is independent of the training observations.

In the TPRD model [68], we let the noise vector $\varvec{\epsilon }:= (\epsilon _1, \epsilon _2,\ldots , \epsilon _n)^T$ follow an n-dimensional MVT distribution with correlation matrix dependent on how well the noise-free model $\textbf{y} = f(\mathbb {X})$ fits the data. Define $f:= (f(\textbf{x}_1), f(\textbf{x}_2), \dots , f(\textbf{x}_n))^T$. Then, assuming zero mean, the noise vector is distributed as:

$$\begin{aligned} \varvec{\mathcal {E}} | \beta \sim MVT_n \Bigg [ \textbf{0}, \ \left( 1 + \frac{1}{\nu } \textbf{f}^T \mathbb {K}^{-1} \textbf{f} \right) \frac{1}{\beta } \mathbb {I}_n, \ \nu + n \Bigg ], \end{aligned}$$

(13)

where $\beta$ is a constant scaling factor and $\mathbb {I}_n$ is the $(n \times n)$ identity matrix. The quantity $\frac{1}{\beta } \mathbb {I}_n$ thus ensures that the covariance matrix of the noise distribution is indeed a matrix, as is required from the definition of the multivariate Student’s t-distribution.

Given $\textbf{F} \sim MVT_n(\textbf{m}, \mathbb {K}, \nu )$ and Eq. (13), we obtain the likelihood derived from the multivariate Student’s t-distribution:

$$\begin{aligned} \textbf{Y} | \textbf{F}, \beta \sim MVT_n \Bigg [ \textbf{f}, \ \left( 1 + \frac{1}{\nu } \textbf{f}^T \mathbb {K}^{-1} \textbf{f} \right) \frac{1}{\beta } \mathbb {I}_n, \ \nu + n \Bigg ]. \end{aligned}$$

(14)

The joint distribution of $\textbf{y}$ and $\textbf{f}$ is therefore given by

$$\begin{aligned} \mathbb {P}(\textbf{y}, \textbf{f} | \beta )&\propto \Bigg [ 1 + \frac{\beta }{\nu + n} \textbf{y}^T \left( \mathbb {I} - \frac{\beta }{\nu + n} \mathbb {A}^{-1} \right) \textbf{y} \nonumber \\&\quad + (\textbf{f} - \bar{\textbf{f}})^T \mathbb {A} (\textbf{f} - \bar{\textbf{f}}) \Bigg ] ^ {-\frac{\nu + 2n}{2}}, \end{aligned}$$

(15)

where $\mathbb {A} = \frac{1}{\nu } \mathbb {K}^{-1} + \frac{\beta }{\nu + n} \mathbb {I}$ and $\bar{\textbf{f}} = \frac{\beta }{\nu + n} \mathbb {A}^{-1} \textbf{y}$, resulting in the marginal log-likelihood

(16)

as shown by [68].

Comparing with Eq. (4) for the GPR case, the log-likelihood in this case is highly similar. In fact, the first term is related to the data-fit term , while the second and third terms are a model complexity penalty and a normalisation constant respectively. The main difference from GPR in this case is that the first term in the TPRD marginal log-likelihood is a logarithmic, rather than linear, function of . This provides further evidence in favour of the robustness of TPRD, as any outliers in $\textbf{y}$ would disturb the marginal log-likelihood for TPRD less than the equivalent in GPR. The kernel hyperparameters and the optimal value for $\nu$ can then be inferred through numerical optimisation of the derivative of Eq. (16), similarly to the GPR case.

3.2.3 Heteroscedastic regression

Another novel method considered for estimating $H_0$ is heteroscedastic GPR and TPR as described by [70]. The idea behind heteroscedastic GP and TP modelling is to simultaneously model the mean and variance, while allowing the error terms $\epsilon _i$ to have a different variance for each element. In other words, given a vector of observations $(\textbf{x}_i, y_i)$ for $i \in \{1, 2, \dots , n\}$ and $f \sim GP(m, k)$ or $f \sim TP(m, k, \nu )$, the basic model $y_i = f(\textbf{x}_i) + \epsilon _i$ shown in Eq. (3) is assigned error terms $\epsilon _i \sim N(0, \sigma _i^2)$ for each i instead of assuming that the error terms are independent and identically-distributed for all i.

This method, as implemented in the +R+ package +hetGP+ [70], also allows for some optimisations based on the ‘stochastic kriging’ (SK) predictor [71], which lead to large computational savings especially when a large number of observations are available at each $\textbf{x}_i$. However, this assumption of repeated readings is often prohibitive when modelling real-world data. While replication can still help speed up the computation, use of the SK predictor does not inherently require a set minimum dataset size or numbers of replicates.

The log-likelihood for the SK predictor is defined by [72, p. 10] as:

$$\begin{aligned} \log \varLambda = c - \frac{1}{2} \sum _{i=1}^n \big [ (a_i - 1) \log \lambda _i + \log a_i \big ] - \frac{1}{2} \log | \mathbb {K}_n |. \end{aligned}$$

(17)

The SK predictor already includes some in-sample heteroscedasticity by independently calculating the moments for each element; therefore, a different variance value will be assigned to each of the sampled elements. However, this is not extended out-of-sample and is therefore not useful for heteroscedastic interpolation. [71] suggest to incorporate out-of-sample heteroscedasticity fitting another GP or TP on the variances of the sample points to obtain a smoothed variance for use in interpolation. However, [70] go a step further and propose introducing latent variables under a GP or TP prior and performing MCMC inference on their joint distribution in order to obtain this smoothed variance. Let be made up of the latent variance variables corresponding to the $r \le n$ unique observation points. We assign a GP or TP prior to this matrix, i.e.:

or analogously:

where $\mathbb {K}_{(g)}:= \mathbb {C}_{(g)} + g \mathbb {A}_r^{-1}$. Here, the subscript (g) is used to distinguish this process from the one on the latent function f. As for $\beta _0$, the natural estimator to use is . As described by [72], one can opt to use in place of to ensure that $\delta _i$ remains positive for each $i \in \{1, 2, \dots , r\}$.

In heteroscedastic GPR, a joint log-likelihood function over both GPs is defined, i.e.:

$$\begin{aligned} \begin{aligned} \log \mathbb {P}(\textbf{y} | \mathbb {K}_r, \mathbb {K}_{(g)})&= c - \frac{1}{2} \sum _{i=1}^r [(a_i - 1) \log \lambda _i + \log a_i] \\&\quad - \frac{1}{2} \log |\mathbb {K}_r| - \frac{1}{2} \log |\mathbb {K}_{(g)}|, \end{aligned} \end{aligned}$$

(18)

and this likelihood may be optimised numerically with respect to any unknown parameter by differentiating it with respect to that parameter and setting the derivative to zero. For TPR, we can similarly use a joint log-likelihood function over both TPs. In the event that replication is present, the maximum likelihood estimates obtained using the r unique points are equivalent to the full-n estimates [72].

For the application of these techniques on our data, we use the +R+ package +hetGP+ [70], in particular the subroutines +mleHetGP+ and +mleHetTP+ for heteroscedastic GPR and TPR.

4 Results and discussion

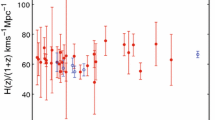
For each of the methods investigated, reconstruction plots of H(z) against z were obtained. As an example, Fig. 1 shows the reconstruction obtained using GPR with the square exponential function, for the dataset CC+SN+BAO and for the priorless case.

Fig. 1

Reconstruction of $\hat{H}(z)$ against z: GPR, square exponential kernel, CC+SN+BAO data, no prior

The results are also presented in tabular form; for example, Table 2 shows the $\hat{H}_0$ values obtained after running the regressions on the different datasets and using the square exponential kernel function, for each of the priors discussed in Table 1. Only the results for the square exponential kernel function are presented here, since each of the kernel functions trialled gave very similar results. The full set of results obtained is available in the Supplementary Material.

Table 2 $H_0$ estimates: GPR with square exponential kernel

For the MCMC-based methods, trace plots showing the evolution of the walkers at each iteration provided a visual confirmation that the desired convergence of the parameter estimates was achieved. An example of one of the trace plots obtained is given in Fig. 2.

Fig. 2

Trace plot: MCMC $\varLambda$CDM, CC+SN+BAO data, no prior

Additionally, corner plots showing the distribution of the parameters in each case were produced. The corner plot for the dataset CC+SN+BAO and the priorless case is presented in Fig. 3. This plot provides a visual confirmation of the decrease in $\hat{\varOmega }_{M0}$ with increasing $\hat{H}_0$, i.e. from the shape of the ‘oval’ in the bottom-left corner of each subplot.

Fig. 3

Corner plot: MCMC $\varLambda$CDM, CC+SN+BAO data, no prior

Since there is a large number of possible combinations of kernel function, method, prior, and dataset, a large number of estimates for $H_0$ were obtained. The different approaches were compared using whisker plots. For example, Fig. 4 contains all the $H_0$ estimates obtained using the CC+SN+BAO dataset, irrespective of the method and prior used. This allows us to determine the effect of different methods and priors given a fixed dataset. Similarly, we present the estimates obtained using the GPR method across all datasets and priors in Fig. 5. We also show the estimates obtained using the priorless case as well as the SH0ES and Planck priors in Figs. 6, 7, 8. Similar figures and tables for the other priors, datasets, and methods considered are presented in the Supplementary Material.

In each case, the estimate for $H_0$ presented is the median of estimates obtained using a given dataset, method, and prior. The same applies for the standard error of this estimate. For each estimate, the actual estimated value is shown using the dot, while the errors are shown using the whisker plots. More uncertain estimates, i.e. those with a higher standard error, consequently have longer whiskers than estimates with low standard error. The pre-established SH0ES and Planck priors $\hat{H}_0^{SH0ES}$ and $\hat{H}_0^P$ are superimposed on the plot as the blue and red bars respectively.

In order to calculate the ‘distance’ between two estimates of $H_0$, we make use of the $\sigma$-distance as in Eq. (19):

$$\begin{aligned} d(\hat{H}_{0,i}, \hat{H}_{0,j}) := \frac{\hat{H}_{0,i} - \hat{H}_{0,j}}{\sqrt{\hat{\sigma }_{\hat{H}_{0,i}}^2 + \hat{\sigma }_{\hat{H}_{0,j}}^2}}, \end{aligned}$$

(19)

where $\hat{H}_{0,i}$ and $\hat{H}_{0,j}$ are the two estimates for $H_0$, and $\hat{\sigma }_{\hat{H}_{0,i}}$ and $\hat{\sigma }_{\hat{H}_{0,j}}$ are their corresponding standard errors. Here, the denominator has a normalising effect since it takes the estimators’ variances into account. This is the same methodology used in [30].

The distance between each $H_0$ estimate and the pre-established SH0ES and Planck priors is also shown in the whisker plot. In particular, for each $H_0$ estimate presented in Figs. 4, 5, 6, 7, 8, 9, the distance between the estimate and the Planck prior is shown on the left of the box and whisker, while the distance between the estimate and the SH0ES prior is shown on the right. A figure of 1.5 on the left-hand side, for example, means that the estimate obtained is at 1.5 units of distance larger than the Planck prior. Lastly, at the bottom of each plot, we show the median of all the values shown in that plot. The median $H_0$ estimate for each plot is also presented within Tables 3, 4, and 5. In order to obtain a suitable standard error for each median value, the median standard error of the relevant estimates is taken.

From these figures, one can immediately notice some patterns. In particular, the estimates obtained using GPR, MCMC $\varLambda$CDM, and MCMC GPR are highly dependent on the prior specification. For these methods, the tensions between each estimate and the pre-established SH0ES and Planck priors are often more than $2\sigma$, and even exceed $4\sigma$ in some cases. On the other hand, TPR as well as heteroscedastic GPR and TPR are less sensitive to the specification of the ‘prior’ $\hat{H}_0$ value, so that the estimates obtained for the Hubble constant using each of the different ‘priors’ are closer to each other. However, for TPR, only a few of the estimated values have more than $2\sigma$ tension with either the SH0ES or Planck priors, owing to the larger standard error associated with the TPR estimates. Therefore, further investigation of TPR with larger datasets is required so that these standard errors are reduced. Regardless of the method used, the standard errors for the priorless case are understandably much larger than for the cases where a prior $\hat{H}_0$ value was specified. This can be seen, for example, by comparing Fig. 6 to Figs. 7 and 8. Additionally, a striking observation that can be made from Fig. 8 is that the estimates for all methods when considering the Planck prior are very close to each other. In this case, the evidence suggests a lower $H_0$ value and one that is very close to $\hat{H}_0^P$.

Additionally, in Fig. 9 we further summarise the results by presenting the median Hubble constant estimates obtained by prior, dataset, and method. In other words, given a fixed ‘prior’, we present the median of all the estimates involving that prior irrespective of the kernel, dataset, and method used. Similarly, given a dataset, we calculate the median over all priors, kernels, and methods, and given a method we get the median over all priors/kernels/datasets. At the bottom of this plot, we present the median estimate obtained across all methods, datasets, kernels, and priors. This value is $\hat{H}_0^{med} = 68.85 \pm 1.67$ km s$^{-1}$ Mpc$^{-1}$. As can be seen from the bottom part of Fig. 9, this value is less than 1 standard deviation from the Planck prior $\hat{H}_0^P$ but is at a tension of more than $2 \sigma$ from the SH0ES prior $\hat{H}_0^{SH0ES}$, which is further evidence in favour of a lower value for the Hubble constant.

Fig. 4

Comparison of estimates and errors obtained using CC+SN+BAO dataset

Fig. 5

Comparison of estimates and errors obtained using GPR method

Fig. 6

Comparison of estimates and errors obtained in priorless case

Fig. 7

Comparison of estimates and errors obtained using SH0ES prior

Fig. 8

Comparison of estimates and errors obtained using Planck prior

Fig. 9

Comparison of estimates and errors obtained: median values for each prior, dataset, and method

We can also compare the median $\hat{H}_0$ value obtained for each method, prior, and dataset in order to determine the effect of the particular method, prior, or dataset on the estimates obtained. The table comparing the different datasets is presented as Table 3, and similarly Tables 4 and 5 respectively compare the methods and priors.

From these tables, we can see that larger datasets generally lead to more confident predictions, i.e. estimates with lower uncertainties. However, it should be noted that only the MCMC $\varLambda$CDM method was applied to the datasets CC+SN_* and CC+SN_*+BAO. When it comes to the method used, we see that GPR, MCMC $\varLambda$CDM, and MCMC GPR give very similar results, indicating that the model-independent GPR is in agreement with the widely-accepted $\varLambda$CDM cosmological model. From the bottom part of Fig. 5, we can see that the median value obtained for GPR is at a distance of 1.3072 standard deviations from $\hat{H}_0^P$, while there is a tension of $2.2341\sigma$ with $\hat{H}_0^{SH0ES}$. This provides some evidence in favour of a lower value for the Hubble constant. The rest of the methods considered, namely TPR and heteroscedastic GPR and TPR, produced even lower estimates for $H_0$. Therefore, these methods provide further evidence in favour of a lower value of $H_0$ that is closer to the Planck and DES priors.

As for the prior used, this naturally has a great effect on the $H_0$ estimates obtained, as the effect of adding a prior is to consider an additional ‘artificial’ data point at $z=0$. As expected, using the Planck and DES priors produced lower values than the SH0ES, H0LiCOW, and CM priors. However, it is to be noted that the estimates obtained when no prior was included are closer to the Planck and DES priors than the SH0ES and H0LiCOW priors – this also suggests a lower value for $H_0$. This is arguably the main finding of our research.

5 Conclusion

In this work, we explore the comparative reconstruction methods as applied to expansion data against a baseline $\varLambda$CDM MCMC approach. We do this using late time survey data involving direct CC data, the Pantheon sample, and BAO data, which collectively have been shown to give strong constraints on cosmological models. In our case, we only consider the $\varLambda$CDM model, which serves as our benchmark for other constraints on cosmological parameters including the increasingly contentious value of $H_0$. These data sets are described in detail in Sect. 2 while the reconstruction methods are explained in Sect. 3. Here, we consider several methods which reconstruct the Hubble diagram independently of a physical cosmological model. This includes GPR which is based on a kernel function that is optimized through a learning process to mimic the underlying data and has been used exhaustively in data analysis pipelines to reduce noise. We also describe our implementation of MCMC and how we use it to fit the GPR kernel hyperparameters. We then describe the TPR method which is a generalization of GPR in that it can address the assumption of Gaussianity in GPR and thus is more applicable to real observational data. This can also help address the problem of overfitting in GPR. Finally, we use the heteroscedastic regression method where both the GPR and TPR methods are reevaluated through the prism of allowing the uncertainty of each reconstructed point to have a separate variance in the determination of its uncertainty. This produces a much more precise reconstruction when tested against real data. The general consistency between the methods helps strengthen the broader coherence of model-independent approaches, and may be useful in constructing parametric models and obtaining constraints on those cosmologies.

The results of each of the different methods with the plethora of data sample combinations and possible trial prior values (Table 1) on the value of the Hubble constant are laid out in Sect. 4. For a square exponential kernel, we show the reconstructions of the Hubble constant in Table 2. Firstly, these are largely invariant up to $1\sigma$ in the choice of kernel function. Another point to appreciate is that the studies that contain a prior are highly dependent on that choice which can readily be observed for the best fits containing a $\hat{H}_0^{SH0ES}$ prior. In all cases, the uncertainties were reasonably good except for the sole instance where only CC data was considered. This is further emphasized when comparing the best fits for specific data sets as in Table 2 as compared with the corresponding result for the scenario in which priors are placed on these analyses, as in Table 5. In Table 4, the methods described here are shown comparatively against their estimates on their constraint value of $H_0$. It is observed that GPR overfits this parameter due to a generic overfitting problem in the method for low redshifts, while TPR fits the real uncertainties much better.

We conducted an exhaustive study of the data set combinations together with priors on $H_0$ and the reconstruction methods, which are shown in Figs. 4, 5, 6, 7, 8, 9. This confirms our previous discussion on the overfitting issue of GPR

Table 3 Median $H_0$ estimate and error obtained by dataset

Table 4 Median $H_0$ estimate and error obtained by method

Table 5 Median $H_0$ estimate and error obtained by prior

which is corrected by the TPR method which contains larger uncertainties that are more consistent with the underlying data. As for the heteroscedastic regression method, this produces intermediary uncertainties which tend to a medium value between the two quoted Hubble constants from literature. We plan to extend this work to probe the comparative behaviour of these methods for large scale structure data, which expresses a mild tension in the value of the $S_8$ parameter. Another important future prospect is to include updated data sets in a future study [73,74,75,76,77,78], as well as other types of observational data including gamma-ray bursts [79, 80] and HII galaxy [81, 82] data samples. We also aim to include more reconstruction methods and expand our diagnostic tests of these methods in future work.