1 Introduction

Gravity is one of the four fundamental interactions known in Nature [1]. The corresponding theory of gravity is used to describe this type of interaction. In particular, general relativity (GR) [2] is the standard theory that describes gravity using the geometrical concept. It was proposed by Einstein in 1915 as an extension of the special theory of relativity to the case of non-inertial reference frames. As any theory, GR has also been well tested in both weak (Solar system tests, weak lensing, etc. [3]) and strong field regimes (using gravitational waves detection [4, 5] and shadow of supermassive black holes M87* [6] and SgrA* [7, 8]).

On the other hand, the GR meets some fundamental problems related to singularity at the origin of corresponding vacuum solutions, non-compatibility with quantum field theories, etc. To resolve these issues, one may modify GR or propose alternative theories of gravity. Fortunately, the current resolutions of experiments and observations allow us to consider these modifications. At the same time, many modifications may create problems for observed phenomena: different parameters may mimic each other  (see, e.g. [8, 9]). One possible solution may come through parameterization of the solutions of the field equations. The parameterization of generic symmetric spherical and symmetric axial spacetime metrics has been proposed in Refs. [10, 11].

One of the modifications of GR has been proposed in Ref. [12]. The main aim was to obtain a convenient approach to the quantum gravity model. The proposed model consists of the scalar and massive vector field and is called scalar-tensor-vector gravity (STVG) [12]. One of the interesting features of this approach is that the massive vector field at the quantum scale represents a repulsive interaction corresponding to the charge \(Q = \sqrt{\alpha G} M \), where G is the gravitational constant, M is the mass of the central object, and \(\alpha \) is the coupling parameter. This model’s spherical and axial symmetric solutions have been obtained in Ref. [13] describing the non-rotating and rotating black holes, respectively. The different properties of these solutions have been explored in [14,15,16,17,18,19,20,21,22,23,24]. Moreover, the dynamics of test particles around different black holes including MOG black holes have been studied in Refs. [25,26,27,28].

Any modifications or alternatives to GR need to be tested. The most convenient and efficient test is based on analysis of the dynamics of the test particles. For any metric theory of gravity, the analysis of massive and/or massless particle motion may provide a deep insight into understanding the physical parameters of solution [29, 30]. It is also worth noting that X-ray data from astrophysical objects are also helpful in testing the solutions for compact objects [31]. The analysis of massless particles may be used to explore the effect of gravitational lensing, which is considered one of the features of GR. The effects of gravitational lensing around compact objects in a plasma environment have been studied in Refs. [32, 33]. The dynamics of electrically charged and neutral test particles near black holes is crucial in astrophysics and has been intensively studied for background geometry features [34,35,36,37,38,39]. The special case of particle motion corresponding to circular orbits may be considered a useful tool for studying the astrophysical phenomenon known as quasi-periodic oscillations (QPOs).

The research in the center of mass energy (CME) in black holes has mostly concentrated on comprehending the fundamental principles responsible for generating ultra-high-energy collisions. This includes investigations into theoretical models and numerical simulations [40,41,42,43,44]. The idea of CME of black holes is crucial for comprehending particle collisions and dynamics in the vicinity of these very intense entities. Recent studies have emphasized the need to study physics at the horizon, where relativistic effects greatly increase collision energy to levels far higher than what can be achieved in terrestrial accelerators such as the Large Hadron Collider. The study conducted by Grib and Pavlov [45] showed that particle collisions in the vicinity of revolving black holes have the potential to attain very high energy. This is primarily attributed to the Penrose process and frame-dragging effects in Kerr black holes. Banados, Silk, and West investigated these high-energy collisions, revealing possible detectable indications in astrophysical events [46]. Recent mathematical simulations and theoretical models, such as the work of Harada and Kimura [47], have further investigated these results. They have examined the circumstances in which these high energies may occur and their consequences for dark matter and basic physics. These advancements indicate that black hole environments may function as a natural high-energy laboratory, providing a unique perspective on particle physics that extends beyond the standard model [48,49,50,51].

This paper aims to investigate the effects of black-bounce and MOG parameters on spacetime geometry, test particle motions, and particle collision near the SV-MOG spacetime. The paper is organized as follows: in Sec. 2, we introduce the SV spacetime in MOG and explore its horizons, spacetime geometry in the \(a-\alpha \) region, and the effective gravitational mass. Moreover, we also investigate its scalar invariants in detail. Section 3 deals with the motion of neutral particles, including the angular momentum, energy, and ISCO. In Sect. 4, we investigate the efficiency of energy extraction under the influence of black-bounce and MOG parameters. In Sect. 5, we discuss the collision of geodesic particles around the SV-MOG spacetime geometry in detail. Finally, in Sect. 6, we conclude our results with concluding remarks. Throughout the paper, we adopt the spacelike signature \((-,+,+,+)\), a system of units in which \(G_{N}=c=1\).

2 Simpson–Visser spacetime in MOG

The field action in the STVG theory has the following several terms [52]:

$$\begin{aligned} S = S_{G}+S_{\phi }+S_{S}+S_{M}, \end{aligned}$$
(1)

where \(S_{M}\) is the action of pressure-less matter, \(S_{G}\) is the original Einstein–Hilbert gravity action, \(S_{S}\) is the action of scalar fields, and \(S_{\phi }\) is the action of vector fields:

$$\begin{aligned} S_{G}= & \frac{1}{16\pi }\int \frac{1}{G} (R+2 \Lambda ) \sqrt{-g}d^4x,\end{aligned}$$
(2)
$$\begin{aligned} S_{\phi }= & -\frac{1}{4\pi } \int \left[ \mathcal {K} + \textrm{V}(\phi _{\mu })\right] \sqrt{-g}d^4x,\end{aligned}$$
(3)
$$\begin{aligned} S_{S}= & \int \frac{1}{G} \Bigg [\frac{1}{2} g^{\alpha \beta } \left( \frac{\nabla _{\alpha }G \nabla _{\beta }G}{G^2} + \frac{\nabla _{\alpha }\mu \nabla _{\beta }\mu }{\mu ^2} \right) \nonumber \\ & - \frac{V_{G}(G)}{G^2} -\frac{V_{\beta }(\mu )}{\mu ^2} \Bigg ] \sqrt{-g}d^4 x,\end{aligned}$$
(4)
$$\begin{aligned} S_{M}= & -\int (\rho \sqrt{u^{\mu }u_{\mu }}+{\mathcal Q}u^{\mu }\phi _{\mu })\sqrt{-g}d^4 x + J^{\mu } \phi _{\mu }, \end{aligned}$$
(5)

with \(R = g^{\mu \nu } R_{\mu \nu } \) is the Ricci scalar, \(g\equiv \)det\((g_{\mu \nu })\) is the determinant of the metric tensor, \(\nabla _{\mu }\) stands for the covariant derivation, and \({\mathcal K}\) is the kinetic term for the scalar field \(\phi _{\mu }\), which reads \({\mathcal K}=B^{\mu \nu } B_{\mu \nu }/4\), where \(B^{\mu \nu } = \partial _{\mu } \phi _{\nu } -\partial _{\nu } \phi _{\mu }.\) The covariant current density is defined to be

$$\begin{aligned} J^{\mu } =\kappa T_M^{\mu \nu } u_{\nu }, \end{aligned}$$
(6)

where \(T_M^{\mu \nu }\) is the energy–momentum tensor for matter with \(\kappa = \sqrt{\alpha G_N},\) \(\alpha = (G-G_N) /G_N\) is a parameter defining the scalar field, \(G_N\) is Newtonian gravitational constant, \(u^{\mu } = dx^{\mu } /d\tau \) is a timelike velocity, and \(\tau \) is the proper time a long time like geodesic. The perfect fluid energy–momentum tensor for matter is given by,

$$\begin{aligned} T^{M\mu \nu } = (\rho _M + p_M) u^{\mu }u^{\nu } -p_Mg^{\mu \nu }, \end{aligned}$$
(7)

where \(\rho _M\) and \(p_M\) are the density and pressure of matter, respectively. From Eqs. (6) and (7) using \(u_\mu u^\mu =1\), we get

$$\begin{aligned} {J^\mu =\kappa \rho _M u^\mu }. \end{aligned}$$
(8)

For the matter-free and pressureless MOG field with \(T_M^{\mu \nu }=0\) in the asymptotically flat (zero-cosmological constant) spacetime, the field equation takes the form,

$$\begin{aligned} G_{\mu \nu }=-\frac{8\pi G}{c^4}T^\phi _{\mu \nu }, \end{aligned}$$
(9)

where \(T^\phi _{\mu \nu }\) is the tensor of massive-vector field. The observational data from galaxy and cluster dynamics show that the mass of the particles in the field \(\phi \) is about \(m_\phi =2.6\times 10^{-28}\) eV, and it is almost zero [14]. One may assume that the vector field is an analog of the electromagnetic field, and its field tensor is defined as

$$\begin{aligned} T^\phi _{\mu \nu }=-\frac{1}{4\pi } \left( B_\mu ^\alpha B_{\nu \alpha } - \frac{1}{4} g_{\mu \nu } B^{\alpha \beta }B_{\alpha \beta }\right) , \end{aligned}$$
(10)

with

$$\begin{aligned} & \Delta _\mu B^{\mu \nu }=0, \end{aligned}$$
(11)
$$\begin{aligned} & \Delta _\alpha B^{\mu \nu }+\Delta _\nu B^{\mu \alpha }+\Delta _\mu B^{\alpha \nu }=0. \end{aligned}$$
(12)

The above assumptions imply that the potential term of the action \(S_\phi \) is zero (\(\textrm{V}(\phi )=(1/2)\mu \phi _\mu \phi ^\mu =0\)), so it has only a kinetic term. One may consider the kinetic term to be a function of the massive-vector field invariant \({\mathcal B}=B_{\mu \nu }B^{\mu \nu }\) as \({\mathcal K}=f({\mathcal B})\).

The geometry around the static and spherically symmetric black hole in MOG is described by the following form of spacetime metric [53,54,55,56]

$$\begin{aligned} ds^2=-g(r)dt^2+\frac{1}{g(r)}dr^2+r^2d\Omega ^2, \end{aligned}$$
(13)

with the metric function

$$\begin{aligned} g(r)= 1-\frac{2(1+\alpha ) M}{r}-\frac{\alpha (1+\alpha ) M^2}{r^2}, \end{aligned}$$
(14)

where \(\alpha \) is the coupling parameter of the modified gravity (hereafter, we call it the MOG parameter) and \(d\Omega ^2=(d\theta ^2+\sin ^2\theta d\phi ^2)\). One can see that the spacetime metric (13) turns to flat-Minkowski one when \(\alpha =-1\) and the case when \(\alpha =0\) corresponds to the Schwarzschild solution.

To obtain a black-bounce in MOG, one can apply the SV regularization method using the transformation [57] as \(r^2\rightarrow r^2+a^2\), and called SV-MOG spacetime. The line element can describe the geometry around the SV-MOG spacetime:

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{1}{f(r)}dr^2+(r^2+a^2)d\Omega ^2\ , \end{aligned}$$
(15)

with the metric function,

$$\begin{aligned} f(r)=1 - \frac{2M(1 + \alpha )}{\sqrt{r^2 + a^2}} + \frac{\alpha (1 + \alpha )M^2}{r^2 + a^2}, \end{aligned}$$
(16)

where M is the total mass, and \(\alpha \) is the STVG (MOG) parameter. The horizon of the SV-MOG black hole can be calculated as,

$$\begin{aligned} \frac{r_H^2}{M^2}=2+\alpha ^2+3 \alpha +2 \sqrt{\alpha ^3+3 \alpha ^2+3 \alpha +1}-\frac{a^2}{M^2},\nonumber \\ \end{aligned}$$
(17)

which is always greater than the Schwarzschild radius corresponding to the positive values of the \(\alpha \) parameter.

Fig. 1
figure 1

Radial representation of f(r), at various values of a and \(\alpha \). We fix \(M=1\)

Full size image

In Fig. 1, we plotted the radial profile of the function f(r) at various discrete parameters a and \(\alpha \). The graphical representation reveals some fascinating f(r) behavior in response to the regularization and MOG parameters. The black line corresponds to the Schwarzschild case and crosses zero at the event horizon \(r=2M\). In the presence of \(\alpha =1\), the event horizon sufficiently increases, and in the presence of the regularization parameter, the horizon slightly decreases.

Fig. 2
figure 2

Graphical representation of black hole horizons \(r_H\) along the black-bounce parameter a (top) and \(\alpha \) (bottom) at different choices of parametric values

Full size image

Figure 2 illustrate the behavior of black hole horizons vs. a and \(\alpha \), left and right, respectively. In the graphical description, we noticed that the dimensionless parameter \(\alpha \) contributes to the horizons. On the other hand, the black-bounce parameter diminishes the horizons. Interestingly, the black-bounced regular MOG black holes have the greatest horizons compared to the Schwarzschild black hole. Similarly, the regular black-bounced black hole has smaller horizons than the regular black-bounced MOG black holes (for details, please see the left panel of Fig. 2).

Fig. 3
figure 3

The existence of a black hole/wormhole is determined by the interval of a and \(\alpha \)

Full size image

In Fig. 3, we have shown the possible region by the shaded area for the existence of black hole/wormholes in the a–\(\alpha \) plane. We noticed that the black-bounce and the MOG parameters result in a greater area for its existence.

2.1 The effective gravitational mass of the spacetime

The mass attributed to the stationary asymptotically flat black hole spacetime corresponds to the conserved quantities associated with the asymptotically time-like and space-like Killing vector fields, respectively, \(\eta ^\mu _{(t)}\) and \(\eta ^\mu _{(\phi )}\). A general argument for equality of the conserved Arnowitt-Deser-Misner mass and of the Komar mass for stationary spacetimes having a time-like Killing vector is established in Refs. [58, 59]. Following the Komar definitions of conserved quantities, we consider a spacelike hypersurface \(\sum _t\), extending from the event horizon to spatial infinity, a surface of constant t with unit normal vector \(n_{\mu }\). The two-boundary \(S_t\) of the hypersurface \(\sum _t\) is a constant t and constant r surface with unit outward normal vector \(\sigma _\mu \). The effective mass reads [60]

$$\begin{aligned} M_{eff}=-\frac{1}{8\pi }\int \limits _{S_t}\bigtriangledown ^\mu \eta ^\nu _{(t)}dS_{\mu \nu }, \end{aligned}$$
(18)

where \(dS_{\mu \nu }=-2n{[_\mu \sigma _\nu ]}\sqrt{h}d^2\theta \) is the surface element of \(S_t,h\) is the determinant of \((2\times 2)\) metric on \(S_t,\) and

$$\begin{aligned} n_\mu =-\frac{\delta ^t_\mu }{|{g^{tt}|^{1/2}}}, \quad \sigma _\mu =-\frac{\delta ^r_\mu }{|{g^{rr}|^{1/2}}}, \end{aligned}$$
(19)

are, respectively, the timelike and spacelike unit outward normal vectors. Thus, the mass integral of Eq. (18) turned into an integral over a closed 2-surface at infinity:

$$\begin{aligned} M_{\text {eff}}&=\frac{1}{4\pi }\int _{0}^{2\phi }\int _{0}^{\phi }\frac{\sqrt{g_{\theta \theta }g_{\phi \phi }}}{|g^{tt}g^{rr}|^{1/2}}\nabla ^{t}\eta ^{r}_{(t)}d\theta d\phi \nonumber \\&= \frac{1}{4\pi }\int _{0}^{2\phi }\int _{0}^{\phi }\frac{\sqrt{g_{\theta \theta }g_{\phi \phi }}}{|g^{tt}g^{rr}|^{1/2}}\left( g^{tt}\Gamma ^{r}_{tt}+g^{t\phi }\Gamma ^{r}_{t\phi } \right) d\theta d\phi . \end{aligned}$$
(20)

Using the metric elements in Eq. (15), we obtain the effective mass of the black hole:

$$\begin{aligned} M_{\text {eff}}=M\frac{r(1+\alpha )}{\sqrt{a^2+r^2}} \left( 1-\frac{\alpha }{\sqrt{a^2+r^2}}\right) , \end{aligned}$$
(21)

which is corrected due to the CDF field and goes over to the Kerr black hole case, that is \(M_{\text {eff}}=M\), when \(\alpha =0\).

Fig. 4
figure 4

Graphical illustration of effective mass along the radial distance r for different values of the parameters. The black solid line corresponds to the Schwarzschild black hole, while dots on each curve locate the location of the event horizon

Full size image

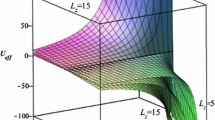
Figure 4 shows the graphical behavior of normalized effective mass along the radial distance r. It behaves differently along r; interestingly, its behavior can be divided into region 1 (\(0 \le r\le 1.5\)), whereas region 2 (\(1.5 \le r\le 3\)). In the first region, \(\alpha \) diminishes, while it contributes to the effective mass in region 2. We also observed that the Schwarzschild black hole has the smallest event horizon compared to the regular black-bounced MOG black holes. Moreover, the black-bounce and MOG parameters contribute to the effective mass outside the event horizon while diminishing it inside.

2.2 Scalar invariants

To explore the properties of spacetime, we may start by studying the scalar invariants of a geometry around a compact gravitating object. Here, we analyze the Ricci scalar, square of the Ricci tensor, and Kretschmann scalar of the spacetime metric given with the lapse function given by Eq. (13). We calculate and examine these quantities by observing their graphical behaviors.

2.2.1 Ricci scalar

Ricci scalar, or the so-called scalar curvature, is one of the simplest curvature invariants of curved spacetime, and it is defined as \(R=g^{\mu \nu } R_{\mu \nu }\), where \(R_{\mu \nu }\) is the Ricci tensor. The positive and negative values of the Ricci scalar correspond to the sunken and convex forms of spacetime, respectively. After some simple mathematics, one may quickly get the following form of the Ricci scalar:

$$\begin{aligned} R= & \frac{1}{\left( a^2+r^2\right) ^{7/2}}\Big [2 a^2 \Big (\alpha (\alpha +1) M^2 \sqrt{a^2+r^2}\nonumber \\ & +a^2 \left( (1+\alpha )M-\sqrt{a^2+r^2}\right) -r^2 \sqrt{a^2+r^2}\nonumber \\ & +(\alpha +1) M r^2\Big )\Big ]. \end{aligned}$$
(22)

At \(r\rightarrow 0\),

$$\begin{aligned} \lim _{r\rightarrow 0}R=\frac{2 (\alpha +1) M (a+\alpha M)}{a^4}-\frac{2}{a^2}. \end{aligned}$$
(23)

2.2.2 Square of the Ricci tensor

Consider the second scalar invariant: the so-called square of Ricci tensor is responsible for the square of the energy–momentum tensor of a field in the spacetime of a black hole. It can be defined as \({\mathcal R}=R_{\mu \nu }R^{\mu \nu }\equiv (8\pi G)T_{\mu \nu }T^{\mu \nu }\) for the spacetime. The square of the Ricci tensor takes the following form for the solution:

$$\begin{aligned} {\mathcal R}&=\frac{2}{\left( a^2+r^2\right) ^{13/2}} \Big [2 \alpha ^2 (\alpha +1)^2 M^4 r^4 \sqrt{a^2+r^2}\nonumber \\&\quad +2 \alpha (\alpha +1)^2 a^2 M^3 r^2 \left( 3 r^2-2 \alpha M \sqrt{a^2+r^2}\right) \nonumber \\&\quad +a^8 \left( \sqrt{a^2+r^2}-4 (\alpha +1) M\right) \nonumber \\&\quad +a^6 \left( (\alpha +1) (11 \alpha +10) M^2 \sqrt{a^2+r^2}\right. \nonumber \\&\quad \left. +2 r^2 \sqrt{a^2+r^2}-12 \alpha (\alpha +1)^2 M^3-8 (\alpha +1) M r^2\right) \nonumber \\&\quad +a^4 \Big (5 \alpha ^2 (\alpha +1)^2 M^4 \sqrt{a^2+r^2}\nonumber \\&\quad +(\alpha +1) (11 \alpha +10) M^2 r^2 \sqrt{a^2+r^2}+r^4 \sqrt{a^2+r^2}\nonumber \\&\quad -6 \alpha (\alpha +1)^2 M^3 r^2-4 (\alpha +1) M r^4\Big )\Big ]. \end{aligned}$$
(24)

At \(r\rightarrow 0\),

$$\begin{aligned} \lim _{r\rightarrow 0}{\mathcal R}= & \frac{2}{a^9} \Big [a^4 (a-4 (\alpha +1) M)-12 \alpha (\alpha +1)^2 a^2 M^3\nonumber \\ & {+}(\alpha +1) a M^2 \Big ((11 \alpha {+}10) a^2{+}5 \alpha ^2 (\alpha {+}1) M^2\Big )\Big ].\nonumber \\ \end{aligned}$$
(25)

2.2.3 Kretchmann scalar

Now we consider the Kretchmann scalar defined as \({\mathcal K}=R_{\mu \nu \sigma \rho }R^{\mu \nu \sigma \rho }\). Usually, the square root of the Kretschmann scalar can be interpreted as an effective gravitational energy density \(\sqrt{{\mathcal K}} \sim \rho _M\). One can easily calculate the Kretchmann scalar for the spacetime metric in the form:

$$\begin{aligned} {\mathcal K}= & \frac{4}{\left( a^2+r^2\right) ^{13/2}} \Big [-2 (\alpha +1) a^2 M r^2 \Big (\alpha ^2 (\alpha +1)\nonumber \\ & M^3 \sqrt{a^2+r^2}+M r^2 \Big (12 \alpha (\alpha +1) M-(7 \alpha +8)\nonumber \\ & \sqrt{a^2+r^2}\Big )-r^4\Big )+2 (\alpha +1)^2 M^2 r^4 \Big (7 \alpha ^2 M^2\sqrt{a^2+r^2}\nonumber \\ & +6 r^2 \left( \sqrt{a^2+r^2}-2 \alpha M\right) \Big ) +a^8 \Big (\sqrt{a^2+r^2}-4 (\alpha \nonumber \\ & +1) M\Big )+a^6 \Big ((\alpha +1) (13 \alpha +11) M^2\sqrt{a^2+r^2}\nonumber \\ & +2 r^2 \sqrt{a^2+r^2}-14 \alpha (\alpha +1)^2 M^3-6 (\alpha +1) M r^2\Big )\nonumber \\ & +a^4 \Big (5 \alpha ^2 (\alpha +1)^2 M^4 \sqrt{a^2+r^2}+15 (\alpha +1)^2\nonumber \\ & M^2 r^2 \sqrt{a^2+r^2}+r^4 \sqrt{a^2+r^2}\nonumber \\ & -14 \alpha (\alpha +1)^2 M^3 r^2\Big )\Big ]. \end{aligned}$$
(26)

At \(r\rightarrow 0\),

$$\begin{aligned} \lim _{r\rightarrow 0}{\mathcal K}= & \frac{4}{a^9} \Big [a^4 (a-4 (\alpha +1) M)-14 \alpha (\alpha +1)^2 a^2 M^3\nonumber \\ & +(\alpha +1) a M^2 \Big ((13 \alpha +11) a^2\nonumber \\ & +5 \alpha ^2 (\alpha +1) M^2\Big )\Big ]. \end{aligned}$$
(27)
Fig. 5
figure 5

Plots illustrate the dependence of the Ricci and square of the Ricci scalar, left and middle, respectively, while the Kretschmann scalar (right) on r as a changes

Full size image

In Fig. 5, we have plotted the dependence of the values of Ricci and the square of the Ricci scalar (left and middle, respectively) and the Kretschmann scalar (right) in the center from the black-bounce parameter for the different values \(\alpha \). It is observed that at \(a\rightarrow 0\), all scalar invariants’ limits go to infinity. An increase in the scalar invariants of the spacetime, including the Ricci scalar and the square of the Riemann tensor, while diminishing the Kretchmann scalar. On the other hand, small values of \(\alpha \) increase them all, and the Ricci scalar takes negative due to the combined effects of a and \(\alpha \) changing the spacetime from oblate to prolate.

3 Neutral particle motion

Neutral particle motion refers to the movement of particles that possess no net electric charge. Electric fields do not influence these particles due to their lack of charge. However, they may still be subject to other forces, such as gravitational, magnetic, or particle interactions. Examples of neutral particles include neutrons, neutrinos, and certain atoms or molecules with equal protons and electrons. Understanding the motion of neutral particles is crucial in various scientific fields, including nuclear physics, astrophysics, and materials science. Studying how neutral particles move and interact with their surroundings provides insights into the behavior of matter under different conditions and helps understand fundamental processes in the universe.

The Hamilton–Jacobi equation, which takes into account both interactions between the magnetized particles with scalar and magnetic fields, has the form

$$\begin{aligned} g^{\mu \nu }\left( \frac{\partial S}{\partial x^\mu }-q\Phi _\mu \right) \left( \frac{\partial S}{\partial x^\nu }-q\Phi _\nu \right) =-m^2, \end{aligned}$$
(28)

where \(q=\sqrt{\alpha }m\) is gravitational test particle charge, and \(q\Phi _\mu \) is the term that defines MOG interaction between the particles and the scalar field. There is an additional interaction between the particles and the scalar field,

$$\begin{aligned} \Phi _\mu =\frac{\sqrt{\alpha } M}{r}\left( -1,0,0,0\right) . \end{aligned}$$
(29)

The Lagrangian of the magnetized particles near the black-bounced black holes in MOG has a form that includes the MOG interaction,

$$\begin{aligned} {\mathcal L}=\frac{1}{2}mg_{\mu \nu } u^\mu u^\nu +q \Phi _\mu u^\mu \ . \end{aligned}$$
(30)

Using the above Lagrangian, one can easily find the integrals of motion of magnetized particles (\(p_\phi =L=mu^\phi \) and \(p_t=-E=mu^t\) denoting the total angular momentum and total energy of the particle, respectively) in the following form,

$$\begin{aligned} -{\mathcal E}= & g_{tt}\dot{t}+\frac{q}{m}\Phi _t,\end{aligned}$$
(31)
$$\begin{aligned} l= & g_{\phi \phi }\dot{\phi }, \end{aligned}$$
(32)

where \({\mathcal E}=E/m\) and \(l=L/m\) are the specific energy and angular momentum. In solving the above Eqs. (31) and (32), we obtain

$$\begin{aligned} {\dot{t}}= & \frac{{\mathcal E}+\frac{q}{m} {\Phi _t}}{- g_{tt}},\end{aligned}$$
(33)
$$\begin{aligned} {\dot{\phi }}= & \frac{l}{ g_{\phi \phi }}. \end{aligned}$$
(34)

The Hamilton–Jacobi action for the motion of magnetized particles in the equatorial plane (\(\theta =\pi /2\)) can be separated as follows

$$\begin{aligned} S=-Et+L\phi +S_r(r). \end{aligned}$$
(35)

By making use of the Hamilton–Jacobi equation (28), we can easily obtain the equation of radial motion of the magnetized particles:

$$\begin{aligned} g_{rr} \dot{r}^2= & -\Big [g^{tt}\left( \mathcal {E}+\frac{q\Phi _t}{m}\right) ^2+g^{\phi \phi }l^2+1\Big ] \nonumber \\= & \left[ {\mathcal {E}}-V^+_\textrm{eff}(r)\right] \left[ {\mathcal {E}}-V^-_\textrm{eff}(r)\right] . \end{aligned}$$
(36)

After certain calculations, we obtain the effective potential in the following form:

$$\begin{aligned} V_\textrm{eff}^\pm =\frac{\alpha M}{r} \pm \sqrt{-g_{tt}\left( 1+g^{\phi \phi }l^2\right) } \ . \end{aligned}$$
(37)

In case we do not consider the MOG interaction, the effective potential takes the value

$$\begin{aligned} V_\textrm{eff}={-g_{tt}\left( 1+g^{\phi \phi }l^2\right) }. \end{aligned}$$
(38)
Fig. 6
figure 6

Radial dependence of the effective potential at various discrete values of the parameters a and \(\alpha \)

Full size image

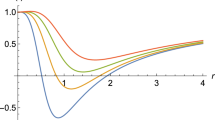
Figure 6 shows the radial behavior of the effective potential in the presence and absence of the MOG interaction, in red and blue curves, respectively. It is observed that the MOG interaction and the parameter \(\alpha \) reduce the instability and increase the stability along r. Furthermore, the MOG interaction further enhances the stability of orbits, resulting in more stable orbits than Schwarzschild black holes and black holes without the MOG interaction. It is also worth noting that, compared to other cases, the Schwarzschild black hole exhibits the most unstable orbits. The length parameter a does not change the maximum effective potential but shifts it toward the black hole.

3.1 Circular motion

Here, we describe the circular motion of particles around the SV-MOG spacetime. To express the above idea, we use the following criteria for circular motion:

$$\begin{aligned} V_\textrm{eff}={\mathcal E}, \qquad V_\textrm{eff}'=0. \end{aligned}$$
(39)

Ensure that the effective potential reaches a minimum to determine the stability of circular orbits around a compact gravitating object.

Fig. 7
figure 7

Radial dependence of \({\mathcal E}_c\) along r at various discrete values of the black-bounce and MOG parameters. The blue and red curves (indicating scenarios with MOG interaction) are labeled as “With MOG int,” while the orange and black curves (indicating scenarios without MOG interaction) are labeled as “Without MOG int”

Full size image

Figure 7 shows the radial dependence of \({\mathcal E}_c\) on r at various options of the black-bounce and MOG parameters. Interestingly, the MOG interaction contributes to \({\mathcal E}_c\), while a diminishes \({\mathcal E}_c\) near the horizons. Compared to the black-bounce parameter, the MOG interactions have a much more substantial impact on the behavior of \({\mathcal E}_c\) near horizons. Furthermore, the spacetime without black-bounce effects has higher \({\mathcal E}_c\) values than black-bounce one.

Fig. 8
figure 8

Graphs depict the behavior of angular momentum \({\mathcal L}/M\) as a function of r/M at various discrete parametric values of \(\alpha \) and a. The upper panel is for \({\mathcal L}< 0\), whereas the lower one is for \({\mathcal L}> 0\)

Full size image
Fig. 9
figure 9

Graphical representation of the ISCO radius along the dimensionless parameter \(\alpha \) for two different values of the black-bounce parameter

Full size image
Fig. 10
figure 10

The graph illustrates the behavior of angular momentum at ISCO along \(\alpha \) (left) and \(r_{\text {ISCO}}\) (right), both with and without considering the MOG interactions

Full size image

Figure 8 shows the graphical interpretation of angular momentum as a function of r/M. We noticed that the MOG parameter contributes significantly, while the black-bounce parameter decreases the angular momentum along the radial profile r. Moreover, compared with negative angular momentum, the MOG parameter has a much more prominent influence on its positive case (\({\mathcal L}> 0\)).

3.2 ISCO

The ISCO can mathematically be represented by the equation \(\partial _{rr}V_\textrm{eff}=0\). Typically, this criterion is combined with the circularity condition given in Eq. (39), which defines the Innermost Stable Circular Orbit (ISCO). As a result, the equation for the effective potential provided in Eq. (37) undergoes modification to fulfill these conditions.

Figure 9 illustrates the graphical description highlighting the significant impact of both MOG interactions and the black-bounce parameter on the ISCO radius. Particularly, the MOG interactions amplify the increase in \(r_{\text {ISCO}}\) along \(\alpha \), and this effect becomes more intense in the absence of black-bounce impacts (\(a=0\)). The black-bounce parameter decreases the \(r_{\text {ISCO}}\) in both cases, i.e., in the presence and absence of the MOG interactions. Thus, one can have higher \(r_{\text {ISCO}}\) values for the Schwarzschild case at \(a=\alpha =0\). Furthermore, it is worth noting that the MOG interactions vanish at \(\alpha =0\) and the \(r_{\text {ISCO}}\) of “With MOG int” meets the \(r_{\text {ISCO}}\) of “Without MOG int” case. It is also observed that MOG interaction weakens the black-bounce effects.

In Fig. 10, we have plotted the graphical behavior of angular momentum at ISCO of particles in the SV-MOG spacetime along \(\alpha \) and \(r_{\text {ISCO}}\) in the left and right panels, respectively. We noted that for \(a=0\), \( {\mathcal L}_{\text {ISCO}}\) increases along \(\alpha \) in both cases (with and without MOG interaction). However, in the absence of MOG interactions, the increase becomes more pronounced. Hence, we can conclude that the MOG interactions diminish the angular momentum along \(\alpha \). In addition, the black-bounce parameter increases \({\mathcal L}_{\text {ISCO}}\). As a result, the blue dashed curves (with MOG interaction) show higher \({\mathcal L}_{\text {ISCO}}\) values than the blue curves for the same \(\alpha \). The angular momentum at ISCO behaves similarly along \(r_{\text {ISCO}}\); it has smaller values when MOG interactions are taken into account than when they are not (for details, please see Fig. 10). Furthermore, it increases linearly for both \(a=0\) and \(a \ne 0\) along \(r_{\text {ISCO}}\) for both cases (with and without MOG interactions). Notably, black holes with non-zero black-bounce parameters have higher \({\mathcal L}_{\text {ISCO}}\) than those without black-bounce effects.

Fig. 11
figure 11

Graphs showing the behavior of \({\mathcal E}_{\text {ISCO}}\) along \({\mathcal L}_{\text {ISCO}}\) (right panel) and along \(r_{\text {ISCO}}\) (middle panel), while along \(\alpha \) (left panel)

Full size image

The graphical illustration of Fig. 11 shows the radial dependence of energy at the ISCO along \({\mathcal L}_{\text {ISCO}}\) (right panel) and \(r_{\text {ISCO}}\) (left). For both \(a=0\) and \(a\ne 0\), energy at the ISCO reveals the same behavior along \({\mathcal L}_{\text {ISCO}}\) and \(r_{\text {ISCO}}\). As in both cases, the \({\mathcal E}_{\text {ISCO}}\) decreases without considering the MOG interaction while showing a much higher increase by considering the MOG interaction along \({\mathcal L}_{\text {ISCO}}\). In addition, the black-bounce parameter considerably contributes to the \({\mathcal E}_{\text {ISCO}}\) in both cases. In contrast, it impacts on \({\mathcal E}_{\text {ISCO}}\) decrease effects of the MOG interactions, particularly at higher values of \({\mathcal L}_{\text {ISCO}}\). Moreover, the left panel shows how the ISCO energy changes with the parameter \(\alpha \) under different conditions. For instance, the MOG interaction and a have influenced these relationships.

4 The energy extraction efficiency

The Novikov-Thorn accretion disc model explains keplerian accretion around astrophysical compact gravitating objects like black holes/wormholes as a geometrically thin disk. The efficiency of the energy extraction process in the accretion disk around the gravitating objects refers to the maximum amount of energy that matter falling into the central black hole from the disk extracts as radiation energy. The efficiency of the accretion of the particle can be calculated \(\eta =1-{\mathcal E}_{\text {ISCO}}\), \({\mathcal E}_{\text {ISCO}}\) is characterized by the ratio of the binding energy (black hole-particle system) and rest energy of the test particle [61].

Indeed, the bolometric luminosity of the brightness emanating from the accretion disk is directly linked to the energy efficiency of the central black hole, as expressed by the equation \(\eta =L_\textrm{bol}/ (\dot{M}c^2)\), where \(\dot{M}\) signifies the accretion rate [62]. Here, we also study the efficiency of released energy at various values of parameters \(\alpha \) and a. The effects of the MOG parameter on the efficiency of the accretion of test particles around regular black holes in MOG are plotted in Fig. 12 along \(\alpha \). Interestingly, both MOG interaction and the length parameter a significantly impact energy efficiency. The efficiency increases gradually without considering the MOG interaction, whereas it diminishes rapidly in the case of MOG interactions along \(\alpha \). Furthermore, the black-bounce parameter reduces the efficiency along \(\alpha \) in both cases. Consequently, the efficiency reaches its maximum at \(\alpha =1\) without considering MOG interactions.

Fig. 12
figure 12

The graph shows how the energy efficiency (\(\eta \)) changes along the parameter \(\alpha \) under different conditions

Full size image

5 Collision of geodesic particles

Explicit explanation of physical mechanisms, energy extraction processes, and the role of gravity in processes is an important task in theoretical astrophysics. The classical Penrose process suggested by R. Penrose is an accepted mechanism. Later, the electric Penrose process is an advanced method of extracting energy from electrically charged black holes. This process involves a particle splitting near the event horizon of a charged black hole, where one fragment is absorbed by the black hole and the other, carrying more energy, escapes to infinity. The black hole’s electric charge enhances this energy extraction by affecting particle behavior. Even a small charge can significantly improve energy extraction compared to an uncharged black hole. These findings enhance our understanding of black hole thermodynamics and astrophysical jets, highlighting the complex relationship between electric charge and energy dynamics in intense gravitational fields. Various Penrose processes, including magnetic and electric versions, have been developed for different black hole models [63,64,65].

Fig. 13
figure 13

Radial dependence of the square of radial velocity for different values of angular momentum of the particle

Full size image

In this scenario, the study by Banados (in 2009) was the first to investigate the acceleration of particles colliding near rotating Kerr black holes, showing that the center of mass energy of colliding particles can become infinite in an extremely fast-spinning Kerr black hole [66, 67]. Subsequent research has explored the impact of external magnetic fields on the acceleration of charged particles near black holes in various gravity models and scenarios [40, 68,69,70,71,72,73]. These studies indicate that energy extraction is more efficient during head-on collisions.

The CME is essential for generating new particles that arise from the collision of particles in the center-of-mass frame. This energy is acquired by adding the masses and kinetic energies of the collide particles. Black holes can be effective particle accelerators, accelerating particle collisions to an infinite CME. This creates favorable circumstances for high-energy physics events that are otherwise difficult to reproduce. In this section, we examine the collision between two particles within the framework of a regular black hole in MOG, especially on an equatorial plane. This configuration is critical because it provides valuable knowledge of the mechanics and interplay in intense gravitational conditions. Such insights are critical for understanding basic physics and the properties of matter near black holes.

Fig. 14
figure 14

Radial dependence of the critical angular momentum with and without MOG interaction

Full size image

Before analyzing the CME plots, it is important to note a fascinating phenomenon related to angular momentum, referred to as a “critical value” essential for approaching a black hole. The critical value of angular momentum may be calculated by satisfying two conditions: (a) \(\dot{r}=0\) and (b) \(d\dot{r}/dr=0\). This is shown in Fig. 13. An increase in the angular momentum results in a negative value for the square of the radial velocity, indicating that the particles cannot approach the center object from that particular value. Consequently, we examined the permissible values of the angular momentum and identified the critical values. Figure 14 illustrates the radial dependence of the critical angular momentum with and without MOG interaction. The graph demonstrates that the critical angular momentum range is broader in the presence of MOG interaction than when there is no MOG interaction. Additionally, the plot indicates that the Schw. Black hole case allows for the maximum range of angular momentum.

For CME plots, it is important to establish the energy of the two particles colliding in the frame of reference known as the center of mass. These particles possess the energies \(\mathcal {E}_1\) and \(\mathcal {E}_2\) at an infinite distance. Let’s examine two particles with masses \(m_1\) and \(m_2\) traveling along geodesics in a black hole spacetime. Their energy in the center of the mass frame is determined (see, for example, [74, 75]),

$$\begin{aligned} \mathcal {E}^2_{cm} = -g_{\mu \nu } (u^\mu _1 + u^\mu _2)(u^\nu _1 + u^\nu _2), \end{aligned}$$
(40)

which simplifies to:

$$\begin{aligned} \mathcal {E}^2_{cm} = m^2_1 + m^2_2 - 2g_{\mu \nu } u^\mu _1 u^\nu _2. \end{aligned}$$
(41)

The symbols \(u^{\mu }_i\) represent the four velocities of the particles involved in the collision, where \(i=1,2\).To simplify computations, we will assume that both particles have the same mass \((m_1 = m_2 = m_0)\) and the same energy \((\mathcal {E}_1 = \mathcal {E}_2 = 1)\) while at an infinite distance. This assumption facilitates the concentration on the inherent characteristics of the collision process while avoiding the complexities arising from varying initial conditions. We can construct the expressions and conditions for CME using the above parameters. This derivation will include an analysis of the combined effects of the particles’ rest mass and kinetic energy as they approach and interact inside the gravitational field of the black hole. This investigation aims to understand better the possible results of high-energy collisions and the consequent creation of new particles in this extreme setting. Therefore, using Eqs. (33), (34) and (36) final expression for the collision energy in the center of the mass frame takes the form [75]

$$\begin{aligned} \frac{\mathcal {E}^2_{\text {cm}}}{2m_0^2} = 1 - \frac{l_1 l_2}{h(r)} + \frac{(\mathcal {E}_1+\frac{q_1}{m}\phi _t) (\mathcal {E}_2+\frac{q_2}{m}\phi _t) \sqrt{R_1(r) R_2(r)}}{f(r)}, \end{aligned}$$
(42)

where for \(( i = 1, 2 )\),

$$\begin{aligned} R_i^2 = \left( \mathcal {E}_i+\frac{q_i}{m}\phi _t\right) ^2 - f(r) \left( 1 + \frac{l_i^2}{h(r)}\right) . \end{aligned}$$
(43)
Fig. 15
figure 15

Graph illustrating the center of mass energy as a function of the radial coordinate (r) around a black hole

Full size image

The graphical representation of the CME as a function of the radial coordinate (r) near a black hole is shown in Fig. 15. The graph shows a decline in the CME as the distance from the black hole grows. The existence of a MOG interaction, as shown by the red curves, leads to an increase in the CME compared to circumstances where this interaction is absent, as depicted by the blue curves. Moreover, the regularization parameter “a” of the black hole, shown by the dashed lines, substantially impacts the CME. It results in distinct energy profiles compared to the other cases when \(a=0\). For both situations of the regularization parameter \(a = 0\) and \(a = 1.5\), the inclusion of the MOG interaction (\(\alpha = 0.3\)) leads to a greater CME compared to conventional scenarios without the MOG interaction (\(\alpha = 0\)).

6 Conclusions and discussions

In the present work, we have studied the spacetime properties and event horizon of black-bounce in MOG. It has been shown that the black-bounce parameter causes an increase in scalar invariants of the spacetime of the black hole, such as the Ricci scalar and square of the Riemann tensor, whereas it decreases the Kretchmann scalar. To better understand the motions of neutral particles, we have also explored their effective potential, critical energy, angular momentum, and specific energy under the impact of both MOG and black-bounce parameters. Moreover, we have studied their ISCO radius, angular momentum, and energy at the ISCO. We have shown that the MOG parameter’s effect on the ISCO radius is similar to that of the Kerr black hole and that the MOG parameter can mimic the spin of the Kerr black hole, providing the same values for the ISCO radius of test particles. Some of our key findings are as follows:

  • the MOG interactions and \(\alpha \) reduce the instability and increase the stability of effective potential along r.

  • The MOG interaction enhances the stability of orbits, resulting in more stable orbits than Schwarzschild black holes and black holes without the MOG interaction.

  • The length parameter a does not change the maxima of the effective potential but shifts it toward the black hole.

  • Compared to the black-bounce parameter, the MOG interactions have a much more substantial impact on the behavior of \({\mathcal E}_c\) near horizons.

  • The MOG parameter contributes significantly, while the black-bounce parameter reduces the angular momentum. Compared to the negative angular momentum, the MOG parameter has a much more prominent influence on its positive case (\({\mathcal L}> 0\)).

  • For \({\mathcal L}< 0\), the energy remains almost unaffected in response to both \(\alpha \) and a at a greater radial distance. In contrast, for \({\mathcal L}>0\), the impact of MOG parameter is very prominent on \({\mathcal E}\).

  • The energy profile along \({\mathcal L}\) shows two different regions. For some specific values of \({\mathcal L}\), it has two energy profiles: one is increasing rapidly, while the other is slowly.

  • The MOG interactions amplify the increase in \(r_{\text {ISCO}}\) along \(\alpha \), which becomes more intense in the absence of black-bounce impacts.

  • The length parameter a decreases \(r_{\text {ISCO}}\), resulting in higher values of ISCO for the Schwarzschild black holes.

We also investigated the energy efficiency of the accretion disk using the Novikov and Thorne approach and found that both the MOG interaction and the length parameter a significantly influence it. The efficiency increases gradually without considering the MOG interaction, whereas it diminishes rapidly in the case of MOG interactions. The efficiency reaches its maximum at \(\alpha = 1\) without considering MOG interactions.

Finally, we analyze the collision between two particles within the context of a black-bounce black hole in MOG and illustrate the findings graphically. The graph demonstrates a decrease in the CME outside black hole horizons along the radial distance r. The presence of MOG interactions results in a higher CME compared to situations when there are no MOG interactions. Furthermore, the regularization parameter significantly affects the CME, leading to unique energy profiles compared to the other cases. When considering both instances of the regularization parameter (\(a = 0\) and \(a = 1.5\)), the presence of the MOG interaction results in a higher CME compared to typical scenarios without the MOG interaction.