1 Introduction

The study of the late-time accelerated expansion of the Universe is one of the most interesting areas of modern cosmology. This phenomenon has been confirmed and supported by different cosmological observations, including the supernova type Ia (SNIa) measurements [1, 2], cosmic microwave background [3, 4], baryon acoustic oscillations [5, 6], and large-scale structure [7, 8]. To explain the acceleration phase of the Universe, an exotic negative-pressure component, dubbed dark energy (DE), is added to the Universe’s energy budget in the context of general relativity. Dark energy causes repulsive gravity behavior on large cosmological scales, initially described by the cosmological constant, \(\Lambda \) [9], with an equation of state (EoS) parameter, \(\omega =-1\). This model, called the Lambda cold dark matter (\(\Lambda \)CDM) model, is widely accepted on the basis of recent observational data [10,11,12]. Unfortunately, the \(\Lambda \)CDM model has some serious theoretical problems, including fine-tuning issues [13,14,15] and the coincidence problem [16, 17], in addition to various observation issues, called cosmological tensions [18,19,20]. Several dynamical dark energy (DDE) models have been proposed in order to overcome these problems, including the quintessence model [21, 22], k-essence [23,24,25], Chaplygin gas [26, 27], holographic dark energy [28,29,30,31,32], generalized holographic dark energy [28, 31, 33, 34], and phantom dark energy, where the EoS parameter is slightly less than \(-1\) [35,36,37]. Phantom DE models have some drawbacks, as their energy density increases with the scale factor and becomes infinite at some point in the future, which leads the Universe to end in a Big Rip singularity [35]. Among the models proposed to resolve this issue, we cite the little sibling of the Big Rip (LSBR), which has been proposed as one of the mildest models of the possible apocalypse and perfectly describes the current acceleration of the Universe [38]. Several works have studied this model in F(R) cosmology [39] and in quantum cosmology [40, 41] (see also [42,43,44,45]). Moreover, it has recently been shown that this model is well supported by cosmological observational data [46], and can reduce the Hubble tension compared to the \(\Lambda \)CDM model [47].

Another way of explaining this late acceleration is to modify the structure of the Einstein–Hilbert gravitational Lagrangian itself by considering scalar tensor theories [48, 49] or by replacing the Ricci scalar with a single-variable f(R) [50], two-variable f(R, T) [51, 52], or even three-variable [53] f(R, T, P), where R is the Ricci scalar, T is the trace of the energy-momentum tensor, and P is the Kretschmann scalar. These approaches have led to many important extensions of general relativity, including F(R) gravity [54], F(G) gravity [55], where G is the Gauss-Bonnet term, F(P) gravity [56], Horndeski scalar-tensor theories [57], etc. However, from a general differential geometric point of view, and taking into account the affine properties of manifolds, the curvature is not the only geometric object that may be used within a geometrical framework to construct gravitational theories. Indeed, torsion and non-metricity are two other essential geometric objects connected to a metric space, along with the curvature. They can be used to obtain \(F({\mathcal {T}})\) [58] and F(Q) [59,60,61] gravity theories, where \({\mathcal {T}}\) and Q are the torsion and the non-metricity scalar, respectively.

Many different applications of F(Q) gravity have recently been studied. Among these, the authors of [62] found an interesting result for the current value of the Hubble parameter, which was close to Planck’s estimate, by considering the F(Q) Lagrangian as a polynomial function of redshift. To demonstrate the late-time acceleration of the Universe, a new parameterization of the EoS parameter in the context of F(Q) was established in [63]. Based on the energy conditions, the authors of [64] restricted the families of F(Q) models compatible with the accelerated expansion of the Universe. A new class of F(Q) theories, in which the non-metricity scalar is coupled non-minimally to the matter Lagrangian, was proposed by [65], where the cosmological solutions are considered in two general classes of models, and are characterized by the accelerated expansion at late time. In addition, the authors of [66] showed that the F(Q) model is well supported by the background and perturbation data, using a particular form of F(Q). For further studies related to the applications of F(Q) gravity, see for instance [61, 66,67,68,69,70,71,72].

In this paper, we aim to reexamine the current understanding of the accelerated expansion of the Universe by considering the specific DDE model [38] in the context of F(Q) gravity. Indeed, in the context of general relativity, this kind of dark energy mimics a phantom-like behavior and smooths the Big Rip singularity, in good agreement with the observational data [36, 42, 46, 47]. Furthermore, this dark energy model predicts more dark matter in the past [47] and reproduces \(\Lambda \)CDM in the current time. As we will show, some of these properties will undergo a change in the context of F(Q) gravity [73,74,75]. Among these, this dark energy will behave as a quintessence, the expansion will decelerate, and the Universe will face a bounce in the future.

Along these lines, we estimate constraints of the cosmological parameters of our setup. We first perform cosmological analysis with the Markov chain Monte Carlo (MCMC) approach [76], using the most recent supernovae type Ia data, namely \(\hbox {Pantheon}^{+}\) [77], combined with H(z) data [78]. We then perform a statistical comparison between our model and \(\Lambda \)CDM using the Akaike information criterion (AIC) [79, 80] and the Bayesian information criterion (BIC) [81]. In addition, we present a cosmographic analysis of the model, including the evolution of the deceleration parameter (q), jerk parameter (j), and snap (s) parameter [82,83,84].

This article is organized as follows: In Sect. 2, we provide a brief review of F(Q) gravity, and in Sect. 3, we present the modified Friedman equations in the F(Q) gravity. In Sect. 4, we describe the methodology of the datasets. In Sect. 5, we present and discuss the results. Section 6 is devoted to a cosmographic analysis of the model. Finally, in Sect. 7 we summarize our results.

2 Overview of F(Q) gravity

In this section, we provide a brief introduction to the formalism of F(Q) gravity. We consider F(Q) modified gravity, in which the basic object is the non-metricity tensor \(Q_{\lambda \mu \nu }\), given by [59]

$$\begin{aligned} \Delta _{\lambda }g_{\mu \nu }=Q_{\lambda \mu \nu }. \end{aligned}$$
(2.1)

The non-metricity scalar, which is an important quantity in this theory, is defined in terms of the disformation tensor, \(L_{\mu \nu }^{\lambda }\), as

$$\begin{aligned} Q=-g^{\mu \nu }(L_{\beta \nu }^{\alpha } L_{\nu \alpha }^{\beta }-L_{\beta \alpha }^{\alpha }L_{\mu \nu }^{\beta }), \end{aligned}$$
(2.2)

where the deformation tensor is symmetrical with respect to lower indices and is defined by

$$\begin{aligned} L_{\mu \nu }^{\lambda }=-\frac{1}{2}g^{\lambda \gamma }(Q_{\mu \gamma \nu }+Q_{\nu \gamma \mu }-Q_{\gamma \mu \nu }). \end{aligned}$$
(2.3)

In terms of the non-metricity conjugate, the non-metricity scalar is given by

$$\begin{aligned} Q=-P^{\alpha \beta \gamma }Q_{\alpha \beta \gamma }, \end{aligned}$$
(2.4)

where the non-metricity conjugate, \(P^{\alpha \beta \gamma }\), is defined in terms of the non-metricity tensor and its two independent traces, \(Q_{\alpha }={{Q_{\alpha }}^{ \beta }}_{\beta }\) and \(\tilde{Q}^{\alpha }={Q_{\beta }}^{\ \alpha \beta }\), as

$$\begin{aligned} P^{\alpha }_{\mu \nu }=\frac{1}{4}\left( -Q^{\alpha }_{\mu \nu }+2 Q^{\alpha }_{(\mu \nu )}-Q^{\alpha }g_{\mu \nu }-\tilde{Q}^{\alpha }g_{\mu \nu }-\delta ^{\alpha }_{(\mu } Q_{\nu )}\right) .\nonumber \\ \end{aligned}$$
(2.5)

The action of the F(Q) modified gravity is written as [60]

$$\begin{aligned} S=\int {d^4x\sqrt{-g}}\left( -\frac{1}{2\kappa ^2}{F}(Q)+{\mathcal {L}}_m \right) , \end{aligned}$$
(2.6)

where F(Q) is a function of the non-metricity scalar Q, g is the determinant of the metric \(g_{\mu \nu }\), and \({\mathcal {L}}_m\) is the Lagrangian density of matter. The field equation of the F(Q) gravity is obtained by varying the action with respect to \(g_{\mu \nu }\), and it takes the form

$$\begin{aligned}{} & {} -\frac{2}{\sqrt{-g}}\nabla _{\alpha }(\sqrt{-g}F_QP^{\alpha }_{\mu \nu } )\nonumber \\{} & {} \quad +\frac{1}{2}g_{\mu \nu }F+F_Q(P^{\alpha \beta }_{\nu }Q_{\mu \alpha \beta } -P^{\alpha \beta }_{\mu }Q_{\alpha \beta \nu })=\kappa ^2 T_{\mu \nu },\nonumber \\ \end{aligned}$$
(2.7)

where \(F_Q = \frac{\partial F}{\partial Q}\), and the energy-momentum tensor, \(T_{\mu \nu }\), is given by

$$\begin{aligned} T_{\mu \nu }=-\frac{2}{\sqrt{-g}}\frac{\delta \sqrt{-g}{\mathcal {L}}_m}{\delta \sqrt{g_{\mu \nu }}}. \end{aligned}$$
(2.8)

By varying the action with respect to the affine connection [61], we obtain the equation

$$\begin{aligned} \nabla _{\mu }\nabla _{\nu }(\sqrt{-g}F_QP^{\mu \nu }_{\alpha })=0. \end{aligned}$$
(2.9)

3 Cosmological model

To examine the cosmological consequences of F(Q) gravity, we consider the Friedmann-Lemaître-Robertson-Walker (FLRW) line element, which describes the flat, homogeneous, and isotropic Universe, given by

$$\begin{aligned} ds^{2}=-dt^{2}+a^{2}(t)\left( dx^{2} +dy^{2}+dz^{2}\right) , \end{aligned}$$
(3.1)

where t is the cosmic time, x, y and z denote the Cartesian coordinates, a(t) is the cosmic scale factor, and the Hubble parameter H(t) is defined by \(H(t) = \frac{\dot{a}}{a}\), with \(\dot{a}\) denoting the derivative of the scale factor with respect to the cosmic time.

3.1 The generalized Friedmann equations

In the FLRW geometry, we obtain the non-metricity scalar as \(Q = 6\,H^2\). We consider the matter content of the Universe as consisting of a perfect and isotropic fluid, with the energy momentum tensor given by

$$\begin{aligned} T_{\mu \nu }=(p+\rho )u_{\mu }u_{\nu }+pg_{\mu \nu }, \end{aligned}$$
(3.2)

where p and \(\rho \) are the pressure and the energy density of the fluid, respectively, and \(u_{\mu }\) is the four-velocity vector normalized according to \(u^{\mu }u_{\nu }=-1\).

To better fulfill our goal, we consider the splitting of F (Q) as \({F (Q) =Q + f(Q)}\). Using the FLRW metric, we obtain two Friedmann equations as [60, 67]

$$\begin{aligned} -\frac{f}{2}+3H^{2}+Qf_Q= & {} \rho , \end{aligned}$$
(3.3)
$$\begin{aligned} (12f_{QQ}H^{2}+1+f_{Q})\dot{H}= & {} -\frac{\rho +p}{2}, \end{aligned}$$
(3.4)

where we have set \(\kappa ^2=1\). According to the above equations, we recover the standard model, for \(f=0\) (i.e., \(F(Q)=Q\)). The same equations, Eqs. (3.3) and (3.4), can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{l} 3H^{2}=\rho +\rho _{DE},\\ -2 \dot{H}-3H^{2}=p+p_{DE}, \end{array} \right. \end{aligned}$$
(3.5)

where we have introduced a geometrical dark energy density, \(\rho _{DE}\), and its pressure, \(p_{DE}\), as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \rho _{DE}=\frac{f}{2}-Qf_Q,\\ p_{DE}=2 \dot{H}(f_Q+2Qf_{QQ})-\frac{f}{2}+Qf_Q. \end{array} \right. \end{aligned}$$
(3.6)

Furthermore, the effective EoS using Eq. (3.5) can be written as

$$\begin{aligned} \omega _{\text {eff}}=\frac{-2 \dot{H}-3H^{2}}{3H^{2}}. \end{aligned}$$
(3.7)

3.2 Dynamical dark energy

In order to understand the characteristic properties of the dark energy driving the recent acceleration of the Universe, we need to parameterize its EoS. To this end, we consider one of the main studied dynamical dark energies given by [38]

$$\begin{aligned} \rho _{\textrm{DE}}+p_{\textrm{DE}}=-\frac{A}{3}, \end{aligned}$$
(3.8)

where \(\rho _{\textrm{DE}}\), \(p_{\textrm{DE}}\), and A are the energy density, the pressure, and a constant characterizing the dark energy model, respectively.

The primary motivation for taking into account this parameterization form is its advantage in smoothing the Big Rip singularity. Indeed, in this scenario, the size of the observable Universe and its expansion rate grow to infinity, while the cosmic time derivative of the Hubble parameter converges to a constant value. Furthermore, this model deviates slowly from the standard model, by the constant A, and it behaves as phantom-like dark energy models. The EoS of this DDE model, dubbed the little sibling of the Big Rip (LSBR) in [38], is given by

$$\begin{aligned} \omega _{\textrm{DE}}=-\left( 1+\frac{A}{3(\rho _{{\textrm{DE}},0}+A\ln {(\frac{a}{a_0})})}\right) . \end{aligned}$$
(3.9)

According to Eq. (3.9), the DDE model describes a phantom DE for positive values of A (i.e., \(\omega _{\textrm{DE}}<-1\)). For negative values of A, the model describes a quintessence DE (i.e., \(\omega _{\textrm{DE}}>-1\)) and mimics the standard model in the limit \(A\rightarrow 0\). Despite the aforementioned advantages, the DDE model faces some drawbacks. Indeed, this DDE model is unable to describe the very early expansion of the Universe as its energy density becomes negative, i.e., it is not supported by high redshifts [47].

Using Eqs. (3.6) and (3.8), we obtain

$$\begin{aligned} 2 \dot{H}(f_Q+2Qf_{QQ})=-\frac{A}{3}, \end{aligned}$$
(3.10)

where the dot (.) indicates the derivative with respect to cosmic time. Using the relation between the derivative of H and the non-metricity scalar Q

$$\begin{aligned} \dot{H}=H \frac{dH}{dx}=\frac{1}{12}\frac{dQ}{dx}, \end{aligned}$$
(3.11)

where \(x=\ln {(a)}\), Eq. (3.10) becomes

$$\begin{aligned} \frac{1}{6}\frac{dQ}{dx}(f_Q+2Qf_{QQ})=-\frac{A}{3}. \end{aligned}$$
(3.12)

In order to illustrate our purpose, we consider the following form of f(Q) [61]

$$\begin{aligned} f(Q)=6 \gamma H_0^2\Bigg (\frac{Q}{Q_0}\Bigg )^{n}, \end{aligned}$$
(3.13)

where \(\gamma \), n and \(Q_0=6H_0^2\) are constants. In this case, Eq. (3.12) becomes

$$\begin{aligned} \frac{{n}}{2}\frac{dQ}{dx}(\frac{Q}{Q_0})^{n-1}\gamma (2n-1)=-A. \end{aligned}$$
(3.14)

We also can write this equation in the form

$$\begin{aligned} \frac{d(\frac{Q}{Q_0})^{n}}{dx}=-\frac{2A}{Q_0\gamma (2n-1)}. \end{aligned}$$
(3.15)

By integration, we obtain

$$\begin{aligned} \Bigg (\frac{Q}{Q_0}\Bigg )^{n}=-\frac{2A}{Q_0\gamma (2n-1)}x+1. \end{aligned}$$
(3.16)

Combining Eqs. (3.13) and (3.6) gives the form of \(\rho _{\textrm{DE}}\) in terms of Q as

$$\begin{aligned} \rho _{\textrm{DE}}= \gamma Q_0 \Bigg (\frac{1}{2}-n\Bigg )\Bigg (\frac{Q}{Q_0}\Bigg )^{n}, \end{aligned}$$
(3.17)

which in terms of x becomes

$$\begin{aligned} \rho _{\textrm{DE}}= Ax+\gamma Q_0 \Bigg (\frac{1}{2}-n\Bigg ) . \end{aligned}$$
(3.18)

We finally obtain the Friedmann equation, from Eq. (3.5), as

$$\begin{aligned} E^2=\Omega _{m_0}(1+z)^3+\Omega _{r_0}(1+z)^4-{\Omega _{x}}\ln {(1+z)} +{\Omega _{\Lambda }}, \nonumber \\ \end{aligned}$$
(3.19)

where \(E = H/H_{0}\) is the dimensionless Hubble rate, \(\Omega _x=2A/Q_0\) and \(\Omega _\Lambda =\gamma (1-2n)\), and we have used \(x=-\ln (1+z)\).

The last two terms in Eq. (3.19) represent the dimensionless parameters of dark energy density, which can be expressed as

$$\begin{aligned} \Omega _{DE}=-\Omega _{x}\ln (1+z) +\Omega _{\Lambda }. \end{aligned}$$
(3.20)

From Eq. (3.19), the model predicts an increase in dark matter density as \( z \rightarrow \infty \). However, in the future, the model is dominated by dark energy, and its behavior is characterized by the sign of \(\Omega _{x}\). Equation (3.19) can be approximated as follows: \(E^2 \approx -\Omega _{x}\ln (1+z)+\Omega _{\Lambda }\). For \(\Omega _{x}\) being positive, the Hubble rate \( H \) diverges while its derivative \( \dot{H} \) remains constant [38]. This abrupt event, the LSBR, smooths the Big Rip singularity in the future. This phenomenon has been extensively studied in references [38, 40, 41, 47]. However, if \(\Omega _{x}\) is negative, the Universe’s dynamical behavior undergoes a bounce, as we will illustrate in Sect. 5. From now on, we will refer to our setup as F(Q)-DDE.

4 Statistical analysis

In order to obtain optimal constraints on cosmological parameters of the F(Q)-DDE model and compare them with those of the \(\Lambda \)CDM model, we perform a Markov chain Monte Carlo (MCMC) analysis, using the last data from \(\hbox {Pantheon}^+\) and Hubble parameter data (H(z)). We consider a parameter space composed of the Hubble constant, \(H_0\), the density parameter of total matter, \(\Omega _m\), the two parameters that describe the F(Q) gravity, \(\gamma \) and n, and the DDE parameter, A, by means of the dimensionless parameter \(\Omega _x=2A/Q_0\). The prior related to the free parameters is given in Table (1)

Table 1 Prior imposed on different parameters for the F(Q)-DDE and \(\Lambda \)CDM models
Full size table

4.1 \(\hbox {Pantheon}^+\) dataset

We use the latest \(\hbox {Pantheon}^+\) measurements [77], composed of 1701 light curves of 1550 distinct supernovae type Ia (SNIa) confirmed by spectroscopy, ranging in z interval, \(z\in [0.001, 2.26]\).

The \(\chi _{\text {Pan}^+}\) function is written as

$$\begin{aligned} \chi _{\text {Pan}^+}^2=\Delta \mu ^T{\mathcal {M}}_{\text {Pan}^+}^{-1}\Delta \mu , \end{aligned}$$
(4.1)

where \({\mathcal {M}}_{\text {Pan}^+}\) is the covariance matrix and \(\Delta \mu \) is a vector where each of its elements refers to the \(i^{\text {th}}\) distance modulus of SNIa, given by

$$\begin{aligned} \Delta \mu ^i= {\left\{ \begin{array}{ll} \mu ^i-\mu ^i_{\text {ceph}}, &{} i\in \text { Cepheid host},\\ \mu ^i-\mu _{\text {theo}}(z_i), &{} \text { Otherwise}, \end{array}\right. } \end{aligned}$$
(4.2)

where \(\mu ^i_{\text {ceph}}\) is the distance modulus for the Cepheid calibrated host-galaxy of the \(i^{th}\) SNIa provided by SH0ES [85], and \(\mu _{\text {theo}}\) is the theoretical distance modulus, defined as

$$\begin{aligned} \mu _{\text {theo}}(z_i)=m_b-M=5\log _{10}{\frac{d_L}{\text {Mpc}}}+25, \end{aligned}$$
(4.3)

where M is the absolute magnitude, \(m_b\) is the apparent magnitude, and \(d_L\) is the luminosity distance, defined as

$$\begin{aligned} d_L=(1+z) c\int _{0}^{z}\frac{dz}{H(z)}, \end{aligned}$$
(4.4)

where c is the speed of light.

4.2 H(z) data

Next, we use Hubble expansion rate data [78] to impose tighter constraints on our F(Q)-DDE model. Generally, H(z) data can be obtained either through the clustering of galaxies and quasars, measured via baryon acoustic oscillations (BAO) in the radial direction [86], or through the differential age method [87]. In our current analysis, we have employed a compilation of 36 data points of the Hubble parameter which exhibit no correlation. The \(\chi ^2_{{\text {H(z)}}}\) function is given by

$$\begin{aligned} \chi ^2_{{\text {H(z)}}}=\sum _{i=1}^{36}\left[ \frac{H_{\text {theo}}(z_i)-H_{\text {obs}}(z_i)}{ \sigma _i}\right] ^2, \end{aligned}$$
(4.5)

where \(H_{\text {theo}}(z_i)\) is the theoretical values, \(H_{\text {obs}}(z_i)\) is the observed values at \(z_i\) and \(\sigma _i\) is the standard deviation.

To analyze both the H(z) data and SNIa samples simultaneously, we use the total chi-square function \(\chi ^2_{\text {tot}}\) given by

$$\begin{aligned} \chi ^2_{\text {tot}}=\chi ^2_{\text {Pan+}}+\chi ^2_{\text {H(z)}}. \end{aligned}$$
(4.6)

4.3 Information criteria

The aim of this work, besides the parameter estimations, is to select the best model supported by the observational data. In fact, a model with a smaller value of \(\chi ^2\) indicates that the model is fitted well to the observational data. However, a large number of parameters can increase the quality of the fit and therefore lead to a smaller \(\chi ^2\). In this case, the \(\chi ^2\) statistic is not an appropriate way to compare models. To confidently predict the goodness of the fit between the F(Q)-DDE and \(\Lambda \)CDM models, we use another statistical tool, namely the Akaike information criterion (AIC) [79, 80], which depends on the number of parameters, \({\mathcal {N}}\), given by

$$\begin{aligned} AIC = \chi ^2_{min}+2{\mathcal {N}}. \end{aligned}$$
(4.7)

As with the \(\chi ^2\) statistic, a model with a smaller AIC value indicates that the model is best supported by the observational data. For this we calculateFootnote 1

$$\begin{aligned} \Delta AIC = AIC_{\text {model}}- AIC_{\Lambda CDM}. \end{aligned}$$
(4.8)

The model selection rule of \(\Delta \)AIC is as follows: a value of 0\(\leqslant \Delta \)AIC<2 suggests that the model has nearly the same level of support from the observational data as \(\Lambda \)CDM; a value of 2\(\leqslant \Delta \)AIC<4 indicates that the model has slightly less support than the \(\Lambda \)CDM model; a value of 4\(\leqslant \Delta \)AIC<10 indicates that the data still support the model but less than the preferred one; and for \(\Delta AIC>10\), the model is not supported by the observational data compared to the \(\Lambda \)CDM model.

We also calculate the Bayesian information criterion (BIC), given by [81]

$$\begin{aligned} BIC = \chi ^2_{min}+{\mathcal {N}}\log {(k)}, \end{aligned}$$
(4.9)

where a smaller BIC value indicates that the model is best supported by the observational data. For this we calculate

$$\begin{aligned} \Delta BIC = BIC_{\text {model}}- BIC_{\Lambda CDM}. \end{aligned}$$
(4.10)

A positive (negative) value of \(\Delta \)BIC shows that the F(Q)-DDE (\(\Lambda \)CDM) model is preferred. The selection rules of the BIC are as follows: a value of 0 \(\leqslant \) \(\Delta \) BIC < 2 means that the evidence is insufficient, a value of 2 \(\leqslant \) \(\Delta \) BIC < 6 indicates that there is a positive evidence, while a value of 6 \(\leqslant \) \(\Delta \) BIC < 10 indicates solid evidence.

5 Results and discussion

In Table 2, we present the 68% C.L. constraints on the cosmological parameters of the \(\Lambda \)CDM and F(Q)-DDE models obtained using the combination of \(\hbox {Pantheon}^+\) and H(z) data. Figure 1 shows the 1D posteriori distributions and 2D marginalized contours at \(1\sigma \) and \(2\sigma \) for the \(\Lambda \)CDM and F(Q)-DDE models. From Table 2, the Hubble constant values are \(H_0=71.42\pm 0.88\) km/s/Mpc for the F(Q)-DDE model and \(H_0=70.27\pm 0.66\) km/s/Mpc for \(\Lambda \)CDM at 68% C.L. The latter is smaller, at around \(1.04\sigma \) from the value obtained by F(Q)-DDE. In Table 2, we also list constraints on the two parameters describing the F(Q) gravity, i.e., (\(\gamma \), n)=( \(0.346^{+0.061}_{-0.087}\), \(-0.65^{+0.21}_{-0.24}\)). We observe a strong correlation between these two parameters in Fig. 1. Furthermore, we note that in F(Q)-DDE gravity, the DDE parameter value is negative, i.e., \(\Omega _{\text {x}}=-0.44\pm 0.14\) at 68% C.L., which from Eq. (3.9) leads to \(\omega _{\text {de}}>-1\). This shows that in the context of F(Q) gravity, the DDE model behaves like a quintessence model, contrary to the results found in [38, 42, 46, 47], where it was shown that observational data prefer the phantom-like behaviors of DDE.

Table 2 Summary of the mean\(\pm 1\sigma \) values of the cosmological parameters for the \(\Lambda \)CDM and F(Q)-DDE models, using \(\hbox {Pantheon}^+\) and H(z) combined, as well as the \(\chi _{\text {min}}^2\), \(\Delta \)AIC, and \(\Delta \)BIC
Full size table

Moreover, the future evolution of the Universe depends strongly on the sign of \(\Omega {x}\), \(\gamma \), and n. Indeed, in the future (i.e., \(-1<z<0\)), the asymptotic behavior of the Friedmann equation (Eq. 3.19) can be simplified to

$$\begin{aligned} E^2\approx -\Omega _{x} \ln {(1+z)} +\gamma (1-2n), \end{aligned}$$
(5.1)

and \(E^2\) is an increasing function of z. This means that \(E^2\) decreases as the Universe expands and, consequently, the Universe will bounce (i.e., \(E^2 = 0\)) at some point in the future where the redshift can be approximated to \(\ln (1+z_{B})\approx \gamma (1-2n)/\Omega _{x}\). Using the numerical values from Table 2 for \(\Omega _{x}\), \(\gamma \), and n, the redshift \(z_{B}\) corresponding to the bounce can be estimated to \(z_{B}\approx -0.835\). This scenario can be interpreted as follows: The dark energy density, described by Eq. (3.18), which drives the current accelerated expansion of the Universe, decreases as the Universe expands. At this point, the Universe undergoes a bounce and starts contracting. In the context of general relativity, this dark energy density smooths the Big Rip singularity.

In the same table, we present the value of \(\chi _{\text {min}}^2\), \(\Delta \)AIC, and \(\Delta \)BIC. According to the \(\chi _{\text {min}}^2\) value, we see that the DDE model in the context of F(Q) gravity increases the goodness of fit to the observational data over \(\Lambda \)CDM, with \(\Delta \chi _{\text {min}}^2=\chi _{\text {model}}^2-\chi _{\Lambda \text {CDM}}^2=-10.76\). However, a large number of parameters can lead to a smaller value of \(\chi ^2\) and thus increase the quality of the fit. To confidently predict the goodness of fit between models, we use the AIC and BIC, which depend on the number of parameters. According to Table 3, we obtain \(\Delta \text {AIC}=\text {AIC}_{\text {model}}-\text {AIC}_{\Lambda \text {CDM}}=-6.76\), which gives a statistical preference for our model. However, the positive sign of \(\Delta \text {BIC}\) shows a preference for the \(\Lambda \)CDM model over our model, as this criterion penalizes models with additional parameters.

Figure 2 shows the theoretical evolution of the distance modulus \(\mu (z)\) (left panel) and the Hubble function H(z) (right panel), predicted by the F(Q)-DDE model as a function of z, using the results presented in Table 2. For comparison, both data samples are also presented in the same figure according to the theoretical prediction of the \(\Lambda \)CDM model. This figure shows that the F(Q)-DDE model behaves identically to \(\Lambda \)CDM, and that both models are in good agreement with the observational data.

Fig. 1
figure 1

The 1\(\sigma \) and 2\(\sigma \) confidence contours and the 1D posterior distributions obtained for the F(Q)-DDE and \(\Lambda \)CDM models, using \(\hbox {Pantheon}^+\) and H(z) combined. The figure was obtained with the Getdist package [93]

Full size image

6 Cosmographic analysis

6.1 Cosmographic parameters

Given the large number of cosmological models that have been proposed to explain the late accelerated expansion of the Universe, a mathematical tool, without assuming a dark energy model, is useful for discriminating between all of the proposed dark energy models. An approach called cosmography has been proposed for this reason [88,89,90]. Cosmographic analysis makes it possible to compare several cosmological models using the derivatives of scale factor a by means of the Taylor series expansion of the scale factor [84, 91, 92].

The aim of this part is to study the Taylor series expansion of the scale factor a with respect to cosmic time, t, by introducing the following cosmographic parameters: the Hubble parameter, deceleration parameter, jerk parameter, and snap parameter, defined respectively as follows

$$\begin{aligned}{} & {} H(t)=\frac{1}{a}\frac{da}{dt}, \end{aligned}$$
(6.1)
$$\begin{aligned}{} & {} q(t)=-\frac{1}{a{H^{2}}}\frac{d^2a}{dt^2}, \end{aligned}$$
(6.2)
$$\begin{aligned}{} & {} j(t)=\frac{1}{a{H^{3}}}\frac{d^3a}{dt^3}, \end{aligned}$$
(6.3)
$$\begin{aligned}{} & {} s(t)=\frac{1}{a{H^{4}}}\frac{d^4a}{dt^4}. \end{aligned}$$
(6.4)
Table 3 Summary of the mean\(\pm {1\sigma }\) values of the current cosmographic parameters as derived parameters
Full size table

Figure 3 shows the evolution of the mean value of the deceleration parameter q(z) and its uncertainty at 1\(\sigma \) and 2\(\sigma \) as a function of redshift for the F(Q)-DDE and \(\Lambda \)CDM models (left panel) and the evolution of \(\omega _{\text {eff}}\) for the F(Q)-DDE model (right panel). The q(z) parameter measures the rate at which the expansion of the Universe is accelerating or decelerating. In particular, positive values of q(z) indicate that the expansion is decelerating, which also corresponds to \(\omega _{\text {eff}}>-\frac{1}{3}\), while negative values of q(z) indicate that the expansion is accelerating, and \(\omega _{\text {eff}}<-\frac{1}{3}\). Figure 3 shows that the expansion of the Universe is characterized by a transition phase, from deceleration to acceleration, in the recent past. For our model, the phase transition (i.e., \(q(z_{\text {tr}})=0\)) occurs at redshift \(z_{\text {tr}}=0.938\), while the redshift transition for \(\Lambda \)CDM is less than that for F(Q)-DDE, at \(z_{\text {tr}}^{\Lambda \text {CDM}}=0.728\). For our model, we obtain the actual value of the deceleration parameter, \(q_0=-0.4315\pm 0.0507\), with a difference of \(3.01\sigma \) compared to the \(\Lambda \)CDM model, where \(q_0=-0.5914\pm 0.0158\). The most important result in Fig. 3 is that a phase transition in the future from accelerating to decelerating expansion at the \(1\sigma \) confidence level, in the redshift \(z<-0.5\), is possible. This result is also confirmed by the equation of state, \(\omega _{\text {eff}}\), where \(\omega _{\text {eff}}>-\frac{1}{3}\) at \(1\sigma \) in the redshift \(z<-0.5\) (see the right panel of Fig. 3). This conclusion was recently found in [94]. We also note that \(\omega _{\text {eff}}>-1\) and that the model is in the quintessence region for all redshifts.

Fig. 2
figure 2

Th= error bar for 1701 data points from the \(\hbox {Pantheon}^{+}\), together with the fit of the \(\mu (z)\) function with respect to redshift for F(Q)-DDE and \(\Lambda \)CDM (left panel), and the error bar for 57 points from the H(z) datasets, including the fit of the Hubble function H(z) versus redshift for F(Q)-DDE and \(\Lambda \)CDM (right panel)

Full size image
Fig. 3
figure 3

Evolution of q(z) in a confidence interval \(1\sigma \) and \(2\sigma \) for the \(\Lambda \)CDM and \(F(Q)-DDE\) models (left panel) and the evolution of \(\omega _{\text {eff}}\) for the F(Q)-DDE model, using the chains of the free parameters obtained by \(\hbox {Pantheon}^+\) and H(z) combined (right panel)

Full size image

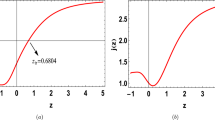
Figure 4 shows the evolution of the jerk parameter (left panel) and the snap parameter (right panel) as functions of the redshift. The red and blue points represent the present time (\(z=0\)) for the \(\Lambda \)CDM and F(Q)-DEE models, respectively. The left panel of Fig. 4 shows that the jerk parameter approaches unity, \(j\simeq 1\), in the near past (i.e., \(z>4\)). Therefore, our model behaves identically to the \(\Lambda \)CDM, as the jerk parameter always remains constant, \(j_{\Lambda \text {CDM}}=1\). At the present time, we obtain a positive value of the jerk parameter \(j_0 = 0.3401 \pm 0.2073\), with a difference of \(3.1\sigma \) compared to the \(\Lambda \)CDM model, and we can see a significant deviation between F(Q)-DDE and \(\Lambda \)CDM for low and negative redshifts (see the left panel of Fig. 3). The right panel of Fig. 4 shows the evolution of the snap parameter. From this figure, we observe significant deviations between F(Q)-DDE and \(\Lambda \)CDM for all redshifts. The present value of the snap parameter for our model is \(s_0=-0.9804 \pm 0.2043\), with a difference of \(4.79\sigma \) compared to the \(\Lambda \)CDM model.

Fig. 4
figure 4

The evolution of the jerk parameter j(z) (left panel) and the snap parameter s(z) (right panel) as functions of the redshift

Full size image

6.2 Statefinder diagnostic

In this section, we use the statefinder diagnostic technique, which is an alternative tool, to compare and distinguish between different models of dark energy [95, 96]. This geometric technique uses the pair of parameters \(\left\{ s,r \right\} \), where r is the jerk parameter and s is snap parameter, defined as follows [95, 96]

$$\begin{aligned} r{} & {} =\frac{\dddot{a}}{aH^3}, \end{aligned}$$
(6.5)
$$\begin{aligned} s{} & {} =-\frac{r-1}{3(q-0.5)}. \end{aligned}$$
(6.6)

In order to evaluate the behavior of our model, the trajectories of the pairs \(\left\{ s,r \right\} \) and \(\left\{ q,r \right\} \) are presented in Fig. 5, where the arrows represent the time evolution from the past to the future. The left panel of Fig. 5 displays the evolutionary trajectory of the \(\left\{ s,r \right\} \) plane. From this figure, our model is located in the quintessence region (i.e., \(r<1\) and \(s>0\)). The right panel of Fig. 5 shows the evolutionary trajectory of the \(\left\{ q,r \right\} \) plane. We notice that the evolution of our model starts from the region where the Universe is dominated by matter abbreviated by SCDM (\(q = 0.5\) and \(r = 1\)), and converges to a point (\(q = -0.55\), \(r = 0\)), representing the late-time evolution of the Universe.

Fig. 5
figure 5

The evolutionary trajectory of the \(\left\{ s,r \right\} \) plane (left panel). The statefinder of the \(\Lambda \)CDM model is indicated by a fixed point (red color), and the blue point indicates the F(Q)-DDE model in the present time. The right panel presents the evolutionary trajectory of the \(\left\{ q,r \right\} \) plane for the F(Q)-DDE model

Full size image

7 Conclusions

In this study, we reevaluate the dynamical dark energy (DDE) model in F(Q) gravity. This dark energy model has been previously studied in the context of general relativity, exhibiting phantom behavior [38]. The model predicts more dark matter density in the past. However, in the future, the model is dominated by dark energy and exhibits distinctive behavior depending on the sign of \(\Omega _{x}\). Specifically, for a positive value of \(\Omega _{x}\), this abrupt event is dubbed the little sibling of the Big Rip, as it smooths the Big Rip singularity. Conversely, this event leads the Universe to bounce when \( \Omega _{x} \) is negative.

To understand the nature of the DDE model within F(Q) gravity, we constrained the model parameters by performing a Markov chain Monte Carlo analysis using a combination of two different background datasets, namely the \(\hbox {Pantheon}^+\) and Hubble parameter data. We found that for the \(\Lambda \)CDM model, \(\Omega _m = 0.281 \pm 0.011\) and \(H_0 = 70.27 \pm 0.66\). However, for the F(Q)-DDE model, \(\Omega _m = 0.232 \pm 0.020\), \(H_0 = 71.42 \pm 0.88\), \(n = -0.65^{+0.21}_{-0.24}\), and \(\gamma = 0.346^{+0.061}_{-0.087}\). In particular, we obtained a negative value for the DDE parameter, \(\Omega _{\text {x}} = -0.44 \pm 0.14\) at 68% C.L., indicating that the DDE model in F(Q) gravity is oriented strictly toward a quintessence region, and in the future the Universe will bounce.

In addition, wee obtained \(\chi _{\text {model}}^2 < \chi _{\Lambda \text {CDM}}^2\), indicating that the model fits the observational data well. However, relying solely on \(\chi _{\text {min}}^2\) to compare models with different numbers of free parameters is inadequate. Therefore, we also evaluated the AIC and BIC values. Our findings show that the F(Q)-DDE model is slightly more preferable in terms of AIC than \(\Lambda \)CDM, where \(\Delta \)AIC = \(-\)6.76. Conversely, our model is less favored in terms of BIC, where \(\Delta \)BIC = +4.16 in favor of \(\Lambda \)CDM. Additionally, the theoretical predictions of the distance modulus \(\mu (z)\) and the Hubble function H(z) from the F(Q)-DDE model are in good agreement with both data samples.

Unlike the case in the context of general relativity, we observed that our setup in the context of F(Q) gravity behaves as a quintessence and faces a bounce in the future at \(z_{B}\approx -0.835\). We found that the phase transition from deceleration to acceleration in F(Q)-DDE starts later than in \(\Lambda \)CDM. We also evaluated the current cosmographic parameters including the deceleration parameter \(q_{0}=-0.4315\pm 0.0507\), jerk parameter \(j_{0}=0.3401\pm 0.2073\), and snap parameter \(s_{0}=-0.9804\pm 0.2043\). Finally, we analyzed the statefinder diagnostics in the \(\left\{ s,r \right\} \) and \(\left\{ q,r \right\} \) planes. We found that from the statefinder diagnostic \(\left\{ s,r \right\} \), our model is located in the quintessence region, while from the \(\{q,r\}\) plane, the DDE model evolves from a state where the Universe is dominated by matter in the past to a late-time state of the Universe.