Mass spectra of $0^{--}$ and $0^{+-}$ hidden-heavy baryoniums

Abstract

In this work, the spectra of the prospective exotic hidden-charm and hidden-bottom baryonium, viz. the baryon–antibaryon states, with $J^{PC}=0^{--}$ and $0^{+-}$ are investigated in the framework of QCD sum rules. The non-perturbative contributions up to dimension 12 are taken into account. Numerical results indicate that there might exist 3 possible $0^{--}$ hidden-charm baryonium states with masses $(5.22\pm 0.26)$, $(5.52\pm 0.25)$, and $(5.46\pm 0.24)$ GeV, and 5 possible $0^{+-}$ hidden-charm baryonium states with masses $(4.76\pm 0.28)$, $(5.24\pm 0.28)$, $(5.16\pm 0.27)$, $(5.52\pm 0.27)$, and $(5.69\pm 0.27)$ GeV, respectively. The corresponding hidden-bottom partners are found lying in the range of $11.68-12.28$ GeV and $11.38-12.33$ GeV, respectively. The possible baryonium decay modes are analyzed, which are hopefully measurable in LHC experiments.

1 Introduction

Since the observation of X(3872) [1], many novel hadronic states or candidates, denoted as XYZ and $P_c$ states, have been observed in experiments. These novel hadronic states can hardly be well understood by conventional quark model [2, 3], and exploring their properties and finding more possible states may greatly enrich the hadron family and our knowledge of the nature of quantum chromodynamics(QCD). With the more novel hadronic states discovering and the deepening of our understanding of strong interaction, it is reasonable to believe that the renaissance of hadron physics will come sooner or later, which attracts more and more interests from theorists and experimentalists.

Among the novel hadronic states, special attention ought be paid to the states possess some exotic quantum numbers (like $0^{--}$, $0^{+-}$, $1^{-+}$, $2^{+-}$, and so on), since they cannot mix with the conventional ones. In the literature, many theoretical investigations on exotic hadronic states were made, including tetraquarks [4,5,6,7,8,9,10], hybrid tates [11,12,13,14,15], glueballs [16,17,18,19,20,21,22,23,24]. On the other hand, exotic hadronic states have gradually been observed in experiment, like the most recently observed $\eta _1(1855)$ [25, 26]. It is highly expected that more novel hadronic structures with exotic quantum numbers will emerge soon afterwards.

While the theoretical investigations on hexaquark with exotic quantum number are still rare. Up to now, most of studies on hexaquark are focus on conventional quantum numbers, such as the deuteron. Deuteron created at the beginning of Universe and its stability is responsible for the production of other elements, is a well-established dibaryon molecular state composed of a proton and a neutron, withe $J^P=1^+$ and binding energy $E_B=2.225$ MeV [27,28,29]. On the other hand, the baryon–antibaryon systems (baryonium) is another special class of heaxquark configuration. Actually, the history of the investigation on baryon–antibaryon system can date back to the proposal by Fermi and Yang that $\pi$-mesons may be composite particles formed by a nucleon–antinucleon pair in 1940s [30], and their scenario was later on replaced by the quark model. Entering the new millennium, the heavy baryonium were proposed and employed to explain the extraordinary nature of Y(4260) [31, 32] and other charmonium-like states observed in experiments. Later on, more investigations on baryonium are performed from various aspects [33,34,35,36,37,38,39,40,41]. Especially, our previous work [41] of the investigation of light baryonium states predicted that the mass of the $\Lambda -\bar{\Lambda }$ baryonium state with $J^{PC}$ of $1^{--}$ is about 2.34 GeV, which is consistent with the experimental observation of the structure in $\Lambda \bar{\Lambda }$ mass spectra with mass of $(2356\pm 24)$ MeV with quantum number of $1^{--}$ by BESIII [42].

In this work, we investigate the hidden-heavy baryonium states with the exotic quantum numbers of $J^{PC}=0^{--}$ and $0^{+-}$ in the framework of QCD sum rules (QCDSR). In past 40 years, the QCDSR technique [43, 44] as a model independent approach has achieved a lot in the study of hadron spectroscopy. To establish the QCDSR, one need to construct the proper interpolating currents corresponding to hadrons of interest, which possesses the foremost information of the concerned hadrons, like quantum numbers and structure components. With the interpolating currents, the two-point correlation function can be readily established and by equating the operator product expansion (OPE) side and the phenomenological side of the two-point correlation, we can then obtain the mass of the hadron.

The rest of the paper is arranged as follows. After the introduction, a brief interpretation of QCD sum rules and some primary formulas in our calculation are presented in Sect. 2. The numerical analysis and results are given in Sect. 3. The possible decay modes of the exotic baryonium states are analyzed in Sect. 4. The last part is left for a brief summary.

2 Formalism

For the $0^{--}$ baryonium state, the interpolating currents in molecular configuration can be constructed as:

$$\begin{aligned} j_{0^{--}}^A(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C q^\prime _b(x)][{\bar{q}}_e (x)\gamma _5 C {\bar{q}}^{\prime T}_f(x)] \nonumber \\{} & {} -[{\bar{Q}}_d(x) Q_c(x)][q^T_a(x) C \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) C {\bar{q}}^{\prime T}_f(x)] {\Big \}}, \end{aligned}$$

(1)

$$\begin{aligned} j_{0^{--}}^B(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}}{\Big \{}[{\bar{Q}}_d(x) Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu q^\prime _b(x)][{\bar{q}}_e(x) \gamma _\mu \gamma _5 C {\bar{q}}^{\prime T}_f(x)] \nonumber \\{} & {} -[{\bar{Q}}_d(x) Q_c(x)][q^T_a(x) C \gamma _\mu \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu C {\bar{q}}^{\prime T}_f(x)] {\Big \}}, \end{aligned}$$

(2)

$$\begin{aligned} j_{0^{--}}^C(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu q^\prime _b(x)][{\bar{q}}_e (x) \gamma _5 C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} +[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)][q^T_a(x) C \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu C {\bar{q}}^{\prime T}_f (x)] {\Big \}}, \end{aligned}$$

(3)

$$\begin{aligned} j_{0^{--}}^D(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu \gamma _5 q^\prime _b(x)][{\bar{q}}_e (x) C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} +[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)][q^T_a(x) C q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu \gamma _5 C {\bar{q}}^{\prime T}_f (x)] {\Big \}}, \end{aligned}$$

(4)

$$\begin{aligned} j_{0^{--}}^E(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu \gamma _5 q^\prime _b(x)][{\bar{q}}_e (x) \gamma _5 C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} -[{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)][q^T_a(x) C \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu \gamma _5 C {\bar{q}}^{\prime T}_f (x)] {\Big \}}, \end{aligned}$$

(5)

$$\begin{aligned} j_{0^{--}}^F(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}}{\Big \{} [{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu q^\prime _b(x)][{\bar{q}}_e (x) C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} - [{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)][q^T_a(x) C q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu C {\bar{q}}^{\prime T}_f (x)] {\Big \}}. \end{aligned}$$

(6)

The interpolating currents for $0^{+-}$ in molecular configuration are found to be in forms:

$$\begin{aligned} j_{0^{+-}}^A(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) \gamma _5 Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C q^\prime _b(x)][{\bar{q}}_e (x)\gamma _5 C {\bar{q}}^{\prime T}_f(x)] \nonumber \\{} & {} -[{\bar{Q}}_d(x) \gamma _5 Q_c(x)][q^T_a(x) C \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) C {\bar{q}}^{\prime T}_f(x)] {\Big \}}, \end{aligned}$$

(7)

$$\begin{aligned} j_{0^{+-}}^B(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}}{\Big \{}[{\bar{Q}}_d(x)\gamma _5 Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu q^\prime _b(x)][{\bar{q}}_e(x) \gamma _\mu \gamma _5 C {\bar{q}}^{\prime T}_f(x)] \nonumber \\{} & {} -[{\bar{Q}}_d(x) \gamma _5 Q_c(x)][q^T_a(x) C \gamma _\mu \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu C {\bar{q}}^{\prime T}_f(x)] {\Big \}}, \end{aligned}$$

(8)

$$\begin{aligned} j_{0^{+-}}^C(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu q^\prime _b(x)][{\bar{q}}_e (x) C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} +[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)][q^T_a(x) C q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu C {\bar{q}}^{\prime T}_f (x)] {\Big \}}, \end{aligned}$$

(9)

$$\begin{aligned} j_{0^{+-}}^D(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu \gamma _5 q^\prime _b(x)][{\bar{q}}_e (x) \gamma _5 C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} +[{\bar{Q}}_d(x) \gamma _\mu Q_c(x)][q^T_a(x) C \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu \gamma _5 C {\bar{q}}^{\prime T}_f (x)] {\Big \}}, \end{aligned}$$

(10)

$$\begin{aligned} j_{0^{+-}}^E(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}} {\Big \{}[{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu q^\prime _b(x)][{\bar{q}}_e (x) \gamma _5 C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} -[{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)][q^T_a(x) C \gamma _5 q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu C {\bar{q}}^{\prime T}_f (x)] {\Big \}}, \end{aligned}$$

(11)

$$\begin{aligned} j_{0^{+-}}^F(x)= & {} \frac{\epsilon _{a b c}\epsilon _{d e f}}{\sqrt{2}}{\Big \{} [{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)]\nonumber \\{} & {} \times [q^T_a(x) C \gamma _\mu \gamma _5 q^\prime _b(x)][{\bar{q}}_e (x) C {\bar{q}}^{\prime T}_f (x)]\nonumber \\{} & {} - [{\bar{Q}}_d(x) \gamma _\mu \gamma _5 Q_c(x)][q^T_a(x) C q^\prime _b(x)]\nonumber \\{} & {} \times [{\bar{q}}_e (x) \gamma _\mu \gamma _5 C {\bar{q}}^{\prime T}_f (x)] {\Big \}}. \end{aligned}$$

(12)

Here, the subscripts $a\cdots f$ are color indices, q and $q^\prime$ stand for light quark u and d, respectively, Q represents the heavy quark c or b, and C is the charge conjugation matrix.

With the currents (1)-(6), the two-point correlation function can be readily established, i.e.,

$$\begin{aligned} \Pi _{J^{PC}}^k(q^2)= & {} i \int d^4 x e^{i q \cdot x} \langle 0 | T \{ j_{J^{PC}}^k(x),\; j_{J^{PC}}^k (0)^\dagger \} |0 \rangle ,\nonumber \\ \end{aligned}$$

(13)

where $|0 \rangle$ denotes the physical vacuum, and k runs from A to F.

On the OPE side, correlation function $\Pi (q^2)$ can be expressed by the dispersion relation as

$$\begin{aligned} \Pi ^{OPE,\;k}_{J^{PC}} (q^2) = \int _{s_{min}}^{\infty } d s\frac{\rho ^{OPE,\;k}_{J^{PC}}(s)}{s - q^2}. \end{aligned}$$

(14)

Here, $s_{min}$ is the kinematic limit, which usually corresponds to the square of the sum of current-quark masses of the hadron [45], $\rho ^{OPE,\;k}_{J^{PC}}(s) = \text {Im} [\Pi ^{OPE,\;k}_{J^{PC}}(s)] / \pi$, and

$$\begin{aligned} \rho ^{OPE}(s)= & {} \rho ^{pert}(s) +\rho ^{\langle G^2 \rangle }(s)\nonumber \\{} & {} + \rho ^{\langle {\bar{q}} G q \rangle }(s) + \rho ^{\langle {\bar{q}} q \rangle ^2}(s) +\rho ^{\langle G^3 \rangle }(s)\nonumber \\{} & {} + \rho ^{\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }(s) + \rho ^{\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }(s) + \rho ^{\langle {\bar{q}} G q \rangle ^2}(s).\nonumber \\ \end{aligned}$$

(15)

The Feynman diagrams corresponding to each term of Eq. (15) are schematically shown in Fig. 1. The analytical expressions of $\rho ^{OPE,\;k}_{J^{PC}}(s)$ can be calculated and given in appendix A.

Fig. 1

The typical Feynman diagrams related to the correlation function, where the thick solid line represents the heavy quark, the thin solid line stands for the light quark, and the spiral line denotes the gluon. There is no heavy quark condensate due to the large heavy quark mass

On the phenomenological side, the correlation function $\Pi (q^2)$ can be expressed as a dispersion integral over the physical regime after isolating the ground state contribution from the baryonium state, i.e.,

$$\begin{aligned} \Pi ^{phen,\;k}_{J^{PC}}(q^2)= & {} \frac{{\lambda ^k_{J^{PC}}}^2}{{M^k_{J^{PC}}}^2 - q^2} + \frac{1}{\pi } \int _{s_0}^\infty d s \frac{\rho ^k_{J^{PC}}(s)}{s - q^2} , \end{aligned}$$

(16)

where M denotes the mass of baryonium state, $\lambda$ is the coupling constant, and $\rho (s)$ is the spectral density that contains the contributions from higher excited states and the continuum states above the threshold $s_0$.

Performing Borel transform on Eqs. (14) and (16), and matching the OPE side with the phenomenological side of the correlation function $\Pi (q^2)$, one can finally obtain the mass of the tetraquark state,

$$\begin{aligned} M^k_{J^{PC}}(s_0, M_B^2) = \sqrt{- \frac{L^k_{J^{PC},\;1}(s_0, M_B^2)}{L^k_{J^{PC},\;0}(s_0, M_B^2)}} . \end{aligned}$$

(17)

Here $L_0$ and $L_1$ are respectively defined as

$$\begin{aligned} L^k_{J^{PC},\;0}(s_0, M_B^2) = \int _{s_{min}}^{s_0} d s \; \rho ^{OPE,\; k}_{J^{PC}}(s) e^{- s / M_B^2}, \end{aligned}$$

(18)

and

$$\begin{aligned} L^k_{J^{PC},\;1}(s_0, M_B^2) = \frac{\partial }{\partial {\frac{1}{M_B^2}}}{L^k_{J^{PC},\;0}(s_0, M_B^2)} . \end{aligned}$$

(19)

3 Numerical analysis

In performing the numerical calculation, the broadly accepted inputs are taken [45,46,47,48,49,50]:

$$\begin{aligned} \begin{aligned}&m_c(m_c)={\overline{m}}_c=(1.275\pm 0.025)\; \text {GeV},\\&m_b(m_b)={\overline{m}}_b=(4.18\pm 0.03)\; \text {GeV} ,\\&\langle {\bar{q}} q \rangle = - (0.24 \pm 0.01)^3 \; \text {GeV}^3 ,\\&\langle g_s^2 G^2 \rangle = (0.88\pm 0.25) \; \text {GeV}^4 , \\&\langle {\bar{q}} g_s \sigma \cdot G q \rangle = m_0^2 \langle {\bar{q}} q \rangle ;, \\&\langle g_s^3 G^3 \rangle = (0.045 \pm 0.013) \;\text {GeV}^6 ,\\&m_0^2 = (0.8 \pm 0.1) \; \text {GeV}^2. \end{aligned} \end{aligned}$$

(20)

Here, ${\overline{m}}_c$ and ${\overline{m}}_b$ represent heavy-quark running masses in $\overline{\text {MS}}$ scheme. For light quark, the chiral quark limit mass $m_q=0$ is adopted. Furthermore, as the discussion in Ref. [51], we cannot discard the on-shell quark masses which are $m_c\approx 1.5$ GeV and $m_b\approx 4.7$ GeV, so the on-shell quark masses are also taken into consideration in our calculation.

Moreover, two additional parameters $s_0$ and $M_B^2$ introduced in establishing the sum rules need to be exacted. We can fix them in light of the so-called standard procedures by fulfilling the following two criteria [43, 44, 50, 52]. One asks for the convergence of the OPE, which is to compare relative contribution of higher dimension condensate to the total contribution on the OPE side, and then a reliable region for $M_B^2$ will be chosen to retain the convergence. The other one requires that the pole contribution (PC) is more than $15\%$ of the total for hexaquark states [35, 39, 41]. Mathematically, the two criteria can be formulated as:

$$\begin{aligned} R^{OPE}= & {} \left| \frac{L_{J^{PC},0}^{k,dim=12}(s_0, M_B^2)}{L_{J^{PC},0}^k(s_0, M_B^2)}\right| , \end{aligned}$$

(21)

$$\begin{aligned} R^{PC}= & {} \frac{L_{J^{PC},0}^k(s_0, M_B^2)}{L_{J^{PC},0}^k(\infty , M_B^2)} . \end{aligned}$$

(22)

To find a proper value for continuum threshold $s_0$, a similar analysis as in Refs. [53,54,55,56,57] is performed. Therein, one needs to find the proper value, which has an optimal window for the mass curve of the baryonium state. Within this window, the physical quantity, that is the mass of the baryonium state, should be independent of the Borel parameter $M_B^2$ as much as possible. In practice, we will vary $\sqrt{s_0}$ by 0.2 GeV to obtain the lower and upper bounds, and hence the uncertainties of $\sqrt{s_0}$.

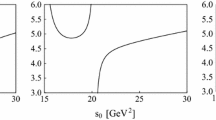
With the above preparation the mass spectrum of exotic baryonium states can be numerically evaluated. For the $0^{--}$ hidden-charm exotic baryonium state in Eq. (1), the ratios $R^{OPE,A}_{0^{--}}$ and $R^{PC,A}_{0^{--}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 2a with different values of $\sqrt{s_0}$, i.e., 5.2, 5.6 and 6.0 GeV. The reliant relations of $M^{A}_{0^{--}}$ on parameter $M_B^2$ are displayed in Fig. 2b. The optimal Borel window is found in range $3.1 \le M_B^2 \le 4.1\; \text {GeV}^2$, and the mass $M^{A}_{0^{--}}$ can then be obtained:

$$\begin{aligned} M^{A}_{0^{--}}= & {} (5.22\pm 0.26)\; \text {GeV}. \end{aligned}$$

(23)

Fig. 2

a The ratios of ${R_{A}^{OPE}}$ and ${R_{A}^{PC}}$ as functions of the Borel parameter $M_B^2$ for different values of $\sqrt{s_0}$, where blue lines represent ${R_{A}^{OPE}}$ and red lines denote ${R_{A}^{PC}}$. b The mass $M^{A}$ as a function of the Borel parameter $M_B^2$ for different values of $\sqrt{s_0}$

For the $0^{--}$ hidden-charm exotic baryonium state in Eq. (2), the ratios $R^{OPE,B}_{0^{--}}$ and $R^{PC,B}_{0^{--}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 3a with different values of $\sqrt{s_0}$, i.e., 5.5, 5.9 and 6.3 GeV. The reliant relations of $M^{B}_{0^{--}}$ on parameter $M_B^2$ are displayed in Fig. 3b. The optimal Borel window is found in range $3.2 \le M_B^2 \le 4.3\; \text {GeV}^2$, and the mass $M^{B}_{0^{--}}$ can then be obtained:

$$\begin{aligned} M^{B}_{0^{--}}= & {} (5.52\pm 0.25)\; \text {GeV}. \end{aligned}$$

(24)

Fig. 3

The same caption as in Fig. 2, but for the current in Eq. (2)

For the $0^{--}$ hidden-charm exotic baryonium state in Eq. (3), the ratios $R^{OPE,C}_{0^{--}}$ and $R^{PC,C}_{0^{--}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 4a with different values of $\sqrt{s_0}$, i.e., 5.4, 5.8 and 6.2 GeV. The reliant relations of $M^{C}_{0^{--}}$ on parameter $M_B^2$ are displayed in Fig. 4b. The optimal Borel window is found in range $4.1 \le M_B^2 \le 5.1\; \text {GeV}^2$, and the mass $M^{C}_{0^{--}}$ can then be obtained:

$$\begin{aligned} M^{C}_{0^{--}}= & {} (5.46\pm 0.24)\; \text {GeV}. \end{aligned}$$

(25)

Fig. 4

The same caption as in Fig. 2, but for the current in Eq. (3)

For the $0^{+-}$ hidden-charm exotic baryonium state in Eq. (7), the ratios $R^{OPE,A}_{0^{+-}}$ and $R^{PC,A}_{0^{+-}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 5a with different values of $\sqrt{s_0}$, i.e., 4.7, 5.1 and 5.5 GeV. The reliant relations of $M^{A}_{0^{+-}}$ on parameter $M_B^2$ are displayed in Fig. 5b. The optimal Borel window is found in range $2.8 \le M_B^2 \le 3.8\; \text {GeV}^2$, and the mass $M^{A}_{0^{+-}}$ can then be obtained:

$$\begin{aligned} M^{A}_{0^{+-}}= & {} (4.76\pm 0.26)\; \text {GeV}. \end{aligned}$$

(26)

Fig. 5

The same caption as in Fig. 2, but for the current in Eq. (7)

For the $0^{+-}$ hidden-charm exotic baryonium state in Eq. (8), the ratios $R^{OPE,B}_{0^{+-}}$ and $R^{PC,B}_{0^{+-}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 6a with different values of $\sqrt{s_0}$, i.e., 5.2, 5.6 and 5.9 GeV. The reliant relations of $M^{B}_{0^{+-}}$ on parameter $M_B^2$ are displayed in Fig. 6b. The optimal Borel window is found in range $3.0 \le M_B^2 \le 4.1\; \text {GeV}^2$, and the mass $M^{B}_{0^{+-}}$ can then be obtained:

$$\begin{aligned} M^{B}_{0^{+-}}= & {} (5.24\pm 0.28)\; \text {GeV}. \end{aligned}$$

(27)

Fig. 6

The same caption as in Fig. 2, but for the current in Eq. (8)

For the $0^{+-}$ hidden-charm exotic baryonium state in Eq. (9), the ratios $R^{OPE,C}_{0^{+-}}$ and $R^{PC,C}_{0^{+-}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 7a with different values of $\sqrt{s_0}$, i.e., 5.2, 5.6 and 5.9 GeV. The reliant relations of $M^{C}_{0^{+-}}$ on parameter $M_B^2$ are displayed in Fig. 7b. The optimal Borel window is found in range $3.3 \le M_B^2 \le 4.3\; \text {GeV}^2$, and the mass $M^{C}_{0^{+-}}$ can then be obtained:

$$\begin{aligned} M^{C}_{0^{+-}}= & {} (5.16\pm 0.27)\; \text {GeV}. \end{aligned}$$

(28)

Fig. 7

The same caption as in Fig. 2, but for the current in Eq. (9)

For the $0^{+-}$ hidden-charm exotic baryonium state in Eq. (10), the ratios $R^{OPE,D}_{0^{+-}}$ and $R^{PC,D}_{0^{+-}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 8a with different values of $\sqrt{s_0}$, i.e., 5.5, 5.9 and 6.3 GeV. The reliant relations of $M^{D}_{0^{+-}}$ on parameter $M_B^2$ are displayed in Fig. 8b. The optimal Borel window is found in range $3.9 \le M_B^2 \le 4.9\; \text {GeV}^2$, and the mass $M^{D}_{0^{+-}}$ can then be obtained:

$$\begin{aligned} M^{D}_{0^{+-}}= & {} (5.52\pm 0.27)\; \text {GeV}. \end{aligned}$$

(29)

Fig. 8

The same caption as in Fig. 2, but for the current in Eq. (10)

For the $0^{+-}$ hidden-charm exotic baryonium state in Eq. (11), the ratios $R^{OPE,E}_{0^{+-}}$ and $R^{PC,E}_{0^{+-}}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 9a with different values of $\sqrt{s_0}$, i.e., 5.7, 6.1 and 6.5 GeV. The reliant relations of $M^{E}_{0^{+-}}$ on parameter $M_B^2$ are displayed in Fig. 9b. The optimal Borel window is found in range $3.8 \le M_B^2 \le 5.2\; \text {GeV}^2$, and the mass $M^{E}_{0^{+-}}$ can then be obtained:

$$\begin{aligned} M^{E}_{0^{+-}}= & {} (5.69\pm 0.27)\; \text {GeV}. \end{aligned}$$

(30)

Fig. 9

The same caption as in Fig. 2, but for the current in Eq. (5)

The $\overline{\text {MS}}$ quark mass are used above. The errors in results mainly stem from the uncertainties in quark masses, condensates and threshold parameter $\sqrt{s_0}$. For the currents $j_{0^{--}}^D$, $j_{0^{--}}^E$, $j_{0^{--}}^F$, and $j_{0^{+-}}^F$, no matter what values of $M_B^2$ and $\sqrt{s_0}$ take, no optimal window for stable plateaus exist. That means the currents in Eqs. (4), (5), (6), and (12) do not support the corresponding hidden-charm baryonium states. For the convenience of reference, a collection of Borel parameters, continuum thresholds, and predicted masses for hidden-charm exotic baryonium states are tabulated in Table 1.

Table 1 The continuum thresholds, Borel parameters, and predicted masses of hidden-charm baryonium for $m_c=1.275 \text {GeV}$

For the $0^{--}$ hidden-bottom exotic baryonium state in Eq. (1), the ratios $R^{OPE,A}_{0^{--},b}$ and $R^{PC,A}_{0^{--},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 10a with different values of $\sqrt{s_0}$, i.e., 11.9, 12.3 and 12.7 GeV. The reliant relations of $M^{A}_{0^{--},b}$ on parameter $M_B^2$ are displayed in Fig. 10b. The optimal Borel window is found in range $8.3 \le M_B^2 \le 10.2\; \text {GeV}^2$, and the mass $M^{A}_{0^{--},b}$ can then be obtained:

$$\begin{aligned} M^{A}_{0^{--},b}= & {} (11.82\pm 0.27)\; \text {GeV}. \end{aligned}$$

(31)

Fig. 10

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (7)

Fig. 11

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (2)

Fig. 12

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (3)

Fig. 13

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (7)

For the $0^{--}$ hidden-bottom exotic baryonium state in Eq. (2), the ratios $R^{OPE,B}_{0^{--},b}$ and $R^{PC,B}_{0^{--},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 11a with different values of $\sqrt{s_0}$, i.e., 12.2, 12.6 and 13.0 GeV. The reliant relations of $M^{B}_{0^{--},b}$ on parameter $M_B^2$ are displayed in Fig. 11b. The optimal Borel window is found in range $8.5 \le M_B^2 \le 10.6\; \text {GeV}^2$, and the mass $M^{B}_{0^{--},b}$ can then be obtained:

$$\begin{aligned} M^{B}_{0^{--},b}= & {} (12.14\pm 0.26)\; \text {GeV}. \end{aligned}$$

(32)

For the $0^{--}$ hidden-bottom exotic baryonium state in Eq. (3), the ratios $R^{OPE,C}_{0^{--},b}$ and $R^{PC,C}_{0^{--},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 12a with different values of $\sqrt{s_0}$, i.e., 12.1, 12.5 and 12.9 GeV. The reliant relations of $M^{C}_{0^{--},b}$ on parameter $M_B^2$ are displayed in Fig. 12b. The optimal Borel window is found in range $9.5 \le M_B^2 \le 12.5\; \text {GeV}^2$, and the mass $M^{C}_{0^{--},b}$ can then be obtained:

$$\begin{aligned} M^{C}_{0^{--},b}= & {} (11.95\pm 0.31)\; \text {GeV}. \end{aligned}$$

(33)

Fig. 14

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (8)

Fig. 15

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (9)

For the $0^{+-}$ hidden-bottom exotic baryonium state in Eq. (7), the ratios $R^{OPE,A}_{0^{+-},b}$ and $R^{PC,A}_{0^{+-},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 13a with different values of $\sqrt{s_0}$, i.e., 11.6, 12.0 and 12.4 GeV. The reliant relations of $M^{A}_{0^{+-},b}$ on parameter $M_B^2$ are displayed in Fig. 10b. The optimal Borel window is found in range $8.0 \le M_B^2 \le 10.0\; \text {GeV}^2$, and the mass $M^{A}_{0^{+-},b}$ can then be obtained:

$$\begin{aligned} M^{A}_{0^{+-},b}= & {} (11.53\pm 0.27)\; \text {GeV}. \end{aligned}$$

(34)

For the $0^{+-}$ hidden-bottom exotic baryonium state in Eq. (8), the ratios $R^{OPE,B}_{0^{+-},b}$ and $R^{PC,B}_{0^{+-},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 14a with different values of $\sqrt{s_0}$, i.e., 12.0, 12.4 and 12.8 GeV. The reliant relations of $M^{B}_{0^{+-},b}$ on parameter $M_B^2$ are displayed in Fig. 11b. The optimal Borel window is found in range $8.5 \le M_B^2 \le 10.9\; \text {GeV}^2$, and the mass $M^{B}_{0^{+-},b}$ can then be obtained:

$$\begin{aligned} M^{B}_{0^{+-},b}= & {} (11.92\pm 0.28)\; \text {GeV}. \end{aligned}$$

(35)

Fig. 16

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (10)

Fig. 17

The same caption as in Fig. 2, but for the hidden-bottom baryonium state with current in Eq. (11)

For the $0^{+-}$ hidden-bottom exotic baryonium state in Eq. (9), the ratios $R^{OPE,C}_{0^{+-},b}$ and $R^{PC,C}_{0^{+-},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 15a with different values of $\sqrt{s_0}$, i.e., 11.8, 12.2 and 12.6 GeV. The reliant relations of $M^{C}_{0^{+-},b}$ on parameter $M_B^2$ are displayed in Fig. 12b. The optimal Borel window is found in range $7.9 \le M_B^2 \le 10.3\; \text {GeV}^2$, and the mass $M^{C}_{0^{+-},b}$ can then be obtained:

$$\begin{aligned} M^{C}_{0^{+-},b}= & {} (11.69\pm 0.29)\; \text {GeV}. \end{aligned}$$

(36)

For the $0^{+-}$ hidden-bottom exotic baryonium state in Eq. (10), the ratios $R^{OPE,D}_{0^{+-},b}$ and $R^{PC,D}_{0^{+-},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 16a with different values of $\sqrt{s_0}$, i.e., 12.1, 12.5 and 12.9 GeV. The reliant relations of $M^{D}_{0^{+-},b}$ on parameter $M_B^2$ are displayed in Fig. 11b. The optimal Borel window is found in range $9.4 \le M_B^2 \le 11.4\; \text {GeV}^2$, and the mass $M^{D}_{0^{+-},b}$ can then be obtained:

$$\begin{aligned} M^{D}_{0^{+-},b}= & {} (12.02\pm 0.26)\; \text {GeV}. \end{aligned}$$

(37)

Table 2 The continuum thresholds, Borel parameters, and predicted masses of hidden-bottom baryonium for $m_b=4.18 \text {GeV}$

Table 3 The continuum thresholds, Borel parameters, and predicted masses of hidden-charm baryonium for $m_c\approx 1.5 \text {GeV}$

For the $0^{+-}$ hidden-bottom exotic baryonium state in Eq. (11), the ratios $R^{OPE,E}_{0^{+-},b}$ and $R^{PC,E}_{0^{+-},b}$ are presented as functions of Borel parameter $M_B^2$ in Fig. 17a with different values of $\sqrt{s_0}$, i.e., 12.3, 12.7 and 13.1 GeV. The reliant relations of $M^{E}_{0^{+-},b}$ on parameter $M_B^2$ are displayed in Fig. 9b. The optimal Borel window is found in range $10.0 \le M_B^2 \le 12.1\; \text {GeV}^2$, and the mass $M^{E}_{0^{+-},b}$ can then be obtained:

$$\begin{aligned} M^{E}_{0^{+-},b}= & {} (12.19\pm 0.27)\; \text {GeV}. \end{aligned}$$

(38)

Table 4 The continuum thresholds, Borel parameters, and predicted masses of hidden-bottom baryonium for $m_b\approx 4.7 \text {GeV}$

Table 5 typical decay modes of the exotic hidden-heavy baryonium

The $\overline{\text {MS}}$ quark mass are used above. The errors in results mainly stem from the uncertainties in quark masses, condensates and threshold parameter $\sqrt{s_0}$. For the currents $j_{0^{--}}^D$, $j_{0^{--}}^E$, $j_{0^{--}}^F$, and $j_{0^{+-}}^F$, no matter what values of $M_B^2$ and $\sqrt{s_0}$ take, no optimal window for stable plateaus exist. That means the currents in Eqs. (4), (5), (6), and (12) do not support the corresponding hidden-bottom baryonium states. For the convenience of reference, a collection of Borel parameters, continuum thresholds, and predicted masses for hidden-charm exotic baryonium states are tabulated in Table 2.

We also evaluate the exotic hidden-charm and hidden-bottom baryonium states with the pole quark masses. By using the obtained analytical results but with pole quark masses, the corresponding masses are readily obtained and tabulated in Tables 3 and 4.

4 Decay analyses

To finally ascertain these exotic hidden-heavy baryonium states, the straightforward procedure is to reconstruct them from their decay products, though the detailed characters stills ask for more investigation. The typical decay modes of these exotic baryonium are given in Table 5, and these processes are expected to be measurable in the running LHC experiments.

5 Summary

In summary, we have investigated the exotic hidden-heavy baryonium states with $J^{PC}=0^{--}$ and $0^{+-}$ in the framework of QCD sum rules. Our numerical results are tabulated in Table 1 and 2 for charm and bottom sector, respectively. Results indicate that there might exist 3 possible $0^{--}$ hidden-charm baryonium states with masses $(5.22\pm 0.26)$, $(5.52\pm 0.25)$, and $(5.46\pm 0.24)$ GeV, and 5 possible $0^{+-}$ hidden-charm baryonium states with masses $(4.76\pm 0.28)$, $(5.24\pm 0.28)$, $(5.16\pm 0.27)$, $(5.52\pm 0.27)$, and $(5.69\pm 0.27)$ GeV, respectively. The corresponding hidden-bottom partners are found lying in the range of $11.68-12.28$ GeV and $11.38-12.33$ GeV, respectively. Moreover, the possible exotic baryonium decay modes are analyzed, which might serve as a guide for experimental exploration.

It should noted that, as the discussion in Ref. [51], lowest order of $\overline{\text {MS}}$ quark masses is ill-defined such that one can equally use the running or the pole masses. One way to solve this problem is to consider the next-to leading and next-to-next-to leading order QCD corrections in the analysis. While, in the work, we just naively perform our calculation by taking consideration on both $\overline{\text {MS}}$ quark mass and the pole masses. The numerical results by using the pole masses are tabulated in Tables 3 and 4, which is bigger than the results in tabulated in Tables 1 and 2.

It also should be noted that we list six $0^{--}$ and six $0^{+-}$ different interpolating operators exotic baryonium states, while they are very different states. From the structures of the interpolating operators, it’s not hard to see that, for the $0^{--}$ states the Eq. (1) is coupled to $\Lambda _c\bar{\Lambda }_c(2595)-c.c.$ molecular state, Eq. (2) is coupled to $\Lambda _c(2625)\bar{\Lambda }_c(2860)-c.c.$ molecular state, Eq. (3) is coupled to $\Lambda _c\bar{\Lambda }_c(2860)+c.c.$ molecular state, Eq. (4) is coupled to $\Lambda _c(2625)\bar{\Lambda }_c(2595)+c.c.$ molecular state, the Eq. (5) is coupled to $\Lambda _c\bar{\Lambda }_c(2625)-c.c.$ molecular state, and the Eq. (6) is coupled to $\Lambda _c(2595)\bar{\Lambda }_c(2860)-c.c.$ molecular state. On the other hand, for the $0^{+-}$ states the Eq. (7) is coupled to $\Lambda _c\bar{\Lambda }_c(2595)-c.c.$ molecular state, Eq. (8) is coupled to $\Lambda _c(2625)\bar{\Lambda }_c(2860)-c.c.$ molecular state, Eq. (9) is coupled to $\Lambda _c(2595)\bar{\Lambda }_c(2860)+c.c.$ molecular state, Eq. (10) is coupled to $\Lambda _c\bar{\Lambda }_c(2625)+c.c.$ molecular state, Eq. (11) is coupled to $\Lambda _c(2595)\bar{\Lambda }_c(2625)-c.c.$ molecular state, and Eq. (12) is coupled to $\Lambda _c\bar{\Lambda }_c(2860)-c.c.$ molecular state. Thus the experiments can discriminate those states.

Appendix A: The spectral densities for \(0^{--}\) and \(0^{+-}\) baryonium states

1.1 1. The spectral densities for $0^{--}$ baryonium state in Eqs. (1) and (2)

$$\begin{aligned}{} & {} \rho ^{pert}(s)=\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \int _{\beta _{min}}^{1-\alpha } \nonumber \\{} & {} \quad \times d \beta \bigg \{\frac{{{\mathcal {F}}}_{\alpha \beta }^{6}(\alpha +\beta -1)^{4}(-5{{\mathcal {F}}}_{\alpha \beta } +7m_Q^2(\alpha +\beta -1)}{3\times 7\times 5^2\times 2^{19}\pi ^{10} \alpha ^{6} \beta ^{6}}\bigg \}, \end{aligned}$$

(A1)

$$\begin{aligned}{} & {} \rho ^{\langle G^2 \rangle }(s)=\frac{\langle G^2 \rangle }{\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \int _{\beta _{min}}^{1-\alpha }\nonumber \\{} & {} \quad \times d \beta \bigg \{{{\mathcal {N}}}_i \frac{{{\mathcal {F}}}_{\alpha \beta }^{4} (\alpha +\beta -1)^{2} (5 m_Q^{2}(\alpha +\beta -1)-3{{\mathcal {F}}}_{\alpha \beta })}{3\times 5\times 2^{19} \alpha ^{4} \beta ^{4}}\nonumber \\{} & {} \qquad +\frac{{{\mathcal {F}}}_{\alpha \beta }^{3}m_Q^{2}(\alpha +\beta -1)^{4}}{5\times 3^2\times 2^{21} \alpha ^{6} \beta ^{6}}\left( 4 m_Q^{2}\left( \alpha ^{4}+\alpha ^{3}(\beta -1)\right. \right. \nonumber \\{} & {} \qquad \left. \left. +\alpha \beta ^{3}+(\beta -1) \beta ^{3}\right) \right. -{{\mathcal {F}}}_{\alpha \beta }\left( 2 \alpha ^{3}\right. \nonumber \\{} & {} \qquad \left. -3 \alpha ^{2}(\beta -1)-3 \alpha \beta ^{2}+\beta ^{2}(3+2 \beta )) \right) \bigg \}, \end{aligned}$$

(A2)

$$\begin{aligned}{} & {} \rho ^{\langle G^3 \rangle }(s) =\frac{-\langle G^3 \rangle }{5\times 3^2\times 2^{23}\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} \frac{d \alpha }{ \alpha ^6} \nonumber \\{} & {} \qquad \times \int _{\beta _{min}}^{1-\alpha } \frac{d \beta }{ \beta ^6} {{\mathcal {F}}}_{\alpha \beta }^2 (\alpha +\beta -1)^4 \bigg \{5 {{\mathcal {F}}}_{\alpha \beta }^2(\alpha ^3+\beta ^3)\nonumber \\{} & {} \quad +8 {{\mathcal {F}}}_{\alpha \beta } m_Q^2 (2 \alpha ^4 -3\alpha ^3(\beta -1)-3\alpha \beta ^3 \nonumber \\{} & {} \quad +3\beta ^3+2\beta ^4)-24 m_Q^4 (\alpha +\beta -1)(\alpha ^4+\beta ^4)\bigg \}, \end{aligned}$$

(A3)

$$\begin{aligned}{} & {} \rho ^{\langle {\bar{q}} q\rangle ^4}=\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \frac{{{\mathcal {H}}}_\alpha }{48 \pi ^{2}}\langle {\bar{q}} q\rangle ^4, \end{aligned}$$

(A4)

where $M_B$ is the Borel parameter introduced by the Borel transformation, $Q = c$ or b, and the factor ${{\mathcal {N}}}_i$ has the following definition: ${{\mathcal {N}}}_A=1$ and ${{\mathcal {N}}}_B=0$. Here, we also have the following definitions:

$$\begin{aligned} {{\mathcal {F}}}_{\alpha \beta }= & {} (\alpha + \beta ) m_Q^2 - \alpha \beta s , {{\mathcal {H}}}_\alpha = m_Q^2 - \alpha (1 - \alpha ) s , \end{aligned}$$

(A5)

$$\begin{aligned} \alpha _{min}= & {} \left( 1 - \sqrt{1 - 4 m_Q^2/s} \right) / 2, ,\nonumber \\ \alpha _{max}= & {} \left( 1 + \sqrt{1 - 4 m_Q^2 / s} \right) / 2 , \end{aligned}$$

(A6)

$$\begin{aligned} \beta _{min}= & {} \alpha m_Q^2 /(s \alpha - m_Q^2). \end{aligned}$$

(A7)

1.2 2. The spectral densities for $0^{--}$ baryonium state in Eqs. (3) and (4)

$$\begin{aligned} \rho ^{pert} (s)= & {} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \int ^{1 - \alpha }_{\beta _{min}} d \beta \nonumber \\{} & {} \times \frac{{{\mathcal {F}}}^6_{\alpha \beta } (\alpha + \beta - 1)^4 \Big (7 m_Q^2 (\alpha + \beta - 1)+ 10{{\mathcal {F}}}_{\alpha \beta } \Big ) }{3\times 7 \times 5^2 \times 2^{18}\pi ^{10} \alpha ^6 \beta ^6}, \end{aligned}$$

(A8)

$$\begin{aligned} \rho ^{\langle G^2 \rangle }(s)= & {} \frac{\langle g_s^2 G^2\rangle }{\pi ^{10}} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \bigg \{- \frac{{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha + \beta -1)^2}{3\times 5\times 2^{21}\alpha ^5\beta ^5}\Big (5m_Q^2(\alpha +\beta -1)^2\nonumber \\{} & {} \times (\alpha +\beta )+4{{\mathcal {F}}}_{\alpha \beta } \big (\alpha ^2+\beta (\beta -1)-\alpha (4\beta +1)\big ) \Big )\nonumber \\{} & {} +\frac{{{\mathcal {F}}}_{\alpha \beta }^3 m_Q^2 (\alpha + \beta -1)^4 }{3^2\times 5\times 2^{20}\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg ( 4 m_Q^2 \Big (\alpha ^4 +\alpha ^3(\beta -1)\nonumber \\{} & {} +\alpha \beta ^3+\beta ^3(\beta -1)\Big )+{{\mathcal {F}}}_{\alpha \beta }\Big (13 \alpha ^3 +3 \alpha ^2 (\beta -1) \nonumber \\{} & {} +3\alpha \beta ^2 +\beta ^2(13\beta -3) \Big ) \bigg ) \bigg \}, \end{aligned}$$

(A9)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle ^2}(s)= & {} {{\mathcal {N}}}_i \frac{\langle {\bar{q}} q \rangle ^2}{2^{10}\pi ^6} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \frac{2 m_Q^2 {{\mathcal {F}}}_{\alpha \beta }^3 (\alpha +\beta -1)^2+{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha +\beta - 1)}{\alpha ^3\beta ^3}, \end{aligned}$$

(A10)

$$\begin{aligned} \rho ^{\langle G^3 \rangle }(s)= & {} \frac{\langle G^3 \rangle }{5\times 3^2\times 2^{21}\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{ {{\mathcal {F}}}_{\alpha \beta }^2 (\alpha +\beta -1)^4}{\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg ( 5(\alpha ^3+\beta ^3) {{\mathcal {F}}}_{\alpha \beta }^2\nonumber \\{} & {} +4 {{\mathcal {F}}}_{\alpha \beta } m_Q^2 \Big ( 13\alpha ^4+3\alpha ^3(\beta -1)+3\alpha \beta ^3\nonumber \\{} & {} +\beta ^3(13\beta -3) \Big )+12 m_Q^4 \Big (\alpha ^5+\alpha ^4(\beta -1)\nonumber \\{} & {} +\alpha \beta ^4+\beta ^4(\beta -1) \Big )\bigg ), \end{aligned}$$

(A11)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }(s)= & {} \frac{-{{\mathcal {N}}}_i\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }{2^9\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{{{\mathcal {F}}}_{\alpha \beta }^{3}+3 m_Q^{2}{{\mathcal {F}}}_{\alpha \beta }^2(\alpha +\beta -1)}{ \alpha ^{2} \beta ^{2}}, \end{aligned}$$

(A12)

$$\begin{aligned} \rho ^{\langle {\bar{q}} G q \rangle ^2}= & {} \frac{{{\mathcal {N}}}_i\langle {\bar{q}} G q \rangle ^2}{2^{11}\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \bigg \{ \frac{3{{\mathcal {H}}}_\alpha ^{2} }{2 (1-\alpha ) \alpha }\nonumber \\{} & {} +\int _{\beta _{min}}^{1-\alpha } d \beta \frac{3{{\mathcal {F}}}_{\alpha \beta } m_Q^{2} }{ \alpha \beta }\bigg \} , \end{aligned}$$

(A13)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q\rangle ^4}= & {} \int _{\alpha _{min}}^{\alpha _{max}} d \alpha \frac{{{\mathcal {H}}}_\alpha -m_Q^2}{24 \pi ^{2}}\langle {\bar{q}} q\rangle ^4, \end{aligned}$$

(A14)

where ${{\mathcal {N}}}_C=1$ and ${{\mathcal {N}}}_D=-1$.

1.3 3. The spectral densities for $0^{--}$ baryonium state in Eqs. (5) and (6)

$$\begin{aligned} \rho ^{pert} (s)= & {} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \int ^{1 - \alpha }_{\beta _{min}} d \beta \nonumber \\{} & {} \times \frac{{{\mathcal {F}}}^6_{\alpha \beta } (\alpha + \beta - 1)^4 \Big ( 10{{\mathcal {F}}}_{\alpha \beta }-7 m_Q^2 (\alpha + \beta - 1) \Big ) }{3\times 7 \times 5^2 \times 2^{18}\pi ^{10} \alpha ^6 \beta ^6}, \end{aligned}$$

(A15)

$$\begin{aligned} \rho ^{\langle G^2 \rangle }(s)= & {} \frac{\langle g_s^2 G^2\rangle }{\pi ^{10}} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \bigg \{ \frac{{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha + \beta -1)^2}{3\times 5\times 2^{21}\alpha ^5\beta ^5}\Big (5m_Q^2(\alpha +\beta -1)^2\nonumber \\{} & {} \times (\alpha +\beta )-4{{\mathcal {F}}}_{\alpha \beta } \big (\alpha ^2+\beta (\beta -1)-\alpha (4\beta +1)\big ) \Big )\nonumber \\{} & {} +\frac{{{\mathcal {F}}}_{\alpha \beta }^3 m_Q^2 (\alpha + \beta -1)^4 }{3^2\times 5\times 2^{20}\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg ( -4 m_Q^2 \Big (\alpha ^4 +\alpha ^3(\beta -1) +\alpha \beta ^3+\beta ^3(\beta -1)\Big )\nonumber \\{} & {} +{{\mathcal {F}}}_{\alpha \beta }\Big (7 \alpha ^3 -3 \alpha ^2 (\beta -1) \nonumber \\{} & {} -3\alpha \beta ^2 +\beta ^2(7\beta +3) \Big ) \bigg ) \bigg \}, \end{aligned}$$

(A16)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle ^2}(s)= & {} - \frac{\langle {\bar{q}} q \rangle ^2}{2^{10}\pi ^6} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \frac{2 m_Q^2 {{\mathcal {F}}}_{\alpha \beta }^3 (\alpha +\beta -1)^2+{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha +\beta - 1)}{3\alpha ^3\beta ^3}, \end{aligned}$$

(A17)

$$\begin{aligned} \rho ^{\langle G^3 \rangle }(s)= & {} \frac{\langle G^3 \rangle }{5\times 3^2\times 2^{21}\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{ {{\mathcal {F}}}_{\alpha \beta }^2 (\alpha +\beta -1)^4}{\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg ( 5(\alpha ^3+\beta ^3) {{\mathcal {F}}}_{\alpha \beta }^2\nonumber \\{} & {} +4 {{\mathcal {F}}}_{\alpha \beta } m_Q^2 \Big ( 13\alpha ^4+3\alpha ^3(\beta -1)+3\alpha \beta ^3\nonumber \\{} & {} +\beta ^3(13\beta -3) \Big )+12 m_Q^4 \Big (\alpha ^5+\alpha ^4(\beta -1)\nonumber \\{} & {} +\alpha \beta ^4+\beta ^4(\beta -1) \Big )\bigg ), \end{aligned}$$

(A18)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }(s)= & {} \frac{-{{\mathcal {N}}}_i\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }{2^9\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{{{\mathcal {F}}}_{\alpha \beta }^{3}+3 m_Q^{2}{{\mathcal {F}}}_{\alpha \beta }^2(\alpha +\beta -1)}{ \alpha ^{2} \beta ^{2}}, \end{aligned}$$

(A19)

$$\begin{aligned} \rho ^{\langle {\bar{q}} G q \rangle ^2}= & {} \frac{{{\mathcal {N}}}_i\langle {\bar{q}} G q \rangle ^2}{2^{11}\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \bigg \{ \frac{3{{\mathcal {H}}}_\alpha ^{2} }{2 (1-\alpha ) \alpha }\nonumber \\{} & {} +\int _{\beta _{min}}^{1-\alpha } d \beta \frac{3{{\mathcal {F}}}_{\alpha \beta } m_Q^{2} }{ \alpha \beta }\bigg \} , \end{aligned}$$

(A20)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q\rangle ^4}= & {} \int _{\alpha _{min}}^{\alpha _{max}} d \alpha \frac{{{\mathcal {H}}}_\alpha -m_Q^2}{24 \pi ^{2}}\langle {\bar{q}} q\rangle ^4. \end{aligned}$$

(A21)

1.4 4. The spectral densities for $0^{+-}$ baryonium state in Eqs. (7) and (8)

$$\begin{aligned} \rho ^{pert}(s)= & {} \int _{\alpha _{min}}^{\alpha _{max}} d \alpha \int _{\beta _{min}}^{1-\alpha } d \beta \nonumber \\{} & {} \times \bigg \{\frac{{{\mathcal {F}}}_{\alpha \beta }^{6}(\alpha +\beta -1)^{4}(5{{\mathcal {F}}}_{\alpha \beta }+7m_Q^2(\alpha +\beta -1)}{3\times 7\times 5^2\times 2^{19}\pi ^{10} \alpha ^{6} \beta ^{6}}\bigg \}, \end{aligned}$$

(A22)

$$\begin{aligned} \rho ^{\langle G^2 \rangle }(s)= & {} \frac{\langle G^2 \rangle }{\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \bigg \{{{\mathcal {N}}}_i \frac{{{\mathcal {F}}}_{\alpha \beta }^{4} (\alpha +\beta -1)^{2} (5 m_Q^{2}(\alpha +\beta -1)+3{{\mathcal {F}}}_{\alpha \beta })}{3\times 5\times 2^{19} \alpha ^{4} \beta ^{4}}\nonumber \\{} & {} +\frac{{{\mathcal {F}}}_{\alpha \beta }^{3}m_Q^{2}(\alpha +\beta -1)^{4}}{5\times 3^2\times 2^{21} \alpha ^{6} \beta ^{6}} \Big (4 m_Q^{2}\Big (\alpha ^{4}\nonumber \\{} & {} +\alpha ^{3}(\beta -1)+\alpha \beta ^{3}+(\beta -1) \beta ^{3}\Big ) \nonumber \\{} & {} +{{\mathcal {F}}}_{\alpha \beta }\left( 2 \alpha ^{3}-3 \alpha ^{2}(\beta -1)-3 \alpha \beta ^{2}+\beta ^{2}(3+2 \beta )) \right) \bigg \}, \end{aligned}$$

(A23)

$$\begin{aligned} \rho ^{\langle G^3 \rangle }(s)= & {} \frac{\langle G^3 \rangle }{5\times 3^2\times 2^{23}\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} \frac{d \alpha }{ \alpha ^6} \int _{\beta _{min}}^{1-\alpha } \frac{d \beta }{ \beta ^6} {{\mathcal {F}}}_{\alpha \beta }^2 (\alpha +\beta -1)^4 \nonumber \\{} & {} \times \bigg \{5 {{\mathcal {F}}}_{\alpha \beta }^2(\alpha ^3+\beta ^3)+8 {{\mathcal {F}}}_{\alpha \beta } m_Q^2 (8 \alpha ^4 +3\alpha ^3(\beta -1)+3\alpha \beta ^3 \nonumber \\{} & {} -3\beta ^3+8\beta ^4)+24 \alpha m_Q^4 (\alpha +\beta -1)(\alpha ^4+\beta ^4)\bigg \}, \end{aligned}$$

(A24)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q\rangle ^4}= & {} -\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \frac{3{{\mathcal {H}}}_\alpha -2m_Q^2}{144 \pi ^{2}}\langle {\bar{q}} q\rangle ^4, \end{aligned}$$

(A25)

where ${{\mathcal {N}}}_A=1$ and ${{\mathcal {N}}}_B=0$.

1.5 5. The spectral densities for $0^{+-}$ baryonium state in Eqs. (9) and (10)

$$\begin{aligned} \rho ^{pert} (s)= & {} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \frac{{{\mathcal {F}}}^6_{\alpha \beta } (\alpha + \beta - 1)^4 \Big (7 m_Q^2 (\alpha + \beta - 1)+ 10{{\mathcal {F}}}_{\alpha \beta } \Big ) }{3\times 7 \times 5^2 \times 2^{18}\pi ^{10} \alpha ^6 \beta ^6}, \end{aligned}$$

(A26)

$$\begin{aligned} \rho ^{\langle G^2 \rangle }(s)= & {} \frac{\langle g_s^2 G^2\rangle }{\pi ^{10}} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \bigg \{- \frac{{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha + \beta -1)^2}{3\times 5\times 2^{21}\alpha ^5\beta ^5}\Big (5m_Q^2(\alpha +\beta -1)^2\nonumber \\{} & {} \times (\alpha +\beta )+4{{\mathcal {F}}}_{\alpha \beta } \big (\alpha ^2+\beta (\beta -1)-\alpha (4\beta +1)\big ) \Big ) \nonumber \\{} & {} +\frac{{{\mathcal {F}}}_{\alpha \beta }^3 m_Q^2 (\alpha + \beta -1)^4 }{3^2\times 5\times 2^{20}\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg ( 4 m_Q^2 \Big (\alpha ^4 +\alpha ^3(\beta -1) +\alpha \beta ^3+\beta ^3(\beta -1)\Big )\nonumber \\{} & {} +{{\mathcal {F}}}_{\alpha \beta }\Big (13 \alpha ^3 +3 \alpha ^2 (\beta -1) \nonumber \\{} & {} +3\alpha \beta ^2 +\beta ^2(13\beta -3) \Big ) \bigg ) \bigg \}, \end{aligned}$$

(A27)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle ^2}(s)= & {} \frac{{{\mathcal {N}}}_i \langle {\bar{q}} q \rangle ^2}{3\times 2^{10}\pi ^6} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \frac{2 m_Q^2 {{\mathcal {F}}}_{\alpha \beta }^3 (\alpha +\beta -1)^2-{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha +\beta - 1)}{\alpha ^3\beta ^3}, \end{aligned}$$

(A28)

$$\begin{aligned} \rho ^{\langle G^3 \rangle }(s)= & {} \frac{\langle G^3 \rangle }{5\times 3^2\times 2^{21}\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{ {{\mathcal {F}}}_{\alpha \beta }^2 (\alpha +\beta -1)^4}{\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg ( 5(\alpha ^3+\beta ^3) {{\mathcal {F}}}_{\alpha \beta }^2+4 {{\mathcal {F}}}_{\alpha \beta } m_Q^2 \Big ( 7\alpha ^4-3\alpha ^3(\beta -1)-3\alpha \beta ^3\nonumber \\{} & {} +\beta ^3(7\beta +3) \Big )-12 m_Q^4 \Big (\alpha ^5+\alpha ^4(\beta -1)+\alpha \beta ^4+\beta ^4(\beta -1) \Big )\bigg ), \end{aligned}$$

(A29)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }(s)= & {} \frac{\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }{3\times 2^9\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{{{\mathcal {F}}}_{\alpha \beta }^{3}+3 m_Q^{2}{{\mathcal {F}}}_{\alpha \beta }^2(\alpha +\beta -1)}{ \alpha ^{2} \beta ^{2}}, \end{aligned}$$

(A30)

$$\begin{aligned} \rho ^{\langle {\bar{q}} G q \rangle ^2}= & {} \frac{\langle {\bar{q}} G q \rangle ^2}{2^{11}\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \bigg \{ \frac{{{\mathcal {H}}}_\alpha ^{2} }{2 (\alpha -1) \alpha }-\int _{\beta _{min}}^{1-\alpha } d \beta \frac{{{\mathcal {F}}}_{\alpha \beta } m_Q^{2} }{ \alpha \beta }\bigg \} , \end{aligned}$$

(A31)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q\rangle ^4}= & {} -\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \frac{m_Q^2+3{{\mathcal {H}}}_\alpha }{72 \pi ^{2}}\langle {\bar{q}} q\rangle ^4, \end{aligned}$$

(A32)

where ${{\mathcal {N}}}_C=1$ and ${{\mathcal {N}}}_D=-3$.

1.6 6. The spectral densities for $0^{+-}$ baryonium state in Eqs. (11) and (12)

$$\begin{aligned} \rho ^{pert} (s)= & {} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \frac{{{\mathcal {F}}}^6_{\alpha \beta } (\alpha + \beta - 1)^4 \Big (10{{\mathcal {F}}}_{\alpha \beta }-7 m_Q^2 (\alpha + \beta - 1) \Big ) }{3\times 7 \times 5^2 \times 2^{18}\pi ^{10} \alpha ^6 \beta ^6}, \end{aligned}$$

(A33)

$$\begin{aligned} \rho ^{\langle G^2 \rangle }(s)= & {} \frac{\langle g_s^2 G^2\rangle }{\pi ^{10}} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \bigg \{ \frac{{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha + \beta -1)^2}{3\times 5\times 2^{21}\alpha ^5\beta ^5}\Big (5m_Q^2(\alpha +\beta -1)^2\nonumber \\{} & {} \times (\alpha +\beta )-4{{\mathcal {F}}}_{\alpha \beta } \big (\alpha ^2+\beta (\beta -1)-\alpha (4\beta +1)\big ) \Big )\nonumber \\{} & {} +\frac{{{\mathcal {F}}}_{\alpha \beta }^3 m_Q^2 (\alpha + \beta -1)^4 }{3^2\times 5\times 2^{20}\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg (- 4 m_Q^2 \Big (\alpha ^4 +\alpha ^3(\beta -1) +\alpha \beta ^3+\beta ^3(\beta -1)\Big )\nonumber \\{} & {} +{{\mathcal {F}}}_{\alpha \beta }\Big (7 \alpha ^3 -3 \alpha ^2 (\beta -1) \nonumber \\{} & {} -3\alpha \beta ^2 +\beta ^2(7\beta +3) \Big ) \bigg ) \bigg \}, \end{aligned}$$

(A34)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle ^2}(s)= & {} \frac{{{\mathcal {N}}}_i \langle {\bar{q}} q \rangle ^2}{2^{10}\pi ^6} \int ^{\alpha _{max}}_{\alpha _{min}} d \alpha \nonumber \\{} & {} \times \int ^{1 - \alpha }_{\beta _{min}} d \beta \frac{ {{{\mathcal {F}}}_{\alpha \beta }^4 (\alpha +\beta - 1)-2 m_Q^2{\mathcal {F}}}_{\alpha \beta }^3 (\alpha +\beta -1)^2}{\alpha ^3\beta ^3}, \end{aligned}$$

(A35)

$$\begin{aligned} \rho ^{\langle G^3 \rangle }(s)= & {} \frac{\langle G^3 \rangle }{5\times 3^2\times 2^{21}\pi ^{10}}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{ {{\mathcal {F}}}_{\alpha \beta }^2 (\alpha +\beta -1)^4}{\alpha ^6\beta ^6} \nonumber \\{} & {} \times \bigg ( 5(\alpha ^3+\beta ^3) {{\mathcal {F}}}_{\alpha \beta }^2\nonumber \\{} & {} +4 {{\mathcal {F}}}_{\alpha \beta } m_Q^2 \Big ( 7\alpha ^4-3\alpha ^3(\beta -1)-3\alpha \beta ^3\nonumber \\{} & {} +\beta ^3(7\beta +3) \Big )-12 m_Q^4 \Big (\alpha ^5+\alpha ^4(\beta -1)\nonumber \\{} & {} +\alpha \beta ^4+\beta ^4(\beta -1) \Big )\bigg ), \end{aligned}$$

(A36)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }(s)= & {} \frac{{{\mathcal {N}}}_i\langle {\bar{q}} q \rangle \langle {\bar{q}} G q \rangle }{2^9\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \nonumber \\{} & {} \times \int _{\beta _{min}}^{1-\alpha } d \beta \frac{-{{\mathcal {F}}}_{\alpha \beta }^{3}+3 m_Q^{2}{{\mathcal {F}}}_{\alpha \beta }^2(\alpha +\beta -1)}{ \alpha ^{2} \beta ^{2}}, \end{aligned}$$

(A37)

$$\begin{aligned} \rho ^{\langle {\bar{q}} G q \rangle ^2}= & {} \frac{-3{{\mathcal {N}}}_i\langle {\bar{q}} G q \rangle ^2}{2^{11}\pi ^6}\int _{\alpha _{min}}^{\alpha _{max}} d \alpha \bigg \{ \frac{{{\mathcal {H}}}_\alpha ^{2} }{2 (\alpha -1) \alpha }\nonumber \\{} & {} +\int _{\beta _{min}}^{1-\alpha } d \beta \frac{{{\mathcal {F}}}_{\alpha \beta } m_Q^{2} }{ \alpha \beta }\bigg \} , \end{aligned}$$

(A38)

$$\begin{aligned} \rho ^{\langle {\bar{q}} q\rangle ^4}= & {} \int _{\alpha _{min}}^{\alpha _{max}} d \alpha \frac{m_Q^2+3{{\mathcal {H}}}_\alpha }{72 \pi ^{2}}\langle {\bar{q}} q\rangle ^4, \end{aligned}$$

(A39)

where ${{\mathcal {N}}}_C=1$ and ${{\mathcal {N}}}_D=-1$.