1 Introduction

The theory of gravity, as postulated by Albert Einstein in 1915, posits that the gravitational interaction arises from the curvature of spacetime caused by the existence of heavy objects. The theory of general relativity, which is mathematically well defined, has been effectively tested under both weak [1] and strong field [2,3,4] conditions. However, with the resolution of experiments and observations currently employed to test general relativity [5, 6], it is possible to contemplate modifications and alternative theories to advance the development of gravitational field theory. The Einstein action is modified by including the KR field [7], which is represented as a self-interacting second-rank antisymmetric tensor. The KR modification may be associated with heterotic string theory [8] and can be understood as stimulating closed strings. The Lorentz symmetry may be violated due to the nonminimal connection between the tensor field and Ricci scalar [9]. The KR field exhibits various characteristics, including deriving the third-rank antisymmetric tensor. This tensor may be understood as a cause of spacetime torsion, as stated in reference [10]. The KR field has been extensively investigated in gravity and particle physics [11,12,13,14]. The strong similarity between the KR field and spacetime torsion confirms that Einstein’s theory of gravity, coupled with the KR field as a source, is comparable to a modified theory of gravity that includes spacetime torsion.

By the conclusion of the 1960s, it was widely accepted that BHs were highly compact celestial bodies possessing a powerful gravitational force surrounded by an imaginary one-way barrier called the event horizon. This event horizon permits matter and radiation to enter the BH but prevents their escape, concealing a singularity. A BH may be fully characterized by three classical parameters: mass, charge, and angular momentum. A Schwarzschild BH is characterized by the absence of both angular momentum and charge. Kerr BHs are rotating BHs; if they are also charged, they are called Kerr-Newman BHs [15]. In the exterior region of a rotating BH, the reference frame would also rotate, resulting in a phenomenon known as frame dragging. The region is known as the ergosphere of the BH [16]. Roger Penrose contributed to advancing the understanding of BHs in the 1960s. He demonstrated that BHs would inevitably arise due to the theory of general relativity [17, 18]. In 1969, he presented an approach to extracting energy from a BH [19]. The Penrose process occurs inside the ergosphere when a particle falling from infinity undergoes a division into two separate particles. One particle would be drawn into the BH, but the other particle would escape with greater mass energy than it originally had. As a result, the rotational energy of the BH would be transferred to the motion of this particle outside the ergosphere [20]. A BH’s energy extraction process would not be infinite, but it would slow it down and reduce its mass.

The study of particle dynamics surrounding BHs is very significant and may be used to examine the physical characteristics of BHs. This area of research has been extensively researched by several scholars [21,22,23,24,25,26,27,28,29]. The capture of massless and massive particles by parameterized BHs is studied in Refs. [30,31,32,33]. The orbital and epicyclic frequencies in axially symmetric and stationary spacetime are considered in Refs. [34,35,36,37,38]. Analytical and numerical solutions for the geodesic problem can be achieved. They can transmit crucial information and reveal the abundant creation of underlying geometric patterns. Hagihara [39] pioneered the development of an analytical solution for geodesics. Grunau and Kagramanova [40] investigated the RN spacetime and examined analytical solutions for test particles that are magnetically and electrically charged. Chandrasekhar [41] was one of the early researchers who studied the paths followed by objects in the curved spacetime around Schwarzschild, Reissner–Nordström, and Kerr BHs. Circular geodesics may also be used to comprehend and investigate the quasinormal modes of BHs, as discussed by Nollert [42]. The integration and separation of electrically charged particle motion can be achieved easily, as has been extensively studied by several researchers [43,44,45,46,47,48,49,50,51,52,53]. The study examines the collision of particles inside the ergoregion and the movement of particles in the braneworld Kerr and Kerr–Newman–Kasuya BHs [54,55,56,57]. Recent research on RN spacetime has shown that the external magnetic field and electric charge exhibit properties similar to the magnetic charge of a BH [58,59,60,61,62].

In this study, we use the signature \((-,+,+,+)\) to represent the spacetime and utilize the geometrized unit system where \(G_\textrm{N}= c = 1\). The Latin indices range from 1 to 3, whereas the Greek indices go from 0 to 3. In the next part, we shall review the spacetime geometry of BH. We will extensively analyze the equations of motion for charged particles in an ionized BH environment and the concept of the innermost stable circular orbit (ISCO) for charged particles. Section 3 will mostly examine the Penrose process in the KR BH. Section 4 will mainly investigate the interaction of electrically charged particles near the event horizon of the BH. In the final section, concluding remarks are provided, discussing all the results and findings obtained.

2 Charged BHs in KR gravity

The action for the theory, which includes gravity non-minimally coupled to a self-interacting KR field, is given by [63]

$$\begin{aligned} S= & {} \frac{1}{2}\int d^4 x\sqrt{-g}\Big [R-2\varLambda -\frac{1}{6}H^{\mu \nu \rho }H_{\mu \nu \rho }\nonumber \\{} & {} -V(B^{\mu \nu }B_{\mu \nu }\pm b^2) + \xi _2 B^{\rho \mu }{B^{{\nu }}}_\mu R_{\rho \nu }\nonumber \\{} & {} +\xi _3B^{\mu \nu }B_{\mu \nu }+R\mathcal {L}_M\Big ] \end{aligned}$$
(1)

where \(\varLambda \) is the cosmological constant, \(\xi _{2,3}\) are the non-minimal coupling constants between gravity and the KR field, \(8\pi {G} = 1\). \(B_{\mu \nu }\) is a second-rank antisymmetric tensor field \(B_{\mu \nu }=-B_{\nu \mu }\). \(H_{\mu \nu \rho } \equiv \partial _{[\mu }B_{\nu \rho ]}\) is field strength. The field strength is invariant under the gauge invariance \(B_{\mu \nu } \rightarrow B_{\mu \nu } + \partial _{[\mu }\varGamma _{\nu ]}\).

The potential \(V(B^{\mu \nu }B_{\mu \nu }\pm b^2)\) depends on \(B^{\mu \nu }B_{\mu \nu }\) to maintain the theory invariance under the local Lorentz transformation of the observer. As the cosmological constant \(\varLambda \) is counted separately, the potential is set to zero at its minimum. The minimum is determined by the condition \(B^{\mu \nu }B_{\mu \nu }=\pm {b}^{2}\), with the sign ± chosen such that \(b^{2}\) is a positive constant.

Now, we focus on deriving the equation of motion of electrically charged particles around the static-charged BHs. The charged BH solution with spherically symmetric spacetime geometry is obtained in Ref. [63] using through spherical coordinates, (\(x^{\alpha }=\{t,r,\theta ,\phi \}\)) in the following form,

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{1}{f(r)}dr^2+r^2\left( d\theta ^2+\sin ^2\theta d\phi ^2\right) , \end{aligned}$$
(2)

where the radial functions f(r) is given by [63],

$$\begin{aligned} f(r)=\frac{1}{1-l}-\frac{2M}{r} +\frac{ Q^2}{r^2(1-l)^2}. \end{aligned}$$
(3)

Here, M represents the total mass of the BH, whereas Q represents its electric charge. Classical gravitational measurements undertaken in the Solar System have shown that the dimensionless parameter l, which represents the Lorentz-violating impact generated by the non-zero vacuum expectation value of the KR field, must have a very small value [64]. When \(l=0\), it will converge to the standard RN-like metric. One can solve \( f(r)= 0\) to get the boundary of a BH. We have

$$\begin{aligned} \frac{r_h}{1-l}=M\pm \sqrt{M^2-\frac{Q^2}{(1-l)^2}}. \end{aligned}$$
(4)
Fig. 1
figure 1

Radius of the event and Cauchy horizons of the charged BH in KR gravity as a function of the BH charge and the KR parameter

Full size image

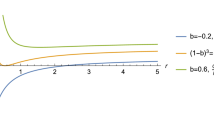
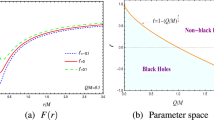
The dependencies of horizon radii of the spacetime (2) from the BH charge and the parameter l are shown in Fig. 1. The positive (negative) values of l cause the event horizon to decrease (increase). In addition, the extreme value of the BH increases and decreases in the negative and positive cases of the parameter l. One can now test the characteristics of the extremes in the BH charge and the minimum in the event horizon radius using the condition \(f(r)=f'(r)=0\), and we have

$$\begin{aligned} r_{min}=1-l, Q^2_{extr}=(1-l)^3. \end{aligned}$$
(5)
Fig. 2
figure 2

The dependence of extreme values of the BH charge Q from l

Full size image

In Fig. 2, we show relationships between extreme BH charge and the KR parameter. The light-blue shaded area implies the value of Q and l in which the spacetime (3) has an event horizon that belongs to a BH. In the values of Q and l out of the shaded area, the BH turns into an object without an event horizon.

It also is worth noting that it has been assumed that the vector and the dilaton fields depend on the radial coordinate only [65], in the following form:

$$\begin{aligned} A_t(r)=\frac{Q}{(1-l)r}. \end{aligned}$$
(6)

2.1 Equations of motion of charged particles in ionized BH environment

Here, we investigate the dynamics of charged particles along circular orbits around an electrically BH in KR gravity using the Hamilton–Jacobi equation,

$$\begin{aligned} g^{\mu \nu }\Big (\frac{\partial {{\mathcal {S}}}}{\partial x^{\mu }}-q A_{\mu }\Big )\Big (\frac{\partial {{\mathcal {S}}}}{\partial x^{\nu }}-q A_{\nu }\Big )=-m^2. \end{aligned}$$
(7)

The action for charged particles at a constant plane (where \(\theta =const\) and \(\dot{\theta }=0\)) can be described by the following separable form,

$$\begin{aligned} {{\mathcal {S}}}=-Et+L \phi +{{\mathcal {S}}}_r+{{\mathcal {S}}}_\theta , \end{aligned}$$
(8)

that allows for separating the variables in the Hamilton-Jacobi equation. Here, E and L are the energy and angular momentum of the charged particle at infinity, respectively. \({{\mathcal {S}}}_r\) and \({{\mathcal {S}}}_\theta \) are the radial and angular functions. After some calculations, we obtain the following:

$$\begin{aligned}{} & {} - \frac{1}{f(r)} \left( E - q A_t\right) ^2 + f(r) \left( \frac{\partial {{\mathcal {S}}}_r}{\partial r}\right) ^2 + \frac{1}{r^2} \left( \frac{\partial {{\mathcal {S}}}_\theta }{\partial \theta }\right) ^2 \nonumber \\{} & {} \quad +\frac{L^2}{r^2 \sin ^2 \theta } = - m^2. \end{aligned}$$
(9)

One can notice that Eq. (6) is fully separable into radial and angular parts,

$$\begin{aligned}{} & {} \bigg (\frac{\partial {{\mathcal {S}}}_\theta }{\partial \theta }\bigg )^2 + \frac{L^2}{ \sin ^2 \theta } = K, \end{aligned}$$
(10)
$$\begin{aligned}{} & {} f(r) \bigg (\frac{\partial {{\mathcal {S}}}_r}{\partial r}\bigg )^2 - \frac{1}{f(r)} \bigg (E - q A_t\bigg )^2 + \frac{K}{r^2} = -m^2, \end{aligned}$$
(11)

where K is the Carter separability constant.

In our further calculation, we use the notations,

$$\begin{aligned} \mathcal {E} = \frac{E}{m},\quad \mathcal {L} = \frac{L}{m},\quad \kappa = \frac{K}{m^2}. \end{aligned}$$
(12)

We now calculate the components of momentum as, \(p^\alpha = g^{\alpha \beta } (\frac{\partial S}{\partial x^\beta })\), and \(p^\alpha = m \dot{x}^\alpha = m (dx^\alpha /d\lambda )\), where the affine parameter is \(\lambda \). Using all the above considerations, we express the equation of motion as follows,

$$\begin{aligned} \dot{t}= & {} \frac{1}{f(r)} \big (\mathcal {E} - q A_t\big ), \end{aligned}$$
(13)
$$\begin{aligned} \dot{\phi }= & {} \frac{\mathcal {L}}{r^2 \sin ^2\theta },\end{aligned}$$
(14)
$$\begin{aligned} \dot{r}^2= & {} \big (\mathcal {E} - q A_t\big )^2 - f(r) \bigg (1 + \frac{\kappa }{r^2}\bigg ),\end{aligned}$$
(15)
$$\begin{aligned} \dot{\theta }^2= & {} \frac{1}{r^4} \bigg (\kappa - \frac{\mathcal {L}^2}{\sin ^2\theta }\bigg ) . \end{aligned}$$
(16)

Restricting the particle’s motion to a constant \(\theta \) plane and \(\dot{\theta }=0\), and the Carter constant reads \(\kappa = {{\mathcal {L}}}^2/\sin ^2\theta \).

Now, we can rewrite Eq. (9) as

$$\begin{aligned} g_{rr}\dot{r}^2=\left[ {{\mathcal {E}}}-V^+_\textrm{eff}(r)\right] \left[ {{\mathcal {E}}}-V^-_\textrm{eff}(r)\right] , \end{aligned}$$

where, the effective potential (\( V_\textrm{eff}\)) of the radial motion of the charged particles reads in the equatorial plane (\(\theta =\pi /2\)) as,

$$\begin{aligned} V^{\pm }_\textrm{eff} = qA_t \pm \sqrt{f(r) \bigg (1 + \frac{\mathcal {L}^2}{r^2}\bigg )}. \end{aligned}$$
(17)

The effective potential consists of two parts: Coulomb and gravitational interaction. It has symmetry according to the sign of q, the specific charge of the charged particles. We use \(V^{+}_\textrm{eff}\) as the effective potential throughout the paper unless otherwise stated.

Fig. 3
figure 3

Radial dependence of the effective potential for positive and negative charges of BH in KR gravity

Full size image

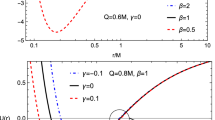
Figure 3 shows the radial dependence of the effective potential of positive (top panel) and negative (bottom panel) charged particles for the dimensionless parameter l of the charged KR BH and comparison with RN BH and Schwarzschild BH. For cases with a positively charged particle, the positive dimensionless parameter l contributes the maximum effective potential value compared to RN BH and Schwarzschild BH, and the negative dimensionless parameter l gives the minimum effective potential value, while the distance where the effective potential takes maximum shifts towards the BH. A negatively charged particle’s effective potential value decreases due to negative Coloumb interaction. Also, at \(l<-0.15\), there is no minimum effective potential.

The orbit circularity of test-charged particles orbiting around charged black holes in KR can be investigated assuming the conditions \(V_{\textrm{eff}}={{\mathcal {E}}}\) and \(V_{\textrm{eff}}'=0\), where the prime’ represents the partial derivative with respect to r. Using these conditions, we determine the angular momentum of a charged particle in circular orbits.

Following the above conditions, we obtain the expression for the angular momentum for circular motion that satisfies the conditions

$$\begin{aligned} \mathcal {L}^2_\pm= & {} \frac{1}{[2r f(r) - r^2 f'(r)]^2} \bigg \{ 2r^5 f(r) f'(r) \pm 2 q r^4 f(r) A_t' \nonumber \\{} & {} \times \, \sqrt{(q r^2 A_t')^2-2r[r^2 f'(r) - 2r f(r)]} \nonumber \\{} & {} +\,r^6 \bigg [2q^2 f(r) A_{t}'^{2} - f'(r)^2\bigg ] \bigg \}, \end{aligned}$$
(18)

the ± sign in Eq. (18) represents the symmetry with the charge coupling parameter sign qQ. The specific angular momentum can only be real if the term under the square root is positive. This eventually implies,

$$\begin{aligned} (qr^2 A'_t)^2\ge 2r[r^2 f'(r) - 2r f(r)]. \end{aligned}$$
(19)
Fig. 4
figure 4

Radial dependence of specific angular momentum for positive and negative charges of BH in KR gravity

Full size image

We study the radial dependence of the specific angular momentum for differently charged dimensionless parameters of l for KR BH for the motion of positive and negatively charged particles. We also compared the results with those of the RN BH and Schwarzschild BH. The top panel of Fig. 4 considers the case for a positively charged particle. It shows that positive l reduces the minimum in angular momentum and shifts the orbit where the minimum occurs toward the charged KR BH. It is observed from the comparisons that, in the Schwarzschild case, the angular momentum has a greater value than the KR BH and RN BH. In the case of negatively charged particle motion (see bottom panel), the influence of l on the minimum of the angular momentum behaves similarly to the previous case. However, compared to other BHs, the Schwarzschild BH has minimal angular momentum.

The energy of the test particle at circular orbits can be found using the expression:

$$\begin{aligned} {{\mathcal {E}}}_{\pm } = qA_t \pm \sqrt{f(r) \bigg (1 + \frac{\mathcal {L}^2_\pm }{r^2}\bigg )}. \end{aligned}$$
(20)
Fig. 5
figure 5

The relationships between the energy \({{\mathcal {E}}}\) and angular momentum \(\mathcal {L}\) (bottom panel) and radial dependence of energy (top panel) of the charged particles at circular orbits around the KR BH

Full size image

In the bottom panel of Fig. 5, we present the relation between the angular momentum and energy of the charged particles corresponding to the circular orbits around the charged KR BH with a positive charge of the particle for different values of the dimensionless parameter l. It is noticed that with an increase in l, the angular momentum of stable circular orbits decreases, and the particle’s energy, on the contrary, increases. The top panel shows the radial energy dependence for different parameter values of l. Increasing the parameter l contributes to an increase in energy.

2.2 Innermost stable circular orbit (ISCO) of charged particle

We now examine the ISCO of the charged particle around the chosen charged BHs. It is now well established that, for stable circular orbits, the following conditions must be obeyed,

$$\begin{aligned} V_\textrm{eff}=\mathcal {E},\quad \partial _r V_\textrm{eff}=0,\quad \partial _{rr}V_\textrm{eff}=0, \end{aligned}$$
(21)

here \(\partial _{rr}\) refers to the second order derivative w.r.t. r. The first-order derivative represents the stationary points, and the last condition corresponds to the minimum of the potential.

Fig. 6
figure 6

Dependence of ISCO radius on BH charge Q for different values of dimensionless parameters l and particle charges for KR BH

Full size image

Figure 6 shows the dependence of the ISCO radius on the charge of the KR BH for positively (upper left) and negatively (lower left) charged test particles, as well as in neutral particles (upper right). The graphs show that the ISCO radius, in all cases, increases with negative values of the parameter l and decreases with increasing parameter l (the dependence is the same for all particles). It is also observed that the minimum value in ISCO radius slightly increases (decreases) in the case of \(l<0\) (\(l>0\)). Moreover, the maximum in the KR BH charge is greater than 1 at \(l<0\). However, it is less than 1 when \(l>0\). The bottom-right panel shows the dependence of the ISCO radius on the parameter l for neutral, positively, and negatively charged particles. This panel shows that the particle charge makes a small contribution to the values of the ISCO radius.

Figure 7 shows charged particles’ angular momentum and energy corresponding to their ISCO for various charged particles and the parameter l.The top left panel shows the dependence of the angular momentum of charged particles in the ISCO on the parameter l. We see that a negative value of the particle charge gives a larger value of angular momentum, and an increase in the parameter l reduces the value of the angular momentum of the ISCO. When considering the dependence of the angular momentum on the ISCO radius of a charged particle (top right panel), it can be seen that an increase in the ISCO radius increases the angular momentum of the particles at the ISCO. Increasing the dimensionless parameter l increases the energy of the charged particle in the ISCO (bottom left panel). The relationship between angular momentum and energy in the ISCO of the charged particles (bottom right panel) for various values of the particle charge, for the fixed values of BH charge and l, at l \(\in \) (-0.3 \(\div \) 0.3).

3 Electric Penrose process

The electric Penrose process is an intriguing method of extracting energy from BHs, that expands upon the conventional Penrose process to include BHs that are electrically charged [66, 67]. Within this framework, the process entails the degradation of particles close to the event horizon of an electrically charged BH. The Electric Penrose Process involves fragmenting an entering particle into two separate pieces inside the BH’s ergosphere. The BH draws one piece into itself, while the other fragment, carrying more energy than the initial particle, moves away towards infinity. The electric charge of the BH facilitates the energy extraction process by influencing the behavior of the involved particles. If a BH has a small electric charge, extracting energy from it may improve greatly compared to a BH that is not charged [68, 69].

Fig. 7
figure 7

ISCO parameters as a function of the dimensionless parameter l for charged particles in KR gravity. In all cases, we fix \(Q=0.5M\)

Full size image

Researchers have recently explored this phenomenon in various scenarios, such as positioning a reflective mirror outside the event horizon to capture particles and facilitate multiple interactions. This results in forming a “BH bomb,” which refers to the possibility of uncontrollable energy extraction [70]. Furthermore, studies have examined how the electric charge of a BH affects the effective potential and the innermost stable circular orbits (ISCO) of charged particles. These investigations have shown that even minor electric charges may replicate the effects of angular momentum [71]. These findings on the electric Penrose process not only improve our understanding of BH thermodynamics and astrophysical jets, but also emphasize the complex relationship between electric charge and energy dynamics in very intense gravitational fields. Researchers have developed several Penrose processes, including magnetic and electric Penrose processes, for different BH models [72,73,74]. This section examines the electric Penrose process, which entails the interaction between charged particles and charged BHs in the context of KR gravity theory.

3.1 Angular velocity, conservation laws and maximum energy of ionized particle

Consider a test particle that decays on the equatorial plane and is characterized by the four-velocity, \(v^{\alpha }=v^t(1,dr/dt,0,d\phi /dt)\). Let us define the radial velocity dr/dt as \(\mu \) and angular velocity \(d\phi /dt\) as \(\zeta \). By imposing the normalization condition \(v^{\alpha }v_{\alpha }=-\lambda \), the expression for the angular velocity becomes

$$\begin{aligned} (v^t)^2\left[ \frac{\mu ^2}{f(r)}-f(r)+\zeta ^2 r^2\right] =-\lambda , \end{aligned}$$
(22)

here \(\lambda \) represents massless (\(=0\)) and massive (\(=1\)) particle. Now, we will deduce an expression describing the angular velocity of the decayed particles as seen by a static observer positioned at an infinite distance. For this, we have

$$\begin{aligned} \zeta =\pm \frac{1}{v^t r}\sqrt{(v^t)^2\left[ f(r)-\frac{\mu ^2}{f(r)}\right] -\lambda }. \end{aligned}$$
(23)

The range of potential values for \(\zeta \) is limited by,

$$\begin{aligned} \zeta _{-}\le \zeta \le \zeta _+,\quad \zeta _{\pm }=\pm \sqrt{\frac{f(r)}{r^2}}, \end{aligned}$$
(24)

that corresponds to the Keplerian orbits.

Subsequently, we examine a situation wherein a charged particle approaches a charged BH from infinity in KR gravity theory and undergoes breakdown into two charged particles in the equatorial plane close to the event horizon. We consider that the conservation rules of energy, momentum, and charge are satisfied by the decay process.

$$\begin{aligned} E_1= & {} E_2 + E_3,\quad L_1 = L_2 + L_3,\quad q_1 = q_2 + q_3, \end{aligned}$$
(25)
$$\begin{aligned} m_1\dot{r_1}= & {} m_2\dot{r_2} + m_3\dot{r_3},\quad m_1 \ge m_2 + m_3, \end{aligned}$$
(26)

Using the above equations, we have

$$\begin{aligned} m_1{v_1^\phi } = m_2{v_2^\phi } + m_3{v_3^\phi }, \end{aligned}$$
(27)

where \(v^\phi =\zeta {v^t}=\zeta {e}/r^2\), \(e_i=(E_i+q_i A_{t})/m_i\) for \(i = 1,2,3\) denotes the number of particles, The Eq. (27) can be expressed as follows,

$$\begin{aligned} \zeta _1m_1e_1=\zeta _2m_2e_2+\zeta _3m_3e_3. \end{aligned}$$
(28)

The angular velocity of the ith particle, denoted by \(\zeta _i=d\phi _i/dt\), is determined by Eq. (23) and is subject to the limitations specified in Eq. (24). The determination of the energy of a particle [75], such as \(E_3\), is possible by solving Eq. (28). We have

$$\begin{aligned} E_3=\frac{\zeta _1-\zeta _2}{\zeta _3-\zeta _2}(E_1 + q_1A_t)-q_3A_t. \end{aligned}$$
(29)

Lastly, to optimize the energy of the escape energy of the accelerated ionized particle from the BH, we assume that particle 1 is neutral (i.e., \(q_1 = 0\)) and starts from infinity with an initial energy equal to its mass energy at rest \(E_1 = m_1\) (\(\mathcal {E} = 1\)). In this particular scenario, the angular velocity (23) of the particles may be expressed straightforwardly as [76],

$$\begin{aligned} \zeta _1^2= & {} \frac{f(r)(1-f(r))}{r^2},\nonumber \\ \zeta _2= & {} \zeta _{-}, \nonumber \\ \zeta _3= & {} \zeta _{+}. \end{aligned}$$
(30)

It is believed that particle 3 departs with more energy than the first decaying particle. To determine the highest energy value of particle 3, we optimize the formula \((\zeta _1-\zeta _2)/(\zeta _3-\zeta _2)\). This is accomplished by adjusting the angular momentum of components \(\zeta _i\) to their highest values. Subsequently, we may readily determine the utmost energy of particle 3.

$$\begin{aligned} \frac{\zeta _1-\zeta _2}{\zeta _3-\zeta _2}=\frac{1}{2}+\frac{\sqrt{1-f(r_{i})}}{2}. \end{aligned}$$
(31)

Here, \(r_{i}\) represents the radius for the ionized particle. Ultimately, we will formulate the equation representing the ionized particle energy in the specified format as [77].

$$\begin{aligned} E_3=\Big [\frac{1}{2}+\frac{\sqrt{1-f(r_{i})}}{2}\Big ] (E_1 + q_1 A_t) - q_3 A_t. \end{aligned}$$
(32)

For \(q_2 = -q_3\) and \(q_1=0\) we have

$$\begin{aligned} E_3=\left( \frac{1}{2}+\frac{\sqrt{1-f(r_{i})}}{2}\right) E_1 - q_3 A_t, \end{aligned}$$
(33)

this simplifies to

$$\begin{aligned} \frac{E_3}{E_1}=\left( \frac{1}{2}+\frac{\sqrt{1-f(r_{i})}}{2}\right) - \frac{q_3 A_t}{E_1}. \end{aligned}$$
(34)

The energy of the ionized particle is at its maximum when \(q_3\) and Q have the same sign, as the time component of the electromagnetic four potential is dependent on Q. This corresponds to the anticipated outcome, in which the charged particle experiences acceleration due to the coulomb repulsion force operating between the BH and the particle. Determining the ionized to neutral particle energies ratio is valuable for assessing the acceleration process’s effectiveness. By formulating the BH mass and speed of light explicitly and replacing them with \(q_3 = Z e\) and \(m_1 \approx A{m_n}\), where Z and A denote the atomic and mass quantities, e represents an elementary charge, and \(m_n\) signifies the nucleon mass, we arrive at the following result:

$$\begin{aligned} \frac{E_3}{E_1}=\left( \frac{1}{2}+\frac{\sqrt{1-f(r_{i})}}{2}\right) -\frac{Z e A_t}{A{m_n}c^2}. \end{aligned}$$
(35)

We may compute the final equation for \(E_3/E_1\) by directly expressing the BH mass and the speed of light in terms of the time component of the electromagnetic four potential and metric functions. This equation is intricate and challenging to solve.

Fig. 8
figure 8

Ratio of energies plotted against the BH charge Q for different values of spacetime parameters. \(l=0\) shows the standard RN BH solution (lower panel) results

Full size image

Consequently, we visually represent its reliance on the BH parameters in Fig. 8. Figure 8 (upper plot) displays the efficiency of the acceleration mechanism, which is the ratio of the energies of ionized and infalling particles with \(Z/A = 1\). The figure shows this efficiency at different ionization sites as a function of the BH’s charge per solar mass. The efficiency significantly declines as the charge of the BH increases. Moreover, it declines as the distance between the BH and the ionization point increases. Similar behavior can be observed in the case of varying parameter l (lower plot).

4 Collisions of charged particles near the event horizon of the KR BHs

The study by Banados in [78] first examined the acceleration of particles colliding near spinning Kerr BHs. It was shown that the center of mass energy of colliding particles might become infinite in an extremely revolving Kerr BH. Various authors have studied the effects of external magnetic fields on the acceleration of charged particles near BHs in different gravity models and situations. These investigations may be found in references such as [79,80,81,82,83]. Research has shown that the energy extraction process is more efficient in head-on collisions.

Our current objective is to examine several instances of charged particle collisions in the equatorial plane under various conditions from the observer’s perspective in motion. Two conditions permit the determination of the critical value of the angular momentum: (i)\(\dot{r}=0\) and (ii) \(d\dot{r}/dr=0\).

Figure 9 illustrates this. A negative radial velocity results from an increase in the angular momentum. The particles cannot approach the central object from that value due to large centrifugal forces.

Consequently, we examined the permissible values of the angular momentum to determine the critical values. The dependency of the critical angular momentum for different values of the BH’s parameters and particle charge is shown in Fig. 10. The upper panels show the relationship between the critical angular momentum and the parameter (q) between different values of the parameter l (on the left) and Q (on the right). The top left panel illustrates that as the value of l increases, the allowable range of angular momentum declines, and there is a linear relation with the q parameter. Similarly, the bottom panel depicts the critical angular momentum with a BH Q charge, considering different parameters l (on the left) and q (on the right). Similar behavior can be observed for both cases.

The general expression for the energy of the center of mass can be expressed as [84, 85]

$$\begin{aligned} \{E_{c},0,0,0\}=m_1u_1^{\mu }+m_2u_2^{\mu }, \end{aligned}$$
(36)

here, the variables \(u_1^{\alpha }\) and \(u_2^{\beta }\) represent the four-velocity of the two particles involved in the collision, with masses \(m_1\) and \(m_2\) correspondingly. It is straightforward to compute the square of the center of mass energy, as described in Eq. (36), and get the result.

$$\begin{aligned} E^2_{c}= & {} m_1^2+m_2^2-2m_1m_2g_{\mu \nu } u^{\mu }u^{\nu }, \end{aligned}$$
(37)
$$\begin{aligned} \frac{E^2_{c}}{m_1m_2}= & {} \frac{m_1}{m_2}+\frac{m_2}{m_1}-2g_{\mu \nu } u^{\mu }_1u^{\nu }_2. \end{aligned}$$
(38)

If the masses of the colliding particles are denoted as \(m_1=A m\) and \(m_2=B m\). Then we have

$$\begin{aligned} \frac{E^2_{cm}}{m^2c^4}=A^2+B^2-2g_{\mu \nu } u^{\mu }_1u^{\nu }_2. \end{aligned}$$
(39)

Now, we will investigate the collision of particles with identical initial energies and masses (\(E_1=E_2=m\)). We shall examine the acceleration of charged particles near a KR BH by applying the standard equation for the center of mass energy of two colliding particles of equal mass. As a consequence, the equation for the center-of-mass energy becomes.

$$\begin{aligned} {{\mathcal {E}}}_\textrm{c}^2=\frac{E^2_\textrm{c}}{4m^2 c^4}=1-g_{\alpha \beta }u_1^{\alpha }u_2^{\beta }. \end{aligned}$$
(40)

Consequently, by using the constituents of the four-velocity, the ultimate equation for the energy of the center of mass in the equatorial plane (where \(\theta =\pi /2\)) may be expressed as follows:

$$\begin{aligned} {{\mathcal {E}}}^2_\textrm{c}= & {} 1+\frac{1}{f(r)}\left( {{\mathcal {E}}}_1-q_1 A_t \right) \left( {{\mathcal {E}}}_2-q_2 A_t \right) \nonumber \\{} & {} +\frac{\mathcal {L}_1{{\mathcal {L}}}_2}{r^2} +\frac{1}{f(r)}\sqrt{\left( {{\mathcal {E}}}_1-q_1 A_t\right) ^2-f(r)\Big (1+\frac{{{\mathcal {L}}}_1^2}{r^2}\Big )}\nonumber \\{} & {} \times \sqrt{\left( {{\mathcal {E}}}_2-q_2 A_t\right) ^2-f(r)\Big (1+\frac{{{\mathcal {L}}}_2^2}{r^2}\Big )}. \end{aligned}$$
(41)
Fig. 9
figure 9

Radial dependence of the square of radial velocity for different values of angular momentum of the particle

Full size image
Fig. 10
figure 10

Dependence of the critical angular momentum on q (top panels) and Q (bottom panels) for different values of the BH and particle parameters

Full size image
Fig. 11
figure 11

Radial dependence of CME for parameters l (top row), L (middle row), and Q (bottom row) for different values of spacetime parameters

Full size image

In Fig. 11, we have illustrated the radial profiles of the center-of-mass energies of charged particles that collide with varying signatures. The graphs depict three distinct scenarios in which the particle charges remain constant: (i) a positive-positive configuration (left column), (ii) a positive-negative configuration (middle column), and (iii) a negative-negative configuration (right column). The graph representing the energy of the center of mass shows a downward trend as the value of the parameter l (upper row) and the angular momentum L (middle row) increase. Note that the energy increases most significantly in the collision of negatively charged particles compared to the other two cases. Moreover, we can observe the same behavior of the center-of-mass energy by varying the parameter Q (lower row).

5 Conclusions

A better understanding way to probe the spacetime geometry of BHs in modified/alternative gravity theories is through investigations of test particle dynamics and energetic processes. For this, in the present work, we aimed to explore spacetime geometry around charged BHs in KR gravity obtained in Ref. [63]. We have started our studies by investigating the KR parameter on the event horizon radius and the extreme value of the BH charge. Then, we derived the equations of motion of charged particles and analyzed the effective potential for circular orbits. It is shown that in the positively charged particle cases, the positive (negative) parameter l contributes (decreases) to the maximum effective potential compared to the RN BH and Schwarzschild BH cases. Meanwhile, the distance where the effective potential takes maximum shifts towards the central BH. A negatively charged particle’s effective potential value decreases due to negative Coloumb interaction. Also, at \(l>-0.15\), there is no minimum effective potential.

We have analyzed the radial profiles of the specific angular momentum and energy of particles corresponding to circular orbits for different l and the charge of KR BH in the cases of positively and negatively charged particles. It is obtained that in \(l>0\) cases, the minimum of the angular momentum decreases, and the orbit where the minimum occurs shifts towards the BH.

The ISCO for charged particles around charged BHs in KR gravity has also been studied. The effect of the BH charge and the KR parameter on the ISCO radius have been analyzed, and it found that the ISCO increases in the presence of \(l>0\) and decreases for \(l<0\). It is also observed that the minimum value in ISCO radius slightly increases (decreases) in the case of \(l<0\) (\(l>0\)). Moreover, the maximum charge of the KR BH is greater than 1 at \(l<0\). However, it is less than 1 when \(l>0\).

There are two types of Penrose process: in the classical Penrose process, a particle decays by two in the ergoregion of a rotating BH, so one of them falls into the BH, and another part goes out with increased energy. In this scenario, the energy efficiency is proportional to the BH spin. In the magnetic Penrose process, the particle decays into two charged particles, and the magnetic field causes the escaping charged particles to increase in time due to the induced electric field. We have also explored the electric Penrose process around the charged BH in KR gravity. Finally, we have considered collisions of charged particles. In doing this, we have first investigated the critical angular momentum of charged particles, providing their collision. The critical value decreases (increases) due to the presence of attractive (repulsive) Coulomb interaction and also decreases (increases) at \(l>0\) (\(l<0\)) cases. We have also studied collisions between positively charged particles and those with positive and negative electric charges. Our findings have shown that a negative value of l causes an increase in the center of mass-energy. The energy is slightly greater in the negatively charged particle collisions when \(Q>0\).