The anatomy of $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ distributions

Abstract

The excellent experimental prospects to measure the invisible mass spectrum of the $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ decay opens a new path to test generalised quark–neutrino interactions with flavour changing $s\rightarrow d$ transitions and as such to novel probes of Physics beyond the Standard Model. Such signals can be a consequence of new lepton-number violating or lepton-number conserving interactions, with their interpretations depending on the Majorana versus Dirac nature of the neutrinos. Furthermore, the possible existence of new massive sterile neutrinos can be tested via their distinctive imprints in the invariant mass spectrum. Within the model-independent framework of the weak effective theory at dimension-six, we study the New Physics effects of Majorana and Dirac neutrinos on the differential distribution of $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ allowing for lepton-number violating interactions and potential new sterile neutrinos. We determine the current and expected future sensitivity on the corresponding $\Delta S=1$ neutral-current Wilson coefficients using the distribution measured by the NA62 collaboration and accounting for expected improvements based on the HIKE experiment. We present single-operator fits and also determine correlations among different type of operators. Even though we focus on $s\rightarrow d\nu \nu$ transitions, the operator bases for Majorana and Dirac and the classification of lepton-number-violating/conserving interactions is applicable also for the study of $b\rightarrow s/d\nu \nu$ and $c\rightarrow u\nu \nu$ transitions relevant in current phenomenology.

1 Introduction

The branching ratio of the rare $K^+ \rightarrow \pi ^+ \nu \bar{\nu }$ decay is currently being measured at ${\mathcal {O}}(35\%)$ accuracy at the NA62 experiment [1, 2], while improved upper limits for the corresponding neutral decay mode, $K_L\rightarrow \pi ^0\nu {\bar{\nu }}$, are provided from the KOTO experiment [3, 4]. Each event of the charged decay mode has a so-called missing neutrino mass squared, which leads to a decay spectrum that can be measured with increased experimental statistics. The existing measurements already play an important role in current phenomenology. They are sensitive to modifications of the Standard Model (SM) that are generated via effective operators at ${\mathcal {O}}(100 \,\text {TeV})$ and also constrain feebly interacting particles that can provide new final states contributing to the invisible mass spectrum [5,6,7,8].

This exceptional sensitivity to New Physics (NP) is due to the high suppression of these decay rates in the SM and the precision reached in their theory predictions. Both rare $K \rightarrow \pi \nu \bar{\nu }$ decay modes are flavour-changing neutral-current (FCNC) processes, and as such loop-induced in the SM and additionally suppressed by products of off-diagonal Cabibbo–Kobayashi–Maskawa Matrix (CKM) elements. The fact that the neutrinos are only interacting with the weak sector of the SM results in a hard Glashow–Iliopoulos–Maiani (GIM) mechanism [9], which highly suppresses light-quark contributions. This generates a severe CKM suppression in the SM and facilitates a precise theory prediction, where, to a very good approximation, only a single local charged-current operator contributes below the charm scale. The evaluation of the operator matrix element and its Wilson coefficient through an ongoing theoretical effort has lead to a theory uncertainty of only $3\%$ and $1\%$ for the charged and neutral decay modes, respectively [10,11,12,13,14,15]. This uncertainty includes the contribution of higher-dimensional operators and light-quark contributions, which have been estimated in chiral perturbation theory [16] and can be evaluated on the lattice [17, 18]. The overall uncertainty in the current SM prediction for the charged decay mode [19] is still dominated by the CKM input parameters, yet current input values [20] result in an overall theory uncertainty of $\simeq 6\%$. This has to be compared with the expected uncertainty of $15\%$ and $5\%$ for the branching-ratio measurement at the end of NA62 and after the first phase of the proposed HIKE experiment [21], respectively. These improved measurements, together with the ones for the $K_L$ mode [22], will result in even tighter probes of potential NP scenarios with flavour violation in the $s-d$ sector.

The present work is motivated by the fact that a more detailed measurement of the missing-mass spectrum will become available at the end of the NA62 experiment and during the run of HIKE. In anticipation of this data, we will consider scenarios with heavy NP, including the possibility of additional massive sterile neutrinos, that can impact the missing-mass spectrum of $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$. We discuss their effect in a mostly model-independent manner by considering all the relevant weak effective theory operators up to dimension six for both Majorana and Dirac neutrinos that generate a $s \rightarrow d \nu \bar{\nu }$ transition at tree level. Here, non-zero contributions of (pseudo-)scalar and tensor operators can distinctively modify the invariant mass spectrum from the SM-like spectrum generated by vector and axial-vector operators. These generalised neutrino interactions have recently received considerable attention in the context of neutrino oscillations [23,24,25,26] and correlations to charged current decays have for example been studied in Ref. [27] in the context of the Standard Model Effective Field Theory (SMEFT). In this work, we will study their impact on the FCNC golden Kaon decay. The impact of sterile neutrinos on (axial-)vector type operators has been studied in Ref. [28]. Working with the two, physically distinct scenarios of Dirac and Majorana neutrinos allows us to incorporate mass effects of sterile neutrinos for all operators, which would not be possible in a basis where neutrinos are represented as Weyl fields [29]. This distinction has the benefit of providing a transparent interpretation of a possible NP signal in terms of lepton-number conserving (LNC) or lepton-number violating (LNV) NP interactions. Dirac and Majorana weak effective theories originate from different UV theories, e.g., in the SMEFT only three Majorana neutrinos are present in the weak effective theory. Instead three Dirac neutrinos in WET can originate from a LNC extension of SMEFT with at least three additional Weyl ($\nu$SMEFT). Constraints on scalar-type SMEFT operators on the $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ distributions, but only using the total branching ratio, were also studied in Refs. [30, 31] for the case of three massless Majorana neutrinos. Generalised neutrino interactions and their impact in $K\rightarrow \pi \nu \nu$ have been discussed in the context of the Weak Effective Theory (WET) in Ref. [32]. The bounds are set employing the total branching ratio for three massless Majorana neutrinos. However, an analysis that utilizes the measured distribution in the lab frame and also incorporates the experimental cuts and backgrounds is hitherto missing.

With the current work we close this gap: we classify all WET operators for both massive Majorana and Dirac neutrinos that can impact $K\rightarrow \pi \nu \nu$ at dimension-six, we derive the differential decay rate in the lab frame of NA62, i.e., as a function of the pion momentum and the invariant neutrino mass, and provide for the first time a fit that incorporate the full experimental information currently available both for massless or massive Majorana or Dirac neutrinos as well as additional sterile neutrinos. We perform a full statistical analysis of the sensitivity to probe the different NP Wilson coefficients accounting for the single-event sensitivity and available background information at the current and future-planned experimental setup. The WET setup allows us to separate the discussion of LNC and LNV-type of interactions by imposing LNC on the Dirac basis. The resulting constraints on dimension-six WET Wilson coefficients have a direct translation to SMEFT or the parameter space of concrete UV completions of the SM. If the overarching theory is assumed to be SMEFT, which does not contain more than the three Weyl neutrinos, neutrinos are necessarily Majorana. In this case, scalar and tensor operators contributing to $K\rightarrow \pi \nu \nu$ are necessarily LNV and thus dimension-seven. If more degrees of freedom are included ($\nu$SMEFT) the corresponding operators can be dimension-six. Both cases match to the dimension-six Wilson coefficient studied in the current work.

The paper is organised as follows. In Sect. 2 we classify the weak effective theory relevant for $q\rightarrow q'\nu \nu$ FCNCs and count the independent Wilson coefficients that contribute to flavour-changing quark into neutrino decays. In the following Sect. 3 we provide the relevant decay rates for zero neutrino masses, and explain our statistical treatment including the treatment of theoretical uncertainties. In the next Sect. 4 we provide the current and expected future sensitivities for the cases in which a single operator contributes (single-operator fits) as well as the correlated constraints on pairs of different operators. After the conclusion we also provide in Appendix A further formulae for the double differential distributions ${\textrm{d}}^2{\textrm{Br}}/{\textrm{d}}q^2{\textrm{d}}k^2$.

2 Weak effective theories for $K \rightarrow \pi \nu \bar{\nu }$

The focus of this work is to study the possible impact of heavy New Physics (NP) scenarios in the distributions of $K^+ \rightarrow \pi ^+\nu \bar{\nu }$. The goal is to also include the possibility that the existence of additional heavy neutrinos could provide further final states with missing energy. To this end, it is useful and necessary to distinguish the conceptually different cases of having Majorana-type versus Dirac-type neutrino masses for the three light neutrinos or the possible extra sterile neutrinos. Both Majorana and Dirac operator basis have a direct correspondence in terms of the basis written using chiral (or equivalently two-component Weyl) fermion fields [29]. However, unless the dimension-four mass terms are specified, the chiral basis with more than three neutrino fields leaves the question of neutrino masses unspecified: The additional right-handed neutrinos can combine with the left-handed ones to give Dirac masses without the need for lepton-number-violating mass terms. Alternatively, the observed neutrinos are Majorana particles in which case their masses originate from Majorana mass terms and the extra, sterile neutrinos have their own independent mass.

We will thus separately discuss two cases:

• (i) Three or more Majorana neutrinos with dimension-six interactions with $s-d$ FCNC interactions that can include lepton-number violation.

• (ii) Dirac neutrinos with dimension-six interactions with $s-d$ FCNC interactions that conserve lepton-number.

Each of these cases will have a distinct low-energy effective theory. We thus decompose the effective Lagrangian relevant for quark-FCNC transitions with neutrinos, i.e., $d_i\rightarrow d_j\nu \nu$ or $u_i\rightarrow u_j\nu \nu$, at the dimension-six level as

$$\begin{aligned} {\mathscr {L}}^{\nu \text {WET}}_{q\rightarrow q'\nu \nu }\Big |_{\nu \text {-type}}= & {} {\mathscr {L}}^{(4)}_{\text {QCD}} + {\mathscr {L}}^{(4)}_{\nu }\Big |_{\nu \text {-type}} \nonumber \\{} & {} +{\mathscr {L}}^{(6),\text {SM}}_{q\rightarrow q'\nu \nu } + {\mathscr {L}}^{(6)}_{q\rightarrow q'\nu \nu }\Big |_{\nu \text {-type}}, \end{aligned}$$

(1)

where the superscript “(n)” indicates the mass-dimension of the operators and $\nu \text {-type}$ labels the case of Majorana or Dirac neutrinos. Apart from the usual dimension-four QCD Lagrangian involving quarks and gluons, the kinetic and mass term of the neutrinos reads

(2)

where $a\ge 3$ runs over the different neutrino flavours, and $\nu _{Ma}$ and $\nu _{Da}$ denote four-component Majorana and Dirac fields, respectively. Equation (2) is already written in terms of mass-eigenstates for the neutrinos fields. Throughout this work we work in the mass-eigenstate basis for the neutrinos. This choice of basis implicitly also fixes the basis for the definition of the dimension-six Wilson coefficients.

In the present work we focus on $K\rightarrow \pi \nu \nu$. In this case the SM induces a single dimension-six operator below the charm mass [19, 33]. For the $s\rightarrow d$ transition the SM contribution can be written both in terms of Majorana or Dirac fields

$$\begin{aligned} {\mathscr {L}}^{(6),\text {SM}}_{s\rightarrow d\nu \nu }= & {} \sum \limits _{\begin{array}{c} a,b = \left\{ 1,2,3 \right\} \end{array}} \left\{ \begin{array}{c} C^{A,\,L, \,\text {SM}}_{ab 21}~ O^{A, \, L }_{ab 21}\\ C^{V,\,LL,\,\text {SM}}_{ab 21}~ O^{V, \, LL}_{ab 21} \end{array}\right\} +\text {h.c.}\nonumber \\= & {} -\frac{4G_F}{\sqrt{2}}\frac{\alpha }{2\pi s^2_w} \sum \limits _{\begin{array}{c} \ell = \left\{ e,\mu ,\tau \right\} \\ a,b =\left\{ 1,2,3 \right\} \end{array}} U_{\ell a}^{*} U_{\ell b} \left( \lambda _c X^\ell + \lambda _tX_t \right) \nonumber \\{} & {} \times \left\{ \begin{array}{l} - O^{A, \, L}_{ab 21} \\ O^{V, \, LL}_{ab 21} \end{array}\right\} +\text {h.c.}, \end{aligned}$$

(3)

where $G_F$ denotes the Fermi constant, $\alpha$ is the fine-structure constant, and $s_w$ is the sine of the weak-mixing angle. The elements of the quark-mixing matrix are comprised in the parameters $\lambda _i = V^*_{is}V_{id}$, while $U_{\ell a}$ is the Pontecorvo–Maki–Nakagawa–Sakata (PMNS) matrix. The short-distance physics is described by the loop functions $X_t$ and $X^\ell$, where the dependence on the $\tau$ mass introduces a small off-diagonal neutrino coupling, which we ignore in the following. The operator induced in the SM case reads

$$\begin{aligned} O^{A, \, L}_{ab ij}&= \frac{1}{2}({\overline{\nu }}_{Ma}\gamma _\mu \gamma _5\, \, \nu _{Mb})({\overline{d}}_i\,\gamma ^\mu \,P_L\, {d}_j ) ,\nonumber \\ O^{V, \,LL}_{\,ab ij}&=({\overline{\nu }}_{Da}\gamma _\mu \, P_L\, \nu _{Db})({\overline{d}}_i\,\gamma ^\mu \,P_L\, {d}_j ). \end{aligned}$$

(4)

in the Majorana and Dirac case, respectively. We have intentionally decided to directly separate the SM from NP contributions in Eq. (1) in order to present the constraints on the NP effects more transparently.

We discuss the dimension-six operator basis for the Majorana and Dirac case in Sects. 2.1 and 2.2, respectively. There are further possibilities, e.g., mixed Dirac–Majorana cases or Dirac masses with lepton-number-violating dimension-six interactions, but as we shall see the main effects can be illustrated within the two aforementioned cases. The basis of operators can be equally well be adjusted by trivial flavour renaming to study $b\rightarrow s/d\nu \nu$ or $c\rightarrow u\nu \nu$ transitions relevant, e.g, for $B\rightarrow K\nu \nu$ or rare charm FCNC with decays to neutrinos.

2.1 Majorana-$\nu$ EFT with lepton-number violation

The dimension-six effective Lagrangian relevant for $d_i\rightarrow d_j \nu \nu$ transitions for the case in which all neutrinos are Majorana particles, can be written as

$$\begin{aligned}&{\mathscr {L}}^{(6)}_{d\rightarrow d^\prime \nu \nu }\Big \vert _{\text {Majorana}} \nonumber \\&\quad = \sum _{\begin{array}{c} I= \left\{ V,A \right\} \\ \tau =\left\{ L,R\right\} \end{array}} \sum _{f} C^{I,\tau }_f O^{I,\tau }_f+\Biggl (\sum _{\begin{array}{c} I= \left\{ S,P,T \right\} \end{array}} \sum _{f} C^{I,L}_f O^{I,L}_f + \text {h.c.} \Biggr ), \end{aligned}$$

(5)

where I denotes the type of interaction, $I = \{V,A,S,P,T\}$, which stand for V for vector-, A for axial-vector-, S for scalar-, P for pseudoscalar-, and T for tensor-type interactions. $\tau =\{L,R\}$ indicates the chirality of the quark currents, and f comprises all neutrino and quark flavour indices, $f=\{abij\}$. The full set of independent operators read

$$\begin{aligned} O^{V, \, L}_{ab ij}&=\frac{1}{2}({\overline{\nu }}_{Ma}\gamma _\mu \, \nu _{Mb})({\overline{d}}_i\,\gamma ^\mu \,P_L\, {d}_j ),\nonumber \\ O^{V, \, R}_{ab ij}&=\frac{1}{2}({\overline{\nu }}_{Ma}\gamma _\mu \, \nu _{Mb})({\overline{d}}_i\,\gamma ^\mu \,P_R\, {d}_j ),\nonumber \\ O^{A, \, L}_{ab ij}&=\tfrac{1}{2} ({\overline{\nu }}_{Ma}\gamma _\mu \gamma _5\, \, \nu _{Mb})({\overline{d}}_i\,\gamma ^\mu \,P_L\, {d}_j ) ,\nonumber \\ O^{A, \, R}_{ab ij}&=\frac{1}{2}({\overline{\nu }}_{Ma}\gamma _\mu \,\gamma _5\, \nu _{Mb})({\overline{d}}_i\,\gamma ^\mu \,P_R\, {d}_j ),\nonumber \\ O^{S, \, L}_{ab ij}&=\frac{1}{2}({\overline{\nu }}_{Ma} \, \nu _{Mb})({\overline{d}}_i \,P_L\, {d}_j ),\nonumber \\ O^{P, \, L}_{ab ij}&=\frac{1}{2}({\overline{\nu }}_{Ma} \,i\gamma _5\, \nu _{Mb})({\overline{d}}_i \,P_L\, {d}_j ),\nonumber \\ O^{T, \, L}_{ab ij}&=\frac{1}{2}({\overline{\nu }}_{Ma} \,\sigma _{\mu \nu }\,\nu _{Mb})({\overline{d}}_i \,\sigma ^{\mu \nu }\,P_L\, {d}_j ), \end{aligned}$$

(6)

with $i,j=1,2,3$.

Apart from the quark-flavour dependence, the operators $O^{V/A, \, L/R}$ are self-adjoint after considering standard relations for four-component Majorana fields [34]. This is not the case for the $O^{S/P/T, \, L}$ operators. We ensure the hermiticity of the Lagrangian by imposing additional conditions on the flavour structure of the Wilson coefficients. The hermiticity condition on the Wilson coefficients $C^{V/A,\,L/R}_f$ is

$$\begin{aligned} C^{V/A,\,L/R}_{abij} = \left( C^{V/A,\,L/R}_{baji} \right) ^*. \end{aligned}$$

(7)

Additionally, there are the further conditions originating from standard relations specific to four-component Majorana fields [34]

$$\begin{aligned} C^{I,\,\tau }_{\,ab ij} = \eta \, C^{I,\,\tau }_{\,ba ij} \quad \text {where} \ \eta = {\left\{ \begin{array}{ll} +1, &{} \text {for} \ I = A,\,S,\,P\\ -1, &{} \text {for} \ I = V,\, T . \end{array}\right. } \end{aligned}$$

(8)

The SM contribution to $K^+\rightarrow \pi ^+\nu \nu$ (${{\bar{s}}}\rightarrow {{\bar{d}}}\nu \nu$ transition) in the Majorana case is induced by the $O^{A, \, L}_{ab ij}$ operators with $i=1$ (down quark) and $j=2$ (strange quark), as discussed in Eq. (3). Note that imposing lepton-number conservation forbids the neutrinos mass-term but also the $O^{S/P/T, \, L}$ interactions, which are thus lepton-number violating.

For $s \rightarrow d \nu \nu$ transitions and the case of three Majorana neutrinos, the number of independent interactions that are symmetric in the flavour of the three Majorana neutrinos are parametrised by $6 \cdot 6$ independent complex Wilson coefficients contained in $C^{A, \, L/R}_{ab 21}$, $C^{S/P, \, L}_{ab 21}$, and $C^{S/P, \, L}_{ab 12}$, with $a \ge b$. In addition, the interactions that are anti-symmetric in the neutrino flavours are parametrised by $3 \cdot 4$ complex Wilson coefficients contained in $C^{V,\,L}_{ab 21}$, $C^{V,\,R}_{ab 21}$, $C^{T,\,L}_{ab 21}$, and $C^{T,\,L}_{ab 12}$, with $a > b$. The same number of 48 independent complex Wilson coefficients contributes to $b \rightarrow s \nu \nu$ decays, after the quark-flavour indices are appropriately changed.

2.2 Dirac-$\nu$ EFT with lepton-number conservation

For the case of Dirac neutrinos, the dimension-six effective Lagrangian with lepton-number conservation relevant for $d_i\rightarrow d_j \nu {\bar{\nu }}$ transitions can be written as

$$\begin{aligned} {\mathscr {L}}^{(6)}_{d\rightarrow d'\nu \nu }\Big \vert _{\text {Dirac}}&=\sum _{\tau ,\tau '=\left\{ L,R\right\} } \!\!\sum _{f} C^{V,\,\tau \tau '}_ f O^{V,\,\tau \tau '}_f \nonumber \\&\quad +\sum _{f}\Bigl (C^{S,\,LL}_f O^{S,\,LL}_f +C^{S,\,LR}_f O^{S,\,LR}_f \nonumber \\&\quad +C^{T,\,LL}_f O^{T,\,LL}_f + \text {h.c.}\Bigr ), \end{aligned}$$

(9)

where $\tau ,\tau '=\{L,R\}$ indicate the chirality of the neutrino and/or quark currents and f comprises all neutrino and quark flavour indices, $f=\{abij\}$. The independent, lepton-number conserving operators read

$$\begin{aligned} O^{V, \,LL}_{\,ab ij}&=({\overline{\nu }}_{Da}\gamma _\mu \, P_L\, \nu _{Db})({\overline{d}}_i\,\gamma ^\mu \,P_L\, {d}_j ),\nonumber \\ O^{V, \,LR}_{\,ab ij}&=({\overline{\nu }}_{Da}\gamma _\mu \, P_L\, \nu _{Db})({\overline{d}}_i\,\gamma ^\mu \,P_R\, {d}_j ), \end{aligned}$$

(10)

$$\begin{aligned} O^{V, \,RL}_{\,ab ij}&=({\overline{\nu }}_{Da}\gamma _\mu \, P_R\, \nu _{Db})({\overline{d}}_i\,\gamma ^\mu \,P_L\, {d}_j ),\nonumber \\ O^{V, \,RR}_{\,ab ij}&=({\overline{\nu }}_{Da}\gamma _\mu \, P_R\, \nu _{Db})({\overline{d}}_i\,\gamma ^\mu \,P_R\, {d}_j ), \end{aligned}$$

(11)

$$\begin{aligned} O^{S,\,LL}_{\,ab ij}&=({\overline{\nu }}_{Da} \, P_L\, \nu _{Db})({\overline{d}}_i \,P_L\, {d}_j ),\nonumber \\ O^{S,\,LR}_{\,ab ij}&= ({\overline{\nu }}_{Da} \, P_L\, \nu _{Db})({\overline{d}}_i \,P_R\, {d}_j ), \end{aligned}$$

(12)

$$\begin{aligned} O^{T,\,LL}_{\,ab ij}&= ({\overline{\nu }}_{Da} \,\sigma _{\mu \nu }\,P_L\,\nu _{Db})({\overline{d}}_i \,\sigma ^{\mu \nu }\,P_L\, {d}_j ). \end{aligned}$$

(13)

In the Dirac case, the $O^{V, \,\tau \tau '}$ operators are all self-adjoint if their flavour structure is neglected. The hermiticity condition on their Wilson coefficients reads

$$\begin{aligned} C^{V,\,\tau \tau '}_{abij} = \left( C^{V,\,\tau \tau '}_{ba ji} \right) ^*. \end{aligned}$$

(14)

In the Dirac basis, the SM contribution to $K^+\rightarrow \pi ^+{\bar{\nu }}\nu$ is induced by the operators $O^{V, \,LL}_{ab ij}$ with $i=1$ (down quark) and $j=2$ (strange quark) and discussed in Eq. (3). In the strict SM case of three massless neutrinos, neutrinos can be described by three left-handed fields without right-handed partners. In this case, the scalar and tensor operators vanish by construction. They do not, however, vanish if the small neutrino masses are due to Dirac masses for which right-handed neutrinos are required. In this case, scalar and tensor interactions are possible without the need for lepton-number violation in contrast to the Majorana case.

For $s \rightarrow d \nu {\bar{\nu }}$ transitions and the case of three Dirac neutrinos, the interactions are parametrised by a total of $9 \cdot 10$ independent complex Wilson coefficients $C^{V, \, \tau \tau '}_{ab 21}$, $C^{S, \, LL/LR}_{ab 21}$, $C^{S, \, LL/LR}_{ab 12}$, $C^{T, \, LL}_{ab 21}$, $C^{T, \, LL}_{ab 12}$, where $\tau ,\tau ' \in \left\{ L,R \right\}$. The same number of 90 complex Wilson coefficients contributes to $b \rightarrow s \nu \nu$ decays, after the quark flavour indices are appropriately changed.

3 Rates and distributions for $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ at NA62

In this section, we derive the decay rates and the resulting distributions for the decay $K^+\rightarrow \pi ^+\nu \nu$ for the cases of Majorana and Dirac neutrinos. We also discuss the treatment of theory and experimental uncertainties used throughout the analysis. Finally, we describe the statistical procedure that we shall use to constrain the parameter-space of the effective theories based on current and expected data from NA62 and HIKE, respectively.

3.1 Decay rates

To derive the differential decay rates for $K^+\rightarrow \pi ^+\nu \overset{\scriptscriptstyle (-)}{\nu }$ we evaluate the matrix element

$$\begin{aligned} {{{\mathcal {M}}}} = {\big \langle {\pi ^+(p_\pi ) \overset{\scriptscriptstyle (-)}{\nu }_{\!\!\!a} \nu _b| H_{\textrm{eff}} |K^+(p_K)}\big \rangle } , \end{aligned}$$

(15)

where the effective Hamiltonian $H_{\textrm{eff}}$ follows either from the Lagrangian in Eq. (5) or from the one in Eq. (9). To be precise, for the Dirac case we compute the amplitude for the transition $K^+\rightarrow \pi ^+{\bar{\nu }}_a \nu _b$, while for the Majorana case the one for $K^+\rightarrow \pi ^+\nu _a \nu _b$. We will mention differences between the Majorana and the Dirac computation when they arise.

Table 1 Numerical values of the form factor parameters used. The values for the scalar and vector form factor are taken from Refs. [13, 36], while the parameters of the tensor form factor are taken from Ref. [37]

The amplitude factorizes into a hadronic part $\big \langle \pi ^+| O^{\textrm{had}}_{sd} |K^+\big \rangle$ and a leptonic part ${\big \langle { \overset{\scriptscriptstyle (-)}{\nu }_{\!\!\!a} \nu _b| O^\textrm{lep}_{ab} | 0}\big \rangle }$. The leptonic part is obtained using standard techniques; in particular we employ Feynman rules for Majorana fields [35] to treat the case of massive Majorana neutrinos. The hadronic parts of the decay are determined by three form factors [13, 36, 37]

$$\begin{aligned}&{\big \langle {\pi ^+|{\bar{d}}\gamma ^\mu s|K^+}\big \rangle } = (p_K + p_\pi )^\mu f^V(q^2)+ \frac{m_{K}^2 - m_{\pi }^2}{q^2}\nonumber \\&\!\qquad \qquad \qquad \qquad \qquad \times (p_K - p_\pi )^\mu \left( f^S(q^2) - f^V(q^2)\right) , \end{aligned}$$

(16)

$$\begin{aligned}&{\big \langle {\pi ^+|{\bar{d}}s|K^+}\big \rangle } = \frac{m_{K}^2 - m_{\pi }^2}{m_s - m_d} f^S(q^2) , \end{aligned}$$

(17)

$$\begin{aligned}&{\big \langle {\pi ^+|{\bar{d}}\sigma ^{\mu \nu }s|K^+}\big \rangle }= \left( p^{\mu }_{\pi }p^{\nu }_{K} - p^{\nu }_{\pi } p^{\mu }_{K} \right) \frac{f^T(q^2)}{m_{K}+ m_{\pi }} , \end{aligned}$$

(18)

with $m_p$ denoting the masses of mesons and quarks, $p_\pi$ and $p_K$ the $\pi ^+$ and $K^+$ momentum, respectively, and $q^2\equiv (p_K-p_\pi )^2$. To obtain the tensor form factor, $f^T(q^2)$, we use isospin symmetry to relate it to the neutral form factor, finding $f^T(q^2) = 2f^T_{0}(q^2)$, with ${\big \langle {\pi ^0|{\bar{s}}\sigma ^{\mu \nu }d|K^0}\big \rangle } = \left( p^{\mu }_{\pi } p^{\nu }_{K} - p^{\nu }_{\pi } p^{\mu }_{K} \right) \sqrt{2}f^T_{0}(q^2)/(m_{K} + m_{\pi })$ evaluated in Ref. [37]. Note, that the parity violating axial parts of the hadronic matrix elements do not contribute to the decay due to the parity conservation of QCD. The $q^2$-dependence of the remnant scalar form-factor functions reads [13, 37]

$$\begin{aligned} f^V(q^2)&= f^+_0\left( 1 + \lambda '_+ \frac{q^2}{m_\pi ^2} + \lambda ''_+ \frac{q^4}{2 m_\pi ^4}\right) ,\nonumber \\ f^S(q^2)&= f^+_0\left( 1 + \lambda _0 \frac{q^2}{m_\pi ^2}\right) ,\nonumber \\ f^T(q^2)&= \frac{2f^T_0(0)}{1 - \lambda _T \, q^2}. \end{aligned}$$

(19)

Table 1 contains the numerical input for the form factors. For notational brevity we also define

$$\begin{aligned} F^S(q^2)&\equiv \frac{m_{K}^2 - m_{\pi }^2}{m_s - m_d} f^S(q^2) ,\nonumber \\ F^T(q^2)&\equiv \frac{f^T(q^2)}{m_{K} + m_{\pi }} . \end{aligned}$$

(20)

The differential partial decay rate for the three-body decay is then given by [20]

$$\begin{aligned}{} & {} {\textrm{d}}\Gamma \left( K^+ \rightarrow \pi ^+ \overset{\scriptscriptstyle (-)}{\nu }_{\!\!\!a} \nu _b\right) \nonumber \\{} & {} \quad = \frac{(2 \pi )^4}{2 E_K} \left| \overline{{{{\mathcal {M}}}}} \right| ^2 \frac{{\textrm{d}}^3\vec {p}_\pi }{(2 \pi )^3 E_\pi }\frac{{\textrm{d}}^3\vec {p}_{\nu ,a}}{(2 \pi )^3 E_{\nu ,a}} \frac{{\textrm{d}}^3\vec {p}_{\nu ,b}}{(2 \pi )^3 E_{\nu ,b}}, \end{aligned}$$

(21)

where $\left| \overline{{{{\mathcal {M}}}}} \right|$ indicates that we have summed over the polarisations of the final-state neutrinos. Starting from this equation, one can derive the differential distribution ${\textrm{d}}^2 \Gamma _{ab}/{\textrm{d}}q^2{\textrm{d}}k^2$ in terms of the Lorentz invariant parameters $q^2 \equiv (p_{\nu ,a} + p_{\nu ,b})^2$ and $k^2 \equiv (p_\pi + p_{\nu ,a})^2$ to obtain the characteristic for three-body decays Dalitz plot. The corresponding expressions in the Majorana and Dirac case are provided in Appendix A.

However, NA62 measures the differential branching ratio ${\textrm{d}},{\textrm{Br}}/{\textrm{d}}|\vec {p}_\pi |$ in the lab frame. To arrive at this expression, we recursively write the three-body phase-space integration into a convolution of two two-particle phase-space integrations. This introduces an additional integration over the variable $q^2 = (p_{\nu ,a} + p_{\nu ,b})^2$ but allows one to trivially perform the integration over both neutrino momenta. After the integration over the angular part of the pion momentum in the lab frame, we are left with the double differential decay rate ${\textrm{d}}^2\Gamma _{ab}/{\textrm{d}}|\vec {p}_\pi |{\textrm{d}}q^2$ in the lab frame.

For the case of a decay to two massless neutrinos, $\nu _a$ and $\nu _b$, the double differential partial decay width of $K^+\rightarrow \pi ^+\nu _a\nu _b$ in the Majorana basis then reads

$$\begin{aligned}&\frac{{\textrm{d}}^2\Gamma _{ab}}{{\textrm{d}}|\vec {p}_\pi | {\textrm{d}}q^2}\Bigg |_{\text {Majorana}}\nonumber \\&\quad =\frac{|\vec {p}_\pi |}{6144 \pi ^3 E_K E_\pi |\vec {p}_K| \left( 1 + \delta _{ab}\right) }\nonumber \\&\qquad \times \Theta (|\vec {p}_\pi |,q^2)\Bigl |_{m_a = m_b = 0} \Bigg {[} +8 \lambda _{K\pi q^2} \left| f^V(q^2)\right| ^2\nonumber \\&\qquad \times \left( \left| C^{A,\,L,\,\text {SM}}_{ab12} + C^{A,\,L}_{ab12} + C^{A,\,R}_{ab12}\right| ^2 + \left| C^{V,\,L}_{ab12} + C^{V,\,R}_{ab12}\right| ^2\right) \nonumber \\&\qquad +12 q^2 \left| F^S(q^2)\right| ^2 \Big (\left| C^{P,\,L}_{ab12} {+} C^{P,\,L*}_{ab21}\right| ^2 + \left| C^{S,\,L}_{ab12} + C^{S,\,L*}_{ab21}\right| ^2 \Big )\nonumber \\&\qquad +3 q^2 \lambda _{K\pi q^2}\left| F^T(q^2)\right| ^2 \Big (\left| C^{T,\,L}_{ab12} - C^{T,\,L*}_{ab21}\right| ^2\Big ) \Bigg {]} \end{aligned}$$

(22)

with $\lambda _{K\pi q^2}\equiv \lambda (m_K^2,m_\pi ^2,q^2)$ and the Källén function $\lambda (x,y,z)\equiv x^2+y^2+z^2-2xy-2yz-2zx$. The additional factor $1/(1 + \delta _{ab})$ accounts for the reduction of the phase space in the case of identical particles in the final state. We stress that in Eq. (22) we have already used the hermiticity and Majorana conditions to obtain all contributions to the neutrino final state $\nu _a\nu _b$. Therefore, the total rate corresponds to the “constrained” sum of channels $\sum _{\begin{array}{c} a,b\\ a\le b \end{array}}$ of all independent final states. In Eq. (22), $\Theta (|\vec {p}_\pi |,q^2)$ is a shorthand for the theta-functions

$$\begin{aligned}{} & {} \Theta (|\vec {p}_\pi |,q^2) \nonumber \\{} & {} \quad \equiv ~ \theta (E_K-E_\pi ) \theta \left( \sqrt{q^2}-m_a-m_b\right) \nonumber \\{} & {} \qquad \times ~\theta \left( 1-\frac{m_K^2+m_\pi ^2-2 E_K E_\pi -q^2}{2 |\vec {p}_K| |\vec {p}_\pi | }\right) \nonumber \\{} & {} \qquad \times ~\theta \left( 1+\frac{m_K^2+m_\pi ^2-2 E_K E_\pi -q^2}{2 |\vec {p}_K| |\vec {p}_\pi | }\right) . \end{aligned}$$

(23)

Analogously, we compute the differential partial decay width of $K^+\rightarrow \pi ^+{\bar{\nu }}_a\nu _b$ for the massless Dirac-neutrino case

$$\begin{aligned}&\frac{{\textrm{d}}^2\Gamma _{ab}}{{\textrm{d}}|\vec {p}_\pi | {\textrm{d}}q^2}\Bigg |_\text {Dirac}\nonumber \\&\quad =\frac{|\vec {p}_\pi |}{3072 \pi ^3 E_K E_\pi |\vec {p}_K|} \Theta (|\vec {p}_\pi |,q^2)\Bigl |_{m_a = m_b = 0} \nonumber \\&\qquad \times \Bigg {[}+ 2 \lambda _{K\pi q^2} |f^V(q^2)|^2 \Bigl (\bigl |C^{V,\,LL,\,\text {SM}}_{ab12} + C^{V,\,LL}_{ab12} \nonumber \\&\qquad +C^{V,\,LR}_{ab12}\bigr |^2 + \bigl |C^{V,\,RL}_{ab12} + C^{V,\,RR}_{ab12}\bigr |^2\Bigr )+ 3 q^2 |F^S(q^2)|^2 \nonumber \\&\qquad \times \Bigl (\bigl |C^{S,\,LL}_{ab12}+C^{S,\,LR}_{ab12}\bigr |^2+\bigl |C^{S,\,LL}_{ba21}+C^{S,\,LR}_{ba21}\bigr |^2\Bigr )\nonumber \\&\qquad +q^2\lambda _{K\pi q^2} |F^T(q^2)|^2 \Bigl (\bigl |C^{T,\,LL}_{ab12}\bigr |^2 +\bigl |C^{T,\,LL}_{ba21}\bigr |^2\Bigr ) \Bigg {]}. \end{aligned}$$

(24)

Similarly to the Majorana case, also here we have used the hermiticity conditions on the Wilson coefficients in order to include all contributions to the ${\bar{\nu }}_a \nu _b$ final state. However, contrarily to the Majorana case, particles are not the same as antiparticles and thus the total rate is given by the unconstrained sum of channels $\sum _{a,b}$.

The total branching ratio for $K^+\rightarrow \pi ^+\nu \overset{\scriptscriptstyle (-)}{\nu }$ is then the sum of the different neutrino channels

$$\begin{aligned} {\textrm{Br}}\left( K^+\rightarrow \pi ^+\nu \overset{\scriptscriptstyle (-)}{\nu }\ \right) = \Gamma _{\text {tot}}^{-1} \int _{\Omega (|\vec {p}_\pi |, q^2)} {\textrm{d}}|\vec {p}_\pi | {\textrm{d}}q^2 \overline{\sum _{a,b}}\frac{{\textrm{d}}^2\Gamma _{ab}}{{\textrm{d}}|\vec {p}_\pi | {\textrm{d}}q^2},\nonumber \\ \end{aligned}$$

(25)

where $\Omega (|\vec {p}_\pi |, q^2)$ denotes the signal region of the NA62 experiment, $\Gamma _{\text {tot}}$ the total decay width in the lab frame, and the overline in ${\overline{\sum }}$ indicates that for the Majorana case the sum is constrained, i.e., $a\le b$, while for the Dirac case it is unconstrained.

3.1.1 Uncertainties in theory predictions

There are two main sources of uncertainties in the theory predictions for the $K\rightarrow \pi \nu \nu$ rates and distributions: (i) uncertainties associated to the SM Wilson coefficient and (ii) uncertainties associated to the form-factors.

For (i), i.e., SM Wilson coefficient, we follow Ref. [19]. We include all state-of-the-art perturbative corrections and include in our analysis both pure theory uncertainties, associated to residual scale dependencies, and parametric uncertainties. At the current level of precision, the dominant uncertainties are parametric, mainly originating from the CKM input. All these uncertainties are due to short-distance dynamics and thus do not depend on $q^2$. We also note that in the SM a significant part of the CKM uncertainties drop out in the ratio of the charged decay mode and $\varepsilon _K$ [38]. This ratio is also theoretically very clean, given recent progress [39,40,41,42] in the theory prediction of $\varepsilon _K$ and has an overall uncertainty of $5\%$, which is similar to the $6\%$ uncertainty for the SM prediction of the charged decay branching ratio.

Fig. 1

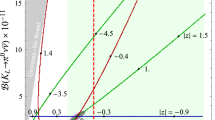
The $q^2$ dependence of the form-factor functions and their uncertainties as given in Table 1. The coloured bands correspond to the $1\sigma$ bands for the vector, scalar and tensor form-factors. The lower panel shows the dependence of the relative uncertainty $\Delta f/f$ of each form-factor function

For (ii), i.e., the form factors, we use their numerical values and uncertainties as published in the original literature and summarised in Table 1. The numerical evaluation of the form factors shows that their relative uncertainties are roughly constant within the $q^2$ signal regions of NA62. This is illustrated in Fig. 1, where we show the $q^2$ dependence of the three form-factor functions and their uncertainties in the NA62 signal regions. The lower panel shows the $q^2$ dependence of their relative uncertainties ${\Delta f}/{f}$. Since these uncertainties are roughly flat in $q^2$, we can consider them as global relative uncertainties, which speeds up the evaluation of the profile likelihood ratio test. This simplifies accounting for them in the likelihood evaluation. Concretely, we use throughout the whole signal region an overall relative error of $0.4\%$, $0.8\%$, and $4\%$ for the vector, scalar, and tensor form factor, respectively, cf., Fig. 1.

The input for CKM parameters and form factors involves fits to experimental data. The operators considered in Eqs. (6) and (10) will not impact these fits, since they comprise only a product of down-quark and neutrino field bilinears. This can in principle change in concrete UV completions or if the overarching EFT is the SMEFT or $\nu$SMEFT theory. In the latter case their Wilson coefficients would be correlated to other weak-effective-theory operators. This can result in correlations with charged-current processes and $\epsilon _{K}$ through weak-isospin symmetry of SMEFT and double insertions of SMEFT operators, respectively. However, the numerical impact of these correlations is negligible, given that the relevant SMEFT Wilson coefficients are already tightly constrained by the currently measured $K^+\rightarrow \pi ^+\nu {\bar{\nu }}$ branching ratio.

3.2 Statistical treatment for EFT fit

To quantify the agreement between the experimental data and the different NP scenarios, we perform a statistical test using a profile likelihood ratio as test statistic that is sampled in a full frequentist manner. The number of signal events, $s_i$, in a category i is given as

$$\begin{aligned} s_i = \frac{{\textrm{BR}}_{K\rightarrow \pi \nu \nu }^{i}(\{C_{\textrm{NP}}\})}{ \textrm{SES}_i} , \end{aligned}$$

(26)

where ${\textrm{BR}}_{K\rightarrow \pi \nu \nu }^{i}(\{C_{\textrm{NP}}\})$ denotes the branching ratio of $K^+\rightarrow \pi ^+\nu \nu$ within the category i for a set of Wilson coefficients $\{C_{\textrm{NP}}\}$ corresponding to the NP scenario under consideration. Further, the variable $\textrm{SES}_i$ denotes the single-event sensitivity of category i taken from Ref. [43]. Note that in Refs. [2, 43], the $\textrm{SES}_i$ are defined such that multiplied with the total branching ratio one obtains the number of expected events in bin i. This is in contrast to our definition in Eq. (26) where we use the branching ratio within the corresponding categories. We, thus, remove the phase-space information from the original definition of the $\textrm{SES}_i$, cf. Table 2.

Table 2 The single-event sensitivities, $\textrm{SES}_i$, for the respective categories provided by the NA62 collaboration [1, 2, 43, 44], as well as the corresponding sensitivities with the phase-space information removed. The definition of each category is given in the original NA62 publications

The number of expected background events, $b_i$, and observed data, $n_i$, in each category are taken from the NA62 measurement [2]. The events in the different categories are uncorrelated, which implies that the total likelihood is a product of Poisson distributions in the number of signal plus background events $s_i + b_i$. We further neglect possible correlations between experimental parameters like the $\textrm{SES}_i$, which—if non-zero—are not provided by the NA62 collaboration. We account for theory and experimental statistical uncertainties in the likelihood by including the corresponding parameters as global observables associated to auxiliary measurements. The uncertainties of the parameters for the theory predictions described in Sect. 3.1 are all assumed to be Gaussian even though some of them, e.g., scale dependencies are of non-statistical nature. However, the numerical impact of this assumption on the analysis is negligible. The sensitivities, $\textrm{SES}_i$, are constrained to follow uncorrelated Gaussian terms while the number of expected background events follows a Poisson distribution.

Let us now denote the total likelihood with the shorthand notation ${\mathcal {L}}(x|\{C_{{\textrm{NP}}}\},\nu )$, with x being the outcome, i.e., the observed data, $\{C_{\textrm{NP}}\}$ the parameters of interest, i.e., the NP Wilson coefficients, and $\nu$ the nuisance parameters. Under the assumption that the NP scenario under consideration is realised in nature, one can determine the confidence intervals on the model parameters $\{C_{\textrm{NP}}\}$ at a given confidence level using the profile likelihood ratio $\lambda$ as a test statistic

$$\begin{aligned} \lambda _{\{C_{{\textrm{NP}}}\}} = \frac{{\mathcal {L}}(x|\{C_{{\textrm{NP}}}\}, {\hat{\hat{\nu }}}(\{C_{{\textrm{NP}}}\}))}{{\mathcal {L}}(x|\{{\hat{C}}_{{\textrm{NP}}}\},\hat{\nu })} . \end{aligned}$$

(27)

The parameters with a single hat are the parameter values that maximise the likelihood. The value for the nuisance parameters $\nu$ that maximise the likelihood for given values of the parameters of interest $\{C_{{\textrm{NP}}}\}$ are denoted with a double-hat. For given parameters of interest $\{C_{{\textrm{NP}}}\}$, we calculate the corresponding p-value via

$$\begin{aligned} p_{\{C_{{\textrm{NP}}}\}} = \int _{\lambda ^{\textrm{obs}}_{\{C_{{\textrm{NP}}}\}}}^{\infty } {\textrm{d}}\lambda _{\{C_{{\textrm{NP}}}\}} \, f(\lambda _{\{C_{{\textrm{NP}}}\}} | \{C_{{\textrm{NP}}}\},\nu ) , \end{aligned}$$

(28)

where f denotes the test-statistic distribution that we sample by means of a Monte-Carlo method under the assumption of $\{C_{{\textrm{NP}}}\}$, and with $\lambda ^{\textrm{obs}}_{\{C_{{\textrm{NP}}}\}}$ the observed value of the test statistic. In order to determine the upper limit on a single Wilson coefficient $C_{\textrm{NP}}$ at a confidence level of $100(1 - \alpha )\%$, we solve for $p_{C_{\textrm{NP}}} = \alpha$. For the procedure on how to estimate two-dimensional confidence regions from the profile likelihood ratio see, e.g., Ref. [45]. For further references, see Refs. [20, 46]

4 New Physics sensitivities

Fig. 2

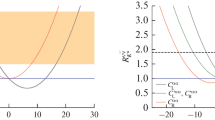
Distributions of ${\textrm{Br}}(K^+ \rightarrow \pi ^+ \nu \nu )$ for different NP scenarios containing three massless Majorana or Dirac neutrinos. The left and middle panel shows differential $q^2$ distributions integrated over the whole physical phase space for $|\vec {p}_\pi |$ and over $|\vec {p}_\pi |$ signal region of NA62, respectively. The right panel shows the lab frame $|\vec {p}_\pi |$ distribution inside the NA62 $q^2$ signal regions as currently done at NA62. All NP Wilson coefficients that affect the rates are displayed in the legend. In each panel we use the values for the given Wilson coefficients that saturate the bound at $90\%$ CL. Therefore, there is no distinction between $a=b$ and $a\ne b$ cases. The gray, dashed line corresponds to the SM case. The dashed, vertical lines indicate the different NA62 signal regions

In this section, we use the NP distributions from Sect. 3.1 together with the binned likelihood from Sect. 3.2 to determine NA62’s sensitivity on constraining the independent NP operators given in Sects. 2.1 and 2.2 for Majorana and Dirac neutrinos, respectively. We shall discuss the sensitivity based on the current experimental data of NA62 [2] and also provide estimates for the future sensitivity based on the prospects in future experiments like HIKE. In Sect. 4.1 we switch on one NP operator at a time, while in Sect. 4.2 we also show correlations by switching on pairs of operators. The limits on all Wilson coefficients are always determined in addition to the Standard Model contribution, which is always included.

4.1 Single-operator fits

For the single-operator fits we discuss three different scenarios:

• (i) Dirac effective theory with three light neutrinos, i.e.,

  $a,b=1,2,3$ with $m_{\nu ,1}\!\approx \!m_{\nu ,2}\!\approx \!m_{\nu ,3}\!\approx \!0$ (operator basis of Sect. 2.2).

• (ii) Majorana effective theory with three light neutrinos, i.e., $a,b=1,2,3$

  with $m_{\nu ,1}\!\approx \!m_{\nu ,2}\!\approx \!m_{\nu ,3}\!\approx \!0$ (operator basis of Sect. 2.1).

• (iii) Majorana effective theory with three light neutrinos and one additional sterile neutrino with mass $m_{\nu ,4}$, i.e., $a,b=1,2,3,4$, (operator basis of Sect. 2.1).

Since in this section we switch on one operator at a time, the bounds are only sensitive to the absolute value of the respective Wilson coefficients and insensitive to their CP violating phases. The exceptions are NP contributions that induce the same operator as the SM, i.e., $O^{A,\,L}_{aa12}$ and $O^{V,\,LL}_{aa12}$, for which the interference term with the SM depends on the relative phase between the NP and the SM Wilson coefficient. Since $K^+\rightarrow \pi ^+\nu \nu$ is a CP conserving decay we choose for concreteness to align the NP with SM phase in the numerical analysis that follows.

Even though the cases (i) and (ii) are physically distinguishable due to the different number of degrees of freedom there will always be a scenario in (i) that leads to the same NP distribution as a scenario in (ii) in the limit of $m_\nu \rightarrow 0$ if a single NP operator is switched on. This is best seen by comparing the Majorana to the Dirac distributions for massless neutrinos in Eqs. (22) and (24) and is illustrated also in Fig. 2, where we present all the independent differential distributions possible for the case (i) and (ii). Throughout Fig. 2, the value of the Wilson coefficients is chosen to saturate the current experimental limit at $90\%$ Confidence Level (CL). The limits are determined from the prescription of Sect. 3.2.

In the left panel and middle panel of Fig. 2, we show the different ${\textrm{dBr}}(K^+ \rightarrow \pi ^+\nu \nu )/{\textrm{d}}q^2$ distributions. The difference between left and middle panel is that the former shows the distributions integrated over the whole pion-momentum, $|\vec {p}_\pi |$, phase space while in the latter we have integrated over the pion-momentum signal region of NA62. A comparison of the different shapes shows how a differential measurement can be used to distinguish different operators. The right panel shows the distributions ${\textrm{dBr}}(K^+ \rightarrow \pi ^+\nu \nu )/{\textrm{d}}|\vec {p}_\pi |$ in the NA62 lab frame after integrating over the $q^2$ signal region of NA62. This corresponds exactly to the categories 3–8 currently employed by NA62 [2]. This plot also makes it evident that a binning in the missing-momentum square, $q^2$, is able to distinguish between the different NP scenarios within the Majorana or the Dirac basis but not between the Majorana or Dirac nature of the neutrinos. In Tables 3 and 4 we collect the constraints at $90\%$ CL on the different Wilson coefficients for the case of three Majorana neutrinos, i.e., scenario (i), and three Dirac neutrinos, i.e, scenario (ii), respectively.

Table 3 Current and estimated future experimental lower limit at $90\%$ CL for the different NP operators in the case of three massless Majorana neutrinos. A single operator is turned on at a time. The case labelled by $\sum a=b$ corresponds to taking neutrino-flavour universal Wilson coefficients, whereas in the case labelled by $a=b$ a single Wilson coefficient is switched on. Note that in case of interference with the SM Wilson coefficient, the CP phase of the NP Wilson coefficient has been aligned to the SM. See text for the details on the different future scenarios

Table 4 Current and estimated future experimental lower limit at $90\%$ CL for the different NP operators in the case of three massless Dirac neutrinos. A single operator is turned on at a time. The case labelled by $\sum a=b$ corresponds to taking neutrino-flavour universal Wilson coefficients, whereas in the case labelled by $a=b$ a single Wilson coefficient is switched on. Note that in case of interference with the SM Wilson coefficient, the CP phase of the NP Wilson coefficient has been aligned to the SM. See text for the details on the different future scenarios

Fig. 3

Distributions of ${\textrm{Br}}(K^+ \rightarrow \pi ^+ \nu \nu )$ for different NP scenarios containing an additional fourth massive Majorana neutrino with mass, $m_{\nu , 4} = 50 \, \text {MeV}$. Similarly to Fig. 2, the left and middle panel shows differential $q^2$ distributions integrated over the whole physical phase space for $|\vec {p}_\pi |$ and over the $|\vec {p}_\pi |$ signal region of NA62, respectively. The right panel shows the lab frame $|\vec {p}_\pi |$ distribution inside the NA62 $q^2$ signal regions as currently done at NA62. All NP Wilson coefficients that affect the rates are displayed in the legend. In each panel we use the values for the given Wilson coefficients that saturate the bound at $90\%$ CL. The gray, dashed line corresponds to the SM case. The dashed, vertical lines indicate the different NA62 signal regions

Additionally, we perform first estimates of the future sensitivity reach based on the proposed HIKE experiment. To this end we use the expected improvements highlighted in the letter of intent for HIKE [21, 47] and perform a naive upscaling of the luminosity such that the expected number of signal events reach 400–500 while also reducing the number of background events to ensure that the intended signal to background ratio of $B/S\sim 0.5{-}0.7$ is achieved.¹ Apart from this, we assume the same experimental setup as NA62. We take the expected data to be the sum of the expected SM contribution plus the upscaled background of NA62 after the aforementioned reduction. The resulting limits are shown in the column labeled “future” in Tables 3 and 4 for the Majorana and Dirac case, respectively.

For the NP scenarios (i) and (ii), we also estimate the expected limits on the Wilson coefficients by choosing an alternative categorisation of the events. For this we integrate over pion-momentum signal region, but choose to bin the data in the current low-$q^2$ and high-$q^2$ signal region NA62 in two and four equidistant $q^2$-bins, respectively. To achieve this, we rescale the $\textrm{SES}$ of the 2018-NEWCOL sample (category 3–8) under the assumption that the efficiencies entering the $\textrm{SES}$ and the background distributions are flat in $q^2$. The expected data is taken to be the sum of the expected SM contribution plus the upscaled background. The estimated sensitivities to the NP operators are shown in the right column of Tables 3 and 4 for the Majorana and Dirac case, respectively. In both future scenarios, we observe an increase of approximately 50–60% for all NP operators apart from the diagonal vector ones that interfere with the Standard Model. For them we observe an increase in sensitivity of 100–130%.

Fig. 4

Current (left) and future (right) lower limits of $1/\sqrt{C}$ at $90\%$ CL for the scenarios with an additional massive fourth neutrino interacting solely via one of the given NP Wilson coefficients as a function of its mass $m_{\nu ,4}$

Finally, in the context of single-operator fits we also study scenario (iii). Namely, the case of having a fourth massive Majorana neutrino, $\nu _4$, with a mass such that the decays $K^+\rightarrow \pi ^+\nu \nu _4$ or $K^+\rightarrow \pi ^+\nu _4\nu _4$ are kinematically possible. To illustrate the possible impact of a fourth massive neutrino on the distributions we choose the benchmark mass $m_{\nu ,4}=50$ MeV and show in Fig. 3 the analogous distributions as for the three massless neutrino cases.

Figure 4 shows the current constraints at $90\%$ CL as a function of the fourth neutrino mass $m_{\nu ,4}$. The left panel shows the current sensitivity while the right one the projected sensitivity. All limits are given at $90\%$ CL. Here we observe an increase of 50–60% in the sensitivities depending on the NP operator. Note that the kinematic endpoint of the contribution of the diagonal operators, i.e., $O^{S/P,\,L}_{4412/21}$ and $O^{A,\,L/R}_{4412}$ (dashed lines), lies at around $\sim 130~\text {MeV}$ as the final state necessarily contains two massive neutrinos.

Fig. 5

Allowed parameter space at $68\%$ CL (dark blue) and $90\%$ CL (light blue) in the plane of two NP Wilson coefficients corresponding to various combinations of scenario (i), i.e. the case of three massless Dirac neutrinos. Note that here $a\ne b$. The dashed line corresponds to the future projection for the HIKE experiment at 90% CL

Fig. 6

Allowed parameter space at $68\%$ CL (dark blue) and $90\%$ CL (light blue) in the plane of two NP Wilson coefficients corresponding to various combinations of scenario (ii), i.e. the case of three massless Majorana neutrinos. Note that here $a\ne b$. The dashed line corresponds to the future projection for the HIKE experiment at $90\%$ CL

4.2 Multi-operator correlations

Next we study the correlations of probing different operators by considering the effect of switching on pairs of different operators simultaneously. For concreteness we cover (almost) all different non-trivial combinations for the case of three massless Dirac or Majorana neutrinos, scenario (i) and (ii), respectively. For these correlations it can be important to specify the phase we chose for the NP Wilson coefficients, since relative phases can be relevant for interferences. We assume there is no new CP-violating phases beyond the SM, i.e., all NP phases are aligned to the SM one. Additionally, in the discussion of neutrino-flavour diagonal operators, e.g., $O^{V,\,LL}_{aa12}$, we consider the flavour-universal case in which we switch on all operators of the category simultaneously but with universal Wilson coefficients, e.g., $C^{V,\,LL}_{1112} =C^{V,\,LL}_{2212} =C^{V,\,LL}_{3312}$. This additional assumption of flavour universality reduces the number of different combinations.

The results are shown in Figs. 5 and 6. For each case we determine the allowed region at $68\%$ CL (dark blue region) and $90\%$ CL (light blue region) in the plane of two Wilson coefficients assuming that the NP scenario is realised in nature. The dashed, black lines correspond to the $90\%$ CL future projection.

5 Discussion and conclusions

The golden, rare kaon decays $K\rightarrow \pi \nu \nu$ provide an excellent test of the Standard Model and are already placing stringent constraints on the parameter space of New Physics. The expected and planned experimental activities will test modifications of the SM operators at energies of ${\mathcal {O}}(300~\text {TeV})$ and will also allow to extract additional information from the invariant mass spectrum of the neutrinos. In the weak effective theory, scalar and tensor operators induce a modified invisible mass distribution, c.f. Fig. 2. We we have classified all independent Majorana and Dirac operators that contribute to these FCNC decays to neutrinos. We have derived the sensitivity to each operator for the current and expected future experimental situation including experimental and theoretical uncertainties, see Tables 3 and 4. The expected constraints on the NP scale range from ${\mathcal {O}}(40 ~\text {TeV})$ for tensor operators to ${\mathcal {O}}(300 ~\text {TeV})$ for axial-vector Majorana and vector Dirac operators. We have studied the impact of a massive sterile neutrino on the invisible mass spectrum and have discussed the correlation of various operators by analysing the allowed parameter space for pairs of different NP operators.

Majorana and Dirac neutrinos, which can be generated from a lepton-number violating SMEFT or a lepton-number conserving $\nu$SMEFT theory with additional right-handed neutrinos, have a completely different UV origin. Therefore, the relevant weak effective theories also contain different number of independent parameters. This implies that concrete UV models could be tested from the data of the spectrum in future searches. The NP sensitivity of the invisible spectrum provides a strong motivation for the future Kaon program and we plan to study the discriminating power of the charged decay mode spectrum on different realisations of the SMEFT and $\nu$SMEFT in the future [48].

Appendix A: Decay rates

The full expressions for the double differential decay widths ${\textrm{d}}^2\Gamma _{ab}/{\textrm{d}}q^2{\textrm{d}}|\vec {p}_\pi |$ and ${\textrm{d}}^2\Gamma _{ab}/{\textrm{d}}q^2{\textrm{d}}k^2$ for massive Majorana and Dirac neutrinos are openly available in a git repository on GitLab [49]. Here we give expressions for the double differential partial decay width in terms of the Lorentz invariant Dalitz variables $q^2 = (p_K - p_\pi )^2$ and $k^2 = (p_\pi + p_{\nu ,a})^2$ for massless neutrinos. In the Majorana case we find

$$\begin{aligned}&\frac{{\textrm{d}}^2\Gamma _{ab}}{{\textrm{d}}q^2{\textrm{d}}k^2}\Bigg |_{\text {Majorana}}\nonumber \\&\quad =\frac{1}{512 \pi ^3 m_K^3 (1 + \delta _{ab})} \Theta _{\text {L.inv.}}\left( q^2,k^2\right) \Bigl |_{m_a = m_b = 0}\nonumber \\&\qquad \times \Bigg [ -4 \left| f^V(q^2)\right| ^2 (k^4 - k^2 (m_K^2 + m_\pi ^2 - q^2) + m_K^2 m_\pi ^2) \nonumber \\&\qquad \times \left( \left| C^{A,\,L, \,\text {SM}}_{ab 12} + C^{A,\,L}_{ab12} + C^{A,\,R}_{ab12}\right| ^2 + \left| C^{V,\,L}_{ab12} + C^{V,\,R}_{ab12}\right| ^2\right) \nonumber \\&\qquad +q^2 \left| F^S(q^2)\right| ^2 \Big (\left| C^{P,\,L}_{ab12} + C^{P,\,L*}_{ab21}\right| ^2+\left| C^{S,\,L}_{ab12} + C^{S,\,L*}_{ab21}\right| ^2 \Big ) \nonumber \\&\qquad +q^2 \left| F^T(q^2)\right| ^2 (-2 k^2 + m_K^2 + m_\pi ^2 - q^2)^2\nonumber \\&\qquad \times \Big (\left| C^{T,\,L}_{ab12} - C^{T,\,L*}_{ab21}\right| ^2 \Big ) +2 q^2 (2 k^2 - m_K^2 - m_\pi ^2 + q^2) \nonumber \\&\qquad \Big (- F^S(q^2) F^T(q^2) {\textrm{Im}}\Big (C^{S,\,L}_{ab12} C^{T,\,L}_{ab21} + C^{S,\,L}_{ab21} C^{T,\,L}_{ab12}\Big ) \nonumber \\&\qquad +F^S(q^2) \left( F^T(q^2)\right) ^* {{\textrm{Im}}}\Big (C^{S,\,L}_{ab21} C^{T,\,L*}_{ab21} + C^{S,\,L}_{ab12} C^{T,\,L*}_{ab12}\Big ) \Big ) \Bigg ], \end{aligned}$$

(29)

with the theta function in terms of $q^2$ and $k^2$ defined as

$$\begin{aligned}{} & {} \Theta _{\text {L. inv.}}\left( q^2,k^2\right) \Bigl |_{m_a = m_b = 0} \nonumber \\{} & {} \quad = \theta (q^2) \theta \bigl ((m_K - m_\pi )^2 - q^2\bigr )\nonumber \\{} & {} \qquad \times \theta \left( k^2 - \frac{1}{2}\left( m_K^2 + m_\pi ^2 - q^2 - \lambda ^{1/2}_{K\pi q^2}\right) \right) \nonumber \\{} & {} \qquad \times \theta \left( \frac{1}{2}\left( m_K^2 + m_\pi ^2 - q^2 + \lambda ^{1/2}_{K\pi q^2}\right) - k^2\right) . \end{aligned}$$

(30)

For massless Dirac neutrinos we similarly find

$$\begin{aligned}&\frac{{\textrm{d}}^2 \Gamma _{ab}}{{\textrm{d}}q^2{\textrm{d}}k^2} \nonumber \\&\quad = \frac{1}{256 \pi ^3 m_K^3}\Theta _{\text {L. inv.}}\left( q^2,k^2\right) \Bigl |_{m_a = m_b = 0}\nonumber \\&\qquad \times \Bigg ( -(f^V(q^2))^2 (k^4 - k^2 (m_K^2 + m_\pi ^2 - q^2) + m_K^2 m_\pi ^2) \nonumber \\&\qquad \times \left( \left| C^{V,\,LL,\,\text {SM}}_{ab 12} + C^{V,\,LL}_{ab 12} + C^{V,\,LR}_{ab 12}\right| ^2 + \left| C^{V,\,RL}_{ab 12} + C^{V,\,RR}_{ab 12}\right| ^2\right) \nonumber \\&\qquad + \frac{q^2}{4} \left( (F^S(q^2))^2 \left( \left| C^{S,\,LL}_{ab12}+C^{S,\,LR}_{ab12}\right| ^2 +\left| C^{S,\,LR}_{ba21}+C^{S,\,LL}_{ba 21}\right| ^2\right) \right. \nonumber \\&\qquad +(F^T(q^2))^2 (-2 k^2+m_K^2+m_\pi ^2-q^2)^2\nonumber \\&\qquad \times \left. \left( \left| C^{T,\,LL}_{ab12}\right| ^2+\left| C^{T,\,LL}_{ba 21}\right| ^2\right) \right) - \frac{q^2}{2} (-2 k^2+m_K^2+m_\pi ^2-q^2) \nonumber \\&\qquad \Big (+ F^S(q^2) F^T(q^2) {\textrm{Im}}\left( C^{T,\,LL}_{ab12} \left( C^{S,\,LL}_{ba21}+C^{S,\,LR}_{ba21}\right) \right) \nonumber \\&\qquad + F^S(q^2) (F^T(q^2))^* {\textrm{Im}}\left( C^{T,\,LL*}_{ba21} \left( C^{S,\,LL}_{ba21}+C^{S,\,LR}_{ba21}\right) \right) \nonumber \\&\qquad + (F^S(q^2))^* F^T(q^2) {\textrm{Im}}\left( C^{T,\,LL}_{ab12} \left( C^{S,\,LL}_{ab12}+C^{S,\,LR}_{ab12}\right) ^*\right) \nonumber \\&\qquad + (F^S(q^2))^* (F^T(q^2))^* {\textrm{Im}}\left( C^{T,\,LL*}_{ba21} \left( C^{S,\,LL}_{ab12}+C^{S,\,LR}_{ab12}\right) ^*\right) \Big ) \Bigg ). \end{aligned}$$

(31)

Note, that for massless neutrinos the interference term between the scalar and tensor operators vanishes for both Majorana, and Dirac neutrinos, after integration over the full $k^2$ phase space, which is why such terms do not appear in Eqs. (22) and (24).