1 Introduction

The study of heavy flavor production has been of particular interest at experiments in hadron colliders, where the dynamics of Quantum Chromodynamics (QCD) can be investigated. Given the higher cross sections of heavy flavor production, the datasets collected may provide an insight on its nature. For instance, measurements considering the bottom quark production at lower energies had been reported by UA1 at CERN [1, 2] and CDF and D0 at Fermilab [3,4,5,6,7,8,9,10,11,12] assuming center of mass energies of 0.63, 1.8, and 1.96 TeV in proton–antiproton collisions, respectively. The Large Hadron Collider (LHC) has allowed us to investigate the high-energy limit of heavy meson production in unprecedented accuracy. The analysis of the cross sections and particle distributions of heavy quarks can be used to restrain backgrounds to new physics investigations [13, 14]. Particularly, the corresponding predictions can be obtained by perturbative QCD (pQCD) calculations in which the heavy quark mass defines a hard scale ensuring the validity of the perturbative method. On the other hand, some aspects in the theoretical calculations are associated to significant uncertainties. One can mention the choice concerning the factorization scale, the value of the bottom quark mass, order of perturbative expansion, and also the corresponding theoretical framework considered for the calculation (collinear factorization, \(k_{\perp }\)-factorization, color dipole picture, Color Glass Condensate formalism and so on). The study of the bottom hadron (b-hadron) production can be further investigated considering higher energies in proton-proton (pp) collisions at the LHC, where a larger kinematic region in transverse momentum and rapidity can be achieved. Focusing on B-mesons production, the ATLAS and CMS Collaboration at the LHC reported measurements of B-mesons cross sections in central rapidity region while the LHCb experiment provided measurements covering forward rapidities. This strongly motivates the evaluation of the theoretical predictions including initial-state transverse momentum distributions and benefit from the high-precision measurements provided by the LHC experiments [15, 16].

One well established approach of the pQCD calculations to study the B-meson production is the \(k_{T}\)-factorization [17,18,19,20,21]. The respective cross sections are calculated by means of the parton densities associated to the unintegrated gluon distribution (UGD). In the literature, several parameterizations regarding the UGDs can be found, which consider the transverse momenta of the initial partons. Moreover, the UGDs are expressed in terms of the Bjorken variable x and the factorization scale \(\mu _{F}\). It is expected that the B-meson production in the available energies at the LHC probes small values of the momentum fraction x, reaching a kinematic region where the QCD nonlinear effects and higher-order corrections need to be accounted for. One possible nonlinear QCD phenomenon is the gluon recombination process associated to the high-density regime where the parton saturation physics takes place. A well established formalism applied to the small-x phenomenology is the color dipole approach [22,23,24,25], where the associated dipole amplitude is connected to the dipole transverse momentum distribution (TMD), that is, the intrinsic dipole \(k_{\perp }\)-distribution. In addition, in the case of large transverse momentum, the dipole TMD and the UGD can be interpreted as nearly equivalent. Here, by using the color dipole framework in transverse momentum representation along with UGDs models, we provided predictions for the B-meson differential cross section considering pp collisions at the LHC domain and models with/without saturation effects are compared. This is complementary to our previous studies done in Refs. [26,27,28,29], where D-meson production has been addressed within the very same formalism.

The paper is organized as follows: In Sect. 2 the theoretical formalism is presented together with the models for the UGDs in order to obtain the B-meson production cross section in pp collisions. In Sect. 3 the corresponding results are compared to the measurements reported by the ATLAS, CMS, and LHCb Collaborations. Predictions for the nuclear modification factor in proton-nucleus collisions are also discussed. In Sect. 4 our main conclusions are summarized.

2 Theoretical formalism

In our framework the B-meson production cross section is obtained assuming the process \(g+p \rightarrow Q\bar{Q}+X\), where a virtual gluon in singlet or color-octet state fluctuates into a heavy quark \(Q\bar{Q}\) pair establishing a color dipole. The latter interacts with the color field of the proton, considered at the rest frame by the QCD dipole framework. The associated hadronic cross section, \(pp \rightarrow Q\bar{Q}X\), is determined by a convolution of the \(gp \rightarrow Q\bar{Q}X\) cross section and the projectile gluon UGD plus the probability that a heavy quark fragments into a meson in order to obtain the B-meson cross section. Consequently, the transverse momentum distribution is given by [25],

$$\begin{aligned} \frac{d^{3}\sigma _{pp \rightarrow BX}}{dYd^{2}P_T} = \int _{z_{\textrm{min}}}^1 \frac{dz}{z^2} B_{Q/B} (z,\mu _{F}^2) \int _{\alpha _{\textrm{min}}}^1 d\alpha \frac{d^{4}\sigma _{pp \rightarrow Q\bar{Q}X}}{dyd\alpha d^2p_T} , \nonumber \\ \end{aligned}$$
(1)

where the B-meson carries a fraction of the heavy quark transverse momentum denoted by z and \(P_{T}\) is the transverse momentum of the B-meson. There is an expression that connects the transverse momenta of the heavy quark to the meson given by \(p_{T} = P_{T}/z\). The meson fragmentation function is represented by \(B_{Q/B}(z,\mu _{F}^2)\) and we will take into account the parameterization from Ref. [16], known as KKKS fragmentation function. Furthermore, the lower limits of integration over z and \(\alpha \) that enter in Eq. (1) have the form,

$$\begin{aligned} z_{\textrm{min}}= & {} \left( \sqrt{m_{B}^2 + P_{T}^2}/\sqrt{s}\right) e^{Y} , \end{aligned}$$
(2)
$$\begin{aligned} \alpha _{\textrm{min}}= & {} (z_{\textrm{min}}/z)\sqrt{(m_{Q}^2 z^2 + P_{T}^2)/m_{B}^2 + P_{T}^2}, \end{aligned}$$
(3)

with \(m_B\) and Y being the mass and rapidity associated with the B-meson produced, respectively, \(m_Q\) is the heavy quark mass, and \(\sqrt{s}\) is the proton-proton center of mass energy. Also in Eq. (1) one has the hadronic cross section of the process \(pp \rightarrow Q\bar{Q}X\) is written in the following way,

$$\begin{aligned} \frac{d^{4}\sigma _{pp \rightarrow Q\bar{Q}X}}{dy d\alpha d^2p_T} = g(x_1,\mu _{F}^2)\, \frac{d^{3}\sigma _{gp \rightarrow Q\bar{Q}X}}{d\alpha d^2p_T} . \end{aligned}$$
(4)

The heavy quark momentum distribution derived within the framework of the color dipole picture in transverse momentum representation is given by [25]:

$$\begin{aligned} \frac{d^3\sigma _{gp \rightarrow Q\bar{Q}X}}{d\alpha d^2 p_T }= & {} \int \frac{d^2 \kappa _{\perp }}{6\pi \kappa ^{4}_{\perp }} \alpha _s(\mu _{F}^2)\, \mathcal{T}_{\textrm{dip}}(x_2,\kappa ^{2}_{\perp })\,\nonumber \\{} & {} H(\alpha ,\bar{\alpha },p_T,\kappa _{\perp }), \nonumber \\ H(\alpha ,\bar{\alpha },p_T,\kappa _{\perp })= & {} \bigg [\frac{9}{8}\mathcal{{I}}_0(\alpha ,\bar{\alpha },p_T) - \frac{9}{4} \mathcal{{I}}_1(\alpha ,\bar{\alpha },\vec {p}_T,\vec {\kappa }_{\perp })\nonumber \\{} & {} + \mathcal{{I}}_2(\alpha ,\bar{\alpha },\vec {p}_T,\vec {\kappa }_{\perp }) \nonumber \\{} & {} +\frac{1}{8}\mathcal{{I}}_3(\alpha ,\bar{\alpha },\vec {p}_T,\vec {\kappa }_{\perp })\bigg ]\nonumber \\{} & {} + \left[ \alpha \longleftrightarrow \bar{\alpha }\right] . \end{aligned}$$
(5)

In the expression above the running coupling at one-loop level, \(\alpha _s(\mu _{F}^2 = M^{2}_{Q\bar{Q}})\), is dependent on the invariant mass of the heavy quark pair written as \(M_{Q\bar{Q}}\simeq 2\sqrt{m_{Q}^2+p_T^2}\). Still, in Eq. (5), \(\alpha \) (\(\bar{\alpha } = 1 - \alpha \)) is the fractional gluon momentum exchanged with the quark (antiquark). Moreover, Refs. [25,26,27,28,29] provide the expressions associated to the auxiliary quantities \(\mathcal{{I}}_i\) (\(i=0,1,2,3\)).

The heavy quark transverse momentum distribution is therefore obtained in terms of the gluon dipole TMD, \(\mathcal{T}_{\textrm{dip}}\) [25]. When \(\kappa _\perp \gg \Lambda _\textrm{QCD}\) is satisfied, namely, when the momentum of the gluon in the target is large enough, we have correspondence between the \(k_\perp \)-factorization and the dipole approach [30,31,32,33], \(\mathcal{T}_\textrm{dip}(x_2,\kappa _{\perp }^2)\simeq \alpha _s\,\mathcal{F}(x_2,\kappa _{\perp }^2)\), where \(\mathcal{F}\) is the target UGD. Additionally, the dimensionless gluon UGD \(\mathcal{F}(x,k_{\perp }^2)\) is related to the quantity \(g(x,Q^2)\), the collinear gluon distribution, which appears in Eq. (4),

$$\begin{aligned} g(x_1,\mu _{F}^2) = \int ^{\mu ^2_F}\frac{dk_{\perp }^2}{\pi k_{\perp }^2}\mathcal{{F}}(x_1,k_{\perp }^2), \end{aligned}$$
(6)

being \(x_{1}\) and \(x_{2}\) fractions of the longitudinal momentum of the projectile and the target, respectively, obtained as a function of the heavy quark pair rapidity y, \(x_{1,2} = (M_{Q\bar{Q}}/\sqrt{s})e^{\pm y}\).

The UGDs can not be derived from first principles; they have to be parameterized, where various models are provided in the literature considering different underlying physical assumptions, such as dependence on rapidity, \(Y = \textrm{ln}(1/x)\), as well as transverse momentum, \(k_{\perp }\). In order to consider analytical models including parton recombination effects, we will take into account the gluon UGD model proposed by Golec-Biernat and Wüsthoff (GBW) based on saturation approach [30],

$$\begin{aligned} \mathcal{F}_{GBW}(x,k_{\perp }^2)=\frac{3\,\sigma _{0}k_{\perp }^2}{4 \pi ^2\alpha _{s}} \tau \,\textrm{exp}\left( -\tau \right) , \end{aligned}$$
(7)

where \(\tau = k_{\perp }^2/Q_{s}^2(x)\) and \(\alpha _{s} = 0.2\). The saturation scale in the proton, \(Q_{s}\), is written as \(Q_{s}^2(x) = (x_0/x)^{\lambda }\,\textrm{GeV}^2\). In present analysis, the model parameter (including heavy quarks) are taken from Ref. [34], where \(\sigma _{0} = 27.43\) mb, \(x_{0} = 0.40 \times 10^{-4}\), and \(\lambda = 0.248\). We are aware that the GBW model is an oversimplification but is quite successful in describing ep data at small-x at low and intermediate photon virtualities \(Q^2\), and is suitable to describe at least the low \(P_T\) part of the B-meson spectrum.

The range of transverse momentum available at the LHC extends far from the strict saturation region,\(P_T^2\le Q_s^2(x_2)\simeq 1\,\textrm{GeV}^2\). This means that the QCD evolution in the dipole cross section or UGD is in order. Hence, we considered a second analytical parameterization discussed in Ref. [35], inspired by the method of virtual quanta proposed by Weizsäcker and Williams (hereafter, WW parametrization). The corresponding model considers the hard gluon TMD with the asymptotic behavior of one gluon exchange between a point-like parton and a hard probe. The WW UGD has the form:

$$\begin{aligned} \mathcal{F}_{WW}(x,k_{\perp }^2)= & {} k_{\perp }^2(N_1/k_0 ^2)(1-x)^7\nonumber \\{} & {} \times {\left\{ \begin{array}{ll} (x^{\lambda } k_{\perp }^2 / k_0^2)^{-b} &{} k_{\perp }^2 \ge k_0^2, \\ x^{-\lambda b} &{} k_{\perp }^2 < k_0^2, \end{array}\right. } \end{aligned}$$
(8)

where \(N_1 = 0.24\) represents the normalization constant together with \(k_0 = 1\) GeV and \(\lambda = 0.29\). In addition, the factor \((1 - x)^7\) is associated with the suppression of the gluon distribution at large x while b is a phenomenological quantity that defines the \(k_{\perp }\)-scaling of the gluon distribution.

Fig. 1
figure 1

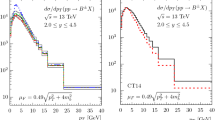
The \(B^0 + \bar{B}^0 \) (left) and \(B^{+} + B^{-}\) (right) double-differential production cross sections in pp collisions as a function of \(P_T\) and Y considering \(\sqrt{s} = 7\) TeV and forward rapidity bins. The predictions with the GBW, JMRT, and WW parameterizations are compared with the experimental measurements from the LHCb Collaboration [37]

Full size image

Finally, we construct a parametrization for the UGD based on the fits of the DLA gluon distribution applied to heavy meson production in photon-proton scattering proposed in Ref. [36]. It will be used in our numerical calculations (hereafter named JMRT parametrization). The authors estimate the gluon distribution at low-x by performing a combined description of the HERA and LHCb data for the \(J/\Psi \) production. The scale dependence of gluon PDF has the following form,

$$\begin{aligned} xg(x,\mu _{F}^2)= & {} Nx^{-a}\left( \frac{\mu _{F}^2}{Q_0^2}\right) ^b\nonumber \\{} & {} \quad \times \exp \left[ \sqrt{16(N_c/\beta _0)\ln (1/x)\ln (G)}\right] , \end{aligned}$$
(9)
$$\begin{aligned} G= & {} \frac{\ln (\mu _{F}^2/\Lambda ^2_\textrm{QCD})}{\ln (Q_0^2/\Lambda ^2_\textrm{QCD})} , \end{aligned}$$
(10)

being the parameters \(N=0.29\), \(a=-0.10\), and \(b=-0.20\) defined by a fit to the small-x data [36]. The parameters a and b account for the x and \(\mu _{F}\) dependence, respectively. The others quantities have the values of \(N_c = 3\), \(\beta _0 = 9\), \(\Lambda _\textrm{QCD} = 0.2\) GeV, and \(Q_0 =1\) GeV. The corresponding UGD is determined by means of the differential of the gluon distribution expressed as follows,

$$\begin{aligned} \mathcal{F}(x,k_{\perp }^2) =k_{\perp }^2\frac{\partial xg(x,\mu _{F}^2)}{\partial \mu _{F}^2}\biggr |_{\mu _{F}^2 =k_{\perp }^2}. \end{aligned}$$
(11)

This way, the JMRT UGD is obtained in the form:

$$\begin{aligned} \mathcal{F}_{JMRT}(x, k_{\perp }^2)= & {} \alpha _{s}k_{\perp }^2Nx^{-a}\left( \frac{k_{\perp }^2}{Q_0^2}\right) ^b \exp \left[ \sqrt{16(N_c/\beta _0)\textrm{ln}(1/x)\ln (C)}\right] \nonumber \\{} & {} \quad \times \left[ \frac{b}{k_{\perp }^2} + \left( \frac{16(N_c/\beta _0)\textrm{ln}(1/x)}{2k_{\perp }^2 \textrm{ln}\left( \frac{k_{\perp }^2}{\Lambda ^2_\textrm{QCD}}\right) \left[ \sqrt{16(N_c/\beta _0)\textrm{ln}(1/x)\textrm{ln}(C)}\right] }\right) \right] , \end{aligned}$$
(12)

where \(C = \frac{\textrm{ln}(k_{\perp }^2/\Lambda ^2_\textrm{QCD})}{\textrm{ln}(Q_0^2/\Lambda ^2_\textrm{QCD})} \).

In the next section by applying Eq. (1) we will investigate the B-meson production in high energies considering pp collisions at the LHC. Despite the validity of the color dipole picture to be restricted to small-\(x_2\) and moderate \(P_T\), the predictions are extrapolated to the full set of measurements. We checked that in the more problematic situation of central rapidities the \(x_2\) value is small than \(x_\textrm{cut}=10^{-2}\) for most part of data points. Namely, \(x_2\le x_\textrm{cut}\) for \(Y=0\) corresponds to the constraint \(P_T^2\le [(x_\textrm{cut}\sqrt{s}/2)^2-m_Q^2]\,z^2\). By using the average \(\langle z\rangle \sim 0.8 \) from the KKKS fragmentation functions [16] this gives \(P_T\lesssim 28\) GeV at 7 TeV and \(P_T\lesssim 52\) GeV at 13 TeV.

3 Results and discussions

In this work we evaluate the B-meson production in pp collisions covering the kinematic regime available by the LHC experiments. Prediction are presented based on the color dipole formalism in the transverse momentum representation. The analytical parametrizations presented before have been compared. In what follows the transverse momentum and rapidity distributions are evaluated for pp collisions and an exploratory analysis is done for the nuclear modification factor in pA collisions.

3.1 Transverse momentum and rapidity distributions

We start showing results for the \(B^0\) and \(B^{+}\) production with its respective charge conjugate as a function of the transverse momentum at forward rapidity region. A comparison is done with the experimental measurements in pp collisions reported by the LHCb [37] experiment considering the rapidity bins, \(2< Y < 2.5\), \(2.5< Y < 3\) and \(3< Y < 3.5\) at \(\sqrt{s} = 7\) TeV. Figure 1 shows the results for GBW (dashed curves), JMRT (solid curves), and WW (dot-dashed curves) parametrizations for \(B^0 + \bar{B}^0 \) (left panel) and \(B^{+} + B^{-}\) (right panel). Considering both cases, the models provide similar results at low \(P_T\). On the other hand, the results lose the concordance with the data as the \(P_T\) assumes large values. The GBW and JMRT models underestimate data. One exception is the WW prediction, which presents an agreement with the experimental measurements even at high \(P_T\) with a better description achieved in very forward rapidities. Consequently, for small \(P_T\) we can not single out the better result. However, a distinction in magnitude becomes visible at large \(P_T\) domain, being the main contrast obtained by JMRT and WW predictions.

In Fig. 2 the theoretical predictions are shown considering \(\sqrt{s} = 13\) TeV for the \(P_T\)-differential cross section that accounts the \(B^{+} + B^{-}\) mesons and the same rapidity bins as before. The corresponding data is provided by LHCb [38]. Results present the same pattern found at \(\sqrt{s} = 7\) TeV. However, some difference regarding the previous scenario can be pointed out. Now the approaches provide an enhancement in the data description at small \(P_T\) region, \(P_T < 4\) GeV.

Fig. 2
figure 2

The \(B^{+} + B^{-}\) double-differential cross sections in pp collisions in terms of \(P_T\) and Y considering \(\sqrt{s} = 13\) TeV and forward rapidity bins. The predictions with the GBW, JMRT, and WW parameterizations are compared with the experimental measurements from the LHCb Collaboration [38]

Full size image

Here some comments are in order. Recently, the description of the LHCb forward rapidity data has been studied also in Ref. [39]. There, the authors include both the gluon induced production, \(gp\rightarrow b\bar{b}X\), as the intrinsic bottom (IB) contributions. The latter is evaluated by using the so called CGC hybrid formalism [40, 41]. It was found that the kinematic range probed by the LHCb data is not sensitive to the IB effects. The spectra has been investigated only in the range \(P_T\le 15\) GeV and the quantity \(\mathcal{T}_{\textrm{dip}}(x_2,\kappa _{\perp }^2)\) in Eq. (5) is obtained in terms of a solution of the running coupling Balitsky–Kovchegov (BK) equation. In addition, the rapidity distribution is overestimated at central rapidities. The B-production has been also analysed in Refs. [42,43,44] by using the color dipole picture in the usual mixed (z, r) representation. Different mechanisms of open-heavy flavor meson production which contribute to inclusive and single diffractive cross-sections are discussed. The investigation includes the contributions of the leading twist two-pomeron fusion and higher twist corrections associated to three-pomeron fusion. The former is the contribution considered here. It was shown that the three-pomeron fusion effect is significant at small transverse momenta. Both contributions are written in terms of the dipole scattering amplitude, \(N(x,\vec {r})\), and in the numerical calculations [42] the CGC parametrization [45] has been used. The integrated gluon distribution, \(xg(x,Q^2)\) is calculated directly in term of the dipole amplitude,

$$\begin{aligned}{} & {} xg(x,Q^2) = \frac{C_FQ}{2\pi ^2 \bar{\alpha }_S} \int d^2\vec {r}\, \frac{J_1(Qr)}{r}\,\nabla ^2_r N(x,\vec {r}), \nonumber \\{} & {} \quad \mathcal{{F}}(x,k^2) = \left. \frac{\partial xg(x,Q^2)}{\partial \ln Q^2}\right| _{Q^2=k^2}, \end{aligned}$$
(13)

where \(C_F = (N_c^2-1)/2N_c\) and \(\bar{\alpha }_s=\alpha _sN_c/\pi \). We believe that the GBW parametrization used in present calculations is very close to the results obtained in Ref. [42]. In the context of \(k_T\)-factorization formalism, B production has been analyzed in Ref. [46] using a variable-flavor-number scheme. Prediction for 7 TeV are presented there and in general the large \(p_T\) region is better described as in our case. The possible reason is the inclusion of subprocesses like \(gQ\rightarrow gQ\) and \(q\bar{q}\rightarrow Q\bar{Q}\) which can contribute at large transverse momentum. Similar results are obtained within the parton reggeization approach [47] as well as in the CASCADE MC predictions [48].

Let us now move to the predictions where the B-meson production cross section is obtained in terms of the rapidity. In Fig. 3 (left panel) the results for \(B^0\) production in pp collisions consider the kinematic region of the data collected by the CMS [49] experiment, namely, center of mass energy of 7 TeV with \(P_T > 5\) GeV. The theoretical calculations show that the considered parameterizations underestimate the measurements at central rapidity and forward rapidities. By comparing the predictions with those found in the literature, see Ref. [49], they are similar to the calculations using Monte Carlo simulations [13]. In [49] Monte Carlo MC@NLO has been used assuming the bottom quark mass as \(m_b = 4.75\) GeV, and the CTEQ6M for the parton distribution functions. On the other hand, in Fig. 3 (right panel) the results are compared to the \(B^{+} + B^{-}\) measurements from LHCb [38] at \(\sqrt{s} = 13\) TeV. The transverse momentum is integrated over the interval \(0< P_T < 40\) GeV. Now, the predictions give a reasonable description of the data. This is probably due to inclusion of the low-\(P_T\) region in the integration interval which is well described by the models and the smaller values of \(x_2\) obtained in high energies and very forward rapidities. The JMRT UGD result is more compatible with data within the uncertainties, while the prediction with WW presents an improvement in the data description considering the large-Y domain.

Fig. 3
figure 3

The \(B^0\) (left panel) and \(B^{+} + B^{-}\) (right panel) differential cross sections in pp collisions in terms of meson rapidity Y. The predictions with the GBW, JMRT, and WW parameterizations are compared with the data provided by the CMS Collaboration at \(\sqrt{s} = 7\) TeV [49] and by the LHCb Collaboration at \(\sqrt{s} = 13\) TeV [38]

Full size image

In Fig. 4 results are shown for the B-meson \(P_T\) spectrum with the rapidity integrated over different intervals. In Fig. 4 (left panel) predictions are provided for \(\sqrt{s} = 13\) TeV and \(2< Y < 4.5\) which is the kinematic accessible in the LHCb [38] detector for \(B^{+} + B^{-}\) measurements. Data is fairly described at low \(P_T\) whereas the large transverse momentum region is underestimated. This is a similar trend as verified in Fig. 2. On the other hand, in Fig. 4 (right panel) the data for \(B^{+}\) measured by the ATLAS [50] at \(\sqrt{s} = 7\) TeV (\(|Y| < 2.25\)) and by the CMS [51, 52] (\(|Y| < 2.4\) and two values for the center of mass energy, \(\sqrt{s} = 5.02\) and 7 TeV) are compared to the theoretical predictions. It is important to stress that in the ATLAS data the differential cross section is multiplied by the branching ratio to the final state, which is \(6.03 \times 10^{-5}\). It seems that the predictions can describe the shape of the \(P_T\) data taking into account the corresponding uncertainties. The difference in the results is small between the JMRT and GBW models. Particularly, at 5.02 TeV this difference starts to growth moderately for large \(P_T\). The predictions fall slightly faster than the measured \(P_T\) spectrum. Additionally, the WW UGD does a better job in high \(P_T\) data description in all cases.

Fig. 4
figure 4

The \(B^{+} + B^{-}\) (left panel) and \(B^{+}\) (right panel) differential cross sections in pp collisions in terms of \(P_T\). The predictions with the GBW, JMRT, and WW parameterizations are compared with the data provided by the LHCb Collaboration at \(\sqrt{s} = 13\) TeV [38], by the ATLAS Collaboration at \(\sqrt{s} = 7\) TeV [50] and by the CMS Collaboration at \(\sqrt{s} = 5.02\) and 7 TeV [51, 52]

Full size image

Worth mentioning that the ratios between different B-mesons cross sections could show evidence of \(P_T\) and Y dependencies and it can be suggested as a future measurement in data taking. This possibly helps to extract information between the fragmentation functions of bottom quarks to \(B^0\), \(B^{+}\), and \(B^{-}\) mesons and also allows comparison with others fragmentation function models.

3.2 Nuclear modification factor

We will study the B-meson production in pA collisions by performing an analysis regarding the nuclear modification factor, \(R_{pA}\). This observable is defined by means of the quotient between pA to pp cross sections being scaled through the mass number A of the target nucleus,

$$\begin{aligned} R_{pA}(Y,P_T) = \frac{d^{3}\sigma _{(pA \rightarrow BX)}/dY d^2P_T}{A \cdot d^{3}\sigma _{(pp \rightarrow BX)}/dY d^2P_T}. \end{aligned}$$
(14)

Our purpose of investigation consists in applying the geometric scaling property as well as by using a nuclear UGD version based on the Glauber–Gribov formalism. The QCD nuclear effects that take place in heavy nuclei collisions can be accounted by geometric scaling (GS) property derived from parton saturation [53] within the color dipole picture. The geometric scaling considers that the nuclear effects are included in the nuclear saturation scale (\(Q_{s,A}\)) as well as in the nucleus transverse area (\(S_A\)) taking the proton (\(S_p\)) as reference. As a consequence, one can replace the proton saturation scale by the respective nuclear one,

$$\begin{aligned} Q_{s,A}^2=Q_{s,p}^2\left( \frac{AS_p}{S_A}\right) ^{\Delta }, \end{aligned}$$
(15)

where \(\Delta = (0.79)^{-1}\), \(S_p=\sigma _0/2=\pi R_p^2\), and \(S_A=\pi R_A^2\) with \(R_A\simeq 1.12 A^{1/3}\) fm. Following this approach one arrives to a simplified expression for the pA cross section assuming that the UGD for protons presents scaling, which is the case for GBW model [the results using GS will be labeled as GS (GBW)]. Correspondingly, the B-meson cross section in pA collisions is given by,

$$\begin{aligned}{} & {} \frac{d^{3}\sigma {(pA \rightarrow BX)}}{dY d^2P_T} \nonumber \\{} & {} \qquad = \left( \frac{S_A}{S_p}\right) \left. \frac{d^{3}\sigma {(pp \rightarrow BX)}}{dY d^2P_T}\right| _{Q_{s,p}^2(x_2)\rightarrow Q_{s,A}^2(x_2)}. \end{aligned}$$
(16)

On the other hand, the B-meson spectrum can be obtained by considering the nuclear form for the unintegrated gluon distribution. In Ref. [54] the nuclear UGD is dependent on the impact parameter and it is derived by assuming the Glauber–Gribov description for the dipole-nucleus cross section taking the GBW model as input. Therefore, based on the assumptions reported, the nuclear UGD is given by

$$\begin{aligned}{} & {} \mathcal{{F}}_{nuc}(x,k_{\perp },b) = \frac{3}{\pi ^2\alpha _{s}}\frac{k^{2}_{\perp }}{Q_{s,p}^2} \sum _{n=1}^{\infty } \frac{(-B)^{n}}{n!} \nonumber \\{} & {} \quad \times \sum _{\ell =0}^{n} C_{n}^{\ell }\frac{(-1)^\ell }{\ell } \,\textrm{exp}\left( -\frac{k_{\perp }^2}{\ell \,Q_{s,p}^2}\right) , \end{aligned}$$
(17)

where \(\mathcal{{F}}_A(x_2,k_{\perp }^2) = \int d^2b\, \mathcal{{F}}_{nuc}(x_2,k_{\perp },b)\) and the series is rapidly convergent for heavy nucleus. Moreover, \(B = AT_{A}(b)\sigma _{0}/2\) and \(T_{A}(b)\) is the nuclear thickness function. The obtained nuclear UGS will be labeled as UGDnuc.

We are now in conditions to show the numerical results for the nuclear modification factor accounting the \(B^{+}\) meson produced in pPb collisions at \(\sqrt{s} = 8.16\) TeV. In Fig. 5 the associated predictions are compared directly to the measurements obtained by the LHCb experiment [55] in terms of \(P_T\). As one can observe considering forward rapidity bin, \(2.5< Y < 3.5\), the measured nuclear modification factor presents an suppression at low \(P_T\) range. However, for high \(P_T\), \(R_{pPb}\) is consistent with unity within the uncertainties, implying that the nuclear effects do not have an influence role for \(B^{+}\) production at large \(P_T\) and forward rapidity range. Additionally, our results demonstrated a weakly dependence as a function of \(P_T\), and the corresponding approaches do not indicate the presence of important nuclear effects in this particular kinematic regime. This is explicitly verified by the predictions reproducing numerically \(R_{pPb}\simeq 1.2\) for GS (GBW) and \(R_{pPb}\simeq 1\) for UGDnuc.

Let us compare our calculations with other approaches in the literature. A study performing the reweighting of the two referred nPDFs (nCTEQ15 and EPPS16) using the LHC data for D, \(J/\psi \), B and \(\Upsilon (1S)\) production in proton-lead collisions at LHC has been done in Ref. [56]. Respect to B production, as the data are not precise enough in the kinematic region where reweighting has been applied the results presented marginal deviation from the original nPDFs. The predictions are in good agreement within the experimental and theoretical uncertainties. Conversely, the role played by the nuclear effects driven by the fully coherent energy loss (FCEL) in cold nuclear matter on the open heavy-flavour production has been investigated in Ref. [57]. It was shown that the FCEL effects on D and B production are quite relevant and similar to those quantified in quarkonium and light hadron production. It is argued that the effect corresponds to about half of the nuclear suppression measured at the LHC at forward rapidities and low \(P_T\) [57]. Our results are compared to FCEL approach as shown in Fig. 5. The UGDnuc result is fairly similar to that from FCEL calculation.

In the context of the CGC framework, Ref. [58] presents the nuclear modification factor \(R_{pA}^{B}(Y,P_T)\) at forward rapidities. The calculations make use of the Glauber model to obtain the dipole-nucleus cross section, \(\sigma _{dA}(x,r,b)\). The transverse momentum dependent multi-point Wilson line correlators are used to describe the target nucleus and proton projectile. The corresponding UGDs are obtained from the numerical solution of the running coupling Balitsky–Kovchegov (rcBK) equation. The results are consistent with data and a significant dependence on the initial nuclear saturation scale, \(Q_{s0,A}^2\), for the amount of nuclear shadowing appearing in \(R_{pA}^B\) as a function of \(P_T\).

Fig. 5
figure 5

The nuclear modification factor for \(B^{+}\) production considering the kinematic regime \(\sqrt{s} = 8.16\) TeV and \(2.5< Y < 3.5\) in pPb collisions. The predictions are obtained using the GS (GBW) and UGDnuc approaches. Result from FCEL approach is also presented as a matter of comparison, together with experimental data from the LHCb Collaboration [55]

Full size image

Recently, in the context of the \(k_T\)-factorization approach analytical unintegrated gluon and sea quark densities in nuclei have been are derived [59]. A rescaling model has been considered to construct the nuclear distributions from the proton ones. They were used to evaluate the inclusive heavy flavor production in proton-lead collisions at the LHC. The evaluated nuclear modification factor for \(B^+\) meson at 5.02 TeV integrated over the rapidity and \(p_T\) is \( R^{B^+}= 0.77\,^{+0.02}_{-0.03}\), where estimated theoretical uncertainties are due to \(\mu _F^2\) scale variation. Similar results are also obtained within the general-mass variable-flavour-number scheme (GM-VFNS) at same energy [60]. In both cases, \(R_{pA}\) does not reveal the presence of significant nuclear initial-state interaction effects. This is in line with the study in Ref. [61], where the NLO SACOT-\(m_T\) scheme has been used in the case of B-production. The \(R_{pPb}\) at 8.16 TeV has been computed using the EPPS21 and nNNPDF3.0 nuclear PDFs and the predictions agree very well with the data.

4 Summary

We performed an investigation on the B-meson production at high energies in pp collisions at the LHC. The theoretical formalism is the color dipole in transverse momentum representation equipped with different unintegrated gluon distributions parametrizations. We verified that the results fairly describe the momentum distribution at small \(P_T\), while a deviation from the measurements becomes apparent towards high values of \(P_T\); this is particularly more intense when using the GBW and JMRT models. At the same time, considering the \(P_T\) and Y distributions, the WW result is more suitable regarding the measured spectrum. The model seems to be consistent when extrapolated to high \(P_T\) and very forward rapidity region. Moreover, an exploratory study is done concerning the B-meson production in pA collisions. The respective results regarding the nuclear modification factor do not show a suppression behavior considering the \(P_T\) spectrum measured in forward rapidity range.

The B-meson production in pp case can be addressed in the color dipole transverse momentum representation which can be convenient for further investigation aiming the heavy-ion mode. The phenomenology associated to the dipole formalism and the UGDs can be refined in order to develop a better description of large \(P_T\) contributions.