1 Introduction

Modified gravity theories have emerged as contenders to address several shortcomings of general relativity (\(\mathcal{G}\mathcal{R}\)) [1, 2]. A key objective of these theories is to elucidate the enigma of dark matter (\(\mathcal{D}\mathcal{M}\)) and dark energy (\(\mathcal{D}\mathcal{E}\)) in our observable universe. In addition, another point of concern is the accelerated expansion of the universe. While \(\mathcal{G}\mathcal{R}\) effectively explains various cosmological phenomena, such as the recent detection of gravitational waves, modified gravity theories seek to refine or provide alternative explanations that better accommodate these observations. By proposing variations in the laws of gravity, these theories offer avenues for testing in extreme regimes, thereby probing fundamental physics beyond the predictions of \(\mathcal{G}\mathcal{R}\). Some variants aim to unify gravity with other fundamental forces, like the strong, weak, and electromagnetic forces, into a cohesive framework, striving for a unified theory of fundamental interactions.

\(\mathcal{G}\mathcal{R}\) predicts singularities, like those at the center of black holes, where our current understanding of physics falters. Modified gravity theories often endeavor to address these singularities and investigate the interplay between gravity and quantum mechanics in extreme gravitational conditions. Several modified theories of gravity have been proposed so far. Among them, models such as \(F({\mathcal {R}})\) [3], \(F({\mathcal {T}})\) [4], and \(F(\mathcal {{\mathcal {T}}, {\mathcal {R}}})\) [5], \(F({\mathcal {G}})\)-gravity [6] and other gravity theories represent alternatives to \(\mathcal{G}\mathcal{R}\), aiming to account for certain cosmological observations. However, despite their potential to reconcile observational discrepancies, these theories encounter challenges such as consistency with experimental data, the ability to explain a broad spectrum of observations, and passing stringent tests like precision gravity tests within the solar system, as well as the predictive success of \(\mathcal{G}\mathcal{R}\), including phenomena like gravitational waves. The pursuit of modified gravity models remains an active and vibrant field within modern physics [7,8,9,10,11,12].

In this study, our focus centers on a distinctive variant of modified gravity theory known as \(\mathcal{R}\mathcal{I}\) gravity, which was recently introduced in [13]. This model hinges on the introduction of a geometric quantity termed the anti-curvature scalar, denoted as \({\mathcal {A}}=g_{\mu \nu }\,A^{\mu \nu }\), where \({\mathcal {A}}\) represents the trace of the anti-curvature tensor \(A^{\mu \nu }\). This tensor is intricately linked with the Ricci tensor, \(R_{\mu \nu }\), through the relationship \(A^{\mu \nu }\,R_{\mu \sigma }=\delta ^{\nu }_{\sigma }\). In a related work [14], two distinct classes of \(\mathcal{R}\mathcal{I}\) models were explored: Class-I and Class-II models. Class-I models take the form \(f({\mathcal {R}}, {\mathcal {A}})\), where f represents a function of the Ricci scalar (\({\mathcal {R}}\)) and the anti-curvature scalar (\({\mathcal {A}}\)). On the other hand, Class-II models are expressed as \(f({\mathcal {R}}, A^{\mu \nu }\,A_{\mu \nu })\), where f denotes a function of the Ricci scalar and the square or quadratic invariant of the anti-curvature tensor. In another study [15], the necessity of modified gravity theories was thoroughly discussed and compared with the standard \(\mathcal{G}\mathcal{R}\) theory. Recently, there has been a surge of interest in investigating this \(\mathcal{R}\mathcal{I}\) gravity theory across various physical scenarios, as documented in the literature [16,17,18,19,20,21,22,23,24,25,26,27,28]. These investigations underscore the growing relevance and applicability of \(\mathcal{R}\mathcal{I}\) gravity in diverse contexts.

The existence of closed time-like curves (CTCs) in a space-time within the context of general relativity is typically considered problematic as it leads to violations of causality, which can result in paradoxes. Several space-time models have been constructed, including the Gödel rotating solutions and Kerr solutions in general relativity. It is also well-known that the presence of closed time-like curves in a space-time leads to the possibility of time travel. To address this issue, Hawking proposed a Chronology Protection Conjecture (CPC). However, to date, there is no rigorous proof of this conjecture. In the context of \(f({\mathcal {R}}, {\mathcal {A}})\) gravity, if the theory permits the existence of CTCs, it would likely require some form of modification to avoid the associated causality violations or it existences can not be discarded analogue to the general relativity. One possible approach to modifying the theory to avoid CTCs could involve imposing constraints on the form of the function \(f({\mathcal {R}}, {\mathcal {A}})\) or introducing additional terms in the action that prevent the emergence of closed time-like curves. For example, one might impose conditions on the curvature scalar to ensure that CTCs do not arise. Another approach could involve incorporating quantum effects or additional fields into the theory to resolve the causality issues associated with CTCs. This might involve considering the effects of matter fields or quantum corrections on the geometry of space-time. Overall, modifying the \(f({\mathcal {R}}, {\mathcal {A}})\) gravity theory to avoid CTCs would likely require careful consideration of the theory’s mathematical structure and physical implications, and may involve introducing new constraints or additional degrees of freedom.

The Gödel metric in the cylindrical coordinates \((t, r, \phi , z)\) is given by the following line-element [29]:

$$\begin{aligned} ds^2= & {} 4\,a^2\Big [dt^2-dr^2-dz^2-\sinh ^2 r (1-\sinh ^2 r)\,d\phi ^2\nonumber \\{} & {} +2\,\sqrt{2}\,\sinh ^2 r\,dt\,d\phi \Big ], \end{aligned}$$
(1)

where a is a constant. It’s noteworthy that the determinant of the Ricci tensor \(R_{\mu \nu }\) derived from the metric tensor \(g_{\mu \nu }\) of this space-time is zero, that means, \(\det (R_{\mu \nu })=0\). This property leads to the presence of circular closed time-like curves (CTCs) at certain finite radial distances \(r > r_0(=\ln (\sqrt{2}+1))\). Despite the violation of causality norms by the formation of CTCs in the Gödel cosmological solution (1), simply imposing the Chronology Protection Conjecture (CPC) isn’t sufficient to discard this solution in GR. At \(r=r_0\), this space-time allows closed null curves or geodesics (CNCs or CNGs). The existence of closed time-like curves in general relativity contravenes the causality principles. However, this cosmological solution becomes invalid within the framework of the newly proposed Ricci-inverse gravity theory due to the absence of the anti-curvature tensor for this space-time model since \(\det (R_{\mu \nu })=0\). Consequently, the formation of CTCs is precluded within the context of Ricci-inverse gravity.

In this study, we investigate an example of axially symmetric cosmological space-time, an exact solution to Einstein’s field equations in general relativity. This axially symmetric space-time forms closed time-like curves, thereby breaching causality constraints. These closed time-like curves emerge at a specific time instance satisfying \(t=t_0>0\) from an initial spacelike hypersurface in a causally permissible manner. A Cauchy horizon delineates the causal regions from the non-causal one. We intend to employ this axially symmetric space-time model within the framework of modified gravity, specifically in Ricci-inverse gravity, to ascertain whether this chosen cosmological model constitutes a valid solution in this novel theory. If we can demonstrate that the selected cosmological model is also a plausible solution in this new theory, it would corroborate the possibility of CTCs formation akin to general relativity within Ricci-inverse gravity.

The paper is structured as follows: In Sect. 2, we address an axially symmetric space-time within the framework of modified gravity theory. Specifically, we focus on Ricci-inverse gravity of class-II models, where the function \(f({\mathcal {R}}, A^{\mu \nu }\,A_{\mu \nu })\) is incorporated into the Einstein-Hilbert action. We rigorously analyze the implications of this modified theory on the chosen space-time metric. Moving on to Sect. 3, we explore the same space-time metric within the realm of Ricci-inverse gravity of class-III models. Here, we introduce the function \(f({\mathcal {R}}, {\mathcal {A}}, A^{\mu \nu }\,A_{\mu \nu })\) into the EH-action and investigate its consequences. In both sections, we meticulously derive the modified field equations corresponding to the respective classes of Ricci-inverse gravity models and proceed to solve them to elucidate the behavior of the system. Lastly, in Sect. 4, we summarize our findings and draw conclusions. Notably, we remark that the investigated cosmological space-time stands as a valid solution within the framework of Ricci-inverse gravity theory in both class of models. This implies the admissibility of closed time-like curves within this modified gravitational framework, that is, Ricci-inverse gravity thereby giving rise to a time-travel possibility.

2 Axially symmetric metric in Ricci-inverse gravity: Class-II models

In this section, the main objective is to investigate an axially symmetric metric in Ricci-inverse gravity. However, for such an analysis, different classes of this gravitational theory will be considered. Ricci-inverse gravity Class II consists of a function that depends on the Ricci scalar R and the square of anti-curvature tensor, i.e. \(f(R,A^{\mu \nu }A_{\mu \nu })\). The action that describes this gravitational theory is given as

$$\begin{aligned} S= & {} \int d^4x \sqrt{-g}\left[ f(R, A^{\mu \nu }A_{\mu \nu })-2\,\Lambda +{{{\mathcal {L}}}}_m\right] , \end{aligned}$$
(2)

where \(A^{\mu \nu }\) is the anti-curvature tensor which is the inverse of the Ricci tensor \(R_{\mu \nu }\), that means, \(A^{\mu \nu }=R^{-1}_{\mu \nu }\). Also \({\mathcal {A}}\) is the anti-curvature scalar defined by \({\mathcal {A}}=g_{\mu \nu }\,A^{\mu \nu } \ne R\).

To obtain the modified Einstein equations, we perform a variation with respect to the metric tensor, leading to

$$\begin{aligned}{} & {} f_R R^{\mu \nu } - \frac{1}{2}fg^{\mu \nu }+\Lambda g^{\mu \nu } - 2f_{A^2}A^{\rho \nu }A^{\mu }_{\rho }\nonumber \\{} & {} \quad - \nabla ^{\mu } \nabla ^{\nu }f_{R} + g^{\mu \nu } \nabla ^{\lambda }\nabla _{\lambda }f_{R} + g^{\rho \nu } \nabla _{\alpha } \nabla _{\rho }( f_{A^2}A_{\sigma \kappa } A^{\sigma \alpha }A^{\kappa \mu })\nonumber \\{} & {} \quad - \nabla ^2(f_{A^2}A_{\sigma \kappa } A^{\sigma \mu }A^{\kappa \nu }) - g^{\mu \nu } \nabla _{\alpha } \nabla _{\rho }(f_{A^2}A_{\sigma \kappa } A^{\sigma \alpha }A^{\kappa \rho }) \nonumber \\{} & {} \quad + 2g^{\rho \nu } \nabla _{\rho } \nabla _{\alpha }( f_{A^2}A_{\sigma \kappa } A^{\sigma \mu }A^{\kappa \alpha } ) \nonumber \\{} & {} \quad -g^{\rho \nu } \nabla _{\alpha } \nabla _{\rho }(f_{A^2}A_{\sigma \kappa } A^{\sigma \mu }A^{\kappa \alpha }) =T^{\mu \nu } \,, \end{aligned}$$
(3)

with \(f=f(R, A^{\mu \nu }A_{\mu \nu })\), \(f_R=\partial f/\partial R\), \(f_{A^2}=\partial f/\partial (A^{\mu \nu }A_{\mu \nu })\) and \(T^{\mu \nu }\) being the energy–momentum tensor which is defined as

$$\begin{aligned} T^{\mu \nu }=\frac{1}{\sqrt{-g}}\frac{\delta (\sqrt{-g}{\mathcal {L}}_{m})}{\delta g_{\mu \nu }}. \end{aligned}$$
(4)

In order to express the field equations more succinctly, let’s define the following tensors

$$\begin{aligned} Y^{\mu \nu }\equiv 2f_{A^2}A^{\rho \nu }A^{\mu }_{\rho } \end{aligned}$$
(5)

and

$$\begin{aligned} U^{\mu \nu }\equiv & {} - \nabla ^{\mu } \nabla ^{\nu }f_{R} + g^{\mu \nu } \nabla ^{\lambda }\nabla _{\lambda }f_{R} \nonumber \\{} & {} + g^{\rho \nu } \nabla _{\alpha } \nabla _{\rho }( f_{A^2}A_{\sigma \kappa } A^{\sigma \alpha }A^{\kappa \mu }) \nonumber \\{} & {} - \nabla ^2(f_{A^2}A_{\sigma \kappa } A^{\sigma \mu }A^{\kappa \nu }) \nonumber \\{} & {} - g^{\mu \nu } \nabla _{\alpha } \nabla _{\rho }(f_{A^2}A_{\sigma \kappa } A^{\sigma \alpha }A^{\kappa \rho }) \nonumber \\{} & {} + 2g^{\rho \nu } \nabla _{\rho } \nabla _{\alpha }( f_{A^2}A_{\sigma \kappa } A^{\sigma \mu }A^{\kappa \alpha } ) \nonumber \\{} & {} -g^{\rho \nu } \nabla _{\alpha } \nabla _{\rho }(f_{A^2}A_{\sigma \kappa } A^{\sigma \mu }A^{\kappa \alpha }) \,. \end{aligned}$$
(6)

Then the field equation (3) becomes

$$\begin{aligned} f_R R^{\mu \nu } - \frac{1}{2}fg^{\mu \nu }+\Lambda g^{\mu \nu } - Y^{\mu \nu } +U^{\mu \nu } =T^{\mu \nu }. \end{aligned}$$
(7)

Now, our objective is to solve this field equation, considering an axially symmetric metric as the cosmological background, which exhibits Closed Timelike Curves (CTCs) [30] (see also Ref. [31] for CTCs). The line element that defines this solution is given as follows

$$\begin{aligned} \textrm{d}s^2 = \frac{\textrm{d}r^2}{\alpha ^2 r^2} + r^2 \textrm{d}z^2 +\left( -2r^2\textrm{d}t + \frac{\beta z \textrm{d}r}{r^2}-tr^2 \textrm{d}\phi \right) \textrm{d}\phi ,\nonumber \\ \end{aligned}$$
(8)

where \(\alpha \) and \(\beta \) are non-zero constants, with \(\beta >0\). To solve Eq. (7) let’s calculate the non-zero components of the Ricci tensor which are given as

$$\begin{aligned} R_{02} = R_{20}= & {} 3 \alpha ^2 r^2 \,,\nonumber \\ R_{11}= & {} -\frac{3}{r^2} \,,\nonumber \\ R_{12} = R_{21}= & {} -\frac{3 \alpha ^2 \beta z}{2 r^2} \,,\nonumber \\ R_{22}= & {} \frac{\alpha ^2 \left( \beta ^2+24 r^6 t\right) }{8 r^4}\,,\nonumber \\ R_{33}= & {} -3 \alpha ^2 r^2 \,, \end{aligned}$$
(9)

and the contravariant components are

$$\begin{aligned} R^{00}= & {} \frac{\alpha ^2 \left[ \beta ^2 \left( 1-6 \alpha ^2 r^2 z^2\right) -24 r^6 t\right] }{8 r^8} \,,\nonumber \\ R^{01} = R^{10}= & {} -\frac{3 \alpha ^4 \beta z}{2 r^2} \,,\nonumber \\ R^{02} = R^{20}= & {} \frac{3 \alpha ^2}{r^2} \,,\nonumber \\ R^{11}= & {} -3 \alpha ^4 r^2 \,,\nonumber \\ R^{33}= & {} -\frac{3 \alpha ^2}{r^2}\,. \end{aligned}$$
(10)

The Ricci scalar is given as

$$\begin{aligned} R=g_{\mu \nu }R^{\mu \nu }= & {} -12 \alpha ^2. \end{aligned}$$
(11)

In addition, the Kretschmann scalar for the space-time (8) is calculated. Its value given by

$$\begin{aligned} R_{\rho \sigma \mu \nu }R^{\rho \sigma \mu \nu }= & {} 24 \alpha ^4 \end{aligned}$$
(12)

is a constant. The considered space-time (8) appears to be free from curvature singularities. However, it is worth noting that the metric components \(g_{rr}\) and \(g_{r\phi }\) exhibit a divergence at \(r=0\), indicating a coordinate singularity.

Another important ingredient is the anti-curvature tensor defined as \(A^{\mu \nu }=R_{\mu \nu }^{-1}\). To find the non-zero components of the anti-curvature tensor the following definition is used

$$\begin{aligned} A^{\mu \nu }= \frac{1}{det[R_{\mu \nu }]}adj[R_{\mu \nu }]. \end{aligned}$$
(13)

To calculate this quantity, it is necessary to analyze whether the determinant of the Ricci tensor is non-zero, as the inversion of \(R_{\mu \nu }\) is impossible if it is zero. Then for the metric (8) we have

$$\begin{aligned} det[R_{\mu \nu }] = -81 \alpha ^6 r^4 \,. \end{aligned}$$
(14)

Then using definition (13) the non-zero contravariant components of the anti-curvature tensor are given as

$$\begin{aligned} A^{00}= & {} -\frac{6 \alpha ^2 \beta ^2 r^2 z^2+\beta ^2+24 r^6 t}{72 \alpha ^2 r^8} \,,\nonumber \\ A^{01} = A^{10}= & {} -\frac{\beta z}{6 r^2} \,,\nonumber \\ A^{02} = A^{20}= & {} \frac{1}{3 \alpha ^2 r^2} \,,\nonumber \\ A^{11}= & {} -\frac{r^2}{3} \,,\nonumber \\ A^{33}= & {} -\frac{1}{3 \alpha ^2 r^2} \end{aligned}$$
(15)

and the covariant components are

$$\begin{aligned} A_{02} = A_{20}= & {} \frac{r^2}{3 \alpha ^2} \,,\nonumber \\ A_{11}= & {} -\frac{1}{3 \alpha ^4 r^2} \,,\nonumber \\ A_{12} = A_{21}= & {} -\frac{\beta z}{6 \alpha ^2 r^2} \,,\nonumber \\ A_{22}= & {} -\frac{\beta ^2-24 r^6 t}{72 \alpha ^2 r^4} \,,\nonumber \\ A_{33}= & {} -\frac{r^2}{3 \alpha ^2} \,. \end{aligned}$$
(16)

In addition, the anti-curvature scalar is

$$\begin{aligned} A=g_{\mu \nu }A^{\mu \nu }= & {} -\frac{4}{3 \alpha ^2}. \end{aligned}$$
(17)

Comparing Eqs. (11) and (17) it is verified that

$$\begin{aligned} A\ne R^{-1}. \end{aligned}$$
(18)

With these ingredients, let’s proceed to solve the field equation (7), considering the Ricci-inverse function as follows

$$\begin{aligned} f(R,A^{\mu \nu }A_{\mu \nu }) = R+k\, A^{\mu \nu }A_{\mu \nu } \,, \end{aligned}$$
(19)

that leads to

$$\begin{aligned} f_R=1 \,,\quad \quad \quad f_{A^2}=k \,. \end{aligned}$$
(20)

Then the field equation reads

$$\begin{aligned}{} & {} R^{\mu \nu } - \frac{1}{2}R\, g^{\mu \nu } -\frac{1}{2}\kappa \, A^{\alpha \beta }A_{\alpha \beta } \, g^{\mu \nu } -Y^{\mu \nu } + U^{\mu \nu } + \Lambda \, g^{\mu \nu } \nonumber \\{} & {} \quad = T^{\mu \nu }\,. \end{aligned}$$
(21)

The non-zero components of the tensor \(Y^{\mu \nu }\) are given as

$$\begin{aligned} Y^{00}= & {} \frac{\kappa \left[ \beta ^2 \left( 3 \alpha ^2 r^2 z^2+1\right) +12 r^6 t\right] }{54 \alpha ^4 r^8}\,,\nonumber \\ Y^{01}= & {} \frac{\beta \kappa z}{9 \alpha ^2 r^2}\,,\nonumber \\ Y^{02}= & {} -\frac{2 \kappa }{9 \alpha ^4 r^2}\,,\nonumber \\ Y^{11}= & {} \frac{2 \kappa r^2}{9 \alpha ^2}\,,\nonumber \\ Y^{33}= & {} \frac{2 \kappa }{9 \alpha ^4 r^2}\,. \end{aligned}$$
(22)

While the only non-zero component of the tensor \(U^{\mu \nu }\) is

$$\begin{aligned} U^{00} = \frac{2 \beta ^2\kappa }{27 \alpha ^4 r^8}. \end{aligned}$$
(23)

Therefore, all geometric ingredients have been accounted for. Now, it is necessary to choose the content of matter. Here the pure radiation is chosen as the matter content whose energy–momentum tensor is defined as

$$\begin{aligned} T^{\mu \nu }=\rho \zeta ^{\mu } \zeta ^{\nu }\,, \end{aligned}$$
(24)

where

$$\begin{aligned} \zeta ^{\mu } = (1,0,0,0) \, \end{aligned}$$
(25)

is a null vector and \(\rho \) is the energy density.

Therefore, Eq. (21) leads to the set of equations

$$\begin{aligned} \rho= & {} \frac{1}{72 \alpha ^4 r^8}\Bigl [54 \alpha ^8 \beta ^2 r^2 z^2+9 \alpha ^6 \left[ \beta ^2 \left( 2 \Lambda r^2 z^2+1\right) +24 r^6 t\right] \nonumber \\{} & {} +72 \alpha ^4 \Lambda r^6 t-8 \alpha ^2 \beta ^2 \kappa r^2 z^2+4 \kappa \left( \beta ^2-8 r^6 t\right) \Bigl ]\,,\end{aligned}$$
(26)
$$\begin{aligned} 0= & {} \frac{\beta z \left( 27 \alpha ^6+9 \alpha ^4 \Lambda -4 \kappa \right) }{18 \alpha ^2 r^2}\,,\nonumber \\ 0= & {} -\frac{27 \alpha ^6+9 \alpha ^4 \Lambda -4 \kappa }{9 \alpha ^4 r^2}\,,\nonumber \\ 0= & {} \frac{r^2 \left( 27 \alpha ^6+9 \alpha ^4 \Lambda -4 \kappa \right) }{9 \alpha ^2}\,,\nonumber \\ 0= & {} \frac{27 \alpha ^6+9 \alpha ^4 \Lambda -4 \kappa }{9 \alpha ^4 r^2}\,, \end{aligned}$$
(27)

Solving these equations for \(\rho \) and \(\Lambda \), we obtain

$$\begin{aligned} \rho= & {} \frac{\beta ^2 \left( 9 \alpha ^6+4 \kappa \right) }{72 \alpha ^4 r^8} \,, \end{aligned}$$
(28)
$$\begin{aligned} \Lambda= & {} -\frac{27 \alpha ^6-4 \kappa }{9 \alpha ^4}\,. \end{aligned}$$
(29)

The first conclusion drawn from these results is that when the coupling constant \(\kappa =0\), the solution in general relativity is recovered, namely \(\rho = \frac{\alpha ^2 \beta ^2}{8 r^8}\) and \(\Lambda =-3 \alpha ^2\). Thus, in Ricci-inverse gravity - Class II, causality violation is permitted by this metric, albeit altering the standard result of general relativity. Additionally, if \(\kappa \) is positive, the energy density satisfies the energy condition, meaning it is always positive, and the cosmological constant is entirely negative, consistent with general relativity. It’s worth noting that the energy–density \(\rho (r)\) diverse at \(r=0\), indicating a coordinate singularity, given that the space-time is devoid of any curvature singularity.

3 Axially symmetric metric in Ricci-inverse gravity: Class-III models

In this study, we explore a different class of the Ricci-inverse gravity model, namely Class III using the same space-time (8). In this class, the function in the gravitational action takes the form \(f(R, A, A^{\mu \nu }\,A_{\mu \nu })\). Then the corrections due to the anti-curvature tensor are of first and second-order. In this way the action describing this theory is given as

$$\begin{aligned} S = \int \textrm{d}x^4 \sqrt{-g}\,[ f(R,A,A^{\mu \nu }A_{\mu \nu })-2\,\Lambda ]+ S_M \,. \end{aligned}$$
(30)

By varying the action (30) with respect to the metric, the field equation is

$$\begin{aligned}{} & {} -\frac{1}{2}\, f\, g^{\mu \nu } + f_R \, R^{\mu \nu }-f_A \, A^{\mu \nu } - 2f_{A^2}\, A^{\rho \nu }A^{\mu }_{\rho } \nonumber \\{} & {} \quad +P^{\mu \nu }+ M^{\mu \nu } + U^{\mu \nu } + \Lambda g^{\mu \nu } = T^{\mu \nu } \,, \end{aligned}$$
(31)

where

$$\begin{aligned} P^{\mu \nu }= & {} g^{\mu \nu } \nabla ^2 \, f_R-\nabla ^{\mu } \nabla ^{\nu }\, f_R \,, \end{aligned}$$
(32)
$$\begin{aligned} M^{\mu \nu }= & {} g^{\rho \mu }\nabla _{\alpha } \nabla _{\rho } (f_{A} A_{\sigma }^{ \alpha } A^{\nu \sigma }) - \frac{1}{2} \nabla ^2 (f_{A}A^{\mu }_{\sigma } A^{\nu \sigma }) \nonumber \\{} & {} - \frac{1}{2} g^{\mu \nu } \nabla _{\alpha } \nabla _{ \rho } ( f_{A}A_{\sigma }^{ \alpha } A^{\rho \sigma })\,,\end{aligned}$$
(33)
$$\begin{aligned} U^{\mu \nu }= & {} g^{\rho \nu }\nabla _{\alpha } \nabla _{\rho }(f_{A^2}A_{\sigma \kappa }A^{\sigma \alpha }A^{\mu \kappa })-\nabla ^{2}(f_{A^2}A_{\sigma \kappa }A^{\sigma \mu }A^{\nu \kappa })\nonumber \\{} & {} - g^{\mu \nu }\nabla _{\alpha } \nabla _{\rho }(f_{A^2}A_{\sigma \kappa }A^{\sigma \alpha }A^{\rho \kappa })\nonumber \\{} & {} + 2g^{\rho \nu }\nabla _{\rho } \nabla _{\alpha }(f_{A^2}A_{\sigma \kappa }A^{\sigma \mu }A^{\alpha \kappa })\nonumber \\{} & {} - g^{\rho \nu }\nabla _{\alpha } \nabla _{\rho }(f_{A^2}A_{\sigma \kappa }A^{\sigma \mu }A^{\alpha \kappa })\,. \end{aligned}$$
(34)

Here have been use \(f=f(R,A,A^{\mu \nu }A_{\mu \nu })\), \(f_R=\partial f/\partial R\), \(f_A=\partial f/\partial A\) and \(f_{A^2}=\partial f/\partial (A^{\mu \nu }A_{\mu \nu })\).

In order to investigate the cosmological solution (8) in the Einstein equation (30), let’s assume that function f is defined as

$$\begin{aligned} f(R,A,A^{\mu \nu }A_{\mu \nu }) = R+a\, R^2+b \, A + c\, A^{\mu \nu }A_{\mu \nu } \, \end{aligned}$$
(35)

with a, b and c being arbitrary constants. This leads to

$$\begin{aligned} f_R= & {} 1+2 a R \,, \nonumber \\ f_A= & {} b \,,\nonumber \\ f_{A^2}= & {} c. \end{aligned}$$
(36)

Assuming that the content of matter is the pure radiation, whose the energy–momentum tensor is given in Eq. (24), and using the ingredients define above, it is found that

$$\begin{aligned} P^{\mu \nu }= & {} 0, \end{aligned}$$
(37)

and the only non-zero component of the tensor \(M^{\mu \nu }\) and \(U^{\mu \nu }\) are

$$\begin{aligned} M^{00}= & {} -\frac{2 \beta ^2}{9 \alpha ^2 r^8}, \end{aligned}$$
(38)
$$\begin{aligned} U^{00}= & {} \frac{2 \beta ^2}{27 \alpha ^4 r^8} \,. \end{aligned}$$
(39)

Thus the field equation (31) leads to the set of equations

$$\begin{aligned} \rho= & {} \frac{1}{72 \alpha ^4 r^8}\Bigl [-54 \alpha ^8 \beta ^2 \left( 4 a-r^2 z^2\right) \nonumber \\{} & {} +9 \alpha ^6 \left[ \beta ^2 \left( 2 \Lambda r^2 z^2+1\right) +24 r^6 t\right] \nonumber \\{} & {} +18 \alpha ^4 \left( \beta ^2 b r^2 z^2+4 \Lambda r^6 t\right) \nonumber \\{} & {} +\alpha ^2 \left[ -\beta ^2 \left( 7b+8 c r^2 z^2\right) +72 b r^6 t\right] \nonumber \\{} & {} +4 c \left( \beta ^2-8 r^6 t\right) \Bigl ] \end{aligned}$$
(40)
$$\begin{aligned} 0= & {} \frac{\beta z \left( 27 \alpha ^6+9 \alpha ^4 \Lambda +9 \alpha ^2 b-4 c\right) }{18 \alpha ^2 r^2}\,,\end{aligned}$$
(41)
$$\begin{aligned} 0= & {} -\frac{27 \alpha ^6+9 \alpha ^4 \Lambda +9 \alpha ^2 b-4 c}{9 \alpha ^4 r^2} \,,\end{aligned}$$
(42)
$$\begin{aligned} 0= & {} \frac{r^2 \left( 27 \alpha ^6+9 \alpha ^4 \Lambda +9 \alpha ^2 b-4 c\right) }{9 \alpha ^2} \,,\end{aligned}$$
(43)
$$\begin{aligned} 0= & {} \frac{27 \alpha ^6+9 \alpha ^4 \Lambda +9 \alpha ^2 b-4 c}{9 \alpha ^4 r^2} \,. \end{aligned}$$
(44)

Solving these equations, the energy density and the cosmological constant are found as

$$\begin{aligned} \rho= & {} -\frac{\beta ^2 \left( 216 \alpha ^8 a-9 \alpha ^6+7\alpha ^2 b-4 c\right) }{72 \alpha ^4 r^8}\,, \end{aligned}$$
(45)
$$\begin{aligned} \Lambda= & {} -\frac{27 \alpha ^6+9 \alpha ^2 b-4 c}{9 \alpha ^4}\,. \end{aligned}$$
(46)

This result highlights some interesting points:

  • The Ricci-inverse theory - Class III allows for closed timelike curves (CTCs), leading to causality violations.

  • If the constants a, b, and c are set to zero, the results of general relativity are recovered.

  • Taking a and c equal to zero, the results for Class I are obtained. Hence, the study developed here represents a generalization of the investigation conducted in Ref. [32].

  • When a and b are both set to zero, the results for Class II are obtained.

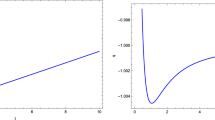
  • The weak energy condition can be violated, as the energy density is not positively defined. In order to analyze this case in more detail, the energy density as given in Eq. (45) is plotted as a function of the radius r choosing different values for the coupling constant, see Fig. 1. The results in the figure show that the energy density can be positive or negative depending on the combination of coupling constant values.

  • The cosmological constant can be positive or negative, depending on the parameters. Therefore, a transition from Anti-de Sitter (AdS) to de Sitter (dS) space is possible.

Fig. 1
figure 1

Energy density versus radius is plotted with the parameters \(\alpha =1\) and \(\beta =0.1\)

Full size image

Beyond the null dust or Vaidya radiation, however, one can consider other energy–momentum tensors within this Ricci-inverse gravity and analyze the result. Here are a few examples of alternative matter-energy contents that could be explored:

  • Electromagnetic field:

    The energy–momentum tensor associated with the electromagnetic field is given [33]

    $$\begin{aligned} {\mathcal {T}}^{\mu \nu }=\Big (F^{\mu \sigma }\,F^{\nu \lambda } \,g_{\sigma \lambda }-\frac{1}{4}\,g^{\mu \nu }\,F_{\gamma \delta } \,F^{\gamma \delta }\Big ), \end{aligned}$$
    (47)

    where \(F_{\gamma \delta }=\partial _{\gamma }\,A_{\delta }-\partial _{\delta }\,A_{\gamma }\) is the electromagnetic field tensor and \(A_{\mu }\) is the the four-vector potential.

  • Anisotropic fluid:

    The energy–momentum tensor associated anisotropic fluid is given by [33]

    $$\begin{aligned} {\mathcal {T}}^{\mu \nu }=(\rho +p_{t})\,U^{\mu }\,U^{\nu }+p_{t} \,g^{\mu \nu }+(p_{r}-p_{t})\,\eta ^{\mu }\,\eta ^{\nu }.\nonumber \\ \end{aligned}$$
    (48)

    Here, \(\rho \) represents the energy density, while \(p_{r}\) and \(p_{t}\) denote the pressure components of the fluid. The vector field \(U^{\mu }\) is a time-like vector, and \(\eta ^{\mu }\) is a space-like vector aligned with the r-direction, satisfying the following relations

    $$\begin{aligned} U_{\mu }\,U^{\mu }=-1,\quad \eta _{\mu }\,\eta ^{\mu }=1,\quad U_{\mu }\,\eta ^{\mu }=0. \end{aligned}$$
    (49)

  • Type-II fluid:

    The energy–momentum tensor of a Type-II fluid is given by [33,34,35,36]

    $$\begin{aligned} {\mathcal {T}}^{\mu \nu }=\epsilon \,k^{\mu }\,k^{\nu }+(\rho +p)\, (k^{\mu }\,\ell ^{\nu }+k^{\nu }\,\ell ^{\mu })+p\,g^{\mu \nu }, \end{aligned}$$
    (50)

    where \(\epsilon \) is the energy density of null dust fluid, and \(\rho \) and p, respectively, represents the energy density and isotropic pressure of this Type-II fluid. Here \((\mathbf{k, \ell })\) are the null vector that satisfies the following relation

    $$\begin{aligned} k^{\mu }\,k_{\mu }=0=\ell ^{\mu }\,\ell _{\mu },\quad k^{\mu }\,\ell _{\mu }=-1. \end{aligned}$$
    (51)

    When \(\epsilon =0\), then the energy–momentum tensor \({\mathcal {T}}^{\mu \nu }\) reduces to degenerate Type I fluid [33] and further it represents string dust for \(\epsilon =0=p\). For Type-II fluid, different energy condition are given in Ref. [33].

  • Charged Anisotropic fluid:

    The energy–momentum tensor of charged anisotropic fluid which is the combination of anisotropic fluid and electromagnetic field tensor is given by

    $$\begin{aligned} {\mathcal {T}}^{\mu \nu }= & {} (\rho +p_{t})\,U^{\mu }\,U^{\nu }+p_{t} \,g^{\mu \nu }+(p_{r}-p_{t})\,\eta ^{\mu }\,\eta ^{\nu }\nonumber \\{} & {} +\Big (F^{\mu \sigma }\,F^{\nu \lambda }\,g_{\sigma \lambda } -\frac{1}{4}\,g^{\mu \nu }\,F_{\gamma \delta }\,F^{\gamma \delta }\Big ), \end{aligned}$$
    (52)

    where different symbols are stated earlier.

    It is important to note that a different choice of the content of matter leads to different analyses and results. In this work, only one form of matter has been chosen. Other matter contents can be investigated in future studies.

4 Conclusions

Observational data indicate that the universe is expanding at an accelerated rate. This is a significant issue in current times, as within the context of the theory of general relativity, there is no consistent explanation for this phenomenon. To address this problem, several alternative theories to general relativity have been proposed. In this paper, the Ricci-inverse gravity theory is considered as the gravitational theory. This theory involves modifying the Einstein-Hilbert action by replacing the Ricci scalar with a function \(f(R, {\mathcal {A}})\), where f represents a function of the Ricci scalar (R) and the anti-curvature scalar (\({\mathcal {A}}\)). Various classes of this theory have been studied in the literature (see, Refs. [14, 15]). Basically, the following classes of models are used in investigating physical problems.

  • Class-I models: In this class, the function f is defined by \(f(R, {\mathcal {A}})=(R+a_1\,R^2+a_2\,R^3+\cdots )+(b_1\,{\mathcal {A}}+b_2\,{\mathcal {A}}^2+b_3\,{\mathcal {A}}^3+\cdots )\), where \(a_i, b_i\) are the coupling constants. The simplest example of this function in class-I models is given by \(f(R, {\mathcal {A}})=(R+a\,{\mathcal {A}})\), where a is the coupling constant. However, one can consider higher order terms of the anti-curvature scalar in this function and would investigate the physical problems.

  • Class-II models: In this class, the function f is defined by \(f(R, A^{\mu \nu }\,A_{\mu \nu })=(R+a_1\,R^2+\cdots )+\left\{ c_1\,A^{\mu \nu }\,A_{\mu \nu }+c_2\,(A^{\mu \nu }\,A_{\mu \nu })^2+\cdots \right\} \), where \(a_i, c_i\) are the coupling constants. The simplest example of this function in class-II models is given by \(f(R, A^{\mu \nu }\,A_{\mu \nu })=(R+\kappa \,A^{\mu \nu }\,A_{\mu \nu })\), where \(\kappa \) is the coupling constant. One can consider higher order terms of the anti-curvature tensor in this function and would investigate the physical problems.

  • Class-III models: In this class, the function f is defined by \(f(R, {\mathcal {A}}, A^{\mu \nu }\,A_{\mu \nu })=(R+a_1\,R^2+\cdots )+(b_1\,{\mathcal {A}}+b_2\,{\mathcal {A}}^2+\cdots )+\left\{ c_1\,A^{\mu \nu }\,A_{\mu \nu }+c_2\,(A^{\mu \nu }\,A_{\mu \nu })^2+\cdots \right\} \), where \(a_i, b_i, c_i\) are the coupling constants. Form this general expression, one can choose various forms of the function f. We see that for \(c_i \rightarrow 0\), one can recover class-I models and for \(b_i \rightarrow 0\), we will get back class-II models from this general class-III models.

The primary objective here was to examine the possibility of causality violation due to the presence of closed time-like curves (CTCs) in a four-dimensional space-time. An example of an axially symmetric cosmological space-time, which is an exact solution to Einstein’s field equations in general relativity and exhibits CTCs, is investigated. This cosmological solution is then analyzed within two different classes of Ricci-inverse gravity, specifically class-II & III models. The most general class is the Class-III models, where the function f is taken as \(f(R, {\mathcal {A}}, A^{\mu \nu }\,A_{\mu \nu })=(R+a\,R^2+b\,{\mathcal {A}}+c\,A^{\mu \nu }\,A_{\mu \nu })\); the other two classes are particular cases of this class. Our results demonstrate that in all classes, the axially symmetric cosmological space-time remains a solution in Ricci-inverse gravity. Consequently, the violation of causality arises in Ricci-inverse theory as it does in general relativity.

Throughout the analysis, we have seen that the energy–density of the null dust or radiation field gets modification by the coupling parameters of the Ricci scalar, the anit-curvature tensor and its scalar. The obtained expression of the energy–density \(\rho (r)\) diverse at \(r=0\), indicating a coordinate singularity, given that the space-time is devoid of any curvature singularity. The space-time model within the Ricci-inverse gravity constitutes a non-vacuum solution featuring null dust or radiation field and a negative cosmological constant as the matter-energy contents. It’s evident that when the coupling parameter \(\kappa \) tends towards zero in Class-II models, and a, b, and c approaches zero in Class-III models, the derived outcomes align with those obtained in general relativity theory.

Notably, one can explore alternative matter-energy contents beyond the null dust or Vaidya radiation field, as mentioned previously, within Ricci-inverse gravity using the same space-time model, which remains open for future investigation. Another point to consider is that one may examine different forms of the function f within all three classes of models and investigate various physical systems. In such cases, different forms of f will naturally alter the outcome of a physical system. However, for the present problem under investigation in this paper, we realized that the energy–density (\(\rho \)) of null dust or radiation field and the cosmological constant (\(\Lambda \)) are modified by the coupling parameters in all three classes, regardless of the specific form of the function f.