Insights on Granda–Oliveros holographic dark energy: possibility of negative dark energy at $z\gtrsim 2$

Abstract

In holographic dark energy (HDE) models, infrared cut-offs with derivatives of the Hubble parameter, such as the Granda–Oliveros cut-off, offer a coherent explanation for late-time acceleration while ensuring causal consistency. We show that such HDE will inevitably mimic the dominant energy forms unless we forcefully calibrate the free parameters. This feature reveals the dependency between the model’s ability to explain the late-time acceleration and the integration constant, highlighting that one cannot arbitrarily set this constant to zero. We see that the origins of HDE and the Friedmann equations from the first law of horizon thermodynamics offer a natural explanation for this behaviour. Thus, the holographic principle naturally extends to all energy components, diverging from the prevalent notion in HDE models. The model also allows dark energy to transit from an early negative energy to a present positive value, with a singular dark energy equation of state parameter, which can relax the tension in the BAO Lyman-$\alpha$ observations. Furthermore, we present observational constraints utilizing Pantheon$^+,$ OHD, CMB Shift parameter, QSO and BAO data, indicating the presence of early negative energy as an unavoidable consequence. Upon using the SH0ES prior, we see that the model accounts for the Hubble parameter at the cost of affecting the matter density while simultaneously relaxing the tensions in BAO Lyman-$\alpha$ observations and the age estimations. This study also underscores notable features stemming from the comprehensive utilization of the covariance matrix within cosmic chronometers, BAO and CMB distance prior and clarifies the implications of negative dark energy density derived from the high redshift Pantheon$^+$ sample. Additionally, we provide a brief overview of the theoretical framework surrounding linear perturbation within the wGOHDE model.

1 Introduction

Established by notable observations, the late-time accelerated expansion of our universe prompts debates regarding its driving force, anointed “dark energy” [1,2,3,4]. While its origin remains obscure, a constant energy density with sufficient negative pressure can reasonably explain this observation. Most theories of gravity can incorporate such a constant, but often, this leads to tussling with the cosmological constant problems [5,6,7,8]. The simplest solution is to consider a dynamic dark energy with minimal extra parameters. The barest choice of w Cold Dark Matter (CDM) or its parametrisations uplifts the constant $\Lambda$ in the vanilla $\Lambda$CDM model to a dynamical form, and there are several attempts to define the physical origin of such extensions [9,10,11]. This article explores the characteristics of the Granda–Oliveros holographic dark energy (GOHDE) model built on the holographic principle, offering observational constraints alongside compelling new insights.

Based on the holographic principle, which limits the maximum possible entropy in a given volume of space, together with the first law of horizon thermodynamics, one can propose an effective “total” energy density as,

$$\begin{aligned} \Lambda ^4\sim \rho \lesssim \frac{S}{L^4}. \end{aligned}$$

(1)

Hereafter referred to as the CKN bound based on its authors Cohen et al. [12], Eq. (1) yields an energy density consistent with observational data when applied in a universe “dominated” by dark energy. Their approach claims to resolve the fine-tuning problem and leads to the description of the holographic dark energy (HDE) [13,14,15,16,17,18,19,20,21,22]. Hsu [23] showed that the above relationship yields an incorrect equation of state for the dark energy with the Hubble scale as IR cut-off. Further, Li [24] showed that the particle horizon encountered the same issues highlighted in [23], and Myung [25] noted that the event horizon brings circular reasoning. Thus, the correct equation of the state is more of a consistency condition than a derived result [25], and the choice of IR cut-off remained an open problem. To resolve the challenges posed by the standard HDE paradigm, Granda and Oliveros introduced a comprehensive IR cut-off, including derivatives of the Hubble parameter [26], hereafter the GOHDE. The notion of the Ricci HDE aligns with this effort [27,28,29,30], and they demonstrate strong physical justifications [31]. Several versions of HDE using GO cut-off have been proposed and scrutinised [32,33,34,35,36].

This article shows that GOHDE will mimic the dominant energy forms, which reveals the dependency between the model’s ability to explain the late-time acceleration and the integration constant. We attribute this nature to the common origin of HDE and the Friedmann equations from the first law of horizon thermodynamics. Thus, the holographic principle naturally extends to all energy components, diverging from the prevalent notion in HDE models. Interestingly, the GOHDE model allows dark energy to transit from an early negative energy to a present positive value, relaxing the tension in the BAO Lyman-$\alpha$ observations. We present observational constraints utilising Pantheon$^+,$ OHD, CMB Shift parameter, and BAO data, indicating early singular dark energy equation of state as an inevitable consequence. Upon using the SH0ES prior, we see that the model accounts for the Hubble parameter at the cost of affecting the matter density while simultaneously improving the BAO Lyman-$\alpha$ observations and the age predictions.

The article is as follows. We build our model and explain its implications in Sects. 2 and 3. In Sects. 4 and 5, we employ observational data to estimate the model’s free parameters and investigate its statistical properties. In Sect. 6, we highlight some aspects to be cautious about using specific data sets. We then analyse the cosmological behaviour and discuss its features in Sect. 7, followed by a brief outlook on linear perturbation and growth function in Sect. 8. Finally, we summarise our findings in Sect. 9.

2 UV/IR see-saw to holographic dark energy

The vacuum energy is the immediate candidate for a cosmological constant. However, addressing the UV and IR divergences of vacuum energy independent of each other does not resolve the cosmological constant problems [37]. Although accounting for the background spacetime geometry improves the rigour of calculations, more is needed to eliminate the original problems [38, 39]. At this juncture, drawing inspiration from black hole mechanics, a crucial insight is to tackle UV and IR divergences simultaneously. The correlation between the area of a black hole’s event horizon with its total energy, along with the Bekenstein–Hawking entropy conjecture, establishes a UV-IR connection [40,41,42,43,44]. The implications of this connection are visible in several milestone works [45,46,47,48] and recently in addressing gravitational entropy [49].

The existence of a UV-IR see-saw led to the construction of the holographic dark energy density $(\rho _{\Lambda }),$ and is given as [13],

$$\begin{aligned} \rho _{\Lambda }={3C^2M^2_{\text {\tiny P}}L^{-2}}. \end{aligned}$$

(2)

Here, L denotes the IR cut-off, C is a constant, and $M_\text {\tiny P}$ represents the reduced Planck mass. The Planck mass comes into the picture because of the choice of units with $\hbar =c=1,$ where $8\pi G=1/M^2_{\text {\tiny P}}.$ This relation originates from the CKN bound [12], which for a dark energy-dominated universe establishes a correlation between the UV cut-off $(\rho _{\Lambda })$ and the IR cut-off (L) via the constrains imposed by the horizon entropy (S),  given by $\rho {_\Lambda } L^4\lesssim S.$

Given the dark energy density, the conventional approach utilises the standard Friedmann equations to study the universe. For a homogeneous and isotropic universe, we begin with the standard Friedmann–Lemaître–Robertson–Walker (FLRW) metric,

$$\begin{aligned} ds^2=c^2dt^2-a^2\left( \frac{dr^2}{1-kr^2}+r^2d\theta ^2+r^2\sin ^2\theta d\phi ^2\right) .\nonumber \\ \end{aligned}$$

(3)

Here, $a\equiv a(t)$ represents the scale factor, k signifies the spatial curvature, and $\left( r,\theta ,\phi \right)$ denotes the conventional spherical polar coordinates with t as the cosmic time. Now, the Friedmann equations and the continuity equation for a 3+1 dimensional spacetime reads,

$$\begin{aligned} H^2&=\frac{8\pi G}{3}\rho , \end{aligned}$$

(4)

$$\begin{aligned} \dot{H}+H^2&=\frac{-4\pi G}{3}\left( \rho +3p\right) , \end{aligned}$$

(5)

$$\begin{aligned} \dot{\rho }&=-3H\left( \rho +p\right) . \end{aligned}$$

(6)

In the above expressions, $\rho$ represents the total energy density, which consists of different components, including matter $(\rho _m),$ radiation $(\rho _r),$ dark energy $(\rho _\Lambda ),$ and other cosmic members if any. Meanwhile, p represents pressure, and H denotes the Hubble parameter.

Here, we will maintain the behaviour of energy densities such as matter or radiation unchanged. In other words, the characteristics of every cosmic component, except dark energy, are determined by established physics. Notably, the behaviour of matter or radiation components is contingent upon the knowledge or assumption of their respective barotropic pressure. Strikingly, this vital information is absent in the construction of standard HDE [25].

3 Granda–Oliveros IR cut-off

There are two primary elements when formulating an HDE model using Eq. (2). The first is the boundary entropy, and the second is the infrared (IR) cut-off. Various options exist for boundary entropy, ranging from the Bekenstein–Hawking entropy to several others [50]. One can employ the Hubble scale as an IR cut-off and account for late-time acceleration, albeit at the expense of relying on generalized entropies [51].

However, there isn’t a universally accepted golden rule for the IR cut-off. The CKN’s original motivation presumed a cosmological “constant” with an equation of state ‘$-1$’ when they employed the Hubble scale, a detail overlooked in [23]. The sole deduction from [12] is that a universe with a large IR cut-off may have a small cosmological constant [52]. In [12] the bound is applied specifically to the universe solely dominated by dark energy, neglecting other forms of energies. Thus the bound recovers the first Friedmann equation of a de Sitter universe through the lens of horizon thermodynamics.

While the Hubble, particle, and future event horizons cannot faithfully construct a dynamic HDE, one way to save the formalism is to include derivatives of the Hubble parameter to define the length scale. The most apparent choice in this context is the Ricci curvature, as demonstrated in [27, 28] or curvature invariants [53, 54]. In pursuit of a more comprehensive approach, Granda and Oliveros introduced a generalized IR cut-off, expressed as [26],

$$\begin{aligned} L_{\text {GO}}=\left( \alpha H^2+\beta \dot{H}\right) ^{-1/2}. \end{aligned}$$

(7)

With this IR cut-off in place, we can define the HDE density using Eq. (2) as,

$$\begin{aligned} \rho _{\Lambda }=3M^2_{\text {\tiny P}}\left( \alpha H^2+\beta \dot{H}\right) . \end{aligned}$$

(8)

Here, we’ve absorbed the constant C into the $\alpha$ and $\beta .$ An apparent assumption inherent in constructing HDE is the choice of the entropy form. To obtain the HDE in the above form, we assumed that S scales as $L^2.$ Any modification to the entropy will alter this assumption. Thus, the Bekenstein–Hawking area law is integrated into the construction of the HDE using Eq. (2), and the only option is to play with different IR cut-offs. Using $L_{\text {GO}}$ to define energy density and then assuming Hubble horizon to study thermodynamics is not a self-consistent approach.

Now, in the standard HDE paradigm, one uses Eqs. (4) and (5) to investigate cosmic evolution. When we substitute Eq. (8) into the first Friedmann equation, we obtain a differential equation of the form,

$$\begin{aligned} H^2 = \frac{8\pi G}{3}\left[ \rho _m+\rho _r-\frac{k}{a^{2}} + 3M^2_{\text {\tiny P}}\left( \alpha H^2 + \beta \dot{H}\right) \right] . \end{aligned}$$

(9)

Assuming that both ordinary matter and dark matter exhibit the same gravitational behaviour, we can express the total matter density as $\rho _m = \rho _{m0}(a)^{-3}.$ Similarly, the radiation goes as $\sim a^{-4}$ and curvature scales like $\sim a^{-2}.$ To simplify further, we can normalize the expression by the present value of the Hubble parameter, denoted as $H_0,$ and substitute $8\pi G\rho _{i0}/(3H_0^2)$ with $\Omega _{i0}.$ For convenience, we shall drop the zero from the subscript. Thus, unless otherwise noted, all $\Omega _i$ represents the current density parameter.

Choosing $x = \ln (a)$ we have $\dot{H}$ as H(dH/dx),  and we represent a in terms of z as $a=1/(1+z)$ when needed. With these, we rewrite the previous equation as

$$\begin{aligned} h^2=\Omega _{r}e^{-4x}+\Omega _{m}e^{-3x}+\Omega _{k}e^{-2x}+\alpha h^2+\beta h\frac{dh}{dx}. \end{aligned}$$

(10)

The above relation is a first-order non-linear differential equation in h,  for which finding an analytical solution might be challenging. However, we could solve it as a first-order ordinary differential equation in $h^2$ with $h^2(x=0)=1+\Omega _k,$ which we can assume by construction. Thus, solving for $h^2$ we get,

$$\begin{aligned} h^2&= \frac{{\Omega _{r}}e^{-4 x}}{-\alpha +2 \beta +1}+\frac{2 {\Omega _{m}}e^{-3 x}}{-2 \alpha +3 \beta +2}+\frac{ {\Omega _{k}}e^{-2 x}}{-\alpha +\beta +1}\nonumber \\&\quad +\text {C}_1e^{-\frac{2 (\alpha -1) x}{\beta }}, \end{aligned}$$

(11)

with

$$\begin{aligned} \text {C}_1&=\frac{\alpha +{\Omega _{k}}}{\alpha -\beta -1}-\frac{2 {\Omega _{m}}}{-2 \alpha +3 \beta +2}+\frac{{\Omega _{r}}}{\alpha -2 \beta -1}\nonumber \\&\quad +\frac{\beta }{-\alpha +\beta +1}+\frac{1}{-\alpha +\beta +1}. \end{aligned}$$

(12)

We will call the cosmological model described by Eq. (11) the Granda–Oliveros holographic dark energy (GOHDE) model.

Equation (11) has four terms with various scaling properties. For instance, in the first term, if we redefine $\frac{\Omega _{r}}{-\alpha +2 \beta +1}$ as $\tilde{\Omega _{r}},$ it is exactly same as radiation. If we repeat the same for all, one could argue that the GOHDE model is effectively similar to w(z)CDM. However, instead of redefining the terms, we will trace the known parameters and attribute everything else as dark energy. Here, we get,

$$\begin{aligned} \Omega _{\Lambda }(x)&=~e^{-4 x} \left\{ e^{\frac{2 x (-\alpha +2 \beta +1)}{\beta }} \left[ \frac{(\alpha -\beta )(\Omega _k+1)-1}{\alpha -\beta -1}\right. \right. \nonumber \\&\quad \left. +\frac{ \Omega _m}{\alpha -\frac{3}{2} \beta -1}+\frac{\Omega _r}{\alpha -2 \beta -1}\right] \nonumber \\&\quad +e^{2 x} \Omega _k \left( \frac{1}{-\alpha +\beta +1}-1\right) \nonumber \\&\quad +e^x \Omega _m\left( \frac{2}{-2 \alpha +3 \beta +2}-1\right) \nonumber \\&\quad \left. +\Omega _r \left( \frac{1}{-\alpha +2 \beta +1}-1\right) \right\} . \end{aligned}$$

(13)

Clearly, the $\Omega _{\Lambda }(x)$ depends on all the free parameters and x,  giving us a dynamic dark energy. The behaviour of dark energy, scaling like different cosmic fluids across various epochs, can be attributed to the shared foundation of the CKN relation and the first Friedmann equation in the first law of thermodynamics. To make this evident, we shall explore the features of the dark energy equation of state parameter. Here, the GOHDE density is a function of z. This aspect allows us to parametrize the model in terms of an energy density with a varying equation of state parameter. In general, for non-interacting fluids, we can write,

$$\begin{aligned} \Omega _\Lambda (z)=\Omega _\Lambda (z=0)\times \exp \left[ 3\int _{0}^{z}\frac{1+w(z')}{1+z'}dz'\right] . \end{aligned}$$

(14)

The above expression holds for all forms of non-interacting energy density. Based on our prior knowledge, we set the equation of state parameters to 0 and 1/3 for matter and radiation, respectively. From the above relation, we can deduce that the dark energy equation of state parameter is a function of redshift and is given as,

$$\begin{aligned} w(z)= -1+\left( \frac{1+z}{3}\right) \partial _z\ln \Omega _\Lambda (z). \end{aligned}$$

(15)

The equation of state of dark energy is contingent upon the values of $\alpha ,$ $\beta ,$ and $\Omega _{\text {i}}$s.

Here lies a vital decision point. Setting $\alpha ,$ $\beta ,$ and $\Omega _{i}$s as free parameters fixes the behaviour of w(z). However, it’s worth noting that w(z) carries more physical significance than, for instance, $\alpha .$ To accommodate this, we find a free parameter from w(z) at the expense of losing control over $\alpha .$ A crucial aspect to consider is that $\alpha$ remains constant throughout cosmic evolution, while w(z) does not. To reconcile this, we logically choose the present value of the equation of state, denoted as $w(z=0)=w_{z_0},$ as the free parameter. Consequently, instead of $\alpha ,$ we introduce a new free parameter, $w_{z_0},$ which serves as a free variable. It’s worth noting that $w_{z_0}=-1$ can be considered a consistency factor, as pointed out in [25]. In the parameter estimation section of this manuscript, we will refer to two distinct cases. One is the GOHDE with $w_{z_0}=-1$ and the other is wGOHDE, where $w_{z_0}$ is a free parameter. Here we have,

$$\begin{aligned} w_{z0}=\frac{-2 \alpha (\Omega _k+1)}{3 \beta (\Omega _m+\Omega _r-1)}+\frac{2 \Omega _k+\Omega _r+3}{3 (\Omega _m+\Omega _r-1)}-\frac{2}{3\beta }.\nonumber \\ \end{aligned}$$

(16)

Here, we get $w_{z0}=-2/(3\beta )$ for a de Sitter universe with no other components. Clearly, our universe is not de Sitter (yet), but very close to one. Hence, a good guess for the $\beta$ value would be 2/3. If one is interested in deducing the value of the original parameter $\alpha ,$ we have,

$$\begin{aligned} \alpha&=~\frac{\beta \left[ -3 w_{z0} (\Omega _{m}+\Omega _{r}-1)+2 \Omega _{k}+\Omega _{r}+3\right] }{2 (\Omega _{k}+1)}\nonumber \\&\quad -\frac{(\Omega _{m}+\Omega _{r}-1)}{ (\Omega _{k}+1)}. \end{aligned}$$

(17)

Given these background equations and their features, one can compute and study the features of other cosmic variables of interest for different values of free parameters. However, we shall move to constrain the values of the free parameters based on the observational data.

4 Data and methodology

In this section we will outline the data sets, methodologies, and statistical quantifiers used to constrain the model’s free parameters by leveraging publicly accessible observational datasets. In the analysis, we will consider a flat universe with $\Omega _{k}=0.$

Data sets

a. Cosmic Chronometer (CC) data set: The dataset encompasses 31 distinct observations of the Hubble parameter across redshifts up to 2,  derived through the differential age method [55,56,57,58,59,60]. This methodology relies on the expression $(1+z)H(z)=-{dz}/{dt},$ as elaborated in [61].

b. BAO galaxy clustering + Lyman-$\alpha$-forest (BAO Gal + Ly${{\alpha }})$ data set: Contained within this dataset are 26 autonomous observations of Baryon Acoustic Oscillations (BAO), extracted from the BAO peaks within the matter power spectrum and analyses of galaxy clustering. This compilation comprises four data points pertaining to the BAO Lyman-$\alpha$ group including Ly$\alpha$-forest of BOSS quasars, SDSS DR12 Ly$\alpha$-forest, Ly$\alpha$-forests of BOSS DR11 quasars [62,63,64], with the remainder attributed to the BAO galaxy clustering set derived from SDSS-III BOSS DR12 galaxy sample, WiggleZ Dark Energy Survey, SDSS DR7 LRG sample [65,66,67,68,69,70,71].

The combined contributions of both the Cosmic Chronometers (CC) and Baryon Acoustic Oscillations Galaxy Clustering plus Lyman-$\alpha$ (BAO Gal + Ly$\alpha )$ datasets yield the observational Hubble data set comprising 57 data points. This dataset will be used as a unified set called Observational Hubble Data (OHD). The entirety of the data is sourced from [72].

c. CMB Shift parameter $({{\varvec{\mathcal {R}}}}){:}$ For a flat universe, the quantity ${\mathcal {R}}$ is defined as the integral ${\mathcal {R}}=\sqrt{\Omega _m}\int _{0}^{z_r}{h^{-1}(z)}dz,$ where $z_r$ denotes the recombination redshift. The value of ${\mathcal {R}}$ provides stringent constraints on $\Omega _m$ based on the Hubble flow. Here, we adopt ${\mathcal {R}}=1.7502\pm 0.0046$ with $z_r=1089.92,$ obtained from the Planck 18 analysis as detailed in [73]. It is important to note that although the shift parameter and the acoustic peak exhibit a linear relationship, they are not degenerate and can complement each other. Similarly, the drag epoch $(r_s)$ also adheres to this relationship, as discussed in [74]. Therefore, we will utilize the CMB shift parameter alongside Baryon Acoustic Oscillation (BAO) and Quasi-Stellar Object (QSO) datasets. By employing ${\mathcal {R}}$ in this manner, we assume that our model’s recombination physics and sound horizon remain unchanged, implying indifference to the acoustic horizon at the time of last scattering [75].

d. Type Ia supernovae (SNe Ia) data: Supernovae type Ia (SNe Ia) are recognized as valuable cosmic entities for investigating cosmic distances. They are commonly referred to as standard candles in cosmology due to their consistent luminosity, offering a dependable method for distance measurement. Numerous datasets of SNe Ia have been compiled, beginning with significant projects such as the milestone Supernova Project [1, 2]. A comprehensive compilation known as the Pantheon sample lists each survey along with corresponding references [76]. The Pantheon sample, comprising 1048 SNe Ia within the redshift range $0.01< z < 2.3,$ is one of the most extensive datasets in this field. A subsequent compilation, Pantheon$^+,$ includes 1550 SNe Ia with 1701 data points calibrated with and without SH0ES prior is also available with full covariance matrix [77]. Both Pantheon and Pantheon$^+$ datasets (with and without SH0ES prior) will be considered to extract the free parameters of our model.

Supernova data, in general, cannot singularly determine the value of $H_0$ due to a degeneracy between $H_0$ and supernova absolute magnitude (M) in the fitting expression for SNe Ia light curves, unless SH0ES prior is employed. It necessitates a combination with other observations to estimate $H_0.$ Reporting $H_0$ by solely using Pantheon or Pantheon$^+$ (without SH0ES prior) is wrong [76, 78], and in its predecessor, the 580 Union2.1 dataset, $H_0$ is presumed [79]. All SNe Ia dataset comprises apparent magnitude $(\mu ),$ corresponding redshift (z),  and the standard deviation in $\mu$ or the covariance matrix. Thus, we aim to compute $\mu$ using the relevant cosmological model for analysis. Here, the apparent magnitude is,

$$\begin{aligned} \mu (z)=5\log _{10}\left[ \frac{d_L(z)}{\text {Mpc}}\right] +M+25. \end{aligned}$$

(18)

Here, M denotes absolute magnitude, requiring calibration using other datasets, and $d_L$ represents luminosity distance given as,

$$\begin{aligned} d_L(z)=c(1+z)\int _{0}^{z}\frac{1}{H(z')}dz'. \end{aligned}$$

(19)

Utilizing the Hubble parameter H(z) at a specific redshift z,  we can estimate $d_L$ and calculate the apparent magnitude. When employing the Dirac SH0ES prior, there are stringent constraints on M,  leading to a large value of $H_0$ and contributing to the Hubble tension.

e. Correlated (BAO) data set: The BAO data has become a fundamental observational tool for constraining cosmological models. These data predominantly stem from surveys of the large-scale structure power spectrum, such as the SDSS-III with DR12 galaxy sample [65], and are extensively documented in [80]. In our analysis, we focus on data points corresponding to two specific parameters: the transverse comoving distance $D_M(z),$ which coincides with $D_c(z)$ in a flat universe, and the volume-averaged angular diameter distance $D_V(z).$ It’s worth noting that all of these distance parameters are scaled by the values of ${\mathcal {R}}$ and $r_s,$ enabling us to integrate the CMB shift parameter mentioned earlier into our analysis. This enhances our ability to achieve a more refined constraint on the cosmological model. The relevant expressions are,

$$\begin{aligned} D_M(z)&=D_c(z)=c\int _{0}^{z}\frac{1}{H(z')}dz', \end{aligned}$$

(20)

$$\begin{aligned} D_V(z)&=\left[ \frac{cz}{H(z)}D_M^2(z)\right] ^{1/3}. \end{aligned}$$

(21)

Here, we use data points from [65, 74, 80]. Given that these data points are correlated, we utilise the covariance matrix provided in [65] for our analysis.

f. The (QSO) data set: This dataset encompasses 120 data points, representing angular sizes and redshifts observed in intermediate-luminosity quasars, spanning a redshift range from 0.46 to 2.76,  as elaborated in the work by [81]. These quasars exhibit minimal dependence on redshift and intrinsic luminosity when observed at 2.29 GHz, establishing a standardised ruler with a linear size of approximately $11.03\pm 0.25$ parsecs. The relationship between the angular size $(\theta ),$ linear length scale $(l_m),$ and angular diameter distance $(D_A)$ for a given redshift is,

$$\begin{aligned} \theta (z)=\frac{l_m}{D_A(z)}. \end{aligned}$$

(22)

Here, we employ the angular diameter distance $(D_A)$, which is defined as the luminosity distance divided by $(1+z)^2,$ and the luminosity distance is determined using Eq. (19). By the methodology and dataset described in [81], we introduce an additional 10% error to the angular size standard deviation. Given that both the QSO and BAO datasets inherently incorporate the drag redshift, we anticipate synergising effectively with the CMB Shift parameter, enhancing our ability to estimate our free parameters.

Our analysis utilises a baseline data amalgamation, which we call the D4 data set, encompassing four primary datasets: OHD, CMB ${\mathcal {R}},$ BAO, and QSO. The analysis strategy entails estimating the model parameters using the D4 exclusively and in tandem with Pantheon, Pantheon$^+$ excluding the SH0ES prior, and Pantheon$^+$ including the SH0ES prior.

Parameter estimation with ${\varvec{\chi }}^{2}$

The parameter estimation process hinges upon the model function, which, in our particular case, represents the Hubble parameter of each respective model. Specifically, we will examine the $\Lambda$CDM, wCDM, GOHDE with a fixed $w_{z0}$ value of $-1,$ and wGOHDE with $w_{z0}$ treated as a free parameter. Consequently, the parameters $\Omega _m$ and $H_0$ are shared across all models, while wCDM introduces the parameter w and GOHDE introduces $\beta$ as additional free parameters. Moreover, in the case of wGOHDE, both $w_{z0}$ and $\beta$ are included alongside $\Omega _m$ and $H_0.$ In our analysis, we maintain $\Omega _r h^2\sim 4.1\times 10^{-5},$ $\Omega _\gamma h^2 \sim 2.4\times 10^{-5},$ and $\Omega _b h^2\sim 0.02$ [82] to be consistent with early physics.

Once we have the Hubble parameter of the model, we proceed to derive the relevant observables. For instance, observational data on the Hubble parameter offers a tangible measure of its value at different redshifts. Similarly, in the context of SNe Ia data, we regard the apparent magnitude as our key observable, computed through the previously outlined equations with respect to a given redshift and the Hubble parameter. Consequently, we formulate expressions for our observables $(A_{\text {theory}})$ across all datasets, each intimately tied to the Hubble flow and contingent upon the model’s free parameters.

The main objective is identifying the optimal free parameters that collectively account for all observables. This simultaneous consideration is paramount since specific free parameters may not influence certain observables. For instance, in the flat $\Lambda$CDM model, the CMB shift parameter ${\mathcal {R}}$ remains independent of $H_0.$ Furthermore, when analyzing the CMB shift parameter, we incorporate radiation density due to its integral spanning from the recombination epoch to the present. Conversely, radiation density plays a negligible role in estimating the luminosity distance in SNe Ia data, thus allowing for its omission to reduce computational expenses. Additionally, some datasets may exhibit preferences for particular combinations of free parameters over others. For instance, while the QSO data indicate a higher value for matter density $\Omega _m,$ other datasets lean towards relatively lower values. Therefore, simultaneous fitting of the data remains essential.

We utilize the chi-square $(\chi ^2)$ minimization approach to determine the free parameters. This process entails constructing the chi-square using specific equations tailored to each dataset. For datasets such as BAO and Pantheon$^+,$ which provide a covariance matrix instead of standard deviation, we use

$$\begin{aligned} \chi ^2 = (A_{\text {observed}} - A_{\text {theory}})^T {\mathbb {C}}^{-1} (A_{\text {observed}} - A_{\text {theory}}). \end{aligned}$$

(23)

Here, $A_{\text {observed}}$ represents the observed data vector, $A_{\text {theory}}$ denotes the theoretical estimate derived from the model and free parameter values, and ${\mathbb {C}}$ represents the corresponding covariance matrix. An additional systematic error of 10% is considered for the QSO data set [81]. The modified chi-square formula for these datasets is as follows:

$$\begin{aligned} \chi ^2=\sum _{i=1} \frac{(A_{\text {observed}_i} - A_{\text {theory}})^2}{(\sigma _i + 0.1A_{\text {observed}_i})^2}. \end{aligned}$$

(24)

Here, the index (i) corresponds to the data point. Finally, we use the conventional chi-square formula for datasets providing standard deviation, given as,

$$\begin{aligned} \chi ^2=\sum _{i=1} \frac{(A_{\text {observed}_i} - A_{\text {theory}})^2}{\sigma _i^2}. \end{aligned}$$

(25)

After constructing the $\chi ^2_j$ for each dataset j,  we compute the combined $\chi ^2_{\text {total}}$ by summing up individual contributions as,

$$\begin{aligned} \chi ^2_{\text {total}} = \sum _{j}\chi ^2_j. \end{aligned}$$

(26)

We then employ the Markov Chain Monte Carlo (MCMC) technique to identify the parameter combination that minimizes the $\chi ^2_{\text {total}}.$ This method iteratively samples parameters and converges towards the parameter set that yields the lowest chi-square value. The implementation of this process relies on Python modules such as emcee [83] and lmfit [84]. Subsequently, upon obtaining the results from the analysis, we generate chi-square distributions and confidence contours from the processed chains.

${\varvec{\chi }}^{2}$ degrees of freedom (DOF)

The $\chi ^2$ statistic quantifies the disparity between the model and observed data, accounting for the errors associated with each datum in a dataset comprising N observations. In an optimal scenario where the model perfectly accounts for all data points, the $\chi ^2$ value would register as zero. Consequently, a lower $\chi ^2$ denotes a superior model alignment with the data. Given that our parameter estimation hinges on minimising $\chi ^2,$ we can readily derive the $\chi ^2$ distribution from the converged Markov Chain Monte Carlo (MCMC) chain.

However, it is essential to recognise that $\chi ^2$ alone does not address the trade-off in introducing additional parameters to enhance the model fit. As an initial step towards model comparison, given the minimum $\chi ^2_{\text {min}},$ we use $\chi ^2$ degrees of freedom, expressed as

$$\begin{aligned} \text {DOF}\equiv \chi ^2_{\text {\tiny {dof}}}:= \frac{\chi ^2_{\text {min}}}{N - N_p}, \end{aligned}$$

(27)

where $N_p$ is the count of independent parameters within the model. Nevertheless, while $\chi ^2_{\text {dof}}$ penalises the inclusion of extra parameters in the model, in situations where the number of data points significantly exceeds the count of free parameters, the addition of an additional parameter may not substantially impact its value.

Information criterion

In response to the challenges of model selection, H. Akaike introduced an information criterion in 1974, subsequently recognized as the Akaike Information Criterion (AIC) [85], while G. Schwarz proposed the Bayesian Information Criterion (BIC) in 1978 [86]. These methodologies serve as valuable aids in selecting an appropriate model. AIC primarily considers the number of free parameters, whereas BIC is rooted in Bayesian principles. Though they share similarities, BIC tends to favour models with fewer dimensions, rendering it preferable for model selection over AIC. The formulas for AIC and BIC are:

$$\begin{aligned} \text {AIC}&= N\log \left( \frac{\chi ^2_{\text {min}}}{N}\right) + 2N_p, \end{aligned}$$

(28)

$$\begin{aligned} \text {BIC}&= N\log \left( \frac{\chi ^2_{\text {min}}}{N}\right) + \left[ \frac{1}{2}\log (N)\right] 2N_p. \end{aligned}$$

(29)

Both AIC and BIC exhibit qualitative similarities, albeit with the distinctive feature of BIC incorporating a multiplicative factor $\log (N)/2$ applied to the count of free parameters, affording BIC an advantage over AIC [86].

Bayes factor

The statistical measures under discussion have not factored in the prior range of analysis. Recognizing that introducing an explicit prior can significantly influence both the optimal values and the significance of the model, we have undertaken a Bayesian analysis between the models. This approach relies on the Bayes theorem, which posits that the posterior probability $({\mathcal {P}})$ is derived from the Likelihood $({\mathcal {L}})$ multiplied by the Prior $(\pi )$ and divided by the Evidence of data $({\mathcal {E}})$. The Bayesian evidence $({\mathcal {E}})$ for the data (D) and model $({\mathcal {M}})$ within a specified parameter space (p) takes the form,

$$\begin{aligned} {\mathcal {E}}(D|{\mathcal {M}})=\int dp {\mathcal {L}}(D|p,{\mathcal {M}}) \pi (p,{\mathcal {M}}). \end{aligned}$$

(30)

The Bayes factor between models ${\mathcal {M}}_i$ and ${\mathcal {M}}_j$ is defined as,

$$\begin{aligned} B_{ij}=\frac{{\mathcal {E}}(D|{\mathcal {M}}_i)}{{\mathcal {E}}(D|{\mathcal {M}}_j)}. \end{aligned}$$

(31)

This metric provides a quantitative estimate of the Evidence supporting one model over another. To facilitate model comparison, we adopt the Jeffreys scale, named after Harold Jeffreys, as outlined in the following Table 1.

Table 1 The Jeffreys’ scale of Bayesian evidence [87]

In this context, we will refrain from calculating the Bayes factor with the Dirac SH0ES prior, as it would inherently introduce significant bias as noted in [88] for [89].

Fig. 1

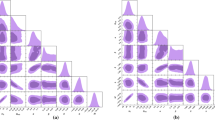
Histograms illustrating the $\chi ^2$ distribution are derived from the final burned MCMC chains for the $\Lambda$CDM, wCDM, GOHDE, and wGOHDE models. Each plot corresponds to different combinations of datasets. The top left diagram utilizes the OHD, BAO, CMB Shift parameter, and QSO datasets (D4 data combination). All other diagrams involve various compilations of SNe Ia data known as Pantheon, Pantheon$^+,$ and Pantheon$^+$ + SH0ES prior, along with the baseline D4 combination. $N_f$ is the normalised frequency of occurrence

Establishing the prior range is vital in MCMC data analysis. In this study, we’ve opted for uniform prior values, as shown in the Table 2.

Table 2 Prior values of all free parameters in the MCMC analysis

For $\beta ,$ we set a range above zero to avoid potential pole at zero. The upper limit is three times that of the de Sitter limit. The ranges for $H_0$ and M are chosen to avoid bias towards any reported values in the Hubble tension, falling within [50, 100] and $[-25, -15],$ respectively. Ranges for w and $w_{z_0}$ include extreme values than those found in the literature. Lastly, the range for present matter density is to exclude zero.

5 Observational constraints

We’ll examine how each model’s $\chi ^2$ distribution changes with different data sets. Looking at histograms in Fig. 1, it’s evident that both the GOHDE and wGOHDE models offer consistent results and demonstrate a better fit than the $\Lambda$CDM model. One notable aspect is that when we include all the data from the Pantheon$^+$ dataset, including its full covariance matrix, it dramatically affects our analysis compared to using just the Pantheon data. Additionally, the SH0ES prior shows a clear difference between the models, with almost no overlap. This suggests that the prior assumption strongly influences the model outcomes. The sudden shift in the $\chi ^2$ values is due to the usage of Dirac SH0ES prior. However, the analysis without the SH0ES prior is generally preferred, as shown by the minimum values of the $\chi ^2$ statistic. It’s also essential to observe the behaviour of the GOHDE model.

Table 3 Constraints (best-fit ± 1$\sigma )$ on the free parameters of the models $(\Lambda$CDM, wCDM, GOHDE, and wGOHDE) using various combinations of data sets along with the best fit estimate of the negative energy transition redshift $z_{\dagger }$ and age

Fig. 2

Confidence contour (1$\sigma$ and 2$\sigma )$ of $\Omega _m$ and $\beta$ for GOHDE model, using various combinations of data sets. The Planck 2018 and Pantheon$^+$+SH0ES estimates of $\Omega _m\pm 1\sigma$ is given in the red and grey shaded portion. The dashed line denotes $\beta =2/3$

Except for the case where the SH0ES prior is considered, GOHDE is practically identical to the $\Lambda$CDM model. However, when we include the SH0ES prior, GOHDE also provides substantial evidence in favour of itself over the $\Lambda$CDM model. This implies that the SH0ES prior is also preferred by other datasets, particularly the BAO Ly-$\alpha$ observations.

Fig. 3

Confidence contour (1$\sigma$ and 2$\sigma )$ of $w_{z0}$ and $\beta$ for wGOHDE model, using various combinations of data sets. The Pantheon$^+$ + SH0ES estimates of $w_0$ is given in the grey shaded portion. The dashed line denotes $\beta =2/3$ and $w_{z_0}=-1$ for their respective axis

The best-fit values are presented in Table 3. Evidently, across all models, whether considering D4 alone, D4 combined with Pantheon, or with Pantheon$^+,$ the results consistently align with the values for $H_0$ and $\Omega _m$ from Planck [90] and TRGB [91] constraints. Upon including the SH0ES prior, the estimated value for $H_0$ aligns with those reported in [77, 78], whereas the $\Omega _m$ value for GOHDE and wGOHDE models notably drops compared to existing literature [78].

Fig. 4

Confidence contour (1$\sigma$ and 2$\sigma )$ of $H_0$ and $\beta$ for GOHDE model, with $w_{z0}=-1,$ using various combinations of data sets. The Planck 2018 and Pantheon$^+$ + SH0ES estimates of $H_0$ are given in red and grey shaded portion. The dashed line denotes $\beta =2/3$

Fig. 5

Confidence contour (1$\sigma$ and 2$\sigma )$ of $H_0$ and $\beta$ for wGOHDE model, using various combinations of data sets. The Planck 2018 and Pantheon$^+$ + SH0ES estimates of $H_0$ are given in red and grey shaded portion. The dashed line denotes $\beta =2/3$

Fig. 6

Confidence contour (1$\sigma$ and 2$\sigma )$ of $H_0$ and $w_{z0}$ for wGOHDE model, using various combinations of data sets. The Pantheon$^+$ + SH0ES estimates of $w_0$ is given in the grey shaded portion. The Planck 2018 and Pantheon$^+$ + SH0ES estimates of $H_0$ are given in red and grey shaded portion. The dashed line denotes $w_{z_0}=-1$

This shows how $\Omega _m$ relates to $\beta$ in both models. When using the SH0ES prior, we also find that the best-fit value of $w_{z0}$ closely matches the GOHDE model. So, when we narrow down the equation of state, changes are largely affected by how $\Omega _m$ and $\beta$ are correlated. This is evident in the confidence plots for $\Omega _m$ and $\beta$ in the GOHDE model shown in Fig. 2. Thus $\beta$ adds additional correlation to $\Omega _{m}$ over $H_0.$ This significantly improves the age estimation for GOHDE and wGOHDE models, making it consistent with globular cluster observations [92].

It is important to observe that, without SH0ES prior, the value of $\beta \sim 2/3$ falls within one standard deviation of the estimated best-fit values in the GOHDE model. However, a notable inverse relationship between $\beta$ and $\Omega _m$ emerges prominently in GOHDE. Consequently, alternative data combinations yield relatively diminished values of $\beta ,$ and incorporation of the SH0ES prior results in an elevation of $\beta$ and a corresponding reduction in $\Omega _m.$ This correlation becomes more intricate with the wGOHDE model. When $w_{z0}$ is treated as a variable parameter, as in the wGOHDE model, an additional positive correlation between $\beta$ and $w_{z0}$ emerges, contributing to the reduction of $\Omega _m.$ Nevertheless, these correlations are notably less pronounced within the framework of wGOHDE. The marginal confidence plots illustrating relationships between different parameters are presented in Figs. 3, 4, 5, and 6. Additionally, Table 3 includes an additional estimation, denoted as $z_{\dagger },$ which corresponds to the singularity in the dark energy equation of state parameter. The implications of this term will be discussed in detail after examining the statistical evidence.

Regarding the age estimation, we have

$$\begin{aligned} \text {Age} = \int _{0}^{a=1}\frac{1}{a'H(a')}da'. \end{aligned}$$

(32)

By substituting the best-fit parameter values, one can calculate the age of the relevant model as detailed in the final column of Table 3. Notably, GOHDE and wGOHDE models yield higher age estimates than $\Lambda$CDM, and the variation across datasets is minimal. With the inclusion of the SH0ES prior, the age estimate for $\Lambda$CDM decreases significantly compared to estimates without this prior. Conversely, the deviation observed for GOHDE and wGOHDE models is minor when incorporating the SH0ES prior. A significant observation is that when using SH0ES prior, while $\Lambda$CDM and wCDM models exhibit considerable tension with the Planck 2018 age estimate of 13.8 billion years [90], GOHDE and wGOHDE models demonstrate improved alignment with this benchmark. The lower value of matter density while using the SH0ES prior improves the age estimation of GOHDE and wGOHDE significantly, thus making the model agree with the estimates from globular clusters [92].

Table 4 Statistical quantifiers (DOF, AIC, BIC and Bayes factor) of the models $(\Lambda$CDM, wCDM, GOHDE, and wGOHDE) using the complete data set without SH0ES prior

Finally, the statistical metrics are enumerated and presented in Table 4. In the absence of SNe Ia data, it is evident that the $\Lambda$CDM model emerges as the most favoured. The elevated $\chi ^2$ degrees of freedom can be attributed to the covariance matrix utilised for the BAO data set. If we relied solely on statistical uncertainties across all data sets, this value would decrease markedly. Specifically regarding the D4 data set, $\Lambda$CDM exhibits superior performance compared to wCDM and GOHDE, while wGOHDE demonstrates the lowest value, primarily due to its increased parameterisation. Despite penalising additional parameters by the $\chi ^2$ degrees of freedom, this metric may not accurately reflect model preference if the number of data points outweighs the surplus parameters. Hence, although the degrees of freedom suggest wGOHDE as the best fit, this may not necessarily hold. To delve further into this matter, we calculate the AIC and BIC values and compare them with those of $\Lambda$CDM. The model with the lowest IC value is deemed optimal.

Coming to the Bayes factor, all models exhibit negative evidence against $\Lambda$CDM under D4 and Pantheon data sets. Both wCDM and GOHDE yield comparable results, given their equivalent degrees of freedom, performing similarly in statistical analyses. When considering the Pantheon$^+$ data, both wCDM and wGOHDE yield the lowest AIC and BIC values, accompanied by Bayes factors ranging between 1 and 3, indicating weak evidence against $\Lambda$CDM. Hence, thus far, $\Lambda$CDM emerges as the optimal model based on statistical metrics. However, when factoring in the SH0ES prior, the model’s Bayes factor will be exceedingly high due to the stringent nature of the Dirac SH0ES prior. Consequently, testing and reporting such values, as done in [89], may not be appropriate. In the analysis presented in [89], they employed sharp one and two-sigma priors, yielding exceptionally high values favouring their model over $\Lambda$CDM. Nonetheless, as reported in [88], their model proves to be less effective under scrutiny.

6 Remarks on data analysis

A key aspect we can observe in GOHDE and wGOHDE is the potential presence of negative dark energy in the recent past. The idea of negative dark energy in a model has caught attention because it could help resolve cosmological tensions. These issues often lead to unconventional features. For example, one way to address the Hubble tension is by considering $w_{\Lambda }<-1,$ which means the possibility of phantom dark energy remains open. Similarly, studies suggest that the BAO Ly$\alpha$ Anomaly could be explained by the existence of negative dark energy in the past [93,94,95,96,97]. Models with negative dark energy often exhibit a non-monotonic evolution of the Hubble parameter, although confirming this behaviour is challenging [93]. An analysis not tied to a specific model but aimed at resolving cosmological tensions exhibits poles in the dark energy equation of state parameter indicating negative dark energy [98]. We will explore these traits shortly. Before that, let’s clarify certain aspects of data analysis a bit further.

We showed how cosmological data could constrain a specific model. However, using various datasets itself is an active area of research. Here, we discuss the outlook of employing different datasets. Firstly, we examine a unique feature observed when using high redshift Pantheon$^+$ data, as reported in [99]. Then, we explore the implications of combining CC, BAO, and CMB datasets with complete covariance matrices, as studied in [56, 59, 100] for cosmic chronometer data, [73] for CMB distance priors, and BAO analyses in [65, 74, 80, 101]. These additional examples highlight the complexities that need to be considered when conducting the analysis.

6.1 Using Pantheon$^+$ with $z>1$

Recently, supernova data has also suggested negative dark energy, with reports indicating a significant shift in cosmological parameters [99, 102]. Moreover, even in the analysis of the $\Lambda$CDM model, it has been reported that $\Omega _{\text {m}}>1$ cannot be ruled out [103, 104].

Fig. 7

Diagrams illustrating the posterior distribution of $\Omega _{\text {m}}$ and $H_0$ for Pantheon$^+$ sample with $z>1$ for $\Lambda$CDM model

So far, the negative energy density has been considered a model feature, hinted mostly by the BAO data. However, [99] has shown that is not the case and even within Pantheon$^+$ sample, the prior values and redshift selection may also lead to similar effects. In this section we reproduce the results obtained in [99] in a slightly different approach and repeat the same analysis with the wGOHDE model.

Fig. 8

Diagrams illustrating the posterior distribution of $\Omega _{\text {m}}$ and $H_0$ for Pantheon$^+$ sample with $z>1$ for wGOHDE model. Here $\Lambda$CDM line in the bottom panel corresponds to the posterior with prior $\Omega _m\in [0.01,8], H_0\in [10,100]$

Here, we analyze the Pantheon$^+$ sample at a redshift of $z=1$ and focus on data points beyond $z>1.$ In their study [99], they categorized the data into three sets. The first set comprises 77 data points calibrated with Cepheid hosts in galaxies, while the remaining data is sorted based on various redshifts. The set calibrated with Cepheids is crucial for determining the absolute magnitude M and establishes a prior for M. Since our interest lies in high redshift data, we employ a Gaussian prior for M and include only data points at $z>1$ for our analysis. We replicate the study by exploring different prior ranges for $H_0$ and $\Omega _{\text {m}},$ thus effectively reproducing the findings reported in [99]. The results are shown in Fig. 7. Subsequently, we conduct the same analysis for our wGOHDE model, considering different prior ranges for additional free parameters. The posteriors are illustrated in Fig. 8.

The Pantheon$^+$ supernova data alone cannot tightly constrain the present value of the Hubble parameter $(H_0)$ due to a degeneracy with the absolute magnitude (M). By employing a Gaussian prior for M,  one can anticipate some constraint on $H_0.$ However, there exists a negative correlation between $H_0$ and the matter density parameter $(\Omega _{\text {m}})$. When setting the prior value of $\Omega _{\text {m}}$ below 1, a higher $H_0$ is obtained, as noted in [77]. In our analysis with the $\Lambda$CDM model, focusing on data with redshifts $z>1$ and varying prior values, deviations from the standard Gaussian posterior are observed. For $\Omega _{\text {m}}\in [0.01,5]$ and $H_0\in [50,100],$ the best-fit value of $H_0$ is approximately 50, with $\Omega _{\text {m}}$ tending towards unity despite having a Gaussian posterior. Extending the prior range for $\Omega _{\text {m}}$ and $H_0\in [10,100]$ results in an unconstrained $\Omega _{\text {m}},$ allowing for $\Omega _{\text {m}}>1.$ Further extension of the prior range for $\Omega _{\text {m}}$ suggests a potential negative dark energy density.

We proceed to analyze the wGOHDE model with $\Omega _{\text {m}}\in [0.01,8]$ and $H_0\in [10,100],$ alongside varying prior ranges for additional free parameters $\beta$ and $w_{z_0}.$ As we expand the prior range, lower $H_0$ values and higher $\Omega _{\text {m}}$ values gain non-zero evidence. An interesting observation is the emergence of bimodal posteriors, indicating similar evidence for higher and lower $H_0$ values as parameter priors are extended. This behaviour also differs from conventional HDE and other dark energy models. Unlike $\Lambda$CDM, the wGOHDE model tends to favor $\Omega _{\text {m}}<1,$ while $\Omega _{\text {m}}>1$ is not fully rejected. Although kernel density plots appear smooth around $\Omega _{\text {m}}=1,$ the posterior distribution reveals a sharp jump, suggesting a preference for $\Omega _{\text {m}}<1.$ Thus, high redshift Pantheon$^+$ data do not predominantly influence the negative dark energy density observed in wGOHDE, while its contribution cannot be disregarded. Here, we restrict the prior range for wGOHDE to $\Omega _{\text {m}}\in [0.01,8]$ and $H_0\in [10,100].$ Exploring additional features of Pantheon$^+$ data under the wGOHDE model and replicating the full analysis outlined in [99] are prospects for future research. All discussed features are presented in Figs. 7 and 8. Throughout our analysis, we employ a Gaussian prior for M with a mean of $-19.249$ and a standard deviation of 0.030. The y-axis in all diagrams represents normalized number density, with solid/dotted lines denoting kernel density estimates.

6.2 Using cosmic chronometers, BAO and CMB distance prior data with covariance matrix

Table 5 Constraints (best-fit ± 1$\sigma )$ on the free parameters of the GOHDE, and wGOHDE models using various combinations of data sets

By incorporating additional systematic uncertainties, regardless of the model used, the constraints are expected to change. While the best-fit values may remain similar, the confidence interval will become broader. A crucial tool for comprehending the universe’s evolution is estimating the Hubble parameter at various redshifts. The technique of estimating the Hubble parameter through the differential age of galaxies is widely employed and offers the advantage of being independent of cosmological models. Previously, we utilized the data derived from this method, known as the Cosmic Chronometer (CC) dataset [56, 59, 100]. However, our study only considered the standard deviation of each data point for the analysis, which is a common practice in the literature and serves as an initial estimation step.

Although the CC method is independent of background cosmology, it relies on factors such as the initial mass function, stellar library, etc. Consequently, stellar population synthesis models introduce systematic uncertainties to the entire dataset. In [105], it was found that the stellar population synthesis model predominantly contributes to the overall error on H(z). Specifically, the initial mass function contributes less than $0.5\%,$ while the stellar library contributes approximately $6.6\%$”, among other factors. Therefore, accounting for these additional uncertainties, the study conducted in [105] laid the groundwork for utilizing CC with a comprehensive covariance matrix construction protocol. In essence, the covariance matrix associated with the CC method is,

$$\begin{aligned} \text {Cov}_{ij}=\text {Cov}_{ij}^{\text {stat}}+\text {Cov}_{ij}^{\text {young}}+ \text {Cov}_{ij}^{\text {model}}+\text {Cov}_{ij}^{\text {met}}. \end{aligned}$$

(33)

Here, the sources contributing to the covariance are represented by “stat,” “young,” “model,” and “met”: statistical errors, contamination from residual young components in galaxy spectra, reliance on chosen models, and stellar metallicity, respectively. Specifically, the selected models encompass further decomposition as,

$$\begin{aligned} \text {Cov}_{ij}^{\text {model}}=\text {Cov}_{ij}^{\text {SFH}}+ \text {Cov}_{ij}^{\text {IMF}}+\text {Cov}_{ij}^{\text {st.lib}}+\text {Cov}_{ij}^{\text {SPS}}. \end{aligned}$$

(34)

Here, “SFH” represents star formation history, “IMF” corresponds to the initial mass function used, “st.lib” denotes the adopted stellar library, and “SPS” signifies the dependency on the stellar population synthesis model. Metallicity and young components are uncorrelated and only have diagonal elements, while the model accounts for the main correlated components. References [105, 106] provide a comprehensive illustration of these procedures.

The main question we aim to address in this section is how much this affects our analysis. Utilizing the full covariance matrix alters the confidence limits, although the mean value stays relatively consistent. When integrated with other datasets, the impact becomes much less significant, yielding no noticeable difference.

Fig. 9

Posterior distribution of $H_0$ with and without considering systematics due to SPS models [105] using Cosmic Chronometer data alone for GOHDE and wGOHDE models. The black dashed line indicates the value from Planck 2018

Figure 9 displays the posteriors of the Hubble parameter with (w/) and without (w/o) the additional systematic uncertainties. Both our GOHDE and wGOHDE models align with the conclusions drawn in [105], indicating larger error bars for $H_0.$ Furthermore, the analysis suggests a higher value for $\Omega _{\text {m}}$ with errors of approximately $\mathcal {O}(1).$ Thus, consistent with the findings of [105], the estimation of matter density is minimally impacted by the utilization of the covariance matrix. Moreover, the CC data alone inadequately constrains $\Omega _{\text {m}}$ in general, and additional free parameters remain unconstrained when using CC data alone. The best-fit values using CC data are tabulated in Table 5. Incorporating additional datasets is crucial to enhance the constraint on our model.

An additional consideration pertains to utilizing BAO datasets. BAO signatures provide highly precise spectroscopic measurements, facilitating comprehensive evaluations of cosmological models. Various approaches have been employed in the literature to incorporate BAO data, and in our analysis, we utilized data providing the Hubble parameter and the correlated transverse co-moving distance separately. A more effective approach involves incorporating BAO data along with the covariance matrix. By utilizing BAO data sourced from publications such as [65, 74, 80, 101], along with their respective covariances, we analyzed our models. The best-fit estimates from this joint analysis are presented in Table 5. Incorporating CC data along with BAO measurements significantly enhances the confidence interval, reducing the influence of the stellar population synthesis (SPS) model present in the systematic errors of CC.

For the GOHDE model, the inclusion of BAO data improves the constraints on the free parameters $\beta$ and $\Omega _{\text {m}},$ yielding estimates similar to those presented in Table 3. Hence, CC data, with or without systematics, combined with BAO data, can effectively constrain the GOHDE model. In the case of the wGOHDE model, constraints on the Hubble parameter are enhanced by including BAO data. However, due to correlations between $\beta ,$ $w_{z_0},$ and $\Omega _{\text {m}},$ other constraints tend to worsen. To address this, a stronger constraint on $w_{z_0}$ could improve constraints on the wGOHDE model. For this purpose, we incorporate the CMB shift parameter ${\mathcal {R}}$ and the full CMB distance prior, which includes covariance between the shift parameter, acoustic peak, and baryon density.

Another significant consideration is using the CMB shift parameter, which assumes the $\Lambda$CDM model for result estimation. However, the choice of cosmology is not a serious concern given that ${\mathcal {R}}$ and the acoustic scale $(l_A)$ are effective observables. Additionally, the model-independent constraints on $\Omega _{\text {b}}h^2$ from BBN make it reasonable to consider ${\mathcal {R}},$ $l_A,$ and $\Omega _{\text {b}}h^2$ as effective observables [73]. Hence, they are suitable for analysing alternative cosmologies [107].

We now examine the effects of incorporating the CMB distance prior, based on the method outlined in [73]. In our previous analysis, we only considered the shift parameter; however, incorporating it alongside other measurements, such as QSO data, makes is appropriate [75]. Here, we intend to use the shift parameter alongside CC and BAO data as one set and then utilize the CMB distance prior with its respective covariance matrix as the second set.

The best-fit values are provided in Table 5. Clearly, in the GOHDE model, using the shift parameter alone yields a result very close to $\Lambda$CDM, while the utilization of the CMB distance prior results in a very low value of matter density. In the case of the wGOHDE model, the matter density aligns closely with other major observations, but we obtain a very low value for $\beta$ and an extremely low value for $w_{z_0}.$ Consequently, even without utilizing the SH0ES prior, we obtain a Hubble parameter close to local observations. However, this comes at the expense of a very low $w_{z_0}$ value. The baryon density, however, remains close to the Planck results, with wGOHDE providing a similar value. The best fit values of are $0.02295\pm 0.00015$ and $0.02340\pm 0.00015$ for wGOHDE and GOHDE respectively.

It would be interesting to explore various combinations of datasets and assess these models further. Additionally, one could employ the complete CMB data and fit the model to the CMB power spectrum. Nevertheless, this endeavour is computationally intensive and falls beyond the scope of the present study.

7 Implications of negative dark energy

Given the parameter values derived from fitting our model to various data combinations, it is crucial to explore the empirical implications. An essential factor in understanding a barotropic fluid’s behaviour is its equation of state parameter. By employing the density parameter described in Eq. (13), we can deduce the equation of state for our dark energy using Eq. (15), and is given as,

$$\begin{aligned} w_{\Lambda }=-1+\frac{\left[ \frac{(2 \alpha -2)}{\beta } \left( \frac{1}{z+1}\right) ^{\frac{2-2 \alpha }{\beta }}{\mathcal {G}}+(z+1)\partial _z{\mathcal {F}}\right] }{3 \left[ \left( \frac{1}{z+1}\right) ^{\frac{2-2 \alpha }{\beta }} {\mathcal {G}}+ {\mathcal {F}}\right] }, \end{aligned}$$

(35)

with

$$\begin{aligned} {\mathcal {F}}&:=~\Omega _k \left[ \frac{(z+1)^2}{-\alpha +\beta +1}-1\right] +\Omega _m \left[ \frac{2(z+1)^3}{-2 \alpha +3 \beta +2}-1\right] \\&\quad +\Omega _r \left[ \frac{(z+1)^4}{-\alpha +2 \beta +1}-1\right] ,\\ {\mathcal {G}}&:=~\frac{(\alpha -\beta )(\Omega _k+1)-1}{\alpha -\beta -1}+ \frac{ \Omega _m}{\alpha -\frac{3}{2} \beta -1}+\frac{\Omega _r}{\alpha -2 \beta -1}. \end{aligned}$$

To establish the $\Lambda$CDM model from the expression above, we need to satisfy the following condition:

$$\begin{aligned} \frac{(2 \alpha -2)}{\beta } \left( \frac{1}{z+1}\right) ^{\frac{2-2 \alpha +\beta }{\beta }} {\mathcal {G}}=-\partial _z{\mathcal {F}}. \end{aligned}$$

(36)

This condition relies on the specific values of the parameters and poses a challenging task. However, there is a straightforward solution that emerges asymptotically. When $\alpha =1,$ the condition simplifies to $\partial _z{\mathcal {F}}=0.$ Solving for z,  we find two solutions: $z=-1$ and $z=(-\Omega _{m}-2\Omega _{r}\pm \sqrt{\Omega _{m}^2-4\Omega _{k}\Omega _{r}})/(2\Omega _{r}).$ Importantly, the latter solution reduces to $-1$ for a universe with zero curvature. Therefore, when $\alpha =1,$ we obtain an asymptotic de Sitter universe for $\Omega _{k}=0.$ Another straightforward scenario arises when there is initially no fluid other than dark energy, which does not accurately depict our universe. Thus, $\Lambda$CDM can only be an approximation in the GOHDE framework.

Two significant observations are derived from the analysis of the dark energy equation of state parameter. Firstly, its dynamic nature exhibits considerable variation from the early to late phases. Secondly, the presence of singularities within the dark energy equation of state parameter is notable. Of these, the latter observation holds particular importance for us, as it suggests the potential existence of negative energy density. Let us look into each observation individually.

The term “dark energy” denotes the force driving the accelerated expansion of the universe in its later stages. This characteristic does not inherently entail any distinct properties during the early phase, as its density is expected to diminish rapidly according to conventional understanding. Thus, regardless of its behaviour in the past, it seems irrelevant to explain the present and future in most dark energy models. However, within the framework of HDE models, matters take on a more intriguing complexion. In our analysis, while our focus primarily lies in modelling dark energy akin to a cosmological constant, we discover that our approach permits it to exhibit behaviours akin to other fluid types. This phenomenon significantly enhances the concept of holography. Consequently, the driving force behind late-time acceleration becomes the integration constant due the presence of $\sim \beta \dot{H}$ in the formulation. Without this term, we are left with a standard HDE model, which cannot explain late-time acceleration unless we fine-tune the infrared cut-off or redefine the entropy.

Furthermore, there exists a notion that often goes unnoticed. The original concept driving the development of HDE aimed to encompass the entire energy density [12]. However, this aspect is frequently overlooked in the formulation of most HDE models. Consequently, rather than being inherently fundamental, most of these models should be viewed as phenomenological. It is plausible that a more fundamental underpinning for dark energy and holography exists, wherein these models emerge as specific instances. The observation that our GOHDE model mimics other energy components underscores the universality of the holographic principle and the effectiveness of employing infrared cutoffs with derivatives of the Hubble parameter. These insights can be traced back to the shared origin of the CKN bound and the Friedmann equation, stemming from the first law of horizon thermodynamics.

In the context of GOHDE, upon examining the characteristics given by Eq. (13), it becomes apparent that dark energy exhibits scaling properties similar to the dominant energy conditions during respective epochs. This outcome stems from our deliberate approach of formulating dark energy by systematically eliminating terms such as $\Omega _{m}a^{-3},$ $\Omega _{r}a^{4},$ and $\Omega _{k}a^{-2}$ from the Hubble flow. Were we to opt for alternative formulations involving the redefinition of other fluid components, we might arrive at a scenario closely resembling the w(z)CDM model, where w(z) denotes a function dependent on redshift and other parameters within the model. However, such redefinitions may not represent the most optimal initial hypothesis. We intended to preserve these components in their original state, leading to the emergence of an energy component exhibiting behaviour reminiscent of radiation during early epochs, transitioning to a matter-like scaling during epochs dominated by matter, and eventually resembling dark energy in the present epoch. Consequently, our approach encapsulates a hitherto unexplored aspect of HDE, showing its universality.

Fig. 10

Dark energy equation state $(w_{\Lambda })$ as a function of redshift (z) for the best fit estimates of GOHDE and wGOHDE models with different data combinations. The Phantom divide $(-1)$, pressure less matter (zero) and radiation states (1/3) are denoted with dashed horizontal lines

In Ricci dark energy, noteworthy instances arise where $\beta$ is defined as $\alpha /2,$ resulting in a dark energy that never scales like radiation in any epochs [27, 28]. Within the framework outlined in this manuscript, such observations can be directly inferred from the Hubble flow equation, as detailed in Eq. (11). Specifically, when $\beta =\alpha /2,$ the term scaling as $\Omega _re^{-4x}/(-\alpha +2\beta +1)$ simplifies to $\Omega _re^{-4x},$ eliminating any radiation-like scaling when isolating dark energy by removing other parameters from consideration. Similarly, when $\beta =2\alpha /3,$ the manifestation of matter-like behaviour is precluded, and setting $\beta =\alpha$ obviates curvature-like scaling. Should we adopt $\beta$ and $\alpha$ as constants, it becomes apparent that fulfilling the conditions above simultaneously is unattainable. This implies that our dark energy fluid possesses a highly dynamic equation of state parameter, capable of transitioning from 1/3 to zero to less than $-1/3$ within our universe. Such transitions may occur smoothly or exhibit singular characteristics. The presence of singular points signifies a shift from negative to positive energy density, suggesting the existence of negative energy density in the universe’s past.

In Fig. 10, we present the dark energy equation of state $(w_{\Lambda })$ plotted against redshift (z) for the best-fit estimates of the GOHDE and wGOHDE models utilizing various data combinations (Fig. 11).

Fig. 11

Dark energy equation state $(w_{\Lambda })$ as a function of redshift (z) for the best fit estimates of wGOHDE with “D4 + Pantheon$^+$ + SH0ES”. The grey line indicates the 1$\sigma$ deviation. $\Lambda _s$CDM is the signswitching $\Lambda$CDM, and the dark and light red band corresponds to 1 and 2 $\sigma$ regions

It is evident that both the GOHDE and wGOHDE models’ best-fit values indicate a transition of our HDE fluid from an early radiation-like behaviour to that of matter and subsequently from matter to quintessence, phantom, or de Sitter-like fluid. Notably, the best-fit values do not precisely correspond to $\beta$ being equal to 1,  1/2,  or 2/3,  although the possibility of 2/3 cannot be entirely dismissed. Furthermore, the presence of singular points in the equation of state signifies a transition from early negative energy to a present positive value. Thus, while the fluid behaves like matter or radiation in the earlier epoch, it does not necessarily correspond to ordinary matter or radiation that conforms to the weak energy condition, suggesting the potential existence of something novel [108]. Negative energies are plausible within the cosmological context, and diverse perspectives exist regarding their existence [109,110,111,112,113,114,115,116].

Returning to the analyses in Fig. 10, the pole in the dark energy equation of state parameter resides in the past. Except for the GOHDE model combined with the Pantheon$^+$ dataset, all optimal parameter estimates indicate a transition within the redshift range of $2<z<5.$ Regardless of the specific model or dataset utilized, this transition redshift, denoted as $z_{\dagger },$ occurs during the matter domination. Remarkably, this transition alleviates the tension observed in BAO Lyman-$\alpha$ measurements.

Among the prominent issues in contemporary cosmology, the Hubble tension stands out, representing an approximately $5\sigma$ disparity between the observed Hubble parameter value and the one derived from the CMB using the best-fit $\Lambda$CDM model [77]. Any attempt to address this tension necessitates comprehensive fitting of the entire CMB dataset using the respective model and subsequently predicting a higher value than that obtained from the $\Lambda$CDM best-fit. Notably, a plethora of literature is discussing this topic, with [117] offering a comprehensive review.

In addition to the Hubble tension, there is a noticeable tension in observations related to the BAO within the Lyman-$\alpha$ forest [96]. While this tension falls around the $2\sigma$ threshold when considering the $\Lambda$CDM model, it is apparent that conventional approaches, such as the parameterization of dark energy through the CPL model, struggle to resolve it adequately [118]. The discrepancy observed in the BAO Ly-$\alpha$ manifests as differences in the measured values of the Hubble parameter at redshifts $\gtrsim 2.3$ when compared to predictions from the $\Lambda$CDM or wCDM models. Regrettably, conventional strategies addressing the original Hubble parameter tension do not inherently rectify the BAO tension [119]. Consequently, there is a compelling motive for investigating a new class of dark energy models that can potentially mitigate both sources of tension simultaneously.

Recently, two noteworthy studies have emerged, each proposing early negative dark energy densities as potential solutions to these tensions. In one such study [120], the authors advocate for dark energy within the framework of Horndeski gravity, which incorporates self-interactions and nonminimal coupling of a dynamical scalar field. Their model addresses cosmological tensions by introducing negative dark energy densities at high redshifts. While their primary focus was alleviating the Hubble tension, their approach inadvertently relieves the BAO Ly-$\alpha$ tension. A more promising model was introduced in another study [121], featuring a spontaneous sign-switching cosmological constant designed to address these tensions. Remarkably, both [120, 121] demonstrate evidence of negative dark energy at redshifts exceeding 2, despite differing origins and constructions of their respective models. The first stringent constraint on the switching redshift was reported around $z\sim 2.5$ [122], later refined to $z\sim 2$ [123]. Notably, when incorporating the absolute magnitude prior from the SH0ES team [77], the sign-switching cosmological constant significantly outperformed the $\Lambda$CDM model in addressing these tensions. Dynamical analysis of similar models advocating negative energy can be found in [124]. Consequently, early negative energy densities are emerging as compelling solutions for tensions in cosmology [125].

Fig. 12

The comoving Hubble flow for $\Lambda$CDM, wCDM, GOHDE, and wGOHDE models with various data combinations using different best fit estimates. The data points are taken from [72] with reference to [62,63,64] for the BAO Ly-$\alpha$ set and [65,66,67,68,69,70,71] for the BAO galaxy clustering set. The colour band corresponds to 1$\sigma$ confidence region

In Fig. 12, we see the behaviour of the comoving Hubble flow, using the best-fit parameters derived from our MCMC chains. The curves are complemented by data points sourced from [72], referencing [62,63,64] for the BAO Ly-$\alpha$ dataset, and [65,66,67,68,69,70,71] for the BAO galaxy clustering dataset. Undoubtedly, the GOHDE and wGOHDE models exhibit enhanced capability in resolving the BAO Ly-$\alpha$ tension even without using the SH0ES prior.

The projections derived from the best-fit parameters notably fall within the $1\sigma$ confidence interval. Particularly noteworthy is the substantial mitigation of tension observed with the inclusion of the SH0ES prior, rendering it practically negligible. The analysis incorporates the SH0ES prior, utilizing the Tripp-1998 corrected distance modulus [126], where the fiducial SNe Ia magnitude (M) is derived from the Cepheid host distances [77, 127]. The disparity between the predicted and observed values of BAO Ly-$\alpha ,$ expressed in terms of standard deviations $(\sigma )$, is detailed in Table 6. Notably, employing the wGOHDE model, tension is essentially absent regardless of the combination of data utilized. Consequently, models featuring a negative energy density exhibit a notable capacity to alleviate the BAO Ly-$\alpha$ tension. Whether yielding a higher $H_0$ value or not, the wGOHDE model accounts for the BAO dataset.

Table 6 Deviation between prediction and observations of BAO Ly-$\alpha$ in terms of respective $\sigma$ based on the best-fit values

The use of the SH0ES prior, particularly as the Dirac prior, may raise questions. Initially, the model may not appear to address the Hubble tension. However, it exhibits a characteristic observed in models capable of resolving the Hubble tension, namely the presence of early negative dark energy density. Without the SH0ES prior, the transition from negative to positive dark energy density occurs around a redshift close to 5. In existing literature, models that resolve the Hubble tension display similar transitions at redshifts just above 2. When employing the SH0ES Dirac prior, we also observe this transition around redshift 2.9. Therefore, the use of the Dirac SH0ES prior serves to highlight this feature.

Further insights regarding the transition redshift $(z_{\dagger })$ can be seen from Tables 3 and 6. In the case of the GOHDE model, when utilizing the D4 + Pantheon$^+$ dataset combination, a value of $z_{\dagger }\sim 232$ was identified, with the BAO Ly-$\alpha$ tension closely resembling that of $\Lambda$CDM or wCDM models. This suggests that in order to alleviate tension, the transition from negative to positive energy density must have occurred relatively recently. Thus, our analysis for the first time establishes upper and lower bounds for the value of $z_{\dagger }.$

$$\begin{aligned} 2.9\lesssim z_{\dagger }&\lesssim 232\text { with GOHDE model},\\ 2.9\lesssim z_{\dagger }&\lesssim 5\text { with }w\text {GOHDE model}. \end{aligned}$$

The values presented in [120, 122, 123] exhibit a notable convergence with our findings. Although our methodology diverges significantly from that employed in [120, 122, 123], it is noteworthy that the observed transition aligns closely with their reported best-fit parameters. The refinement of constraints is anticipated with the incorporation of complete CMB data, which is a promising avenue for future investigation.

7.1 Recent progresses on the transition from AdS to dS vacua

In discussions involving negative dark energy density, recent advancements in the field are noteworthy. A significant development is the concept of a sign-switching cosmological constant with CDM, denoted as $\Lambda _s$CDM. In this model, the cosmological constant changes sign around a specific redshift, denoted as $z_{\dagger }.$ Here, $z_{\dagger }$ represents an extra parameter of the model (although not physical), and $\Lambda _s$ is defined as $\Lambda _s\equiv \Lambda _{s0}\text {sgn}[z_{\dagger }-z].$ This approach has been explored in various studies [122, 123, 128]. A notable aspect of $\Lambda _s$CDM is its ability to address multiple cosmological tensions simultaneously. Sequential research has demonstrated its potential in resolving tensions related to $H_0,$ $S_8,$ and the BAO Ly$\alpha$ disparity.

In $\Lambda _s$CDM, despite the dark energy becoming negative, it remains constant. Recent studies have introduced string-motivated cosmologies and constructions to motivate the physical processes underlying these transitions. For example, [129] propose a motivation for $\Lambda _s$CDM using type-II minimally modified gravity, which preserves spatial diffeomorphism invariance while disrupting $3+1$ diffeomorphism invariance on cosmological scales [130]. Type-II minimally modified gravity shows promise in resolving the Hubble tension, aligning well with $\Lambda _s$CDM. However, implementing $\Lambda _s$CDM within this framework often results in a pole in $\dot{H},$ posing challenges for perturbation theories. Strategies to overcome this issue are discussed in [129]. Additionally, studies propose that Casimir forces can account for these transitions, albeit with implications for the number of relativistic neutrino-like species $(N_{eff})$ and dark dimensions [131, 132].

Here, our manuscript illustrates how negative energy density can intrinsically address the BAO Ly$\alpha$ inconsistency. While the model outlined in [122, 123] adopts a sign-switching mechanism, ours and the approach in [120] demonstrate substantial similarities. Both our framework and that of [120] describe a fluid exhibiting characteristics of pressure-less negative energy matter in the recent past, transitioning to supercritical positive energy matter. The similarity in this transition redshift will have profound significance in connecting $\Lambda _s$CDM with our wGOHDE or other HDE variants and thus bringing the ideas of AdS space into HDE settings, which appears to be interesting. Another explanation for this situation could arise from the geometry of the universe [133], which warrants further exploration.

8 Linear perturbation and growth function

Analysing a cosmological model involves testing its capacity to explain the evolution of cosmological structures. This necessitates an understanding of cosmic fluids and their dynamics. In the standard $\Lambda$CDM model, the growth of perturbations is governed by a straightforward second-order differential equation solely involving matter density perturbations. However, when considering dynamical dark energy with an equation of state different from $-1,$ its perturbations have a non-negligible impact on the growth function, requiring a study of the coupled system. Even in the simplest case of the wCDM model, we can neglect these perturbations when the dark energy equation of state is very close to $-1,$ as the dark energy density is significantly lower than that of matter density. However, when it exhibits a significant deviation from $\Lambda$CDM, it becomes appropriate to consider dark energy perturbations.

In [134], the author has simplified the consideration of dark energy perturbations by enabling the transformation of the model of interest into models discussed therein. In our scenario, we can express our wGOHDE model as an effective wmCDM model, where mCDM represents the modified matter component. Following the approach outlined in [134], the coupled matter-dark energy perturbation equations for a constant $w_{\Lambda }$ are,

$$\begin{aligned}&\delta ''_{\text {m}}+\frac{3}{2a}\left( 1-w_{\Lambda }\Omega _{\Lambda }(a)\right) \delta '_{\text {m}}\nonumber \\&\quad =\frac{3}{2a^{2}} \Bigg [\Omega _{\text {m}}(a)\delta _{\text {m}}+\Omega _{\Lambda }(a)\delta _{\Lambda }\left( 1+3c_{\text {eff}}^{2}\right) \Bigg ] \end{aligned}$$

(37)

$$\begin{aligned}&\delta ''_{\Lambda }+\frac{3}{2a}\Bigg [1-w_{\Lambda }(2+\Omega _{\Lambda }(a)) \Bigg ]\delta '_{\Lambda } \nonumber \\&\qquad +\frac{1}{2a^2}\Bigg [w_{\Lambda }\left( 3w_{\Lambda }\Omega _{\Lambda }(a)-1\right) \Bigg ]\delta _{\Lambda } \nonumber \\&\quad =\frac{3}{2a^{2}} \left( 1+w_{\Lambda }\right) \Bigg [\Omega _{\text {m}}(a)\delta _{\text {m}}+\Omega _{\Lambda }(a)\delta _{\Lambda }\left( 1+3c_{\text {eff}}^{2}\right) \Bigg ]. \end{aligned}$$

(38)

Now the question is how to map our wGOHDE model to wmCDM model. Form the expression for the Hubble parameter we have, ignoring radiation and curvature,

$$\begin{aligned} h^2=\frac{2 \varvec{\Omega _{m}}e^{-3 x}}{2-2 \tilde{\alpha } +3 \tilde{\beta }}+\left( 1-\frac{2 \varvec{\Omega _{m}}}{2-2 \tilde{\alpha } +3 \tilde{\beta }}\right) e^{-\frac{2 (\tilde{\alpha } -1) x}{\tilde{\beta }}}.\nonumber \\ \end{aligned}$$

(39)

To map our wGOHDE model to the wmCDM model, we introduce new parameters $\tilde{\alpha }$ and $\tilde{\beta },$ representing the modified parameters in the transformed model. Previously, we defined dark energy by removing the matter density term $\Omega _{\text {m}}e^{-3x}$ from the expression for the Hubble parameter and introduced a new set of free parameters $w_{z_0}$ and $\beta .$ This formulation enabled the dark energy to exhibit behaviour akin to matter in the matter-dominated era and radiation in the radiation-dominated era. Consequently, the dark energy density defined earlier possessed a dynamic equation of state parameter transitioning from 1/3 to 0 and eventually to a value $<-1/3.$ This transition occasionally led to singularities in the equation of state parameter, indicating negative dark energy density.

Fig. 13

Evolution f(z) against z for different values of $\tilde{\alpha }$ and $\tilde{\beta }.$ The data points corresponds to compilation of 11 f(z) measurements taken from TABLE (1) of [135] for illustration purpose alone

In our formulation of dark energy, we imposed the condition that other fluids remain unaffected by the modelling of dark energy. However, this condition resulted in dark energy being influenced by other fluids. Nevertheless, to understand the system’s dynamical characteristics, it is unnecessary to distinguish between what constitutes our dark energy and matter. Instead, the focus should be on scaling behaviour and constructing an effective fluid description. Thus, by allowing modification of our matter sector, we can avoid the occurrence of negative dark energy densities. The presence of supercritical matter or radiation typically accompanies the occurrence of negative dark energy density. Therefore, it was apparent that a supercritical fluid with an identical equation of state parameter offset the negative energy density of dark energy. To elaborate further, when the dark energy density becomes negative in a matter-dominated era, not only does the density become negative, but the equation of state also approaches zero, resembling some form of diffused dark matter. Consequently, this creates a negative overdensity in the matter sector. However, the supercritical value of $\Omega _{\text {m}}a^{-3}/H^2$ serves to cancel it out, ensuring compliance with the law of conservation of energy.

Indeed, when we modify the matter sector, dark energy and matter density exhibit unconventional features. In our case, modifying the matter component results in an effective model resembling wCDM. Consequently, the free parameters behave differently, leading us to utilize $\tilde{\alpha }$ and $\tilde{\beta }$ instead of $\alpha$ and $\beta .$ Furthermore, one can define the new matter density as,

$$\begin{aligned} \tilde{\Omega }_{\text {m}}=\Omega _{\text {m}}\left( \frac{2}{2-2\tilde{\alpha } +3 \tilde{\beta }}\right) , \end{aligned}$$

(40)

and the dark energy equation of state as,

$$\begin{aligned} \tilde{w}_{\Lambda }=-1+\frac{2(\tilde{\alpha }-1)}{3\tilde{\beta }}. \end{aligned}$$

(41)

Thus, the Hubble parameter becomes

$$\begin{aligned} h^2=\tilde{\Omega }_{\text {m}}e^{-3x}+\left( 1-\tilde{\Omega }_{\text {m}}\right) e^{-3(1+\tilde{w}_{\Lambda })x} \end{aligned}$$

(42)

which is nothing but a wCDM model.

The difference in the free parameters $\alpha$ and $\beta$ arises from how we define the structure of dark energy. In the equation of state given by Eq. (15), we compute the derivative of the logarithm of the dark energy density. In our earlier parametrization, where the matter and other cosmic components remained unchanged, the features of the dark energy density influenced the equation of state. Consequently, the equation of state became a function not only of $\alpha$ and $\beta$ but also depended on $\Omega _{\text {i}}$s, representing the densities of various cosmic components. However, in the parametrization convenient for studying perturbations, such dependencies are not evident. As a result, the former free parameters and those used in the current context are practically different.

Now that we have the Hubble parameter, we can readily compute the density perturbations using Eqs. (37) and (38). In these equations, we have,

$$\begin{aligned} \Omega _{\text {m}}(a)=\frac{\tilde{\Omega }_{\text {m}}}{h^2}a^{-3}\text { and }\Omega _{\Lambda }(a)=\frac{\left( 1-\tilde{\Omega }_{\text {m}}\right) }{h^2}a^{-3(1+\tilde{w}_{\Lambda })}. \end{aligned}$$

(43)

Now, by employing various values of $\tilde{\alpha }$ and $\tilde{\beta },$ we can compute $\tilde{\Omega }_{\text {m}}$ and $\tilde{w}$ and numerically evaluate $\delta _{\text {m}}$ and $\delta _{\Lambda }.$

One of the most straightforward derived functions from $\delta$ is the linear growth rate of matter perturbations, denoted as f(z),  defined as,

$$\begin{aligned} f(z)=\frac{d\ln \delta _{\text {m}}}{d \ln a}=-\frac{(1+z)}{\delta _{\text {m}}} \frac{d\delta _{\text {m}}}{dz}. \end{aligned}$$

(44)

For illustration, we will plot f(z) against z for different values of $\tilde{\alpha }$ and $\tilde{\beta }.$ In this parametrization, when $\tilde{\alpha }=1$ and $\tilde{\beta }=2/3,$ we recover the $\Lambda$CDM model. This holds true for the previous parametrization as well. The numerical analyses were conducted for both clustered $(c_{\text {eff}}\simeq 0)$ and non-clustered $(c_{\text {eff}}\simeq 1)$ dark energy on the growth of matter perturbations. For the numerical analysis, we utilized the initial conditions described in [134], which are,

$$\begin{aligned} a_i&=10^{-3} \end{aligned}$$

(45)

$$\begin{aligned} \delta _{\text {m}i}&=1.4\times 10^{-4},~ \delta _{\text {m}i}'=\delta _{\text {m}i}/a_i \end{aligned}$$

(46)

$$\begin{aligned} \delta _{\Lambda i}&=\frac{1+\tilde{w}_{\Lambda }}{1-3\tilde{w}_{\Lambda }}\delta _{\text {m}i},~ \delta _{\Lambda i}'=\frac{1+\tilde{w}_{\Lambda }}{1-3\tilde{w}_{\Lambda }}\delta _{\text {m}i}'. \end{aligned}$$

(47)

Here we consider three different possibilities of $\tilde{\beta }\in \{1/2,2/3,1\}$ and $\tilde{\alpha }\in \{0.75,1.00,1.25\}$ and we took $\Omega _{\text {m}}=0.3$ for simplicity. The results are shown in Fig. 13. Clearly, $\tilde{\alpha }>1$ and $\tilde{\beta }<2/3$ deviate a lot from the $\Lambda$CDM estimate, and all other combinations can reasonably account for the data. The data points corresponds to compilation of 11 f(z) measurements taken from TABLE (1) of [135] for illustration purpose alone. While the model diverges from wCDM due to alterations in the matter sector, the matter equation of state parameter remains fixed at zero. Consequently, the modification essentially amounts to a multiplicative factor of around one, unaffected by redshift (z). Further analysis taking the $f\sigma _8$ data and the estimation of $S_8$ are left for future work.

9 Conclusions

To summarise, we study Granda–Oliveros holographic dark energy within a flat FLRW universe, aiming to provide observational constraints on model parameters and evidence for early negative energy that alleviates the BAO Ly-$\alpha$ anomaly. We define the GOHDE density and re-parameterise the parameter $\alpha$ as $w_{z0},$ representing the present value of the dark energy equation of state parameter. Subsequently, we employ $\chi ^2$ minimisation with the MCMC method to estimate the free parameters using various observational data sets. Statistically, both GOHDE and wGOHDE models indicate weak evidence against the standard $\Lambda$CDM model. Additionally, we showcase specific characteristics of various datasets, highlighting any distinctive aspects they reveal. Our focus centres particularly on the Pantheon$^+,$ CC, BAO, and CMB distance prior datasets. Furthermore, we explore the features of linear perturbations and growth functions using an alternative parametrization.

Regarding cosmological implications, we report for the first time the potential of an HDE model to alleviate the BAO Ly-$\alpha$ anomaly. We emphasise the significance of the transition from early negative energy to positive energy as a critical indicator for easing various cosmological tensions, noting that this transition must have occurred relatively recently to be effective. Consequently, we establish upper and lower bounds for this transition region, consistent with other models exhibiting similar properties.

Furthermore, we demonstrate that HDE models inherently mimic dominant energy forms unless the free parameters are rigorously calibrated. This observation underscores the dependence between a model’s capability to explain late-time acceleration and the integration constant, highlighting the impossibility of arbitrarily setting this constant to zero. The origins of HDE and the Friedmann equations from the first law of horizon thermodynamics offer a natural explanation for this behaviour, extending the holographic principle to all energy components, diverging from prevalent notions.

It is crucial to acknowledge that plugging the expression for any HDE density into the first Friedmann equation may be one of many approaches for constructing holographic dark energy models. As discussed in prior studies [136, 137], the choice of entropy can modify the form of the first law and, consequently, the derived Friedmann equations, suggesting that different entropy formulations lead to distinct cosmology. Furthermore, this analysis did not consider any interaction between the dark sectors, which could significantly impact the results and yield unforeseen outcomes. Previous research [138] has examined a generic interaction term with the simplest IR cut-off, demonstrating its potential to explain late-time acceleration while producing a CMB power spectrum significantly different from that of $\Lambda$CDM. Future inquiries may examine the impacts of modifying the entropy definition and including various interaction terms.

Use of AI tools: I acknowledge the assistance of ChatGPT 3.5 and Grammarly in enhancing the grammar and English language usage in this article. Following these tools, I reviewed and edited the full content, assuming full accountability for the accuracy and quality.

Python modules used: Numpy [139], Pandas [140], Scipy [141], Emcee [83], Lmfit [84], PyMC [142], Scienceplots [143], Corner [144], Seaborn [145] and Matplotlib [146]. Sample codes showcasing the methodology utilizing the emcee module can be accessed at https://emcee.readthedocs.io/en/stable/tutorials/line/, while those utilizing the lmfit module are available at https://lmfit.github.io/lmfit-py/fitting.html. The datasets employed in this study have been identified beforehand, and the MCMC algorithms were run on a moderately equipped workstation with 12 cores and 64 GB of RAM. The codes and datasets utilized in this analysis are accessible upon reasonable request. The cosmological analyses’ chains are available for reference at https://github.com/manoshmanoharan/GOHDE-Cosmology.