Abstract
We present for the first time a Friedmann-like construction in the framework of an osculating Finsler–Randers–Sasaki (F–R–S) geometry. In particular, we consider a vector field in the metric on a Lorentz tangent bundle, and thus the curvatures of horizontal and vertical spaces, as well as the extra contributions of torsion and non-linear connection, provide an intrinsic richer geometrical structure, with additional degrees of freedom, that lead to extra terms in the field equations. Applying these modified field equations at a cosmological setup we extract the generalized Friedmann equations for the horizontal and vertical space, showing that we obtain an effective dark energy sector arising from the richer underlying structure of the tangent bundle. Additionally, as it is common in Finsler-like constructions, we obtain an effective interaction between matter and geometry. Finally, we consider a specific model and we show that it can describe the sequence of matter and dark-energy epochs, and that the dark-energy equation of state can lie in the quintessence or phantom regimes, or cross the phantom divide.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
General Relativity (GR) has been proved a successful theory of gravity, tested with high precision at Earth-based and Solar System experiments (perihelion precession of Mercury, gravitational redshift, Shapiro time-delay effect, etc) [1]. Nevertheless, at the theoretical level one faces the problem of non-renormalizability [2], since GR cannot be incorporated in a quantum description [3]. Additionally, at the cosmological level we still have the open issues of dark matter and dark energy [4, 5], as well as possible tensions between predictions and observations, such as the \(H_0\) [6] and \(\sigma _8\) tensions [7] (for a review see [8]). Hence, a large amount of research was devoted in the construction of various gravitational modifications, namely theories that possess general relativity at as a particular limit, but which in general exhibit richer behavior, theoretically and cosmologically improved [9,10,11,12].
The basic procedures towards modified gravity constructions is to start from the Einstein-Hilbert Lagrangian and add extra terms, resulting to f(R) gravity [13, 14], f(G) gravity [15], Weyl gravity [16], Lovelock gravity [17], etc. Furthermore, one can consider alternative geometries, beyond the Riemannian one, such is the torsional formulation of gravity, and construct extensions such as f(T) gravity [11], \(f(T,T_G)\) gravity [18], f(T, B) gravity, etc. In similar lines, one can use non-metricity, resulting to symmetric teleparallel gravity [19, 20], f(Q) gravity [21], etc.
However, one can proceed to more radical geometrical modifications, namely use Finsler and Finsler-like geometries, which have richer structure than Riemannian framework, and use them in order to construct gravitational theories [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. These modified theories of gravity use generalized metric structures, where a vector field is incorporated in the geometrical construction, and have contributed with different directions in the development of locally anisotropic models for the gravitational field theory and cosmology.
In Finsler and Finsler-like geometries more than one connection and curvature appear, which depend on the position and velocity, in contrast to GR in which there is only the Levi-Civita connection and the curvature of the Riemannian space. Therefore, gravity can be studied in a different way in the framework of an 8-dimensional Lorentz tangent bundle or a vector bundle which includes the observer (velocity/tangent vector) with extra internal/dynamical degrees of freedom [25,26,27,28,29,30, 54], as well as in an osculating Riemannian and Barthel framework [55,56,57].
Concerning this approach, all kinds of generalized metric theories belong to the larger class of the so called “anisotropic field theories”, since Lorentz violations, velocity fields and torsions produce anisotropies in the space and the matter sector [40, 42, 58, 59]. Hence, these internal geometrical anisotropies, which should not be confused with spacetime anisotropies that may appear in Riemannian geometry too (e.g. in Bianchi cases) are induced by internal direction/velocity y-variables in addition to the position x-variables in the structure of the base manifold. In these lines, geometrical anisotropies can be considered as a “potential” or a tidal field in the matter sector [60]. In cases where an anisotropy is included in the metric structure of spacetime, as it appears in Finsler and Finsler-like cosmologies, it is incorporated in the effective energy–momentum tensor of the anisotropic structure, which could potentially lead to energy exchange between geometry and matter [61]. Finally, similarly to general relativity, geometrical effects are produced not only by the distribution of mass-energy but also by its motion [62].
In this work we propose a novel geometrical structure, namely that of Finsler–Randers–Sasaki type, in order to extract generalized gravitational field equations. Then, applying them in a cosmological framework we construct Finsler–Randers–Sasaki cosmology, which is characterized by modified Friedmann equations with new terms that depend on the underlying geometry and the tangent bundle features. As we will show, these terms can lead to interesting cosmological implications, and describe the thermal history of the Universe, as well as the effective dark energy sector. The plan of the work is the following: In Sect. 2 we provide the basic concepts of Finsler–Randers–Sasaki geometry, and we extract the general gravitational field equations. Then, in Sect. 3 we proceed to the application at a cosmological framework, and we extract the modified Friedmann equations for the horizontal and vertical subspaces, investigating also specific examples. Finally, in Sect. 4 we discuss our main results.
2 Finsler–Randers–Sasaki geometry and gravity
In this section we present the basics of Finsler–Randers–Sasaki geometry and gravity. We will start by introducing some geometrical aspects from Finsler geometry and the oscullating Riemannian metric, and then we will use it to construct a gravitational theory.
2.1 Finsler–Randers–Sasaki geometry with oscullating Riemannian metric
We consider an n-dimensional bundle M, as well as its tangent bundle TM, with a fibered and differentiable (smooth) metric function F(x, y) with the following properties:
-
1.
F is continuous on TM and smooth on \( \widetilde{TM}\equiv TM{\setminus } \{0\} \), namely the tangent bundle minus the null set \( \{(x,y)\in TM | F(x,y)=0\}\).
-
2.
F is positively homogeneous of first degree on its second argument:
$$\begin{aligned} F(x^\mu ,ky^\alpha ) = kF(x^\mu ,y^\alpha ), \qquad k>0 . \end{aligned}$$(1) -
3.
For each \(x\in M\) the fundamental metric tensor:
$$\begin{aligned} g_{ij}(x,y) =\pm \dfrac{1}{2}\dfrac{\partial ^2 F^2}{\partial y^i \partial y^j} \end{aligned}$$(2)is non-singular, with \(i,j=0,1,\ldots ,n-1\).
A Lorentz tangent bundle TM over a spacetime 4-dimensional manifold M is a fibered 8-dimensional manifold with local coordinates \(\{x^\mu ,y^ a\}\), where the Greek indices of the spacetime variables x are \(\kappa ,\lambda ,\mu ,\nu ,\ldots = 0,\ldots ,3\) and the Latin indices of the fiber variables y are \( a, b,\ldots ,f = 0,\ldots ,3\). An extended Lorentzian structure on TM can be provided if the background manifold is equipped with a Lorentz metric tensor of signature \((-1,\ldots ,1)\). As it is known, a metric following the above three properties is called a Finsler metric [22, 23].
Additionally, one can introduce the oscullating Riemannian metric on a differentiable manifold [63]. In particular, this can be defined by a tangent vector field \(Y:U\rightarrow TU\), where \(U\subset M\) is an open neighborhood on M with the property \(Y(x)\ne 0\) \(\forall x\in U\). In such a case the metric can be defined by the relation:
In the following we will consider that all non-vanishing global vector fields, defined on the spacetime manifold, satisfy M \(y(x)=Y(x)\) [64]. The pair \((U,g_{ij}(x,y(x))\) is called Y-oscullating Riemannian metric associated to (M, F) manifold.
As it is known, the length of a curve c in a Finsler space is given by the integral
with \(y=\frac{dx}{d\tau }\) and \(\tau \) an affine parameter along the curve. In a Finsler–Randers (FR) spacetime [65] the metric is given by the relation [66, 67]:
where \(a_{\mu \nu }(x)\) is a Riemannian pseudo-metric and \(f_{\alpha }\) a covector with \(||f_{\alpha }||\ll 1\). Note that the 1-form \(f_{\alpha }dx^{\alpha }\) can be interpreted as the “energy” produced by the anisotropic force field \(f_{\alpha }\), and hence due to (4) and (5) the integral \(\int _{a}^{b}F(x,dx)\) represents the “total work” that a particle requires in order to move along a path with proper time \(\tau \).
We proceed by writing the corresponding Lagrangian function of an FR space with an oscullating Riemannian metric, which is
with \(||f_{\alpha }||\ll 1\). We mention here that in the above expression the second term \(f_{\alpha }(x)y^{\alpha }(x)\) can be interpreted as the “power” that is produced due to propagation of particles through the force-field \(f_{\alpha }(x)\). Now, from (2), (3) and (6) we can extract the metric tensor \(v_{\alpha \beta }(x,y(x))\) as
where
with \(L = \sqrt{-g_{\alpha \beta }y^{\alpha }(x)y^{\beta }(x)}\) and \(||A_{\gamma }||<<1\). Due to relation (8), the metric (7) can be called “weak Finslerian metric” [67]. Hence, as we can see from (7), the term \(h_{\alpha \beta }(x,y)\) can be considered as a perturbation. For convenience, and in order to make notation lighter, in the following we will write y instead of y(x).
Let us now introduce the Sasaki-type metric on TM [68]. Such a metric has the form:
In our approach we consider that the Finslerian metric \(v_{\alpha \beta }(x,y)\) is given by (7), and the unified adapted frame is defined in the form \(E_A = \,\{\delta _\mu ,{\dot{\partial }}_\alpha \} \) with
and
and where \(E_A\) is the adapted basis of the tangent space \(T_{x}M\). Furthermore, we define the dual basis \({E^{A}}=(dx^{\mu },\delta y^{\alpha })\) with
where \(E^{A}\) is the adapted basis of the cotangent bundle \(T^{*}M\) and \(N^{\alpha }_{\lambda }\) are the components of the nonlinear connection with \(\alpha ,\lambda = (0,1,2,3)\). The nonzero coefficients of a canonical and distinguished d-connection \({\mathcal {D}}\) on TM read as [22]:
Finally, concerning the non-linear connection, we choose a Cartan-type of the form:
which is known to have interesting applications [69].
We now have all the geometrical quantities in order to calculate the curvature tensors. In particular, in such a framework the Riemann and Ricci curvature tensors of the horizontal space are defined as [22, 23]:
where \(\Omega ^\alpha _{\nu \kappa }\) represents the curvature of the nonlinear connection and is defined as
Moreover, the curvature tensors of the vertical space are given by:
Thus, the generalized Ricci scalar curvature in the adapted basis is:
where
In the same lines, one can define the torsion tensor as
where \(L_{\beta \nu }^{\alpha }\) is given in (14).
2.2 Finsler–Randers–Sasaki gravity
Having presented the Finsler–Randers–Sasaki geometrical framework, we can use it in order to construct a gravitational theory. An Einstein-Hilbert-like action on TM can be defined as
for some closed subspace \({\mathcal {N}}\subset TM\), where \( L_M\) is the standard matter Lagrangian and \(\kappa \) is the gravitational constant. Note that
while the absolute value of the metric determinant \(|{\mathcal {G}}|\) is \(\sqrt{|{\mathcal {G}}|} = \sqrt{-g}\sqrt{-v}\), with g, v the determinants of the metrics \(g_{\mu \nu }, v_{\alpha \beta }\) respectively, as it follows from the form of (9).
Performing variation of the above action in terms of \(g_{\mu \nu }\), \(v_{\alpha \beta }\) and \(N^\alpha _\kappa \) we extract the field equations as (the details are presented in Appendix A):
where we have defined the “energy–momentum tensors”
where \(\delta ^\mu _\nu \) and \( \delta ^\alpha _\beta \) are the Kronecker symbols.
Note that the second field equation (29) is simplified to:
where in our case \(S_{\alpha \beta }\) and S are zero and the mixed Cartan symbols \(C^{\mu }_{\nu \gamma }\) are also zero as we can see from (15). Additionally, we mention that the third field equation (30) is identically zero since the coefficients \(L^{\rho }_{\mu \nu }\) are identical to the classical to Christoffel coefficients of the FRW model, thus they do not depend on the vertical coordinates \(y^{\alpha }\). The mixed Cartan coefficients \(C^{\mu }_{\nu \gamma }\) are zero as we mentioned and the mixed energy–momentum tensor \(Z^{\kappa }_{\alpha }\) is also zero from relation (33) since we do not consider the matter field to depend on the non-linear connection \(N^{\alpha }_{\kappa }\).
Let us make some remarks in order to give a physical interpretation of Eqs. (28), (29) and (30). As one can see, they may contain a source of local-matter creation and contribute to the anisotropic energy–momentum tensors \(T_{\mu \nu }\) and \(Y_{\alpha \beta }\) of the horizontal and vertical spaces. Hence, the energy–momentum tensor \(T_{\mu \nu }\) includes additional information of the action of the local anisotropy of matter fields. \(Y_{\alpha \beta }\), on the other hand, is an object with no equivalent in Riemannian gravity, and it incorporates more information of intrinsic anisotropy, which is produced from the vertical metric structure \(v_{\alpha \beta }\), and it includes additional gravitational field in the framework of the osculating tangent bundle. Finally, the energy–momentum tensor \({\mathcal {Z}}^{\kappa }_{\alpha }\) reflects the dependence of matter fields on the nonlinear connection \(N^{\alpha }_{\mu }\), a structure which induces an interaction between internal and external spaces. This tensor is different from \(T_{\mu \nu }\) and \(Y_{\alpha \beta }\), which depend on just the external or internal structure respectively.
Lastly, we introduce a new tensor, quantifying the covariant derivative of the torsion tensor, namely
Using this definition we can re-write (28) as:
where we have omitted from the above relation the term \(\mathcal T^\gamma _{\kappa \gamma }{\mathcal {T}}^\beta _{\lambda \beta }\) since it is of second order. Hence, taking the covariant derivative of (36) we extract the continuity equation for our theory, namely
As expected, and as we discussed in the Introduction, Finsler–Randers–Sasaki gravity, similarly to other Finsler-like models, gives rise to an effective interaction between geometry and matter, which can have interesting cosmological implications.
3 Cosmology
In this section we apply the Finsler–Randers–Sasaki geometry and the oscullating Riemannian framework at a cosmological setup, and using the general field equations we derive the generalized Friedmann equations. Then we will provide specific examples.
3.1 General case
We consider the usual homogeneous and isotropic Friedmann–Robertson–Walker (FRW) metric
with a(t) the usual scale factor and \(k=0,\pm 1\) the spatial curvature, and substituting it in (9) we find:
For simplicity, in the following we focus on the spatially-flat case \(k=0\).
We consider the energy momentum tensor for a perfect fluid in the horizontal and the vertical space:
where \(\rho _m\) and \(p_m\) are respectively the energy density and pressure of the matter perfect fluid, while \(u^{\mu }\) and \(y^{\alpha }\) are the velocities of the fluid in the horizontal and vertical space respectively. We notice from relations (41) and (7), (8), that the energy momentum tensor \(Y^{\alpha \beta }\) of the vertical space constitutes an anisotropic perturbation of the horizontal energy momentum tensor \(T^{\mu \nu }\).
In order to proceed, we have to consider an ansatz for \(A_{\gamma }\) and \(y^{\gamma }\). Firstly, it proves convenient to introduce the following scalars:
and as we can see, \(W_{0}\) represents the time-anisotropic contribution of our space while \(W_{1}\),\(W_{2}\),\(W_{3}\) express the directional components of the anisotropic contribution. In this work we will focus on the case considering \(y^{2}=y^{3}=0\) in order to have only a dependance on the parameter t:
with \(y^{0}\), \(y^{1}\) constants, and \(A_{0}(t)\), \(A_{1}(t)\) time-dependent functions, in agreement with FRW symmetries.
Inserting the G-metric from (39) into the horizontal field equation (28) of the previous section we finally extract the generalized Friedmann equations of the horizontal and vertical space (extracted as (B15), (B16) and (B22), (B23) in Appendix B) as
and
with \(L(t)=\sqrt{(y^{0})^{2}-a(t)^{2}(y^{1})^{2}}\). Finally, the continuity equation (37) under the above considerations becomes:
As expected and as usual, out of the three Eqs. (48), (49), (52) only two are independent, while out of the (50), (51), (52) only two are independent.
As we observe, in Finsler–Randers–Sasaki cosmology we obtain extra terms in the Friedmann equations, arising from the richer geometrical structure. In particular, the anisotropic torsion terms quantified by the covector field \(A_{\mu }\) introduce additional degrees of freedom on the tangent bundle of spacetime, which provide the extra contributions in the Friedmann equations. In the case where the internal geometrical structure disappears, namely when \(W_{0}\) and \(W_{1}\) become zero, the above equations recover the standard Friedmann equations. Additionally, as it was discussed above, in the scenario at hand we obtain an interaction between geometry and matter, which is now clear by the form of (52), and which in the case \(W_{0}=W_{1}=0\) recovers the standard conservation equation too.
We can re-write the Friedmann equations (48), (49) in their standard form
with \(H(t)={\dot{a}}(t)/a(t)\) the Hubble function, and where we have introduced an effective dark energy density and pressure of the form
where we have emitted the explicit time-dependence of the various quantities in order to make the notation lighter. Thus, the dark-energy equation-of-state parameter is defined as
Additionally, the conservation equation (52) can be written as
where the interaction term Q is given by
Hence, differentiating (48) and inserting into (49) using (59) we also acquire
One can now clearly see that in the scenario of Finsler–Randers–Sasaki gravity and cosmology we obtain an interaction between geometry and matter, and therefore an interaction between the effective dark energy and matter sectors. Such an interaction is common in Finsler-like cosmologies [27, 51, 53, 59, 70] and it is very interesting since interacting cosmologies [71,72,73,74,75] are known to have many advantages, including solving the coincidence problem [76, 77] as well as alleviating cosmological tensions [78, 79].
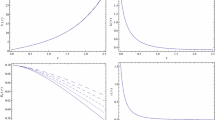
Upper graph: The effective dark energy density parameter \(\Omega _{DE}\) (green-solid), and the matter density parameter \(\Omega _{m}\) (blue-dashed), as a function of the redshift z, for Finsler–Randers–Sasaki cosmology under the ansätze (46), (47), with \(y^0=1\), \(y^1=10^{-6}\) in units where \(\kappa =1\). Middle graph: The corresponding dark-energy equation-of-state parameter \(w_{DE}\). Lower graph: The corresponding deceleration parameter q. We have set the initial conditions \(\Omega _{DE}(z=0)\equiv \Omega _{DE0}\approx 0.69\) [80]
3.2 Specific model
For completeness, in this subsection we will examine a specific model. As one can see from the general Friedmann equations (48), (49), or equivalently from the effective dark-energy sector (55), (56), the appearance of the arbitrary functions \(W_0(t)\) and \(W_1(t)\), i.e. of \(A_0(t)\), \(A_1(t)\), makes the resulting cosmological phenomenology very capable. The only point that one should be careful is that the argument of the square root in L(t) should be positive, and thus \(y^1\) should be suitably smaller than \(y^0\).
Let us investigate a specific example. For simplicity we focus on dust matter, namely we assume that \(p_m=0\). We solve the Eqs. (48), (50) and (52) numerically, and as independent variable we use the redshift \(1+z=1/a\) (we set the present scale factor \(a_0=1\)). Furthermore, we introduce the matter and dark energy density parameters, \(\Omega _{m}\equiv \kappa \rho _{m}/(3H^2)\) and \(\Omega _{DE}= \kappa \rho _{DE}/(3\,H^2)\) respectively. Lastly, we impose \(\Omega _{DE}(z=0)\equiv \Omega _{DE0}\approx 0.69\) and \(\Omega _m(z=0)\equiv \Omega _{m0}\approx 0.31\) in agreement with observations [80].
We present the evolution of \(\Omega _{m}(z)\) and \(\Omega _{DE}(z)\) in the upper graph of Fig. 1. As we can see, we can recover the universe thermal history, i.e. the succession of matter and dark energy epochs. Moreover, in the middle graph Fig. 1 we show the evolution of the corresponding effective dark-energy equation-of-state parameter \(w_{DE}(z)\) according to (57). For this specific example \(w_{DE}\) lies in the quintessence regime. Nevertheless, note that according to the form of (55), (56), one could have other scenarios, in which \(w_{DE}\) can be phantom-like, or experience the phantom divide crossing during the evolution. Finally, for completeness, in the lower graph of Fig. 1 we depict the deceleration parameter q, defined as \(q=-1-\frac{{\dot{H}}}{H^2}\). As we can see, the transition from acceleration to deceleration happens at \(z_{tr}\approx 0.7\), in agreement with observations.
4 Discussion and concluding remarks
In this work we presented for the first time a Friedmann-like construction in the framework of an osculating Finsler–Randers–Sasaki geometry, building the corresponding gravitational theory and applying it at a cosmological setup. In particular, we considered a vector field in the metric on the total structure of a Lorentz tangent bundle, which depends on the position coordinates. In this approach, the curvatures of horizontal and vertical spaces, the extra contributions of torsion, non-linear connection and the vector field, that depend on x and y(x), provide an intrinsic richer geometrical structure, with additional degrees of freedom, that lead to extra terms in the field equations.
Applying these modified field equations at a cosmological setup, considering explicit ansätze for the Finsler–Randers–Sasaki metric functions, we extracted the generalized Friedmann equations for the horizontal and vertical parts of R-S spacetime, in which we have the appearance of extra terms, which can be collected to build an effective dark energy sector. Hence, in the framework of Finsler–Randers–Sasaki geometry and gravity, we obtain an effective dark energy density and pressure arising from the richer underlying structure of the tangent bundle. Additionally, as it is common in Finsler-like constructions, we acquire an effective interaction between the matter and the geometrical sectors, and in particular of the extra Finsler–Randers–Sasaki degree of freedom and matter energy density.
We elaborated the generalized Friedmann equations numerically for a specific model, replicating the thermal evolution of the universe, encompassing distinct matter and dark energy epochs. Our analysis revealed that the dark-energy equation-of-state parameter could occupy the quintessence or phantom regime, or undergo a phantom-divide crossing during the evolution.
Several crucial steps remain to be comprehensively explored. Firstly, a thorough investigation into cosmological applications is imperative, involving data confrontation from Type Ia Supernovae (SNIa), Baryon Acoustic Oscillations (BAO), and Cosmic Microwave Background (CMB) observations. Additionally, one could consider different and more complicated ansätze for the Finsler–Randers–Sasaki metric functions. Another interesting subject is the investigation of spherically symmetric and black hole solutions in the theory at hand. These essential and intriguing inquiries are reserved for future research projects.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: Data sharing not applicable to this article as no datasets were generated or analysed during the current study.]
Code Availability Statement
This manuscript has no associated code/software. [Author’s comment: Code/Software sharing not applicable to this article as no code/software was generated or analysed during the current study.]
References
C.M. Will, Living Rev. Relativ. 17, 4 (2014). arXiv:1403.7377 [gr-qc]
A. Addazi, J. Alvarez-Muniz, R. Alves Batista, G. Amelino-Camelia et al., Prog. Part. Nucl. Phys. 125, 103948 (2022). arXiv:2111.05659 [hep-ph]
R. Alves Batista, G. Amelino-Camelia, D. Boncioli, J.M. Carmona et al., arXiv:2312.00409 [gr-qc]
E.J. Copeland, M. Sami, S. Tsujikawa, Int. J. Mod. Phys. D 15, 1753 (2006). arXiv:hep-th/0603057
Y.F. Cai, E.N. Saridakis, M.R. Setare, J.Q. Xia, Phys. Rep. 493, 1–60 (2010). arXiv:0909.2776 [hep-th]
E. Di Valentino, L.A. Anchordoqui, O. Akarsu, Y. Ali-Haimoud, L. Amendola, N. Arendse, M. Asgari, M. Ballardini, S. Basilakos, E. Battistelli et al., Astropart. Phys. 131, 102605 (2021). arXiv:2008.11284 [astro-ph.CO]
E. Di Valentino, L.A. Anchordoqui, Ö. Akarsu, Y. Ali-Haimoud, L. Amendola, N. Arendse, M. Asgari, M. Ballardini, S. Basilakos, E. Battistelli et al., Astropart. Phys. 131, 102604 (2021). arXiv:2008.11285 [astro-ph.CO]
E. Abdalla, G. Franco Abellán, A. Aboubrahim, A. Agnello, O. Akarsu, Y. Akrami, G. Alestas, D. Aloni, L. Amendola, L.A. Anchordoqui et al., JHEAP 34, 49–211 (2022). arXiv:2203.06142 [astro-ph.CO]
E.N. Saridakis et al. [CANTATA], Modified Gravity and Cosmology: An Update by the CANTATA Network (Springer, 2021). arXiv:2105.12582 [gr-qc]
S. Capozziello, M. De Laurentis, Phys. Rep. 509, 167–321 (2011). arXiv:1108.6266 [gr-qc]
Y.F. Cai, S. Capozziello, M. De Laurentis, E.N. Saridakis, Rep. Prog. Phys. 79(10), 106901 (2016). arXiv:1511.07586 [gr-qc]
S. Nojiri, S.D. Odintsov, V.K. Oikonomou, Phys. Rep. 692, 1–104 (2017). arXiv:1705.11098 [gr-qc]
A.A. Starobinsky, Phys. Lett. B 91, 99 (1980)
S. Capozziello, Int. J. Mod. Phys. D 11, 483 (2002). arXiv:gr-qc/0201033
S. Nojiri, S.D. Odintsov, Phys. Lett. B 631, 1 (2005). arXiv:hep-th/0508049
P.D. Mannheim, D. Kazanas, Astrophys. J. 342, 635 (1989)
D. Lovelock, J. Math. Phys. 12, 498 (1971)
G. Kofinas, E.N. Saridakis, Phys. Rev. D 90, 084044 (2014). arXiv:1404.2249 [gr-qc]
S. Bahamonde, C.G. Böhmer, M. Wright, Phys. Rev. D 92(10), 104042 (2015). arXiv:1508.05120 [gr-qc]
J. Beltrán Jiménez, L. Heisenberg, T. Koivisto, Phys. Rev. D 98(4), 044048 (2018). arXiv:1710.03116 [gr-qc]
F.K. Anagnostopoulos, S. Basilakos, E.N. Saridakis, Phys. Lett. B 822, 136634 (2021). arXiv:2104.15123 [gr-qc]
R. Miron, M. Anastasiei, The Geometry of Lagrange Spaces, Theory and Applications (Springer Science and Business Media, Dordrecht, 1994)
S. Vacaru, P. Stavrinos, E. Gaburov, D. Gonta, arXiv:gr-qc/0508023 [gr-qc]
A.P. Kouretsis, M. Stathakopoulos, P.C. Stavrinos, Phys. Rev. D 86, 124025 (2012). arXiv:1208.1673 [gr-qc]
A. Triantafyllopoulos, P.C. Stavrinos, Class. Quantum Gravity 35(8), 085011 (2018). arXiv:1903.12521 [gr-qc]
G. Minas, E.N. Saridakis, P.C. Stavrinos, A. Triantafyllopoulos, Universe 5, 74 (2019). arXiv:1902.06558 [gr-qc]
S. Konitopoulos, E.N. Saridakis, P.C. Stavrinos, A. Triantafyllopoulos, Phys. Rev. D 104(6), 064018 (2021). arXiv:2104.08024 [gr-qc]
P.C. Stavrinos, S.I. Vacaru, Class. Quantum Gravity 30, 055012 (2013). arXiv:1206.3998 [astro-ph.CO]
S.I. Vacaru, Int. J. Mod. Phys. D 21, 1250072 (2012). arXiv:1004.3007 [math-ph]
M. Hohmann, C. Pfeifer, N. Voicu, Phys. Rev. D 100(6), 064035 (2019). arXiv:1812.11161 [gr-qc]
A.P. Kouretsis, M. Stathakopoulos, P.C. Stavrinos, Phys. Rev. D 82, 064035 (2010). arXiv:1003.5640 [gr-qc]
N.E. Mavromatos, S. Sarkar, A. Vergou, Phys. Lett. B 696, 300 (2011). arXiv:1009.2880 [hep-th]
S. Basilakos, A.P. Kouretsis, E.N. Saridakis, P. Stavrinos, Phys. Rev. D 88, 123510 (2013). arXiv:1311.5915 [gr-qc]
S. Basilakos, P. Stavrinos, Phys. Rev. D 87(4), 043506 (2013). arXiv:1301.4327 [gr-qc]
P. Stavrinos, S.I. Vacaru, Universe 7(4), 89 (2021)
Z. Chang, X. Li, Phys. Lett. B 663, 103 (2008). arXiv:0711.0056 [hep-th]
S.I. Vacaru, Gen. Relativ. Gravit. 44, 1015–1042 (2012). arXiv:1010.5457 [math-ph]
V.A. Kostelecky, M. Mewes, Astrophys. J. 689, L1 (2008). arXiv:0809.2846 [astro-ph]
N.E. Mavromatos, V.A. Mitsou, S. Sarkar, A. Vergou, Eur. Phys. J. C 72, 1956 (2012). arXiv:1012.4094 [hep-ph]
A. Kostelecky, Phys. Lett. B 701, 137 (2011). arXiv:1104.5488 [hep-th]
C. Pfeifer, M.N.R. Wohlfarth, Phys. Rev. D 85, 064009 (2012). arXiv:1112.5641 [gr-qc]
V. Alan Kostelecky, N. Russell, R. Tso, Phys. Lett. B 716, 470 (2012). arXiv:1209.0750 [hep-th]
J. Foster, R. Lehnert, Phys. Lett. B 746, 164 (2015). arXiv:1504.07935 [physics.class-ph]
M. Hohmann, C. Pfeifer, Phys. Rev. D 95(10), 104021 (2017). arXiv:1612.08187 [gr-qc]
C. Pfeifer, Int. J. Geom. Meth. Mod. Phys. 16(supp02), 1941004 (2019). arXiv:1903.10185 [gr-qc]
G. Papagiannopoulos, S. Basilakos, A. Paliathanasis, S. Pan, P. Stavrinos, Eur. Phys. J. C 80(9), 816 (2020). arXiv:2005.06231 [gr-qc]
M. Hohmann, C. Pfeifer, N. Voicu, Universe 6(5), 65 (2020). arXiv:2003.02299 [gr-qc]
P.C. Stavrinos, S. Ikeda, Rep. Math. Phys. 44, 221–230 (1999)
P.C. Stavrinos, S. Ikeda, Bull. Calcutta Math. Soc. 8, 1–2 (2000)
P.C. Stavrinos, M. Alexiou, Int. J. Geom. Methods Mod. Phys. 15, 1850039 (2018)
S. Ikeda, E.N. Saridakis, P.C. Stavrinos, A. Triantafyllopoulos, Phys. Rev. D 100(12), 124035 (2019). arXiv:1907.10950 [gr-qc]
S. Vacaru, P. Stavrinos, Spinors and Space-time Anisotropy (Athens University Press, Athens, 2002). arXiv:gr-qc/0112028
G. Papagiannopoulos, S. Basilakos, A. Paliathanasis, S. Savvidou, P.C. Stavrinos, Class. Quantum Gravity 34(22), 225008 (2017). arXiv:1709.03748 [gr-qc]
A. Triantafyllopoulos, E. Kapsabelis, P. Stavrinos, Eur. Phys. J. Plus 135(7), 557 (2020). arXiv:2004.00356 [gr-qc]
R. Hama, T. Harko, S.V. Sabau, Eur. Phys. J. C 83(11), 1030 (2023). arXiv:2310.09067 [gr-qc]
A. Bouali, H. Chaudhary, R. Hama, T. Harko, S.V. Sabau, M.S. Martín, Eur. Phys. J. C 83(2), 121 (2023). arXiv:2301.10278 [gr-qc]
R. Hama, T. Harko, S.V. Sabau, Eur. Phys. J. C 82(4), 385 (2022). arXiv:2204.04506 [gr-qc]
P.C. Stavrinos, A.P. Kouretsis, M. Stathakopoulos, Gen. Relativ. Gravit. 40, 1403–1425 (2008). arXiv:gr-qc/0612157 [gr-qc]
A.P. Kouretsis, M. Stathakopoulos, P.C. Stavrinos, Phys. Rev. D 79, 104011 (2009). arXiv:0810.3267 [gr-qc]
C. Misner, K. Thorne, J.A. Wheeler, Gravitation (Princeton University Press, Princeton, 1973)
R. Hama, T. Harko, S.V. Sabau, S. Shahidi, Barthel–Randers geometry. Eur. Phys. J. C 81(8), 742 (2021). arXiv:2108.00039 [gr-qc]
S. Weinberg, Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity (Wiley, New York, 1972)
Roman S. Ingarden, Makoto Matsumoto, Rep. Math. Phys. 32(1), 35–48 (1993)
H. Rund, The Differential Geometry of Finsler Spaces (Springer, Berlin, 2012)
G. Randers, Phys. Rev. 59, 195–199 (1941)
E. Kapsabelis, P.G. Kevrekidis, P.C. Stavrinos, A. Triantafyllopoulos, Eur. Phys. J. C 82(12), 1098 (2022). arXiv:2208.05063 [gr-qc]
A. Triantafyllopoulos, S. Basilakos, E. Kapsabelis, P.C. Stavrinos, Eur. Phys. J. C 80(12), 1200 (2020). arXiv:2006.05913 [gr-qc]
S. Sasaki, Tohoku Math. J. 10, 338–354 (1958)
E. Kapsabelis, A. Triantafyllopoulos, S. Basilakos, P.C. Stavrinos, Eur. Phys. J. C 81(11), 990 (2021). arXiv:2111.00952 [gr-qc]
P. Stavrinos, C. Savvopoulos, Universe 6(9), 138 (2020). arXiv:2101.00657 [gr-qc]
G.R. Farrar, P.J.E. Peebles, Astrophys. J. 604, 1–11 (2004). arXiv:astro-ph/0307316 [astro-ph]
B. Wang, J. Zang, C.Y. Lin, E. Abdalla, S. Micheletti, Nucl. Phys. B 778, 69–84 (2007). arXiv:astro-ph/0607126 [astro-ph]
X.M. Chen, Y.G. Gong, E.N. Saridakis, JCAP 04, 001 (2009). arXiv:0812.1117 [gr-qc]
V. Salvatelli, N. Said, M. Bruni, A. Melchiorri, D. Wands, Phys. Rev. Lett. 113(18), 181301 (2014). arXiv:1406.7297 [astro-ph.CO]
M.A. Buen-Abad, M. Schmaltz, J. Lesgourgues, T. Brinckmann, JCAP 01, 008 (2018). arXiv:1708.09406 [astro-ph.CO]
W. Zimdahl, D. Pavon, Phys. Lett. B 521, 133–138 (2001). arXiv:astro-ph/0105479 [astro-ph]
M. Jamil, E.N. Saridakis, M.R. Setare, Phys. Rev. D 81, 023007 (2010). arXiv:0910.0822 [hep-th]
S. Pan, W. Yang, E. Di Valentino, E.N. Saridakis, S. Chakraborty, Phys. Rev. D 100(10), 103520 (2019). arXiv:1907.07540 [astro-ph.CO]
W. Khyllep, J. Dutta, S. Basilakos, E.N. Saridakis, Phys. Rev. D 105(4), 043511 (2022). arXiv:2111.01268 [gr-qc]
N. Aghanim et al. [Planck], Astron. Astrophys. 641, A6 (2020) [Erratum: Astron. Astrophys. 652, C4 (2021)]. arXiv:1807.06209 [astro-ph.CO]
Acknowledgements
The authors acknowledge the contribution of the LISA CosWG, and of COST Actions CA18108 “Quantum Gravity Phenomenology in the multi-messenger approach” and CA21136 “Addressing observational tensions in cosmology with systematics and fundamental physics (CosmoVerse)”.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Action variation and general field equations
In this Appendix we extract the general field equations, performing variation of the action (26) on the Finsler–Randers–Sasaki geometry. In particular, varying (26) we acquire
with
In the above expressions we have defined: \({\overline{R}}_{\mu \nu } = R_{(\mu \nu )} + \Omega ^\alpha _{\kappa (\mu } C^\kappa _{\nu )\alpha }\) and
Applying the Stoke theorem on the Lorentz tangent bundle we obtain
where we have also used the Leibniz rule. Applying the Stokes theorem again and eliminating the new boundary terms, we find
As a last step, the matter part of the action yields
Finally, combining Eqs. (A1)–(A6), (A8), (A10), (A11) and setting \(\Delta K = 0\), we result to the field equations, namely
where we have defined the “energy–momentum tensors”
where \(\delta ^\mu _\nu \) and \( \delta ^\alpha _\beta \) are the Kronecker symbols.
Appendix B: Friedmann equations
In this Appendix we show how the general field equations (28)–(30), under the cosmological metric (38) and (39) give rise to the Friedmann equations on the horizontal and vertical space.
Let us start from the horizontal space. First we will calculate the trace of the torsion \({\mathcal {T}}^{\beta }_{\nu \beta }\) that is required inside (35), (36). From the torsion definition (25) we have that:
If we substitute the non-linear connection (17) and the components of \(L_{\alpha \kappa }^{\alpha }\) from (14) we find:
where h is the trace of the metric \(h_{\alpha \beta }\) from (8). From the above relation we can see that the torsion tensor is of first order in terms of the weak metric \(h_{\alpha \beta }\).
As a next step we use (8) in order to express the \(h_{\alpha \beta }\)-terms in terms of \(A_{\alpha }\) and \(L = \sqrt{-g_{\alpha \beta }y^{\alpha }(x)y^{\beta }(x)}\). In this way we finally find
where we have set
Additionally, we calculate the \(\delta \)-derivatives of the terms \(B_{\kappa }\) and \(\Lambda _{\kappa }\) as
In order to proceed, we have to consider an ansatz for \(A_{\gamma }\) and \(y^{\gamma }\). As we mentioned in (46), (47), in this work we will focus on the case \(A_{\gamma }=(A_{0}(t),A_{1}(t),0,0)\) and \( y^{\gamma }=(y^{0},y^{1},0,0)\), with \(y^{0}\), \(y^{1}\) constants and \(A_{0}(t)\), \(A_{1}(t)\) time-dependent functions, which is consistent with FRW symmetries. Under these ansätze, (B4), (B5) give
where \(L=\sqrt{(y^{0})^{2}-(y^{1})^{2}a^{2}}\). Similarly, (35) becomes
Hence, inserting the FRW metric (38), the time-component and the trace of the (B10) finally gives
with \(W_{1}(t)=A_{1}(t)y^{1}\) according to definition (43).
As a last step we take the time component of (36) and its trace, inserting all the above expressions, and substituting the FRW metric (38). After some straightforward manipulations we obtain two equations, namely
where \(\rho _m\) and \(p_m\) are respectively the energy density and pressure of the perfect fluid energy–momentum tensor \(T_{\mu \nu }\). Lastly, inserting (B11), (B12) we obtain
In order to extract the cosmological equations arising from the vertical space we begin from (7) and (8). From those we can calculate:
where
The vertical energy–momentum tensor is:
where we used relations (B17) and (B18).
Hence, starting from the vertical field equation (34), by raising the indices and substituting (B20), we obtain:
where \(R=\frac{\ddot{a}}{a}+\frac{{\dot{a}}^{2}}{{a}^{2}}\).
If we take \(\alpha =\beta =0\) and \(\alpha =\beta =1\) in the above Eq. (B21) we finally extract the vertical cosmological equations:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
About this article
Cite this article
Kapsabelis, E., Saridakis, E.N. & Stavrinos, P.C. Finsler–Randers–Sasaki gravity and cosmology. Eur. Phys. J. C 84, 538 (2024). https://doi.org/10.1140/epjc/s10052-024-12924-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-024-12924-1