Strong gravitational lensing by $Sgr A^*$ and $M87^*$ black holes embedded in dark matter halo exhibiting string cloud and quintessential field

Abstract

We investigate the strong gravitational lensing phenomena caused by a black hole with a dark matter halo in the presence of cloud string and quintessence. This study examines strong gravitational lensing with two significant dark matter models: the universal rotation curve model and the cold dark matter model. To do this, we first numerically estimate the strong lensing coefficients and strong deflection angles for both the universal rotation curve and cold dark matter models. It is observed that the deflection angle, denoted as $\alpha _D$, increases with the parameter $\alpha$ while holding the value of $2M \gamma$ constant. Additionally, it increases with the parameter $2M \gamma$ while keeping the value of $\alpha$ constant. The strong deflection angle $\alpha _D$, for the black hole with a dark matter halo, with parameters $\alpha$ and $2\,M \gamma$, greatly enhances the gravitational bending effect and surpasses the corresponding case of the standard Schwarzschild black hole ($A=B=0=\alpha =2M\gamma$). Furthermore, we investigate the astrophysical consequences through strong gravitational lensing observations, using examples of two supermassive black holes, namely $M87^{*}$ and $Sgr A^{*}$, located at the center of nearby galaxies. It is observed that black holes with dark matter halos in the presence of cloud string and quintessence can be quantitatively distinguished and characterized from the standard Schwarzschild black hole ($A=B=0=\alpha =2M\gamma$). The findings in our analysis suggest that observational tests for black holes influenced by dark matter halos, cloud string and quintessence are indeed feasible and viable.

1 Introduction

The most fascinating prediction of general relativity is black holes, which became a theoretical possibility when Karl Schwarzschild first provided a solution to Einstein’s field equations. This solution described the gravitational field outside a spherically symmetric, non-rotating and static object in space [1]. In 1939, Oppenheimer, Snyder, and Datt [2] studied spherically symmetric and homogeneous dust collapse, concluding that it inevitably leads to the formation of Schwarzschild black holes. This provided the first possible astrophysical origin for black holes. Since then, Einstein’s general theory of relativity has gained much popularity in recent years, passing multiple observational tests and establishing itself as the current best theory of gravity. Notably, the announcement of gravitational waves [3, 4], the first black hole shadow image of $M87^*$ and Sag A* by the EHT collaboration [5,6,7], and the motion of S-stars around the galactic center [8,9,10] have sparked much interest in the scientific community to study further the causal structure of spacetime and the dynamical environment around compact objects. One such effect of general relativity is the deflection of light by massive bodies. This leads to a phenomenon called gravitational lensing, first observed by the astronomer Walsh et al. in 1979 [11]. It is currently an active research field with dedicated projects such as the Kilo-Degree survey [12], Gaia Gravitational Lenses group [13], and the strong lensing insights into Dark Energy Survey [14], among others. Our analysis in this paper focuses on strong gravitational lensing, which occurs when the source is almost exactly behind a very massive object, i.e., the lens. This phenomenon produces multiple images, arcs and even Einstein rings. With improvements in observational astronomy, strong lensing has become of prime importance in testing various theories of gravity [15,16,17,18,19,20,21].

Consequently, the theory of gravitational lensing can be classified into two distinct scenarios. In the first scenario, when a photon’s radial distance greatly exceeds the gravitational lens’s radius, the deflection of the light ray is very small. This results in two slightly distorted images on both sides of the lens. In the second scenario, referred to as strong gravitational lensing, the photon follows multiple orbits around the lens before reaching the observer. In this case, an infinite series of highly magnified images appears on both sides of the lens. The study of gravitational lensing in the vicinity of relativistic objects, such as a star orbiting in the Kerr spacetime [22] or an accretion disk surrounding a Schwarzschild black hole, was initially conducted in the 1970s [23]. The concept of gravitational lensing was first introduced in the weak field limit [24,25,26,27]. It was later widely explored in the strong field limit [28,29,30,31]. Darwin conducted pioneering research on the paths of photons as they traverse the vicinity of a black hole, revealing the substantial bending of light rays. This work led to the development of a precise lens equation, as discussed later by Frittelli et al. in [32] and by Virbhadra and Ellis in 2000. Subsequently, in further studies, Virbhadra et al. [33] and Virbhadra and Ellis [15] embarked on numerical investigations, focusing on the phenomenon of lensing caused by static, spherically symmetric naked singularities. These investigations involved a meticulous examination of various lensing observables. Inspired by their works, Perlick [34] delved into the study of lensing within spherically symmetric and static spacetime, employing the light-like geodesic equation without employing any approximations. Virbhadra [35] comprehensively studied the relativistic images produced by the gravitational lensing of a Schwarzschild black hole using numerical methods.

The research has unveiled the profound significance of gravitational lensing, particularly in the context of black holes, as an invaluable tool in astrophysics. It allows for the exploration of the strong gravitational effects in the vicinity of these massive celestial objects and provides valuable insights into distant and faint stars. Due to its critical importance, gravitational lensing by various black holes has garnered considerable attention over recent decades. Researchers have employed functional and analytical techniques, as introduced by Bozza et al. in their 2001 work [30], which was founded on the strong deflection of light rays. These techniques have revealed that the deflection angle exhibits a logarithmic divergence as light rays approach the photon sphere of a Schwarzschild black hole. Bozza’s approach has not been limited to Schwarzschild black holes but has also been extended to other scenarios. For example, it has been applied to the study of Reissner–Nordström black holes [36] and implemented in metric systems that are both static and spherically symmetric [37]. The extensive research on gravitational lensing is motivated by the understanding that the paths of light near black holes provide valuable insights into the fundamental features and characteristics of the underlying spacetime geometry. Numerous studies have been dedicated to examining gravitational lensing caused by a variety of sources, including the distribution of structures. [38,39,40], dark energy [41,42,43], dark matter (DM) [44,45,46], quasars [47,48,49,50], gravitational waves [51,52,53] and various other compact celestial objects [54,55,56,57,58]. Recently, the Event Horizon Telescope collaboration successfully achieved an angular resolution that enables the observation of the image of the supermassive black hole situated at the center of the M87 galaxy. This development marks the onset of a new era in the exploration of gravitational lensing within the context of strong gravitational fields [59,60,61,62,63,64]. Additionally, the anticipation that relativistic images can serve as a means to test gravity in the strong deflection limit has prompted the application of this technique to a wide range of black hole metrics. This includes both the context of general relativity and modified theories. Such an approach has led to diverse investigations involving various black hole metrics. This is evident from the contributions of researchers such as Fernando and Roberts [65], Bozza [66], Majumdar and Mukherjee [67], Eiroa and Romero[68], Bozza [69], Sahu et al. [70], and Islam and Ghosh [71].

Furthermore, there has been considerable interest in studying gravitational lensing in the context of naked singularities or spacetimes without a horizon [72]. The quantitative aspects of gravitational lensing have proven to be a valuable means of distinguishing between horizonless compact objects and black holes [72, 73]. In 2019, Shaikh et al. [74] conducted an analytical investigation into the phenomenon of strong gravitational lensing caused by such horizon-less compact objects. Their study aimed to derive precise expressions for lensing observables pertaining to images formed from within the photon sphere and then compared these results with images formed from outside the photon sphere. The astrophysical implications concerning various observables like image position, separation, magnification, the occurrence of Einstein rings and time delays in the formation of relativistic images have been investigated in connection with several supermassive black holes [75,76,77,78,79,80,81,82,83,84,85,86,87,88]. Virbhadra and Keeton investigated the time delay and magnification centroid caused by gravitational lensing from black holes and naked singularities [89]. Recently, the distortion of images due to gravitational lensing has been studied in detail by Virbhadra [90, 91]. The influence of string cloud and quintessential field on optical properties of a black hole is also considered in detail in [92,93,94].

In this paper, we aim to expand upon the study of strong gravitational lensing by the supermassive black holes, $Sgr A^*$ and $M87^*$, which are surrounded by DM halos exhibiting string clouds and quintessential fields. Also, our objective is to explore how this phenomenon can be distinguished from other astrophysical black holes. Additionally, we will compare the observable signatures of black holes in DM halos with string clouds and quintessential fields to those of Schwarzschild black holes. This comparison will take into consideration the supermassive black holes, $Sgr A^*$ and $M87^*$, as the gravitational lenses.

The true nature of DM remains unclear to this day, making it a highly active research field in astrophysics, astronomy and cosmology. Current indirect evidence for DM has been found through various means, including galactic rotation curves of spiral galaxies [95, 96], gravitational lensing [45], large-scale structure formation [97], baryon acoustic oscillations (BAO) and cosmic microwave background radiation [98, 99]. The rotation curves of spiral galaxies reveal that the velocity of stars in the outer regions of galaxies becomes constant [100]. This is in contrast to Newtonian dynamics, which predicts that the outermost stars must be rotating faster. The most logical explanation for this discrepancy is the presence of an unseen extra mass that causes such behavior. Observations from the cosmic microwave background show that 26.8% of our universe comprises DM, while the remaining 68.3% is made up of dark energy [98]. The matter distribution in our galaxy is divided into different parts. The region from $10^{4}$ pc to $10^{5}$ pc is dominated by DM, often referred to as the outer halo [101]. The most promising candidates for DM are particles beyond the standard model, such as Weakly Interacting Massive Particles (WIMP), axions, and dark photons [102,103,104,105]. Micro and primordial black holes [106, 107] and sterile neutrinos are also among the possible candidates. Various modifications of Newton’s theory of gravitation and the general theory of relativity have been proposed in the literature to explain the peculiar behavior of galactic rotation curves [108,109,110,111,112,113,114,115].

The paper is structured as follows: Sect. 2 offers a concise description of black hole spacetime structure and DM halos. Section 3 outlines the gravitational lensing setup, including the lens equation, strong deflection angle, and strong lensing coefficients for two different black hole solutions exhibiting DM halos in the background of the cloud of strings and quintessence field. Additionally, this section covers strong lensing observables such as the position of the innermost image, image separation, brightness differences among relativistic images, and the time delay for supermassive black holes $M87^*$ and $Sgr A^*$. In Sect. 4, we compare the strong lensing observables among the standard Schwarzschild black hole and black hole spacetime with a DM halo in two different models: the universal rotation curve (URC) and cold dark matter (CDM) halo with Navarro-Frenk-White (NFW), within the background of the cloud of strings and quintessence field. Finally, in Sect. 5, we summarize our findings and draw conclusions.

2 Black hole geometry and DM Halo

In this section, we start with the spherically symmetric static spacetime to discuss the black hole geometry, which is described by the metric as,

$$\begin{aligned} ds^2 = - f(r) dt^2 + \frac{1}{f(r)} dr^2 + r^2 d\theta ^2 + r^2 \sin ^2\theta d\varphi ^2. \end{aligned}$$

(1)

In the above equation, f(r) defines the lapse function of a black hole. For the current study, we shall consider the following lapse function [116, 117]:

$$\begin{aligned} f(r)=\left( 1-\alpha -\frac{2 M G_N}{c^2 r}-\frac{\gamma }{r^{3\omega _{q}+1}}\right) . \end{aligned}$$

(2)

In the above equation, $\alpha$, $\gamma$ and $\omega _{q}$ represent a cloud of strings, quintessence and quintessence field, respectively, with mass M, speed of light c and the gravitational constant $G_N$. For the current analysis, we shall consider only one case, i.e., quintessence dark energy, by fixing $\omega _{q}=-\frac{2}{3}$ [116, 117]. Now, we will include the effect of two different kinds of DM halos in the above black hole geometry: URC profile and CDM halo with NFW profile.

2.1 URC profile

This subsection will briefly discuss the well-known DM halo-like URC profile. URC matter distribution was described in [118] and it is defined with the following expression

$$\begin{aligned} \rho (r) = \frac{\rho _0 r_0^3}{(r+r_0)(r^2+r_0^2)}. \end{aligned}$$

(3)

In the above matter distribution, $r_0$ denotes the characteristic radius, and $\rho _0$ is the central density of the URC DM halo. According to the literature reviews [119, 120], the best fit values within the recent observations of M87 galaxy for the parameters of the URC DM profile are $\rho _0 = 6.9\times 10^6 \text {M}_{\odot }/\textrm{kpc}^{3}$ and $r_0 = 91.2\; \textrm{kpc}$. For the Milky Way galaxy, both the involved parameters in URC DM halo are measured as $\rho _0 = 5.2 \times 10^7 \text {M}_{\odot }/\textrm{kpc}^{3}$ and $r_0 = 7.8\; \textrm{kpc}$ [121]. With this halo profile, the function f(r) in the metric (2) is given by [122]

$$\begin{aligned} {\begin{matrix} &{}f(r) = e^{-\frac{2 \pi ^2 \rho _0 r_{0}^2 G_N}{c^2}} \left( \frac{r^2}{r_{0}^2}+1\right) ^{-\frac{\left( 1-\frac{r}{r_{0}}\right) \left( 2 \pi \rho _0 r_{0}^3 G_N\right) }{c^2 r}}\\ &{}\left( \frac{r}{r_{0}}+1\right) ^{-\frac{\left( \frac{r}{r_{0}}+1\right) \left( 4 \pi \rho _0 r_{0}^3 G_N\right) }{c^2 r}} e^{\frac{4 \pi \rho _0 r_{0}^3 G_N \tan ^{-1}\left( \frac{r \left( \frac{r}{r_{0}}+1\right) }{r_{0}}\right) }{c^2 r}}\\ &{}-\frac{2 M G_N}{c^2 r}-\frac{\gamma }{r^{-1}}-\alpha .\\ \end{matrix}} \end{aligned}$$

(4)

Here $M = 6.5 \times 10^9~\text {M}_{\odot }$ for the $M87^*$ central black hole and $M = 4.3 \times 10^6~\text {M}_{\odot }$ for the $Sgr A^*$ black hole. The lapse function in the Eq. (4) is very complicated. In order to discuss strong gravitational lensing, we shall use the series solution just for the sack of simplicity, which is straightaway calculated as:

$$\begin{aligned} {\begin{matrix} f(r)&{}=\left( 1-2 \pi ^2 A B\right) \left( 1-4 \pi A B \left( \frac{B c^2 r}{M G_N}+1\right) \right) \\ &{} \quad \times \left( 4 \pi A B \left( \frac{B c^2 r}{M G_N}+1\right) +1\right) \\ &{} \quad \times \left( \frac{2 \pi A B^2 c^2 r \left( B c^2 r-M G_N\right) }{M^2 G_N^2}+1\right) \\ &{} \quad -\frac{2 M G_N}{c^2 r}-\frac{\gamma }{r^{-1}} -\alpha ,\\ \end{matrix}} \end{aligned}$$

(5)

where $A=\frac{\rho _0 r_{0}^{3}}{M}$ and $B=\frac{M G_N}{c^2 r_{0}}$. Now, the involved parameters A and B under the observational well-fitted values for $M87^*$ are calculated as: $A=\frac{\rho _0 r_{0}^{3}}{M}=805.231$, $B=\frac{M G_N}{c^2 r_{0}}=3.40611\times 10^{-9}$. Further, for $Sgr A^*$ the parameters A and B are calculated as: $A=\frac{\rho _0 r_{0}^{3}}{M}=5738.77$, $B=\frac{M G_N}{c^2 r_{0}}=2.6346\times 10^{-11}.$

2.2 The CDM halo with NFW profile

The CDM halo model with NFW profile was calculated by using N-body simulations, which is also known as universal spherically averaged density profile [123] and it is expressed as:

$$\begin{aligned} \rho (r) = \frac{\rho _0}{(r/r_0)(1+r/r_0)^2}. \end{aligned}$$

(6)

In the above Eq. (5), $\rho _0$ represents the density of the universe at the stage of collapsing of halo, and $r_0$ denotes the characteristic radius. The recent observational data for the Milky Way galaxy [121], the best-fit values for the involved parameters, i.e., $\rho _0$ and $r_0$ for CDM halo model with NFW are measured as $\rho _0 = 5.23 \times 10^7 \text {M}_{\odot }/\textrm{kpc}^{3}$ and $r_0=8.1 \; \textrm{kpc}$. For the other black hole model say $M87^*$ galaxy, the involved parameters are measured as $\rho _0 = 0.008 \times 10^{7.5}~\text {M}_{\odot }/ \text {kpc}^3$ (see [124]) and ${r_0} = 130~\text {kpc}$ [122]. Within scope of CDM halo profile, the function f(r) in the metric by Eq. (2) is provided by [125] with the following form:

$$\begin{aligned} f(r)=\left( 1+\frac{r}{{r_0}}\right) ^{-\frac{8 \pi G_N \rho _0 r_0^3}{c^2 r}} - \frac{2 G_N M}{c^2 r}-\frac{\gamma }{r^{-1}}-\alpha . \end{aligned}$$

(7)

In the above equation, $M = 4.3 \times 10^6~\text {M}_{\odot }$ is the mass for $Sgr A^*$ black hole model and $M = 6.5 \times 10^9~\text {M}_{\odot }$ is the mass for $M87^*$ central black hole. Due to the involvement of the exponential function in the lapse function by Eq. (7), it isn’t very easy for the discussion of strong gravitational lensing. Again, one can use the series solution for the lapse function of the black hole under the effect of the CDM halo model with the NFW profile; we have the following revised form of the lapse function:

$$\begin{aligned} f(r)= & {} 1-\frac{2 M G_N}{c^2 r}-\frac{\gamma }{r^{-1}} -\alpha +32 \pi ^2 A^2 B^2\nonumber \\ {}+ & {} \frac{4 \pi A B (B r+2 M)}{M}, \end{aligned}$$

(8)

where the value of parameters A and B for $M87^*$ are measured as: $A=\frac{\rho _0 r_{0}^{3}}{M}=85.508$, $B=\frac{M G_N}{c^2 r_{0}}=2.38952\times 10^{-9}$. Further for the $Sgr A^*$ black model values of A and B are calculated as: $A=\frac{\rho _0 r_{0}^{3}}{M}=6463.81$, $B=\frac{M G_N}{c^2 r_{0}}=2.537\times 10^{-11}$.

3 Strong gravitational lensing and its observable by black hole with DM halos

Here, we study the strong gravitational lensing by black holes with two different DM halo models. Here, we investigate the deflection of photon rays in the equatorial plane ($\theta =\frac{\pi }{2}$) due to URC and CDM halos models. To study the deflection angle of photon rays in the equatorial plane ($\theta =\frac{\pi }{2}$), we write the Eq. (1) by the transformations, $t\rightarrow \frac{t}{2M}$, $r\rightarrow \frac{r}{2\,M}$, $2\,M\gamma \rightarrow \gamma$ as:

$$\begin{aligned} d\bar{s}^2=-P(r)dt^2+ R(r) dr^2 +S(r) d\phi ^2 . \end{aligned}$$

(9)

Now, by using the Eq. (9), one can write the lapse function by Eq. (5) for the URC halo model within the scope of Eq. (9) is expressed as:

$$\begin{aligned} {\begin{matrix} P(r)&{}=(1-2 \pi ^2 A B) (4 \pi A B^2 r (2 B r-1)+1)\\ &{} \quad \times (4 \pi A B (2 B r + 1)+1)\\ &{} \quad \times (1-4 \pi A B (2 B r+1))-\frac{1}{r} -\gamma r-\alpha .\\ \end{matrix}} \end{aligned}$$

(10)

Further, we have the following expressions:

$$\begin{aligned} {\begin{matrix} R(r) &{}=\bigg [-\alpha +\left( 1-2 \pi ^2 A B\right) \\ &{} \quad \times \left( 4 \pi A B^2 r (2 B r-1)+1\right) \\ &{} \quad \times (4 \pi A B (2 B r+1)+1) (1-4 \pi A B (2 B r+1))\\ &{} \quad -\frac{1}{r} -\gamma r-\alpha \bigg ]^{-1} \end{matrix}} \end{aligned}$$

(11)

and

$$\begin{aligned} S(r)=r^2. \end{aligned}$$

(12)

The lapse function by Eq. (8) for the CDM with NFW profile model as:

$$\begin{aligned} P(r)= & {} 1-\frac{1}{r}+32 \pi ^2 A^2 B^2+8 \pi A B (B r+1)\nonumber \\ {}{} & {} -\gamma r -\alpha . \end{aligned}$$

(13)

According to Eq. (1) and Eq. (9), we have the following relations

$$\begin{aligned} R(r)= & {} \bigg [1-\frac{1}{r}+32 \pi ^2 A^2 B^2+8 \pi A B (B r+1)\nonumber \\ {}{} & {} -\gamma r -\alpha \bigg ]^{-1} \end{aligned}$$

(14)

and

$$\begin{aligned} S(r)=r^2. \end{aligned}$$

(15)

By utilizing Eq. (9), one can derive null geodesics with respect to the affine parameter $\tau$ using the following equations

$$\begin{aligned}{} & {} \dot{t}=\frac{dt}{d\tau }=\frac{E}{P(r)}, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \dot{\phi }= \frac{d\phi }{d\tau }=\frac{L}{r^2}, \end{aligned}$$

(17)

$$\begin{aligned}{} & {} \biggr ( \frac{dr}{d\tau }\biggr )^2 = \dot{r}^2=E^2-\frac{L^2 }{r^2}P(r). \end{aligned}$$

(18)

Here, the constants E and L represent the energy and angular momentum of the particle, respectively. Because the spacetime described by Eq. (1) is static and spherically symmetric, these two quantities also serve as conserved quantities. The function P(r) is defined by Eqs. (10) and (13) for the cases of URC and CDM halos respectively. The Eq. (18) can be written as

$$\begin{aligned} \left( \frac{dr}{d\tau }\right) ^2+V_{eff} =E^2, \end{aligned}$$

(19)

where the effective potential of a photon is given by

$$\begin{aligned} V_{eff}=\frac{L^2 }{r^2}P(r). \end{aligned}$$

(20)

For the unstable circular photon orbit of radius $r_{ph}$, the conditions for the effective potentials are $\frac{dV_{eff}}{dr}|_{r_{ph}}=0$ and $\frac{d^2V_{eff}}{dr^2}|_{r_{ph}}<0$. Thus, the radius of the photon sphere $r_{ph}$ is the largest real root of the equation

$$\begin{aligned} {2P(r_{ph})-r_{ph}~P^{\prime }(r_{ph})=0}. \end{aligned}$$

(21)

Note that at $r=r_{ph}$, the condition $\frac{d^2V_{eff}}{dr^2}|_{r_{ph}}<0$ is satisfied for the black hole spacetime (9). Because these orbits are unstable against small perturbations, photons coming from infinity and approaching the black hole with a specific impact parameter denoted as u ultimately return to infinity after reaching their closest distance $r_0$. When the particle reaches this minimum distance $r_0$, closest to the central black hole, at which point $\frac{dr}{d\tau }=0$, we can express the ratio $\frac{L}{E}$ as a function of the impact parameter u in relation to the closest distance $r_0$ as [37]

$$\begin{aligned} u=\frac{L}{E}=\frac{r_0}{\sqrt{P(r_0)}}. \end{aligned}$$

(22)

The strong deflection angle experiences an infinite increase as $r_0 \rightarrow r_{ph}$ and remains finite only when $r_0 > r_{ph}$. Thus, the critical impact parameter, denoted as $u_{ph}$, is precisely defined by

$$\begin{aligned} u_{ph} =\frac{r_{ph}}{\sqrt{P(r_{ph})}}. \end{aligned}$$

(23)

Note that throughout this paper, the photon sphere radius $r_{ph}$ and the critical impact parameter $u_{ph}$ are respectively estimated as $r_{ph}/R_S$ and $u_{ph}/R_S$, where $R_S$ is known as the Schwarzschild radius. For impact parameters less than $u_{ph}$, photons are drawn into the black hole, while for impact parameters greater than $u_{ph}$, photons approach their nearest distance to the black hole, denoted as $r_0$. However, when the impact parameter equals $u_{ph}$, photons follow an unstable circular orbit around the black hole, resulting in the formation of a photon sphere with a radius $r_{ph}$. The expression for the deflection angle in terms of the nearest approach distance $r_0$, within the context of the spacetime Eq. (9), can be described as follows [33, 126]:

$$\begin{aligned} \alpha _D(r_0)=I(r_0)- \pi , \end{aligned}$$

(24)

where $r_0$ is the closest approach distance of photons trajectory and $I(r_0)$ is defined as

$$\begin{aligned} I(r_0) = 2\int _{r_0}^\infty \frac{\sqrt{R(r)}}{\sqrt{S(r)} \sqrt{ \frac{P(r_0)S(r)}{S(r)S(r_0)}-1} } ~dr. \end{aligned}$$

(25)

In the strong field limit, the deflection angle $\alpha _D(r_0)$ is influenced by the relationship between $r_0$ and $r_{ph}$. Notably, when $r_0\approx r_{ph}$, it experiences an augmentation. So, we define a new variable z as [37, 79, 127]

$$\begin{aligned} z=1-\frac{r_0}{r}. \end{aligned}$$

(26)

The total azimuthal angle, expressed in relation to these newly introduced variables, can be formulated as follows:

$$\begin{aligned} I(r_0)=\int _{0}^1 F(z,r_0)H(z,r_0)dz, \end{aligned}$$

(27)

where

$$\begin{aligned}{} & {} F(z,r_0)= \frac{2r^2\sqrt{S(r_0)}}{r_{0} S(r)}\sqrt{P(r)R(r)}, \end{aligned}$$

(28)

$$\begin{aligned}{} & {} \quad H(z,r_0)=\frac{\sqrt{S(r)}}{\sqrt{S(r)P(r_0)-P(r)S(r_0)}}. \end{aligned}$$

(29)

For all values of z and $r_0$, the function $F(z,r_0 )$ becomes regular but the function $H( z,r_0)$ diverges at $z=0$ only. The integral (27) can be expressed as

$$\begin{aligned} I(r_0) = I^{D}(r_0)+I^{R}(r_0), \end{aligned}$$

(30)

with the regular part

$$\begin{aligned} I^{R}(r_0)=\int _{0}^1 g(z,r_0) dz \end{aligned}$$

(31)

and the divergent part

$$\begin{aligned} I^{D}(r_0)=\int _{0}^1 F(0,r_{ph})H_0(z,r_{0}) dz, \end{aligned}$$

(32)

where $g(z,r_0)=F(z,r_0)H(z,r_0) - F(0, r_{ph}) H_0(z,r_0)$. To obtain the divergence of the integrand in Eq. (25), one can expand the portion of square root in $H(z,r_0)$ as

$$\begin{aligned} H_0(z,r_0)= \frac{1}{\sqrt{\eta (r_0) z +\zeta (r_0) z^2 + \mathcal {O}(z^3) }}, \end{aligned}$$

(33)

where

$$\begin{aligned} {\begin{matrix} \eta (r_0) = \frac{r_0}{ S(r_0)} \bigg ( P(r_0) S^\prime (r_0) - P^\prime (r_0) S(r_0) \bigg ), \end{matrix}} \end{aligned}$$

(34)

$$\begin{aligned} {\begin{matrix} \zeta (r_0) &{}= \frac{1}{ 2S^2(r_0)}\biggr ((2 r_0 S(r_0)-2r^2_0 S^\prime (r_0))\\ &{} \quad \times ( P(r_0) S^\prime (r_0) - P^\prime (r_0) S(r_0) )\\ &{} \quad +r^2_0 ~S(r_0)(P(r_{0})S^{\prime \prime }(r_{0})-P^{\prime \prime }(r_{0}) S(r_{0})) \biggr ).\\ \end{matrix}} \end{aligned}$$

(35)

Here, the prime symbol represents differentiation with respect to the variable r. When $r_0 \approx r_{ph}$, the coefficient $\eta (r_0)$ vanishes and the order of divergence is $z^{-1}$ which leads the integral divergence logarithemcally. For, $r_0 \approx r_{ph}$, the strong deflection angle becomes [128,129,130,131,132]

$$\begin{aligned} \alpha (u)= -\bar{a}~ log\left( \frac{u}{u_{ph}}-1\right) +\bar{b} +\mathcal {O}((u -u_{ph})log(u -u_{ph})), \end{aligned}$$

(36)

where

$$\begin{aligned} \bar{a}=\frac{F(0,r_{ph})}{2\sqrt{\zeta (r_{ph})}} =\sqrt{\frac{2P(r_{ph}) R(r_{ph})}{P(r_{ph})S^{\prime \prime }(r_{ph})-P^{\prime \prime }(r_{ph}) S(r_{ph})}} \end{aligned}$$

(37)

and

$$\begin{aligned} \bar{b}=-\pi + a_R + \bar{a} ~log \biggr ({\frac{2\zeta (r_{ph})S(r_{ph})}{ u^2_{ph}P^2(r_{ph})}}\biggr ), \end{aligned}$$

(38)

where $a_R=I^{R}(r_{ph})= \int _{0}^{1} g(z,r_{ph} ) dz$ which is numerically obtained.

Now, we discuss some strong lensing observables quantities with the help of strong lensing coefficients ${u_{ph}}$, ${\bar{a}}$, ${\bar{b}}$ and strong deflection angle $\alpha _D$. In this context, we examine a scenario in which the source, the black hole acting as a lens, and the receiver are perfectly aligned, and both the receiver and source are positioned at a very far from the black hole (lens). Thus, one can express the lens equation as [30]

$$\begin{aligned} \beta =\tilde{\alpha }-\frac{d_{ls}}{d_{os}}\Delta \alpha _{n}. \end{aligned}$$

(39)

Here, we use the angles $\beta$ and $\tilde{\alpha }$ to represent the angular positions of the source and the image, respectively, relative to the optical axis. Additionally, we denote the distances between the lens and the source as $d_{ls}$, between the receiver and the lens as $d_{ol}$, and between the receiver and the source as $d_{os}$, respectively such that $d_{os} = d_{ol} + d_{ls}$. Here, we define $\Delta \alpha _{n}$ as the angular offset of deflection angle, where $\Delta \alpha _{n} = \tilde{\alpha } - 2n\pi$ and the variable n signifies the number of complete loops made by the light ray. Using the Eqs. (36) and (39), the angular separation between the $n^{th}$ relativistic and the black hole (lens) can be written as

$$\begin{aligned} \theta _n = \theta ^0 _n - \frac{u_{ph} e_n d_{os}(\theta _n^0-\beta )}{\bar{a}d_{ls}d_{ol}}, \end{aligned}$$

(40)

where

$$\begin{aligned}{} & {} e_n=e^{\frac{\bar{b}-2n\pi }{\bar{a}}},\\{} & {} \quad \theta ^0_n=\frac{ u_{ph}(1+e_n)}{d_{ol}}, \end{aligned}$$

and $\theta ^0_n$ is the image position for $\alpha =2n\pi$. The magnification for the n-th relativistic image, is defined as [37]

$$\begin{aligned} \mu _n=\biggr (\frac{\beta }{\tilde{\alpha }}\frac{d\beta }{d\tilde{\alpha }}\biggr )^{-1}\biggr |_{\theta _n^0}=\frac{e_n u^2_{ph}(1+e_n)d_{os}}{\bar{a}\beta d_{ls}d^2_{ol}}. \end{aligned}$$

(41)

Clearly, the initial (i.e., first) relativistic image shines the brightest, and the magnification decreases exponentially as we move to higher image orders denoted by n. Importantly, as $\beta \rightarrow 0$, Eq. (41) exhibits divergence. Consequently, perfect alignment significantly enhances the possibility of detecting the images. If we designate $\theta _n$ as the asymptotic position where a cluster of images converges as n approaches infinity, then the brightest image, specifically the outermost image denoted as $\theta _1$, can be individually distinguished. All other images become tightly grouped at the position $\theta _{\infty }$, representing the asymptotic location of the set of relativistic images as in the limit $n \rightarrow \infty$. By utilizing the deflection angle as described in Eq. (36) and the lens equation provided in Eq. (39), we have derived three observable quantities such as the angular position of the set of images $\theta _{\infty }$, angular separation S between the outermost image and remaining the inner set of images and the flux ratio between the outermost relativistic image and the remaining inner set of relativistic images can be expressed as [37, 81]

$$\begin{aligned}{} & {} \theta _{\infty }=\frac{u_{ph}}{d_{ol}}, \end{aligned}$$

(42)

$$\begin{aligned}{} & {} S= \theta _1-\theta _{\infty }\approx \theta _{\infty }e^\frac{(\bar{b} -2\pi )}{\bar{a}}, \end{aligned}$$

(43)

$$\begin{aligned}{} & {} r_{mag}=\frac{\mu _1}{\Sigma ^\infty _{n=2}\mu _{n}}\approx \frac{5\pi }{\bar{a}~log(10)}. \end{aligned}$$

(44)

If the observables quantities $\theta _{\infty }$, S and $r_{mag}$ are obtained from the observation, the strong lensing coefficients $\bar{a}$, $\bar{b}$ and the minimum impact parameter $u_{ph}$ can be obtained easily by the Eqs. (42), (43) and (44), and also, this value can be compared to the predictions from theoretical models. Thus, one can identify the characterization of the black hole in the presence of a DM halo. Another important observable quantity is the time delays $\Delta T_{2,1}$ between two different relativistic images. Time travel along the photon path varies for different relativistic images, resulting in time differences between these images. This time delay serves as a crucial observable, derived from the disparity in image formation times. By distinguishing the time signals of the first and second images during observations, it is possible to calculate the time delay between these two signals [66]. As a photon travels from the source to an observer, the time it takes to traverse a path around the black hole can be determined using the formula provided by [66]

$$\begin{aligned} \tilde{T}=\tilde{a}log\biggr (\frac{u}{u_{ph}}-1\biggr )+\tilde{b}+\mathcal {O}(u-u_{ph}). \end{aligned}$$

(45)

Employing the Eq. (45) makes it feasible to calculate the time disparity between the two relativistic images. In the context of spherically symmetric spacetime, the time delay between two relativistic images (first and second) positioned on the same side of the black hole can be expressed as [66]

$$\begin{aligned} \Delta T_{2,1}=2\pi u_{ph}=2\pi d_{ol} \theta _{\infty }. \end{aligned}$$

(46)

Using the above formula (46), it is beneficial to investigate the time delay associated with various black holes positioned at the center of neighboring galaxies. This paper investigates the time delay associated with two supermassive black holes $M87^*$ and $Sgr A^{*}$ in the context of a black hole with two significant URC and CDM halos.

3.1 Strong lensing observables for URC halo

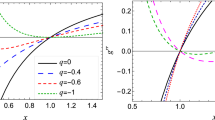
Here, we discuss strong gravitational lensing and its various observables with URC DM halo in the presence of cloud string and quintessence. The behavior of the photon sphere radius ${r_{ph}}$ in Fig. 1a and the minimum impact parameter ${u_{ph}}$ in Fig. 1b are described as a function of both the parameters $\alpha$ and $2M \gamma$ for the case of URC model. From Fig. 1a, it is observed that the photon sphere radius ${r_{ph}}$ increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increases with the parameter $2M \gamma$ for the fixed value of $\alpha$. From Fig. 1 b and Tables 1 and 2, it is observed that the minimum impact parameter ${u_{ph}}$ increases with the parameter $\alpha$ for the fixed value of $2\,M \gamma$ and also increases with the parameter $2\,M\gamma$ for the fixed value of $\alpha$. It also observes that when $A=0$, $B=0$, $\alpha =0$ and $2\,M \gamma =0$, the photon sphere radius $r_{ph}=1.5$ and the minimum impact parameter $u_{ph}=2.59808$ correspond to the case of Schwarzschild black hole [37].

Fig. 1

The behavior of the photon sphere radius ${r_{ph}}$ (left panel) and the minimum impact parameter ${u_{ph}}$ (right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the URC model. It’s worth noting that the photon sphere radius ${r_{ph}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$exhibit nearly identical behavior and also the minimum impact parameter ${u_{ph}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$ exhibit nearly identical behavior

Table 1 Estimation of strong lensing coefficients with the different value of black hole parameters $\alpha$ and $2M\gamma =1.2\times 10^{-16}$ for the case of URC for $M87^*$ black hole where $A=805.231$, $B=3.40611\times 10^{-9}$ and $\omega _q=- \frac{2}{3}$

Table 2 Estimation of strong lensing coefficients with the different value of black hole parameters $\alpha$ and $2M\gamma =1.2\times 10^{-16}$ for the case of URC for the case of $Sgr A^{*}$ black hole where $A=5738.7, B=2.6346\times 10^{-11}$and $\omega _q=-\frac{2}{3}$

Fig. 2

The behaviour of the deflection limit coefficients ${\bar{a}}$(left panel) and ${\bar{b}}$(right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the URC model. It’s worth noting that the deflection limit coefficient ${\bar{a}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$exhibit nearly identical behavior and also the deflection limit coefficient ${\bar{b}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$exhibit nearly identical behavior

Fig. 3

The behaviour of the strong deflection angle ${\alpha _{D}}$ as a function of both the parameters $\alpha$ and $2M \gamma$ for the URC model. It’s worth noting that the strong deflection angle ${\alpha _{D}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$ exhibit nearly identical behavior

The behavior of deflection limit coefficient ${\bar{a}}$ in Fig. 2a and the deflection limit coefficient ${\bar{b}}$ in Fig. 2b are described as a function of both the parameters $\alpha$ and $2M \gamma$ for the case of URC model. From Fig. 2a and Tables 1 and 2, it is observed that deflection limit coefficient ${\bar{a}}$ increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increase with the parameter $2\,M \gamma$ for the fixed value of $\alpha$. From Fig. 2b and Tables 1 and 2, it is observed that deflection limit coefficient ${\bar{b}}$ increase with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increase with the parameter $2M \gamma$ for the fixed value of $\alpha$. It is also observed that when $A=0$, $B=0$, $\alpha =0$ and $2\,M \gamma =0$ the deflection limit coefficient ${\bar{a}}=1$ and the deflection limit coefficient ${\bar{b}}=-0.40023$ correspond to the case of Schwarzschild black hole [37].

The behavior of the deflection angle in Fig. 3 is described as a function of the parameters $\alpha$ and $2\,M \gamma$ for the case of the URC model. It is observed that the deflection angle $\alpha _D$ increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increases with the parameter $2M \gamma$ for the fixed value of $\alpha$. It’s worth noting that the photon sphere radius ${r_{ph}}$, minimum impact parameter ${u_{ph}}$, deflection limit coefficient ${\bar{a}}$, deflection limit coefficient ${\bar{b}}$ and the strong deflection angle ${\alpha _D}$ for the cases of $M87^{*}$ and $Sgr A^{*}$ exhibit nearly identical behavior for the URC model.

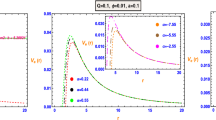
The behavior of observable quantities such as angular image position $\theta _{\infty }$ in Fig. 4, image separation S in Fig. 5, relative magnification $r_{mag}$ in Fig. 6 of the relativistic images and the time delays $\Delta T_{2,1}$ between two different relativistic images in Fig. 7, are described as a function of both the parameters $\alpha$ and $2M \gamma$ for the case of the URC model. From Figs. 4 and 5, it is observed that observable quantities such as angular image position $\theta _{\infty }$ and image separation S increase with the parameter $\alpha$ for the fixed value of $2M \gamma$ and they also increase with the parameter $2M \gamma$ for the fixed value of $\alpha$. However, in Fig. 6, the observable quantity relative magnification $r_{mag}$ decreases with the parameter $\alpha$ for the fixed value of $2M \gamma$, and it also decreases with the parameter $2M \gamma$ for the fixed value of $\alpha$ for both the cases of the supermassive black holes $M87^{*}$ and $Sgr A^{*}$ (cf. Table 3). From Fig. 7a and b and Table 3, it is observed that the time delays $\Delta T_{2,1}$ between two different relativistic images increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increases with the parameter $2M \gamma$ for the fixed value of $\alpha$ in the context of URC DM halo.

Fig. 4

The behaviour of the observable quantity angular image position ${\theta _{\infty }}$ for $M87^{*}$ (left panel) and for $Sgr A^*$(right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the URC model

Fig. 5

The behaviour of the observable quantity angular image separation S for $M87^{*}$ (left panel) and for $Sgr A^*$(right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the URC model

Fig. 6

The behaviour of the relative magnification ${r_{mag}}$ as a function of both the parameters $\alpha$ and $2M \gamma$ for the URC model. It’s worth noting that the relative magnification ${r_{mag}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$ exhibit nearly identical behavior

3.2 Strong lensing observables for CDM Halo with NFW

Here, we discuss the strong gravitational lensing and its various observable with CDM halo in the presence of cloud string and quintessence.

The behavior of the photon sphere radius ${r_{ph}}$ in Fig. 8a and the minimum impact parameter ${u_{ph}}$ in Fig. 8b are described as a function of both the parameters $\alpha$ and $2M \gamma$ for the case of CDM model. From Fig. 8a, it is observed that the photon sphere radius ${r_{ph}}$ increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increases with the parameter $2\,M \gamma$ for the fixed value of $\alpha$. From Fig. 8b and Tables 4 and 5, it is observed that the minimum impact parameter ${u_{ph}}$ increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increases with the parameter $2M \gamma$ for the fixed value of $\alpha$. It also observes that when $A=0$, $B=0$, $\alpha =0$ and $2M \gamma =0$, the photon sphere radius $r_{ph}=1.5$ and the minimum impact parameter $u_{ph}=2.59808$, correspond to the case of a Schwarzschild black hole [37].

Fig. 7

The behaviour of the time delays $\Delta T_{2,1}$ between two relativistic images for $M87^{*}$ (left panel) and for Sgr $A^*$ (right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the URC model. Time delays $\Delta T_{2,1}$ are measured in minutes

The behavior of deflection limit coefficient ${\bar{a}}$ in Fig. 9a and the deflection limit coefficient ${\bar{b}}$ in Fig. 9b are described as a function of both the parameters $\alpha$ and $2M \gamma$ for the case of CDM model. From Fig. 9a and Tables 4 and 5, it is observed that deflection limit coefficient ${\bar{a}}$ increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increase with the parameter $2\,M \gamma$ for the fixed value of $\alpha$. From Fig. 9b and Tables 4 and 5, it is observed that deflection limit coefficient ${\bar{b}}$ increase with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increase with the parameter $2M \gamma$ for the fixed value of $\alpha$. It also observes that when $A=0$, $B=0$, $\alpha =0$, and $2M \gamma =0$, the deflection limit coefficient ${\bar{a}}=1$ and the deflection limit coefficient ${\bar{b}}=-0.40023$ correspond to the case of a Schwarzschild black hole [37].

The behavior of deflection angle ${\alpha _D}$ in Fig. 10 is described as a function of both the parameters $\alpha$ and $2M \gamma$ for the case of the CDM model. It is observed that the deflection angle $\alpha _D$ increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increases with the parameter $2M \gamma$ for the fixed value of $\alpha$. It’s worth noting that the photon sphere radius ${r_{ph}}$, minimum impact parameter ${u_{ph}}$, deflection limit coefficient ${\bar{a}}$, deflection limit coefficient ${\bar{b}}$ and the strong deflection angle ${\alpha _D}$ for the cases of $M87^{*}$ and $Sgr A^{*}$ exhibit nearly identical behavior for the CDM model.

Table 3 Estimation of strong lensing observables for URC case for the supermassive black holes $M87^*$ and $Sgr A^*$, with the different value of black hole parameter $\alpha$ and $2M\gamma =1.2\times 10^{-16}$. The observable quantity $r_{mag}$ does not depend on the mass or distance of the black hole from the observer

Table 4 Estimation of strong lensing coefficients with the different value of black hole parameter $\alpha$ and $2M\gamma =1.2\times 10^{-16}$ for the case CDM of $M87^*$ black hole where $A=85.508$, $B=2.38952\times 10^{-9}$, $\omega _q=-\frac{2}{3}$

Table 5 Estimation of strong lensing coefficients with the different value of black hole parameter $\alpha$ and $2M\gamma =1.2\times 10^{-16}$ for the case CDM of $Sgr A^*$ black hole where $A=6463.81,B=2.537\times 10^{-11}$and $\omega _q=-\frac{2}{3}$

The behavior of observable quantities such as angular image position $\theta _{\infty }$ in Fig. 11, image separation S in Fig. 12, relative magnification $r_{mag}$ in Fig. 13, and the time delays $\Delta T_{2,1}$ between two different relativistic images in Fig. 14 are described as a function of both the parameters $\alpha$ and $2\,M \gamma$ for the case of the CDM model. From Figs. 11 and 12, it is observed that observable quantities angular image position $\theta _{\infty }$ and angular image separation S increases with the parameter $\alpha$ for the fixed value of $2\,M \gamma$ and also increase with the parameter $2M \gamma$ for the fixed value of $\alpha$; but in Fig. 13, the observable quantity relative magnification $r_{mag}$ decreases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also decreases with the parameter $2M \gamma$ for the fixed value of $\alpha$ for both the cases of $M87^{*}$ and $Sgr A^{*}$ supermassive black hole (cf. Table 6). From Fig. 14a and b and Table 6, it is observed that the time delays $\Delta T_{2,1}$ between two different relativistic images increases with the parameter $\alpha$ for the fixed value of $2M \gamma$ and also increases with the parameter $2M \gamma$ for the fixed value of $\alpha$ in the context of CDM halo.

Fig. 8

The behaviour of the photon sphere radius ${r_{ph}}$ (left panel) and the minimum impact parameter ${u_{ph}}$ (right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the CDM model. It’s worth noting that the photon sphere radius ${r_{ph}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$ exhibit nearly identical behavior and also the minimum impact parameter ${u_{ph}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$exhibit nearly identical behavior

Fig. 9

The behaviour of the deflection limit coefficient ${\bar{a}}$ (left panel) and ${\bar{b}}$(right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the CDM model. It’s worth noting that the deflection limit coefficient ${\bar{a}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$exhibit nearly identical behavior and also the deflection limit coefficient ${\bar{b}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$exhibit nearly identical behavior

4 Comparison with observation

In this paper, we apply the standard method for strong gravitational lensing phenomena developed by Bozza [37], which can be used to distinguish between various types of spherically symmetric black holes and explore the astrophysical implications. The study focuses on the supermassive black holes $M87^{*}$ and $Sgr A^{*}$ located at the centers of nearby galaxies. We evaluate the strong lensing coefficients $\bar{a}$, $\bar{b}$ and $u_{Ph}/R_S$ (see Tables 1, 2, 4, 5, 7), as well as the observable quantities $\theta _{\infty }$, S and $r_{mag}$ (see Tables 3, 6, 7) for the supermassive black holes at the centers of nearby galaxies. We also evaluate these observable quantities for the standard Schwarzschild black hole ($A=B=0=\alpha =2M\gamma$), Schwarzschild black hole with both URC and CDM halos ($\alpha =0=2M\gamma$) and the black hole spacetime with both DM halos with the presence of string cloud and quintessence, by considering the supermassive black hole $M87^*$ with a mass of $M=6.5\times 10^9 M_{\odot }$ and a distance of $d_{ol}=16.8Mpc$ for comparison (see Table 7).

Fig. 10

The behaviour of the strong deflection angle ${\alpha _{D}}$ as a function of both the parameters $\alpha$ and $2M \gamma$ for the CDM model. It’s worth noting that the strong deflection angle ${\alpha _{D}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$ exhibit nearly identical behavior

Fig. 11

The behaviour of the observable quantity angular image position ${\theta _{\infty }}$ for $M87^{*}$ (left panel) and for $Sgr A^*$ (right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the CDM model

Fig. 12

The behaviour of the observable quantity angular image separation S for $M87^{*}$ (left panel) and for $Sgr A^*$(right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the CDM model

Fig. 13

The behaviour of the relative magnification ${r_{mag}}$ as a function of both the parameters $\alpha$ and $2M \gamma$ for the CDM model. It’s worth noting that the relative magnification ${r_{mag}}$ for the cases of $M87^{*}$ and $Sgr A^{*}$exhibit nearly identical behavior

In our estimation, it is found that considering the same mass and distance (see Table 7), the innermost images $\theta _{\infty }$ in the background of a black hole with a DM halo (both URC and CDM cases with $\alpha =0.03$ and $2\,M\gamma =1.2\times 10^{-16}$) are significantly greater than those of the standard Schwarzschild black hole. Also, a black hole with a DM halo has a very large image separation S and smaller relative magnification $r_{mag}$. Their difference value from the standard Schwarzschild black hole respect as $\sim 0.0052~\mu as$ and $\sim 0.14$ magnitude for $\alpha =0.03$. It is also observed that for the black hole with a DM halo, $\theta _{\infty }\in (19.96,21.23) \mu as$ while $S\in (0.0249,0.0322)~ \mu as$ when $2M\gamma =1.2\times 10^{-16}$, $0\le \alpha \le 0.04$). It suggests that the outermost images of the black hole with DM halo are closer to the remaining innermost images and which able to be distinguished from the other black hole images. Furthermore, suppose the outermost image can be resolved. In that case, it will distinguish the black hole with a DM halo, string, and quintessence from the Schwarzschild black hole and characterize the black hole with a DM halo, string, and quintessence using future technology. In our present analysis, we have focused exclusively on the spherically symmetric case, omitting consideration of spin. This decision stems from the understanding that Silhouette’s configuration, as observed from an infinite distance, exhibits only a minor dependence on the black hole’s spin [133, 134]. Despite this constraint, we maintain confidence in the generalizability of our findings concerning gravitational lensing around supermassive black holes, particularly $Sgr A^*$ and $M87^*$. The ngEHT observations offer a valuable opportunity to validate our model in the context of these spherical black holes [135]. In Tables 3, 6 and 7, it is observed that the time delay $\Delta T_{2,1}$ for the case of a black hole with DM halo with the presence of string cloud and quintessence ($2\,M\gamma =1.2\times 10^{-16}$, $\alpha =0.03$) for both the URC and CDM models (e.g.$\sim 18192.8$ minutes for $M87^{*}$ and $\sim 12.0349$ minutes for $Sgr A^{*}$) is significantly more than the case of a Schwarzschild black hole with halo ($\alpha =0=2M\gamma$) and a standard Schwarzschild ($A=B=0 =\alpha =2M\gamma$) black hole. It means that if one can distinguish between the first and second relativistic images, the time delay between these two images might provide a good opportunity to detect a black hole with a DM halo, string, and quintessence from an astrophysical black hole, such as the Schwarzschild black hole. Therefore, the black hole with a DM halo, string and quintessence could be quantitatively distinguished from other astrophysical black holes, such as standard Schwarzschild black holes. It is noted that through the gravitational lensing scenario, detecting the audible boundary of sound waves near the black hole horizon under the influence of DM halos within the scope of string cloud and quintessential field may become easier. The astrophysical consequences resulting from DM halos around black holes may illuminate the correlations between sonic fluid and black hole shape. We anticipate that our analytical findings may prove useful in future research on comparable black holes. These findings may facilitate further exploration into the composition of the near-horizon geometry of typical astrophysical black holes.

Table 6 Estimation of strong lensing observables for CDM case for the supermassive black holes $M87^*$ and $Sgr A^*$, with the different value of black hole parameter $\alpha$ and $2M\gamma =1.2\times 10^{-16}$. The observable quantity $r_{mag}$ does not depend on the mass or distance of the black hole from the observer

Fig. 14

The behaviour of the time delays $\Delta T_{2,1}$ between two relativistic images for $M87^{*}$ (left panel) and for $Sgr A^*$ (right panel) as a function of both the parameters $\alpha$ and $2M \gamma$ for the CDM model. Time delays $\Delta T_{2,1}$ are measured in minutes

5 Discussions and conclusions

In this paper, we have explored the calculations of strong gravitational lensing and focus on supermassive black holes in the central region of a galaxy, which is surrounded by DM halos in the background of Schwarzschild-like spacetimes within the scope of string cloud quintessential field. For the arrangement of two different DM halos, namely URC and CDM models, their lapse functions have been provided in Eqs. (5) and (8), respectively. We have calculated the values of the involved parameters using the observational data of $M87^*$ and $Sgr A^*$, namely $\rho _0$ and $r_0$. We have analyzed the effects of the cloud string parameter $\alpha$ and the quintessence parameter $2M\gamma$ on strong gravitational lensing and its various observables such as the angular image position $\theta _{\infty }$, image separation S, relative magnification $r_{mag}$ of the relativistic images and the time delays $\Delta T_{2,1}$ between two different relativistic images. These effects are compared to the cases of the standard Schwarzschild ($A=B=0=\alpha = 2M \gamma$), Schwarzschild with both URC and CDM DM halos ($\alpha =0$, $2\,M \gamma =0$), black hole with URC DM halo model, and black hole with CDM halo model with the presence of string cloud and quintessence. We first calculate the null geodesic equation for the black hole space-time by Hamilton -Jacobi action, and using this, we obtain the photon sphere radius $r_{ph}$.

It is found that the photon sphere radius ${r_{ph}}$ increases with the parameter $\alpha$ for the fixed value of $2M\gamma$ and also increases with the parameter $2M\gamma$ for the fixed value of $\alpha$, for both the cases of the URC and CDM halo models. We obtained strong lensing coefficients ${u_{ph}}$, ${\bar{a}}$, and ${\bar{b}}$ numerically as well as graphically for both URC and CDM models. It is observed that the strong lensing coefficients ${u_{ph}}$, ${\bar{a}}$, and ${\bar{b}}$ increase with the parameter $\alpha$ for the fixed value of $2M\gamma$, and also they increase with the parameter $2M\gamma$ for the fixed value of $\alpha$, for both the cases of URC and CDM halo models. Using these coefficients, we obtained the deflection angle ${\alpha _D}$ as a function of both the parameters $\alpha$ and $2M\gamma$ for both the URC and CDM models. It is found that the strong deflection angle ${\alpha _D}$ increases with the parameter $\alpha$ for the fixed value of $2M\gamma$ and also increases with the parameter $2M\gamma$ for the fixed value of $\alpha$, for both the URC and CDM halo models. Thus, both parameters $\alpha$ and $2M\gamma$ greatly intensify the gravitational bending effects for both the URC and CDM halo models. Furthermore, it is observed that the strong deflection angle ${\alpha _D}$ for both the URC and CDM halo models is greater than in the case of the standard Schwarzschild black hole. These findings indicate that the gravitational lensing effect due to a black hole with a DM halo, with the presence of string cloud and quintessence, is greatly enhanced compared to the case of a standard Schwarzschild black hole. Thus, a black hole with a DM halo can be more easily detected and distinguished from other ordinary astrophysical black holes, such as standard Schwarzschild black holes. With the help of strong lensing coefficients ${u_{ph}}$, ${\bar{a}}$ and ${\bar{b}}$, the strong lensing observable quantities such as angular image position $\theta _{\infty }$, image separation S, relative magnification $r_{mag}$ of the relativistic images and the time delays $\Delta T_{2,1}$ between two different relativistic images have been obtained for the case of URC and CDM models. We numerically calculate the strong lensing observables: angular image position $\theta _{\infty }$, angular image separation S, relative magnification $r_{mag}$ of the relativistic images, and the time delays $\Delta T_{2,1}$ for the supermassive black holes $M87^{*}$ and $SgrA^{*}$ in the context of black hole spacetime with a DM halo, with the presence of string cloud and quintessence. It is observed that the observable quantities, angular image position $\theta _{\infty }$ and image separation S, increase with the parameter $\alpha$ for the fixed value of $2M\gamma$ and also increase with the parameter $2M\gamma$ for the fixed value of $\alpha$, for both the URC and CDM halo models. Meanwhile, the relative magnification $r_{mag}$ of the relativistic images decreases with the parameter $\alpha$ for the fixed value of $2M\gamma$ and also decreases with the parameter $2M\gamma$ for the fixed value of $\alpha$. In the URC DM halo case, where $2M\gamma =1.2\times 10^{-16}$and $0\le \alpha \le 0.04$, angular position $\theta _{\infty }\in (19.96,21.2256)~ \mu as$ for $M87^{*}$, $\theta _{\infty }\in (26.38,28.0488) \mu as$ for $Sgr A^{*}$; the angular separation $S\in (0.024,0.0321442) \mu as$ for $M87^{*}$, $S\in (0.032,0.042467)~ \mu as$ for $Sgr A^{*}$; and the magnification $r_{mag}\in (6.684,6.822)$ magnitude for $M87^{*}$, $r_{mag}\in (6.684,6.822)$ magnitude for $Sgr A^{*}$. In the CDM halo case, where $2M\gamma =1.2\times 10^{-16}$and $0\le \alpha \le 0.04$, angular position $\theta _{\infty }\in (19.96,21.2238)~ \mu as$ for $M87^{*}$, $\theta _{\infty }\in (26.38,28.0484)~ \mu as$ for $Sgr A^{*}$; the angular separation $S\in (0.024,0.032133)\mu as$ for $M87^{*}$, $S\in (0.032,0.042465)~ \mu as$ for $Sgr A^{*}$; and the magnification $r_{mag}\in (6.68407,6.822)$ magnitude for $M87^{*}$, $r_{mag}\in (6.68407,6.822)$ magnitude for $Sgr A^{*}$.

Table 7 Estimation of observables by taking the supermassive black hole $M87^{*}$ having mass $M=6.5\times 10^9 M_{\odot }$ and distance $d_{ol}=16.8 Mpc$ in the context of Schwarzschild black hole, black hole URC model and black hole CDM model

Another important observable quantity, the time delays $\Delta T_{2,1}$ between two different relativistic images, increases with the parameter $\alpha$ for the fixed value of $2M\gamma$, and also increases with the parameter $2M\gamma$ for the fixed value of $\alpha$, for both the URC model and the CDM model. We have also numerically obtained the time delays $\Delta T_{2,1}$ between the first and second-order relativistic images for the supermassive black holes $M87^{*}$ and $Sgr A^{*}$ in the background of standard Schwarzschild ($A=B=0=\alpha =2M\gamma =0$), Schwarzschild-like with URC and CDM DM halos ($\alpha =0=2M\gamma$) and a black hole with a DM halo with the presence of string cloud and quintessence ($2\,M\gamma =1.2\times 10^{-16}$, $0\le \alpha \le 0.04$) for both URC and CDM models. It is observed that the time delay $\Delta T_{2,1}$ for the case of a black hole with DM halo ($2\,M\gamma =1.2\times 10^{-16}$, $\alpha =0.03$) for both the URC and CDM models (e.g.$\sim 18192.8$ minutes for $M87^{*}$ and $\sim 12.0349$ minutes for $Sgr A^{*}$) is significantly more than the case of a Schwarzschild black hole with halo ($\alpha =0=2M\gamma$) and a standard Schwarzschild ($A=B=0=\alpha =2M\gamma$) black hole.

Therefore, the findings in our investigation suggest how the black hole with DM halo under the effect of string cloud quintessential field is detectable by astronomical observations. Further, we also try to investigate strong gravitational lensing as an extension of the current work by using other DM profiles. It is also our plan to extend our work for the rotating black holes. Finally, we may test the effects of DM halos on various modified theories of gravity.