1 Introduction

In our universe, stars are the original sources of heat and luminosity as well they are considered the fundamental components of galaxies. The residue portion, after exhausting all nuclear fuels of a star, becomes a compact object by a non-equilibrium gravitational collapse. Compact objects are mainly classified into white dwarfs, neutron stars and black holes. Among these objects, neutron stars are most interesting in the present time because of their internal structure and physical features. Although it has been assumed that the interior structure of a celestial object was formed by isotropic fluid but, recently, anisotropic matter distribution has attracted much attention among researchers in modern cosmology. Because of various courses like a magnetic field, phase transition, viscosity, rotation and the mixture of two fluids etc., it has been predicted that in the interior of a stellar body, two pressure components may be presented, such as radial pressure (\(p_{r}\)) and tangential pressure (\(p_{t}\)) with \(p_{r}\ne p_{t}\). In 1972, Ruderman [1] first investigated that interior matter part with density \(10^{15}\) g/cm\(^{3}\) possesses anisotropic nature. To know the mysterious behavior of our current accelerating universe, a big part of research in modern cosmology has attracted many cosmologists. In the present time, it has possible to know that a hidden source of energy plays the main role in the background of this mystery, known as dark energy (DE). Einstein’s relativistic theory (GR) provides a successful mathematical platform for explaining all phenomena in the physical world formed by highly compact astrophysical objects. But this gravitational theory is not sufficient to describe the phenomena regarding repulsive pressure. So to explore the current universe, various DE models and modified theories of gravity (MTG) have been developed. Some of them are stated by modifying the geometry part and some by matter part in the Einstein–Hilbert (E–H) action. Among these theories, the easiest theory is the f(R) theory of gravity, in which the Ricci scalar (R) is replaced by an arbitrary function f(R) in the Einstein–Hilbert (E–H) action [2]. Also, f(G) modified gravity made by including an arbitrary function f(G) in the gravitational action for the Gauss–Bonnet invariant term G [3]. Moreover, Rastall [4] developed a modified gravity theory using the non-conservation equation of motion for the matter part. Besides these, many authors have developed several extended versions of the above MTGs. For example, f(R,T), f(G,T), f(R,G), f(R,G,T), and Generalized Rastall Gravity (GRG), Rastall–Rainbow gravity etc. [5,6,7,8,9,10].

Now all of these gravitational theories, including the original theory of GR has been formulated by assuming the underlying geometry as Riemannian geometry. And several models of physical characteristics of compact objects have been developed in the framework of these modified gravitational theories [11,12,13,14,15,16,17,18,19,20,21]. Here the Riemannian geometry was developed corresponding to a symmetric and metric coherent Levi-Civita connection with non-vanishing curvature. Another type of gravitational theory of Einstein’s GR has been developed in terms of tetrad field (Weitzenb\(\ddot{o}\)ck spacetime) known as the teleparallel equivalent of general relativity (TEGR) [22, 23]. Actually, in the TEGR theory of gravity, to find out the equation of motion, non-vanishing scalar curvature (R) is replaced by torsion scalar (T) in E–H action. Weyl first introduced a generalized version of Riemannian geometry by replacing the metric field as the class of conformally equivalent metrics [24]. He did introduce a connection by which the covariant divergence of the metric tensor is non-zero, and such a property explained mathematically by a new type of geometrical term known as the non-metricity. Geometrically this term describes the variation of the length of a vector in the parallel transport. Then the Weyl–Cartan geometry was introduced by including torsion in the Weyl geometry [25,26,27,28,29,30,31,32,33]. Now, based on this geometry, another alternative, and our main interest here is possible gravity, is Symmetric Teleparallel Gravity (STG). The connection behind this gravity is a curvature-free and torsion-free connection, known as a symmetric teleparallel connection (also known as Weyl–Cartan connection), that is not matric compatible. In this connection, the teleparallel condition implies vanishing curvature, and symmetry implies vanishing torsion. The non-trivial geometry in the background of this gravity (STG) is explored by the non-metricity terms of spacetime. Nester and Yo [34] first introduced such a type of geometry to construct the symmetric teleparallel equivalent of general relativity (STEGR). Here the gravitational interaction is governed by the nonmetricity term (Q) of the metric for stated spacetime.

Now in differential geometry, we can write a general form of a linear affine connection as follows

$$\begin{aligned} \Gamma ^{\xi }_{~\mu \nu }={\big \{}^{\xi }_{~\mu \nu }{\big \}} + K^{\xi }_{~\mu \nu } + L^{\xi }_{~\mu \nu }, \end{aligned}$$
(1)

where \({\big \{}^{\xi }_{~\mu \nu }{\big \}}\) represents the Christoffel symbols, coefficients of Levi-Civita connection, which can be defined as

$$\begin{aligned} {\big \{}^{\xi }_{~\mu \nu }{\big \}}=\frac{1}{2}g^{\xi \chi }\big (\partial _{\mu }g_{\chi \nu } + \partial _{\nu }g_{\chi \mu } - \partial _{\chi }g_{\mu \nu }\big ), \end{aligned}$$
(2)

the contortion tensor is

$$\begin{aligned} K^{\xi }_{~\mu \nu }=\frac{1}{2}T^{\xi }_{~\mu \nu } + T_{(\mu ~\nu )}^{~~\xi }, \end{aligned}$$
(3)

with the torsion tensor \(T^{\xi }_{~\mu \nu }\equiv 2\Gamma ^{\xi }_{~\mu \nu }\) and the deformation tensor can be given in terms of the non-metricity tensor as

$$\begin{aligned} L^{\xi }_{~\mu \nu }=\frac{1}{2}g^{\xi \chi }\big (-Q_{\mu \chi \nu } - Q_{\nu \chi \mu } + Q_{\chi \mu \nu }\big ). \end{aligned}$$
(4)

Here the non-metricity tensor \(Q_{\gamma \mu \nu }\) is defined as \(Q_{\gamma \mu \nu }\equiv \nabla _{\gamma }g_{\mu \nu }\) i.e., the covariant derivative of metric tensor, in the context of Weyl–Cartan connection \(\Gamma ^{\xi }_{\mu \nu }\), and it can be written as

$$\begin{aligned} Q_{\gamma \mu \nu }=-\frac{\partial g_{\mu \nu }}{\partial x^{\gamma }} + g_{\nu \xi }\Gamma ^{\xi }_{~\mu \gamma } + g_{\xi \mu }\Gamma ^{\xi }_{~\nu \gamma }. \end{aligned}$$
(5)

Similar to some MTG like f(R), f(T) gravity STGR also has been generalized by many authors to modified f(Q) gravity [35, 36]. Like f(T) gravity, in f(Q) gravity, one advantage is that the second order differential equation arises instead of the fourth order differential equation in f(R) gravity. Also, it has many similar properties to f(T) gravity.

Now we concentrate on some current papers which are developed in the framework of f(Q) theory of gravity, where Q represents the non-metricity scalar. In the Ref. [37], Lazkoz et al. discussed the f(Q) gravity with an arbitrary function of redshift f(z) and tested the validity of different observational data in the background of this new approach. The cosmic expansion of the universe without a cosmological model, i.e., cosmography discussed in Ref. [38] and a cosmological model in Ref. [39]. The gravitational field equations and a dynamical system have been analyzed in the background of f(Q) gravity [40]. In the Ref. [41] performed a new type of scalar-tensor extended theory of f(Q) gravity. Different types of energy conditions have been discussed in the Ref. [42]. Rui-Hui et al. [43] discussed f(Q) modified gravity in detail and explored its application of it to characterize the configurations of spherically symmetric type objects. An exact solution of anisotropic Bianchi type-I space-time has been investigated and discussed with stability and energy conditions by Koussour et al. [44] in f(Q) gravity. A static and spherically symmetric solution with an anisotropic matter part discussed in Ref. [45]. An anisotropic compact star solution with a quintessence field has been performed and also discussed all required physical attributes to examine the stability and viability of the solutions by Sanjay et al. [46].

In modern cosmological research, the study of Einstein–Maxwell (E–M) spacetime that is actually created by the inclusion of charge with static spacetime in the context of GR, as well as MTG, is attracted more attention to the researchers [47,48,49]. According to Neslu\(\hat{s}\)an [50], when the neutrality of a stellar configuration is broken due to much more escape of electrons from the surface, the resulting stellar configuration would achieve an electric charge. Also, it has been observed that a distinct feature for compact stars in comparison with normal stars is the existence of a strong electromagnetic field, and for this reason, a compact object may be an electrically charged object [51,52,53]. Actually, the addition of electric charge and thermal pressure gradient of fluid creates more repulsion in the interior of a stellar configuration, which averts the gravitational collapse [54, 55]. Again, based on Ivanov’s proposition, electrically charged fluid can prevent the growth of curvature of spacetime, and for this reason, the creation of singularity may be avoided [56]. In the Ref. [57], the author has shown a dust distribution with a small amount of charge may remain in equilibrium due to the repulsion force of charge against the gravitational pull. Also, one can study the literature [58,59,60] to know the importance of charge. Thus, it is important to mention that the existence of an electromagnetic field or electrically charged matter distribution for a static stellar configuration plays an important role in physical existence and also in attaining an equilibrium position.

In a similar way to MTGs like f(R,T) and f(G,T), Yixin Xu et al. [61] constructed an extended theory of f(Q) gravity based on the non-metricity scalar Q, which is coupled nonminimally to T(trace of the energy–momentum tensor), known as f(Q, T) gravity theory. Actually, to construct this gravity, the geometric action of the gravitational field has been modified by taking Lagrangian density as an arbitrary function of Q and T, i.e., \({\mathcal {L}}=f(Q,T)\). Also, in the Ref. [62], the authors discussed f(Q, T) gravitational theory with respect to the Weyl type space-time and its cosmological implications.

The main motivation behind our present work is to study the complete set of Einstein–Maxwell (E–M) field equations that describe the equation of motion for a spherically symmetric object in the modified f(Q, T) gravity and examine the behavior of physical attributes of neutron stars with respect to this gravity. We divide the whole work into some sections as follows: In Sect. 2, we have given a mathematical framework regarding the construction of field equations in f(Q, T) gravity. Thereafter we have constructed a complete set of E–M field equations for a spherically symmetric metric in modified f(Q, T) gravity. Next, in Sect. 3, we have obtained the complete solutions of field equations. The boundary conditions between interior and exterior space-times have been discussed in Sect. 4. In Sect. 5, we have discussed the nature of physical parameters through graphically and analytically in detail. Finally, the valuable conclusions of our whole work have presented in Sect. 6.

2 Basic formulation of gravitational field equations in f(Q, T) gravity

The Einstein–Hilbert action for the modified theories of gravity f(Q, T), which is an extended version of the symmetric teleparallel gravity, in the presence of charge can be written according to the Ref. [61] in the following form

$$\begin{aligned} S= & {} \frac{1}{16 \pi }\int f(Q,T) \sqrt{-g}d^{4}x + \int \mathcal {L}_{m} \sqrt{-g}d^{4}x\nonumber \\{} & {} + \int \mathcal {L}_{e} \sqrt{-g}d^{4}x, \end{aligned}$$
(6)

where f(Q, T) is an arbitrary function of Q and T, which are known as the non-metricity term and the trace of the energy–momentum tensor \(T_{\mu \nu }\) respectively. Also g is the determinant i.e., \(g \equiv \text {det}(g_{\mu \nu })\) for the metric tensor \(g_{\mu \nu }\), \(\mathcal {L}_{m}\) is the Lagrangian density for matter part and \(\mathcal {L}_{e}\) is the Lagrangian density for electromagnetic field.

Now the non-metricity term, Q can be defined as follows

$$\begin{aligned} Q \equiv -g^{\mu \nu }\Big (L^{\xi }_{~\chi \mu }L^{\chi }_{~\nu \xi } - L^{\xi }_{~\chi \xi }L^{\chi }_{~\mu \nu }\Big ) \end{aligned}$$
(7)

with

$$\begin{aligned} L^{\xi }_{~\chi \gamma }\equiv & {} -\frac{1}{2}g^{\xi \lambda }\Big (\bigtriangledown _{\gamma } g_{\chi \lambda } + \bigtriangledown _{\chi } g_{\lambda \gamma }- \bigtriangledown _{\lambda } g_{\chi \gamma }\Big ) \end{aligned}$$
(8)
$$\begin{aligned} Q_{\xi \mu \nu }= & {} \nabla _{\xi }g_{\mu \nu }. \end{aligned}$$
(9)

The independent traces of non-metricity tensor are

$$\begin{aligned} Q_{\xi } \equiv Q_{\xi }^{~\mu }{_\mu }~~~~~\text {and}~~~~ \tilde{Q}_{\xi } \equiv Q^{\mu }_{~\xi \mu }. \end{aligned}$$
(10)

Again the superpotential function is defined in terms of non-metricity tensor as follows

$$\begin{aligned} P^{\xi }_{~\mu \nu }= & {} \frac{1}{4}\Big [-Q^{\xi }_{~\mu \nu } + 2Q_{(\mu ~\nu )}^{~~\xi } + Q^{\xi }g_{\mu \nu } - \tilde{Q}^{\xi }g_{\mu \nu }\nonumber \\{} & {} -\delta ^{\xi }{_(\mu Q_{\nu )}}\Big ], \end{aligned}$$
(11)

here the trace i.e., the non-metricity scalar Q takes the following form

$$\begin{aligned} Q= & {} -Q_{\xi \mu \nu }P^{\xi \mu \nu }. \end{aligned}$$
(12)
$$\begin{aligned} \mathcal {L}_{e}= & {} -\frac{1}{16\pi }F^{\mu \nu }F_{\mu \nu }, \end{aligned}$$
(13)

where the tensor \(F_{\mu \nu }\) is defined as \(F_{\mu \nu }=\frac{\partial \Phi _{\nu }}{\partial x^{\mu }}-\frac{\partial \Phi _{\mu }}{\partial x^{\nu }}\) and \(\Phi _{\mu }=\delta _{\mu }^{t}\Phi _{t}(r)\) is the four potential for electromagnetic field.

If we vary the action (1) then we get

$$\begin{aligned} \delta S= & {} \int {\bigg \{}\frac{1}{16\pi }\bigg (-\frac{1}{2}f g_{\mu \nu }\sqrt{-g}\delta g^{\mu \nu }\nonumber \\{} & {} +f_{Q}\sqrt{-g}\delta Q + f_{T}\sqrt{-g}\delta T\bigg )\nonumber \\{} & {} -\frac{1}{2}\big (T_{\mu \nu } + E_{\mu \nu }\big )\sqrt{-g}\delta g^{\mu \nu }{\bigg \}}d^{4}x, \end{aligned}$$
(14)

where \(f=f(Q,T)\), \(f_{T}=\frac{\partial f(Q,T)}{\partial T}\) and \(f_{Q}=\frac{\partial f(Q,T)}{\partial Q}\). The energy–momentum tensor, characterizes the matter part can be defined as

$$\begin{aligned} T_{\mu \nu }\equiv \frac{-2}{\sqrt{-g}}\frac{\delta (\sqrt{-g}L_{m})}{\delta g^{\mu \nu }}~~~ \text {and its trace}~ T=g^{\mu \nu }T_{\mu \nu }. \end{aligned}$$
(15)

Now the energy–momentum tensor for electromagnetic field can be written as

$$\begin{aligned} E_{\mu \nu }=-\frac{2}{\kappa ^{2}}\left( g^{\delta \omega }F_{\mu \delta }F_{\omega \nu } -\frac{1}{4}g_{\mu \nu }F_{\delta \omega }F^{\delta \omega }\right) . \end{aligned}$$
(16)

The components of the field strength tensor are non-commutative and given by \(F_{tr}=-F_{rt}=-\partial _{r}\Phi _{t}(r)\). Locally the electric field intensity is \(E=\frac{\partial _{r}\Phi _{t}(r)}{\sqrt{-g_{tt}g_{rr}}}\). The corresponding modified form of Maxwell’s electromagnetic field equations are given by

$$\begin{aligned} (\sqrt{-g}~F^{\mu \nu }),_{\nu }=4\pi J^{\mu }\sqrt{-g},~F_{[\mu \nu ,\delta ]}=0 \end{aligned}$$
(17)

where \(J^{\mu }\) is the 4-current vector of electric charge satisfying \(J^{\mu }=\sigma u^{\mu }\), where \(\sigma \) is the charge density. So we can get from the Maxwell’s equation as follows

$$\begin{aligned} \frac{d}{dr}(r^{2}E(r))=4\pi r^{2}\sigma \sqrt{g_{rr}}=4\pi r^{2}\sigma e^{\lambda } \end{aligned}$$
(18)

By integrating the above Eq. (18) we can evaluate the electric field E as follows

$$\begin{aligned} E(r)=\frac{1}{r^{2}}\int _{0}^{r}4\pi r^{2}\sigma (r)e^{\lambda }~dr = \frac{q(r)}{r^2}, \end{aligned}$$
(19)

where q(r) represents the total charge inside a spherical object with radius r. The matrix form for the components of energy–momentum tensor \(E_{\mu \nu }\) can be written as \(E_{\nu }^{\mu }=\frac{E^{2}}{\kappa ^{2}}~diag(+1,+1,-1,-1)\).

Now if we use the variational principle i.e., the variation of gravitational action is zero, then we get the field equation in f(Q, T) gravity as follows

$$\begin{aligned}{} & {} -\frac{2}{\sqrt{-g}}\nabla _{\xi }\big (f_{Q}\sqrt{-g}P^{\xi }_{~\mu \nu }\big )-\frac{1}{2}f g_{\mu \nu }+f_{T}(T_{\mu \nu }+\Theta _{\mu \nu }) \nonumber \\{} & {} \quad -f_{Q}\big (P_{\mu \xi \chi }Q_{\nu }^{~\xi \chi }-2 Q^{\xi \chi }_{~~\mu } P_{\xi \chi \nu }\big )=8\pi \big (T_{\mu \nu } + E_{\mu \nu }\big ),\nonumber \\ \end{aligned}$$
(20)

where \(\Theta _{\mu \nu }=g^{\xi \chi }\frac{\delta T_{\xi \chi }}{\delta g^{\mu \nu }}\).

Now we have chosen the function f(Q, T) in separable form like \(f(Q,T)=f_{1}(Q) + f_{2}(T)\), where \(f_{1}(Q)\) and \(f_{2}(T)\) are arbitrary functions of Q and T respectively. In our present model we take \(f_{1}\) in quadratic form like \(f_{1}(Q)=\alpha Q + \beta (1 + Q^{2})\) and \(f_{2}\) in linear form like \(f_{2}(T)=\lambda T\) with \(\alpha \), \(\beta \) and \(\lambda \) are constant parameters. So we can write the following [43, 44, 61, 63]

$$\begin{aligned} f(Q,T)=\alpha Q + \beta (1 + Q^{2}) + \lambda T. \end{aligned}$$
(21)

For the above function (21) the modified form of gravitational field equation (20) can be written to the following form

$$\begin{aligned}{} & {} \frac{2}{\sqrt{-g}}\nabla _{\xi }\big (f_{Q}\sqrt{-g}P^{\xi }_{~\mu \nu }\big )+\frac{\alpha Q + \beta (1 + Q^{2})}{2} g_{\mu \nu } \nonumber \\{} & {} \quad +f_{Q}\big (P_{\mu \xi \chi }Q_{\nu }^{~\xi \chi }-2 Q^{\xi \chi }_{~~\mu } P_{\xi \chi \nu }\big )=-8\pi \big (T_{\mu \nu }^{eff} + E_{\mu \nu }\big ),\nonumber \\ \end{aligned}$$
(22)

where

$$\begin{aligned} T_{\mu \nu }^{eff}=T_{\mu \nu }+\frac{\lambda }{16\pi }T g_{\mu \nu }-\frac{\lambda }{8\pi }(T_{\mu \nu }+\Theta _{\mu \nu }) \end{aligned}$$
(23)

let us take \(L_{m}=\rho \), the energy density of the matter part and hence we can get \(\Theta _{\mu \nu }=-2T_{\mu \nu }+\rho g_{\mu \nu }\). Also we can write the above equation as follows

$$\begin{aligned} T_{\mu \nu }^{eff}=T_{\mu \nu }+\frac{\lambda }{16\pi }T g_{\mu \nu }+\frac{\lambda }{8\pi }(T_{\mu \nu }-\rho g_{\mu \nu }). \end{aligned}$$
(24)

The connection equation of motion can be established by taking the variation of the gravitational action with respect to the connection. For this purpose, we have to use the Lagrangian multiplier method with the constraint that the connection is flat and torsion-free, i.e., \(T^{\xi }_{~\mu \nu }=0\) and \(R^{\xi }_{\mu \gamma \nu }=0\). Now for our model, the connection equation of motion, i.e., the field equation after taking the variation of (6) w.r.t. the connection can be given as

$$\begin{aligned} \nabla _{\mu }\nabla _{\nu }\left( \sqrt{-g}f_{Q}P^{\mu \nu }_{~\xi } + 4\pi H_{\xi }^{~\mu \nu }\right) =0. \end{aligned}$$
(25)

Here the term \(H_{\xi }^{~\mu \nu }\) defined as Hypermomentum tensor density with

$$\begin{aligned} H_{\xi }^{~\mu \nu }=\frac{\sqrt{-g}}{16\pi }f_{T}\frac{\delta T}{\delta \Gamma ^{\xi }_{~\mu \nu }} + \frac{\delta \sqrt{-g}\left( \mathcal {L}_{m}+ \mathcal {L}_{e}\right) }{\delta \Gamma ^{\xi }_{~\mu \nu }}. \end{aligned}$$
(26)

For more details of explicit calculations see the Refs. [45, 61].

In the General Theory of Relativity (GR), one important fundamental consideration is \(T_{\mu ;\nu }^{\nu }=0\) i.e., the covariant divergence of the energy–momentum tensor is zero. In a gravitational theory, the matter energy–momentum tensor becomes conserved if \(T_{\mu ;\nu }^{\nu }=0\) hold. After confirming the experimental evidence for the existence of DM and DE, several alternatives or modified theories of gravity are developed. But these theories of gravity may be obeyed or disobeyed conservation law of energy–momentum. In the Ref. [61], it has been discussed in detail that the matter energy–momentum is not conserved in f(Q,T) theory. In the present model, we are discussing f(Q,T) theory in the presence of the electromagnetic field. Again the covariant derivative of \(E_{\mu \nu }\) is non-zero. Hence in our present study, the matter energy–momentum is not conserved.

Phenomenologically, the non-conservation of energy–momentum confirms a production process of physical particle [64,65,66,67,68]. In this regard, P. Rastall [4] developed a gravitational theory as an extension of GR with the simplest form of non-conservation equation energy–momentum that is the covariant derivative of energy–momentum tensor is proportional to the Ricci scalar. Again the main point of Rastall and its generalization [9] theories is the ordinary conservation law is verified only for flat spacetime (Minkowski) or specifically in a weak gravitational field limit. Actually, the violation of classical conservation law comes from some features of quantum effects in gravitational systems [64, 69, 70]. In the Ref. [71] the authors discussed the impact of non-conservation of energy–momentum on strange star configuration. So, physically there is an energy exchange between geometry and cosmic fluid. Also, it may be an initial base of the primary inflation era and the current accelerating phase of the universe expansion.

Let us consider a spherically symmetric space-time to describe the interior region with radial co-ordinate r from the center of symmetry. Next we describe the interior geometry of the stellar object in the co-ordinate system (t, r, \(\theta \), \(\phi \)) by the following line element

$$\begin{aligned} ds^{2}=e^{\zeta }dt^{2}-e^{\eta }dr^{2}-r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(27)

Where \(\zeta \) and \(\eta \) are functions of radial co-ordinate r only. We have taken that the matter distribution as anisotropic type inside the whole region of star. So, the energy–momentum tensor, describing the anisotropic matter portion, can be given as

$$\begin{aligned} T_{\mu \nu }^{M}=(\rho +p_{t})u_{\mu }u_{\nu }+p_{t}g_{\mu \nu }+(p_{r}-p_{t})v_{\mu }v_{\nu }, \end{aligned}$$
(28)

where \(g_{\mu \nu }\) represents the metric tensor, \(v^{\mu }\) is the space-like 4-vector, \(u^{\mu }\) is the 4-velocity and it is orthogonal to \(v^{\mu }\) vector i.e., \(u_{\mu }v^{\mu }=0\). Also they are satisfying some relations like \(u_{\mu }u^{\nu }=-1\) and \(v_{\mu }v^{\nu }=1\). So we can write the components of \(T_{\mu \nu }\) for anisotropic fluid in a matrix form as \((T_{\nu }^{\mu })^{M}=diag(\rho ,-p_{r},-p_{t},-p_{t})\).

In the Refs. [72,73,74], the authors studied the most general form of static spherical metric and the connection in the context of symmetric spacetime and the postulates of symmetric teleparallelism. And also discussed the field equations and the non-metricity scalar Q depending on two types sets of connection coefficients. One is dependent on some initial constant, and the other is purely a function of radial coordinate r. In our model, we will consider only r dependent connection coefficients with respect to the particular spherical symmetric metric (27). Because it is more compact and easier due to the absence of initial constants for the case of field equation reduction and examination of physical characteristics of spherical symmetric objects. Now in the following, we will discuss the connection and field equations.

The authors in the Ref. [43] have discussed clearly that the inertial connection \(\Gamma ^{\xi }_{~\mu \nu }\) should not effected whether the gravity is canceled or not. This implies the following

$$\begin{aligned} \Gamma ^{\xi }_{~\mu \nu }=\Gamma ^{\xi }_{~\mu \nu }\mid _{G=0} = {\big \{}^{\xi }_{~\mu \nu }{\big \}}\mid _{G=0}. \end{aligned}$$
(29)

Now by using the above relation (29) we can obtain the following non-vanishing components of \(\Gamma \) for the metric (27).

$$\begin{aligned}{} & {} \Gamma ^{\theta }_{~r\theta }=\Gamma ^{\phi }_{~r\phi }=\frac{1}{r},~~~ \Gamma ^{r}_{~\phi \phi }=\sin ^{2}\theta \Gamma ^{r}_{~\theta \theta }=-r\sin ^{2}\theta ,~~~ \nonumber \\{} & {} \quad \Gamma ^{\theta }_{~\phi \phi }=-\cos \theta \sin \theta ,~~~ \Gamma ^{\phi }_{~\theta \phi }=\cot \theta . \end{aligned}$$
(30)

So, the non-vanishing components of \(Q_{\xi \mu \nu }\) and \(L^{\xi }_{~\mu \nu }\) corresponding to the metric (27) are as follows

$$\begin{aligned} Q_{rrr}= & {} -e^{\eta }\eta ',~~ Q_{rtt}=e^{\zeta }\zeta ',~~Q_{\theta r \theta }=Q_{\theta \theta r}=r(1-e^{\eta }),\nonumber \\ Q_{\phi r \phi }= & {} Q_{\phi \phi r}=(1-e^{\eta })r\sin ^{2}\theta \end{aligned}$$
(31)

and

$$\begin{aligned} L^{r}_{~rr}= & {} -\frac{1}{2}\eta ',~~~ L^{t}_{~tr}=L^{t}_{~rt}=-\frac{1}{2}\zeta ',~~~L^{r}_{~tt}=-\frac{1}{2}e^{\zeta - \eta }\zeta ',\nonumber \\ L^{r}_{~\theta \theta }= & {} (e^{-\eta }-1)r,~~~L^{r}_{~\phi \phi }=e^{-\eta }(1-e^{\eta })r\sin ^{2}\theta . \end{aligned}$$
(32)

Therefore, the simplified form of non-metricity scalar with respect to the metric (27) can be obtained as follows

$$\begin{aligned} Q=\frac{\big (e^{-\eta }-1\big )(\zeta ' + \eta ')}{r}, \end{aligned}$$
(33)

where the prime \('\) represents the derivative with respect to r.

The componentwise field equations using the metric (27) and function (21) (with \(G,~c=1\)) can be written as

$$\begin{aligned}&-\frac{e^{-\eta }}{2r^{2}}\bigg [ 4r \beta Q' \big (e^{\eta } - 1\big ) + (\alpha + 2\beta Q) {\Big \{} \big (e^{\eta } - 1\big )(2 + r \zeta ') \nonumber \\&\qquad + \big (1 + e^{\zeta }\big )r \eta ' {\Big \}}\bigg ] - \frac{\alpha Q + \beta (1 + Q^{2})}{2} = 8\pi \rho ^{eff} + E^{2}, \end{aligned}$$
(34)
$$\begin{aligned}&\frac{e^{-\eta }}{2r^{2}}\bigg [4r \beta Q' \big (e^{\eta } - 1\big ) + (\alpha + 2\beta Q){\Big \{} \big (e^{\eta } - 1\big )\nonumber \\&\qquad \times (2 + r \zeta ' + r \eta ') - 2r \zeta ' {\Big \}}\bigg ]\nonumber \\&\qquad + \frac{\alpha Q + \beta (1 + Q^{2})}{2} = 8\pi p_{r}^{eff} -E^{2}, \end{aligned}$$
(35)
$$\begin{aligned}&\frac{e^{-\eta }}{4r} \bigg [ - 4r\beta Q' + (\alpha + 2 \beta Q){\Big \{}2\zeta ' \big ( e^{\eta } -2\big ) - r \zeta '^{2} \nonumber \\&\qquad + \eta '\big (2e^{\eta } + r \zeta '\big ) - 2r\zeta '' {\Big \}}\bigg ] + \frac{\alpha Q + \beta (1 + Q^{2})}{2}\nonumber \\&\quad = 8\pi p_{t}^{eff} + E^{2}, \end{aligned}$$
(36)

where

$$\begin{aligned} \rho ^{eff}=\rho +\frac{\lambda }{16\pi }(\rho -p_{r}-2p_{t}), \end{aligned}$$
(37)
$$\begin{aligned} p_{r}^{eff}=p_{r}+\frac{\lambda }{16\pi }(\rho +3p_{r}+2p_{t}), \end{aligned}$$
(38)
$$\begin{aligned} p_{t}^{eff}=p_{t}+\frac{\lambda }{16\pi }(\rho +p_{r}+4p_{t}). \end{aligned}$$
(39)

3 Solution of field equations

The set of field equations (34)–(39) contains six unknowns. Hence to close the set of the field equations we have to some considerations. Let us consider the metric potential functions by Krori–Barua (K–B) space-time [75] as follows

$$\begin{aligned} e^{\zeta }=e^{B r^{2} + C} ~~~~\text {and}~~~~ e^{\eta }=e^{A r^{2}}, \end{aligned}$$
(40)

where A, B and C are unknown constants.

Again we use a workable relation between radial pressure (\(p_{r}\)) and energy density (\(\rho \)) of matter arrangements in the whole interior of compact objects as follows

$$\begin{aligned} p_{r} = w \rho , \end{aligned}$$
(41)

where w is the EoS parameter that lies between 0 and 1, i.e., \(0<w<1\). Now by solving the field equations we get the following expressions.

$$\begin{aligned} \rho (r)= & {} \frac{2(A + B)e^{-2A r^{2}}\big (-4(A + B)\beta + e^{Ar^{2}}(-\alpha + 4(A + B)\beta )\big )}{(1 + w)(8\pi + \lambda )}. \end{aligned}$$
(42)
$$\begin{aligned} p_{r}(r)= & {} \frac{2(A + B)e^{-2A r^{2}} w \big (-4(A + B)\beta + e^{Ar^{2}}(-\alpha + 4(A + B)\beta )\big )}{(1 + w)(8\pi + \lambda )}. \end{aligned}$$
(43)
$$\begin{aligned} p_{t}(r)= & {} \frac{1}{8\pi + 3\lambda }\Big [ 2(A + B)\big (e^{-A r^{2}} - 1\big )\alpha + \big (1 + 4(A + B)^{2} e^{-2A r^{2}}\big (e^{A r^{2}} - 1\big )^{2}\big )\beta + 4(A + B)e^{-2A r^{2}}\big (-3B + A r\nonumber \\{} & {} + (A -B)B r^{2} \big )\beta + (A + B)(\alpha - 4(A + B)\beta ) + e^{-A r^{2}}\big ( B \big (-3 + (A - B)r^{2} \big ) \alpha + 4(A + B) \big (A + 4B \nonumber \\{} & {} + B(B - A)r^{2}\big )\beta \big ) + \frac{e^{-2A r^{2}}}{r^{2}}\big (4(A + B) (-1 + (A - 3B)r^{2})\beta + e^{2A r^{2}} (1 + (A + B)r^{2})(\alpha - 4(A + B)\beta ) \nonumber \\{} & {} - e^{A r^{2}} (\alpha + (A + 3B)r^{2} \alpha - 8(A + B)(1 + 2B r^{2})\beta )\big ) \nonumber \\{} & {} + \frac{2(A + B)e^{-2A r^{2}} \big (4(A + B)\beta + e^{A r^{2}}(\alpha - 4(A + B)\beta )\big )(8\pi w + \lambda + 2w \lambda )}{(1 + w)(8\pi + \lambda )}\Big ]. \end{aligned}$$
(44)
$$\begin{aligned} E^{2}(r)= & {} \frac{e^{-2A r^{2}}}{2r^{2}(1 + w)(8\pi + 3\lambda )}\Big [4(A + B)\beta \big (8\pi (2(1 + w) + B r^{2}(5 + w) - A r^{2} (3 + 7w) ) \nonumber \\{} & {} + \big (B r^{2} (3 - 5w) + 4(1 + w) - 2B^{2}r^{4} (1 + w) + A r^{2}\big (-7 - 15w + 2r(1 + w) + 2B r^{2} (1 + w)\big )\big )\lambda \big ) \nonumber \\{} & {} - e^{2A r^{2}} (1 + w) \big (16\pi \alpha - 8\pi \big (8B - r^{2} 4A^{2}r^{2} + 8A\big (1 + B r^{2}\big )\big )\beta \nonumber \\{} & {} + 4\alpha \lambda - \big (16B - r^{2} + 4A^{2}r^{2} + 4B^{2}r^{2} + 8A\big (2 + B r^{2}\big )\big )\beta \lambda \big ) + 2e^{A r^{2}} \big (8\pi (1 + 2B r^{2} + w - 2A r^{2}w)\alpha \nonumber \\{} & {} + 32(A + B)\pi \big (-2(1 + w) - B r^{2} (3 + w) \big )\beta + \big (2 + \big (2 - 4A r^{2}\big )w - B^{2}r^{4}(1 + w) + B r^{2}\big (1 - 3w \nonumber \\{} & {} + A r^{2} (1 + w)\big )\big )\alpha \lambda - 4(A - B)\big (-2 B r^{2}(w - 1)+ 4(1 + w) \nonumber \\{} & {} - B^{2}r^{4} (1 + w) + A r^{2} \big (-3 -7w +B r^{2}(1 + w)\big )\big )\beta \lambda \big )\Big ]. \end{aligned}$$
(45)
$$\begin{aligned} \triangle (r)= & {} \frac{e^{-2A r^{2}}}{r^{2}(1 + w)(8\pi + \lambda )(8\pi + 3\lambda )}\Big [e^{2A r^{2}}(1 + w)\big (\alpha - \big (4(A + B) + \big (4(A + B)^{2} - 1 \big )r^{2}\big )\beta \big )(8\pi + \lambda ) + 4(A + B)\beta \nonumber \\{} & {} \times \big (8\pi \big (-1 - w + r^{2}\big (-B\big (5 + w + B r^{2}(1 + w)\big ) + A(2 + 6w + r(1 + B r)(1 + w))\big )\big ) + \big (-1 -w + r^{2}\nonumber \\{} & {} \times \big (-B \big (3 - 5w + B r^{2}(1 + w)\big ) + A(4 + 12w + r(1 + B r)(1 + w))\big )\big )\lambda \big )\nonumber \\{} & {} + e^{A r^{2}}\big (8\pi \big (-1 -w + r^{2} \big (-B\big (4 + B r^{2}(1 + w)\big ) + A\big (1 + 5w + B r^{2}(1 + w)\big )\big )\big )\alpha \nonumber \\{} & {} - 32(A + B)\pi \big (-2(1 + w) + r^{2}\big (A\big (1 + 5w + B r^{2} (1 + w)\big )- B\big (B r^{2}(1 + w) + 2(3 + w)\big )\big )\big )\beta \nonumber \\{} & {} + \big (-1 -w + r^{2}\big (-B\big (2 - 6w + B r^{2}(1 + w)\big ) + A \big (3 + 11w + B r^{2} (1 + w)\big )\big )\big )\alpha \lambda - 4(A + B)\big (-2(1 + w) \nonumber \\{} & {} + r^{2}\big (-B\big (4 - 4w + B r^{2}(1 + w)\big ) + A\big (3 - 11w + B r^{2}(1 + w)\big )\big )\big )\beta \lambda \big )\Big ]. \end{aligned}$$
(46)

4 Matching conditions

For physically existence of a stellar structure there should be a smooth connection between interior geometry (\(\mathcal {M^{-}}\)) and exterior geometry (\(\mathcal {M^{+}}\)) of the star. Due to the absence of matter distribution at the outside of the star, many vacuum solutions have been evaluated to describe the exterior geometry of a stellar system. For example (i) Schwarzschild vacuum solution (for static, non-charge) [76], (ii) Reissner–Nordstr\(\ddot{\textrm{o}}\)m (for static, charge) [77, 78], (iii) Kerr (for rotation, non-charge) [79] and (iv) Kerr–Newman (for rotation, charge) [80, 81], etc. Actually we discuss the smooth connection between two geometries by smoothly connectedness of metric coefficients (\(g_{\mu \nu }\)) for interior and exterior line elements at the boundary of the star. Here our goal is to evaluate the expression of unknown constant parameters A, B, and C. Now using the continuity of metric coefficients \(g_{tt}\), \(g_{rr}\) and its derivative \(\frac{\partial g_{tt}}{\partial r}\) at the boundary (\(r=R\)) we can write the following conditions

$$\begin{aligned} g_{tt}^{-}=g_{tt}^{+},~~~~~g_{rr}^{-}=g_{rr}^{+},~~\text {and}~~~~~\frac{\partial g_{tt}^{-}}{\partial r}=\frac{\partial g_{tt}^{+}}{\partial r}, \end{aligned}$$
(47)

where the signs \(+\) and − indicate the exterior and interior geometries respectively.

Now we want to know about the spherically symmetric vacuum solution corresponding to our considered model in f(Q,T) gravity. For the vacuum case we must have \(T_{\mu \nu }=0\) i.e., matter part is zero and hence f(Q,T) reduces to f(Q). Again by simplifying the reduced form of field Eqs. (34)–(36), we can get

$$\begin{aligned} \frac{e^{-\eta }(\alpha + 2\beta Q)(\eta ' + \zeta ')}{r}=0. \end{aligned}$$
(48)

From the above equation it follows that \(\eta ' + \zeta ' = 0\), which implies \(g_{rr}=g_{tt}^{-1}\). Now comparing (48) and (33), we can say that for spherical vacuum, Q i.e., non-metricity scalar always zero. Also we can get the following equation

$$\begin{aligned} \alpha (e^{\eta } - 1 + r \eta ') + r^{2} e^{\eta } E^{2}=0. \end{aligned}$$
(49)

Let us take \(E(r)=\frac{q(r)}{r^{2}}\), where q(r) represents the charge within a sphere of radius r and \(\mathcal {Q}=\)total charge. By integrating the above Eq. (49), we can get

$$\begin{aligned} e^{-\eta }=1-\frac{H}{r} - \frac{\mathcal {Q}^{2}}{\alpha r^{2}}=e^{\zeta }, \end{aligned}$$
(50)

where H is integration constant. Now if we take \(H=2M\) and \(\alpha <0\), then we will get Reissner–Nordstr\(\ddot{\textrm{o}}\)m (R–N) metric as a vacuum solution corresponding to our assumed model. In our present study, we have considered that the star is electrically charged and non-rotating. So, the exterior vacuum space-time in the context of our consideration can be described by Reissner–Nordstr\(\ddot{\textrm{o}}\)m (R–N) metric. And this metric represents an asymptotically flat space-time because when the distance from the body approaches infinity, the metric becomes Minkowski metric. Now we define the R–N metric as

$$\begin{aligned} ds^{2}= & {} \left( 1 - \frac{2M}{r} + \frac{\mathcal {Q}^{2}}{r^{2}} \right) dt^{2} - \left( 1 - \frac{2M}{r} + \frac{\mathcal {Q}^{2}}{r^{2}} \right) ^{-1} dr^{2}\nonumber \\{} & {} - r^{2}\big (d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}\big ), \end{aligned}$$
(51)

where M and \(\mathcal {Q}\) are respectively represents total mass and charge. Analysing the above conditions (Eq. 47) we have obtained the following expressions

$$\begin{aligned} \left. \begin{aligned} A&=-\frac{1}{R^{2}}\ln \bigg (1-\frac{2M}{R}+ \frac{\mathcal {Q}^{2}}{R^{2}}\bigg )\\ B&=\bigg (\frac{M}{R^3}-\frac{\mathcal {Q}^{2}}{R^{4}}\bigg )\bigg (1-\frac{2M}{R}+\frac{\mathcal {Q}^{2}}{R^{2}}\bigg )^{-1}\\ C&=\ln \bigg (1-\frac{2M}{R}+\frac{\mathcal {Q}^{2}}{R^{2}}\bigg )-\bigg (\frac{M}{R}-\frac{\mathcal {Q}^{2}}{R^{2}}\bigg )\bigg (1-\frac{2M}{R}+ \frac{\mathcal {Q}^{2}}{R^{2}}\bigg )^{-1} \end{aligned} \right\} \nonumber \\ \end{aligned}$$
(52)

5 Physical analysis

In this section, we will inspect about some physical features in details. Our goal is to investigate physical validity and stability of our considered stellar system in modified f(Q, T) gravity by concentrating on some necessary physical properties and conditions for well-behaved stellar interior solutions. In this connection, the behavior of physical parameters of our dedicated model will also be delivered by a fruitful graphical representation of obtained solutions. Now we are taking some pulsars like neutron stars with mass (M), radius (R) and charge (\(\mathcal {Q}\)), which are given in the following Table 1 [82,83,84,85]. Also we have evaluated the numerical values of required unknown constants like A, B, included in that table. Here actually we have taken four neutron stars like 4U1820-30, Vela X-1, 4U1538-52 and SAXJ 1808.4-3658, which are indicated by PS1, PS2, PS3 and PS4 respectively for simplicity.

Table 1 The assumed values of total mass (M), total radius (R) and total charge (\(\mathcal {Q}\)) for different compact stars candidates and the calculated numerical values of constants A, B and C
Full size table
Fig. 1
figure 1

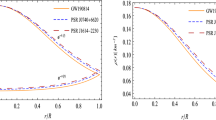
Behavior of energy density (\(\rho \)), derivative (\(\frac{d\rho }{dr}\)) and double derivative (\(\frac{d^2 \rho }{dr^2}\)) with radial co-ordinate r for Table 1

Full size image
Fig. 2
figure 2

Behavior of radial pressure (\(p_{r}\)), derivative (\(\frac{d p_{r}}{dr}\)) and double derivative (\(\frac{d^2 p_{r}}{dr^2}\)) with radial co-ordinate r for Table 1

Full size image

5.1 Energy density and pressure

In our presenting model, the main physical quantities governing the acceptance and validness of a stellar model are energy density (\(\rho \)), radial pressure (\(p_{r}\)) and tangential pressure (\(p_{t}\)). For a well-behaved physical characteristics of compact object (as well neutron star) these parameters values should be finite, non-negative and strictly monotonically decreasing in direction of surface boundary throughout the whole interior region. Now we have calculated the expressions of central density (\(\rho ^{c}\)), central radial pressure (\(p_{r}^{c}\)) and central tangential pressure (\(p_{t}^{c}\)) i.e., the values of parameters \(\rho \), \(p_{r}\) and \(p_{t}\) at \(r=0\) as follows.

$$\begin{aligned} \rho ^{c}= & {} \rho (r=0)=\frac{-2(A + B)\alpha }{(1 + w)(8\pi + \lambda )}. \end{aligned}$$
(53)
$$\begin{aligned} p_{r}^{c}= & {} p_{r}(r=0)=\frac{-2(A + B)w\alpha }{(1 + w)(8\pi + \lambda )}=w \rho _{c}. \end{aligned}$$
(54)
$$\begin{aligned} p_{t}^{c}= & {} p_{t}(r=0)=\frac{1}{3 \lambda +8 \pi }\Big [2 \alpha (A-2 B)\nonumber \\{} & {} +\frac{2 \alpha (A+B) (\lambda +2 \lambda w+8 \pi w)}{(\lambda +8 \pi ) (w+1)}+\beta \Big ]. \end{aligned}$$
(55)

Now for the parameters \(\rho \), \(p_{r}\) and \(p_{t}\) of a compact stellar structure to attain the maximum value at the center and strictly monotonically decreasing behavior in the whole interior region of the star, the following conditions should be satisfied at every point along radius of the star.

$$\begin{aligned} \left. \begin{aligned}&\frac{d\rho }{dr}<0,~~ \frac{d\rho }{dr}(r=0)=0~~\text {and}~~\frac{d^{2}\rho }{dr^{2}}(r=0)<0\\&\frac{dp_{r}}{dr}<0 ,~~ \frac{dp_{r}}{dr}(r=0)=0~~\text {and}~~\frac{d^{2}p_{r}}{dr^{2}}(r=0)<0\\&\frac{dp_{t}}{dr}<0 ,~~ \frac{dp_{t}}{dr}(r=0)=0~~\text {and}~~\frac{d^{2}p_{t}}{dr^{2}}(r=0)<0 \end{aligned} \right\} \nonumber \\ \end{aligned}$$
(56)
Fig. 3
figure 3

Behavior of tangential pressure (\(p_{t}\)), derivative (\(\frac{d p_{t}}{dr}\)) and double derivative (\(\frac{d^2 p_{t}}{dr^2}\)) with radial co-ordinate r for Table 1

Full size image

In the Figs. 1, 2 and 3, we have depicted the behaviors of \(\rho \), \(p_{r}\), \(p_{t}\) with first derivatives like \(\frac{d\rho }{dr}\), \(\frac{dp_{r}}{dr}\), \(\frac{dp_{t}}{dr}\) and second derivatives like \(\frac{d^{2}\rho }{dr^{2}}\), \(\frac{d^{2}p_{r}}{dr^{2}}\), \(\frac{d^{2}p_{t}}{dr^{2}}\) for variations of r. From these figures we can easily checked that energy density, radial pressure and tangential pressure satisfied the conditions of Eq. (56) and positive at each point in interior region of PS1, PS2, PS3 and PS4. So with respect to our solutions for stellar structure the values of \(\rho \), \(p_{r}\) and \(p_{t}\) becomes maximum at the center and decreases in the direction of surface boundary for the stars (Table 2).

Table 2 The numerical values of \(\rho ^{c}\), \(\rho ^{s}\), \(p_{r}^{c}\) and \(p_{t}^{s}\) have been calculated in standard units
Full size table

5.2 Energy conditions

Some physical prominent conditions based on density and pressure also determine the respectful matter distribution in the interior of a stellar structure are known as energy conditions. Actually these conditions support to verify the presence of realistic (i.e., not exotic) matter. For anisotropic configuration these conditions are classified as

  • Null Energy Condition (NEC): \(\rho +p_{r}\ge 0\), \(\rho +p_{t} + \frac{E^{2}}{4\pi } \ge 0\),

  • Weak Energy Condition (WEC): \(\rho +p_{r}\ge 0\), \(\rho +p_{t} + \frac{E^{2}}{4\pi } \ge 0\), \(\rho + \frac{E^{2}}{8\pi } \ge 0\),

  • Strong Energy Condition (SEC): \(\rho +p_{r}\ge 0\), \(\rho +p_{t} + \frac{E^{2}}{4\pi } \ge 0\), \(\rho +p_{r}+2p_{t} + \frac{E^{2}}{4\pi } \ge 0\),

  • Dominant Energy Condition (DEC): \(\rho + \frac{E^{2}}{4\pi } \ge |p_{r}|\), \(\rho \ge |p_{t}|\), \(\rho + \frac{E^{2}}{8\pi } \ge 0\).

Fig. 4
figure 4

Behavior of \(\rho \), \(\rho + p_{r}\), \(\rho +p_{t}\), \(\rho + p_{r} +2p_{t}\), \(\rho - p_{r}\) and \(\rho - p_{t}\) with r for Table 1

Full size image

In the Fig. 4, we have shown the behavior of various algebraic compositions for parameters \(\rho \), \(p_{r}\) and \(p_{t}\) with respect to the radius r. Now if we verify all graphs in the Fig. 4 then we can say that all the energy conditions are hold good for neutron stars PS1, PS2, PS3 and PS4 in the context of our considerations. So the stellar configurations representing by our present model contains realistic matter in the interior region.

5.3 Stability

Here we will examine the stability of the present stellar structure system by studying (i) causality conditions and (ii) adiabatic index.

Fig. 5
figure 5

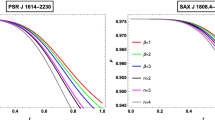
Behavior of radial sound speed square (\(v_{sr}^{2}\)) (left panel), tangential sound speed square (\(v_{st}^{2}\)) (middle panel) and the difference \(v_{st}^{2}-v_{sr}^{2}\) (right panel) against r for Table 1

Full size image

5.3.1 Causality conditions

A compact stellar structure model becomes physically satisfactory if causality conditions are satisfied at every point throughout the interior whole region. Conceptually the principle of causality describes that for anisotropic matter distribution the radial and tangential sound speeds should not exceed the speed of light. Now we define the sound speed as

$$\begin{aligned} \left. \begin{aligned}&v_{sr}=\text {radial sound speed}=\sqrt{\frac{dp_{r}}{d\rho }}\\&v_{st}=\text {tangential sound speed}=\sqrt{\frac{dp_{t}}{d\rho }}. \end{aligned} \right\} \end{aligned}$$
(57)

So, the principle of causality becomes \(0<v_{sr}, v_{st}<1\) [86, 87], as we have taken speed of light (c) \(=1\) throughout the model. Additionally, we can verify the stability by using another strategy based on anisotropic matter distribution, known as the Hererra’s cracking concept [87]. According to the Hererra’s approach, at every stable stellar region point of such matter distribution the condition \(0<|v_{st}^{2} - v_{sr}^{2}|<1\) must be hold, which means no cracking cannot present in that region.

In the Fig. 5, we have illustrated the graphical behavior of radial sound speed square (\(v_{sr}^{2}\)) in the left panel, tangential sound speed square (\(v_{st}^{2}\)) in the middle panel and the difference \(v_{st}^{2}-v_{sr}^{2}\) in the right panel with variations of radius r. Now we have verified that the radial sound speed values are constant and lies in the interval (0,1) for PS1, PS2, PS3 and PS4. As well the graphs of tangential sound speed square are monotonically decreasing and the value of speed lies between 0 and 1 at every point in the interior for all of PS1, PS2, PS3 and PS4. So we can conclude that throughout the interior region of stellar configurations representing by our proposed model satisfy the causality conditions. Moreover, we can easily verify the difference \(v_{st}^{2}-v_{sr}^{2}\) of sound speed squares satisfies the cracking condition \(0<|v_{st}^{2} - v_{sr}^{2}|<1\) inside the stars. Hence we can claim that our considered model is physically stable.

5.3.2 Adiabatic index

In the investigation about the stable status of an anisotropic compact stellar model, the adiabatic index plays a vital role. Actually this index value describes the stiffness of density and pressure ratio for interior matter distribution [88, 89]. Chandrasekhar [90, 91] as a pioneer provided some technics regarding the performance of adiabatic index to examine the dynamical stability of stellar objects against radial perturbation. According to the prediction of another work by Heintzmann and Hillebrandt [92], for dynamically stable compact spherical stellar object the adiabatic index (\(\Gamma \)) value must be greater than \(\frac{4}{3}\) throughout the whole interior region of the object. Now for our proposed system the adiabatic index can be defined in two ways, which are

$$\begin{aligned} \left. \begin{aligned}&\Gamma _{r}=\text {radial adiabatic index}=\Big (1 + \frac{\rho }{p_{r}}\Big )v_{sr}^{2}\\&\Gamma _{t}=\text {tangential adiabatic index}=\Big (1 + \frac{\rho }{p_{t}}\Big )v_{st}^{2}. \end{aligned} \right\} \end{aligned}$$
(58)
Fig. 6
figure 6

Behavior of tangential adiabatic index (\(\Gamma _{t}\)) against r for Table 1

Full size image

In our present study the radial adiabatic index (\(\Gamma _{r}\)) is constant and so we have to check the values of tangential adiabatic index (\(\Gamma _{t}\)) inside the interior region. To understand the values of \(\Gamma _{t}\) in the context of our present model we examine its graphical nature, which is given in the Fig. 6. From this figure we have found that \(\Gamma _{t}>\frac{4}{3}\) in the whole interior region for PS1, PS2, PS3 and PS4. Hence we can say that our model can represents a dynamically stable stellar configurations.

5.4 Electric field

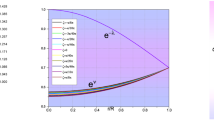
We have given the expression of electric field intensity (E) in square form in the Eq. (45). We have plotted the graphs of \(E^{2}\) with variations of radius r in the Fig. 7 for known neutron stars which are given in the Table 1. Now we have seen that \(E^{2}\) becomes positive in the whole interior region and monotonically increasing nature to outward of the stars. Moreover, electric field satisfies a physically true condition because \(E^{2}=0\) at \(r=0\) i.e., it vanishes at the center of stars for our considerations.

Fig. 7
figure 7

Behavior of electric field intensity (\(E^{2}\)) against r for Table 1

Full size image

5.5 Anisotropy

The anisotropy factor (\(\Delta \)) can defined as

$$\begin{aligned} \Delta (r)=p_{t} - p_{r}. \end{aligned}$$
(59)

The explicit expression of \(\Delta (r)\) is provided in Eq. (50). Physically \(\Delta \) measures the additional stress along the tangential direction over the radial direction. For \(p_{t}>p_{r}\) it leads to \(\Delta > 0\), which represents the anisotropic stress is outward directed i.e., repulsive force in nature. Again \(p_{t}<p_{r}\) yields \(\Delta <0\) that represents an inward directed anisotropic stress i.e., attractive force in nature. For a suitable understanding of the behavior of the anisotropy factor, we examine the graphical nature of \(\Delta \) with respect to the radius of stars. We have given the graphical behavior of \(\Delta \) in Fig. 8. Now we have observed that the values of \(\Delta \) in our model is negative inside the interior region and decreases in the direction of the surface with the increased value of r for known neutron stars. Also \(\Delta (r=0)=0\) i.e., radial pressure (\(p_{r}\)) and tangential pressure (\(p_{t}\)) are equal at the center of the stars. So anisotropic nature becomes attractive and inward-directed, and hence our proposed model represents a more compact stellar configuration.

5.6 EoS parameter

The equation of state parameters corresponding to our model can be defined by

\(w_{r}=\frac{p_{r}}{\rho }\)   and   \(w_{t}=\frac{p_{t}}{\rho }\).

Now for a non-exotic matter distribution, it has been required that EoS parameters must lie in the interval [0,1]. Again Zeldovich’s [93] condition suggests that for a well-behaved stellar system, the condition \(0<w_{r}, w_{t}<1\) should be satisfied. In our considered model \(w_{r}\equiv w\) and it lies between 0 and 1. Again the profile of the Fig. 9 represents the graphical nature of \(w_{t}\) and makes clear that \(0<w_{t}<1\) in the interior of stars. So EoS parameters satisfied physically true conditions in the case of our model.

Fig. 8
figure 8

Behavior of anisotropic factor (\(\Delta \)) against r for Table 1

Full size image
Fig. 9
figure 9

Behavior of tangential EoS (\(w_{t}\)) against r for Table 1

Full size image
Fig. 10
figure 10

Behavior of mass function (\(M_{eff}\)) compactness (\(U_{eff}\)) against r for the Table 1

Full size image

5.7 Mass–radius relation and compactness

The mass–radius relation for our spherical stellar structure can be defined as

$$\begin{aligned} m(r)=\int ^{r}_{0}4\pi \rho r^{2}dr=\int ^{r}_{0}4\pi \Big [\frac{2(A + B)e^{-2A r^{2}}r^{2}\big (-4(A + B)\beta + e^{Ar^{2}}(-\alpha + 4(A + B)\beta )\big )}{(1 + w)(8\pi + \lambda )}\Big ]dr. \end{aligned}$$
(60)

The effective gravitational mass \(M_{eff}\) for our current spherically symmetric charged stellar object can be defined as [94]

$$\begin{aligned} M_{eff}=\int _{0}^{r} 4\pi \left( \rho (r') + \frac{E^{2}}{8\pi }\right) r'^{2}dr', \end{aligned}$$
(61)

where \(\left( \rho (r') + \frac{E^{2}}{8\pi }\right) \) is the effective density due to the additional charge.

Again we can analyze the viability of our compact stellar structure configuration by a physical parameter that is defined as the mass to radius ratio, known as the compactness factor (\(U_{eff}\)). So, \(U_{eff}=\frac{M_{eff}(r)}{r}\). Now for a well-behaved solution of compact stellar configuration, the mass and compactness factor should be zero at the center and monotonically increasing throughout the interior region. According to Buchdahl limit [95], the maximum mass is allowed inside a compact star so that the condition \(U_{eff}<4/9\) must be satisfied at every point in the interior of the star.

The variations of mass function (\(M_{eff}\)) with radius (r) has been depicted in the left panel of the Fig. 10. From this figure it has been cleared that at the center of the stars mass value becomes zero and mass function monotonically increases towards the boundary. Again we have shown the graphical nature of compactness factor (\(U_{eff}\)) inside the stars in the right panel of the Fig. 10. Now one can easily verify that compactness behavior in the stellar interior region satisfies required Buchdahl condition for representing a well-behaved stellar configuration in the context of our assumed model.

5.8 Surface redshift

Here we will check the validity of our stellar system by a physical parameter that measures the amount of force appointed on the light due to the existence of strong gravitational field, known as surface redshift (\(Z_{s}^{eff}\)). The surface redshift is defined as

$$\begin{aligned} Z_{s}^{eff}=(1-2U_{eff})^{-\frac{1}{2}} -1, \end{aligned}$$
(62)

where, \(U_{eff}\) represents the compactness factor \(\frac{M_{eff}(r)}{r}\). Now for physically true stellar configuration, the value of \(Z_{s}^{eff}\) should vanish at the center and increase towards the outward surface. The maximum value of \(Z_{s}^{eff}\) was suggested by 2 for an isotropic stellar structure without cosmological constant [96, 97]. Again in presence of cosmological constant for anisotropic matter distribution, Bohmer and Harko [98] proposed that \(Z_{s}^{eff}\le 5\) whereas Ivanov [56] suggested \(Z_{s}^{eff}\le 5.211\). Now we have illustrated the behavior of surface redshift (\(Z_{s}^{eff}\)) with the variation of radial coordinated r in Fig. 11. From this figure, it is remarkable that \(Z_{s}^{eff}\) vanishes at the center of stars and increases in the direction of the boundary with an increased value of radial coordinate r. Also, the redshift value does not exceed the upper limit for the validity of an anisotropic stellar configuration. So our considered model represents a good stellar configuration in the context of surface redshift.

Fig. 11
figure 11

Behavior of surface redshift (\(Z_{s}^{eff}\)) against r for the Table 1

Full size image
Fig. 12
figure 12

Behavior of all active forces \(F_{g}, F_{h}, F_{a}, F_{m},\text {and} F_{e}\) against the radial co-ordinate r

Full size image

5.8.1 Tolman–Oppenheimer–Volkoff (TOV) equations

In this subsection, we want to investigate whether our current stellar system in a hydrostatically equilibrium state through the TOV equation [99, 100]. The modified form of the TOV equation in f(Q, T) gravitational theory given by

$$\begin{aligned}{} & {} -p_{r}' - \frac{\zeta '}{2}\left( \rho + p_{r}\right) + \frac{2}{r}\left( p_{t}-p_{r}\right) - \frac{\lambda }{16\pi + 2\lambda }\nonumber \\{} & {} \quad \times \left( \rho ' + p_{r}' + 2p_{t}'\right) + \frac{1}{(8\pi + \lambda )r^4}\left( r^{4}E^{2}\right) '=0. \end{aligned}$$
(63)

The above equation can be rewritten in a simplest form as

$$\begin{aligned} F_{h}+ F_{g} + F_{a} + F_{m} + F_{e}=0, \end{aligned}$$
(64)

where

$$\begin{aligned} F_{h}= & {} -p_{r}', F_{g}=- \frac{\zeta '}{2}\left( \rho + p_{r}\right) , F_{a}=\frac{2}{r}\left( p_{t}-p_{r}\right) ,\\ F_{m}= & {} - \frac{\lambda }{16\pi + 2\lambda }\left( \rho ' + p_{r}' + 2p_{t}'\right) ,\nonumber \\ F_{e}= & {} \frac{1}{(8\pi + \lambda )r^4}\left( r^{4}E^{2}\right) '. \end{aligned}$$

The Eq. (63) represents the equilibrium condition for our present charged anisotropic stellar system in f(Q, T) gravity under the combined active forces. Here all active forces are represented as \(F_{h} \equiv \) hydrostatic force, \(F_{g} \equiv \) gravitational force, \(F_{a} \equiv \) anisotropic repulsive force, \(F_{m} \equiv \) force corresponding to the modified gravity and \(F_{e} \equiv \) electric force.

In Fig. 12, we have illustrated the behaviour of all active forces throughout the whole interior region of the stellar structure. By examining this figure, one can easily observe that the positive part of each figure profile contains the forces \(F_{h}\), \(F_{m}\) and \(F_{e}\), whereas the negative portion contains the forces \(F_{a}\) and \(F_{g}\). So, we may claim that the forces \(F_{a}\) and \(F_{g}\) are balanced by the combined action of three other forces like \(F_{h}\), \(F_{m}\) and \(\varvec{F_{e}}\). Thus, the addition of all active forces gives zero value, and the resulting stellar system becomes a physically stable equilibrium state. Therefore, our discussed stellar system is in a hydrostatically equilibrium state in the context of f(Q, T) gravity.

6 Conclusions

In this study, we have explored a new analytical solution of electrically charged spherically symmetric object with interior anisotropic matter distribution in modified f(Q, T) gravity. Following the variational principle to Einstein–Hilbert (E–H) action, we have formulated a complete set of Einstein–Maxwell (E–M) field equations correspondence to a non-linear arbitrary function \(f(Q,T) = \alpha Q + \beta (1 + Q^{2}) + \lambda T \). To obtain the analytical solution of E–M field equations, we have described the interior space-time of stellar structure by K–B metric potentials. Next, with the help of the junction procedure between interior and exterior Reissner–Nordstr\(\ddot{\textrm{o}}\)m metric, the analytical form of constant parameters A, B and C have been obtained. Next, to judge the realisticness of our obtained solutions, we have presented a suitable graphical analysis to test the required viability conditions. For this purpose, we have selected four pulsars like neutron stars with mass, radius and charge, which are included in Table 1.

The behavior of main physical quantities that characterizes the model like energy density (\(\rho \)), radial pressure (\(p_{r}\)) and tangential pressure (\(p_{t}\)) have been depicted in the respective Figs. 1, 2 and  3 and it is observed that the values of these quantities are positive and finite in the interior region of stars. Again with the help of first and second derivatives nature, we have confirmed \(\rho \), \(p_{r}\) and \(p_{t}\) decreases to the boundary surface of considered stars. So with respect to our stellar structure solutions, the quantities \(\rho \), \(p_{r}\) and \(p_{t}\) become maximum at the center and decreases towards the surface of stars.

All energy conditions are satisfied for all selected stars PS1, PS2, PS3 and PS4 (for more details, see Fig. 4) in the presence of charged effect. So normal matter is present in the interior region of the stellar body represented by our proposed model. Also, we have analyzed the behavior of the anisotropic factor that is \(\Delta <0\) and \(\Delta (r=0)=0\). So in the case of our model, anisotropic force is attractive, and that permits the building of a more compact stellar object.

Now we claim that our present solutions fulfill all necessary conditions for stability. Because in Fig. 5, it has been shown that the radial and tangential sound speeds lie in the interval (0,1). Also the inequality \(0<|v_{st}^{2}-v_{sr}^{2}|<1\) holds by all considered neutron stars. That indicates our proposed model is physically stable. Further, Fig. 6 has displayed the behavior of tangential adiabatic index (\(\Gamma _{t}\)), and it is observed that \(\Gamma _{t}>\frac{4}{3}\) within the stellar region. So our stellar structure becomes dynamically stable. Moreover the, Zeldovich’s condition \(0<w_{r}, w_{t}<1\) has satisfied in the context of our solutions in the whole interior region of known stars.

To verify the Buchdahl condition regarding the maximum allowable mass within a compact object, we have examined the behaviour of the mass function, i.e., the effective gravitational mass (\(M_{eff}(r)\)) due to presence of electric field \(E^{2}\) inside considered compact stars. In Fig. 10, it has been shown that at the center of stars, \(M_{eff}(r)\) is zero and increases when radial coordinate r increases. Also the compactness factor (\(U_{eff}=\frac{M_{eff}(r)}{r}\)) satisfies \(U_{eff}<\frac{4}{9}\) at every point in the interior region. So, our considered model can deliver a physically possible existing compact stellar object. Besides, we have verified the physical validity of our solutions through surface redshift (\(Z_{s}^{eff}\)), whose nature has been depicted in Fig. 11. And we have observed that the values of \(Z_{s}^{eff}\) do not exceed 1 throughout the interior region of known stars. So, our solutions become physically valid in the context of surface redshift.

Again, in order to examine the hydrostatic equilibrium position of our current stellar system, we have used the modified TOV Eq. (47). In Fig. 12, we have demonstrated the graphical behavior of all active forces like \(F_{g}, F_{h}, F_{a}, F_{m},\text {and}~ F_{e}\) throughout the whole interior region for considered three stellar objects corresponding to our obtained solutions. By observing the nature of forces, we have the negative nature of the forces \(F_{a}\) and \(F_{g}\) are balanced by the combined action of three other forces like \(F_{h}\), \(F_{m}\) and \(F_{e}\), which are in positive nature. Hence, the sum of all active forces becomes zero. Thus, our proposed stellar system is in an equilibrium position in the context of f(Q, T) gravity.

Now, for a rotating neutron star, i.e., pulsar, there must exist ‘magnetism’, but for a static neutron star, there must not be any associated magnetism. First, we want to clarify that we have used pulsar-like neutron stars to verify the viability of our current model. The main reason behind this is that our proposed neutron star is static and electrically charged, inspired by the Ref. [102]. But there is no any relation with rotation. Now, we present the connection of the electromagnetic field to our considered model as follows: Based on the Ref. [103], we have a self-gravitating stellar system that attained the equilibrium position after some amount of electrons, i.e., lighter particles escape, leaving an electrified star. Again, in the case of cold stars, electrostatic energy is balanced by gravitational energy. For compact stars, i.e., high density and pressure, the effect of net charge plays a definite role in the mass–radius ratio. According to the Ref. [104], such types of stars allow some more charge to be in equilibrium. In our discussing model, we have produced the effective role of the electric field in case of energy conditions, mass, compactness, surface redshift, etc. More importantly, we have shown the definite role of an electric field in attaining the hydrostatic equilibrium position for our stellar system, i.e., the TOV equation is satisfied. Because if the force due to the electric field, i.e., is absent, then the sum of all other forces is not equal to zero, i.e., the hydrostatic equilibrium condition, is not satisfied.

Now, according to the Ref. [101] a charged body always produce an Electromagnetic mass model (EMMM), where mass and other physical parameters have a purely electromagnetic origin and also, both the solutions like, interior and exterior, are of purely electromagnetic origin, i.e., both the spacetimes become flat when charge density vanishes. In this connection, one may study several works on EMMM [105,106,107,108,109,110,111,112,113]. An electromagnetic mass model for a Lorentz extended electron has been obtained in [114, 115]. Also, in the Refs.  [116, 117], authors have constructed several solutions for EMMM via embedding technique in GR. In the Ref. [118], Corne et al. proposed that ’pure electromagnetic mass cannot exist. Again, Arnowitt et al. [119] constructed pure electromagnetic mass as \(m=2|e|\) with electric charge e. In our current study, Einstein–Maxwell field equations (34)–(36) are highly non-linear, and hence they are not easy to solve. Hence, we have used a different technique to solve the field equations via an EoS. As a result, we have the pressure gradient \(p_{t}\) depending on electric field \(E^{2}\) and also, \(E^{2}\) dependent on the mass, i.e., the effective mass has been discussed. So, based on the literature survey, we may claim our current model is not purely EMMM but may be considered a special kind of EMMM.

Now from the whole of our above discussions, we notice that our obtained solutions for describing a spherically symmetric stellar system in f(Q, T) gravity maintains all physical conditions through graphically and analytically for viability and stability. Moreover, we have examined all required physical conditions in case of four selected pulsars like neutron stars viz., PS1, PS2, PS3 and PS4. Hence the configuration of a neutron star can be designed by our considered model in f(Q, T) modified gravity.