1 Introduction

Black holes are celestial bodies predicted by the theory of general relativity, and the concept of black holes was first proposed by scientists such as Michell and Laplace in the early eighteenth century [1, 2]. The proposal of the black hole concept has been indirectly confirmed by physicists through various observational means, such as gravitational lensing effects, the motion of star orbits, the detection of X-rays, and gravitational waves, all of which provide solid support for the real existence of black holes [3,4,5,6]. Black holes are composed of extremely dense matter, among which the most notable feature is the singularity within a black hole. Regarding the singularity of black holes, there are two scenarios: one is the gravitational collapse leading to a naked singularity, and the other is that the end product of gravitational collapse is a black hole, meaning the singularity produced is enveloped by the event horizon of the black hole, thereby not producing a naked singularity. Naked and non naked singularities represent the two possibilities of whether the singularity can be covered by the event horizons. A naked singularity means that the singularity is not covered by the event horizons and can be directly exposed to external observation; whereas a non naked singularity means the singularity is completely surrounded by the event horizons, not affecting the completeness of spacetime causality. This issue actually relates to the weak cosmic censorship conjecture, which is a conjecture about the properties of black holes. The weak cosmic censorship conjecture suggests that all singularities in the universe should be enveloped by the event horizons of black holes, preventing them from affecting the causal laws of spacetime.

In the previous section, we discussed two important concepts: singularities and the Weak Cosmic Censorship Conjecture. There are some connections between them. On one hand, an important result of General Relativity is the Singularity Theorems, proposed by physicists Penrose and Hawking [7, 8], which suggest that matter collapse inevitably leads to singularities, thus causing the breakdown of physical laws. On the other hand, to ensure that physical laws remain unaffected by singularities, Penrose proposed the Weak Cosmic Censorship Conjecture in 1979 [9, 10]. Specifically, the idea behind the Weak Cosmic Censorship Conjecture is that the appearance of singularities is always accompanied by event horizons, thereby preventing singularities from being exposed to the universe. To test this conjecture, physicists have used various methods such as the collapse evolution of matter fields [11,12,13], collisions of supermassive black holes [14,15,16,17], and numerical evolutions of black holes [18, 19]. Here, we will employ the thought experiment proposed by Wald to test the weak cosmic censorship conjecture, by incident test particles into both extreme and near extreme black holes [20], as well as the method proposed by Semiz and others, which involves incident a scalar field into extreme and near extreme black holes to test the weak cosmic censorship conjecture [21]. Research on this conjecture has led to different schools of thought [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41], with some studies suggesting that the Weak Cosmic Censorship Conjecture could be violated, exposing the singularities of black holes, while other studies argue that it is not violated, thus ensuring that black holes’ event horizons encompass them. Therefore, research on the Weak Cosmic Censorship Conjecture is continuously evolving and changing.

On the other hand, through the Einstein field equations, exact solutions for black holes can be obtained, allowing physicists to gain a deeper understanding of the nature of black holes. Typically, the exact solutions for black holes are divided into spherically symmetric and rotating cases. Physicists know through research that gravitational collapse can form black holes, and mass alone can describe the properties of spherically symmetric black holes. However, there is another type of black hole, namely the rotating Kerr black hole, which is described by its mass, angular momentum, and charge, according to the no hair theorem [42,43,44,45,46,47,48,49,50,51,52,53]. Among the many “hairs” of black holes, scalar hair, as the most important one, affects the properties of black holes. Tang and others have used the NJ (Newman–Janis) method to extend the background metric of spherically symmetric short haired black holes to the background metric of rotating short haired black holes [54]. In this work, by injecting test particles and scalar fields into the rotating short haired black holes calculated by Tang and others, the influence of short hair on the Weak Cosmic Censorship Conjecture for Kerr black holes is explored.

The structure of this article is as follows: Sect. 1 is the introduction. Section 2 introduces the exact solutions of rotating short haired black holes. Section 3 discusses the incident of test particles into rotating short haired black holes. Section 4 covers the incident of scalar fields into rotating short haired black holes. Section 5 provides a summary of the article. This article adopts natural units where \(c = G = 1.\)

2 Short haired black holes under rotation

2.1 Precise solution of short haired black holes in the case of rotation

The no hair theorem is a key feature of classical black holes, and the quantum effects of black hole event horizons become particularly significant due to the extreme properties of trapped ergospheric horizons [55,56,57,58,59,60,61]. However, the non trivial matter fields in black hole spacetimes may lead to violations of the no hair theorem. Among them, scalar hair acts as the most significant hair of black holes, affecting the spacetime structure of black holes.

Contreras et al. have utilized the gravitational decoupling method to extend these spherically symmetric black holes with scalar hair to the rotating case, discussing the fundamental physical properties of such spacetimes [62]. This is based on the spherically symmetric hairy background metrics obtained by Ovalle et al. [63]. Using the Newman–Janis (NJ) algorithm, solutions for rotating short haired black holes were obtained, meaning that the NJ method can extend spherically symmetric spacetimes to rotating spacetimes through complex transformations. Therefore, within the NJ algorithm [64,65,66], Tang and Xu [54] obtained the exact solutions for short haired black holes in the rotating case, as follows

$$\begin{aligned} ds^2= & {} -\bigg [1-\frac{2Mr-\frac{Q_m^{2k}}{r^{2k-2}}}{\rho ^2}\bigg ]dt^2+ \frac{\rho ^2}{\Delta }dr^2\nonumber \\{} & {} -\frac{2a \sin ^2\theta (2Mr-\frac{Q_m^{2k}}{r^{2k-2}})}{\rho ^2}dtd\phi + \rho ^2d\theta ^2\nonumber \\{} & {} +\frac{\Sigma \sin ^2\theta }{\rho ^2}d\phi ^2, \end{aligned}$$
(1)

here

$$\begin{aligned} \rho ^2= & {} r^2+a^2\cos ^2\theta , \end{aligned}$$
(2)
$$\begin{aligned} \Delta= & {} r^2-2Mr+\frac{Q_m^{2k}}{r^{2k-2}}+a^2, \end{aligned}$$
(3)
$$\begin{aligned} \Sigma= & {} (r^2+a^2)^2-a^2\Delta (r)\sin ^2\theta . \end{aligned}$$
(4)

The mass of the black hole is denoted by the variable M in the given equation, \(Q_m\) denotes the strength parameter of the hair, where for \(Q_m\ne 0\) and \(k>1,\) it represents a short haired black hole under rotation. Here, a represents the spin parameter of the short haired black hole, namely \(a=J/M,\) where J denotes the angular momentum of the black hole. When \(Q_m=0,\) the metric (1) representing the short haired black hole degenerates to a Kerr black hole.

2.2 Event horizon and angular velocity of a short haired black hole

The event horizons of this short haired black hole can be expressed in a coupled manner, given by \(g^{rr}=\Delta =0.\) This can be obtained through Eq. (3):

$$\begin{aligned} \Delta =r^2-2Mr+\frac{Q_m^{2k}}{r^{2k-2}}+a^2=0. \end{aligned}$$
(5)

By rearranging Eq. (5), we obtain a coupled equation for the event horizons

$$\begin{aligned} r_h=M\pm M\sqrt{1-\frac{\frac{Q_m^{2k}}{r_h^{2k-2}}+a^2}{M^2}}. \end{aligned}$$
(6)

For convenience of analysis, let the coupling term be \(\beta =\frac{Q_m^{2k}}{r_h^{2k-2}}.\) Then Eq. (6) can be rewritten as follows

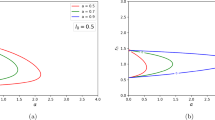
$$\begin{aligned} r_h=M\pm M\sqrt{1-\frac{\beta +a^2}{M^2}}, \end{aligned}$$
(7)

where \(r_h\) represents the event horizons of the rotating short haired black hole. From Eq. (7), we know that when \(\beta +a^2<M^2\) is satisfied, it indicates the existence of a black hole spacetime. However, in the other case when \(\beta +a^2>M^2\) is satisfied, the background metric (1) no longer describes a black hole. This is the point of interest for us because if, after scattering test particles or scalar fields, the metric (1) transitions from describing a black hole to a non black hole spacetime, then it can be said that the metric (1) has undergone super spinning. In other words, at this point, there is a possibility of violating The Weak Cosmic Censorship Conjecture under our conditions.

The formula provided below expresses the area of the event horizons for this particular black hole:

$$\begin{aligned} A=\int \int \sqrt{g_{\theta \theta }g_{\phi \phi }}d\theta d\phi =4\pi (r_h^2+a^2). \end{aligned}$$
(8)

At the event horizons of this black hole, the angular velocity can be determined using the following formula:

$$\begin{aligned} \Omega _h=-\frac{g_{03}}{g_{33}}=\frac{a}{r_h^2+a^2}. \end{aligned}$$
(9)

3 Incident test particles on rotating short haired black holes

This chapter, our main focus is on incident test particles in rotating short haired black holes, aiming to discuss the possibility of disrupting the black hole event horizons in extreme and near extreme black hole scenarios. Through Eq. (7), we can calculate the event horizons of rotating short haired black holes. In this equation, when \(\beta +a^2\le M^2\) satisfies certain conditions, the black hole event horizons exists. However, when it exceeds a certain threshold denoted by \(\beta +a^2>M^2,\) it implies the absence of an event horizons in this spacetime, which is precisely the issue we are primarily discussing. Therefore, in this article, we primarily delve into this problem.

The movement of particles in the spacetime of rotating short haired black holes can be described using the geodesic equation

$$\begin{aligned} \frac{d^2x^{\mu }}{d\tau ^2}+\Gamma _{\alpha \beta }^{\mu }\frac{dx^{\alpha }}{d\tau } \frac{dx^{\beta }}{d\tau }=0. \end{aligned}$$
(10)

The Lagrangian is given by:

$$\begin{aligned} L=\frac{1}{2}mg_{\mu \nu }\frac{dx^{\mu }}{d\tau }\frac{dx^{\nu }}{d\tau }= \frac{1}{2}mg_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }. \end{aligned}$$
(11)

If a test particle moves at a slow pace along the equatorial plane with \(\theta =\frac{\pi }{2},\) it does not exhibit any motion in the \(\theta \)direction, resulting in \(d\theta /d\tau =0,\) which implies that the momentum \(P_\theta \) is zero:

$$\begin{aligned} P_{\theta }=\frac{\partial L}{\partial \dot{\theta }}=mg_{22}\dot{\theta }=0. \end{aligned}$$
(12)

From the equations of motion of the test particle, the angular momentum \(\delta J\) and energy \(\delta E\) can be expressed as the components of the test particle in the \(\phi \) and t directions, respectively. Their expressions are as follows

$$\begin{aligned} \delta J= & {} P_{\phi }=\frac{\partial L}{\partial \phi }=mg_{3\nu }\dot{x}^{\nu }, \end{aligned}$$
(13)
$$\begin{aligned} \delta E= & {} -P_t=-\frac{\partial L}{\partial \dot{t}}=-mg_{0\nu }\dot{x}^{\nu }. \end{aligned}$$
(14)

When a test particle enters the interior of the event horizons of a rotating short haired black hole, the energy and angular momentum of the short haired black hole change. At this point, the changed energy and angular momentum are as follows

$$\begin{aligned} M\rightarrow M^{\prime }= & {} M+\delta E, \end{aligned}$$
(15)
$$\begin{aligned} J\rightarrow J^{\prime }= & {} J+\delta J. \end{aligned}$$
(16)

When the test particle moves outside the event horizons of the short haired black hole, its four velocity is given as follows

$$\begin{aligned} U^{\mu }U_{\mu }{=}\frac{dx^{\mu }}{d\tau }\frac{dx_{\mu }}{d\tau } {=}g_{\mu \nu }\frac{dx^{\mu }}{d\tau }\frac{dx^{\nu }}{d\tau }= \frac{1}{m^2}g^{\mu \nu }P_{\mu }P_{\nu }{=}-1.\nonumber \\ \end{aligned}$$
(17)

Substituting the expressions for angular momentum and energy into the above equation and rearranging, we obtain the following expression

$$\begin{aligned} g^{00}\delta E^2-2g^{03}\delta E\delta J+g^{11}P_r^2+g^{33}\delta J^2=-m^2. \end{aligned}$$
(18)

The equation \(\delta E\) above can be calculated as

$$\begin{aligned} \delta E{} & {} =\frac{g^{03}}{g^{00}}\delta J\nonumber \\{} & {} \pm \frac{1}{g^{00}} \sqrt{(g^{03})^2\delta J^2-g^{00}(g^{33}\delta J^2+g^{11}P_r^2+m^2)}.\nonumber \\ \end{aligned}$$
(19)

As the test particle travels from infinity towards the event horizons, its trajectory must be timelike and oriented towards the future. Therefore, in this case, we need to satisfy the following conditions

$$\begin{aligned} \frac{dt}{d\tau }>0. \end{aligned}$$
(20)

For the two equations of \(\delta J\) and \(\delta E,\) rearranging yields

$$\begin{aligned} \dot{t}=\frac{dt}{d\tau }=-\frac{g_{33}\delta E+g_{03}\delta J}{g_{00}g_{33}-g_{03}^2}. \end{aligned}$$
(21)

The energy is obtained from Eqs. (20) and (21)

$$\begin{aligned} \delta E>-\frac{g_{03}}{g_{33}}\delta J. \end{aligned}$$
(22)

At this point, we need to satisfy the condition of Eq. (22), which means the energy of the test particle takes a negative sign, that is

$$\begin{aligned} \delta E{} & {} =\frac{g^{03}}{g^{00}}\delta J\nonumber \\{} & {} \quad -\frac{1}{g^{00}} \sqrt{(g^{03})^2\delta J^2-g^{00}(g^{33}\delta J^2+g^{11}P_r^2+m^2)}.\nonumber \\ \end{aligned}$$
(23)

In studying the constraints on energy and angular momentum, we conclude that to ensure the test particle can accurately enter the event horizons, its energy and angular momentum must meet specific requirements, that is

$$\begin{aligned} \delta J<-\lim \limits _{r\rightarrow r_h}\frac{g_{33}}{g_{03}}\delta E. \end{aligned}$$
(24)

By combining Eqs. (9) and (24), the solution obtained is

$$\begin{aligned} \delta J<-\lim \limits _{r\rightarrow r_h}\frac{g_{33}}{g_{03}}\delta E= \frac{\delta E}{\Omega _h}=\frac{r^2+a^2}{a}\delta E. \end{aligned}$$
(25)

When the angular momentum is too large, it is impossible for the test particle to fall into the black hole. Therefore, for a test particle to be captured by a rotating short haired black hole, there must be an upper limit to the test particle’s angular momentum, denoted as \(\delta J_{max}.\) Thus, the upper limit of the test particle’s angular momentum \(\delta J,\) given by Eq. (25), is

$$\begin{aligned} \delta J_{max}<\frac{\delta E}{\Omega _h}=\frac{r_h^2+a^2}{a}\delta E. \end{aligned}$$
(26)

From Eq. (7), we know that the event horizons of the rotating short haired black hole disappears only when \(\beta +a^2>M^2.\) Therefore, we can arrange this condition as follows

$$\begin{aligned} a>M\sqrt{1-\frac{\beta }{M^2}}=M\kappa , \end{aligned}$$
(27)

that is

$$\begin{aligned} J>M^2\kappa . \end{aligned}$$
(28)

Here, the parameter \(\kappa =\sqrt{1-\frac{\beta }{M^2}}\) is a function of the hair strength \(\kappa (Q_m^{2k}),\) where \(\beta =\frac{Q_m^{2k}}{r_h^{2k-2}}.\)

Therefore, for test particles entering a rotating short haired black hole to damage the event horizons of the black hole, the following conditions are necessary

$$\begin{aligned} J^{\prime }>\kappa ^{\prime }M^{{\prime }2}. \end{aligned}$$
(29)

Here, the parameter \(\kappa ^{\prime }\) is a physical quantity related to \(\beta \) and the mass M,  and \(\beta \) contains information about the event horizon.Therefore, when neutral test particles enter the interior of the event horizon of a short haired black hole, the corresponding mass M and \(\beta \) in the composite system formed by the short haired black hole will also change.At this point, the mass \(M^{\prime }\) of the composite system becomes \(M+\delta E\) (see Eq. (15)).Analyzing the event horizon (Eq. (5)) of the short haired black hole, when the corresponding mass changes, the coupling term \(\beta ,\) which contains information about the event horizon, also undergoes a slight change, and the change in \(\beta \) is an increasing trend (\(\beta =-r^2+2Mr-a^2,\) when the system is formed, the corresponding \(\beta \) increases). Therefore, the \(\beta ^{\prime }\) of the composite system formed can also be represented as \(\beta ^{\prime }=\beta +\delta E,\) without loss of generality.

At this point, after the neutral particle enters the event horizons and forms a composite system, the parameter \(\kappa ^{\prime }\) can be represented as

$$\begin{aligned} \kappa ^{\prime }=\sqrt{1-\frac{\beta ^{\prime }}{M^{\prime 2}}}= \sqrt{1-\frac{\beta +\delta E}{(M+\delta E)^2}}. \end{aligned}$$
(30)

Here, since \(\delta E \ll M,\) the expansion of the coupling term \(\kappa ^{\prime }\) yields

$$\begin{aligned} \kappa ^{\prime }&\approx \kappa +\left( \frac{\beta }{\kappa M^3}-\frac{1}{2\kappa M^2}\right) \delta E \nonumber \\&\quad + \frac{8\beta ^2-4\beta M-M^2-12\beta M^2+8M^3}{8M^6\kappa ^3}\delta E^2. \end{aligned}$$
(31)

Substituting Eqs. (15), (16), and (31) into Eq. (29) yields

$$\begin{aligned} J+\delta J&>\bigg (\kappa +\bigg (\frac{\beta }{\kappa M^3}- \frac{1}{2\kappa M^2}\bigg )\delta E\nonumber \\&\quad +\frac{8\beta ^2-4\beta M-M^2-12\beta M^2+8M^3}{8M^6\kappa ^3}\delta E^2\bigg )\nonumber \\&\quad \times (M^2+2M\delta E+\delta E^2). \end{aligned}$$
(32)

After rearranging, we obtain

$$\begin{aligned}&\delta J>(M^2\kappa -J){+}\bigg (2\kappa M{+}\frac{\beta }{\kappa M}- \frac{1}{2\kappa }\bigg )\delta E{+}\bigg (\kappa +\frac{2\beta }{\kappa M^2}\nonumber \\&-\frac{1}{\kappa M}{+}\frac{8\beta ^2-4\beta M-M^2-12\beta M^2{+}8M^3}{8M^4\kappa ^3}\bigg ) \delta E^2. \end{aligned}$$
(33)

In Eq. (33) we obtain a lower bound on the event horizons for which the test particle can destroy the short haired black hole in the rotating case. When we do not consider the effects of higher order perturbations, the lower limit of angular momentum at this point can be expressed as

$$\begin{aligned} \delta J_{min}>(M^2\kappa -J)+\bigg (2\kappa M+\frac{\beta }{\kappa M}- \frac{1}{2\kappa }\bigg )\delta E. \end{aligned}$$
(34)

According to the above derivation, only when the selected test particles satisfy both conditions of Eqs. (26) and (34) at the same time, the event horizons of the short hair black hole can be destroyed.

To explore whether neutral test particles can disrupt the event horizons of short hair black holes, we will discuss two cases next, one extreme case and the other near extreme case.

1\(\star \) In the extreme case, where \(\frac{\beta +a^2}{M^2}=1,\) the event horizons of the rotating short haired black hole is as follows

$$\begin{aligned} r_h=M. \end{aligned}$$
(35)

In the case of first order approximation, to disrupt the event horizons of the rotating short haired black hole, the following two conditions need to be satisfied

$$\begin{aligned}{} & {} \delta J_{max}<\frac{\delta E}{\Omega _h}=\frac{r_h^2+a^2}{a}\delta E, \end{aligned}$$
(36)
$$\begin{aligned}{} & {} \delta J_{min}>\bigg (2\kappa M+\frac{\beta }{\kappa M}-\frac{1}{2\kappa }\bigg )\delta E. \end{aligned}$$
(37)

By combining Eqs. (27), (35), and (36), it can be calculated that

$$\begin{aligned} \delta J_{max}&<\frac{r_h^2+a^2}{a}\delta E=\frac{M^2\kappa ^2+M^2\kappa ^2+ \beta }{M\kappa }\delta E\nonumber \\&=\frac{2M^2\kappa ^2+\beta }{M\kappa }\delta E=\bigg (2M\kappa + \frac{\beta }{M\kappa }\bigg )\delta E. \end{aligned}$$
(38)

Analyzing Eqs. (37) and (38), in the case of a first order approximation, it can be intuitively obtained that

$$\begin{aligned} \delta J_{max}-\delta J_{min}&=\bigg (2M\kappa +\frac{\beta }{M\kappa }\bigg )\delta E\nonumber \\&\quad -\bigg (2M\kappa +\frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )\delta E= \frac{1}{2\kappa }\delta E. \end{aligned}$$
(39)

In the case of first order approximation, we get the result of Eq. (39). This result shows that the event horizons of the black hole can be destroyed under the condition of first order approximation (\(\delta J_{max}-\delta J_{min}>0)\). Next, we will explore the second order approximation. When considering second order small quantities, according to Eqs. (33) and (38), it can be obtained.

$$\begin{aligned} \delta J_{max}-\delta J_{min}&=\frac{1}{2\kappa }\delta E- \bigg (\kappa +\frac{2\beta }{\kappa M^2}-\frac{1}{\kappa M}\nonumber \\&\quad +\frac{8\beta ^2-4\beta M-M^2-12\beta M^2+8M^3}{8M^4\kappa ^3}\bigg )\delta E^2\nonumber \\&=\frac{1}{2\kappa }\delta E-(higher\text {-}order\ terms). \end{aligned}$$
(40)

In Eq. (40), the result we calculated is a first order small quantity minus higher order small quantities, and at this point, the final result presented is still a positive value.This also means that even when taking higher order quantities into account, our result remains positive \((\delta J_{max}-\delta J_{min}>0),\) i.e., under extreme conditions, the event horizons of a short haired black hole can be destroyed. At this time, the weak cosmic censorship conjecture is violated.

2\(\star \) In the near extreme case, that is, when \(a=\kappa M,\) the condition for the event horizons of a rotating short haired black hole is

$$\begin{aligned}{} & {} \delta J_{max}<\frac{r_h^2+a^2}{a}\delta E, \end{aligned}$$
(41)
$$\begin{aligned}{} & {} \delta J_{min}>\bigg (2\kappa M+\frac{\beta }{\kappa M}- \frac{1}{2\kappa }\bigg )\delta E+(\kappa M^2-J). \end{aligned}$$
(42)

For \(a\sim \kappa M,\) a dimensionless small quantity \(\epsilon \) can be used to describe the degree of approximation

$$\begin{aligned} \frac{\beta +a^2}{M^2}=1-\epsilon ^2. \end{aligned}$$
(43)

Parameter \(\epsilon \rightarrow 0,\) that is \(\epsilon \ll 1,\) when \(\epsilon =0,\) Eq. (43) degenerates into the extreme case. From Eqs. (41) and (42), it can be concluded that to destroy the event horizons of the spacetime of a short haired black hole in the near extreme case, the following expression must hold.

$$\begin{aligned} \frac{1}{\Omega _h}-2\kappa M-\frac{\beta }{\kappa M}+\frac{1}{2\kappa }>0. \end{aligned}$$
(44)

This indicates that the event horizons of a rotating short haired black hole in the near extreme case can only be destroyed if the test particle makes the composite system satisfy the above condition.

Considering \(\epsilon \ll 1,\) some series expansions can be performed to obtain

$$\begin{aligned} r_h= & {} M(1+\epsilon ), \end{aligned}$$
(45)
$$\begin{aligned} a= & {} M\bigg (\kappa -\frac{\epsilon ^2}{2\kappa }+o(\epsilon ^4)\bigg ), \end{aligned}$$
(46)
$$\begin{aligned} a^2= & {} M^2-M^2\epsilon ^2-\beta . \end{aligned}$$
(47)

Combining Eqs. (43), (44), (45), and (46), the calculation is obtained

$$\begin{aligned}&\frac{1}{\Omega _h}-2M\kappa -\frac{\beta }{\kappa M}+\frac{1}{2\kappa }\nonumber \\&\quad =\frac{1}{2\kappa }+\frac{2M^2\epsilon +\bigg (M^2+\frac{\beta }{2\kappa ^2}\bigg ) \epsilon ^2-o(\epsilon ^4)}{a}\nonumber \\&\quad =\frac{1}{2\kappa }+\frac{2M^2\epsilon }{a}+(higher\text {-}order\ terms). \end{aligned}$$
(48)

Since \(\epsilon \) can be characterized as a first order small quantity, the analysis of the above equation yields

$$\begin{aligned} \frac{1}{\Omega _h}-2M\kappa -\frac{\beta }{\kappa M}+\frac{1}{2\kappa }>0. \end{aligned}$$
(49)

At this point, it represents that in the near extreme case, the event horizons of the short haired black hole can be destroyed (Expressions (49) and (44) are simultaneously satisfied.)

When higher order terms are taken into account, from the spin parameter \(a=J/M,\) it can be obtained that

$$\begin{aligned} M^2\kappa -J=\frac{M^2\epsilon ^2}{2\kappa }-o(\epsilon ^4). \end{aligned}$$
(50)

It is obtained from Eqs. (33) and (48)

$$\begin{aligned}&\delta J_{max}-\delta J_{min}\nonumber \\&\quad =\left( \frac{1}{2\kappa }+\frac{2M^2\epsilon +\bigg (M^2+ \frac{\beta }{2\kappa ^2}\bigg )\epsilon ^2-o(\epsilon ^4)}{a}\right) \delta E\nonumber \\&\qquad -(M^2\kappa -J) -\left( \kappa +\frac{2\beta }{\kappa M^2}-\frac{1}{\kappa M}\right. \nonumber \\&\qquad \left. +\frac{8\beta ^2-4\beta M-M^2-12\beta M^2+8M^3}{8M^4 \kappa ^3}\right) \delta E^2\nonumber \\&\quad =\frac{1}{2\kappa }\delta E+(higher\text {-}order\ terms)). \end{aligned}$$
(51)

Utilizing Eq. (50), Eq. (51) can be transformed into

$$\begin{aligned}&\delta J_{max}-\delta J_{min}\nonumber \\&\quad =\left( \frac{1}{2\kappa }+\frac{2M^2\epsilon +\left( M^2+ \frac{\beta }{2\kappa ^2}\right) \epsilon ^2-o(\epsilon ^4)}{a}\right) \delta E\nonumber \\&\qquad -\frac{M^2\epsilon ^2}{2\kappa } -\left( \kappa +\frac{2\beta }{\kappa M^2}-\frac{1}{\kappa M}\right. \nonumber \\&\qquad + \left. \frac{8\beta ^2-4\beta M-M^2-12\beta M^2+8M^3}{8M^4 \kappa ^3}\right) \delta E^2\nonumber \\&\quad =\frac{1}{2\kappa }\delta E+(higher\text {-}order\ terms). \end{aligned}$$
(52)

In Eq. (52), the result we calculate is a first order small quantity plus higher order small quantities, and the final result presented is still a positive value.This also means that even when considering higher order terms, our result is still positive \((\delta J_{max}-\delta J_{min}>0),\) i.e., in the near extreme case, the event horizons of short haired black holes can be destroyed.

Overall, when a neutral test particle enters the event horizons of a short haired black hole, considering the inclusion of higher order terms in both extreme and near extreme cases (fully consider the back-reaction and the spacetime background), at this time, in the extreme case, Eq. (40) can be approximately obtained.

$$\begin{aligned} \delta J_{max}-\delta J_{min}=\frac{1}{2\kappa }\delta E-(higher\text {-}order\ terms). \end{aligned}$$
(53)

In extreme cases, an approximation can be obtained from formula (52)

$$\begin{aligned} \delta J_{max}-\delta J_{min}=\frac{1}{2\kappa }\delta E+(higher\text {-}order\ terms). \end{aligned}$$
(54)

In both Eqs. (53) and (54), the results are dominated by a first order term. When the spacetime background and back-reaction effects are fully considered,then these backgrounds will influence our analysis of higher order terms. However, because the actual theory behind spacetime is very complex, the specific expressions for these higher-order terms cannot be accurately calculated. These issues are discussed in the literature [67, 68], where their analysis indicates that the influence of back-reaction effects is negligible if the test body is uncharged. The underlying reason is that the electromagnetic self-force back-reaction effects, which contribute most to the back-reaction, can be ignored. In our case, since our test particles carry no charge, the impact of the back-reaction effects is extremely weak (affecting only the higher-order terms in our analysis, not the lower-order terms). This means that even with full consideration of these effects, our conclusions would not change.

4 Incident scalar field in a rotating short haired black hole

In the third section, the weak cosmic censorship conjecture was tested using the method of test particles. This section primarily utilizes the method proposed by Semiz and others [21], introducing a massive scalar field into the spacetime of a rotating short haired black hole to discuss whether the event horizons of the black hole can be disrupted in the cases of extreme and near extreme black holes.

4.1 Scattering of a massive scalar field

In the scalar field, the Klein Gordon equation under curved spacetime is as follows

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu }(\sqrt{-g}g^{\mu \nu }\partial _{\nu }\psi )-\mu ^2\psi =0. \end{aligned}$$
(55)

Based on the metric given by Eq. (1), its determinant can be calculated

$$\begin{aligned} g=-\rho ^4\sin ^2\theta , \end{aligned}$$
(56)

the inverse metric tensor of the metric (1) is given by the following equation

$$\begin{aligned} g^{\mu \nu }=\frac{\Delta ^{\mu \nu }}{g}. \end{aligned}$$
(57)

Let \(\eta =2Mr-\frac{Q_m^{2k}}{r^{2k-2}},\) substituting the metric (1) into the above expression yields the following equation:

$$\begin{aligned}&-\frac{(r^2+a^2)^2-a^2\Delta \sin ^2\theta }{\Delta \rho ^2} \frac{\partial ^2\psi }{\partial t^2}-\frac{2a\eta }{\Delta \rho ^2} \frac{\partial ^2\psi }{\partial t\partial \phi }\nonumber \\&\quad +\frac{1}{\rho ^2}\frac{\partial }{\partial r}\bigg (\Delta \frac{\partial \psi }{\partial r}\bigg )+\frac{1}{\rho ^2\sin \theta } \frac{\partial }{\partial \theta }\bigg (\sin \theta \frac{\partial \psi }{\partial \theta }\bigg )\nonumber \\&\quad +\frac{\Delta -a^2\sin ^2\theta }{\Delta \rho ^2 \sin ^2\theta } \frac{\partial ^2\psi }{\partial \phi ^2}-\mu ^2\psi =0. \end{aligned}$$
(58)

The form of the solution for the scalar field \(\psi \) in the above equation is as follows:

$$\begin{aligned} \psi (t,r,\theta ,\phi )=e^{-i\omega t}R(r)S_{lm}(\theta )e^{im\phi }, \end{aligned}$$
(59)

where \(S_{lm}(\theta )\) are the angular spherical functions, and l, m are constants of the angular separation variables, whose values are positive integers. Substituting Eq. (59) into the scalar field equation (58) yields the angular and radial equations, respectively.

$$\begin{aligned}&\frac{1}{\sin \theta }\frac{d}{d\theta }\bigg (\sin \theta \frac{d S_{lm}(\theta )}{d\theta }\bigg )-\bigg (a^2\omega ^2\sin ^2\theta +\frac{m^2}{\sin ^2\theta }\nonumber \\&\quad +\mu ^2a^2\cos ^2\theta -\lambda _{lm}\bigg )S_{lm}=0, \end{aligned}$$
(60)

and

$$\begin{aligned}&\frac{d}{dr}\bigg (\Delta \frac{dR(r)}{dr}\bigg )+\bigg (\frac{(r^2+a^2)^2}{\Delta } \omega ^2-\frac{2a\eta }{\Delta }m\omega \nonumber \\&\quad +\frac{m^2a^2}{\Delta }-\mu ^2r^2-\lambda _{lm}\bigg )S_{lm}=0. \end{aligned}$$
(61)

The solution to Eq. (60) is a spherical function, which has an integral of 1 when calculating the energy flux. Therefore, we will solve the radial equation, introducing tortoise coordinates in this calculation process

$$\begin{aligned} dr_*=\frac{r^2+a^2}{\Delta }dr. \end{aligned}$$
(62)

By substituting the turtle coordinates into the radial equation (61), we get

$$\begin{aligned}&\frac{\Delta }{(r^2+a^2)^2}\frac{d}{dr}(r^2)\frac{dR(r)}{dr_*}+ \frac{d^2R(r)}{dr_*^2}\nonumber \\&\quad +\bigg [\bigg (\omega -\frac{ma}{r^2+a^2}\bigg )^2+\frac{\Delta 2am\omega }{(r^2+a^2)^2}\nonumber \\&\quad -\frac{\Delta }{(r^2+a^2)^2}(\mu ^2r^2+\lambda _{lm})\bigg ]R(r)=0. \end{aligned}$$
(63)

Near the event horizons \((r\cong r_h),\) namely

$$\begin{aligned} \Delta \cong 0. \end{aligned}$$
(64)

Substituting Eq. (64) into (63) yields

$$\begin{aligned} \frac{d^2R(r)}{dr_*^2}+\bigg (\omega -\frac{ma}{r^2+a^2}\bigg )^2R(r)=0. \end{aligned}$$
(65)

Substituting Eq. (9) into (65) yields

$$\begin{aligned} \frac{d^2R(r)}{dr_*^2}+(\omega -m\Omega _h)^2R(r)=0. \end{aligned}$$
(66)

Expressed in exponential form

$$\begin{aligned} R(r)\sim e^{[\pm i(\omega -m\Omega _h)r_*]}. \end{aligned}$$
(67)

Here, the positive and negative signs correspond to the outgoing and incoming waves, respectively. When we incident a scalar field into a rotating short haired black hole, the spacetime of this black hole will absorb the energy of the perturbation field. Therefore, it is more in line with physical reality to take the negative sign in Eq. (67). At this time, the solution to Eq. (66) is

$$\begin{aligned} R(r)=e^{[-i(\omega -m\Omega _h)r_*]}. \end{aligned}$$
(68)

By substituting Eq. (68) into Eq. (59), we can obtain the approximate solution to the field equation as

$$\begin{aligned} \psi (t,r,\theta ,\phi )=e^{[-i(\omega -m\Omega _h)r_*]}e^{-i\omega t}S_{lm}(\theta )e^{im\phi }. \end{aligned}$$
(69)

Once this solution is acquired, it enables the calculation of the energy and angular momentum that the spacetime of a short haired black hole absorbs when the scalar field is scattered onto it.

The following equation represents the energy momentum tensor of a scalar field \(\psi \) with mass \(\mu \)

$$\begin{aligned} T_{\mu \nu }=\partial _{\mu }\psi \partial _{\nu }\psi ^*-\frac{1}{2}g_{\mu \nu } (\partial _{\mu }\psi \partial ^{\nu }\psi ^*+\mu ^2\psi \psi ^*). \end{aligned}$$
(70)

By substituting the background metric of the short haired black hole from Eq. (1) into Eq. (70), the following tensor is obtained

$$\begin{aligned} T_t^r= & {} \frac{r_h^2+a^2}{\rho ^2}\omega (\omega -m\Omega _h)S_{lm} (\theta )e^{im\phi }S^*_{l^{\prime }m^{\prime }}(\theta )e^{-im\phi },\nonumber \\ \end{aligned}$$
(71)
$$\begin{aligned} T_{\phi }^r= & {} \frac{r_h^2+a^2}{\rho ^2}m(\omega -m\Omega _h)S_{lm} (\theta )e^{im\phi }S^*_{l^{\prime }m^{\prime }}(\theta )e^{-im\phi }.\nonumber \\ \end{aligned}$$
(72)

The energy flux of the event horizons in the spacetime of a short haired black hole

$$\begin{aligned} \frac{dE}{dt}=\int \int T_t^r\sqrt{-g}d\theta d\phi =\omega (\omega -m\Omega _h)[r_h^2+a^2]. \end{aligned}$$
(73)

The angular momentum flux through the event horizons in the spacetime of a short haired black hole

$$\begin{aligned} \frac{dJ}{dt}=\int \int T_{\phi }^r\sqrt{-g}d\theta d\phi =m(\omega -m\Omega _h)[r_h^2+a^2]. \end{aligned}$$
(74)

Between Eqs. (73) and (74), one scenario, as we learn from equation \(\omega -m\Omega _h,\) occurs when \(\omega >m\Omega _h,\) leading to \(\omega -m\Omega _h\) being positive. This indicates that both angular momentum and energy flux are positive, suggesting that the energy dE and angular momentum dJ can be extracted from the scalar field by the rotating short haired black hole. In another scenario, when \(\omega <m\Omega _h,\) both angular momentum and energy are negative, indicating that the energy extracted by the rotating short haired black hole in the scalar field is due to black hole superradiance [69]. During the time interval dt,  the equations \(\delta E\) and \(\delta J\) for the rotating short haired black hole are as follows:

$$\begin{aligned} dE= & {} \omega (\omega -m\Omega _h)[r_h^2+a^2]dt, \end{aligned}$$
(75)
$$\begin{aligned} dJ= & {} m(\omega -m\Omega _h)[r_h^2+a^2]dt. \end{aligned}$$
(76)

From these two equations, the energy and angular momentum extracted by the short haired black hole from the scalar field are derived. Using these equations, one can discuss the impact on the event horizons of the black hole due to the scattering of the scalar field onto the rotating short haired black hole in extreme and near extreme conditions.

4.2 Incident scalar field in a short haired black hole

This section primarily investigates the impact of a scalar field encountering a rotating short haired black hole, exploring whether the scalar field with significant angular momentum can disturb the event horizons of this spacetime. The process of scalar field scattering is discussed using the concept of differentiation, focusing on the time interval dt.

During this process, after the rotating short haired black hole absorbs the energy and angular momentum from the incident scalar field, its mass M and angular momentum J become \(M^{\prime }\) and \(J^{\prime },\) respectively. After obtaining the changed mass and angular momentum, we discuss based on equation \(\kappa ^{\prime }M^{\prime 2}-J^{\prime }.\) If \(\kappa ^{\prime }M^{\prime 2}\ge J^{\prime },\) then \(\kappa ^{\prime }M^{\prime 2}-J^{\prime }\) is positive, meaning the event horizons of the rotating short haired black hole exists. Conversely, the event horizons of this black hole spacetime is disrupted.

Therefore, for the system formed by equation \(\kappa ^{\prime }M^{\prime 2}-J^{\prime },\) after absorbing energy and angular momentum from the scalar field, its state can become

$$\begin{aligned}&\kappa ^{\prime }M^{'2}-J^{\prime }=(M^2\kappa -J)\nonumber \\&\quad +\bigg (2M\kappa +\frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )\delta E\nonumber \\&\quad +\bigg (\kappa +\frac{2\beta }{\kappa M^2}-\frac{1}{\kappa M}\nonumber \\&\quad +\frac{8\beta ^2-4\beta M-M^2-12\beta M^2+M^3}{8M^4 \kappa ^3}\bigg )\delta E^2-\delta J. \nonumber \\ \end{aligned}$$
(77)

When we consider lower-order perturbations, equation (77) becomes

$$\begin{aligned} \kappa ^{\prime }M^{\prime 2}-J^{\prime }{} & {} =(M^2\kappa -J)+\bigg (2M\kappa + \frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )\delta E\nonumber \\{} & {} \quad -\delta J. \end{aligned}$$
(78)

Substituting Eqs. (75) and (76) into Eq. (78) yields

$$\begin{aligned} \kappa ^{\prime }M^{'2}-J^{\prime }&=(M^2\kappa -J)+\bigg (2M\kappa + \frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )\nonumber \\&\quad \times m^2\bigg (\frac{\omega }{m}-\frac{1}{2\kappa M+ \frac{\beta }{M\kappa }-\frac{1}{2\kappa }}\bigg )\bigg (\frac{\omega }{m}- \Omega _h\bigg )\nonumber \\ {}&\quad \times [r_h^2+a^2]dt. \end{aligned}$$
(79)

Here, just as we analyze test particles, we will analyze two types of situations, namely extreme cases and near extreme cases.

1\(\star \) In the extreme case, that is, when \(M^2\kappa =J,\) Eq. (79) then becomes

$$\begin{aligned} \kappa ^{\prime }M^{\prime 2}-J^{\prime }&=\bigg (2M\kappa +\frac{\beta }{M\kappa }- \frac{1}{2\kappa }\bigg )m^2\nonumber \\&\quad \times \bigg (\frac{\omega }{m}-\frac{1}{2\kappa M+\frac{\beta }{M\kappa }- \frac{1}{2\kappa }}\bigg )\bigg (\frac{\omega }{m}-\Omega _h\bigg )\nonumber \\ {}&\quad \times [r_h^2+a^2]dt. \end{aligned}$$
(80)

Then, the angular velocity \(\Omega _h\) can be expressed as

$$\begin{aligned} \Omega _h&=\frac{a}{r_h^2+a^2}=\frac{M\kappa }{2M^2\kappa ^2+\beta }\nonumber \\&=\frac{1}{2M\kappa +\frac{\beta }{M\kappa }}\le \frac{1}{2\kappa M+ \frac{\beta }{M\kappa }-\frac{1}{2\kappa }}. \end{aligned}$$
(81)

Analyzing Eq. (80), if the incident wave mode is considered to be

$$\begin{aligned} \frac{\omega }{m}=\frac{1}{2}\bigg (\frac{1}{2\kappa M+ \frac{\beta }{M\kappa }-\frac{1}{2\kappa }}+\Omega _h\bigg ). \end{aligned}$$
(82)

Then (80) can be rewritten as

$$\begin{aligned} \kappa ^{\prime }M^{\prime 2}-J^{\prime }&=-\frac{1}{4}\bigg (2M\kappa + \frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )m^2\nonumber \\&\quad \times \bigg (\frac{1}{2\kappa M+\frac{\beta }{M\kappa }- \frac{1}{2\kappa }}-\Omega _h\bigg )^2(r_h^2+a^2)dt. \nonumber \\ \end{aligned}$$
(83)

Evaluating the above equation, it is intuitively obtained that, in the extreme case, the incident scalar quantity field is capable of destroying the event horizons of a short haired black hole \((\kappa ^{\prime }M^{\prime 2}-J^{\prime }<0).\) Moreover, due to the deviation in angular velocity at the event horizons of a short haired black hole from that at the event horizons of a Kerr black hole, it becomes possible to disrupt the event horizons of the short haired black hole.Therefore, by reanalyzing Eqs. (81) and (83), it can be determined that the scalar field modes capable of disrupting the event horizon of a short haired black hole constitute a range, i.e.

$$\begin{aligned} \frac{1}{2M\kappa +\frac{\beta }{M\kappa }}<\frac{\omega }{m}< \frac{1}{2\kappa M+\frac{\beta }{M\kappa }-\frac{1}{2\kappa }}. \end{aligned}$$
(84)

In other words, when the modes of the incident wave are confined within the range of expression (84), the event horizons of the short haired black hole will be disrupted. Furthermore, the larger the hair parameter, the wider the wave modes that can disrupt the event horizons of the short haired black hole. It is worth mentioning that since the energy carried by the incident wave that can penetrate into the interior of the event horizons is minimal, the corrections from higher order parts are nearly zero. Therefore, in this section, we will only analyze the lower order correction terms, that is, without considering the higher order terms. In summary, under extreme conditions, the scalar field can disrupt the event horizon of the short haired black hole, and there exists a range of modes for the scalar field within which the weak cosmic censorship conjecture will be violated.

2\(\star \) In the near extreme case, i.e., \(J\ne M^2\kappa ,\) we have the following equation

$$\begin{aligned} \kappa ^{\prime }M^{\prime 2}-J^{\prime }&=(\kappa M^2-J)+ \bigg (2M\kappa +\frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )\nonumber \\&\quad \times m^2\bigg (\frac{\omega }{m}-\frac{1}{2\kappa M+\frac{\beta }{M\kappa }- \frac{1}{2\kappa }}\bigg )\bigg (\frac{\omega }{m}-\Omega _h\bigg )\nonumber \\ {}&\quad \times (r_h^2+a^2)dt. \end{aligned}$$
(85)

Similarly, in the near extreme case, the pattern of the incident scalar field can be written as

$$\begin{aligned} \frac{\omega }{m}=\frac{1}{2}\bigg (\frac{1}{2\kappa M+\frac{\beta }{M\kappa }- \frac{1}{2\kappa }}+\Omega _h\bigg ). \end{aligned}$$
(86)

Then formula (85) can be sorted out

$$\begin{aligned} \kappa ^{\prime }M^{'2}-J^{\prime }&=(\kappa M^2-J)-\frac{1}{4} \frac{1}{\bigg (2M\kappa +\frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )}\nonumber \\&\quad \times m^2\Omega _h^2\bigg (\frac{1}{\Omega _h}-\bigg (2\kappa M+ \frac{\beta }{M\kappa }-\frac{1}{2\kappa }\bigg )\bigg )^2\nonumber \\&\quad \times (r_h^2+a^2)dt. \end{aligned}$$
(87)

Here we use the same method as the analysis in Sect. 3, that is, we use a dimensionless decimal to describe the degree of approximation, which can therefore be written according to the expression (43)

$$\begin{aligned} \frac{a^2+\beta }{M^2}=1-\epsilon ^2, \end{aligned}$$
(88)

where \(\epsilon \) is a small quantity approaching 0. Using Taylor expansion, we can obtain

$$\begin{aligned} a=\frac{J}{M}=M\kappa \bigg (1-\frac{\epsilon ^2}{2\kappa ^2}+o(\epsilon ^4)\bigg ), \end{aligned}$$
(89)

tidy up

$$\begin{aligned} J=M^2\kappa \bigg (1-\frac{\epsilon ^2}{2\kappa ^2}+o(\epsilon ^4)\bigg ), \end{aligned}$$
(90)

\(M^2\kappa -J\) is calculated as

$$\begin{aligned} M^2\kappa -J=\frac{M^2\epsilon ^2}{2\kappa }-o(\epsilon ^4). \end{aligned}$$
(91)

Bring formula (88) and (90) into formula (87)

$$\begin{aligned}&\frac{1}{\Omega _h}-2M\kappa -\frac{\beta }{\kappa M}+\frac{1}{2\kappa }\nonumber \\&\quad =\frac{1}{2\kappa }+\frac{\bigg (2M^2\epsilon +\bigg (M^2+\frac{\beta }{2\kappa ^2} \bigg )\epsilon ^2-o(\epsilon ^4)\bigg )}{a}. \end{aligned}$$
(92)

Combined with formula (91) and (92), formula (87) can be rewritten as

$$\begin{aligned} \kappa ^{\prime }M^{\prime 2}-J^{\prime }&=\bigg (\frac{M^2\epsilon ^2}{2\kappa } -o(\epsilon ^4)\bigg )\nonumber \\&\quad -\frac{1}{4}\frac{1}{(2\kappa M+\frac{\beta }{M\kappa }- \frac{1}{2\kappa })}m^2\Omega _h^2\nonumber \\&\quad \times \left( \frac{1}{2\kappa }+\frac{\bigg (2M^2\epsilon + \bigg (M^2+\frac{\beta }{2\kappa ^2}\bigg )\epsilon ^2-o(\epsilon ^4)\bigg )}{a}\right) ^2\nonumber \\&\quad \times (r_h^2+a^2)dt\approx \frac{M^2\epsilon ^2}{2\kappa }-\left( \frac{1}{2\kappa }\right) ^2dt. \end{aligned}$$
(93)

Since our analysis occurs over an extremely short time interval dt,  at this time, dt can be regarded as a first order small quantity. Analyzing Eq. (93), we know that the largest part of the first term is a second order small quantity \((\frac{M^2\epsilon ^2}{2\kappa }),\) and the largest part of the second term is a first order small quantity \(\bigg (\bigg (\frac{1}{2\kappa }\bigg )^2dt\bigg ).\) Subtracting a first order small quantity from a second order small quantity, the entire expression will exhibit the effect of a negative value, which is to say

$$\begin{aligned} \kappa ^{\prime }M^{\prime 2}-J^{\prime }<0. \end{aligned}$$
(94)

This means that, when a scalar field is incident upon a rotating short haired black hole in the near extreme case, the event horizons of this spacetime can be disrupted, violating the weak cosmic censorship conjecture.

5 Summary

In this paper, we utilize the exact solution of rotating short hair black holes to explore the weak cosmic censorship conjecture.

The results are as follows:

\(\bullet \) Incident test particles into a rotating short haired black hole, discuss whether the spacetime in the case of extreme black holes and near extreme black holes can disrupt the event horizon of the rotating short haired black hole. For the extreme case, when considering first-order and higher-order approximations, the results indicate that neutral test particles can destroy the event horizon of short haired black holes, violating the weak cosmic censorship conjecture. In the near extreme case, considering first-order and higher-order situations, our results are similar to the extreme case, where the event horizon of short haired black holes can be destroyed.

\(\bullet \) Incident a scalar field into a rotating short haired black hole, explore whether the event horizons of the rotating short haired black hole can be disrupted in the case of extreme and near extreme black holes. We find that, in the extreme case, the rotating short haired black hole will be overspun by the incident scalar field, and there exists a range for the incident wave modes, that is \(\frac{1}{2M\kappa +\frac{\beta }{M\kappa }}<\frac{\omega }{m}<\frac{1}{2\kappa M+\frac{\beta }{M\kappa }-\frac{1}{2\kappa }}.\) This means that within this range, the event horizon of the rotating short haired black hole is disrupted. In the near extreme case, the event horizon of the rotating short haired black hole, due to the presence of hair, allows the black hole to be overspun.

In summary, our analysis indicates that the presence of hair has a significant impact on whether a rotating short haired black hole can be overspun. The presence of hair not only makes the applicability of the weak cosmic censorship conjecture in rotating short haired black holes unstable but also holds key significance for the direction of our future research. In the future, we will employ numerical simulation methods, fully considering the impact of spacetime background and back-reaction effects, to obtain precise conditions for overspinning short haired black holes through numerical simulations. This method not only provides us with a new perspective for understanding the weak cosmic censorship conjecture and the no hair theorem of black holes but also lays a solid foundation for the in depth study of the properties of rotating short haired black holes.