Abstract
Upcoming experiments will improve the sensitivity to \(\mu \rightarrow e\) processes by several orders of magnitude, and could observe lepton flavour-changing contact interactions for the first time. In this paper, we investigate what could be learned about New Physics from the measurements of these \(\mu \rightarrow e\) observables, using a bottom-up effective field theory (EFT) approach and focusing on three popular models with new particles around the TeV scale (the type II seesaw, the inverse seesaw and a scalar leptoquark). We showed in a previous publication that \(\mu \rightarrow e\) observables have the ability to rule out these models because none can fill the whole experimentally accessible parameter space. In this work we give more details on our EFT formalism and present more complete results. We discuss the impact of some observables complementary to \(\mu \rightarrow e\) transitions (such as the neutrino mass scale and ordering, and LFV \(\tau \) decays) and draw attention to the interesting appearance of Jarlskog-like invariants in our expressions for the low-energy Wilson coefficients.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The observed neutrino mass matrix \([m_\nu ]\) [1] requires New Physics beyond the Standard Model (SM) which is lepton flavour-changing. Observing lepton flavour-changing processes other than neutrino oscillations, would therefore give complementary information on New Physics in the lepton sector.
Flavour-changing contact interactions among charged leptons (which we refer to as LFV), have not yet been observed, but upcoming experiments aim to improve the sensitivity to a few processes in the \(\mu \rightarrow e\) sector by orders of magnitude, and to probe a wide palet of \(\tau \rightarrow l\) processes with lesser sensitivity. This is summarised in Table 1; it suggests that LFV could be discovered in \(\mu \rightarrow e\), while \(\tau \rightarrow l\) is more promising for distinguishing among models. For a review of \(\mu \rightarrow e\) LFV, see e.g. [2].
The aim of this project is to explore what can be learned about New Physics in the lepton sector from observations of \(\mu \rightarrow e \gamma ,\mu \rightarrow e {\bar{e}} e\) and/or \(\mu A \rightarrow \! eA \). For instance, it would be ideal if the data could indicate properties of the New Physics model, such as whether new particles interact with lepton doublets or singlets or both, whether LFV occurs among SM particles at loop or tree level, or whether LFV is related to \([m_\nu ]\), baryogenesis or New Physics in the quark flavour sector.
In order to quantify what \(\mu \rightarrow e\) data could tell us about models, we study these questions in a bottom-up EFT approach, assuming  TeV. We translate the data from the experimental scale to \(\Lambda _{NP}\) using EFT, then match three “representative” models to the experimentally allowed Wilson coefficient space, and explore which differences among the models can be identified by the data.
TeV. We translate the data from the experimental scale to \(\Lambda _{NP}\) using EFT, then match three “representative” models to the experimentally allowed Wilson coefficient space, and explore which differences among the models can be identified by the data.
Model predictions for LFV have been widely studied; in particular, there is a large literature devoted to calculating LFV rates in neutrino mass models (for a review, see e.g. [3, 4]; or for example [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]) and other Standard Model extensions such as leptoquarks [40,41,42,43,44,45,46,47,48,49]. We hope that our bottom-up EFT approach could give a complementary perspective on the well-studied relations between models and observables. Our study differs from top-down analyses in that firstly, we suppose that upcoming \(\mu \rightarrow e\) experiments will measure 12 Wilson coefficients, and not just three rates. So we are using a more optimistic/futuristic parametrisation of the LFV observables, using as input everything they could tell us. This allowed us to show in a previous publication [50], that the three models we consider could be ruled out by upcoming data. Secondly, model studies frequently scan over the model parameter space; this allows to estimate correlations among LFV observables, but the results depend on the choice of measure on model parameter space. We circumvent the issue of measure and the need to scan by parametrising the models in terms of “Jarlskog-like” invariants [51], which contribute to the observables. Also, the operator coefficients are allowed to be complex, which is consistent with the hints of leptonic CP violation in neutrino observations [52].
This manuscript gives more complete results than presented in [50] – in particular highlighting the appearance of model “invariants” in the coefficients at the experimental scale, and explores the impact of some complementary observables on the model predictions for \(\mu \rightarrow e\). Section 2 reviews \(\mu \rightarrow e\) observables and the EFT formalism implemented here, then Sect. 3 summarises the three TeV-scale models that we consider, which are the type II seesaw [19,20,21,22], an inverse seesaw [29,30,31], and a scalar leptoquark [40,41,42,43,44,45,46,47,48,49] which can fit the \(R_D\) anomaly [53,54,55,56,57]. The matching of the models to the EFT is relegated to Appendix C. Section 4 gives the twelve observable Wilson coefficients at the experimental scale (including the coefficients for \(\mu A \rightarrow \! eA \) on heavy targets, missing in [50]), expressed in terms of “invariant” combinations of model and SM parameters. Section 5 explores the interplay of \(\mu \rightarrow e\) flavour change with some complementary observables in the models we consider. Then we discuss what we learned about bottom-up reconstruction in Sect. 6, and conclude in Sect. 7.
2 Observables and notation
In a bottom-up perspective, one starts from data and how to parametrise it, which is reviewed in Sect. 2.1. Section 2.2 reviews our EFT formalism; it allows to obtain expressions for the observable Wilson coefficients in terms of operator coefficients at the weak scale, which are given in Appendix B.
2.1 Observables
Some models considered here generate a Majorana mass matrix for the three light neutrinos. At energies below the weak scale (taken \(\simeq m_W\)), it can be included in the Lagrangian as [1]
where greek indices indicate the charged lepton mass eigenstate basis, square brackets indicate a matrix, and \([m_\nu ]_{\alpha \beta } = U_{\alpha i} m_i U_{\beta i}\) for \( m_i\) real and positive. The leptonic mixing matrix U is parameterised as in [1] by three mixing angles, one “Dirac” phase and two “Majorana” phases. In our study, we approximate the Dirac phase \(\delta \approx 3\pi /2\) [58], and take the Majorana phases as free parameters. The Majorana phases and the lightest neutrino mass \(m_{min}\) affect the elements of \([m_\nu ]\), but not the flavour-changing elements of
for \(\alpha \ne \beta \in \{e,\mu ,\tau \}\) and \(D_m = \textrm{Diag}\, (m_1,m_2, m_3)\), because the Majorana phases cancel and the \(|m_i^2 -m_j^2|\) are determined in neutrino oscillations.
Lepton flavour changing processes can be broadly classified as: those that change lepton flavour by two units such as muonium–anti-muonium oscillations, those that change both lepton and quark flavour by one unit such as \(K\rightarrow \mu ^\pm e^\mp \), and those that change lepton flavour by one unit and are otherwise flavour diagonal. The three classes are independent under Renormalisation Group running below the scale of the new particles responsible for LFVFootnote 1 We focus on \(\mu \rightarrow e\) interactions from the last class, which are otherwise flavour diagonal. This is motivated by the very restrictive bounds on a handful of processes in this sector, for which the experimental sensitivity is planned to improve by several orders of magnitude in the next few years (see Table 1). This differs from \(\tau \rightarrow l\) \((l\in \{ \mu ,e\})\) processes, where the upper bound on the branching ratio for a large variety of LFV \(\tau \) decays is currently of order \( 10^{-8}\), and Belle II aims for sensitivities \(\mathcal{O} (10^{-9}\rightarrow 10^{-10})\). So from an EFT perspective, the \(\tau \rightarrow l\) sector allows to independently measure almost every Wilson coefficient up to a New Physics scale  TeV (at tree level) [60]; whereas in the \(\mu \rightarrow e\) sector, fewer coefficients are probed at greater accuracy, motivating the use of Renormalization Group Equations (RGEs) in the \(\mu \rightarrow e\) sector.
TeV (at tree level) [60]; whereas in the \(\mu \rightarrow e\) sector, fewer coefficients are probed at greater accuracy, motivating the use of Renormalization Group Equations (RGEs) in the \(\mu \rightarrow e\) sector.
The three processes we consider are \(\mu \rightarrow e \gamma \), \(\mu \rightarrow e {\bar{e}} e\) and \(\mu A \rightarrow \! eA \). In the latter, a \(\mu ^-\) is captured by a nucleus, where it can transform into an electron via various interactions; we restrict to those which are coherent across the nucleus, or “spin-independent”Footnote 2 (some details are given in Appendix A). At the experimental scale, these three processes can be parametrised by the dimensionless operator coefficients \(\{C\}\) of the following Lagrangian [2, 79,80,81]:
where \(\mathcal{O}_{Al} \) is the combination of operators contributing to SI \(\mu \rightarrow e\) conversion on light targetsFootnote 3 such as Titanium (used by SINDRUM [66, 70]) or Aluminium (to be used by COMET [67] and Mu2e [68, 69]), and \( \mathcal{O}_{Au\perp }\) is an independent combination probed by heavy targets such as Gold (used by SINDRUM [70]). At the experimental scale, these operators would describe \(\mu \rightarrow e\) interactions with nucleons, which can be matched to operators involving quarks at a scale \(\sim \) 2 GeV. We use the quark basis here, because it is more convenient for comparing to models. At 2 GeV, the operators areFootnote 4
where \(\theta _A\) is the misalignment angle between the vectors in operator space corresponding to \(\mu \rightarrow e\) conversion on Gold and Aluminium, and Appendix A briefly reviews these results.
The Branching Ratios (BRs) can be written as
where only the Spin Independent contribution to \(\mu A \rightarrow \! eA \) is included based on the results of [79] (we do not use the recent results of [82]), the \(B_A\) are target-nucleus dependent constants discussed in Appendix A, and \(d_A\equiv I_{A,D}/(4|\vec {u}_A|)\) are given after Eq. (A.16). In all cases, the outgoing electrons are approximated as chiral because they are relativistic. The final states containing electrons of different chirality therefore do not interfere, giving independent constraints on the coefficients generating those final states. The experimental limits on \(\mu \rightarrow e \gamma \) and \(\mu \rightarrow e {\bar{e}} e\) therefore constrain eight coefficients – the two dipoles and six four-lepton coefficients – to be in the vicinity of zero. The correlation matrix and resulting bounds are discussed in [83] and we repeat the bounds here for completeness:
where \(B_{process}\) is the experimental upper bound on the Branching Ratio for the process, and \(e^2(64\ln \frac{m_\mu }{m_e}- 136)\) is written as \( 205e^2\). Although the discussion of [83] implicitly supposed the coefficients were real, the same bounds apply for complex coefficients, because the real and imaginary components of the coefficients are constrained to lie inside the same ellipse around the origin.
The dipole coefficient is not constrained by \(\mu A \rightarrow e A\) because it contributes in interference, but the bound on \(|C_{Al,X}|^2 \) (and in principle \(|C_{Au\perp ,X}|^2 \)) is affected in the expected way by the independent bounds on the dipole:
In this work, we do not consider future improvements in the experimental reach for \(\mu A \rightarrow \! eA \) on heavy targets, so the current MEG bound on the dipole coefficient ensures that it is negligible in \(\mu Au \rightarrow e Au\). The current bound on Gold therefore implies
where \(\theta _A\) is the misalignement angle between the vectors in operator space corresponding to \(\mu \rightarrow e\) conversion on Gold and Aluminium and given after Eq. (A.15).
The current bounds on the twelve observable coefficients are given in Table 2, as well as the bounds that could be set, if upcoming experiments do not observe \(\mu \rightarrow e\) processes. The \(\mu A \rightarrow \! eA \) bounds given here differ from our previous paper [50] because \(\mathcal{O}_{Au\perp ,X}\) is here defined in terms of operators with quarks, so differs from the nucleon definition of [50]. The matching of quarks with nucleons is discussed in Appendix A.
In this theoretical study, we optimistically consider that these twelve coefficients can be measured with the same reach that they can be constrained, given in Table 2. Polarising the muon could allow to distinguish between coefficients of operators with an L vs an R projector in the \({\bar{e}}-\mu \) bilinear in \(\mu \rightarrow e \gamma \) and \(\mu \rightarrow e {\bar{e}} e\) [2] as well as in \(\mu A \rightarrow \! eA \) [84, 85]. And in the case of \(\mu \rightarrow e {\bar{e}} e\), the angular distributions of the three-particle final state allow to determine the magnitude of various coefficients and some phases, as discussed in [86,87,88]. Vector operators \(\mathcal{O}_{VXX}\) and scalar operators \(\mathcal{O}_{SYY}\) (for \(Y \ne X\)) induce the same angular distributions, but could in principle be distinguished by measuring final state helicities [86,87,88]. Our models do not generate the scalar operators within the reach of upcoming experiments (see Sect. 5.3).
2.2 Bottom-up EFT
For an introduction to EFT, see for instance [89,90,91,92,93,94,95,96]. Our EFT consists of an operator basis and Renormalisation Group Equations (RGEs) to look after scale evolution. The previous section presented an operator basis describing the observables at low energy; a more complete set of operators is required in translating the observables from the experimental to the New Physics scale, because the RGEs mix operators.
Our New Physics scale is at \(\Lambda _{NP}\approx \) TeV, so we need a QED\(\times \)QCD invariant basis of operators below the weak scale, included in the Lagrangian as
where \(v = 174\) GeV, the superscript \(\zeta \) gives the flavour indices, and the operator subscripts indicate the Lorentz structure and particle content. So for instance
We write the SM Yukawa matrices as \([Y_e], [Y_u]\) and \( [Y_d]\), and the Yukawa eigenvalue of fermion f as \(y_f\).
As discussed in Appendix C1, we did not find a simple and reliable recipe to express the coefficients of the Lagrangian (2.13) in terms of model parameters, because a TeV is not so far from the weak scale. The SMEFT operator basis [97, 98] and RGEs [99, 100] are appropriate above the weak scale, but the EFT expansions (in operator dimension and loop\(\times \)logarithm) are not converging fast. So it is a poor approximation to match to dimension six SMEFT operators, run to the weak scale at one loop, then match to the Lagrangian (2.13). In principle, we could match the model directly to the Lagragian (2.13), but that requires to explicitly calculate all the loop diagrams between the TeV and the weak scale. Finally, we opt to present the matching results in the basis of Eq. (2.13), but at the TeV-scale (such that the RGEs include the QED and QCD loops). So we will not be using the SMEFT basis, but for comparing to the literature, we implement it as
where \([m_\nu ]^{\alpha \beta } = C_5^{\alpha \beta }v \).
The low energy EFT includes all LFV operators of dimension six, and some relevant operators of dimension seven (see [80] for a list). In this low-energy EFT, we ensure that operators appear only once by requiring \(\zeta = e \mu \ldots \). Operators of dimension five and six (\(n= 1,2\)) are included in SMEFT, but without the \(+h.c.\) for hermitian operators. In SMEFT, we follow the convention that each flavour index in \(\zeta \) runs over all three generations (so some operators are repeated in the SMEFT Lagrangian, causing some factor of 2 or 4 differences between coefficients in SMEFT vs the low-energy EFT).
The doublet and singlet leptons are in the charged lepton mass eigenstates \(\{e,\mu ,\tau \}\) [59], which can differ from the diagonal-Yukawa basis as discussed in Appendix C2. The singlet quarks are labelled by their flavour, and the quark doublets are in the u-type mass basis, with generation indices that run \(1\rightarrow 3\).
In quantum field theories, the coefficients of renormalizable and non-renormalizable operators evolve with scale. For non-renormalisable operators, this evolution of the operator coefficients lined up in a row vector \(\vec {C}\) can be described as
where \(t =\ln \mu \), the effects of renormalisable interactions on the non-renormalisable operators are described by the matrix \([\Gamma ]\), and \([\vec {X}]\) is a three-index tensor that schematically represents the effect of non-renormalisable interactions on the evolution of other non-renormalisable interactions (for instance, the mixing of a pair of four-fermion operators into another four-fermion operator via a fish diagram).
The RGEs we implement automatically for the QED\(\times \) QCD-invariant EFT are an improved leading log approximation to \([\Gamma ]\) [101], where most of the anomalous dimension are at one-loop, augmented by the two-loop vector to dipole mixing (because this mixing vanishes at one loop and is \(\mathcal{O} (10^{-3})\) [102]). We also consider the mixing of two dimension six operators into a dimension eight operator described by \([\vec {X}]\), and when relevant, include these contributions by hand in matching the model to EFT at \(\Lambda _{NP}\). Since the dimension eight operators have two additional Higgs legs, they are particularly relevant when the Higgs has \(\mathcal{O} (1)\) couplings to loop particles, such as the top quark in the leptoquark model. These dimension eight contributions are discussed more fully in Sect. 5.3 and Appendix C.
Solving the RGEs allows to translate operator coefficients from the experimental scale to the New Physics scale – where the coefficients can be calculated in a model. We aim to resum the QCD running, and include the electroweak effects in perturbation theory (\(\mathcal{O}(\alpha \ln )\) and occasionally \(\mathcal{O}(\alpha ^2 \ln ^2)\)). If the matrix \([\Gamma ]\) were scale-independent, then the solution would be \(\sim \exp \Gamma t\); however, \([\Gamma ]\) describes SM loop corrections, and SM parameters run in various ways with scale. For \([\Gamma ]\) scale-dependent, the RGEs can be solved by scale-ordering, analogous to the familiar time-ordering that allows to solve a similar equation for the time-translation operator in quantum field theory. We include the scale-dependence of \(\alpha _s\) (at one loop), and the associated running of quark Yukawas, but neglect the running due to other SM couplings (including the top Yukawa). So the effect of QCD is to renormalise some coefficients and rescale some electroweak anomalous dimensions, such that the first terms in the perturbative solution of the RGE (2.15) are
where \({\widetilde{\Gamma }}_{KJ} = f_{KJ} \Gamma _{KJ} (m)\) [103, 104] with \(\Gamma \) the electroweak anomalous dimension matrix, no sum on J, K and:
where \(a_{J} = -\gamma ^s_{J}/2\beta _0\) for \(\alpha _s\gamma ^s_{J}/4\pi \) the QCD anomalous dimension of the coefficients \(C_{J}\) (\(a_T=-4/23\), \(a_S= a_D = 12/23\) with 5 flavours), \(\beta _0\) is the 1-loop QCD beta function coefficient, and the parameters in the electroweak anomalous dimension cause it to run as \(\Gamma _{KJ}(m) = \eta ^{a_I} \Gamma _{KJ}(\Lambda )\). Finally, once the RGEs have been solved, a coefficient at the experimental scale (for instance \(C_{D,X} (m_\mu )\)), can be written at \(\Lambda _{NP}\) as a weighted sum of the coefficients of operators that can contribute via loops to \(\mu \rightarrow e \gamma \).
It can be shown [80] that almost every operator involving 3 or 4 legs that induces a \(\mu \rightarrow e\) interaction (but no other flavour change) contributes to the amplitude for \(\mu \rightarrow e \gamma \), \(\mu \rightarrow e {\bar{e}} e\) and/or \(\mu A \rightarrow \! eA \) suppressed at most by a factor of order \(10^{-3}\). This suggests that the RGEs are relevant to include, because they ensure that a small handful of processes are sensitive to almost any \(\mu \rightarrow e\) operator. Despite that almost all operators can contribute, there remain only 12 constraints. Rather than dealing with a large correlation matrix corresponding to the usual operator basis, we use a scale-dependent basis that corresponds to the twelve experimentally probed directions. This was proposed in [80], and the recipe we follow is outlined in [81].
The RGEs can be solved to express an operator coefficient at the experimental scale, e.g. the dipole coefficient, in terms of operator coefficients at the NP scale:
The directions in coefficient space corresponding to the twelve vectors \(\{e_O\}\) then form a basis for the observable subspace at \(\Lambda _{NP}\). The elements of most of these vectors at or just above the electroweak scale are given in [80] (the coefficient combinations probed by \((\mu Al \rightarrow e Al)\) and \((\mu Au \rightarrow e Au)\) are given for completeness in Appendix B).
3 The models
The three TeV-scale New Physics models that we consider are the type II and inverse seesaw models, and a scalar leptoquark. These models are selected for their diverseFootnote 5 lepton-flavour-changing predictions: LFV is controlled by the neutrino mass matrix in the type II seesaw, is independent of the neutrino mass matrix in the inverse seesaw, and the leptoquark can mediate \(\mu A \rightarrow \! eA \) at tree level, as well as addressing anomalies in the quark flavour sector.
The type II seesaw model [19,20,21,22] is an economical neutrino mass model, where the SM particle content is extended with a colour-singlet, SU(2) triplet scalar \(\Delta \), of hypercharge \(Y=+1\) (in the normalization where the lepton doublets have \(Y=-1/2\)). The SM Lagrangian at the mass scale of the triplet is augmented by
where \(\ell \) are the left-handed SU(2) doublets, \(M_\Delta \) is the triplet mass which we take \(\sim \) TeV, f is a symmetric complex \(3\times 3\) matrix proportional to the light neutrino mass matrix and whose indices \( \alpha ,\beta \) run over \(\{e,\mu ,\tau \}\), \(\{\tau _I\}\) are the Pauli matrices, and the \(\lambda \)’s are real dimensionless couplings. A feature of this model, that is shared with some other neutrino mass models, is that the SU(2) singlet leptons do not acquire new interactions, so LFV is expected to involve the doublet leptons. The phenomenology of the type II seesaw has been widely studied at colliders [106,107,108,109,110,111] and for low-energy LFV [23,24,25,26,27,28, 112,113,114].
In Effective Field Theory, the neutrino mass matrix generated in the type II seesaw model can be obtained by matching, at \(M_\Delta \), the tree-level diagram in the left panel of Fig. 5 onto the dimension five neutrino mass operator appearing in Eq. (2.14). This gives a neutrino mass matrix
which can also be obtained in the model by minimising the potential for the Higgs and the electrically neutral component of the triplet = \((\Delta ^1 + i\Delta ^2)/\sqrt{2}\,\), which obtains a vev \( -\lambda _H v^2/(\sqrt{2}M_\Delta )\). This model is reputed to be predictive for LFV, because the lepton flavour-changing couplings \(f^{\alpha \beta }\) are proportional to the light neutrino mass matrix. However, LFV is not suppressed by the small neutrino mass scale, because lepton number change involves \([f]^{\alpha \beta *} \lambda _H\), so for a sufficiently small Higgs to triplet coupling, \(\lambda _H \sim 10^{-12}\), it is possible to have \(M_\Delta \sim \) TeV and \(f^{\alpha \beta }\) of \(\mathcal{O}(1)\).
The second model we consider is the inverse (type I) seesaw [29,30,31], which, like the type II seesaw, naturally generates small Majorana neutrino masses from new particles that can be at the TeV-scale with \(\mathcal{O}(1)\) LFV couplings. In this model, n gauge singlet Dirac fermions, \(\Psi _a^T = (S_a, N_a)\), are added to the SM particle content, with approximately lepton number conserving interactions. Lepton number changing interactions can be included via Yukawa couplings and/or Majorana masses(see [115] for a “basis-independent” discussion of the options); we choose to allow small Majorana masses for \(S_a\) and write the Lagrangian as

where a, b run from 1..n, \(N_a\) and \(S_a\) are respectively right- and left-handed and in the eigenbases of M, \(Y_\nu \) is a complex \(3\times n\) dimensionless matrix, we take \(M_a\) of \(\mathcal{O}\)(TeV), and \(\mu \) is an \(n\times n\) Majorana mass matrix with \(\mu _{ab}\ll M_c\). For vanishing \(\mu \), lepton number is conserved, and the \(N_a\) combine with the \(S_a\) into Dirac singlet neutrinos, which can have lepton flavour changing interactions \(Y_\nu \) with the SM doublets. Like the type II seesaw, this model is expected to induce LFV among doublet leptons, but unlike the type II seesaw, it has several non-degenerate heavy new particles, and will induce low energy LFV processes via loop diagrams because the flavour-changing \(Y_\nu \) couples \(\ell \) to two heavy particles.
The inverse seesaw models induce LFV [32,33,34,35,36,37,38,39, 116], they can lead to non-unitarity of the lepton mixing matrix [117,118,119,120], and the singlets could be discovered at colliders for suitable mass ranges [121,122,123,124,125,126,127]. With small \(\mu _{ab}\), the leading contribution to the active neutrino mass matrix is
So the flavour-changing \(Y_\nu \) can be \(\mathcal{O}\)(1) because small \(\mu _{ab}\) gives small \(m_\nu \), and the flavour change is expected to be independent of the active neutrino mass matrix as can be seen for n = 3 by solving Eq. (3.4) for \(\mu _{ab}\).
Finally, our third model includes a leptoquark – for a review of this class of coloured and charged bosons, see e.g. [41] – which is chosen to fit the anomalies in \(R_{D^*}\) and/or \(R_D\) [53,54,55,56,57]. It is an SU(2)-singlet scalar denoted \(S_1\) in the notation of [40] – not to be confused with the singlet fermions \(\{S_a\}\) of Eq. (3.3) – and has interactions
where the generation indices are \(\alpha \in \{ e,\mu ,\tau \}\) and \(j\in \{u,c,t\}\), and the sign of the doublet contraction is taken to give \(+ \lambda ^{\alpha j}_L \overline{e_L} (u_L)^c S_1\). The leptoquark mass is \(m_{LQ} \approx \) TeV, consistent with the CMS and ATLAS searches [128,129,130,131,132] which exclude leptoquarks with sub-TeV masses that are pair-produced via strong interactions, and decay to specific final states. Some leptoquark-Higgs interactions are included in Eq. (3.5) because they appear in the matching results of Appendix C3c, but their contributions to LFV observables are negligible assuming perturbative couplings. This Lagrangian does not lead to neutrino masses (as mentioned in Appendix C3c), but features \(\mu A \rightarrow \! eA \) at tree level and LFV interactions for singlet and doublet leptons (so unlike the seesaw models, it induces scalar and tensor operators).
The low-energy phenomenology of leptoquarks (see e.g. [42,43,44,45,46,47,48,49]) attracted attention in recent years due to various B-physics anomalies. In particular, the excesses in the ratios [53,54,55,56,57]
where \(X_c = D, D^*\ldots \), could indicate a new charged-current four-fermion interaction involving b and c quarks, a \(\tau \) and a (tau) neutrino. The \(S_1\) leptoquark can generate this interaction with various Lorentz structures, while preserving lepton flavour (if \(S_1\) only interacts with \(\tau \)’s and \(\nu _\tau \)’s, one could attribute \(\tau \) flavour to the leptoquark.) So fitting \(R_D\) and/or \(R_{D^*}\) involves leptoquark coupling constants that differ from the \(\lambda _X^{e q}\), \(\lambda _X^{\mu q}\) that are relevant for \(\mu \rightarrow e\) processes, and in this manuscript, we neglect the \(\lambda _X^{\tau q}\) couplings and possible correlations among \(\mu \rightarrow e\) and \(\tau \rightarrow l\) processes that could arise in this model.Footnote 6 The LFV predictions of the \(S_1\) leptoquark have been discussed, for instance, in [133, 134].
4 The observables coefficients in terms of model parameters
In this section, we give the coefficients of the observable Lagrangian (2.3) as a function of model and SM parameters. Some of these results were already presented in [50]. The coefficients are expressed in terms of \(\mu \rightarrow e\) flavour-changing combinations of model and SM parameters, which we refer to as “invariants”. These are a convenient stepping-stone between the models and the observables, because they concisely identify the masses and couplings constants that the observables depend on, and give the functional dependance. We briefly discuss the invariants in Sect. 4.1 and list the coefficients in Sect. 4.2.
4.1 Comments on invariants
Invariants were introduced [51, 135] as products of Lagrangian coupling constants (or matrices), in order to have a Lagrangian-basis-independent measure of symmetry breaking in a model. However, it may be unclear how these elegant constructions relate to observable S-matrix elements for symmetry-violating processes, because the mass and scale-dependence of S-matrix elements can be intricate.
For instance, the original invariant constructed to measure CP violation in the quark sector of the Standard Model can be written in terms of Lagrangian Yukawa matrices as [51, 135, 136]
but it is unclear at what scale to evaluate the quark masses (or equivalently, Yukawa couplings). This invariant can be compared to the parameter \(\epsilon _K\) (see e.g. [91] for a brief review) that contributes to CP-violation in \(K-{\bar{K}}\) mixing, and for which the result at next-to or next-to-next-to leading log has been expressed in a rephasing invariant form in [137]. Restricting to the leading log QCD corrections for simplicity, one can write
where \( x_Q = m_Q(m_Q)/m_W\), the Inami-Lim functions [138] are
and \(\eta ^{pq}\) are the appropriate QCD corrections for the Inami-Lim functions (see [137]). So one sees that there is only a remote relation between the Lagrangian invariant of Eq. (4.1), and Eq. (4.2), which allows a numerically precise prediction for the observable \(\epsilon _K\),
In the models considered here, we obtain expressions for the observable coefficients at \(m_\mu \) (which are \(\approx \) S-matrix elements) in terms of “invariants”, which are flavour-changing combinations of Lagrangian parameters at specified scales, and encode the dependence of LFV observables on running SM and model coupling constants and masses. In practice, these combination are frequently products of matrices in flavour space, which are manifestly invariant under flavour-basis transformations, hence we refer to them as “invariants”. For instance, in the type II seesaw model, photon penguin diagrams (contributing to \(\mu \rightarrow e {\bar{e}} e\)) generate the coefficient \(C_{V,LR}^{e\mu ee}\) proportional to the invariant:
where \([\tilde{m}_e]\) is the charged lepton mass matrix, but with its eigenvalues replaced by \(m_\alpha \rightarrow \tilde{m }_\alpha = \max \{m_\alpha ,q^2\}\), which is the kinematic cutoff of the logarithm, with  the (four-momentum)\(^2\) of the photon. (So the cutoff of the \(\tau \) loop is \(m_\tau \), but \(\tilde{m}_e \approx m_\mu \) so the last term in the parentheses of Eq. (4.3) vanishes, or equivalently there is no long-distance contribution to the matrix element, because \(q^2 \sim m_\mu ^2\) in most of the phase space [139].) Equation (4.3) exemplifies our relatively simple invariants, constructed by multiplying matrices, which encode the correct scale evolution of coupling constants and masses, provided that the scale separations are large enough for EFT to be reliable.Footnote 7
the (four-momentum)\(^2\) of the photon. (So the cutoff of the \(\tau \) loop is \(m_\tau \), but \(\tilde{m}_e \approx m_\mu \) so the last term in the parentheses of Eq. (4.3) vanishes, or equivalently there is no long-distance contribution to the matrix element, because \(q^2 \sim m_\mu ^2\) in most of the phase space [139].) Equation (4.3) exemplifies our relatively simple invariants, constructed by multiplying matrices, which encode the correct scale evolution of coupling constants and masses, provided that the scale separations are large enough for EFT to be reliable.Footnote 7
However, our simple invariants apply only for models with a single mass scale for LFV; for models with many heavy LFV particles around the scale \(\Lambda _{NP}\), such as the inverse seesaw, the operator coefficients obtained in matching are not linear products of matrices in flavour space (see e.g. Eqs. 4.10, 4.12). Constructions that involve Inami-Lim functions of mass matrix eigenvalues are no doubt also “invariant” under Lagrangian basis transformations, but like Eq. (4.2), this invariance is not manifest.
Our invariants have other attractive features, beyond the correct scale-dependence to parametrise S-matrix elements. As expected they measure \(\mu \rightarrow e\) flavour change in the model, and they also identify the products of model parameters relevant to observables. This second feature allows to circumvent the necessity of scanning over model parameters. For instance, in the inverse seesaw model, \([Y_\nu ]\) is a 3\(\times \)3 matrix of unknown complex numbers, so naively one must scan over them all, and possibly impose some texture. However, in the case of degenerate singlets, there are only two invariants – \([Y_\nu Y_\nu ^\dagger ]_{e\mu }\) and \([Y_\nu Y_\nu ^\dagger Y_\nu Y_\nu ^\dagger ]_{e\mu }\) – which are complex numbers of magnitude 0\(\rightarrow \)1. This raises the question whether one could reconstruct the model Lagrangian from a sufficient number of invariants?
Finally, the invariant of Eq. (4.3) illustrates an interesting dynamical mechanism to break properties of the model. Recall that \( [m_\nu m_\nu ^\dagger ]^{e \mu }\) is a function only of neutrino oscillation parameters – which are measured – so the second term of the second expression exhibits the log-induced dependence on the unknown Majorana phases and neutrino mass scale. This logarithmic breaking of a relation between model-matrices is reminiscent of the “log-GIM” mechanism in the quark sector [140], where \(\Delta F = 1\) FCNC operators can be mediated by similar penguin diagrams at \(\mathcal{O}(G_F \alpha _e\ln m_W/m_c)\), with a charm quark in the loop.Footnote 8
4.2 Predictions at the experimental scale
This section lists the model predictions for the observable coefficients of the Lagrangian (2.3), partially presented in Ref. [50]. The model parameters are given in the Lagrangians of Sect. 3. The expressions given here occasionally differ from [50], because we made numerically insignificant modifications of the lower cutoff of some logarithms, in order to obtain more elegant invariants with the physically correct cutoffs.
4.3 \(\mu \rightarrow e \gamma \)
In the inverse seesaw model, the dipole coefficients are
where the parentheses include the flavour-universal \(\mathcal{O}(10\%)\) QED running, and M is the singlet mass scale. The couplings \(Y^{\alpha a}_\nu \) can be of order one – which could be especially motivated in the \(\tau \) sector – so \(\mathcal{O}(Y^4)\) combinations can be larger than \(\mathcal{O}(Y^2)\), and could appear at dimension eight when two additional Higgs legs on the sterile neutrino line are replaced by the Higgs vev, or at two-loop when the Higgs legs are closed. We estimate the \({\mathcal {O}}(Y^4)\) terms to be suppressed with respect to the coefficient in Eq. (4.4) by \(\sim v^2/M^2\) or \(\sim 1/(16\pi ^2)\), and we therefore expect them to not modify significantly the correlations between the \(\mu \rightarrow e\) observables that the model can predict [50].
For the type II seesaw,
where the second term in the bracket in Eq. (4.5) arises from the two-loop vector to dipole mixing [102]. In both seesaw models, the coefficient \(C^{e\mu }_{D,L}\) is suppressed by a factor \(m_e/m_\mu \), and can be obtained from Eqs. (4.6, 4.4) by multiplying by \(m_e/m_\mu \).
For the leptoquark, which interacts with singlet and doublet leptons, the dipole coefficients are
where \(X\ne Y\in \{L,R\}\), \(f_{TD}\), \(a_T\) and \(\eta \) are related to the QCD running and defined at Eq. (2.17), and the \(\tilde{m}_Q\) serving as lower cutoff for the logarithms (here and further in the manuscript) is
because the quarks are matched to nucleons at 2 GeV. The first term in Eq. (4.7) is the matching contribution (times its QED running),the second term is the 2-loop mixing of tree vector operators into the dipole, and the third term is the one loop mixing of tensor operators to dipoles.
The last term of Eq. (4.7) requires some discussion, because the first log-enhanced term in the parentheses arises in the RGEs between \(m_{LQ}\rightarrow m_\mu \), but the second “finite”, or not-log-enhanced term is formally of higher order in EFT. It is included because it is of comparable magnitude to the log-enhanced term in the case of internal top quarks – that is, as discussed in Appendix C1, the scale ratio \(m_{LQ}/m_t\) is not large, so our matching conditions at \(\Lambda _{NP}\) are constructed to reproduce the results of matching to a QCD\(\times \)QED invariant EFT at \(m_W\). And finally, although the finite part is only required for the top quark, a quark-flavour-summed expression is given in order to retain the “invariant” formulation. (The light quark contributions are numerically negligible in this expression, which is fortunate because their QCD running is also not correct.)
We do not consider dimension 8 contributions to the dipole, because they are suppressed \(\propto v^2/M^2\), and do not allow to circumvent the parametric suppression of the dimension six term. For instance, in the inverse seesaw, such terms also have the loop and \(y_\mu \) suppression applying to (4.4).
4.3.1 \(\mu \rightarrow e {\bar{e}} e\)
The decay \(\mu \rightarrow e {\bar{e}} e\) can be mediated at the experimental scale by the dipole operators, and vector and scalar four-lepton operators (see Eq. (2.8). We do not give results for the scalar coefficients, because they are effectively vanishing: in matching, all three models induce coefficients that are smaller than the upcoming experimental sensitivity, and SM interactions that could transform some other LFV operator into a scalar are suppressed by lepton Yukawas, so negligible as well. Unfortunately, scalar coefficients \(C_{S,XX}\) are indistinguishable from vectors \(C_{V,YY}\) in the angular distribution of \(\mu \rightarrow e {\bar{e}} e\), so the absence of scalar coefficients in these models would be challenging to test.
For the type II seesaw, the vector four-lepton coefficients arise at tree level, as illustrated in the middle diagram of Fig. 5, and in the RGEs via QED penguin diagrams:
where \(\alpha \) is the index of the intermediate charged lepton. The operators \(\mathcal{O}^{e\mu ff }_{V,RR}\) and \(\mathcal{O}^{e\mu ff }_{V,RL}\), where the flavour-change is among singlet leptons, have coefficients below upcoming experimental sensitivities because they are suppressed \(\propto y_e y_\mu \). This is also the case for the inverse seesaw.
In the case of the inverse seesaw, both vector operators arise via loop diagrams, with propagating singlets and Higgses:
where the first expression for a coefficient is for arbitrary singlet masses  TeV, and after the arrow is the simplified formula when the singlets mass\(^2\) differences are less than \(v^2\) [50]. In the first expression, the first two terms arise from Z and \(\gamma \) penguins above the electroweak scale (the Higgs propagates in the loop), and the last one is from boxes.
TeV, and after the arrow is the simplified formula when the singlets mass\(^2\) differences are less than \(v^2\) [50]. In the first expression, the first two terms arise from Z and \(\gamma \) penguins above the electroweak scale (the Higgs propagates in the loop), and the last one is from boxes.
Finally the leptoquark can generate flavour-changing lepton currents involving either singlet or doublet leptons. We give here the coefficient for left-handed leptons; the result for singlets is obtained by interchanging \(L\leftrightarrow R\):
where \(g^e_L= -1+2\sin ^2\theta _W\), \(g^e_R=2\sin ^2\theta _W\), the first term represents the box diagram at \(m_{LQ}\) (and its QED running to \(m_\mu \), with −/\(+\) for \(X=\)/\(\ne L\)), the second term is the log-enhanced photon penguin that mixes the tree operators \(\mathcal{O}_{VLL}^{QQ}\) (for \(Q\in \{u,c,t\}\)) into 4-lepton operators, and the last term is the contribution of the Z-penguins without the negligible QED running. Since we only retain the part of the Z-penguin that is proportional to \(y_Q^2\)(see Appendix C4), the dominant contribution arises from the top quark, where the “finite” (not log-enhanced) part of the diagrams is included because the logarithm is not large (see the discussion after Eq. (4.7) or in Appendix C1).
4.3.2 \(\mu \textrm{Al}\rightarrow e \textrm{Al}\)
The SINDRUMII experiment searched for \(\mu A \rightarrow \! eA \) on Titanium (\(Z = 22\)) and Gold (\(Z= 79\)), setting the bounds listed in Table 1. Upcoming experiments will start with an Aluminium target, which probes a similar combination of coefficients as Titanium according to the analysis of [79]. So this section gives expressions for the coefficient on Aluminium \(C_{Al,X}\), expressed in the quark operator basis, where the conversion ratio on Aluminium is given in Eq. (A.16).
The photon penguin diagrams in the type II seesaw model generate a vector \(\mu \rightarrow e\) operator on u and d quarks, giving
where \(\tilde{m}_\tau = m_\tau \) and \(\tilde{m}_\alpha = m_\mu \) for \(\alpha \in \{e,\mu \}\) because the logarithm is cut off by the momentum transfer from the leptons to the nucleus [143], which is of order \(m_\mu \). Notice that the penguin diagram of Fig. 5 generates a 2-lepton-2-quark operator at scales above 2 GeV, where quarks are matched to nucleons, then it continues to mix into a 2-lepton-2-proton operator, which is why the logarithm cuts off at \(m_\mu \).
The inverse seesaw generates vector operators, via Z and \(\gamma \) penguins above the weak scale:
For the leptoquark, which induces scalar and vector 2l2q operators, we obtain
where are included the tree vector coefficient on u quarks with its QED running, the electroweak box contribution to the d vector, the QED then Z penguin contributions to the u and d vectors (where we took \(V_{ud} \simeq 1, \sin ^2 \theta _W \simeq 1/4\)), and the scalar u, c and t contributions (where the QCD running of the top contribution is negligible). As in Eq. (4.14), the Z-penguin contribution only includes the diagrams \(\propto y_Q^2\), with their “finite parts”.
4.3.3 \(\mu A \rightarrow \! eA \) on heavy targets
Changing the target in \(\mu A \rightarrow \! eA \) allows to probe a different combination of operator coefficients [79]. This is discussed quantitatively in Appendix A, where Eqs. (A.12, A.13, A.14) give the operators probed by light and heavy targets in the quark basis. The SINDRUM experiment searched for \( \mu A \rightarrow \! eA \) on Gold (see Table 1), and there are plans based on the proposal of Ref. [71, 73] to build experiments that could probe \(\mu A \rightarrow \! eA \) on heavy targets (see Table 1). However, we consider these experiments to be too far in the future for the purposes of our study, so we suppose that the data for Gold remains the bound of SINDRUM given in Table 1. The operator probed by Gold can be decomposed into the operator probed by light targets, plus the remaining part, approximately given in Eq. (2.6). In this section, we discuss the coefficient of this orthogonal part, which can be written as
The type II seesaw only generated a vector operator on protons, (no scalar operators, and no vector operator on neutrons), so once the coefficient is measured on a first target, it can be predicted on any other. That is, Gold probes approximately the same four-fermion operator as light targets, and since the dipole and proton vector coefficients are weighted by approximately 1/4 and 1/2 in both the amplitudes on Gold and Aluminium, the ratio of the rates is
where \({\widetilde{B}}_{Al}\) and \({\widetilde{B}}_{Au}\) are given after Eq. (A.5).
In the inverse seesaw, \(\mu A \rightarrow \! eA \) on heavy targets could give complementary information, because the Z penguin contribution generates vector \(\mu \rightarrow e\) operators on both protons and neutrons:
The coefficient is nonetheless a combination of the same invariants that feature in the other \(\mu \rightarrow e\) operators, and so can be predicted with a combination of \(\mu \rightarrow e\) observations. For instance, in the nearly degenerate limit, it can be written as a linear combination of the light targets coefficient and the dipole.
In the leptoquark model, we neglect the scalar coefficients on d, s and b quarks, because the model does not generate scalar operators with down-type quarks at tree level, and the estimates of Appendix C3c suggest that the loop-induced coefficients are below experimental sensitivity. So we obtain
where the terms, in order, are the scalar up and charm quark contribution with their QED and QCD running, the tree vector up quark contribution with its QED running, the leptoquark-W box matching onto the vector operator for down quarks (neglecting the QED running), then the QED penguin contribution to the vector coefficients for u and d quarks, and finally the Z penguin contributions to both u and d vector coefficients.
In this leptoquark model, different operators contribute to the \(\mu \rightarrow e\) conversion rates on Gold and Aluminum, so \({C}_{Au\perp ,X} \) is independent from \(C_{Al,X} \), implying that \(C_{Au\perp ,X} \) could be just below the current SINDRUMII bound (see Table 2) even if \(\mu \rightarrow e\) flavour change is not observed in upcoming experiments. Furthermore, we anticipate that this will remain true, even if the definition of \( \mathcal{O}_{Au\perp } \) changes as theoretical calculations are updated (the definition of the \( \mathcal{O}_{A} \)s in References [79, 82] appears different.). The point is that cancellations can occur, for instance among vector and scalar coefficients in the coefficient on Aluminium, allowing the coefficient on Gold to be relatively large.
5 Phenomenology
The type II seesaw model is reputed to be predictive, because the lepton flavour-changing couplings of the scalar boson \(\Delta \) are proportional to the observed neutrino mass matrix. However, we observed in [50] that knowing the neutrino oscillation parameters does not predict the observable \(\mu \rightarrow e\) coefficients. So Sects. 5.1 and 5.2 explore the connections between \(\mu \rightarrow e\) processes and other lepton flavour- and number-changing observables in the type II seesaw. The remaining two subsections respectively discuss how \(\mu \rightarrow e \gamma \) constraints suppress dimension eight operators in the leptoquark model (Sect. 5.3), and the impact of allowing operator coefficients to be complex (Sect. 5.4).
5.1 The neutrino mass scale in the type II seesaw
In this section, we explore how the predictions of the type II seesaw model for \(\mu \rightarrow e\) observables are influenced by the lightest neutrino mass scale, denoted as \(m_{\textrm{min}}.\)
The lightest neutrino mass plays a crucial role in determining the relevant coefficients in the model, namely \(C^{e\mu }_{D,R}\), \(C^{e\mu ee}_{V,LL}\), and \(C^{e\mu ee}_{V,LR}\propto C_{Al,L},\ C_{Au\perp ,L}\). The tau mass cut-off in the two-loop vector mixing and one-loop photon penguin introduces a term \(\propto [m^*_\nu ]_{\mu \tau } [m_\nu ]_{e\tau }\) (see Eqs. 4.5 and 4.9) that gives rise to the dipole and \(C^{e\mu ee}_{V,LR}\) dependence on the unknown neutrino parameters. Additionally, the \(\mu \rightarrow 3e_L\) vector depends on \(m_{\textrm{min}}\) from both the tree-level \(\propto [m_{\nu }]_{ee}[m^*_{\nu }]_{\mu e}\) and the photon penguin contributions.
The magnitude of these unknown terms increases with the lightest neutrino mass, making them more relevant when \(m_{\textrm{min}}\) is large. For example, if we allow \(m_{\textrm{min}}\sim 0.2\) eV, the two-loop vector-to-dipole mixing can reach the size of the one-loop matching contribution to the dipole, and certain choices of Majorana phases could allow for a cancellation that suppresses the dipole coefficient. Although this has not been pointed out in the literature before (the dipole cannot vanish in the type II seesaw at the leading order), the cancellation requires a high neutrino mass scale \(m_{\textrm{min}}\). Values \(m_{\textrm{min}}\sim 0.2\) eV are compatible with the laboratory constraint extracted from the tritium decay end-point, which yields \(\sqrt{\sum _i m^2_i |U_{ei}|^2}< 0.8\) eV (\(90\%\) CL) [144], but are disfavored by the cosmological bounds on the neutrino masses sum \(\sum m_i\). Assuming \(\Lambda \)CDM, CMB data constrain the sum to be \(\sum m_i<0.26\) eV (\(95\%\) CL), while combined with the BAO measurements the constraint is stricter \(\sum m_i<0.12\) eV (\(95\%\) CL) [145].
\(\frac{|C^{e\mu ee}_{V,LR}|}{|C^{e\mu }_{D,R}|}\) and \(\frac{|C^{e\mu ee}_{V,LL}|}{|C^{e\mu }_{D,R}|}\) as functions of \(m_{\textrm{min}}\) for normal and inverted ordering in blue and red respectively, for all possible values of the Majorana phases. We consider only the one-loop matching contribution to the dipole since for \(m_{\textrm{min}}\lesssim 0.2\) eV the two-loop vector to dipole mixing is negligible. The shaded blue region corresponds to the values of \(m_{\textrm{min}}\) above the cosmology preferred upper bound \(m_{\textrm{min}}\lesssim 0.04\) eV
By imposing the cosmological upper bound \(m_{\textrm{min}}\lesssim 0.04\) eV, the \(\mu \rightarrow e\) coefficients are also constrained. In this case, the dipole is approximately unaffected by the two-loop contribution and is completely determined from the neutrino oscillation parameters, apart from the overall LFV scale. When the dipole coefficient is non-vanishing, the ratios
are finite for any value of the Majorana phases. Figure 1a, b illustrate that by imposing the upper-bound \(m_\textrm{min}\lesssim 0.04\) eV and allowing the Majorana phases to vary freely, these ratios are bounded from above
The cosmological bound is generally insufficient to constrain the ratios from below, as there exist \(m_{\textrm{min}}\) values for both \(\mu \rightarrow 3e\) vectors such that the operator coefficient can vanish. If \(m_{\textrm{min}}\) is measured, for instance by observing the neutrinoless double beta decay, additional information can be obtained for the \(\mu \rightarrow e\) coefficients. The penguin cannot vanish for \(m_{\textrm{min}}\lesssim 0.02\) eV regardless of the ordering, while the \(\mu \rightarrow 3e_L\) vector is also non-vanishing for \(m_\textrm{min}\lesssim 10^{-3}\) eV:
Therefore, if the ratio of coefficients \(\frac{|C^{e\mu ee}_{V,LR}|}{|C^{e\mu }_{D,R}|}\) or \(\frac{|C^{e\mu ee}_{V,LL}|}{|C^{e\mu }_{D,R}|}\) were observed outside the ranges of Eq. (5.3), it would be possible to infer a lower bound on the neutrino mass scale (if it originates from the type II seesaw mechanism). Since these ranges are significantly narrower in the NO case, measuring the ordering (which is expected to be determined in the upcoming years) would be particularly useful to pinpoint the interplay between the lightest neutrino mass and the \(\mu \rightarrow e\) predictions in the type II seesaw. Furthermore, if the mass ordering is normal, future beta decay experiments might be able to constrain \(m_{\textrm{min}} \lesssim 0.02\, \text{ eV }\) (the Project 8 experiment [146] aims at a 90% C. L. sensitivity of \(40\, \text{ meV }\) on the effective neutrino mass in beta decay, which corresponds to \(m_{\textrm{min}} \simeq 0.04\, \text{ eV }\)). In this case, measuring the ratio of coefficients \(\frac{|C^{e\mu ee}_{V,LR}|}{|C^{e\mu }_{D,R}|}\) outside the range [8.5, 10] would exclude the type II seesaw model.
5.2 \(\tau \) LFV in the type II seesaw
In this section, we explore whether the type II seesaw model can be predictive, when one considers flavour-changing decays of muons and taus. In particular, we focus on observations of \(\tau \rightarrow 3 l \) decays, if one does not see \(\mu \rightarrow e\) decays. So in practise in this section, the Majorana phases are fixed to ensure that the tree contribution to \(\mu \rightarrow e {\bar{e}} e\) vanishes, and we study the \(\tau \rightarrow 3 l \) rates as a function of the neutrino mass scale.
There are four \(\Delta \)LF\(=\)1 \(\tau \rightarrow 3 l \) decays (\(\tau \rightarrow \mu {\bar{\mu }} \mu \), \( \rightarrow e{\bar{e}} e\), \( \rightarrow e {\bar{\mu }} \mu \) and \(\rightarrow e {\bar{e}} \mu \)) and two that are \(\Delta \)LF\(=\)2 (\( \rightarrow e{\bar{\mu }} e\), and \(\rightarrow \mu {\bar{e}} \mu \)), as given in [147]. They can all be mediated at tree level by \(\Delta \) exchange as illustrated in the middle diagram of Fig. 5. The branching ratios for the four \(\Delta \)LF\(=\)1 decays are analogous to Eq. (2.8)
where we restrict to a fixed chirality of the flavour-changing lepton bilinear, \(l,\tilde{l} \in \{e,\mu \}, l\ne \tilde{l}\) and the factor 0.18 accounts for the hadronic \(\tau \) decays: \(\Gamma (\tau \rightarrow e{\bar{\nu }} \nu )/\Gamma (\tau \rightarrow \textrm{all}) \simeq 0.18\). The final pair of branching ratios (Eq. 5.6) are \(\Delta \)LF\(=\)2; we assume such coefficients run with QED like other four-lepton vector operators. The current experimental constraints (see Table 1) are of order

Ratios BR(\(\tau \rightarrow 3l\))/BR(\(\mu \rightarrow e {\bar{e}} e\)) in the type II seesaw model as a function of \(m_1\) in inverted ordering (so \(m_1 \ge \sqrt{\Delta ^2_{atm}}\)) for vanishing \([m_\nu ]_{e \mu }\). This illustrates that Belle II could observe specific \(\tau \rightarrow 3l\) decays, even if \(\mu \rightarrow e {\bar{e}} e\) and \(\mu \rightarrow e \gamma \) are not observed at upcoming experiments because the tree contribution to \(\mu \rightarrow e {\bar{e}} e\) vanishes with \([m_\nu ]_{e \mu }\). Some \(\tau \rightarrow 3l\) processes (in black) also vanish at tree level, and we include \(\tau \rightarrow e \gamma \) and \(\tau \rightarrow \mu \gamma \) to illustrate our claim that they are undetectable at Belle II in the Type II seesaw model(the BR\((l_i\rightarrow l_j \gamma )\) are also divided by BR\((\mu \rightarrow e {\bar{e}} e)\))
Same as Fig. 2 for normal ordering in the case where \(\mu \rightarrow e {\bar{e}} e\) is suppressed because \([m_\nu ]_{e \mu }\) vanishes (so  )
)
The type II seesaw can predict \(\tau \rightarrow 3 l \) within the reach of Belle II, in spite of the current bound BR\((\mu \rightarrow e {\bar{e}} e) \le 10^{-12}\). For instance, in normal ordering with vanishing lightest neutrino mass \(m_1\)
However, in the coming years, the Mu3e experiment will improve the sensitivity to \(\mu \rightarrow e {\bar{e}} e\), so the allowed range for the \(\tau \rightarrow l\) rates will depend on the results of Mu3e. To be concrete, we suppose that \(\mu \rightarrow e\) flavour change is not observed at MEG II or Mu3e. So in the following, we suppose that the Majorana phases (and the lightest neutrino mass \(m_{min}\)) are fixed such that \(C_{VLL}^{e\mu ee}\) vanishes at tree level, implying that the \(\mu \rightarrow e {\bar{e}} e\) rate is suppressed by \(\mathcal{O}(\alpha ^2)\), because it is mediated by the dipole and the penguin-induced \(C_{VLR}^{e\mu ee}\). Recall that the tree-level contribution to the coefficient \(C_{VLL}^{e\mu ee}\), which is proportional to \([m]^*_{\mu e} [m]_{ee}\), can vanish with \([m]_{ee}\) in normal ordering (NO) for  (as is well known from neutrinoless double beta decay [148]), and it can also vanish with \([m]_{e\mu }\) both in normal and inverted ordering for
(as is well known from neutrinoless double beta decay [148]), and it can also vanish with \([m]_{e\mu }\) both in normal and inverted ordering for  .
.
There are six \(\tau \rightarrow 3 l \) decays, whose tree-level amplitudes are proportional to products of only five neutrino mass matrix elements. This suggests at least one relation among these decays for generic \(m_{min}\) and Majorana phases – but this relation could be difficult to test in general, because \(m_{min}\) and the Majorana phases can accidentally suppress almost any element of the neutrino mass matrix (as we saw for \([m_\nu ]_{e \mu }\)). This section considers a scenario where either \( [m_\nu ]_{e\mu } \) or \([m_\nu ]_{ee}\) vanishes in order to suppress \(\mu \rightarrow e\) rates, so testable predictions can be expected.
For \(m_{ee}\rightarrow 0\), one of the \(\Delta LF\) = 2 processes vanishes (at the order we calculate):
Similarly, the tree contribution to \(\tau \rightarrow e {\bar{e}} e\) vanishes, so that only the dipole and penguin contributions to this decay remain. So a signature of the type II seesaw with vanishing \([m_\nu ]_{ee}\), is that these decays are suppressed simultaneously with the matrix element for neutrinoless double beta decay.
In the case where \(\mu \rightarrow e {\bar{e}} e\) is suppressed because \([m_\nu ]^{e\mu }\) vanishes (and  ), there are identities among the tree-level coefficients \({ C}_{V,LL}^{l\tau \sigma \rho } \propto m_{l\sigma }m_{\tau \rho }^* \) ( which by default dominate the rates for the decays \(\tau \rightarrow l{\overline{\rho }} \sigma ):\)
), there are identities among the tree-level coefficients \({ C}_{V,LL}^{l\tau \sigma \rho } \propto m_{l\sigma }m_{\tau \rho }^* \) ( which by default dominate the rates for the decays \(\tau \rightarrow l{\overline{\rho }} \sigma ):\)
As a result, for values of the Majorana phases fixed to suppress \(\mu \rightarrow e {\bar{e}} e\) (and for compatible \(m_{min}\)), ratios of \(\tau \rightarrow 3 l \) decays are predicted. We plot in Figs. 3 (for normal ordering) and 2 (for inverted ordering) the rates of various \(\tau \rightarrow 3 l \) decays, normalised to the rate for \(\mu \rightarrow e {\bar{e}} e\),Footnote 9 for the case where \(\mu \rightarrow e {\bar{e}} e\) is suppressed by \([m_\nu ]_{e\mu } \rightarrow 0\). These figures show [23, 25] that Belle II could see \(\tau \rightarrow 3 l \) decays for BR and BR
and BR , and that the branching ratios follow the predictions of Eq. (5.7). Furthermore, if several \(\tau \rightarrow 3 l \) decays were observed (including \(\tau \rightarrow e {\bar{e}} e\)), we anticipate than one could compare their relative branching ratios with the type II seesaw predictions shown in Figs. 2 and 3, and either exclude the model or deduce constraints on \(m_1\) and the mass ordering.Footnote 10 Regarding \(\mu A \rightarrow \! eA \), we estimate that BR\((\mu Al \rightarrow eAl) \sim 10^2\) BR\((\mu \rightarrow e {\bar{e}} e)\) in the case of vanishing \([m_\nu ]_{e\mu }\) in the type II seesaw, because \(C_{V,LR}^{e\mu ee}\) and \(\tilde{C}_{Al,L}\) are both induced by the photon penguin, see Eqs. (4.9, 4.15).
, and that the branching ratios follow the predictions of Eq. (5.7). Furthermore, if several \(\tau \rightarrow 3 l \) decays were observed (including \(\tau \rightarrow e {\bar{e}} e\)), we anticipate than one could compare their relative branching ratios with the type II seesaw predictions shown in Figs. 2 and 3, and either exclude the model or deduce constraints on \(m_1\) and the mass ordering.Footnote 10 Regarding \(\mu A \rightarrow \! eA \), we estimate that BR\((\mu Al \rightarrow eAl) \sim 10^2\) BR\((\mu \rightarrow e {\bar{e}} e)\) in the case of vanishing \([m_\nu ]_{e\mu }\) in the type II seesaw, because \(C_{V,LR}^{e\mu ee}\) and \(\tilde{C}_{Al,L}\) are both induced by the photon penguin, see Eqs. (4.9, 4.15).
Finally, the decays \(\tau \rightarrow e \gamma \) and \(\tau \rightarrow \mu \gamma \) will not be observed at Belle II if neutrino masses arise via the type II seesaw model, because this requires \(\mu \rightarrow e \gamma \) or \(\mu \rightarrow e {\bar{e}} e\) larger than the current constraints (this conclusion is fully general and does not assume that the tree-level contribution to \(\mu \rightarrow e {\bar{e}} e\) vanishes). The dipole coefficients \(C_{D,R}^{l \tau }\), at the experimental scale \(m_\tau \), can be written analogously to Eq. (4.6), with the index replacement \(e\rightarrow l\) and \(\mu \rightarrow \tau \), and without the second term, because the RG running ends at \(m_\tau \) for all flavours in the loop. At the order we calculate, the \(\tau \) dipole coefficients are therefore given by \([m_\nu m_\nu ^\dagger ]_{l\tau }\), so are independent of the neutrino mass scale and Majorana phases (see Eq. 2.2), and the ratio
is predicted. However, in order to be within the reach of Belle II (BR , see Table 1), these branching ratios need to be much larger than BR(\(\mu \rightarrow e \gamma )\), which can be engineered via a cancellation in \(C_{D,R}^{e\mu }\) for specific Majorana phases at a large neutrino mass scale. However, when this cancellation arises, the model predicts a larger branching ratio for \(\mu \rightarrow e {\bar{e}} e\) than \(\tau \rightarrow l \gamma \), because the coefficient \(C_{VLL}^{e\mu ee} \propto m_1^2\) arises at tree level.
, see Table 1), these branching ratios need to be much larger than BR(\(\mu \rightarrow e \gamma )\), which can be engineered via a cancellation in \(C_{D,R}^{e\mu }\) for specific Majorana phases at a large neutrino mass scale. However, when this cancellation arises, the model predicts a larger branching ratio for \(\mu \rightarrow e {\bar{e}} e\) than \(\tau \rightarrow l \gamma \), because the coefficient \(C_{VLL}^{e\mu ee} \propto m_1^2\) arises at tree level.
5.3 The dipole constraints on boxes for the leptoquark
The leptoquark Lagrangian of Eq. (3.5) allows the leptoquark to interact with doublet and singlet leptons, so it can induce lepton flavour-changing dipole, tensor and scalar operators, without any suppression by the lepton Yukawas. Nonetheless, we neglect four-lepton scalar operators in this model, because the coefficients are suppressed below the upcoming experimental reach by the dipole constraint. This section aims to show that suppression.
We are interested in scalar four-lepton operators \(\mathcal{O}_{S,XX}\), such as those in the observable Lagrangian of Eq. (2.3). These operators occur at dimension eight in SMEFT with a pair of Higgs legs, for instance in the form \(({\overline{\ell }}_eH \mu _R) ({\overline{\ell }}_eH e_R)\) and can be generated in the leptoquark model via box diagrams with Higgs legs, as illustrated on the left in Fig. 4. Equivalently, these operators are generated in the dimension six\(^2 \rightarrow \) dimension eight RGEs of SMEFT or the low energy EFT, respectively by the fish diagrams at the centre or right of Fig. 4. It is straightforward to see from the model diagram, that
so that this coefficient could be \( \sim 3\times 10^{-5}\) for leptoquark couplings of \(\mathcal{O}(1)\) to the top quark. This is marginally above the current experimental bound, which is \(|C_{SRR}^{e \mu ee}|\le 2.8 \times 10^{-6}\) from SINDRUM [64]. So now we want to show that the product \(\lambda _L^{\alpha t} \lambda _R ^{\beta t *}\) is constrained to be  for almost any combination of lepton flavours \(\alpha , \beta \).
for almost any combination of lepton flavours \(\alpha , \beta \).
In the presence of both the \(\lambda _L\) and \(\lambda _R\) interactions, the leptoquark matches onto 2l2q tensor operators involving the up-type quarks (see Eq. C.11). These tensor operators then mix to the dipole (see the last term of Eq. 4.7), generating an “invariant” that is not identical to the one appearing in Eq. (5.8):
However, the term \(\propto y_t\) in \([\lambda _L Y_u^* \eta _{m_Q}\ln \frac{m_{LQ}}{m_Q} \lambda _R^\dagger ]^{e \mu }\) is of comparable magnitude to the term \(\propto y_t\) of \([\lambda _L Y_u^* \lambda _R^\dagger ]^{e \mu }\) from Eq (5.8).
Now we want to argue that this term  , because if its larger it exceeds the experimental bound on \(\Delta C_{DR}^{ \alpha \beta }\), so must be small enough to cancel against next biggest term. In this argument, we assume that
, because if its larger it exceeds the experimental bound on \(\Delta C_{DR}^{ \alpha \beta }\), so must be small enough to cancel against next biggest term. In this argument, we assume that  , and use a different normalisation of the dipole operator:
, and use a different normalisation of the dipole operator:
where the lepton Yukawa is removed. This is more convenient for comparing the experimental bounds [61, 62, 149,150,151,152,153,154] on NP contributions to the coefficient of the redefined dipole operator, expressed as a matrix in flavour space:
where on the diagonal are the \((g-2)_\beta \) constraints [151, 152] using \(|\Delta a_\beta | \simeq 2m_\beta |C_D^{\beta \beta } + C_D^{\beta \beta *}|/(e v)\), and the EDM constraints [153, 154] on \(\mathcal{I}m \{C_D^{\beta \beta }\} \simeq - v d_\beta /2\) [155] are  , and
, and  . The contribution of Eq. (5.9), with
\(\lambda _L^{\alpha t} \lambda _R^{\alpha t *}\) of order 1, is larger than the bounds of Eq. (5.11) on all the dipole coefficients, except possibly
\([{\widetilde{C}}_{D}]^{\tau \tau }\). So the top contribution must cancel against the next largest contribution to the dipole, which is relatively suppressed at least by the charm or
\(\tau \) Yukawa, because the dipole operator requires a single Higgs leg. So this implies that
. The contribution of Eq. (5.9), with
\(\lambda _L^{\alpha t} \lambda _R^{\alpha t *}\) of order 1, is larger than the bounds of Eq. (5.11) on all the dipole coefficients, except possibly
\([{\widetilde{C}}_{D}]^{\tau \tau }\). So the top contribution must cancel against the next largest contribution to the dipole, which is relatively suppressed at least by the charm or
\(\tau \) Yukawa, because the dipole operator requires a single Higgs leg. So this implies that

for all flavour combinations \(\alpha \beta \) except \(\tau \tau \), so the scalar four-lepton coefficients are below upcoming experimental sensiticity and can be neglected.
We also explored the possibility that constraints on vector four-quark operators [156] – for instance from meson–antimeson oscillations – allow to set bounds on the vector four-lepton operators. Our hope was that the quark sector could set bounds on the eigenvalues \(\{\lambda _i\}\) of the leptoquark coupling matrices
where \( D_\lambda =\) diag \(\{\lambda _1, \lambda _2, \lambda _3\}\), and \(V_l\) and \(V_Q\) are unitary matrices. \(K^0\! -\! \overline{K^0}\) and \(D^0\! -\! \overline{D^0}\) mixing constrain two independent combinations of \( V_Q^\dagger D^2_\lambda V_Q \), but in order to set an upper bound on the eigenvalues, at least one more constraint would be required, and we did not find useful constraints involving tops.
5.4 Complex coefficients – what changes?
The coefficients of the observables operator are generally complex numbers, and it is not immediately clear whether experiments can fully determine these coefficients when non-zero phases are present. When considering upper limits on branching ratios, the only difference is that we have two identical 12-dimensional ellipses, each respectively in the space of the real and imaginary parts of the coefficients. This happens because the branching fractions are functions of the absolute values of operator coefficient combinations, which result in a quadrature sum of the real and imaginary components. Therefore, the two do not mix, and the rate is a combination of the same positive defined quadratic forms, to which the upper limit can separately apply.
The complication arises when we consider the possibility of measuring the complex coefficients from data. Expanding the branching ratios of Eqs. (2.7)-(2.10) in terms of the (complex) coefficients of Eq. (2.3), we findFootnote 11
where we have defined \(C_{\square }=|C_\square |e^{i\phi _\square }\), \(X\ne Y\) and A can be Al or Au \(\perp \). The observables only depend on relative phases, so for brevity we relabel \(\phi _\square -\phi _{D,Y}\rightarrow \phi _\square \). We thus have 10 branching fractions that can generally depend on 18 parameters: 10 absolute values and 8 relative phases. For example, observing \(\mu \rightarrow e_X \gamma \) and \(\mu \rightarrow e_X {\overline{e}}_X e_X\) ( \(\mu \rightarrow e_X {\overline{e}}_Y e_Y\)) would not be sufficient to measure the real and imaginary parts of the coefficient \(C^{e\mu ee}_{V,XX}\) ( \(C^{e\mu ee}_{V,XY}\)). However, some observables may be directly related to the coefficient relative phases. For instance, it has been shown in [86,87,88] that the T-odd asymmetry term
is accessible via the angular distribution of the outgoing electrons/positrons, and could assist in determining the relative phase of the \(\mu \rightarrow 3e\) vectors and dipole. In addition, interpreting data assuming specific models can help in reducing the number of relevant parameters, and measurements may still be used to find regions of parameter space that are incompatible with the model predictions. For the three models we considered here:
-
1.
In the type II seesaw the observable coefficients are related to the neutrino mass matrix, which is complex (given the hints of the CP violating Dirac phase \(\delta \simeq 3/2\pi \) and due the potential presence of non-zero Majorana phases). In our analysis of the type II seesaw in [50], we identified the region where the model can sit in the space of the angular variables \(\tan \theta =\sqrt{|C_D|^2+|C_{V,LR}|^2}/|C_{V,LL}|\) and \(\tan \phi =|C_D/C_{V,LR}|\), which depend on the absolute values of the observable coefficients. One may wonder whether experiments can identify a point in this space despite having complex phases, which make three branching fractions depend on five parameters (three absolute values and two phases). Since the flavour changing interactions with electron singlets are negligible, the \(A^T_{\mu \rightarrow 3e}\) asymmetry is given by the relative phases of the \(C_{V,LL}, C_{V,LR}\) vectors with the \(C^{e\mu }_{D,R}\) dipole. Combined with the measurements of the branching fractions for \(\mu \rightarrow e_L \gamma \), \(\mu \rightarrow e_L {\overline{e}}_L e_L\) and \(\mu \rightarrow e_L {\overline{e}}_R e_R\), one of five physical parameters would still remain undetermined. Taking advantage of the fact that in the type II seesaw \(C_{A}\propto C_{V,LR}\), a detection of \(\mu A\rightarrow e A\) could be used to extract the value of the last unknown, resulting in the complete knowledge of the relevant complex coefficients (modulo an overall phase). This also opens the interesting possibility of taking advantage of \(\mu \rightarrow e\) observables to determine the unmeasured neutrino parameters, i.e. the lightest neutrino mass and the Majorana phases. Since the complex EFT coefficients depends on these three unknown, measuring the coefficients could allow to infer their values. Additionally, since the system is over-constrained, with three complex coefficients being a function of four parameters (including the overall magnitude of LFV), we can use experimental results to check for consistency with the type II seesaw.
-
2.
The operator coefficients in the inverse seesaw are given by the off-diagonal elements of Hermitian matrices, which can be in general complex. In the case of nearly degenerate sterile neutrinos, we have found that the coefficients satisfy linear relations of the following form [50]
$$\begin{aligned} C^{e\mu ee}_{V,XY}=a_{XY} C^{e\mu }_{A,L}+b_{XY} C^{e\mu ee}_{D,R} \end{aligned}$$(5.17)where a and b are real numbers, and \(XY=LL,LR\). These relations hold in general and do not assume real coefficients. However, with non-vanishing phases, two observables are not sufficient to fully determine the \(\mu \rightarrow e\) predictions of the inverse seesaw. Observing \(\mu \rightarrow e_L \gamma \) would give the dipole absolute value, and measuring \(\mu A\rightarrow e_L A\) would only yield a combination of \(|C^{e\mu }_{2q,L}|\) and dipole-four fermion relative phase. Taking advantage of Eq. (5.17), a \(\mu \rightarrow e_L {\overline{e}}_R e_R\) signal could allow to solve for \(C^{e\mu }_{2q,L}\) as a complex number. Then, again by means of Eq. (5.17) for \(XY=LR\), we could predict \(BR(\mu \rightarrow e_L {\overline{e}}_R e_R)\) and compare it against experimental results. We conclude that, despite the non-zero phases, the inverse seesaw with degenerate sterile neutrinos is predictive enough that it could be ruled out by a combination of \(\mu \rightarrow e\) observations
-
3.
In the leptoquark model the \(\mu \rightarrow e\) coefficients depend on a number of invariants that is larger than the number of observables. This means that the model could already fill the experimental ellipse (with the exception of the scalar four lepton directions) even in the case of real couplings. Allowing complex couplings would make the model even less constrained, and thus we do not discuss this case further.
6 Discussion
The purpose of bottom-up EFT is to take low-energy experimental information to high-scale models. In this section, we discuss various aspects of this process, in the light of the three models we considered.
6.1 What differences among models can be identified by the data?
We showed in [50] that the data could rule out the models we consider, because the models predict relations between the Wilson coefficients, so are unable to fill the whole ellipse in coefficient space that is accessible to experiments. But it would be more interesting to ask whether \(\mu \rightarrow e\) observations could identify properties of models.
A simple question is whether \(\mu \rightarrow e\) data could distinguish models with LFV couplings to either lepton doublets or singlets, vs models that interact with both. It seems that the answer is yes. If LFV interactions involve only doublets or singlets, the only lepton-chirality-changing interaction in the theory is the Higgs Yukawa. So the coefficients of chirality-changing LFV operators must be proportional to the Yukawa coupling to an odd power. For instance, the dipole coefficients would satisfy
If this relation is not satisfied, it suggests that LFV involves doublets and singlets. If it is satisfied with exponent \(-1\), then it is probable that LFV involves doublets but not singlets. If in addition, the coefficients of other singlet-LFV operators are negligible, it becomes very probable that LFV involves only doublets – although it could result from accidental cancellations in a model with LFV for doublets and singlets.
It would be interesting and useful if the data could also identify other model properties, such as the loop order at which LFV occurs. But our models suggest this is not possible, because loops that occur in matching the model to the EFT are indistinguishable from small couplings, and because coefficients that arise at tree level can be accidentally small, as occurred in the type II seesaw where \(C_{VLL}^{e\mu ee}\) can vanish. For similar reasons, \(\mu \rightarrow e\) observables can not distinguish NP that interacts only with leptons in its renormalisable Lagrangian, from NP that interacts with quarks and leptons.
6.1.1 What is the role of the RGEs?
There are many reasons to use Renormalisation Group Equations in EFT, as is well-known in quark flavour physics. However, the RGEs may not be motivated in the lepton sector, because LFV has yet to be discovered, so precise, scheme-independent predictions are not crucial. Indeed, the RGEs are often not included in the \(\tau \rightarrow l\) sector, where the data separately constrain most coefficients. In the \(\mu \rightarrow e\) sector where there are fewer restrictive bounds, an EFT analysis suggests that the RGEs are relevant because they mix difficult-to-probe operators into well-constrained processes. In this section, we explore whether this occurs in our models.
The inverse seesaw at the TeV-scale is an example of a model where the RGEs are unnecessary, because low-energy LFV operators are generated via loop diagrams in matching, and the RGEs just contribute an \(\mathcal{O}(10\%)\) renormalisation. A few properties of the model contribute to this behaviour: first, the new interactions couple one light SM particle with a heavy new particle and a weak boson, so LFV occurs via loops that contribute in matching. Then, there is no significant operator mixing via the RGEs, because the photon penguin vanishes below the weak scale at one loop; that is, LFV operators are vectors(or \(\propto \) a lepton yukawa coupling) because only the lepton doublet interacts with new particles, and vector operators only mix into each other via the penguins. But in the one-loop penguin diagrams, the gauge boson attaches to the Higgs, so the penguins are only present above the weak scale, and generate 2l2q operators in matching.
The type II seesaw is an example of a model where the leading contribution to some observables arises in matching, and via the RGEs for others. This behaviour can be reproduced in EFT, and can also be obtained in model calculations that judiciously include log-enhanced loops [26]. However, the correct lower limits of the logarithms are crucial to obtain the dependence of LFV observables on the unknown parameters of the neutrino mass matrix in the type II seesaw model. These lower limits should be implemented automatically in EFT, but to our knowledge were previously missing from the literature. So it seems that the RGEs are required in this model, in order to identify the parameter space the model cannot reach.
In the type II seesaw, a careful one-loop model calculation could include all the terms of our leading-log EFT, because we do not resum \((\alpha \lg )^n\) for all n, but rather work to \(\mathcal{O}(\alpha \ln )\). However, our EFT also includes the “leading” vector to dipole mixing at \(\mathcal{O}(\alpha ^2 log)\), which we did not find in the literature about this model. This mixing causes the dipole to depend on the unknown neutrino parameters (Majorana phases and \(m_{min}\)), thereby allowing it to vanish. It is “well known” that the 2-loop electroweak contribution to \((g-2)_\mu \) is comparable to the one-loop part, but it seems that the implications of this may not have been implemented in all model calculations. However, it is relatively simple to implement in EFT [101], illustrating the first reason to do EFT: it is the simpler way to get a more precise result.
The leptoquark is our model where the RGEs are most useful, because they allow to simultaneously include the multitude of relevant electroweak loops and large QCD effects in an organised fashion. The RGEs are required to obtain model predictions, because they mix difficult-to-constrain coefficients – such as tensor operators involving top quarks – into observable coefficients like the dipole, while simultaneously including the QCD running of the operators. so are required to obtain model predictions.
6.1.2 Do cancellations among coefficients occur in models?
It is common to make tables listing the “sensitivity” of observables to operator coefficients (e.g. [80, 101]); these “one-at-a-time-bounds” are simple to obtain by allowing a single operator to have a non-zero coefficient, and computing the experimental constraint upon it. It can also be common to take these sensitivities as bounds, because it is generally considered unlikely that models generate cancellations among operator coefficients, especially since these coefficients run with scale. However, such cancellations can occur, for instance via the equations of motion, so these “sensitivities” are not true upper bounds (instead, they are the value of the coefficient above which it could be detected).
The operator population in EFTs is often reduced via the equations of motion (as pedagogically discussed in [98, 157]). This can sometimes impose “accidental” but precise cancellations among operator coefficients. An example is discussed in Appendix C4: in a model, the Z penguin diagrams can be \(\propto q^2\) (= the momentum-transfer\(^2\) of the Z), or \(\propto v^2\). Both contributions could contribute to the decay \(Z\rightarrow e^\pm \mu ^\mp \), but the part \(\propto q^2\) gives a negligible contribution to \(\mu \rightarrow e {\bar{e}} e\), due to the \(q^2\sim m_\mu ^2\) suppression. However if the model is matched to SMEFT, the equations of motion are used to to transform the \(q^2\) part of the diagrams into four-fermion and penguin operators (\(\mathcal{O}_{HL3}^{e\mu }\) and \(\mathcal{O}_{HL1}^{e\mu }\)), with coefficients whose sum cancels in low-energy matrix elements where \(q^2 \rightarrow 0\). The “one at a time bounds” on penguin and four-fermion operators miss this cancellation, so would instead suggest that both are strictly constrained by \(\mu \rightarrow e {\bar{e}} e\).
In the type II seesaw model, the Z-penguin diagrams give negligible contribution to \(\mu \rightarrow e {\bar{e}} e\) because the \(\propto v^2\) part is suppressed by lepton Yukawas, and the \(\propto q^2\) part is kinematically suppressed as discussed above. So experimental observations do not exclude a \({\bar{e}} \, Z \! \! \! \! / ~ \mu \) interaction just below the sensitivity of the LHC, despite that the “one-at-a-time-bounds” suggest that they do. Nonetheless, the model can not generate such interactions, because they are controlled by the same model parameters as the photon penguin diagrams, which are constrained by \(\mu \rightarrow e {\bar{e}} e\).
So in summary, apparently accidental cancellations can occur among coefficients in EFT; whether this affects the constraints on models is model-dependent.
6.1.3 Does it matter that coefficients are complex?
\(\mu \rightarrow e\) observables define an experimentally accessible 12-dimensional ellipse in the space of the Wilson coefficients, but these are generally complex numbers. Although this does not complicate the analysis when imposing bounds on the coefficients, because the ellipses for the real and imaginary components are identical, allowing for complex phases could generally hinder the determination of the coefficients from data. If the muon polarization and the electron/positron angular observables could in principle identify 12 real coefficients, unobservable directions will be present when considering the full parameter space spanned by coefficients with non-zero phases. Measuring for instance the branching fraction for \(\mu \rightarrow e_X \gamma \) would identify a circle with radius \(\sqrt{BR(\mu \rightarrow e_X \gamma )/384\pi ^2}\) centered at the origin of the complex plane for the dipole coefficient \(C_{DX}\), but without further assumptions the real and imaginary parts would remain undetermined. However, if our goal is to use data to exclude models, the model predictions can help in reducing the number of unmeasurable direction. Interpreting data in light of a particular model can lead to the determination of absolute values as well as relative phases for the coefficient. The neutrino mass models we considered in this paper are an example where this determination is possible.
In the type II seesaw, the LFV operators are complex because their coefficients are directly related to the neutrino mass matrix, which contains up to three phases in the case of Majorana neutrinos. We discussed in Sect. 5.4 how, taking advantage of the model predictions and making use of observables directly related to the coefficient phases (see Eq. 5.16), one could interpret \(\mu \rightarrow e\) data to determine the (complex) coefficients predicted by the type II seesaw.
Similarly, in the inverse seesaw model, the predictions for flavour-changing observables are determined by the magnitude of off-diagonal matrix elements, and the operators can be complex. In Sect. 5.4, we showed that despite the presence of operator phases, we can use the model predictions to identify points in the experimentally accessible ellipse.
7 Summary
The \(\mu \rightarrow e\) sector is promising for the discovery of LFV, due to the exceptional upcoming experimental sensitivity – to three processes. So this project explored what could be learned about the New Physics in the lepton sector from \(\mu \rightarrow e\) observations, by studying some “representative” TeV-scale models described in Sect. 3. We take the data to be 12 Wilson coefficients, which can be individually constrained and distinguished in measurements (with the exception of vector and scalar four-lepton operators which have indistinguishable angular distributions in \(\mu \rightarrow e {\bar{e}} e\), see Sect. 2).
Bottom-up EFT is an appropriate formalism to compare data with models, because data improves slowly while models can evolve more rapidly. It also gave some relevant effects (such as the two-loop vector to dipole mixing in the type II seesaw, see Eq. 4.6) which we did not find in the literature. Our analysis is at leading order in EFT, meaning that we attempt to include the largest contribution of the model to all the operators to which the data can be sensitive. This includes some 2-loop anomalous dimensions and some operators which are dimension eight in SMEFT. Our notation and assumptions are summarised in Sect. 2. Our models are located at the TeV scale in order to profit from many complementary observables, but the ratio \(m_W/\)TeV is not large, which implies that EFT is poorly motivated between \(m_W \rightarrow \) TeV (see the discussion in Appendix C1), so in practise we match our models to the QCD\(\times \)QED-invariant EFT that is relevant below \(m_W\).
The observable operator coefficients are given in Sect. 4 in terms of model parameters at the TeV, which usually appear with SM parameters in elegant combinations that recall Jarlskog invariants. This unforeseen curiosity (discussed in Sect. 4.1) may be an accident of our simple leading order analysis, which allows analytic expressions. Or possibly it indicates an interesting new role for invariants as stepping stones in the reconstruction of models from EFT coefficients. For instance, our models did not fulfill our expectations: we anticipated that the type II seesaw was predictive because the flavour-changing couplings \(f_{\alpha \beta }\) (Eq. 3.1) are determined by the neutrino mass matrix, and that the inverse seesaw was unpredictive because the \(Y^{\alpha a}\) couplings (Eq. 3.3) are unknown. However, Sect. 4.2 shows that \(\mu \rightarrow e\) flavour change is controlled by two invariants in the inverse seesaw with degenerate singlets, whereas three invariants are needed in the type II model. In any case, it is interesting that \(\mu \rightarrow e\) flavour change in these models is controlled by a few complex numbers of magnitude  , which could be obtained for a wide variety of flavour structures in Lagrangians.
, which could be obtained for a wide variety of flavour structures in Lagrangians.
We showed in [50] that \(\mu \rightarrow e\) data has the ability to exclude the models we consider, because they cannot fill the whole ellipse in coefficient space accessible to upcoming experiments. In Sect. 5, we explored the more interesting question of whether observations could indicate a model – specifically, the type II seesaw model – by including some complementary observables. In Sect. 5.1 we showed that, in the type II seesaw model, some ratios of \(\mu \rightarrow e\) Wilson coefficients can be confined to relatively narrow intervals (depending on the mass ordering, see Eq. (5.3)) if the lightest neutrino mass is small enough. Therefore, if these ratios where observed outside the ranges quoted in Sect. 5.1, a lower bound on the neutrino mass scale could be inferred (assuming that neutrino masses arise from the type II seesaw mechanism). In Sect. 5.2, we considered \(\tau \)-LFV at Belle II – still in the type II seesaw model – in the case where neither \(\mu \rightarrow e \gamma \) nor \(\mu \rightarrow e {\bar{e}} e\) are observed in upcoming experiments (see table 1). In this case, the model makes specific predictions for \(\tau \)-LFV ratios that could be observed at Belle II, as a function of the neutrino mass scale and ordering. As a result, Belle II could contribute to constraining the neutrino mass scale and ordering or rule out the type II seesaw model.
Finally, in the discussion Sect. 6, we addressed some questions that arise in a bottom-up EFT attempt to reconstruct New Physics from (low-energy) data.
Data availability
This manuscript has no associated data. [Author’s comment: Data sharing not applicable to this article as no datasets were generated or analysed during the current study.]
Code availability
This manuscript has no associated code/software. [Author’s comment: Code/Software sharing not applicable to this article as no code/software was generated or analysed during the current study.]
Notes
This is obvious for the \(\Delta LF\) = 2 processes, and the quark flavour-changing and diagonal interactions are independent because the CKM mixing is small [59].
We neglect \(\mu e\gamma \gamma \) operators which can contribute to \(\mu A \rightarrow \! eA \) [78].
Notice that the quark currents are not chiral, which introduces factors of 2 as given in Eq. (A.2).
Reference [105] makes an interesting classification of Majorana neutrino mass models into three sets, based on the flavour structures that are multiplied in the definition of \([m_\nu ]\). However, both seesaw models enter the same set.
It is clear that if the leptoquark has couplings \(\lambda _X^{e q}\), \(\lambda _X^{\mu q}\) and \(\lambda _X^{\tau q}\), then it can mediate \(\tau \rightarrow e\), \(\tau \rightarrow \mu \) and \(\mu \rightarrow e\) processes. Furthermore, if \(|\lambda _X^{\tau q}|\sim 0.2\) to fit the B-physics anomalies, then experimental bounds \(B_{(\tau \rightarrow l)}\) on \(\tau \rightarrow l\) processes could constrain \(\lambda _X^{l q}< B_{(\tau \rightarrow l)}/\lambda _X^{\tau q} \). In all the cases we checked, we find
$$\begin{aligned} \frac{B_{(\tau \rightarrow e)}}{\lambda _X^{\tau q}} \frac{B_{(\tau \rightarrow \mu )}}{\lambda _X^{\tau q}} > B_{(\mu \rightarrow e)} \end{aligned}$$that is, that \(\mu \rightarrow e\) processes can probe smaller \(\lambda _X^{l q}\) couplings than \(\tau \rightarrow l\) can exclude.
But notice the impact of phase space: the tilde on \(m_e\) is from kinematics that the Lagrangian does not know about, so the Lagrangian invariant would include a “large” \(\ln \frac{m_\mu }{m_e}\) that the coefficient does not contain because the large log is only relevant in a small phase space.
In the lepton sector below the weak scale, the (quadratic) GIM mechanism suppresses LFV amplitudes \(\propto m^2_\nu /m_W^2\), so implementing log-GIM would be very interesting (\(\ln (m_\nu /m_W)\gg m^2_\nu /m_W^2\)). However, this appears difficult [141, 142], because there are no “penguin diagrams” in the SM with a massless gauge boson attached to a neutrino loop, and because the logarithm in log-GIM is cutoff by the largest of the mass in the loop, or the external momentum traversing the loop, and this latter is of order charged lepton masses in LFV processes.
In the type II seesaw, the overall magnitude of LFV \( \sim |f^2v^2/M_\Delta ^2|\) is unknown, so we plot ratios of rates. This unknown corresponds to \(\lambda _H\) in our parametrisation.
The dip in Fig. 2 in the ratios for \(\tau \rightarrow {\overline{\mu }}ll\) is caused by a partial cancellation in \([m_\nu ]_{\mu \tau }\) engineered by the Majorana phases. But its a less interesting feature because it occurs at a rather large value of the summed neutrino masses,
 0.2 eV.
0.2 eV.We assume that we can distinguish the processes with electron/positrons of different chiralities via the angular distributions. We do not discuss the scalar operator \(C^{e\mu ee}_{S,XX}\) because it is negligible in the models we consider.
The scalar operator with top quarks also matches at \(m_t\) onto \(({\bar{e}} P_R \mu )GG\), whose QCD running we suppose is accounted for by the wavefunction contributions, and which at 2 GeV matches onto nucleons like for the b and c:
$$\begin{aligned} G^{NQ}_S \simeq 0.9 \frac{2m_N }{27m_Q(m_Q) } \frac{\alpha _s(m_Q)}{ \alpha _s(2\textrm{GeV}) }. \end{aligned}$$However, we do not write the top contribution because it is absent from the EFT below the weak scale, so we include it at \(m_t\).
In matching the leptoquark to SMEFT at \(\Lambda _{NP}\), the “higgs-penguin” diagrams of the model correspond to the mixing of the tree-induced scalar \(\mathcal{O}_{LEQU}\) into \(\mathcal{O}_{EH}\). Similarly, the \(\propto v^2\)-Z-penguin diagrams correspond to the mixing of 2l2q vector operators into the penguin operators \(\mathcal{O}_{HL1}\), \(\mathcal{O}_{HL3}\), and/or \(\mathcal{O}_{HE}\). All the operators are of dimension six and involve at most two quarks, so the effect of QCD is as discussed around Eq. (2.17). It is straightforward to see that, for \(\eta \simeq 1+\delta \), this modification of the electroweak anomalous dimension is \(\mathcal{O}(\delta ^2)\), so we neglect this effect. In the QED\(\times \)QCD-invariant EFT, the log-enhanced contribution of box and Z-penguin diagrams arises in the dimension six\(^2\rightarrow \) dimension eight RGEs via “fish diagrams” (see e.g. Fig. 17) combining a Z- or Higgs-induced four-quark operator with a leptoquark-induced two-lepton-two-quark operator. The QCD running for these diagrams is more complicated (four-quark operators mix under QCD), and includes the wrong diagrams. So using the RGEs of QCD and QED between the weak scale and \(\Lambda _{NP}\), would resum the wrong QCD for penguins and boxes. It gives the correct QCD running below \(m_W\), but such fish diagrams have a light (\(\ne t\)) quark in the loop, so are negligible due to the Yukawa suppression (We nonetheless include the light quarks in the formulae, in order to construct attractive “invariants”).
The lower cutoff for the diagram of Fig. 17) is neccessarily 2 GeV, because the quarks are matching to hadrons at that scale. However, below 2 GeV, the u quark can be replaced in the diagram by a proton, and this is equivalent to retaining the u quark, given that the matching of quark onto nucleon vector currents in the nucleus respects charge conservation.
References
R.L. Workman et al. [Particle Data Group], Review of particle physics. PTEP 2022, 083C01 (2022)
Y. Kuno, Y. Okada, Muon decay and physics beyond the standard model. Rev. Mod. Phys. 73, 151 (2001). arXiv:hep-ph/9909265
L. Calibbi, G. Signorelli, Charged lepton flavour violation: an experimental and theoretical introduction. Riv. Nuovo Cim. 41(2), 71–174 (2018). arXiv:1709.00294 [hep-ph]
M. Ardu, G. Pezzullo, Introduction to charged lepton flavor violation. Universe 8(6), 299 (2022). arXiv:2204.08220 [hep-ph]
J. Hisano, T. Moroi, K. Tobe, M. Yamaguchi, Lepton flavor violation via right-handed neutrino Yukawa couplings in supersymmetric standard model. Phys. Rev. D 53, 2442–2459 (1996). arXiv:hep-ph/9510309
S. Antusch, E. Arganda, M.J. Herrero, A.M. Teixeira, Impact of theta(13) on lepton flavour violating processes within SUSY seesaw. JHEP 11, 090 (2006). arXiv:hep-ph/0607263
A. Rossi, Supersymmetric seesaw without singlet neutrinos: neutrino masses and lepton flavor violation. Phys. Rev. D 66, 075003 (2002). arXiv:hep-ph/0207006
W. Altmannshofer, A.J. Buras, S. Gori, P. Paradisi, D.M. Straub, Anatomy and phenomenology of FCNC and CPV effects in SUSY theories. Nucl. Phys. B 830, 17–94 (2010). arXiv:0909.1333 [hep-ph]
V. Cirigliano, A. Kurylov, M.J. Ramsey-Musolf, P. Vogel, Lepton flavor violation without supersymmetry. Phys. Rev. D 70, 075007 (2004). arXiv:hep-ph/0404233
Y. Omura, E. Senaha, K. Tobe, Lepton-flavor-violating Higgs decay \(h \rightarrow \mu \tau \) and muon anomalous magnetic moment in a general two Higgs doublet model. JHEP 05, 028 (2015). arXiv:1502.07824 [hep-ph]
E. Arganda, M.J. Herrero, X. Marcano, C. Weiland, Imprints of massive inverse seesaw model neutrinos in lepton flavor violating Higgs boson decays. Phys. Rev. D 91(1), 015001 (2015). arXiv:1405.4300 [hep-ph]
F. Deppisch, J.W.F. Valle, Enhanced lepton flavor violation in the supersymmetric inverse seesaw model. Phys. Rev. D 72, 036001 (2005). arXiv:hep-ph/0406040
K. Agashe, A.E. Blechman, F. Petriello, Probing the Randall–Sundrum geometric origin of flavor with lepton flavor violation. Phys. Rev. D 74, 053011 (2006). arXiv:hep-ph/0606021
M. Blanke, A.J. Buras, B. Duling, A. Poschenrieder, C. Tarantino, Charged lepton flavour violation and (g-2)(mu) in the littlest Higgs model with T-parity: a clear distinction from supersymmetry. JHEP 05, 013 (2007). arXiv:hep-ph/0702136
T.M. Aliev, A.S. Cornell, N. Gaur, Lepton flavour violation in unparticle physics. Phys. Lett. B 657, 77–80 (2007). arXiv:0705.1326 [hep-ph]
Y. Cai, J. Herrero-García, M.A. Schmidt, A. Vicente, R.R. Volkas, From the trees to the forest: a review of radiative neutrino mass models. Front. in Phys. 5, 63 (2017). arXiv:1706.08524 [hep-ph]
P. Escribano, M. Hirsch, J. Nava, A. Vicente, Observable flavor violation from spontaneous lepton number breaking. JHEP 01, 098 (2022). arXiv:2108.01101 [hep-ph]
M.L. López-Ibáñez, A. Melis, M.J. Pérez, M.H. Rahat, O. Vives, Constraining low-scale flavor models with (g-2)\(\mu \) and lepton flavor violation. Phys. Rev. D 105(3), 035021 (2022). arXiv:2112.11455 [hep-ph]
M. Magg, C. Wetterich, Neutrino mass problem and gauge hierarchy. Phys. Lett. B 94, 61–64 (1980)
G. Lazarides, Q. Shafi, C. Wetterich, Proton lifetime and fermion masses in an SO(10) model. Nucl. Phys. B 181, 287–300 (1981)
J. Schechter, J.W.F. Valle, Neutrino masses in SU(2) \(\times \) U(1) theories. Phys. Rev. D 22, 2227 (1980)
R.N. Mohapatra, G. Senjanovic, Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys. Rev. D 23, 165 (1981)
E.J. Chun, K.Y. Lee, S.C. Park, Testing Higgs triplet model and neutrino mass patterns. Phys. Lett. B 566, 142–151 (2003). arXiv:hep-ph/0304069
M. Kakizaki, Y. Ogura, F. Shima, Lepton flavor violation in the triplet Higgs model. Phys. Lett. B 566, 210–216 (2003). arXiv:hep-ph/0304254
A.G. Akeroyd, M. Aoki, H. Sugiyama, Lepton flavour violating decays tau –\(>\) anti-l ll and mu –\(>\) e gamma in the Higgs Triplet Model. Phys. Rev. D 79, 113010 (2009). https://doi.org/10.1103/PhysRevD.79.113010. arXiv:0904.3640 [hep-ph]
D.N. Dinh, A. Ibarra, E. Molinaro, S.T. Petcov, The \(\mu - e\) conversion in nuclei, \(\mu \rightarrow e \gamma , \mu \rightarrow 3e\) decays and TeV scale see-saw scenarios of neutrino mass generation. JHEP 08, 125 (2012) [Erratum: JHEP 09, 023 (2013)]. arXiv:1205.4671 [hep-ph]
M.M. Ferreira, T.B. de Melo, S. Kovalenko, P.R.D. Pinheiro, F.S. Queiroz, Lepton flavor violation and collider searches in a type I + II seesaw model. Eur. Phys. J. C 79(11), 955 (2019). arXiv:1903.07634 [hep-ph]
L. Calibbi, X. Gao, Lepton flavor violation in minimal grand unified type II seesaw models. Phys. Rev. D 106(9), 095036 (2022). https://doi.org/10.1103/PhysRevD.106.095036. arXiv:2206.10682 [hep-ph]
D. Wyler, L. Wolfenstein, Massless neutrinos in left-right symmetric models. Nucl. Phys. B 218, 205–214 (1983)
R.N. Mohapatra, Mechanism for understanding small neutrino mass in superstring theories. Phys. Rev. Lett. 56, 561–563 (1986)
R.N. Mohapatra, J.W.F. Valle, Neutrino mass and baryon number nonconservation in superstring models. Phys. Rev. D 34, 1642 (1986)
A. Ilakovac, A. Pilaftsis, Flavor violating charged lepton decays in seesaw-type models. Nucl. Phys. B 437, 491 (1995). arXiv:hep-ph/9403398
D. Tommasini, G. Barenboim, J. Bernabeu, C. Jarlskog, Nondecoupling of heavy neutrinos and lepton flavor violation. Nucl. Phys. B 444, 451–467 (1995). arXiv:hep-ph/9503228
A. Ibarra, E. Molinaro, S.T. Petcov, Low energy signatures of the TeV scale see-saw mechanism. Phys. Rev. D 84, 013005 (2011). arXiv:1103.6217 [hep-ph]
R. Alonso, M. Dhen, M.B. Gavela, T. Hambye, Muon conversion to electron in nuclei in type-I seesaw models. JHEP 01, 118 (2013). arXiv:1209.2679 [hep-ph]
A. Abada, V. De Romeri, A.M. Teixeira, Impact of sterile neutrinos on nuclear-assisted cLFV processes. JHEP 02, 083 (2016). arXiv:1510.06657 [hep-ph]
R. Coy, M. Frigerio, Effective approach to lepton observables: the seesaw case. Phys. Rev. D 99(9), 095040 (2019). arXiv:1812.03165 [hep-ph]
A. Crivellin, F. Kirk, C.A. Manzari, Comprehensive analysis of charged lepton flavour violation in the symmetry protected type-I seesaw. JHEP 12, 031 (2022). arXiv:2208.00020 [hep-ph]
D. Zhang, S. Zhou, Complete one-loop matching of the type-I seesaw model onto the Standard Model effective field theory. JHEP 09, 163 (2021). arXiv:2107.12133 [hep-ph]
W. Buchmuller, R. Ruckl, D. Wyler, Leptoquarks in lepton-quark collisions. Phys. Lett. B 191, 442–448 (1987) [Erratum: Phys. Lett. B 448, 320–320 (1999)]
I. Doršner, S. Fajfer, A. Greljo, J.F. Kamenik, N. Košnik, Physics of leptoquarks in precision experiments and at particle colliders. Phys. Rep. 641, 1–68 (2016). arXiv:1603.04993 [hep-ph]
M. Bauer, M. Neubert, Minimal leptoquark explanation for the \(R_{D^{(*)}}\), \(R_K\), and \((g-2)_\mu \) anomalies. Phys. Rev. Lett. 116(14), 141802 (2016). arXiv:1511.01900 [hep-ph]
Y. Sakaki, M. Tanaka, A. Tayduganov, R. Watanabe, Testing leptoquark models in \({{\bar{B}}} \rightarrow D^{(*)} \tau {{\bar{\nu }}}\). Phys. Rev. D 88(9), 094012 (2013). arXiv:1309.0301 [hep-ph]
Y. Cai, J. Gargalionis, M.A. Schmidt, R.R. Volkas, Reconsidering the one leptoquark solution: flavor anomalies and neutrino mass. JHEP 10, 047 (2017). arXiv:1704.05849 [hep-ph]
A. Angelescu, D. Bečirević, D.A. Faroughy, O. Sumensari, Closing the window on single leptoquark solutions to the \(B\)-physics anomalies. JHEP 10, 183 (2018). arXiv:1808.08179 [hep-ph]
H.M. Lee, Leptoquark option for B-meson anomalies and leptonic signatures. Phys. Rev. D 104(1), 015007 (2021). arXiv:2104.02982 [hep-ph]
R.X. Shi, L.S. Geng, B. Grinstein, S. Jäger, J. Martin Camalich, Revisiting the new-physics interpretation of the \(b\rightarrow c\tau \nu \) data. JHEP 12, 065 (2019). https://doi.org/10.1007/JHEP12(2019)065. arXiv:1905.08498 [hep-ph]
N. Desai, A. Sengupta, Status of leptoquark models after LHC Run-2 and discovery prospects at future colliders. arXiv:2301.01754 [hep-ph]
M. Bordone, O. Catà, T. Feldmann, R. Mandal, Constraining flavour patterns of scalar leptoquarks in the effective field theory. JHEP 03, 122 (2021). https://doi.org/10.1007/JHEP03(2021)122. arXiv:2010.03297 [hep-ph]
M. Ardu, S. Davidson, S. Lavignac, Distinguishing models with \(\mu \rightarrow e \) observables. arXiv:2308.16897 [hep-ph]
C. Jarlskog, Commutator of the quark mass matrices in the standard electroweak model and a measure of maximal CP nonconservation. Phys. Rev. Lett. 55, 1039 (1985)
K. Abe et al. [T2K], Constraint on the matter–antimatter symmetry-violating phase in neutrino oscillations. Nature 580(7803), 339–344 (2020) [Erratum: Nature 583(7814), E16 (2020)]. arXiv:1910.03887 [hep-ex]
J.P. Lees et al. [BaBar], Evidence for an excess of \({\bar{B}} \rightarrow D^{(*)} \tau ^-{\bar{\nu }}_\tau \) decays. Phys. Rev. Lett. 109, 101802 (2012). arXiv:1205.5442 [hep-ex]
M. Huschle et al. [Belle], Measurement of the branching ratio of \({\bar{B}} \rightarrow D^{(\ast )} \tau ^- {\bar{\nu }}_\tau \) relative to \({\bar{B}} \rightarrow D^{(\ast )} \ell ^- {\bar{\nu }}_\ell \) decays with hadronic tagging at Belle. Phys. Rev. D 92(7), 072014 (2015). arXiv:1507.03233 [hep-ex]
G. Caria et al. [Belle], Measurement of \({\cal{R}}(D)\) and \({\cal{R}}(D^*)\) with a semileptonic tagging method. Phys. Rev. Lett. 124(16), 161803 (2020). arXiv:1910.05864 [hep-ex]
[LHCb], Measurement of the ratios of branching fractions \({\cal{R}}(D^{*})\) and \({\cal{R}}(D^{0})\). arXiv:2302.02886 [hep-ex]
R. Aaij et al. [LHCb], Test of lepton flavour universality using \(B^0 \rightarrow D^{*-}\tau ^+\nu _{\tau }\) decays with hadronic \(\tau \) channels. arXiv:2305.01463 [hep-ex]
M.A. Ramírez et al. [T2K], Measurements of neutrino oscillation parameters from the T2K experiment using \(3.6\times 10^{21}\) protons on target. arXiv:2303.03222 [hep-ex]
M. Ardu, S. Davidson, What is leading order for LFV in SMEFT? JHEP 08, 002 (2021). arXiv:2103.07212 [hep-ph]
S. Banerjee, V. Cirigliano, M. Dam, A. Deshpande, L. Fiorini, K. Fuyuto, C. Gal, T. Husek, E. Mereghetti, K. Monsálvez-Pozo et al., Snowmass 2021 white paper: charged lepton flavor violation in the tau sector. arXiv:2203.14919 [hep-ph]
A.M. Baldini et al. [MEG], Search for the lepton flavour violating decay \(\mu ^+ \rightarrow \rm e^+ \gamma \) with the full dataset of the MEG experiment. Eur. Phys. J. C 76(8), 434 (2016). arXiv:1605.05081 [hep-ex]
K. Afanaciev et al. [MEG II], A search for \(\mu ^+\rightarrow e^+\gamma \) with the first dataset of the MEG II experiment. arXiv:2310.12614 [hep-ex]
A.M. Baldini et al. [MEG II], The design of the MEG II experiment. Eur. Phys. J. C 78(5), 380 (2018). arXiv:1801.04688 [physics.ins-det]
U. Bellgardt et al. [SINDRUM], Search for the Decay mu+ –\(>\) e+ e+ e-. Nucl. Phys. B 299, 1–6 (1988)
A. Blondel, A. Bravar, M. Pohl, S. Bachmann, N. Berger, M. Kiehn, A. Schoning, D. Wiedner, B. Windelband, P. Eckert et al., Research proposal for an experiment to search for the decay \(\mu \rightarrow eee\). arXiv:1301.6113 [physics.ins-det]
P. Wintz, Results of the SINDRUM-II experiment. Conf. Proc. C 980420, 534–546 (1998)
Y.G. Cui et al. [COMET], Conceptual design report for experimental search for lepton flavor violating mu- - e- conversion at sensitivity of 10**(-16) with a slow-extracted bunched proton beam (COMET), KEK-2009-10
L. Bartoszek et al. [Mu2e], Mu2e Technical Design Report. arXiv:1501.05241 [physics.ins-det]
F. Abdi et al. [Mu2e], Mu2e Run I sensitivity projections for the neutrinoless \(\mu ^- \rightarrow e^-\) conversion search in aluminum. arXiv:2210.11380 [hep-ex]
W.H. Bertl et al. [SINDRUM II], A search for muon to electron conversion in muonic gold. Eur. Phys. J. C 47, 337–346 (2006)
Y. Kuno, PRISM/PRIME, Nucl. Phys. B Proc. Suppl. 149, 376–378 (2005)
M. Aoki et al. [C. Group], A new charged lepton flavor violation program at Fermilab. arXiv:2203.08278 [hep-ex]
Y. Kuno et al. [PRISM collaboration], An experimental search for a \(\mu N\rightarrow e N\) conversion at sensitivity of the order of \(10^{-18}\) with a highly intense muon source: PRISM, unpublished, J-PARC LOI (2006)
Bernard Aubert et al., Searches for lepton flavor violation in the decays tau+- –\(>\) e+- gamma and tau+- –\(>\) mu+- gamma. Phys. Rev. Lett. 104, 021802 (2010)
L. Aggarwal et al. [Belle-II], Snowmass White Paper: Belle II physics reach and plans for the next decade and beyond. arXiv:2207.06307 [hep-ex]
K. Hayasaka et al., Search for lepton flavor violating tau decays into three leptons with 719 million produced tau+tau- pairs. Phys. Lett. B 687, 139–143 (2010)
M. Aiba, A. Amato, A. Antognini, S. Ban, N. Berger, L. Caminada, R. Chislett, P. Crivelli, A. Crivellin, G.D. Maso et al. Science case for the new high-intensity muon beams HIMB at PSI. arXiv:2111.05788 [hep-ex]
S. Davidson, Y. Kuno, Y. Uesaka, M. Yamanaka, Probing \(\mu e \gamma \gamma \) contact interactions with \(\mu \rightarrow e\) conversion. Phys. Rev. D 102(11), 115043. arXiv:2007.09612 [hep-ph]
R. Kitano, M. Koike, Y. Okada, Detailed calculation of lepton flavor violating muon electron conversion rate for various nuclei. Phys. Rev. D 66, 096002 (2002) [Erratum: Phys. Rev. D 76, 059902 (2007)]. arXiv:hep-ph/0203110
S. Davidson, Completeness and complementarity for \(\mu \rightarrow e\gamma \mu \rightarrow e {{\bar{e}}} e\) and \(\mu A \rightarrow eA\). JHEP 02, 172 (2021). arXiv:2010.00317 [hep-ph]
S. Davidson, B. Echenard, Reach and complementarity of \(\mu \rightarrow e\) searches. Eur. Phys. J. C 82(9), 836 (2022). arXiv:2204.00564 [hep-ph]
W.C. Haxton, E. Rule, K. McElvain, M.J. Ramsey-Musolf, Nuclear-level effective theory of \(\mu \rightarrow \)e conversion: formalism and applications. Phys. Rev. C 107(3), 035504 (2023). arXiv:2208.07945 [nucl-th]
S. Davidson, Y. Kuno, M. Yamanaka, Selecting \(\mu \rightarrow e\) conversion targets to distinguish lepton flavour-changing operators. Phys. Lett. B 790, 380–388 (2019). arXiv:1810.01884 [hep-ph]
Y. Kuno, K. Nagamine, T. Yamazaki, Polarization transfer from polarized nuclear spin to \(\mu ^-\) spin in muonic atom. Nucl. Phys. A 475, 615–629 (1987)
R. Kadono, J. Imazato, T. Ishikawa, K. Nishiyama, K. Nagamine, T. Yamazaki, A. Bosshard, M. Dobeli, L. van Elmbt, M. Schaad et al., Repolarization of negative muons by polarized Bi-209 nuclei. Phys. Rev. Lett. 57, 1847–1850 (1986). arXiv:1610.08238 [nucl-ex]
Y. Okada, K. i Okumura, Y. Shimizu, Mu \(\rightarrow \) e gamma and mu \(\rightarrow \) e processes with polarized muons and supersymmetric grand unified theories. Phys. Rev. D 61, 094001 (2000). arXiv:hep-ph/9906446
Y. Okada, Ki. Okumura, Y. Shimizu, CP violation in the mu \(\rightarrow \) 3 e process and supersymmetric grand unified theory. Phys. Rev. D 58, 051901 (1998). arXiv:hep-ph/9708446
P.D. Bolton, S.T. Petcov, Measurements of \(\mu \rightarrow 3e\) decay with polarised muons as a probe of new physics. Phys. Lett. B 833, 137296 (2022). arXiv:2204.03468 [hep-ph]
H. Georgi, Effective field theory. Annu. Rev. Nucl. Part. Sci. 43, 209–252 (1993)
H. Georgi, On-shell effective field theory. Nucl. Phys. B 361, 339–350 (1991)
A.J. Buras, Weak Hamiltonian, CP violation and rare decays. arXiv:hep-ph/9806471
Les Houches Lect. Notes 108 (2020)
A.V. Manohar, Introduction to effective field theories. arXiv:1804.05863 [hep-ph]
A. Pich, Effective field theory with Nambu-Goldstone modes. arXiv:1804.05664 [hep-ph]
L. Silvestrini, Effective theories for quark flavour physics. arXiv:1905.00798 [hep-ph]
M. Balsiger, M. Bounakis, M. Drissi, J. Gargalionis, E. Gustafson, G. Jackson, M. Leak, C. Lepenik, S. Melville, D. Moreno et al. Solutions to problems at Les Houches Summer School on EFT. arXiv:2005.08573 [hep-ph]
W. Buchmuller, D. Wyler, Effective Lagrangian analysis of new interactions and flavor conservation. Nucl. Phys. B 268, 621 (1986)
B. Grzadkowski, M. Iskrzynski, M. Misiak, J. Rosiek, Dimension-six terms in the Standard Model Lagrangian. JHEP 1010, 085 (2010). arXiv:1008.4884 [hep-ph]
R. Alonso, E.E. Jenkins, A.V. Manohar, M. Trott, Renormalization group evolution of the standard model dimension six operators. III: Gauge coupling dependence and phenomenology. JHEP 1404, 159 (2014). arXiv:1312.2014 [hep-ph]
E.E. Jenkins, A.V. Manohar, M. Trott, Renormalization group evolution of the standard model dimension six operators II: Yukawa dependence. JHEP 1401, 035 (2014). arXiv:1310.4838 [hep-ph]
A. Crivellin, S. Davidson, G.M. Pruna, A. Signer, Renormalisation-group improved analysis of \(\mu \rightarrow e\) processes in a systematic effective-field-theory approach. JHEP 05, 117 (2017). arXiv:1702.03020 [hep-ph]
M. Ciuchini, E. Franco, L. Reina, L. Silvestrini, Leading order QCD corrections to b –\(>\) s gamma and b –\(>\) s g decays in three regularization schemes. Nucl. Phys. B 421, 41–64 (1994). arXiv:hep-ph/9311357
S. Bellucci, M. Lusignoli, L. Maiani, Leading logarithmic corrections to the weak leptonic and semileptonic low-energy Hamiltonian. Nucl. Phys. B 189, 329 (1981)
G. Buchalla, A.J. Buras, M.K. Harlander, The anatomy of epsilon-prime/epsilon in the standard model. Nucl. Phys. B 337, 313 (1990)
S. Kanemura, H. Sugiyama, Probing models of neutrino masses via the flavor structure of the mass matrix. Phys. Lett. B 753, 161–165 (2016). https://doi.org/10.1016/j.physletb.2015.12.012. arXiv:1510.08726 [hep-ph]
A.G. Akeroyd, M. Aoki, Single and pair production of doubly charged Higgs bosons at hadron colliders. Phys. Rev. D 72, 035011 (2005). arXiv:hep-ph/0506176
P. Fileviez Perez, T. Han, G.Y. Huang, T. Li, K. Wang, Neutrino masses and the CERN LHC: testing type II seesaw. Phys. Rev. D 78, 015018 (2008). arXiv:0805.3536 [hep-ph]
A. Melfo, M. Nemevsek, F. Nesti, G. Senjanovic, Y. Zhang, Type II seesaw at LHC: the roadmap. Phys. Rev. D 85, 055018 (2012). arXiv:1108.4416 [hep-ph]
F.F. Freitas, C.A. de S. Pires, P.S. Rodrigues da Silva, Inverse type II seesaw mechanism and its signature at the LHC and ILC. Phys. Lett. B 769, 48–56 (2017). arXiv:1408.5878 [hep-ph]
D.K. Ghosh, N. Ghosh, I. Saha, A. Shaw, Revisiting the high-scale validity of the type II seesaw model with novel LHC signature. Phys. Rev. D 97(11), 115022 (2018). arXiv:1711.06062 [hep-ph]
S. Antusch, O. Fischer, A. Hammad, C. Scherb, Low scale type II seesaw: present constraints and prospects for displaced vertex searches. JHEP 02, 157 (2019). https://doi.org/10.1007/JHEP02(2019)157. arXiv:1811.03476 [hep-ph]
W. Konetschny, W. Kummer, Nonconservation of total lepton number with scalar bosons. Phys. Lett. B 70, 433–435 (1977). https://doi.org/10.1016/0370-2693(77)90407-5
E. Ma, M. Raidal, U. Sarkar, Phenomenology of the neutrino mass giving Higgs triplet and the low-energy seesaw violation of lepton number. Nucl. Phys. B 615, 313–330 (2001). arXiv:hep-ph/0012101
S. Mandal, O.G. Miranda, G. Sanchez Garcia, J.W.F. Valle, X.J. Xu, Toward deconstructing the simplest seesaw mechanism. Phys. Rev. D 105(9), 095020 (2022). arXiv:2203.06362 [hep-ph]
E. Fernández-Martínez, X. Marcano, D. Naredo-Tuero, HNL mass degeneracy: implications for low-scale seesaws, LNV at colliders and leptogenesis. JHEP 03, 057 (2023). arXiv:2209.04461 [hep-ph]
D.V. Forero, S. Morisi, M. Tortola, J.W.F. Valle, JHEP 09, 142 (2011). https://doi.org/10.1007/JHEP09(2011)142. arXiv:1107.6009 [hep-ph]
S. Antusch, O. Fischer, Non-unitarity of the leptonic mixing matrix: Present bounds and future sensitivities. JHEP 10, 094 (2014). arXiv:1407.6607 [hep-ph]
E. Fernandez-Martinez, J. Hernandez-Garcia, J. Lopez-Pavon, Global constraints on heavy neutrino mixing. JHEP 08, 033 (2016). arXiv:1605.08774 [hep-ph]
M. Chrzaszcz, M. Drewes, T.E. Gonzalo, J. Harz, S. Krishnamurthy, C. Weniger, A frequentist analysis of three right-handed neutrinos with GAMBIT. Eur. Phys. J. C 80(6), 569 (2020). arXiv:1908.02302 [hep-ph]
M. Blennow, E. Fernández-Martínez, J. Hernández-García, J. López-Pavón, X. Marcano, D. Naredo-Tuero, Bounds on lepton non-unitarity and heavy neutrino mixing. arXiv:2306.01040 [hep-ph]
F. del Aguila, J.A. Aguilar-Saavedra, R. Pittau, Heavy neutrino signals at large hadron colliders. JHEP 10, 047 (2007). arXiv:hep-ph/0703261
A. Atre, T. Han, S. Pascoli, B. Zhang, The search for heavy majorana neutrinos. JHEP 05, 030 (2009). arXiv:0901.3589 [hep-ph]
F.F. Deppisch, P.S. Bhupal Dev, A. Pilaftsis, Neutrinos and collider physics. New J. Phys. 17(7), 075019 (2015). arXiv:1502.06541 [hep-ph]
S. Banerjee, P.S.B. Dev, A. Ibarra, T. Mandal, M. Mitra, Prospects of heavy neutrino searches at future lepton colliders. Phys. Rev. D 92, 075002 (2015). arXiv:1503.05491 [hep-ph]
S. Antusch, E. Cazzato, O. Fischer, Displaced vertex searches for sterile neutrinos at future lepton colliders. JHEP 12, 007 (2016). arXiv:1604.02420 [hep-ph]
A. Das, S. Jana, S. Mandal, S. Nandi, Probing right handed neutrinos at the LHeC and lepton colliders using fat jet signatures. Phys. Rev. D 99(5), 055030 (2019). arXiv:1811.04291 [hep-ph]
K. Mękała, J. Reuter, A.F. Żarnecki, Heavy neutrinos at future linear e\(^{+}\)e\(^{?}\) colliders. JHEP 06, 010 (2022). arXiv:2202.06703 [hep-ph]
A.M. Sirunyan et al. [CMS], Search for pair production of first-generation scalar leptoquarks at \(\sqrt{s} =\) 13 TeV. Phys. Rev. D 99(5), 052002 (2019). arXiv:1811.01197 [hep-ex]
A. Tumasyan et al. [CMS], Inclusive nonresonant multilepton probes of new phenomena at \(\sqrt{s}\)=13 TeV. Phys. Rev. D 105(11), 112007 (2022). arXiv:2202.08676 [hep-ex]
G. Aad et al. [ATLAS], Search for leptoquark pair production decaying into \(te^- {\bar{t}}e^+\) or \(t\mu ^- {\bar{t}}\mu ^+\) in multi-lepton final states in \(pp\) collisions at 13 TeV with the ATLAS detector. arXiv:2306.17642 [hep-ex]
G. Aad et al. [ATLAS], Search for pair production of third-generation scalar leptoquarks decaying into a top quark and a \(\tau \)-lepton in \(pp\) collisions at \( \sqrt{s} \) = 13 TeV with the ATLAS detector. JHEP 06, 179 (2021). arXiv:2101.11582 [hep-ex]
G. Aad et al. [ATLAS], Search for pairs of scalar leptoquarks decaying into quarks and electrons or muons in \( \sqrt{s} \) = 13 TeV \(pp\) collisions with the ATLAS detector. JHEP 10, 112 (2020). arXiv:2006.05872 [hep-ex] and see the plots at: https://atlas.web.cern.ch/Atlas/GROUPS/PHYSICS/PUBNOTES/ATL-PHYS-PUB-2023-006
A. Crivellin, C. Greub, D. Müller, F. Saturnino, Scalar leptoquarks in leptonic processes. JHEP 02, 182 (2021). arXiv:2010.06593 [hep-ph]
I. Bigaran, R.R. Volkas, Getting chirality right: single scalar leptoquark solutions to the \((g-2)_{e,\mu }\) puzzle. Phys. Rev. D 102(7), 075037 (2020). arXiv:2002.12544 [hep-ph]
J. Bernabeu, G.C. Branco, M. Gronau, CP restrictions on quark mass matrices. Phys. Lett. B 169, 243–247 (1986)
G.C. Branco, L. Lavoura, J.P. Silva, CP violation. Int. Ser. Monogr. Phys. 103, 1–536 (1999)
J. Brod, M. Gorbahn, E. Stamou, Standard-model prediction of \(\epsilon _K\) with manifest quark-mixing unitarity. Phys. Rev. Lett. 125(17), 171803 (2020). arXiv:1911.06822 [hep-ph]
T. Inami, C.S. Lim, Effects of superheavy quarks and leptons in low-energy weak processes k(L) —\(>\) mu anti-mu, K+ —\(>\) pi+ neutrino anti-neutrino and K0 \(<\)—\(>\) anti-K0. Prog. Theor. Phys. 65, 297 (1981) [Erratum: Prog. Theor. Phys. 65 (1981), 1772]
W.J. Marciano, A.I. Sanda, Exotic decays of the muon and heavy leptons in gauge theories. Phys. Lett. B 67, 303–305 (1977)
M.B. Gavela, A. Le Yaouanc, L. Oliver, O. Pene, J.C. Raynal, T.N. Pham, CP violation induced by penguin diagrams and the neutron electric dipole moment. Phys. Lett. B 109, 215–220 (1982)
G. Hernández-Tomé, G. López Castro, P. Roig, Flavor violating leptonic decays of \(\tau \) and \(\mu \) leptons in the Standard Model with massive neutrinos. Eur. Phys. J. C 79(1), 84 (2019) [Erratum: Eur. Phys. J. C 80(5), 438 (2020)]. arXiv:1807.06050 [hep-ph]
P. Blackstone, M. Fael, E. Passemar, \(\tau \rightarrow \mu \mu \mu \) at a rate of one out of \(10^{14}\) tau decays? Eur. Phys. J. C 80(6), 506 (2020). https://doi.org/10.1140/epjc/s10052-020-8059-7. arXiv:1912.09862 [hep-ph]
M. Raidal, A. Santamaria, Muon electron conversion in nuclei versus mu –\(>\) e gamma: an effective field theory point of view. Phys. Lett. B 421, 250–258 (1998). arXiv:hep-ph/9710389
M. Aker et al. [KATRIN], Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nat. Phys. 18(2), 160–166 (2022). arXiv:2105.08533 [hep-ex]
N. Aghanim et al. [Planck], Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 641, A6 (2020) [Erratum: Astron. Astrophys. 652 (2021), C4]. arXiv:1807.06209 [astro-ph.CO]
A.A. Esfahani et al. [Project 8], The Project 8 Neutrino Mass Experiment. arXiv:2203.07349 [nucl-ex]
R. Kitano, Y. Okada, P odd and T odd asymmetries in lepton flavor violating tau decays. Phys. Rev. D 63, 113003 (2001). arXiv:hep-ph/0012040
J.D. Vergados, H. Ejiri, F. Simkovic, Theory of neutrinoless double beta decay. Rep. Prog. Phys. 75, 106301 (2012). arXiv:1205.0649 [hep-ph]
K. Hayasaka et al. [Belle Collaboration ], New search for \(\tau \rightarrow e \gamma \) and \(\tau \rightarrow \mu \gamma \), decays at Belle. Phys. Lett. B 666, 16–22 (2008). arXiv:0705.0650 [hep-ex]
B. Aubert et al. [BABAR Collaboration ], Searches for lepton flavor violation in the decays \(\tau ^\pm \rightarrow e^\pm \gamma \) and \(\tau ^\pm \rightarrow \mu ^\pm \gamma \). Phys. Rev. Lett. 104, 021802 (2010). arXiv:0908.2381 [hep-ex]
L. Morel, Z. Yao, P. Cladé, S. Guellati-Khélifa, Determination of the fine-structure constant with an accuracy of 81 parts per trillion. Nature 588(7836), 61–65 (2020). https://doi.org/10.1038/s41586-020-2964-7
B. Abi et al. [Muon g-2], Phys. Rev. Lett. 126(14), 141801 (2021). https://doi.org/10.1103/PhysRevLett.126.141801. arXiv:2104.03281 [hep-ex]
T.S. Roussy, L. Caldwell, T. Wright, W.B. Cairncross, Y. Shagam, K.B. Ng, N. Schlossberger, S.Y. Park, A. Wang, J. Ye et al., A new bound on the electron’s electric dipole moment. arXiv:2212.11841 [physics.atom-ph]
G.W. Bennett et al. [Muon (g-2)], An improved limit on the muon electric dipole moment. Phys. Rev. D 80, 052008 (2009). arXiv:0811.1207 [hep-ex]
M. Pospelov, A. Ritz, Ann. Phys. 318, 119–169 (2005). https://doi.org/10.1016/j.aop.2005.04.002. arXiv:hep-ph/0504231
M. Bona et al. [UTfit], Model-independent constraints on \(\Delta F=2\) operators and the scale of new physics. JHEP 03, 049 (2008). arXiv:0707.0636 [hep-ph]
H. Simma, Equations of motion for effective Lagrangians and penguins in rare B decays. Z. Phys. C 61, 67–82 (1994). arXiv:hep-ph/9307274
V. Cirigliano, R. Kitano, Y. Okada, P. Tuzon, On the model discriminating power of mu –\(>\) e conversion in nuclei. Phys. Rev. D 80, 013002 (2009). arXiv:0904.0957 [hep-ph]
Y. Aoki et al. [Flavour Lattice Averaging Group (FLAG)], FLAG Review 2021. Eur. Phys. J. C 82(10), 869 (2022). arXiv:2111.09849 [hep-lat]
T. Suzuki, D.F. Measday, J.P. Roalsvig, Total nuclear capture rates for negative muons. Phys. Rev. C 35, 2212 (1987)
V. Cirigliano, S. Davidson, Y. Kuno, Spin-dependent \(\mu \rightarrow e\) conversion. Phys. Lett. B 771, 242–246 (2017). arXiv:1703.02057 [hep-ph]
S. Davidson, Y. Kuno, A. Saporta, Spin-dependent \({\mu \rightarrow e}\) conversion on light nuclei. Eur. Phys. J. C 78(2), 109 (2018). arXiv:1710.06787 [hep-ph]
M. Hoferichter, J. Menéndez, F. Noël, Improved limits on lepton-flavor-violating decays of light pseudoscalars via spin-dependent \(\mu \rightarrow e\) conversion in nuclei. arXiv:2204.06005 [hep-ph]
M.A. Shifman, A.I. Vainshtein, V.I. Zakharov, Remarks on Higgs boson interactions with nucleons. Phys. Lett. B 78, 443 (1978)
V. Cirigliano, R. Kitano, Y. Okada, P. Tuzon, On the model discriminating power of \(\mu \rightarrow e\) conversion in nuclei. Phys. Rev. D 80, 013002 (2009). arXiv:0904.0957 [hep-ph]
M. Hoferichter, J. Ruiz de Elvira, B. Kubis, U.G. Meisner, High-precision determination of the pion-nucleon term from Roy-Steiner equations. Phys. Rev. Lett. 115, 092301 (2015). https://doi.org/10.1103/PhysRevLett.115.092301. arXiv:1506.04142 [hep-ph]
A. Crivellin, M. Hoferichter, M. Procura, Phys. Rev. D 89, 093024 (2014). https://doi.org/10.1103/PhysRevD.89.093024. arXiv:1404.7134 [hep-ph]
C.W. Murphy, Low-energy effective field theory below the electroweak scale: dimension-8 operators. JHEP 04, 101 (2021). arXiv:2012.13291 [hep-ph]
H.L. Li, Z. Ren, J. Shu, M.L. Xiao, J.H. Yu, Y.H. Zheng, Complete set of dimension-eight operators in the standard model effective field theory. Phys. Rev. D 104(1), 015026 (2021). arXiv:2005.00008 [hep-ph]
S. Davidson, M. Gorbahn, M. Leak, Majorana neutrino masses in the renormalization group equations for lepton flavor violation. Phys. Rev. D 98(9), 095014 (2018). arXiv:1807.04283 [hep-ph]
I. Doršner, S. Fajfer, A. Greljo, J.F. Kamenik, N. Košnik, I. Nišandžic, New physics models facing lepton flavor violating Higgs decays at the percent level. JHEP 06, 108 (2015). arXiv:1502.07784 [hep-ph]
F.F. Deppisch, S. Kulkarni, H. Päs, E. Schumacher, Leptoquark patterns unifying neutrino masses, flavor anomalies, and the diphoton excess. Phys. Rev. D 94(1), 013003 (2016). arXiv:1603.07672 [hep-ph]
H.K. Dreiner, An introduction to explicit R-parity violation. Adv. Ser. Dir. High Energy Phys. 21, 565–583 (2010). arXiv:hep-ph/9707435
R. Barbier, C. Berat, M. Besancon, M. Chemtob, A. Deandrea, E. Dudas, P. Fayet, S. Lavignac, G. Moreau, E. Perez et al., R-parity violating supersymmetry. Phys. Rep. 420, 1–202 (2005). arXiv:hep-ph/0406039 [hep-ph]
S. Davidson, M. Losada, Basis independent neutrino masses in the R(p) violating MSSM. Phys. Rev. D 65, 075025 (2002). arXiv:hep-ph/0010325 [hep-ph]
G. Aad et al. [ATLAS], Search for the charged-lepton-flavor-violating decay \(Z\rightarrow e\mu \) in \(pp\) collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. Phys. Rev. D 108, 032015 (2023). arXiv:2204.10783 [hep-ex]
M. Ardu, S. Davidson, M. Gorbahn, Sensitivity of \(\mu \rightarrow \)e processes to \(\tau \) flavor change. Phys. Rev. D 105(9), 096040 (2022). arXiv:2202.09246 [hep-ph]
Acknowledgements
We thank Ann-Kathrin Perrevoort for helpful comments about observables in \(\mu \rightarrow e {\bar{e}} e\). The work of SL is supported in part by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 860881-HIDDeN. The work of MA is supported by the Spanish AEI-MICINN PID2020-113334GB-I00/AEI/10.13039/501100011033.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: \(\mu A \rightarrow \! eA \) operators
References [79, 158] observed that the target-dependence of the \(\mu A \rightarrow \! eA \) rate could give information about the contributing operators. So the aim of this Appendix is to identify the independent four-fermion operators \(\mathcal{O}_{Al,X}\) and \(\mathcal{O}_{Au\perp ,X}\), probed by Spin-Independent (SI) \(\mu A \rightarrow \! eA \) on light and heavy targets. We use the formalism of [78] and use the nuclear calculation of [79]. The operators \(\mathcal{O}_{Al,X}\) and \(\mathcal{O}_{Au,X}\) can be constructed in the nucleon basis relevant at the experimental scale, or in a quark basis more relevant for comparing to models. In the following, we first construct these operators in the nucleon basis, where operators, coefficients and parameters wear “tildes”, then express them in the quark basis without tildes. Notice that normalisations change between the bases, so there are numerical differences between, e.g., \({\widetilde{B}}_A\) and \(B_A\).
The results in this Appendix have two peculiarities, arising in the matching of nucleons with quarks. The first is that there is a “loss of information” in going from nucleons to quarks, because the scalar u and d content of a nucleon are comparable: \(\langle N|{\bar{u}} u|N\rangle \approx \langle N|{\bar{d}} d|N\rangle \) (Or in the notation of Eq (A.8), \(G_S^{N,u}\approx G_S^{N,d}\), which is obtained both with lattice and \(\chi \)PT methods [159]). As a result, the coefficients of scalar p and n operators need to be measured accurately, in order to distinguish scalar coefficients involving us vs ds. The second curiosity is that \(\mathcal{O}_{Au\perp ,X}\) is different, when calculated in the quark or nucleon bases. That is, Ref. [83] obtained an orthonormal basis of nucleon operators for the two-dimensional space probed by Gold and Titanium. When these nucleon operators are matching to quarks, they are no longer orthogonal. In Ref. [81], the operators probed by Gold and Titanium were first matching to quarks, then decomposed into orthonormal components. We follow the second approach here, because the aim is to identify the independent information available about models, and that is expressed in the quark basis in our bottom-up perspective.
In the nucleon basis at the experimental scale, the lepton-nucleon operators relevant for Spin-Independent \(\mu A \rightarrow \! eA \) can be added to the Lagrangian as [79]
where \(\widetilde{\mathcal{O}}_{S,X}^{(NN)} = ({\overline{e}} P_X \mu ) ({\overline{N}} N)\) and \(\widetilde{\mathcal{O}}_{V,X}^{(NN)} = ({\overline{e}} \gamma ^\alpha P_X \mu ) ({\overline{N}}\gamma _\alpha N)\). Notice that the nucleon currents are not chiral: \(\widetilde{\mathcal{O}}_{V,X}^{(NN)} = \widetilde{\mathcal{O}}_{V,XL}^{(NN)} + \widetilde{\mathcal{O}}_{V,XR}^{(NN)}\), so
A similar relation holds for the coefficients on quarks used in \(\mu A \rightarrow \! eA \).
The Spin-Independent conversion rate, normalised to the \(\mu \) capture rateFootnote 12\( (\mu + A\rightarrow \nu + A')\), can be written [79]
The nucleus(A) and nucleon(N) -dependent “overlap integrals” \( I_{A,V}^{(N)}\), \(I_{A,S}^{(N)},I_{A,D}\) correspond to the integral over the nucleus of the lepton wavefunctions and the appropriate nucleon density; we use here the results of [79]. We neglect smaller contributions to the \(\mu \rightarrow e\) conversion amplitude, such as the Spin-Dependent part [161,162,163] which is not coherently enhanced by the numerous nucleons, and subdominant Spin-Independent contributions arising from, e.g. \(\mu e\gamma \gamma \) operators [78], or from tensor contributions to the scalar coefficient [161].
Focusing on an outgoing electron of left helicity, the Branching Ratio can be re-expressed as [81, 83] (\({\widetilde{B}}_{A}\) here is written \(B_A\) in [83])
where the coefficients (of operators with outgoing \(e_L\)) are lined up in a vector \(\vec {\tilde{C}}_L\), the overlap integrals are lined up in a five-component vector \(\vec {v}_{A5} = (I_{A,S}^{(p)},I_{A,V}^{(p)},I_{A,S}^{(n)},I_{A,V}^{(n)},\frac{1}{4}I_{A,D})\), and the target-dependent constants \( {\widetilde{B}}_A \) are
with \({\widetilde{B}}_{Al}=142\),\({\widetilde{B}}_{Ti}=250\), and \({\widetilde{B}}_{Au}=300\).
In order to identify the four-fermion operator probed by a target A (as opposed to the combination of coefficients), it is convenient to temporarily neglect the dipole. This implies that \(\mu A \rightarrow \! eA \) on the target nucleus A probes the combination of coefficients \(\tilde{C}_{A,L} \equiv \vec {\tilde{C}}_L \cdot {\hat{v}}_{A4}\) where \( \vec {v}_{A4} \) contains only the four-fermion overlap integrals (so neglects the dipole). So \(\tilde{C}_{A,L} \) is the coefficient of the operator
because the Branching Ratio resulting from \(\delta \mathcal{L} = \tilde{C}_{A,L} \widetilde{\mathcal{O}}_{A,L}\) will be
in agreement with Eq. (A.4). In general,
where on light targets like Aluminium, \(I_A^D/(4|v_{A5}|)= 0.27\) and \(|v_{A4}|/|v_{A5}| \simeq \) 0.96.
In order to express the Al and Au operators in the quark basis, there is one more step. The nucleon operators of Eq. (A.1) can be matched at 2 GeV onto light quark operators \(\mathcal{O}_{S,X}^{qq} = ({\overline{e}} P_X \mu ) ({\overline{q}} q) \), \(\mathcal{O}_{V,X}^{qq} = ({\overline{e}} \gamma ^\alpha P_X \mu ) ({\overline{q}} \gamma _\alpha q) \) using
where the parameters \(G^{N,q}_O\) can be determined from sum rules, lattice calculations or experiment, and we use the values summarised in [81]. Below the heavy quark (b and c) mass scales, there is also a two-step contribution to scalar nucleon operators from scalar quark operators [164, 165], via matching first onto the gluon operator \(({\bar{e}} P_R \mu )GG\), then onto nucleons.Footnote 13 As a result, the nucleon and quark coefficients are related as
for \(q\in \{u,d,s,c,b,t\}\), and \(O\in \{S,V\}\). This allows to define quark “overlap integrals” for target A as
which can be assembled into a “target vector” \(\vec {u}_A\) in the space of operators describing \(\mu \rightarrow e\) conversion on quarks:
Analogously to Eq. (A.6), we use \({\hat{u}}_{Al} \approx {\hat{u}}_{Ti}\) to define \(\mathcal{O}_{Al}\) in Eq. (2.4). The orthogonal direction probed by Gold, \({\hat{u}}_{Au \perp }\) is defined as
where the operators are in the order given in Eq. (A.11), sin\(\theta _{A} \approx 0.093\) and \(\theta _{A}\) is \(\approx \) 5.3 degrees [81]. This gives the definition of \(\mathcal{O}_{Au\perp }\) in Eq. (2.6).
Finally, it can be convenient, in the quark operator basis, to write
where \(B_A\) is defined as is Eq. (A.5) but with \(\vec {v}_{A5} \rightarrow \vec {u}_A\), \(B_{Al} =19363\), \(B_{Ti} =32860\), \(B_{Au} =24519\), and \(d_A = I_D/(4|\vec {u}_A|)= 0.0228, 0.0219,0.0246 \) respectively for Al, Ti and Au.
Appendix B: Observable coefficients at \(\Lambda _{NP}\)
The coefficients of the Lagrangian of Eq. (2.3), which are at the experimental scale \(m_\mu \), are written in [80] as linear combinations of coefficients at some higher scale taken to be \(m_W\). These formulae allows to identify what magnitude of which coefficients needs to be retained in matching to the models. This Appendix gives the linear combination of coefficients probed by \(\mu A \rightarrow \! eA \) on Aluminium, not given in [80] and also on Gold for completeness.
Using the results of [79], the combination of coefficients at the scale \(\Lambda \) which is probed by \(\mu A \rightarrow \! eA \) on Aluminium, for outgoing \(e_L\), is:

where the result for Titanium can be approximately obtained by replacing \( {\widetilde{B}}_{Al} = 142 \longrightarrow {\widetilde{B}}_{Ti} = 250\). The constraint from \(\mu A \rightarrow \! eA \) on Gold is:

where we used the scalar quark densities in the nucleon of Ref. [166, 167], the coefficients are at \(\Lambda \), \(m_f = m_f(m_f)\),
\(\eta \) and \(f_{TS}\) are defined in Eq.(2.17), \({\widetilde{\ln }} \equiv \ln (\Lambda /m_\psi )\) where \(m_\psi \in \{m_b, 2~\textrm{GeV},m_\mu \}\) is a suitably chosen lower cutoff for the logarithm, and the dipole contribution is given at the experimental scale (it can be written in terms of coefficients at \(\Lambda \) as given in [80]). A similar bound applies with L and R interchanged.
Appendix C: Matching the models with the EFT
This section summarises the matching of the models with EFT. We first discuss which EFT to match onto in Sect. C1, and how we define the lepton flavour basis in Sect. C2, then give the matching of our three models onto a QED\(\times \)QCD-invariant EFT in Sect. C3. In Sect. C4, we discuss some curiosities related to the EFT description of penguin diagrams in the models.
1.1 1. Which EFT to match to?
The models we study contain new particles with masses around the TeV, so we need a recipe to match these models onto the QCD\(\times \)QED-invariant EFT appropriate below the weak scale.
A formally correct approach would be to match the models to the EFT at \(m_W\). Indeed, this would be similar to the weak-scale matching in the SM, where one removes the t, W, Z and h at \(m_W\), because there is no “large log” argument for sequential matching out of t, h, Z then W. However, this approach has two drawbacks: first, it implies calculating many loop diagrams involving SM particles and New Physics in the broken SM, and second, resumming QCD from the TeV to the weak scale is unobvious because the loops one calculates are electroweak. (But the QCD issue may be minor, because  varies by \(\sim 30\%\) from \(m_Z\rightarrow \)TeV.) We will follow this approach for the inverse seesaw, where the leading contributions arise in electroweak loops(that induce no field bilinears running under QCD), and below \(m_W\) the RGEs of QED only modify the magnitude of the coefficients.
varies by \(\sim 30\%\) from \(m_Z\rightarrow \)TeV.) We will follow this approach for the inverse seesaw, where the leading contributions arise in electroweak loops(that induce no field bilinears running under QCD), and below \(m_W\) the RGEs of QED only modify the magnitude of the coefficients.
If we match to an EFT at \(\Lambda _{NP}\), there could be fewer diagrams to calculate, and QCD can be resummed. However, the scale ratio TeV/v is not large, so higher order contributions in the EFT expansions in log-enhanced loops and operator dimension can be relevant. For instance, ln(TeV/\(m_W)\simeq \) 2.5 and ln(TeV/\(m_t)\simeq \) 1.75, so one-loop model diagrams with weak-scale particles in the loop can have finite parts comparable to the log-enhanced part – despite that in EFT power-counting, these finite parts should be included at NLL, and not at LL where they can give undesirable dependence on the renormalisation scheme of the operators. Also, by power-counting, dimension eight operators are only suppressed with respect to dimension six by a factor \(v^2/\textrm{TeV}^2\sim \) 0.03.
The obvious EFT to use at a TeV is SMEFT, which can then be matched at \(m_W\) to the low-energy EFT. This two-step matching should allow to correctly resum QCD at all scales. Some of the four-fermion operators present in the low-energy EFT, first arise in SMEFT at dimension eight – an example is the \(\mathcal{O}_{S,XX}^{e\mu ee}\) operator that contributes at tree level to \(\mu \rightarrow e {\bar{e}} e\) (see Eq. 2.3). Matching the models to SMEFT then the low-energy EFT generates contributions to these additional operators at \(\mathcal{O}(v^2/(\Lambda _{NP}^2 v^2))\) via the “penguin” operators (see Eqs. C.26–C.28) or \(\mathcal{O}_{EH}\), but in order to recover contributions at \(\mathcal{O}(v^2/\Lambda _{NP}^4)\), we need to match onto dimension eight operators, and include the dimension six\(^2\rightarrow \) dimension eight mixing in the RGEs. Dimension eight operators are legion in SMEFT [168, 169], so this requires cherry-picking the relevant operators.
We also tried matching out the new particles and the electroweak bosons at \(\Lambda _{NP}\), such that below \(\Lambda _{NP}\), we use the RGEs of QCD and QED. In this approach, there are four-fermion operators induced by the Higgs and the Z in our EFT, and including the dimension six\(^2 \rightarrow \) dimension eight mixing in the RGEs reproduces the \(\mathcal{O}(\alpha \ln )\) terms obtained in SMEFT at dimension six, as well as the \(\mathcal{O}(1/\Lambda _{NP}^4)\) terms. This is simpler than using SMEFT, because there is no intermediate matching, and its easier to pick out the relevant dimension eight operators. However, this approximation of treating electroweak particles as contact interactions when they are dynamical, can in some casesFootnote 14 give the wrong QCD and/or QED running from \(\Lambda _{NP}\rightarrow m_W\). And unfortunately, numerous loop calculations must be performed in the model to obtain the potentially relevant finite part of electroweak loops.
In summary, we aim for the first, correct, approach, augmented by resummed one-loop QCD corrections. But sometimes we neglect finite matching contributions. For conciseness, we give the matching results at \(\Lambda _{NP}\) (rather than \(m_W\)), because the RGEs we implement automatically will include the log-enhanced QED and QCD loops. The finite and log\((\Lambda /m_W)\)-enhanced loops involving h,Z and W, and the dimension six\(^2\rightarrow \) dimension eight mixing are included in the matching. In resumming QCD, we use five flavour anomalous dimensions at all scales.
1.2 2. The Yukawa correction \(\mathcal{O}_{EH}\)
When lepton flavour is not conserved, the charged lepton mass eigenstate basis provides a pragmatic and unambiguous definition of lepton flavour. It is a significant simplification to always work in this basis, not only in the EFT, but also in models. This circumvents a problem that could arise in matching models onto EFT: if the model induces the SMEFT “Yukawa correction” operator
then the mass eigenstate basis that defines lepton flavour is rotated with respect to the Yukawa eigenbasis, which seems the obvious definition of flavour in a model. If the rotation from Yukawa to mass eigenbases is performed in matching, the resulting corrections are at dimension 8 in the EFT(\(\propto C_{EH}\times C_{other}\)), to which some \(\mu \rightarrow e\) observables can be sensitive [59]. However, to obtain self-consistent results at dimension 8 requires including dimension 6 operators in the equations of motion when reducing the operator basis (this is particularily relevant for the mass correction \(\mathcal{O}_{EH}\)). In addition, performing this basis rotation appears daunting.
The simplest solution is define the charged lepton flavours as the “mass” eigenstates also in the model. This means that the Yukawa matrix \(Y_e\) is not quite diagonal, and that the flavour eigenstates cannot be simply obtained from the Lagrangian of the model. Instead, the matrix \( [C_{EH}]^{\alpha \beta }\) must be calculated, then one diagonalises
However, since the Lagrangian is invariant under flavour basis transformations, an explicit calculation of the basis is rarely required. And current LHC constraints on flavour-changing Higgs decays impose that renormalisation group effects of the off-diagonals of \([Y_e]\) are below the sensitivity of upcoming experiments [59]. Following this approach, we include the \(\mathcal{O}_{EH}\) operator in the lepton equations of motion in our EFT, so that we distinguish \([Y_e]\) which appears at Higgs vertices from \([m_e]/v\) which arises from the equations of motion.
1.3 3. Matching results
The matching results are given in the usual theory-motivated operator basis of the EFT, where there are a large number of operators. However, \(\mu \rightarrow e \gamma \), \(\mu \rightarrow e {\bar{e}} e\) and \(\mu A \rightarrow \! eA \) can only probe the coefficients of the 12 operators in the experimentally-observable subspace, which are given in Sect. B. Since the 12 observables have wildly varying overlaps with many high-scale operators, its important to estimate the magnitude of all coefficients obtained in matching. So we list the coefficients that we include in our results, and also estimate subleading corrections to those coefficients, and contributions to coefficients we took to be vanishing.
1.3.1 a. Type II matching-to-QED summary
The type II seesaw model and its Lagrangian are discussed in Sect. 3. We draw the relevant matching diagrams in Fig. 5. At tree level in the model, one obtains the neutrino mass matrix
Above the weak scale, the lepton number changing neutrino mass matrix operator runs, and mixes with itself to generate LFV operators [170] with coefficients \(\propto m_\nu ^2/v^2\). We neglect the running because TeV \(\rightarrow m_W\) is not far, and and the dimension five\(^2 \rightarrow \) dimension six mixing because the effect is tiny.
There are also four-doublet-lepton vector operators with coefficient
where \( \alpha ,\beta ,l\in \{ e,\mu ,\tau \}\) and \(\alpha \ne \beta \). Then at one-loop in the model, there is a contribution to the dipole coefficients:
where we recall that our dipole operator includes a factor \(m_\mu \).
In practise, we neglect \(C^{e\mu }_{DL} \propto m_e\), and the matching contributions to all the other operators; we estimate below the largest matching contributions we neglected for each coefficient.
Representative diagrams of matching contributions that we neglect, because they are subdominant or below upcoming experimental sensitivity: from left to right, a box with two triplets \(\Delta \) that contributes to vector four-lepton operators, a box with a \(\Delta \) and a Higgs, and the Z penguin. \(\ell \) are doublet leptons, and e are singlets
-
1.
Vector four-fermion operators \(\mathcal{O}_{VLX}\) will be generated with log-enhanced coefficients by the photon penguin in renormalisation group running. We list here some other one-loop matching contributions to four lepton operators (illustrated in the first three diagrams of Fig. 6): there are boxes exchanging two \(\Delta \)s (first line of the expression below), or a Higgs and a \(\Delta \) (second line where \(m_\delta = \textrm{max}\{m_\alpha ,m_\beta \}\)) and finally the Z-penguins which are discussed in Appendix C4:
$$\begin{aligned}{} & {} (C^{\alpha \beta ll }_{VLL}, C^{\alpha \beta ll}_{VLR}, C^{\alpha \beta ll }_{VRR}, C^{e\alpha \beta ll }_{VRL}) \\{} & {} \quad \sim -\left( \frac{5( [m_\nu m_\nu ^\dagger ]^{ \alpha \beta } [f^* f]^{ll} + [m_\nu m_\nu ^*]^{\alpha l} [f^* f ]^{ l \beta }) }{64\pi ^2 |\lambda _H|^2 v^2}, 0,0,0 \right) \\{} & {} + \left( 0, [Y_e^\dagger m^*_\nu ]^{ l \beta } [Y^T_e m_\nu ]^{l \alpha } \ln \frac{M_\Delta }{m_l},0, [m^*_\nu Y_e]^{l \beta } [m_\nu Y_e^*]^{l \alpha } \ln \frac{M_\Delta }{m_\delta } \right) \\{} & {} \times \frac{3 }{32\pi ^2 |\lambda _H|^2v^2} \\{} & {} + {\Bigg (}2 g^e_L, 2 g^e_R, 0,0 {\Bigg )}\\{} & {} \quad \times \frac{1 }{ (16 \pi ^2) |\lambda _H|^2 v^4 } {\Bigg [}m_\nu m^*_e \ln \frac{M_\Delta }{m_e} m_e^T m^*_\nu {\Bigg ]}_{ \alpha \beta } \end{aligned}$$where recall that \([m_\nu m_\nu ^*]^{\alpha \beta }\) that appears in the triplet-triplet boxes is determined by the neutrino oscillation parameters so is independent of the neutrino mass scale or Majorana phases. In the Z-penguin diagrams, there are mass insertions on the internal lepton lines, for which we use a Feynman rule \(-i[m_e]_{\alpha \alpha }/v\) rather than \(-i [Y_e]_{\alpha \alpha }\), as discussed in Sect. C2. The \(g^f_X\) couplings here and in the following equations refer to the interactions of the Z boson with a fermion f vector current of chirality X. For instance, the Feynman rule for the Z couplings to leptons reads \(-i g/(2 c_W)\gamma ^\alpha (g^e_L P_L+g^e_R P_R)\)
-
2.
Vector operators with a quark bilinear can also be generated by the Z-penguin:
$$\begin{aligned}{} & {} (C^{e\mu QQ }_{VLL}, C^{e\mu QQ}_{VLR}, C^{e\mu QQ }_{VRR}, C^{e\mu QQ }_{VRL}) \sim {\Bigg (}2 g^Q_L, 2 g^Q_R, 0,0 {\Bigg )}\nonumber \\{} & {} \times \frac{1 }{ (16 \pi ^2) |\lambda _H|^2 v^4 } {\Big [}m_\nu m^*_e \ln \frac{M_\Delta }{m_e} m_e^T m^*_\nu {\Big ]}_{ e \mu } \end{aligned}$$(C.4) -
3.
Scalar four-lepton operators involving a \(\tau \) bilinear can be generated by a box where the Higgs and the triplet scalar \(\Delta \) are exchanged, as illustrated in the middle diagram of Fig. 6. This gives \(\mathcal{O}^{e \tau \tau \mu }_{V XY}\) operators, which can be Fiertz-transformed to LR and RL scalars, given on the first line below:
$$\begin{aligned}{} & {} (C^{e\mu \tau \tau }_{SLL}, C^{e\mu \tau \tau }_{SRR}, C^{e\mu \tau \tau }_{SLR}, C^{e\mu \tau \tau }_{SRL}) \\{} & {} \quad \sim \Big ( 0,0, [ Y^T_e m_\nu ^*]^{\tau \mu } [m_\nu Y^*_e]^{\tau e}, [m_\nu ^* Y_e]^{\tau \mu } [Y_e^\dagger m_\nu ]^{\tau e} \Big )\\{} & {} \quad \times \frac{3 }{32\pi ^2 |\lambda _H|^2v^2} \ln \frac{m_\Delta }{m_\delta } \\{} & {} \quad - y_\tau \Big ( [ m_\nu m_\nu ^* ]_{\mu e} y_e, [ m_\nu m_\nu ^* ]_{e \mu } y_\mu , [ m_\nu m_\nu ^* ]_{\mu e}y_e, \\{} & {} \quad \times [ m_\nu m_\nu ^* ]_{e \mu } y_\mu \Big ) \frac{3 \lambda _4 }{32\pi ^2 |\lambda _H|^2 v^2} \end{aligned}$$where on the first line \(m_\delta \) that provides the lower cutoff of the logarithm is the heaviest internal lepton. The scalar operators on the second line are mediated by “Higgs penguins”, or Higgs exchange with a flavour-changing vertex corresponding to the loop-induced SMEFT coefficient \(C_{EH}^{e\mu } \simeq -3 \lambda _4 [m_\nu m_\nu ^*Y_e]^{e\mu }/(64\pi ^2|\lambda _H|^2 v^2)\), and we used \(m_h^2/v^2 \simeq 1/2\) and a Higgs-triplet interaction \(\delta \mathcal{L}\supset \lambda _4 \Delta ^\dagger \Delta H^\dagger H\).
-
4.
Higgs “penguin diagrams”, as illustrated in Fig. 7 and which generated the second line of the previous equation, can also generate scalar operators involving quarks \(Q \in \{d,u, s,c,b\}\), and other flavours of lepton \(l\in \{e,\mu \}\). They are all suppressed by two Yukawa couplings and a loop:
$$\begin{aligned}{} & {} ( C^{e\mu ll}_{SLL}, C^{e\mu ll }_{SRR} ) \sim - y_l \Big ( [ m_\nu m_\nu ^* ]_{\mu e} y_e, [ m_\nu m_\nu ^* ]_{e \mu } y_\mu \Big )\\{} & {} \frac{3 \lambda _4 }{32\pi ^2 |\lambda _H|^2 v^2}\\{} & {} (C^{e\mu QQ }_{SLL}, C^{e\mu QQ}_{SRR}, C^{e\mu QQ }_{SLR}, C^{e\mu QQ }_{SRL}) \\{} & {} - y_Q \Big ( [ m_\nu m_\nu ^* ]_{\mu e} y_e, [ m_\nu m_\nu ^* ]_{e \mu } y_\mu ,\nonumber \\{} & {} {[} m_\nu m_\nu ^* ]_{\mu e}y_e, [ m_\nu m_\nu ^* ]_{e \mu } y_\mu \Big ) \frac{3 \lambda _4 }{32\pi ^2 |\lambda _H|^2 v^2}. \end{aligned}$$ -
5.
Finally, we neglect the tensor operators in this model. The \(\tau \)-tensors can be induced at two loop, suppressed by two lepton Yukawas, via Higgs exchange with \(\tau \rightarrow \{e,\mu \}\) flavour-changing couplings at both vertices [171] (e.g. as illustrated in Fig. 7).
Representative diagrams generating scalar four-fermion operators via Higgs exchange. If the model is matched to SMEFT, the external fermion current \({\bar{f}}f\) should not be included and the diagrams match onto the operator \(\mathcal{O}^\dagger _{EH}= H^\dagger H {\bar{e}} H^\dagger \ell \), which generates LFV Higgs couplings. Or the diagrams can be matched directly to a QED\(\times \)QCD invariant four-fermion operator
1.3.2 b. Inverse seesaw matching-to-QED summary
The inverse seesaw is introduced in Sect. 3 and the Lagrangian is written in Eq. (3.3). At tree-level, the left diagram of Fig. 8 gives the following neutrino mass matrix
In the following we neglect the matching contributions that are \(\propto m_\nu \), thus suppressed by the small neutrino masses, and we only consider the insertion of lepton number conserving interactions. The right diagram in Fig. 8 gives tree-level matching contribution to the SMEFT penguins \(C_{HL1,3}\), contributing to the difference \(C_{HL1}-C_{HL3}\) but without modifying the fermion Z couplings \(\propto ( C_{HL1}+C_{HL3})\).
Including the one-loop corrections arising from the (representative) diagrams in Fig. 9, we find
where \(g', g\) are respectively the hypercharge and SU(2) gauge couplings.
The vector four lepton operators get contribution from the \(\gamma \) and Z penguins (Fig. 10a, b), as well as from box diagrams (Fig. 10c) when the external leptons are left-handed
where \(\alpha ,\beta ,l\in \{e,\mu ,\tau \}\) and \(\alpha \ne \beta \). Similarly, the two-lepton two-quark vectors matching conditions are
where \(q_Q\) is the electric charge of the \(Q=u,d\) quark and \(\eta _{u}=-\eta _d=1\).
We neglect all vectors with right-handed flavour changing currents because they are suppressed by two insertions of the lepton Yukawas, and arise at dimension eight or at higher-loops
giving contributions below the future experimental sensitivities. Similar Yukawa suppressions are expected for the scalar operators, which we neglect.
The dipole receive matching contributions from diagrams involving virtual sterile neutrinos (Fig. 11a), as well as from the exchange of a virtual active neutrino between flavour conserving and flavour changing (\(\propto C_{HL3}\)) W couplings (Fig. 11b). The resulting dipole coefficients are
As depicted in Fig. 12, matching contributions featuring four neutrino Yukawa matrices can emerge either at dimension eight or via higher-loops. To estimate their magnitude we consider the dimension-six results and account for the appropriate suppression factors, leading to
Although the dimension-eight and two-loop suppressions are insufficient to push these contributions beyond the reach of experiments with no further assumption on the neutrino Yukawas, they nonetheless have a negligible impact on the correlations between \(\mu \rightarrow e\) observables that the model can predict.
1.3.3 c. Leptoquark matching-to-QED summary
The leptoquark model is introduced in Sect. 3, and the Lagrangian is given in Eq. (3.5). The \(S_1\) leptoquark alone does not induce neutrino masses; for instance, adding another leptoquark [172], such as an SU(2)-doublet leptoquark of hypercharge Y=1/6, could generate neutrino masses at one loop via diagrams familiar from R-parity-violating Supersymmetry [173,174,175]. Or, in the presence of a colour-octet Majorana fermion, the \(S_1\) leptoquark can generate neutrino masses at two-loop [44].
At tree level in the model, the leptoquark induces vector, scalar and tensor flavour-changing operators involving u-type quarks and charged leptons of both chiralities. Then at one-loop, there are various penguin and box diagrams, which match onto dimension six operators of SMEFT and dimension eight four-fermion operators in SMEFT.
Diagrams matching the \(S_1\) leptoquark onto, from left to right, two-lepton two-quark operators (vector for \(X=Y\), scalar and tensor for \(X\ne Y\), where \(X,Y \in \{L,R\}\)), a Z-penguin contribution to the 2l2u vector operators, and two diagrams that contribute to the dipole: a finite matching part \(\propto \lambda _X \lambda _X^\dagger y_\mu \), and the tensor\(\rightarrow \) dipole mixing \(\propto \lambda _Y y _Q \lambda _X^\dagger \)
At tree level in the model, tensor and scalar coefficients involving leptons and up-type quarks arise as illustrated in Fig. 13:
The vector 2l2u operators, for \(Q\in \{u,c,t\}\), are
where the second line gives the contribution of the Z-penguin for \(Q\in \{u,c\}\)(illustrated in Fig. 13, and discussed further in Sect. C4), and
There is a finite matching contribution to the dipole coefficients, illustrated in Fig. 13:
where the second term is the finite part of the tensor to dipole mixing (represented in the last diagram of Fig. 13), which will be included via the QED RGEs evolving down from \(m_{LQ}\).
Vector four-lepton operators \(\mathcal{O}_{V,XY}\) can arise via Z-penguins and boxes, as illustrated in Fig. 14, and give
where \(l\in \{ e,\mu ,\tau \}\), the first line is the Z-penguin, and the second is the boxes.
Finally, vector operators involving leptons and d-type quarks can arise via Z-penguins and boxes with a leptoquark and an electroweak boson, which give
where \(F\in \{d,s,b\}\) and the box has no finite part at dimension six.
Scalar 2l2d operators can be generated by “Higgs-penguin” diagrams, as illustrated for instance in the first diagram of Fig. 15. There could also be boxes with a leptoquark and a Higgs, but these would be suppressed by a small quark Yukawa squared, so appear relatively suppressed with respect to the Higgs penguins. Such diagrams can also contribute to scalar 2l2u operators, which already arise at tree level as given in Eq. (C.12):
where \( F \in \{d,s,b\}\), and the lepton-flavour-changing vertex of the Higgs is \(\propto C_{EH}^{e \mu }\). This SMEFT coefficient can be generated at one-loop in the model via various diagrams, and is of order:
where the final log-enhanced term could apparently be large for top quarks in the loop, but \(\mu \rightarrow e \gamma \) imposes  , as discussed in Sect. 5.3. As a result the Higgs penguin contributions to the scalar 2l2q operators are negligible.
, as discussed in Sect. 5.3. As a result the Higgs penguin contributions to the scalar 2l2q operators are negligible.
Scalar four-lepton operators also receive contributions from Higgs penguins, which are simple to extrapolate from the quark results, but not listed because they are negligible due to the lepton Yukawa coupling. For instance, in the case of \(C^{e\mu ee}_{S,XX}\) – the scalar four-lepton operator appearing in the Lagrangian of “observables” (2.3) – the Higgs penguin contribution is \(\propto y_e\) so suppressed below the reach of upcoming experiments.
At \(\mathcal{O}(1/m_{LQ}^4)\), there are log-enhanced box diagrams that generate scalar four-lepton operators (see the right diagram of Fig. 15), with no suppression by small Yukawa couplings when the internal quarks are tops. However, the resulting coefficients are below the sensitivity of upcoming experiments due to dipole constraints, as discussed in Sect. 5.3. Finally, there could be two-loop penguin\(^2\) contributions to XY scalars with a \(\tau \)-bilinear, which are not listed because they seem suppressed with respect to the “Higgs penguin” contribution in this leptoquark model.
We neglect tensor operators involving a pair of \(\tau \)s, or down-type quarks, because they seem at least as suppressed as the scalar operators.
1.4 4. Penguins
“Penguin” is a widely used word in physics. In this manuscript, “penguin diagrams” are broadly understood to have the shape illustrated in Fig. 16: there is a 4-particle interaction mediated by a contact interaction or heavy particle exchange(illustrated as a grey ellipse), then two of the four legs are closed to a loop. One or several boson propagator(s) attach to the loop (drawn as an ellipse surrounding a dashed line), and may connect to an external particle line. This definition includes LFV “Higgs penguins”, which could contribute to the \(\mathcal{O}_{EH}\) SMEFT operator which gives flavour-changing Higgs couplings.
“Penguin” diagrams are often contributions to Z or \(\gamma \) vertices, in which case the external currents must be vector. In the case of photon penguins, the loop is \(\propto q^2\) = the four-momentum\(^2\) of the off-shell photon, which has a vector current bilinear at the other end of its propagator, so the diagram contributes to a vector four-particle operator. For Z penguins, there are two types of diagrams: those \(\propto v^2\), where \(v = \langle H_0 \rangle \) is the Higgs vev, and those \(\propto q^2\).
The curiosity we discuss here arises in SMEFT, where the equations of motion of the Z boson are used to match the \(\propto q^2\) part of the penguin diagrams onto momentum-independent operators; the coefficients of these operators must then cancel precisely in low-energy processes to mimic this kinematic suppression as \(q^2 \rightarrow 0\). This occurs in the type II seesaw model, where the \(q^2\)-Z-penguin diagrams give the dominant contribution to flavour-changing Z decays at the electroweak scale (eg \(Z\rightarrow e^\pm \mu ^\mp \)), but a negligible contribution to low-energy observables. This is generically expected in models where the Z penguin diagrams are \(\propto q^2\), and motivates LHC searches for \(Z\rightarrow e^\pm \mu ^\mp \) [176].
We aim to calculate in EFT the Z-penguin contribution to the low-energy matrix element \(\mathcal{M} (\mu _L u_R \rightarrow e_L u_R)\), that could arise in the leptoquark model or the type II seesaw and contributes to \(\mu A \rightarrow \! eA \). We calculate in three ways: in the model, by matching directly onto the low-energy QCD\(\times \)QED-invariant EFT at \(\Lambda _{NP}\), and by matching to SMEFT at \(\Lambda _{NP}\) then to the low-energy EFT at the weak scale. The diagrams are illustrated in Figs. 17 and 18.
In the models, there are in principle four diagrams contributing to the “Z-penguin”: the Z attached to either external fermion, to the internal scalar or to the internal fermion(as illustrated on the left in Fig. 17). They give a log-enhanced contribution to the coefficient of \( ({\bar{e}} \gamma P_L \mu ) ({\bar{u}}\gamma P_R u) \):
where \(N_c=3\) for the leptoquark and \(N_c=1\) for type II, the mass and couplings of the heavy boson are represented via the vector four-fermion coefficient induced at tree-level \( C_{V XY}^{e\mu ff}\), and \(q^2 \) is the momentum transfer on the Z line. A better approximation for the lower cutoff of the logarithm would be max\(\{m_f^2, q^2_{min}\}\), where \(q^2_{min}\) for \(\mu A \rightarrow \! eA \) is \(m_\mu ^2\).Footnote 15 However, putting \(m_f\) gives a nicer invariant, and the difference is numerically irrelevant for current experimental sensitivities. The \(\propto q^2\) part of the matrix element is negligible for low-energy muon processes where \(q^2 \sim m_\mu ^2\), because  suppresses the coefficients beneath the reach of upcoming experiments.
suppresses the coefficients beneath the reach of upcoming experiments.
In matching the models directly to the QCD\(\times \)QED invariant EFT, four-fermion operators can be generated by the heavy New Physics, and also by electroweak bosons of the SM (Z and h). The (log-enhanced part of the) model amplitude arises in the [dimension 6]\(^2 \rightarrow \) dimension eight running of the EFT is represented in the fish diagram to the right in Fig. 17. Calculating the fish at zero-external-momentum (because \(q^2\) is negligible) gives [177]:
where there is a contribution with an \(m_f\) insertion on both lines connecting the grey bubble to a Higgs, as well as contributions with two mass insertions on one of the f lines, which combine \(\propto |g^f_R - g^f_L| = 1\).
Alternatively, one could match the model to SMEFT at \(\Lambda _{NP}\), run to \(m_W\), then match to the QED\(\times \)QCD-invariant EFT. The penguin diagrams arise in the SMEFT RGEs as illustrated in Fig. 18: the grey blob is a New-Physics induced vector four-fermion operator which mixes via the first two diagrams into the “penguin operators”, defined as
where after the arrows are the flavour-changing Z vertices to which the operators reduce when the Higgs gets a vev (so \(a=3\) in the triplet case, where \(\langle H^\dagger \tau _3 H \rangle = - v^2\)), and we used \(Z^\mu = -s_W B^\mu + c_W W_3^\mu \), where \(s_W =\sin \theta _W = g'/\sqrt{g^2 + g^{'2}}\) and \(2m_Z^2 = (g^2 + g^{'2}) v^2\). In the SMEFT RGEs, the grey blob also mixes via B and \(W_0\) exchange (which can be written as \(\gamma \) and Z exchange by a basis rotation) into other four-fermion operators, as illustrated by the last diagram of Fig. 18. Then at the weak scale, the penguin and four-fermion operators of SMEFT match onto four-fermion operators in the low-energy theory. The component \(\propto m_f^2\) of the penguin matrix element of Eq. (C.24) corresponds to the first diagram of Fig. 18, induces the SMEFT penguin operators, and therefore a four-fermion operator at low-energy. However, the \(\propto q^2\) component of matrix element in the model generates both the penguin operators and four-fermion operators. These coefficients will cancel in low energy four-fermion processes, as one can see by using the equations of motion for the Z:\( (q^2 - m_Z^2) Z^\mu = -\frac{g}{2c_W} \sum _f g^f_X (\overline{f_X}\gamma _\mu f_X)\) (which apply in “on-shell” bases such as SMEFT) in calculating the contribution of a Z vertex \(\propto q^2\) to the S-matrix element \(\langle e f {\bar{f}} | S |\mu \rangle \):
where \(f_X\) is a chiral SM fermion.
So all the calculations give the same result, but in SMEFT, the kinematics of the matrix element is modified by using the equation of motion to reduce the operator basis. That is, the \(\propto q^2\) part of the Z penguin diagrams vanishes as \(q^2\rightarrow 0\) via an increasingly precise cancellation between the penguin and four-fermion operators. This illustrates that models can “naturally” engineer very precise cancellations among operator coefficients.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3.
About this article
Cite this article
Ardu, M., Davidson, S. & Lavignac, S. Constraining new physics models from \(\mu \rightarrow e \) observables in bottom-up EFT. Eur. Phys. J. C 84, 458 (2024). https://doi.org/10.1140/epjc/s10052-024-12782-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-024-12782-x




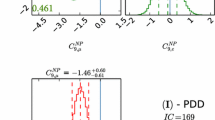




 0.2 eV.
0.2 eV.












