Bouncing and collapsing universes dual to late-time cosmological models

Abstract

We use the Jordan frame–Einstein frame correspondence to explore dual universes with contrasting cosmological evolutions. We study the mapping between Einstein and Jordan frames where the Einstein frame universe describes the late-time evolution of the physical universe, which is driven by dark energy and non-relativistic matter. The Brans–Dicke theory of gravity is considered to be the dual scalar–tensor theory in the Jordan frame. We show that an Einstein frame universe, with cosmological evolution of the $\Lambda$CDM model, always corresponds to a bouncing Jordan frame universe governed by a Brans–Dicke theory. On the other hand, quintessence models of dark energy with non-relativistic matter component are shown to be always dual to a Brans–Dicke Jordan frame with a turn-around, i.e., a bounce or a collapse. The evolution of the equation of state of the quintessence field determines whether the turn-around is a bounce or a collapse. The point of the Jordan frame turn-around for all the cases can be tuned anywhere by choosing an appropriate Brans–Dicke parameter. This essentially leads to alternative descriptions of the late-time evolution of the physical universe, in terms of bouncing or collapsing Brans–Dicke universes in the Jordan frame. Therefore, the effect of dark energy can equivalently be seen as collapse of space in a conformally connected universe. We further study the stability of such conformal maps against linear perturbations. The effective bouncing and collapsing descriptions of the current accelerating universe may have interesting implications for the evolutions of perturbations and quantum fluctuations in the cosmological background.

1 Introduction

It is well-known that some classes of modified theories of gravity, such as scalar–tensor theories [1,2,3] and f(R) theories [4,5,6], can be recast as Einstein gravity with a minimally coupled scalar-field in a conformally connected frame. The universe described by the modified gravity action is referred to as the Jordan frame, whereas, the universe described by the Einstein–Hilbert action in the conformally connected frame is called the Einstein frame.

Einstein and Jordan frames are mathematically equivalent, they essentially describe the same theory in terms of different dynamical variables [7, 8]. However, the equations of motion in these frames may lead to drastically different evolutions of the corresponding universes. Recent studies exploring conformally connected universes with contrasting cosmological evolutions can be found in [9,10,11,12,13,14,15,16,17,18,19,20,21,22]. In [19], it is demonstrated that a decelerating Einstein frame universe can be conformally equivalent to accelerating Jordan frame universes, governed by f(R) and scalar–tensor theories. The duality between an expanding Einstein frame and a collapsing Jordan frame is studied in [22]. It is shown that for some viable quintessence models in the Einstein frame, the corresponding Jordan frame, governed by an f(R) gravity theory, may have a collapsing description. A general condition is derived to predict whether a quintessence model, with a given time-dependent equation of state parameter, leads to such an expansion-collapse duality between the conformally connected frames. In [12] (also see [13]), a cosmological model is introduced where the Jordan frame universe is collapsing during the matter and radiation dominated eras. The model maps to a standard quintessence field with exponential potential in the Einstein frame. In [14], the authors introduced “anamorphic cosmology”, which combines features of both the inflationary and ekpyrotic models of the early universe. The anamorphic universe behaves like an expanding inflationary universe and a contracting ekpyrotic universe at the same time, depending on different conformally invariant criteria. The “conflation” model, introduced in [15], also combines inflationary and ekpyrotic scenarios, where the universe is contracting and expanding in different conformal frames.

In this paper, we explore the Einstein frame–Jordan frame correspondence focusing on the late-time cosmology, where the Jordan frame is governed by a scalar–tensor theory action. We classify scalar–tensor theories based on whether they lead to a collapsing Jordan frame, corresponding to an expanding Einstein frame. The general condition for such expansion-collapse duality is then applied to late-time cosmological models, where the Jordan frame action is considered to be the Brans–Dicke action, and the Einstein frame is modeled to describe the physical universe in the current era.

The late-time acceleration of the physical universe is realized in general relativity by introducing dark energy, an exotic fluid that violates the strong energy condition [23,24,25]. The $\Lambda$CDM $(\Lambda$ + Cold Dark Matter) model of the current universe, often referred to as the concordance model of cosmology, interprets dark energy as the cosmological constant $(\Lambda )$ in the Einstein field equation [26,27,28]. We show that an Einstein frame which effectively describes the evolution of the concordance model of cosmology, always corresponds to a bouncing Jordan frame, governed by a Brans–Dicke theory. The transition of the Einstein frame from a dust-dominated phase to an accelerating phase can be associated with the bounce in the Jordan frame. We also show that quintessence models of dark energy [23, 24, 29] in the Einstein frame are always dual to Brans–Dicke Jordan frames with a turn-around, i.e., a bounce or a collapse. Whether the Jordan frame turn-around is a bounce or a collapse is determined by the evolution of the equation of state of the quintessence field at the turn-around. Moreover, the point of the Jordan frame turn-around for all these cases can be set up anywhere by choosing an appropriate Brans–Dicke parameter. As examples, we demonstrate bouncing and collapsing behaviours in the Brans–Dicke Jordan frames, corresponding to thawing and freezing types of quintessence models with a non-relativistic matter component in the Einstein frame.

In general, bouncing models of cosmology are explored as a theory of the early universe, alternative to the inflationary scenario [30,31,32,33]. For example, bouncing scenarios are realized using scalar–tensor theories in [6, 34, 35]. As for any theory of the early universe, cosmological perturbations play an important role in the bouncing models. The statistical properties of the large-scale structure and CMBR anisotropies as observed today, must be explained from the primordial fluctuation near the bouncing epoch (see, for example, [36,37,38] and references therein). A viable bouncing scenario in the early universe hence needs to be checked for stability under perturbations.

In order to accommodate for cosmological perturbations in the present bouncing model of the late-time universe, the conformal correspondence between the physical Einstein frame and the bouncing Jordan frame should be stable in the perturbative regime. Previous studies have pointed out that for early universe bouncing scenarios, the linear order conformal correspondence may become singular under certain conditions, breaking the Einstein frame–Jordan frame duality (see, for example, [10, 21]). We investigate the stability of the conformal map in the present case, where the bouncing and collapsing universes are dual to the concordance and quintessence models in the Einstein frame. As an concrete example, we demonstrate the stability of the conformal correspondence against linear perturbations for the concordance model. For this case, the Jordan frame perturbations are numerically solved, first via the Einstein frame using the conformal map, then directly in the Jordan frame. The evolution of Jordan frame scalar perturbations obtained in these two ways are in good agreement. This explicitly shows that the map between the linear order perturbations in the conformally connected frames remains valid, even through the bounce in the Jordan frame. The duality between the bouncing universe and the $\Lambda$CDM universe is hence shown to be stable under linear perturbations.

This paper is organized in the following way. In Sect. 2, we briefly introduce the Einstein frame–Jordan frame correspondence, where the Jordan frame is governed by a scalar–tensor theory action. The general condition for an expansion-collapse duality for scalar–tensor theories is obtained in Sect. 3. In Sect. 4, we show that an Einstein frame, effectively describing the evolution of the concordance model of cosmology, always corresponds to a bouncing Jordan frame which is governed by a Brans–Dicke theory. We discuss the duality between Jordan frame universes with turn-arounds and quintessence models in the Einstein frame in Sect. 5. In Sect. 6, we briefly discuss an example of the expansion-collapse duality where a de Sitter expansion in the Jordan frame maps to a collapsing Einstein frame approaching the singularity. A collapsing universe in a well-behaved gravity theory typically supports the growth of perturbations as well as the quantum effects. We investigate whether the duality between a collapsing and an expanding universe survives as the perturbations evolve. At first glance, it might appear that the role of backreactions from the perturbations in an expanding universe diminishes. However, since its dual universe is collapsing where perturbations are expected to grow, it is worthwhile to explore if such a map remains viable when perturbations are included. This helps us understand if the late-time accelerating universe has any appreciable features from the growth of perturbations and quantum effects due to the same being true for its dual universe. The effect of linear scalar perturbation in the conformal map is discussed in Sect. 7. We conclude with summary and discussion in Sect. 8.

Throughout this paper Latin indices represent spacetime components, Greek indices represent spatial components. Metric signature is taken to be $(-,+,+,+).$

2 Jordan and Einstein frames

We begin with a brief review of Jordan and Einstein frames in the context of scalar–tensor theories, for detailed discussion, see [1,2,3, 6].

In scalar–tensor theories, the gravity sector is governed by a scalar field $(\lambda )$ along with the metric tensor field $(g_{ab})$. The action of a general scalar–tensor theory can be written as [1, 3]

$$\begin{aligned} S_{J} = \int \text {d}^4 x \sqrt{-g} \left( f(\lambda )R - \frac{1}{2} h(\lambda ) g^{ab} \partial _a \lambda \partial _b \lambda - U(\lambda ) \right) , \end{aligned}$$

(1)

where $f(\lambda ),$ $h(\lambda ),$ $U(\lambda )$ are arbitrary functions of the scalar field $\lambda .$ The universe described by this action is referred to as the Jordan frame universe. Scalar–tensor theories belong to a class of extended theories of gravity which can be recast as general relativity, with a canonical scalar field, in a conformally connected frame. With the following conformal transformation [1, 3]

$$\begin{aligned} {\tilde{g}}_{ab}&= \Omega ^2(x) g_{ab}, \end{aligned}$$

(2a)

$$\begin{aligned} \Omega ^2&= 16 \pi G f(\lambda ), \end{aligned}$$

(2b)

the action in Eq. (1) can be written as

$$\begin{aligned} S_{J}= & {} \int \text {d}^4 x \sqrt{-{\tilde{g}}} \left[ \frac{1}{16 \pi G} {\tilde{R}} - \frac{1}{2} K[\lambda ] {\tilde{g}}^{ab} \partial _a\lambda \partial _b\lambda \right. \nonumber \\{} & {} - \left. \frac{U(\lambda )}{(16 \pi G f(\lambda ))^2} \right] , \end{aligned}$$

(3)

where,

$$\begin{aligned} K[\lambda ] = \frac{1}{16 \pi G f^2(\lambda )} \left( h(\lambda )f(\lambda ) + 3 f_{,\lambda }^2 \right) . \end{aligned}$$

(4)

The first term in Eq. (3) is the Einstein–Hilbert action with respect to the metric ${\tilde{g}}_{ab}.$ The remaining terms describe a minimally coupled scalar field, with non-canonical kinetic term. One may define a new scalar field $\varphi$ by

$$\begin{aligned} \frac{\text {d}\varphi }{\text {d}\lambda } = \sqrt{K[\lambda ]},\quad K[\lambda ] > 0, \end{aligned}$$

(5)

such that in terms of $\varphi ,$ the action in Eq. (3) becomes [1, 3]

$$\begin{aligned} S_{E} =\int \text {d}^4 x \sqrt{-{\tilde{g}}} \left[ \frac{1}{16 \pi G} {\tilde{R}} - \frac{1}{2} {\tilde{g}}^{ab} \partial _a\varphi \partial _b\varphi - V(\varphi ) \right] , \end{aligned}$$

(6)

where,

$$\begin{aligned} V(\varphi ) = \frac{U(\lambda (\varphi ))}{(16 \pi G f(\lambda (\varphi )))^2}. \end{aligned}$$

(7)

Note that $K[\lambda ]>0$ is necessary for the field $\varphi$ to be real. The action (6) describes a minimally coupled canonical scalar field $\varphi ,$ with potential $V(\varphi ),$ in Einstein’s gravity. The universe governed by this action is referred to as the Einstein frame universe.

We now move on to the expansion-collapse duality between the conformally connected frames.

3 Expansion-collapse duality between Einstein and Jordan frames

As discussed above, a minimally-coupled scalar field in general relativity can have an alternative description given by a scalar–tensor theory in the Jordan frame. In this paper we are interested in a scenario where the Einstein frame is the physical universe, undergoing the dark energy-dominated late time accelerating phase, with non-negligible subdominant presence of non-relativistic matter. Then corresponding to this Einstein frame, we seek a class of scalar–tensor theories leading to a collapsing Jordan frame universe. Such a class of scalar–tensor theories, if exists, can provide an effective description of the expanding physical universe in the Einstein frame, in terms of a collapsing one, in the Jordan frame. In this section we find a general condition for such an expansion-collapse duality between the conformal frames.

Let us consider that both Jordan and Einstein frame spacetimes are described by spatially flat FRW metrics, i.e.,

$$\begin{aligned} g_{ab}&= \text {diag} \left[ -1, a^2(t),a^2(t),a^2(t) \right] \quad \text {and} \end{aligned}$$

(8a)

$$\begin{aligned} {\tilde{g}}_{ab}&= \text {diag} \left[ -1, {\tilde{a}}^{2}({\tilde{t}}), {\tilde{a}}^{2}({\tilde{t}}),{\tilde{a}}^{2}({\tilde{t}}) \right] , \end{aligned}$$

(8b)

respectively. Then, according to the conformal transformation (2), Einstein and Jordan frame scale factors and coordinate times are related by [1]

$$\begin{aligned} {\tilde{a}}&= \Omega a = \sqrt{16 \pi G f(\lambda )} a \end{aligned}$$

(9a)

$$\begin{aligned} \text {d}{\tilde{t}}&= \Omega \text {d}t = \sqrt{16 \pi G f(\lambda )} \text {d}t. \end{aligned}$$

(9b)

The Einstein frame action (6) leads to the usual Friedmann equations

$$\begin{aligned} {\tilde{H}}^2&= \left( \frac{1}{{\tilde{a}}}\frac{\text {d}{\tilde{a}}}{\text {d}{\tilde{t}}} \right) ^2 = \frac{\kappa ^2}{3} \rho _\varphi ({\tilde{a}}) \end{aligned}$$

(10a)

$$\begin{aligned} \frac{\text {d}{\tilde{H}}}{\text {d}{\tilde{t}}}&= - \frac{\kappa ^2}{2} \left( \rho _\varphi + P_\varphi \right) = - \frac{\kappa ^2}{2} \rho _\varphi (1 + w_\varphi ), \end{aligned}$$

(10b)

where $\kappa ^2 = 8 \pi G,$ $\rho _\varphi$ and $P_\varphi$ are the energy density and pressure associated with the scalar field $\varphi ,$

$$\begin{aligned} \rho _\varphi&= \frac{1}{2} \left( \frac{\text {d}\varphi }{\text {d}{\tilde{t}}} \right) ^2 + V(\varphi ), \end{aligned}$$

(11a)

$$\begin{aligned} P_\varphi&= \frac{1}{2} \left( \frac{\text {d}\varphi }{\text {d}{\tilde{t}}} \right) ^2 - V(\varphi ), \end{aligned}$$

(11b)

${\tilde{H}}$ is the Einstein frame Hubble parameter, and $w_\varphi =P_\varphi /\rho _\varphi$ is the equation of state parameter corresponding to the scalar field $\varphi .$ From the above relations, the time derivative of the field can be written as

$$\begin{aligned} \frac{\text {d}\varphi }{\text {d}{\tilde{t}}} = \sqrt{\rho _\varphi (1 + \omega _\varphi )}. \end{aligned}$$

(12)

Starting with the relation between the scale factors in the two conformal frames (9a) and using Eqs. (5) and (12), one can find

$$\begin{aligned} \frac{\text {d}a}{\text {d}{\tilde{a}}} = \frac{1}{\sqrt{16 \pi G}} f^{-\frac{1}{2}} \left( 1 - \frac{1}{2} \frac{f_{,\lambda }}{f} K^{-\frac{1}{2}}[\lambda ] \sqrt{\frac{(1 + w_{\varphi })\rho _\varphi }{{\tilde{H}}^2}}\right) , \end{aligned}$$

(13)

where the subscript $(,\lambda )$ represents derivative with respect to the Jordan frame scalar field $\lambda .$ The condition for the expansion-collapse duality between Jordan and Einstein frames is then obtained by setting

$$\begin{aligned} \frac{\text {d}a}{\text {d}{\tilde{a}}} < 0, \end{aligned}$$

(14)

leading to

$$\begin{aligned} \frac{1}{\sqrt{16 \pi G}} f^{-\frac{1}{2}} \left( 1 - \frac{1}{2} \frac{f_{,\lambda }}{f} K^{-\frac{1}{2}}[\lambda ] \sqrt{\frac{(1 + w_{\varphi })\rho _\varphi }{{\tilde{H}}^2}}\right) < 0. \end{aligned}$$

(15)

Note that $f(\lambda )>0$ is required to ensure that the conformal factor is real, i.e. $\Omega ^2>0.$ Let us further consider $f_{,\lambda }>0,$ then using the Friedmann equation (10a) the expansion-collapse condition can be put in the form

$$\begin{aligned} 1 + w_\varphi > \frac{2}{3} \left( \frac{fh}{f_{,\lambda }^2} + 3 \right) . \end{aligned}$$

(16)

In general, both sides of the above inequality may evolve in time. For a scalar field in the Einstein frame, with arbitrary time-dependent $w_\varphi ({\tilde{a}}),$ and a scalar–tensor theory in the Jordan frame, specified by the functions $f(\lambda ), h(\lambda )$ $(f_{,\lambda } > 0)$, there may exist periods of evolution when $w_\varphi ({\tilde{a}})$ satisfies the above inequality. During such a period, for an expanding (collapsing) Einstein frame universe, the corresponding Jordan frame collapses (expands).

Here we would like to mention that in a previous study [22], we obtained a similar expansion-collapse duality condition between the conformal frames, where the Jordan frame was governed by an f(R) theory. The expansion-collapse condition in the case of f(R) theories is solely determined by the Einstein frame quantities $(w_\varphi , \rho _\varphi , {\tilde{H}})$, the Jordan frame function f(R) does not appear explicitly in the condition. However, in the present case, one requires the expressions for the Jordan frame functions $f(\lambda )$ and $h(\lambda )$ in order to check the validity of the condition (16). This additional requirement in the case of scalar–tensor theories is expected, simply because the Jordan frame action has three unspecified functions (f, h, U), whereas, the Jordan frame action for f(R) theories has a single unspecified function, f(R).

We now explore the expansion-collapse duality between an Einstein frame which describes the late-time evolution of the physical universe, and a suitable scalar–tensor theory in the Jordan frame. Previous studies have considered different aspects of the duality between the standard universe and conformally connected universes with bouncing/collapsing behaviours, governed by scalar–tensor theories [12,13,14,15, 17]. In the present work we show that the dual universes with turn-arounds are not exclusive to specific cosmological models, they are, in fact, generic features of the concordance model and quintessence models of dark energy.

4 Concordance model: bounce in the Jordan frame

The current accelerating expansion of the physical universe is considered to be driven by a strong energy condition-violating exotic dark energy [23,24,25]. The equation of state parameter of dark energy $w_{\text {de}}$ must be smaller than $-1/3$ and the value $w_{\text {de}} \approx -1$ is favoured by observations [39]. The cosmological constant $\Lambda$ is the simplest implementation of dark energy within the framework of general relativity. Although being consistent with observations, the cosmological constant model suffers from several fine-tuning problems [26, 27]. A wide class of dynamical models of dark energy has been explored as an alternative for the $\Lambda$ model (see, for example, [23,24,25] and references therein). A Quintessence field, i.e. a canonical scalar field minimally coupled to gravity with a suitable equation of state parameter, is the simplest of such dynamical models of dark energy [25, 29, 40]. In the following discussion, we will consider the cosmological constant model of dark energy. Quintessence models of dark energy in this context will be discussed in the next section.

4.1 Einstein frame: concordance model

We set up the Einstein frame for it to describe the current accelerating epoch of the universe, consisting of the cosmological constant and a non-relativistic matter component or dust, referred to as the concordance model (see, for example, [28]). For a simple implementation of the concordance model in the Einstein frame, we consider that the Einstein frame scalar field effectively describes both dark energy and non-relativistic matter in the field equation level. This is achieved by taking the energy density of the scalar field, $\rho _\varphi ,$ to be

$$\begin{aligned} \rho _\varphi ({\tilde{a}})&= \rho _\Lambda + \rho _{\text {m}} = \rho _\Lambda + \rho _{\text {m}0} {\tilde{a}}^{-3} \end{aligned}$$

(17a)

$$\begin{aligned}&= \rho _{\text {c}} \left( \Omega _\Lambda + \Omega _{\text {m}0} {\tilde{a}}^{-3} \right) , \end{aligned}$$

(17b)

where $\rho _{\text {m}0}$ is the energy density of dust at the current epoch $({\tilde{a}}=1)$, $\rho _{\text {c}} = 3 {\tilde{H}}^2_0/\kappa ^2$ is the critical density of the universe, ${\tilde{H}}_0 = {\tilde{H}}({\tilde{a}}=1),$ $\Omega _\Lambda = \rho _\Lambda /\rho _{\text {c}},$ and $\Omega _{\text {m}0} = \rho _{\text {m}0}/\rho _{\text {c}}.$ With this role of the Einstein frame scalar field, there is no need to add an extra matter component in the Einstein frame, as the single scalar field takes into account both dark energy, implemented by the cosmological constant, and matter. Since the scalar field is the sole component in the Einstein frame, the Jordan frame action in this case remains a pure gravity action, governed by only the metric $g_{ab}$ and the Jordan frame scalar field $\lambda .$ The Einstein frame scalar field $\varphi$ in this set up is hereafter referred to as the concordance field, in order to distinguish it from a quintessence model.

Starting with the above $\rho _\varphi ({\tilde{a}}),$ one can reconstruct the action of the concordance field as follows. Using the Friedmann equations in the Einstein frame (10), the equation of state $w_\varphi ,$ which is the effective equation of state of the $\Lambda$ CDM model, can be written as a function of the scale factor as (see Fig. 1),

$$\begin{aligned} w_\varphi = - 1 - \frac{2}{3} \frac{1}{{\tilde{H}}^2}\frac{\text {d}{\tilde{H}}}{\text {d}{\tilde{t}}} = - \frac{\Omega _\Lambda {\tilde{a}}^3}{1 - \Omega _\Lambda + \Omega _\Lambda {\tilde{a}}^3}. \end{aligned}$$

(18)

Fig. 1

Equation of state parameter of the concordance field is plotted with respect to the Einstein frame scale factor. At the early times ${\tilde{a}}\rightarrow 0,$ $w_\varphi \rightarrow 0,$ corresponds to the dust-dominated phase of the universe. In the late times $w_\varphi$ approaches $-1,$ describing a $\Lambda$-dominated universe. The vertical line represents the period of dust-dark energy equivalence

This, along with Eq. (12), leads to the concordance field as a function of the scale factor,

$$\begin{aligned} \kappa \varphi ({\tilde{a}})&= \frac{1}{\sqrt{3}} \left[ \ln \left( \sqrt{\frac{\Omega _\Lambda }{1- \Omega _\Lambda } {\tilde{a}}^3 + 1} - 1 \right) \right. \nonumber \\&\quad \left. -\ln \left( \sqrt{\frac{\Omega _\Lambda }{1- \Omega _\Lambda } {\tilde{a}}^3 + 1} + 1 \right) \right] . \end{aligned}$$

(19)

Finally, from Eq. (11), the concordance potential

$$\begin{aligned} V = \frac{1}{2}(1 - w_\varphi ({\tilde{a}})) \rho _\varphi ({\tilde{a}}) \end{aligned}$$

(20)

can be written as a function $\varphi$ as

$$\begin{aligned} V(\varphi ) = \frac{3}{8} \frac{H_0^2}{\kappa ^2} \Omega _\Lambda \left( 6 + \exp \left( - \sqrt{3} \kappa \varphi \right) + \exp \left( \sqrt{3} \kappa \varphi \right) \right) , \end{aligned}$$

(21)

where ${\tilde{a}}$ is replaced with $\varphi$ according to Eq. (19). In other words, a canonical scalar field with the above potential in the Einstein frame leads to equations of motion which are exactly the same as those of the $\Lambda$CDM or the concordance cosmology. One can solve the Friedmann equation for the concordance model to find the Einstein frame scale factor as

$$\begin{aligned} {\tilde{a}}({\tilde{t}}) = \left( \frac{1 - \Omega _\Lambda }{\Omega _\Lambda }\right) ^{\frac{1}{3}} \sinh ^{\frac{2}{3}} \left( \frac{3}{2} \sqrt{\Omega _\Lambda } H_0 ({\tilde{t}}- {\tilde{t}}_i )\right) , \end{aligned}$$

(22)

where,

$$\begin{aligned} {\tilde{t}}_i = \frac{2}{3 H_0\sqrt{\Omega _\Lambda }} {\textrm{arcsinh}} \left( - \sqrt{ \frac{\Omega _\Lambda }{1 - \Omega _\Lambda }} \right) , \end{aligned}$$

(23)

which is, as expected, the scale factor of the $\Lambda$CDM model. Note that the origin of the Einstein frame coordinate time is chosen to be the current epoch ${\tilde{t}}_0,$ i.e. ${\tilde{t}}_0=0$ and ${\tilde{a}}({\tilde{t}}={\tilde{t}}_0=0)=1,$ whereas, at ${\tilde{t}}={\tilde{t}}_i$ the scale factor ${\tilde{a}}({\tilde{t}}={\tilde{t}}_i) = 0.$

Having set up the Einstein frame, we will now move on to a suitable Jordan frame description of the universe.

4.2 Jordan frame: Brans–Dicke theory

The concordance scalar field in the Einstein frame, with potential (21), can be mapped to a wide class of scalar–tensor theories, depending on choices of the functions $f(\lambda ),\ h(\lambda )$ in the Jordan frame action (1). This correspondence is given by the relations (5) and (7), as discussed before. We are interested in an example of the scalar–tensor theories, dual to the concordance model, such that the conformally connected frames possess the expansion-collapse duality feature as discussed in Sect. 3.

The widely-studied Brans–Dicke theory of gravity is the prototype of scalar–tensor theories [1, 3, 41,42,43,44,45]. A Brans–Dicke theory dual to the concordance model may lead to the expansion-collapse duality under certain conditions, as we will see. Apart from this, the Brans–Dicke action is simple enough for the equations of motion in the Jordan frame to be solved analytically. For this reason, we will consider the Brans–Dicke theory as an example of scalar–tensor theories in the Jordan frame for the rest of the discussion.

With the following choice of the functions [1, 3],

$$\begin{aligned} f(\lambda )&= \frac{\lambda }{16 \pi }, \end{aligned}$$

(24a)

$$\begin{aligned} h(\lambda )&= \frac{w_{\text {BD}}}{8 \pi \lambda }, \end{aligned}$$

(24b)

the Jordan frame action (1) becomes the Brans–Dicke action

$$\begin{aligned} S_{J}^{\text {BD}} = \int \text {d}^4 x \sqrt{-g} \left( \frac{\lambda }{16 \pi } R - \frac{w_{\text {BD}}}{16 \pi \lambda } g^{ab} \partial _a \lambda \partial _b \lambda - U(\lambda ) \right) , \end{aligned}$$

(25)

where $w_{\text {BD}},$ the constant Brans–Dicke parameter, must satisfy $w_{\text {BD}}> - 3/2$ in order for the concordance field $\varphi$ to be real (see Eq. (5)). Note that $f_{,\lambda } = \frac{1}{16 \pi },$ $f_{,\lambda }>0$ is ensured for all $\lambda .$ One can then apply Eq. (16) to determine the condition for a collapsing Jordan frame,

$$\begin{aligned} w_\varphi ({\tilde{a}}) > \frac{4}{3} w_{\text {BD}} + 1. \end{aligned}$$

(26)

Fig. 2

Condition for a collapsing Brans–Dicke Jordan frame, dual to the concordance model, determined by $w_{\text {BD}}$ and $w_\varphi ;$ where $w_{\text {BD}}$ is the constant Brans–Dicke parameter specifying the Jordan frame, $w_\varphi$ is the dynamic equation of state of the concordance field. At a given instant, if a pair $(w_\varphi , w_{\text {BD}})$ lies in the shaded region, then the corresponding Brans–Dicke universe is collapsing at that instant

For the Brans–Dicke model, the expansion-collapse duality condition becomes significantly simple, as it only requires the knowledge of the equation of state $w_\varphi ({\tilde{a}}).$ Given the evolution of $w_\varphi ({\tilde{a}}),$ the expanding and collapsing phases of the Jordan frame, determined by the condition (26), can be visualized in Fig. 2. The shaded region in the figure depicts the domain in the $(w_\varphi , w_{\text {BD}})$ space, where the condition (26) is satisfied. That is, for a Brans–Dicke Jordan frame, specified by $w_{\text {BD}},$ at a given value of the Einstein frame scale factor ${\tilde{a}}_*,$ if the pair $(w_\varphi ({\tilde{a}}_*), w_{\text {BD}})$ lies within the shaded region, then we can conclude that the Jordan frame is collapsing at ${\tilde{a}}= {\tilde{a}}_*.$

The Einstein frame is matter dominated at the early-times; i.e. for ${\tilde{a}}\rightarrow 0,$ the equation of state parameter of the concordance field $w_\varphi \approx 0$ (see Fig. 1). Eventually, as the scale factor increases, $w_\varphi$ decreases. In the late-time of the Einstein frame, i.e., as ${\tilde{a}}\rightarrow \infty ,$ $w_\varphi \rightarrow -1$ depicting the dark-energy dominated era. We see from Fig. 2 that for $w_{\text {BD}}> -3/4,$ the Jordan frame is never collapsing. For $-3/2< w_{\text {BD}} <-3/4,$ the points with $w_\varphi = 0$ always lie in the shaded region. This implies that at the beginning of the matter-dominated era of the Einstein frame $(w_\varphi \approx 0)$, the Jordan frame is collapsing. For the same value of $w_{\text {BD}},$ $w_\varphi$ will then monotonically decrease towards $-1$ with increasing ${\tilde{a}}.$ Thus, at some time, the trajectory of the Einstein frame universe in the $(w_\varphi , w_{\text {BD}})$ space will inevitably come out of the shaded region and enter the white region, where the Jordan frame is expanding. The transition of the trajectory from the shaded region (collapsing Jordan frame) to the white region (expanding Jordan frame), represents a bounce in the Jordan frame. The Einstein frame scale factor at the point of the bounce, ${\tilde{a}}_b,$ satisfies

$$\begin{aligned} w_\varphi ({\tilde{a}}_b) = \frac{4}{3} w_{\text {BD}} + 1. \end{aligned}$$

(27)

For the concordance scalar field in the Einstein frame, the equations of motion of the corresponding Jordan frame can be solved analytically. Starting with Eq. (5) and using Eq. (24), one can write the Brans–Dicke field $\lambda$ as a function of the concordance field as,

$$\begin{aligned} \lambda (\varphi ) = \lambda _0 \exp \left( \sqrt{\frac{2}{\varpi }} \kappa \varphi \right) , \end{aligned}$$

(28)

where we define

$$\begin{aligned} \varpi = 2 w_{\text {BD}}+3, \end{aligned}$$

(29)

and $\lambda _0$ is an integration constant such that $\lambda (\varphi =0)=\lambda _0.$ Given the concordance potential (21), one can obtain the corresponding Brans–Dicke potential using Eqs. (7) and (28) as

$$\begin{aligned} U(\lambda ) = \frac{3 G}{64 \pi } H_0^2 \Omega _\Lambda \lambda ^2 \left( 6 + \left( \frac{\lambda }{\lambda _0} \right) ^{\sqrt{\frac{3}{2}\varpi }} + \left( \frac{\lambda }{\lambda _0} \right) ^{-\sqrt{\frac{3}{2}\varpi }} \right) . \end{aligned}$$

(30)

Now, from Eq. (9a), the Brans–Dicke frame scale factor a is related to the Einstein frame scale factor as

$$\begin{aligned} a = \frac{{\tilde{a}}}{\sqrt{G \lambda }}. \end{aligned}$$

(31)

Using Eqs. (19) and (28), we replace $\lambda$ with ${\tilde{a}}$ in the above expression to write the Jordan frame scale factor as a function of the Einstein frame scale factor,

$$\begin{aligned} a({\tilde{a}}) = \sqrt{\frac{8 \pi }{\kappa ^2 \lambda _0}} {\tilde{a}} \left( \frac{\sqrt{\frac{ \Omega _{\Lambda }}{1-\Omega _{\Lambda }}{\tilde{a}}^3 + 1} + 1}{\sqrt{\frac{ \Omega _{\Lambda }}{1-\Omega _{\Lambda }}{\tilde{a}}^3+1}-1}\right) ^{\frac{1}{\sqrt{ 6 \varpi }}}. \end{aligned}$$

(32)

Fig. 3

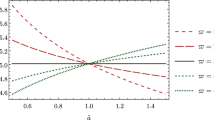
Bouncing behaviour of the Brans–Dicke Jordan frame, dual to the concordance model. Scale factors of different Jordan frames, specified by different $w_{\text {BD}}$ values, are plotted with respect to the Einstein frame scale factor. The gray plot below is the equation of state of the concordance field $w_\varphi ,$ The Vertical gray line represents the epoch of dust-$\Lambda$ equivalence in the Einstein frame. The occurrence of the Jordan frame bounce shifts towards future with decreasing $w_{\text {BD}}$

Evolution of the Jordan frame scale factor $a({\tilde{a}})$ for different values of $w_{\text {BD}}$ is shown in Fig. 3. For all the plots, the Jordan frame universe is seen to be collapsing at the early matter-dominated phase in the Einstein frame. Eventually, the Jordan frame goes through a non-singular bounce and starts expanding with the Einstein frame. One can find the Einstein frame scale factor at the point of bounce in the Jordan frame to be

$$\begin{aligned} {\tilde{a}}_{b} = \left( \frac{1 - \Omega _\Lambda }{ 2 \Omega _\Lambda } \right) ^{\frac{1}{3}} \left( - \frac{3 + 4 w_{\text {BD}}}{3 + 2 w_{\text {BD}}} \right) ^{\frac{1}{3}}, \end{aligned}$$

(33)

for $- \frac{3}{2}< w_{\text {BD}}< - \frac{3}{4}$ (see Fig. 2). We see, depending on $w_{\text {BD}},$ the Jordan frame bounce can occur corresponding to a value of the Einstein frame scale factor anywhere within ${\tilde{a}}_b \rightarrow 0$ (for $w_{\text {BD}}\rightarrow - \frac{3}{4})$ and ${\tilde{a}}_b \rightarrow \infty$ (for $w_{\text {BD}}\rightarrow - \frac{3}{2})$, i.e., anywhere within the entire concordance model era. The time of the Jordan frame bounce shifts to the future with increasing value of $w_{\text {BD}}$ parameter, as it can be seen from Fig. 4. For a given Brans–Dicke model $(w_{\text {BD}})$, the size of the Jordan frame universe at the point of the bounce depends on the dark energy content in the Einstein frame universe $(\Omega _\Lambda )$. Interestingly, even though the concordance model possesses a big bang-like cosmological singularity, i.e., the Einstein frame scale factor ${\tilde{a}} \rightarrow 0$ at a finite coordinate time (Eq. (23)), there is no such singularity in the dual bouncing description, as it can be seen from Fig. 3. Therefore, the appearance of the cosmological singularity can be attributed to the choice of the conformal frame. The conformal frame-dependence of cosmological singularities has been argued in the literature previously, for example in [12], the present result agrees with such a conjecture.

Note that, a similar result was obtained in [16], where, the conformal duality was established between a bouncing Jordan frame and an Einstein frame governed by a scalar field with a quartic potential and a cosmological constant. In the following section, we generalize this result by considering the case of generic quintessence models with arbitrary potentials.

Fig. 4

Einstein frame scale factor at the point of the Jordan frame bounce ${\tilde{a}}_b$ is plotted with respect to the Brans–Dicke parameter $w_{\text {BD}}.$ Different plots are for $\Omega _\Lambda = 0.6, 0.7, 0.8.$ ${\tilde{a}}_b$ can take any possible value depending on $- \frac{3}{2}< w_{\text {BD}}< - \frac{3}{4}.$ For smaller values of $w_{\text {BD}},$ the Jordan frame bounce occurs at later times in the Einstein frame

It is interesting to note that depending on the choice of the constant $\lambda _0$ in Eq. (32), the Jordan frame scale factor can become arbitrarily small at the bounce. However, the bounce can be arranged near the current epoch in the Einstein frame, when the Einstein fame scale factor remains ${\tilde{a}}\sim 1.$ In this scenario, if the Jordan frame scale factor decreases below a sufficiently small scale near the bounce, one may speculate the quantum effects in the Jordan frame to become non-trivial; for example, quantum fluctuations in relevant Jordan frame cosmological operators may grow in this regime. At the same time, the quantum effects in the corresponding Einstein frame is expected to be suppressed due to its relatively large scale. In this case, the conformal correspondence seems to provide a map between a quantum-corrected universe and a universe with negligible quantum effects. Alternatively, one may find the classical conformal map to break down near the bouncing phase [46,47,48]. For example, [48] shows that in the absence of additional matter components, the conformal correspondence between an expanding and collapsing universe survives at the quantum level. Interestingly, quantum fluctuations in different cosmological operators increase both in the collapsing and the expanding frame in similar ways, regardless of the cosmological evolutions therein.

5 Quintessence models: turn-around in the Jordan frame

In the previous section, we demonstrated the duality between the physical universe and bouncing universes by considering the example of the concordance scalar field in the Einstein frame, i.e., a single canonical scalar field that reproduces the background evolution of the $\Lambda$CDM cosmology. We now extend the analysis to general quintessence models with other matter components, such as non-relativistic matter and radiation, added separately. As before, the Einstein frame represents the physical universe, therefore we wish these matter components to be minimally coupled in the Einstein frame. This can be achieved by considering the Jordan frame action with the following form

$$\begin{aligned} S_{J}^{BD}&= \int \text {d}^4 x \sqrt{-g} \left( \frac{\lambda }{16 \pi } R - \frac{w_{\text {BD}}}{16 \pi \lambda } g^{ab} \partial _a \lambda \partial _b \lambda - U(\lambda ) \right) \nonumber \\&\quad + \int \text {d}^4 x \sqrt{-g}\Omega ^4(\lambda ) {\mathcal {L}}_M \left( \psi _M;\Omega ^2(\lambda )g_{ab}\right) , \end{aligned}$$

(34)

where the first term is the Brans–Dicke action same as before; in the second term we introduce the action of a non-minimally coupled matter field $\psi _M.$ The conformal transformation ${\tilde{g}}_{ab} = \Omega ^2 g_{ab}$ removes the $\lambda$ dependency from the matter action, leading to the Einstein frame action

$$\begin{aligned} S_E&= \int \text {d}^4 x \sqrt{-\tilde{g}}\frac{{\tilde{R}}}{2 \kappa ^2} - \int \text {d}^4 x \sqrt{-\tilde{g}}\left( \frac{1}{2} {\tilde{g}}^{ab} \partial _a \varphi \partial _b \varphi + V(\varphi ) \right) \nonumber \\&\quad + \int \text {d}^4 x \sqrt{-\tilde{g}}{\mathcal {L}}_M \left( \psi _M; {\tilde{g}}_{ab} \right) . \end{aligned}$$

(35)

That is, in this convention the matter field is minimally coupled in the Einstein frame, as a consequence of which the matter energy–momentum tensor is conserved in this frame. Similar approach for the Einstein frame can be found in [12, 13]. The scalar field $\varphi$ now takes the role of a quintessence field. Note that, once the quintessence model is specified in the Einstein frame, the Jordan frame action is fixed up to the choice of the Brans–Dicke parameter $w_{\text {BD}}.$ The Brans–Dicke potential is determined from the quintessence potential as in Eq. (7), where the fields themselves are related via Eq. (28), these relations are the same as in the case of the concordance model.

Let us consider non-relativistic matter (dust) and radiation components in the Einstein frame, along with the quintessence field $\varphi .$ The above action leads to the standard Friedmann equation in the Einstein frame

$$\begin{aligned} {\tilde{H}}^2 = \frac{\kappa ^2}{3} \left( \rho _\varphi ({\tilde{a}}) + \rho _M({\tilde{a}}) + \rho _R({\tilde{a}})\right) , \end{aligned}$$

(36)

where $\rho _\varphi ,$ $\rho _M,$ and $\rho _R$ are the energy densities corresponding to the quintessence field, non-relativistic matter and radiation, respectively. Starting with Eq. (13) for Brans–Dicke theory (Eq. (24)) and using the above Friedmann equation we find

(37a)

(37b)

(37c)

where

$$\begin{aligned} {\mathcal {C}}({\tilde{a}}; \varpi ) = \frac{2}{3} \varpi \left( 1 + \frac{\Omega _M({\tilde{a}})}{\Omega _\varphi ({\tilde{a}})} + \frac{\Omega _R({\tilde{a}})}{\Omega _\varphi ({\tilde{a}})} \right) , \end{aligned}$$

(38)

$\Omega _{M,R}({\tilde{a}}) = \rho _{M,R}/\rho _c$ are the time-dependant density parameters of dust and radiation in the Einstein frame. We see that whether the Jordan frame with $\varpi$ is expanding or collapsing is determined by the equation of state of the quintessence field and energy densities of all the components present in the Einstein frame. The Jordan frame goes through a ‘turn-around’, i.e., a bounce or a collapse, when the equation of state satisfies Eq. (37c). From this we define

$$\begin{aligned} \varpi _*({\tilde{a}}_{\text {TA}}) = \frac{3}{2} \left( 1 + w_\varphi ({\tilde{a}}_{\text {TA}}) \right) \left( 1 + \frac{\Omega _M({\tilde{a}}_{\text {TA}})}{\Omega _\varphi ({\tilde{a}}_{\text {TA}})} + \frac{\Omega _R({\tilde{a}}_{\text {TA}})}{\Omega _\varphi ({\tilde{a}}_{\text {TA}})} \right) ^{-1}, \end{aligned}$$

(39)

such that the Jordan frame with $\varpi = \varpi _* ({\tilde{a}}_{\text {TA}})$ corresponding to the quintessence field goes through a turn-around at the Einstein frame scale factor ${\tilde{a}}={\tilde{a}}_{\text {TA}}.$ We see that $\varpi _*({\tilde{a}}_{\text {TA}})>0$ for all ${\tilde{a}}_{\text {TA}}$ (as long as $w_\varphi ({\tilde{a}}_{\text {TA}}) > -1,$ we will ignore cases with $w_\varphi < -1$ as they lead to the phantom regime). Therefore, a positive $\varpi _*({\tilde{a}}_{\text {TA}})$ always exists for any ${\tilde{a}}_{\text {TA}},$ which is required for the quintessence field to be real (see Eq. (5)). From these we can conclude the followings:

• 1. Quintessence models with standard matter components in the Einstein frame always correspond to a Jordan frame governed by a Brans–Dicke model where the Jordan frame goes through a turn-around, i.e., a bounce or a collapse.

• 2. The point of the Jordan frame turn-around, i.e., the value of the Einstein frame scale factor at the time of the Jordan frame bounce or collapse, can be arranged anywhere, determined by the choice of the Brans–Dicke theory $(\varpi )$.

Therefore, the dual bouncing/contracting universe description is a feature generic to a variety of late-time cosmological models, including the quintessence models and the concordance model of the universe. It follows from above that one value of $\varpi$ is somewhat spacial. All observationally consistent quintessence models have a common attribute that all of them lead to the same values of the equation of state parameter and density parameter at the current epoch in the Einstein frame, $w_{\varphi 0},$ $\Omega _{\varphi 0}.$ Putting ${\tilde{a}}= 1$ in (39) we define

$$\begin{aligned} \varpi _0 = \varpi _*({\tilde{a}}_{\text {TA}} = 1) = \frac{3}{2} \left( 1 + w_{\varphi 0} \right) \left( \! 1{+}\frac{\Omega _{M 0}}{\Omega _{\varphi 0}}{+}\frac{\Omega _{R 0}}{\Omega _{\varphi 0}}\! \right) ^{{-}1}.\nonumber \\ \end{aligned}$$

(40)

For any viable quintessence model, its corresponding Jordan frame with $\varpi =\varpi _0$ either goes through a bounce or a collapse at the current epoch $({\tilde{a}}=1)$.

5.1 Turn-around in the Jordan frame: bounce or collapse?

Whether the Jordan frame turn-around is a bounce or a collapse is determined by the conditions Eqs. (37a) and (37b). At the point of the turn-around, when $1+w_\varphi ({\tilde{a}}) = {\mathcal {C}}({\tilde{a}};\varpi )$ is satisfied, if $w_\varphi ({\tilde{a}})$ is decreasing (increasing) with respect to ${\tilde{a}},$ then the Jordan frame is collapsing (expanding) before the turn-around and expanding (collapsing) after the turn-around, or the Jordan frame goes through a bounce (collapse). Thus, whether a quintessence model maps to bouncing Jordan frame or a collapsing Jordan frame is determined by whether the equation of state of the quintessence field is decreasing or increasing function of the scale factor at the point of the Jordan frame turn-around.

Fig. 5

Equation of state $w_\varphi$ and energy contributions of the quintessence field and matter for the freezing quintessence model Eq. (42), with $w_p=0,$ $w_f=-1,$ ${\tilde{a}}_T = 0.17,$ $\tau =0.33.$ Initially $w_\varphi ({\tilde{a}}) \sim 0 ;$ in the late times as dark energy contribution takes over matter contribution, $w_\varphi$ approaches $-1$ asymptotically

Fig. 6

Bouncing behaviour of the Jordan frame scale factor for freezing quintessence model (42), with $w_p=0,$ $w_f=-1,$ ${\tilde{a}}_T = 0.17;$ the bounce is arranged at the current epoch ${\tilde{a}}=1.$ a Before the current era $1+w_\varphi > {\mathcal {C}}$ (collapsing Jordan frame) and $1 + w_\varphi < {\mathcal {C}}$ (expanding Jordan frame) after the current era, leading to the Jordan frame bounce at the current era. b Bouncing behaviour of the Jordan frame scale factor a,  $a_0 = a({\tilde{a}}=1)$

Quintessence models are categorized based on the nature of the evolution of the field, into the freezing and thawing types [23]. In the freezing quintessence models, the field evolution slows down as time increases and it eventually ‘freezes’ in the late times, corresponding to a decreasing equation of state parameter which approaches $w_\varphi \rightarrow -1$ in the late times [23, 29, 49, 50]. In the thawing quintessence models, the field stays frozen in the early times due to the Hubble friction, corresponding to $w_\varphi \rightarrow -1.$ In the late times, the field overcomes the Hubble friction and starts to evolve, resulting in increasing $w_\varphi$ later on. Decreasing and increasing equations of state $w_\varphi$ are features generally associated with freezing and thawing quintessence models, respectively. Therefore, taking into account the previous arguments, we expect freezing and thawing quintessence models to be dual to Brans–Dicke Jordan frames with bounce and collapse, respectively. In the following section we demonstrate these dualities for viable quintessence models.

5.2 Examples: freezing and thawing quintessence models dual to Jordan frames with bounce and collapse

Here we consider examples of freezing and thawing quintess ence models and explicitly show the bouncing and collapsing behaviours of their corresponding Jordan frames. For both cases, the Jordan frame turn-arounds are arranged at the current era in the Einstein frame $({\tilde{a}}= 1)$. The condition for Jordan frame turn-around at the current epoch is very weakly dependent on the radiation contribution, i.e., $\Omega _{R 0}/\Omega _{\varphi 0} \sim 10^{-5}$ is negligible with respect to $\Omega _{M0}/\Omega _{\varphi 0}$ in Eq. (37). Therefore, we can safely ignore radiation and only consider the contribution from non-relativistic matter in the following examples.

Fig. 7

Equation of state $w_\varphi$ and energy contributions of the quintessence field and matter for the thawing quintessence model (44), with $K=2.88,$ $\Omega _{\varphi 0} = .7,$ $w_0=-0.9.$ Initially $w_\varphi ({\tilde{a}}) \sim 0;$ as the dark energy takes over in the late times, $w_\varphi$ deviates from $-1$

As an example of the freezing quintessence models, we consider the ‘double exponential’ potential of the form [23, 49]

$$\begin{aligned} V(\varphi ) = V_1 \exp \left( - \lambda _1 \kappa \varphi \right) + V_2 \exp \left( - \lambda _2 \kappa \varphi \right) , \end{aligned}$$

(41)

with the parameters $\lambda _1 \gg 1$ and $\lambda _2 \lesssim 2.$ The model leads to an initial scaling matter era when dark energy is subdominant $(\Omega _\varphi = 3/\lambda _1^2)$, followed by an accelerating dark energy dominated era. The equation of state for this model can be approximated using the following parameterization [49]

$$\begin{aligned} w_\varphi ({\tilde{a}}) = w_f + \frac{w_p - w_f}{1 + \left( \frac{{\tilde{a}}}{{\tilde{a}}_T} \right) ^{1/\tau }}, \end{aligned}$$

(42)

where the parameters $w_p$ and $w_f$ represent the initial and final values of $w_\varphi ;$ ${\tilde{a}}_T$ and $\tau$ determine the transition from matter era to dark energy era in the Einstein frame. The evolution of the equation of state parameter and energy contribution of the field are shown in Fig. 5 for $w_p=0,$ $w_f=-1.$ We see that $w_\varphi$ initially stays at 0 in the matter dominated era; it decreases later on and eventually approaches $-1$ in the late dark energy dominated era. In Fig. 6a, we plot the condition for expanding and collapsing Jordan frame and Fig. 6b shows the bouncing behaviour of the Jordan frame scale factor. In this example, the Brans–Dicke parameter $\varpi$ is chosen such that the Jordan frame bounce occurs at the current era, i.e. at ${\tilde{a}}=1.$ The plots show that before the current era $w_\varphi$ satisfies the condition for collapse, Eq. (37a), while it satisfies the condition for expansion, Eq. (37b) after the current era, thus leading to a bounce in the Jordan frame at the current era.

We now move on to the case of thawing quintessence models. As an example, we consider the ‘hilltop’ quintessence potential [23, 49]

$$\begin{aligned} V(\varphi ) = \Lambda ^4 \left( 1 + \cos \left( \frac{\varphi }{f} \right) \right) . \end{aligned}$$

(43)

The field evolution for this potential can approximately be implemented with the following parameterization of the equation of state [49]

$$\begin{aligned}&w_\varphi ({\tilde{a}}) = -1 + (1 + w_0) {\tilde{a}}^{3(K-1)} \left[ \frac{\left( K - F\left( {\tilde{a}}\right) \right) \left( F\left( {\tilde{a}}\right) + 1\right) ^K + \left( K + F\left( {\tilde{a}}\right) \right) \left( F\left( {\tilde{a}}\right) - 1\right) ^K }{\left( K - \Omega _{\varphi 0}^{-1/2}\right) \left( \Omega _{\varphi 0 }^{-1/2} + 1\right) ^K + \left( K - \Omega _{\varphi 0}^{-1/2}\right) \left( \Omega _{\varphi 0 }^{-1/2} + 1\right) ^K}\right] , \end{aligned}$$

(44)

where

$$\begin{aligned} F({\tilde{a}}) = \sqrt{1 + \left( \Omega _{\varphi 0}^{-1} - 1 \right) {\tilde{a}}^{-3}}, \end{aligned}$$

(45)

$w_0 = w_\varphi ({\tilde{a}}=1),$ and K is a constant parameter of the model. The evolution of $w_\varphi$ and energy contributions from the quintessence field and matter are shown in Fig. 7a and b, for $w_0=-0.9,$ $\Omega _{\varphi 0}=0.7,$ and $K=2.88$ [49]. The equation of state remains close to $-1$ in the early times, corresponding to an almost frozen field $\varphi .$ As dark energy contribution takes over the matter contribution near the current epoch, the field starts to evolve and $w_\varphi$ increases slightly. The conditions for expanding and collapsing Jordan frame are plotted in Fig. 7a. We choose the Brans–Dicke parameter $\varpi$ for the Jordan frame collapse to occur at the current era. The plot shows that before the current era, $w_\varphi$ satisfies the condition for expansion, Eq. (37b), while it satisfies the condition for collapse, Eq. (37a) after the current era, thus leading to a collapse in the Jordan frame at the current era (Fig. 8).

Fig. 8

Collapsing behaviour of the Jordan frame scale factor for the thawing quintessence model (44), with $K=2.88,$ $\Omega _{\varphi 0} = .7,$ $w_0=-0.9;$ the collapse is arranged at the current epoch ${\tilde{a}}=1.$ a $1+w_\varphi < {\mathcal {C}}$ (expanding Jordan frame) before the current era and $1 + w_\varphi > {\mathcal {C}}$ (collapsing Jordan frame) after the current era, leading to the Jordan frame collapse at the current era. b Collapsing behaviour of the Jordan frame scale factor a,  $a_0 = a({\tilde{a}}=1)$

The duality between an indefinitely contracting Jordan frame and the physical universe in the Einstein frame has interesting consequence on the conformal correspondence at the quantum level, similar to the expansion-bounce scenario discussed in Sect. 4.2. Once the scale factor of the contracting Jordan frame becomes sufficiently small, the Jordan frame universe is expected to develop non-negligible quantum characteristics. As the Jordan frame contracts further, the quantum effects therein are expected to grow. While at the same time, the Einstein frame keeps on expanding with its scale factor becoming arbitrarily large. It is worth exploring whether the quantum effects in the Einstein frame are suppressed due to its large scale, or whether the quantum characteristics are a frame independent effect – both the conformally connected universes develop increasing quantum features regardless the cosmological expansions therein.

6 De Sitter expansion in the Jordan frame: collapsing Einstein frame

In the previous sections, we have explored examples of the expansion-collapse duality, where Einstein frames undergoing accelerating expansion correspond to bouncing or collapsing Jordan frames. It is, however, also possible to construct an opposite scenario, where an expanding universe in the Jordan frame can be described through a collapsing universe in the Einstein frame. In this section, we briefly discuss an example where a de Sitter expansion in the Jordan frame maps to a contracting Einstein frame.

Let us consider the prototype Brans–Dicke theory in the Jordan frame, given by the action in Eq. (25) with $U(\lambda ) = 0.$ One can show that for the Brans–Dicke parameter $w_{\text {BD}}= - \frac{4}{3},$ the Jordan frame equations of motion (see Appendix A) admit de Sitter solution [1],

$$\begin{aligned} a(t)&= a_0 \exp \left( H_0 t \right) , \end{aligned}$$

(46a)

$$\begin{aligned} \lambda (t)&= \lambda _0 \exp \left( - 3 H_0 t \right) , \end{aligned}$$

(46b)

where t is the Jordan frame coordinate time, $H_0$ is the constant Hubble parameter in the Jordan frame, $a_0 = a(t=0),$ and $\lambda _0 = \lambda (t=0).$ In this case, the Jordan frame universe mimics the late-time dark energy-dominated era of the $\Lambda$CDM model, where, the effect of dark energy is produced by the Brans–Dicke field instead of the cosmological constant.

In the corresponding Einstein frame (Eq. (6)), the potential becomes $V(\phi ) = 0$ (from Eq. (7)) and the Einstein frame scalar field describes a stiff fluid with equation of state parameter $w_\varphi = 1$ (from Eq. (11)). With $w_{\text {BD}}= -4/3$ and $w_\varphi = 1,$ the expansion-collapse duality condition in Eq. (26) is always satisfied. Therefore, as the Jordan frame expands exponentially, the corresponding Einstein frame contracts. To see this explicitly, one can reconstruct the solution for the Einstein frame scale factor through its Jordan frame counterpart. Using Eq. (46) in Eq. (9), we find the Einstein frame scale factor as

$$\begin{aligned} {\tilde{a}} = \sqrt{\frac{\kappa ^2}{8 \pi } \lambda _0 a_0^3} \left( 1 - \sqrt{\frac{8 \pi }{\kappa ^2 \lambda _0}} \frac{3}{2} H_0 {\tilde{t}} \right) ^{\frac{1}{3}} , \end{aligned}$$

(47)

where the Einstein frame coordinate time ${\tilde{t}}$ is related to the Jordan frame coordinate time t as (see Eq. (9b))

$$\begin{aligned} {\tilde{t}} = \frac{2}{3 H_0} \sqrt{\frac{\kappa ^2 \lambda _0}{8 \pi }} \left[ 1 - \exp \left( - \frac{3}{2} H_0 t \right) \right] . \end{aligned}$$

(48)

Note that we have chosen the origin of ${\tilde{t}}(t)$ such that ${\tilde{t}}(t = 0) = 0.$ In the late-time limit $(t \rightarrow \infty ),$ the Jordan frame scale factor $a \rightarrow \infty ,$ while in this, limit the Einstein frame coordinate time ${\tilde{t}} \rightarrow \frac{2}{3 H_0} \sqrt{\frac{\kappa ^2 \lambda _0}{8 \pi }}$ and the scale factor ${\tilde{a}}\rightarrow 0.$ Therefore, the de Sitter expansion in the Jordan frame can alternatively be seen in the Einstein frame as a collapsing universe, heading towards a big crunch-like singularity.

The duality between a de Sitter spacetime and a contracting universe can be a helpful tool in further studies. For example, quantum fluctuations in the de Sitter background have been studied extensively as the generator of the large-scale structure in the universe (see for example [51]). It is well-known that quantum fluctuations of a massless scalar field in a de Sitter cosmology show divergent behavior in the infrared limit (see [52,53,54] and references therein). This peculiarity is often associated with the non-existence of de Sitter invariant vacuum state. It has also been shown that similar divergences can arise in a universe with power-law expansion [53]. One may address the issue of the diverging quantum fluctuations in the de Sitter and power-law type expanding spacetimes by posing the problem in a conformally connected frame that is contracting. When the scale factor in the contracting universe becomes sufficiently small and approaches the singularity, the classical description of the system is expected to break down; one may speculate the universe to develop significant quantum characteristics in this regime. Therefore, the conformal frame with the contracting universe may provide a natural framework to study the quantum fluctuation, which, in turn, can be imported to the conformally connected expanding de Sitter spacetime. The study of quantum fluctuations in the de Sitter universe through the contracting universe may provide new insights into the infrared divergence issue, which may not be apparent otherwise.

7 Einstein frame-Jordan frame correspondence: effects of linear perturbations

The Einstein and Jordan frame universes are connected via conformal transformation of the metric. We have so far considered that both the Einstein and Jordan frame metrics take the form of the spatially flat FRW spacetime, as given in Eq. (6). However, in general, both the conformally connected universes can possess small perturbations on the background of FRW spacetime. A robust conformal correspondence should provide a regular map between the perturbations in the Einstein and Jordan frames as well.

The study of cosmological perturbations in several classes of modified theories of gravity, particularly exploring the Einstein frame-Jordan frame mapping, can be found in [55,56,57,58,59,60,61]. In [55,56,57] perturbations in generalized $f(\phi ,R)$ theories are studied using the Einstein frame description. Cosmological perturbations in the early universe f(R) models is explored, for example, in [58].

In this section we introduce linear scalar perturbations in the background metrics of both the conformally connected frames. Following the treatment in [55,56,57,58], we briefly review the relation between metric perturbations in the Einstein and Jordan frames.

7.1 Metric potentials in Einstein and Jordan frames

Let us consider scalar perturbations in the Jordan and Einstein frame metrics. The line elements in the Jordan and Einstein frames, written in the Newtonian gauge, are

$$\begin{aligned} \text {d}s^2&= a^2(\eta ) \left[ - (1 + 2 \Phi ) \text {d}\eta ^2 + (1 - 2 \Psi ) \delta _{\alpha \beta } \text {d}x^\alpha \text {d}x^\beta \right] , \end{aligned}$$

(49a)

$$\begin{aligned} \text {d}{\tilde{s}}^2&= {\tilde{a}}^2(\eta ) \left[ - (1 + 2 {\tilde{\Phi }}) \text {d}\eta ^2 + (1 - 2 {\tilde{\Psi }}) \delta _{\alpha \beta } \text {d}x^\alpha \text {d}x^\beta \right] , \end{aligned}$$

(49b)

where $(\Phi , \Psi )$ and $({\tilde{\Phi }}, {\tilde{\Psi }})$ are the metric potentials in the Jordan and Einstein frames, respectively. Note that we will be using the conformal time $(\eta )$ in this section, which is same for both the frames.¹ The above mentioned perturbed line elements are related via the conformal transformation (2a) as

$$\begin{aligned} \text {d}{\tilde{s}}^2 = \Omega ^2 \text {d}s^2, \end{aligned}$$

(50)

where the conformal parameter is perturbed as well

$$\begin{aligned} \Omega (\eta , x^\alpha ) = {\bar{\Omega }}(\eta ) + \delta \Omega (\eta , x^\alpha ). \end{aligned}$$

(51)

Comparing the first order terms in Eq. (50), one can relate the metric potentials in the two frames as [55,56,57,58]

$$\begin{aligned} \Phi&= {\tilde{\Phi }} - \frac{\delta \Omega }{ {\bar{\Omega }}}, \end{aligned}$$

(52a)

$$\begin{aligned} \Psi&= {\tilde{\Psi }} + \frac{\delta \Omega }{{\bar{\Omega }}}. \end{aligned}$$

(52b)

Let us now come to the example where the Einstein and Jordan frames are governed by the concordance scalar field $(\varphi )$ and the Brans–Dicke field $(\lambda )$, where the fields are now perturbed,

$$\begin{aligned} \lambda \left( \eta , x^\alpha \right)&= {\bar{\lambda }}(\eta ) + \delta \lambda (\eta , x^\alpha ), \end{aligned}$$

(53a)

$$\begin{aligned} \varphi \left( \eta , x^\alpha \right)&= {\bar{\varphi }}(\eta ) + \delta \varphi (\eta , x^\alpha ). \end{aligned}$$

(53b)

Since the Einstein frame is free from anisotropic stress, we further take ${\tilde{\Phi }} = {\tilde{\Psi }}$ [58]. The relations between the metric potentials in the two frames then reduce to

$$\begin{aligned} \Phi&= {\tilde{\Phi }} - \frac{\delta \lambda }{2 {\bar{\lambda }}}, \end{aligned}$$

(54a)

$$\begin{aligned} \Psi&= {\tilde{\Phi }} + \frac{\delta \lambda }{2 {\bar{\lambda }}}, \end{aligned}$$

(54b)

whereas, the two potentials in the Jordan frame are related by

$$\begin{aligned} \Psi = \Phi + \frac{\delta \lambda }{{\bar{\lambda }}}. \end{aligned}$$

(55)

This shows that unlike the Einstein frame, the two metric potentials in the Jordan frame are not equal, which is a well-known characteristic of modified theories of gravity [55, 58].

We now replace the Brans–Dicke field terms $({\bar{\lambda }}, \delta \lambda )$ in Eq. (54) with those of the concordance field. Noting that $\varphi$ and $\lambda$ are related as (see Eq. (5))

$$\begin{aligned} \frac{\text {d}\varphi }{\text {d}\lambda } = \sqrt{K[\lambda ]} = \frac{1}{\sqrt{2 \kappa ^2}} \frac{\sqrt{\varpi }}{\lambda }, \end{aligned}$$

(56)

we get

$$\begin{aligned} \frac{\delta \lambda }{{\bar{\lambda }}}&= \frac{\sqrt{2}\kappa }{\sqrt{\varpi }} \delta \varphi , \end{aligned}$$

(57a)

$$\begin{aligned}&=\frac{\sqrt{2}}{\sqrt{\varpi }} \frac{2}{\kappa {\bar{\varphi }}'} \left( {\tilde{\Phi }}' + {\tilde{\mathcal {H}}} {\tilde{\Phi }} \right) , \end{aligned}$$

(57b)

where the prime denotes derivative with respect to the conformal time $\eta ,$ ${\tilde{\mathcal {H}}} ={\tilde{a}}'/{\tilde{a}}.$ The last line is derived using the space-time component of the perturbed Einstein equation in the Einstein frame [58],

$$\begin{aligned} {\tilde{\Phi }}' + {\tilde{\mathcal {H}}}{\tilde{\Phi }} = \frac{\kappa ^2}{2}{\bar{\varphi }}' \delta \varphi . \end{aligned}$$

(58)

Using Eq. (57b) in Eq. (54) we can write

$$\begin{aligned} \Phi&= {\tilde{\Phi }} - \frac{\sqrt{2}}{\sqrt{\varpi }} \frac{1}{\kappa {\bar{\varphi }}'} \left( {\tilde{\Phi }}' + {\tilde{\mathcal {H}}} {\tilde{\Phi }} \right) \end{aligned}$$

(59a)

$$\begin{aligned} \Psi&= {\tilde{\Phi }} + \frac{\sqrt{2}}{\sqrt{\varpi }} \frac{1}{\kappa {\bar{\varphi }}'} \left( {\tilde{\Phi }}' + {\tilde{\mathcal {H}}} {\tilde{\Phi }} \right) . \end{aligned}$$

(59b)

These are the relations between the metric potentials in the two conformal frames.² Thus, once the evolution of the metric potential in the Einstein frame is known, along with the background quantities ${\tilde{a}}(\eta )$ and ${\bar{\varphi }}(\eta ),$ one can obtain the solutions for the metric potentials in the Jordan frame.

It is, however, possible that under certain circumstances the above relations become singular, breaking the perturbative map between the two conformal frames. This issue is addressed, for example, in [10, 21], in the context of early universe bouncing f(R) theories. It is shown that the relation between the metric potentials can diverge when the background scalar field in the Einstein frame goes through an extremum, i.e., ${\bar{\varphi }}' \rightarrow 0.$ The same issue can potentially arise in the case of Brans–Dicke theory governed Jordan frame. From the relations (59), we see that if the background concordance field goes through an extremum at an instant, i.e. ${\bar{\varphi }}' \rightarrow 0,$ the Jordan frame potentials $(\Phi , \Psi )$ can diverge, even if the Einstein frame potential and its derivative $({\tilde{\Phi }}, {\tilde{\Phi }}')$ remain finite. This can cause the Einstein frame–Jordan frame correspondence to break down in the perturbative regime. We now check whether such a divergence occurs in the present model of the bouncing universe dual to the physical universe.

From Eq. (12), the conformal time derivative of the background field can be written as

$$\begin{aligned} {\bar{\varphi }}' = {\tilde{a}}\sqrt{(1 + w_\varphi ({\tilde{a}})) {\bar{\rho }}_\varphi ({\tilde{a}})}. \end{aligned}$$

(60)

For the case of the concordance model in the Einstein frame, this relation becomes

$$\begin{aligned} {\bar{\varphi }}' = \sqrt{ \rho _{\text {c}} \frac{1 - \Omega _\Lambda }{{\tilde{a}}}}, \end{aligned}$$

(61)

where we have used Eqs. (17b) and (18) to obtain Eq. (61). This shows that ${\bar{\varphi }}'$ is non-zero for any finite value of the Einstein frame scale factor ${\tilde{a}}.$ Also from Eq. (22), ${\tilde{a}}$ is finite-valued as long as the coordinate time ${\tilde{t}}$ is finite, hence ${\bar{\varphi }}'$ never becomes 0 at an instant. Unlike the models explored in [10, 21], the issue of diverging metric potentials caused by ${\bar{\varphi }}' \rightarrow 0$ is not present in the current model.

For quintessence models of dark energy, $\bar{\varphi {}}$ takes the role of the background quintessence field. The relation in Eq. (60) holds true for quintessence models as well, given $w_\varphi ,$ ${\bar{\rho }}_ \varphi$ are the equation of state and background energy density associated with the quintessence field. As long as the quintessence equation of state remains $w_\varphi ({\tilde{a}}) > -1$ at any finite time, $\bar{\varphi {}}'$ remains non-zero and the relations Eq. (59) are non-divergent. For example, for the thawing and freezing types of quintessence models considered in the last section, Eqs. (42) and (44), $w_\varphi \ne -1$ for any finite value of the scale factor ${\tilde{a}}.$ For the thawing model, $w_\varphi$ approaches $-1$ in the asymptotic future $({\tilde{a}}\rightarrow \infty )$; while for the freezing model, $w_\varphi \rightarrow -1$ in the asymptotic past $({\tilde{a}}\rightarrow 0)$ (see Figs. 5a and 7a). Therefore, we expect the Jordan frame–Einstein frame map to behave regularly in the perturbative regime for quintessence models with $w_\varphi > -1,$ even when the Jordan frame goes through the turn-around.

In the following discussion, we mainly focus on the example of the concordance model and explicitly verify the stability of the perturbative conformal map. To do this, we first numerically solve the Einstein frame metric perturbation, the result is then transported to the Jordan frame using the conformal correspondence. For the second case, we solve the perturbations in the Jordan frame directly, the result is then compared with those obtained via the Einstein frame. If the conformal map is robust under perturbations, then the Jordan frame metric potentials obtained in these two cases should be in agreement.

7.1.1 Numerical results in the Einstein frame

Let us first consider the evolution of perturbations in the Einstein frame. Cosmological perturbations in the presence of a canonical scalar field has been studied broadly, both in the context of inflationary models and dark energy models (see, for example, [58, 62] and references therein). For the perturbed Einstein frame metric (49b) and the perturbed concordance field (53b), the Einstein field equation leads to [58]

$$\begin{aligned} {\tilde{\Phi }}'' + 2 \frac{\text {d}}{\text {d}\eta } \left( \frac{{\tilde{a}}}{{\bar{\varphi }}'} \right) \left( \frac{{\tilde{a}}}{{\bar{\varphi }}'} \right) ^{-1} {\tilde{\Phi }}' - \nabla ^2 {\tilde{\Phi }} + 2 {\bar{\varphi }}' \frac{\text {d}}{\text {d}\eta } \left( \frac{\tilde{{\mathcal {H}}}}{{\bar{\varphi }}'} \right) {\tilde{\Phi }} = 0, \end{aligned}$$

(62)

where $\nabla ^2$ is the spatial Laplacian. Following the treatment of [58, 63], the above equation for a Fourier mode k can be put in a relatively simple form,

$$\begin{aligned} u''(\eta ) + \left( k^2 - \frac{\theta ''(\eta )}{\theta (\eta )}\right) u(\eta ) = 0, \end{aligned}$$

(63)

where the first order quantity u and background quantity $\theta$ are defined as

$$\begin{aligned} u(\eta )&= {\tilde{a}}(\eta )\frac{{\tilde{\Phi }}(\eta )}{{\bar{\varphi }}'(\eta )},\end{aligned}$$

(64a)

$$\begin{aligned} \theta (\eta )&= \frac{{\tilde{\mathcal {H}}}}{{\tilde{a}}{\bar{\varphi }}'}. \end{aligned}$$

(64b)

For small scale modes, or for large k $(k^2 \gg \theta ''/\theta )$, the contribution from the $\theta ''/\theta$ term in Eq. (63) becomes minimal, leading to an oscillatory solution for u. The Einstein frame metric potential is then obtained using ${\tilde{\Phi }} = ({\bar{\varphi }}'/{\tilde{a}}) u,$ where, from Eq. (61), the factor $({\bar{\varphi }}'/{\tilde{a}})$ can be shown to decay as $1/{\tilde{a}}^{\frac{3}{2}}.$ Hence, for $k^2 \gg \theta ''/\theta ,$ we expect ${\tilde{\Phi }}$ to have the profile of a damped oscillator.

Fig. 9

Numerical solution for Einstein frame metric perturbation ${\tilde{\Phi }}$ is plotted with respect to the conformal time $\eta ,$ for Fourier mode $k=15,$ where the Einstein frame is governed by the concordance scalar field. $\eta$ is given in the unit of 13.5 Gy, $\eta =0$ corresponds to the current Einstein frame epoch, ${\tilde{a}}=1$

The background quantity $\theta (\eta )$ can be obtained analytically, from Eqs. (22) and (61). Using this, we numerically solve the perturbation equation (63) for such a sufficiently large $k=15,$ with initial conditions

$$\begin{aligned} {\tilde{\Phi }}(\eta = 0) = 10^{-3},\ {\tilde{\Phi }}'(\eta = 0) = 10^{-2}. \end{aligned}$$

(65)

Other background parameters are taken to be $\Omega _\Lambda =0.7,\ H_0 = 70~\text {km}~\text {s}^{-1}~\text {Mpc}^{-1}.$ The origin of the conformal time $(\eta = \int \text {d}{\tilde{t}}/ {\tilde{a}})$ is chosen such that $\eta =0$ coincides with the current epoch, i.e., ${\tilde{a}}({\tilde{t}}={\tilde{t}}_0=0)={\tilde{a}}(\eta =0) = 1$ in the Einstein frame. Figure 9 shows the numerical evolution of the Einstein frame perturbation with conformal time. As discussed above, ${\tilde{\Phi }}$ exhibits oscillation with decreasing amplitude.

Once the evolution of ${\tilde{\Phi }}$ is known, one can obtain the Jordan frame metric perturbations $\Phi ,\ \Psi ,$ from the relations (59). For the numerical results, we choose the Jordan frame with Brans–Dicke parameter $w_{\text {BD}}= - \frac{3}{4} \left( 1 + \Omega _\Lambda \right) .$ For this choice of $w_{\text {BD}},$ the Jordan frame bounce occurs exactly at the current epoch of the Einstein frame, i.e., at ${\tilde{a}}=1.$ The numerical evolutions of $\Phi$ and $\Psi$ are plotted in Fig. 11a and b.

Fig. 10

Jordan frame scale factor a is plotted with respect to the Jordan frame coordinate time t,  dual to the concordance model in the Einstein frame. Here $w_{\text {BD}}= - \frac{3}{4} \left( 1 + \Omega _\Lambda \right) ,$ t is given in the unit of 13.5 Gy. The Jordan frame bounce occurs at $t=0.$ The blue plot is the numerical solution obtained directly in the Jordan frame, whereas, the black dashed plot is the analytical results obtained via the Einstein frame. The Einstein and Jordan frame results are shown to be in agreement

Fig. 11

Jordan frame metric potentials $\Psi$ and $\Phi$ are plotted with respect to the conformal time $\eta$ (in the unit of 13.5 Gy), where Einstein frame is governed by the concordance field. Here $\eta =0$ is the point of the bounce. In both the figures, the blue plots show numerical solutions of the metric potentials obtained directly in the Jordan frame, whereas, the black dashed plots are the corresponding results obtained from Einstein frame, using the conformal correspondence. The Jordan and Einstein frame solutions are in good agreement throughout the evolution

7.1.2 Numerical results in the Jordan frame

Having solved the Jordan frame perturbations using the conformal correspondence, we now study the evolution of perturbations directly in the Jordan frame. We then compare these results with those obtained via the Einstein frame in the previous section. If the Einstein frame–Jordan frame correspondence remains valid in the linear perturbation regime, then the solutions obtained for the two cases are expected to be in agreement.

Let us first consider the background evolution of the Brans–Dicke Jordan frame. Starting with the action (25) and using the background metric (8b), one can obtain the background equations of motion for the Brans–Dicke field and the Jordan frame scale factor as (see Appendix A)

$$\begin{aligned}&{\dot{H}} = - \frac{w_{\text {BD}}}{2} \left( \frac{\dot{{\bar{\lambda }}}}{{\bar{\lambda }}} \right) ^2 + 2 H \frac{{\dot{{\bar{\lambda }}}}}{{\bar{\lambda }}} \nonumber \\&\quad + \frac{1}{2 \varpi {\bar{\lambda }}} 16 \pi \left[ {\bar{\lambda }}U_{,\lambda }({\bar{\lambda }}) - 2 U ({\bar{\lambda }}) \right] , \end{aligned}$$

(66a)

$$\begin{aligned}&\ddot{{\bar{\lambda }}} + 3 H {\dot{{\bar{\lambda }}}} = - \frac{16 \pi }{\varpi } \left[ {\bar{\lambda }}U_{, \lambda }({\bar{\lambda }}) - 2 U({\bar{\lambda }}) \right] , \end{aligned}$$

(66b)

where the overdots represent derivatives with respect to the Jordan frame coordinate time t,  $H = {\dot{a}}/a$ is Jordan frame Hubble parameter. The Brans–Dicke potential $U(\lambda ),$ dual to the concordance potential, is given in Eq. (30). Using this, we numerically solve the coupled Eqs. (66a) and (66b) simultaneously to obtained a(t) and ${\bar{\lambda }}(t).$ For this and all following numerical calculations, the origin of the Jordan frame coordinate time (t) is taken such that it coincides with the Einstein frame coordinate time at the current epoch, i.e., ${\tilde{t}}_0=0,\ t({\tilde{t}}={\tilde{t}}_0) = 0,\ \eta ({\tilde{t}}={\tilde{t}}_0)=0.$ The initial conditions are fixed it $t=0$ such that they coincide with the Einstein frame solutions. Figure 10 shows the evolution of the Jordan frame scale factor with respect to the Jordan frame coordinate time t. For the chosen Brans–Dicke theory, $w_{\text {BD}}= - \frac{3}{4} \left( 1 + \Omega _\Lambda \right) ,$ the Jordan frame bounce occurs at $t=0,$ which corresponds to the current epoch in the physical universe. The same plot also shows the analytical solution for a(t) obtained using the Einstein frame (from Eq. (32), using Eqs. (9b) and (22)). We see that the numerical solution obtained directly in the Jordan frame is in agreement with its counterpart, analytically obtained in the Einstein frame.

Having obtained the background evolution in the Jordan frame, we now move on to the perturbations. For the perturbed Brans–Dicke field

$$\begin{aligned} \lambda = {\bar{\lambda }}(t) + \delta \lambda (t, x^\alpha ), \end{aligned}$$

(67)

and the perturbed Jordan frame metric in the Newtonian gauge (written in terms of the coordinate time t),

$$\begin{aligned} \text {d}s^2 = -\text {d}t^2 (1 + 2 \Phi )+ a^2(t) (1 - 2 \Psi ) \delta _{\alpha \beta } \text {d}x^\alpha \text {d}x^\beta , \end{aligned}$$

(68)

the linear order equations of motions, governing $\delta \lambda$ and $\Phi ,$ can be written for Fourier mode k as (see Appendix A)

$$\begin{aligned}&\ddot{\delta \lambda } +\dot{\delta \lambda } \left( 3 H+\frac{{\dot{{\bar{\lambda }}}}}{{\bar{\lambda }}}\right) \nonumber \\&\quad +\delta \lambda \left( \frac{k^2}{a^2}+\frac{6 H {\dot{{\bar{\lambda }}}}}{{\bar{\lambda }}}-\frac{\dot{{\bar{\lambda }}}^2}{{\bar{\lambda }}^2}+\frac{2 \ddot{{\bar{\lambda }}}}{{\bar{\lambda }}}+\frac{16 \pi {\bar{\lambda }}U_{,\lambda \lambda }}{\varpi }-\frac{16 \pi U_{\lambda }}{\varpi }\right) \nonumber \\&\quad -6 H {\dot{{\bar{\lambda }}}} \Psi -2 \Psi \ddot{{\bar{\lambda }}}-4 {\dot{{\bar{\lambda }}}} {\dot{\Psi }} = 0, \end{aligned}$$

(69)

and

$$\begin{aligned}&-6 {\bar{\lambda }}\varpi \ddot{\Psi } -30 H {\bar{\lambda }}{\dot{\Psi }} \varpi \nonumber \\&\quad +\Psi \left( -\frac{2 k^2 {\bar{\lambda }}\varpi }{a^2}-24 H^2 {\bar{\lambda }}\varpi -12 {\dot{H}} {\bar{\lambda }}\varpi -\frac{2 {\dot{{\bar{\lambda }}}}^2 w \varpi }{{\bar{\lambda }}}\right) \nonumber \\&\quad +\delta \lambda \left( -\frac{2 k^2 \varpi }{a^2}+36 H^2 \varpi -\frac{6 H {\dot{{\bar{\lambda }}}} \varpi }{{\bar{\lambda }}}\right. \nonumber \\&\quad \left. +18 {\dot{H}} \varpi -48 \pi {\bar{\lambda }}U_{,\lambda \lambda } -48 \pi U_{,\lambda }-64 \pi w U_{,\lambda }+\frac{{\dot{{\bar{\lambda }}}}^2 w \varpi }{{\bar{\lambda }}^2}\right) \nonumber \\&\quad +\dot{\delta \lambda } \left( 6 H \varpi +\frac{2 {\dot{{\bar{\lambda }}}} w \varpi }{{\bar{\lambda }}}\right) = 0. \end{aligned}$$

(70)

For the Fourier mode $k=15,$ the coupled Eqs. (69) and (70) are numerically solved together to obtain $\Psi (t)$ and $\delta \lambda (t).$ We choose the following initial conditions at $t=0,$

$$\begin{aligned}&\Psi (0)= 0.0263,\ {\dot{\Psi }}(0)=-0.1623,\ \delta \lambda (0)=0.1130,\nonumber \\&\dot{\delta \lambda }(0)=-0.6745, \end{aligned}$$

(71)

such that they coincide with the Einstein frame initial conditions (65) at $\eta = t =0.$ Using the solutions of $\Psi (t)$ and $\delta \lambda (t),$ the other Jordan frame metric potential $\Phi (t)$ can be obtained from Eq. (55). Figure 11a and b show the evolution of the Jordan frame metric perturbations $(\Phi , \Psi ),$ together with their counterparts obtained from the Einstein frame. Note that the Jordan frame solutions $\Psi (t),$ $\Phi (t)$ are converted to functions of the conformal time $\eta ,$ in order to compare them with the Einstein frame solutions. We see that for both the metric potentials, the Jordan and Einstein frame solutions are in good agreement.

The Einstein frame solutions behave regularly through out the evolution, including the point of the Jordan frame bounce at $\eta =0.$ The conformal map between the Einstein and Jordan frames is thus able to accommodate for cosmological perturbations present in the two frames. Therefore, the bouncing universe description of the concordance model of cosmology is shown to be stable against linear perturbations.

As the final example, we carry out the same analysis for a collapsing Jordan frame (see Fig. 12). For this, we consider a quintessence field in the Einstein frame with logarithmic equation of state parameter,

$$\begin{aligned} w_\varphi ({\tilde{a}}) = w_0 - w' \ln {\tilde{a}}, \end{aligned}$$

(72)

where $(w_0, w')$ are constant parameters of the model [64,65,66]. We ignore the contribution from the ordinary matter component in this example. For $w'<0,$ the equation of state is an increasing function of the scale factor, therefore the corresponding Jordan frame undergoes a collapse. After the collapse, the Jordan frame scale factor continues to contract indefinitely (Fig. 12b), while the Einstein frame expands (Fig. 12a). We perform the same numerical analysis as before and show that the map between the Einstein and Jordan frame perturbations remains well-behaved at the point of the turn-around, and even as the Jordan frame scale factor $a \rightarrow 0$ (Fig. 12c and d).

Fig. 12

Conformal duality at the perturbative regime between the Einstein frame with a quintessence field (without matter) and its dual collapsing Jordan frame with a Brans–Dicke theory. The equation of state of the quintessence field is $w_\varphi ({\tilde{a}}) = w_0 - w' \ln {\tilde{a}},$ where $(w_0, w') = (-0.87, -0.48)$ [64]. All the plots are with respect to the conformal time $\eta$ (in the unit of 13.5 Gy). The Brans–Dicke parameter is chosen such that the Jordan frame turn-around occurs at $\eta =0,$ ${\tilde{a}} = 1.$ In a and b, the Einstein and Jordan frame scale factors ($\tilde{a}$ and a) are plotted with respect to the conformal time. Jordan frame metric potentials $\Psi$ and $\Phi$ are plotted for $k=10$ in c and d. In both the figures, the blue plots show numerical solutions of the metric potentials obtained directly in the Jordan frame, whereas, the black dashed plots are the corresponding results obtained from Einstein frame, using the conformal correspondence. The Jordan and Einstein frame solutions are in good agreement throughout the evolution, even as $a \rightarrow 0$

8 Summary and discussion

The scalar–tensor theories belong to a class of modified theories of gravity, which can be mapped to Einstein’s gravity using the Jordan frame–Einstein frame duality. The Einstein and Jordan frame descriptions are mathematically equivalent, it is, however, possible that the Jordan frame universe goes through a quite distinct cosmological evolution in comparison with its Einstein frame counterpart [9,10,11,12,13,14,15, 17,18,19,20,21,22]. In this paper, we study a class of dual universes with contrasting nature of evolutions. We consider an Einstein frame where the universe goes though the standard late-time cosmological evolution, driven by dark energy and non-relativistic matter. Dual to this, we find a class of scalar–tensor theories which may lead to a collapsing Jordan frame. A general condition for such an expansion-collapse duality is obtained to predict whether, for a given scalar–tensor theory, the Jordan frame is collapsing during a period of evolution.

We first set up the Einstein frame scalar field for it to provide an effective description of the $\Lambda$CDM or the concordance model of cosmology. As an example of the scalar–tensor theories, we consider the Brans–Dicke model in the Jordan frame. Using the general condition for the expansion-collapse duality, we show that concordance model of cosmology can always be mapped to a bouncing Brans–Dicke Jordan frame. This implies that the $\Lambda$CDM model of the late-time universe can have an effective description in terms of the dynamics of a bouncing universe. In the second case, the Einstein frame scalar field is treated as a quintessence field and a non-relativistic matter component is added separately in the Einstein frame. Quintessence models are shown to be always dual to Brans–Dicke Jordan frames with turn-arounds, i.e., a bounce or a collapse. The nature of evolution of the equation of state of the quintessence field at the turn-around determines whether the turn-around is a bounce or a collapse. These results indicate that the effect of dark energy can alternatively be realized as collapse of space in a conformally connected universe, at least classically.

We have also discussed an example of the expansion-collapse duality where a de Sitter expansion in the Jordan frame maps to a collapsing Einstein frame heading towards singularity. The dual description of a de Sitter spacetime through a collapsing universe has potential applications. For example, one may study the infrared divergence of quantum fluctuations in the de Sitter background [52,53,54] by posing the problem in a collapsing universe where the quantum effects are better understood.

Previous studies have explored the expansion-collapse duality between conformal frames in different scenarios [12,13,14,15, 17]. For example, in [12] (also see [13]), the Jordan frame universe is contracting in the radiation and matter dominated phases, while it is expanding in the dark energy era. In the “anamorphic” model, the universe undergoes an initial anamorphic phase, which exhibits features of both contracting (ekpyrotic) and expanding (inflationary) models [14, 17]. After the end of the anamorphic phase the universe enters into the standard hot expanding phase, consistent with general relativity. In the present work, we explore the expansion-collapse duality in the context of late-time cosmology. We show that dual universes with bounce or collapse are not exclusive to specific dark energy models; in fact, quintessence models, in general, can always be mapped to Jordan frames with turn-arounds. Moreover, the expanding and contracting phases in the Jordan frame need not be corresponding to certain eras in the Einstein frame. The Jordan frame can always be tuned to arrange the turn-around anywhere in the Einstein frame.

A robust conformal correspondence between the Einstein and Jordan frames should provide a regular map between cosmological perturbations therein. We investigate whether the dual bouncing and collapsing universe description of the standard cosmology is robust against linear perturbations. The conformal correspondence is found to be stable as long as the Einstein frame scalar field’s equation of state satisfies $w_\varphi >-1.$

To see this explicitly, we primarily consider the example of the concordance field in the Einstein frame. We numerically solve scalar metric perturbations in both the conformal frames. The Einstein frame solutions are then transported to the Jordan frame, using the linear order conformal map. These are compared with the Jordan frame perturbations, directly obtained in the Jordan frame. The solutions of the Jordan frame perturbations in these two cases are in agreement. Therefore, in this case the conformal duality between the late-time physical universe and the bouncing Brans–Dicke Jordan frame universe is shown to be stable under linear perturbations. The same analysis is performed for another example, where the Einstein frame is governed by a quintessence field with logarithmic equation of state. The corresponding Jordan frame undergoes a collapse and then contracts indefinitely. The results here also indicate that the conformal correspondence between the perturbations in the two frames behave regularly, even as the Jordan frame scale factor $a \rightarrow 0.$

Bouncing scenarios, in general, have been explored in the literature as a candidate for the early universe model, alternative to the inflationary theory. In this paper we show that a perturbatively stable, effective bouncing description is also possible for the standard late-time evolution of the universe. This may have interesting implications. As we have seen, the nature of the cosmological evolution depends on the conformal frame, however, it is shown in the literature that physical observables, such as the redshift, galaxy number count [20], Sachs–Wolfe effect, curvature perturbation (see [67, 68] and references therein) are independent of the choice of the conformal frame. One can use these frame invariant observables in the current model to find a map between the late-time cosmological perturbations and fluctuations in a bouncing model. Typically, small perturbations on a collapsing cosmological background tend to grow, whereas the growth of perturbations is suppressed in an expanding space. Therefore, one can speculate that the perturbations in the bouncing universe will grow up to the point of the bounce. On the other hand, the point of the Jordan frame bounce can be arranged at the onset of the cosmological constant dominated era in the Einstein frame. The interpretation of the evolution of perturbations in the bouncing universe may reveal interesting features regarding how dark energy affects the evolution of cosmological perturbations in the standard cosmology, which may not be apparent otherwise. Also, since the Jordan frame scale factor at the point of bounce is sensitive to the dark energy content in the Einstein frame, such a duality may help in a better understanding of the concordance model of cosmology.

The status of the conformal correspondence at the quantum level is explored in the literature in several contexts (see, for example [47, 69,70,71,72,73,74,75,76] and references therein). The duality between the physical universe and bouncing and collapsing universe presented in this paper may provide further insights into the topic. In the bouncing and collapsing descriptions of the late-time cosmological models, the scale factor can become arbitrarily small at a time when the dual universe represents the accelerating and expanding physical universe. As the collapsing universe reaches a sufficiently small scale, it is expected to develop quantum characteristics; for example, the quantum variance in cosmological quantities may become large in these regions. However, the expanding universe is expected to behave classically at this point.

It is shown in [48] that the conformal map between a contracting Brans–Dicke Jordan frame and an expanding Einstein frame holds at the quantum level. Interestingly, the rise in quantum fluctuations is found to be conformally invariant; they take the same value in both frames regardless of the different cosmological evolutions. Given that the effect of dark energy can alternatively be realized as collapse of space, as shown in the present work, the results may indicate that a dark energy-driven large expanding universe can also harbor non-trivial quantum features [77,78,79].

Appendix A: Field equations in the Jordan frame

Here we summarize the derivations of the Brans–Dicke theory equations of motion in the Jordan frame, Eqs. (66), (69) and (70). For detailed derivation see, for example [1].

The variation of the Brans–Dicke action (25) with respect to the metric $g^{ab}$ leads to the field equation

$$\begin{aligned} \lambda G_{ab}&= \frac{w_{\text {BD}}}{\lambda } \left( \nabla _a \lambda \nabla _b \lambda - \frac{1}{2} g_{ab} \nabla ^c \lambda \nabla _c \lambda \right) \nonumber \\&\quad + (\nabla _a \nabla _b \lambda - g_{ab}\Box \lambda ) - 8 \pi U g_{ab}, \end{aligned}$$

(73)

the trace of which is

$$\begin{aligned} \lambda R = \frac{w_{\text {BD}}}{\lambda } \nabla ^c \lambda \nabla _c \lambda + 3 \Box \lambda + 32 \pi U. \end{aligned}$$

(74)

The equation of motion of the Brans–Dicke field $\lambda$ can be derived as

$$\begin{aligned} 2 w_{\text {BD}}\Box \lambda + \lambda R - \frac{w_{\text {BD}}}{\lambda } \nabla _c \lambda \nabla ^c \lambda - 16 \pi \lambda U_{,\lambda } = 0. \end{aligned}$$

(75)

Using Eqs. (74) and (75), one can find the following dynamical equations for the metric and for $\lambda ,$

$$\begin{aligned} \varpi \lambda R&= \varpi \frac{w_{\text {BD}}}{\lambda } \nabla _c \lambda \nabla ^c \lambda + 16 \pi \left( 3 \lambda U_{,\lambda } + 4 w_{\text {BD}}U \right) . \end{aligned}$$

(76a)

$$\begin{aligned} \varpi \Box \lambda&= 16 \pi \left( \lambda U,_\lambda - 2 U \right) . \end{aligned}$$

(76b)

For the homogeneous background field $\lambda (t)$ and spatially flat FRW line element (written in the coordinate time) in the Jordan frame,

$$\begin{aligned} \text {d}s^2 = - \text {d}t^2 + a^2(t) \delta _{\alpha \beta } \text {d}x^\alpha \text {d}x^\beta , \end{aligned}$$

(77)

the above equations lead to

$$\begin{aligned}&{\dot{H}} = - \frac{w_{\text {BD}}}{2} \left( \frac{{\dot{\lambda }}}{\lambda } \right) ^2 + 2 H \frac{{\dot{\lambda }}}{\lambda } + \frac{1}{2 \varpi \lambda } 16 \pi \left[ \lambda U_{,\lambda } - 2 U \right] \end{aligned}$$

(78a)

$$\begin{aligned}&\ddot{\lambda } + 3 H {\dot{\lambda }} = -\frac{16 \pi }{\varpi } \left[ \lambda U_{, \lambda } - 2 U \right] . \end{aligned}$$

(78b)

Similarly, using the perturbed metric (68) and perturbed field (67) in Eqs. (76a) and (76b), one can find the linear order equation

$$\begin{aligned}&-6 {\bar{\lambda }}\varpi \ddot{\Psi } -30 H {\bar{\lambda }}{\dot{\Psi }} \varpi \nonumber \\&\quad +\Psi \left( -\frac{2 k^2 {\bar{\lambda }}\varpi }{a^2}-24 H^2 {\bar{\lambda }}\varpi -12 {\dot{H}} {\bar{\lambda }}\varpi -\frac{2 {\dot{{\bar{\lambda }}}}^2 w \varpi }{{\bar{\lambda }}}\right) \nonumber \\&\quad +\delta \lambda \left( -\frac{2 k^2 \varpi }{a^2}+36 H^2 \varpi -\frac{6 H {\dot{{\bar{\lambda }}}} \varpi }{{\bar{\lambda }}}+18 {\dot{H}} \varpi \right. \nonumber \\&\quad \left. -48 \pi {\bar{\lambda }}U_{,\lambda \lambda }-48 \pi U_{,\lambda }-64 \pi w U_{\lambda }+\frac{{\dot{{\bar{\lambda }}}}^2 w \varpi }{{\bar{\lambda }}^2}\right) \nonumber \\&\quad +\dot{\delta \lambda } \left( 6 H \varpi +\frac{2 {\dot{{\bar{\lambda }}}} w \varpi }{{\bar{\lambda }}}\right) = 0 \end{aligned}$$

(79)

and

$$\begin{aligned}&\ddot{\delta \lambda } +\dot{\delta \lambda } \left( 3 H+\frac{{\dot{{\bar{\lambda }}}}}{{\bar{\lambda }}}\right) \nonumber \\&\quad +\delta \lambda \left( \frac{k^2}{a^2}+\frac{6 H {\dot{{\bar{\lambda }}}}}{{\bar{\lambda }}}-\frac{\dot{{\bar{\lambda }}}^2}{{\bar{\lambda }}^2}+\frac{2 \ddot{{\bar{\lambda }}}}{{\bar{\lambda }}}+\frac{16 \pi {\bar{\lambda }}U_{,\lambda \lambda }}{\varpi }-\frac{16 \pi U_{\lambda }}{\varpi }\right) \nonumber \\&\quad -6 H {\dot{{\bar{\lambda }}}} \Psi -2 \Psi \ddot{{\bar{\lambda }}}-4 {\dot{{\bar{\lambda }}}} {\dot{\Psi }} = 0, \end{aligned}$$

(80)

where all the terms involving $\Phi$ are replaced with $\Psi$ using Eq. (55).