1 Introduction

The Event Horizon Telescope (EHT) collaboration has revolutionized our understanding of black holes by capturing images of M87* and Sgr A*, revealing a striking feature: a bright ring encircling a dark shadow [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. These prominent signatures arise from the strong light deflections occurring near unstable bound photon orbits, which form photon spheres in spherically symmetric spacetimes [15,16,17,18]. These unprecedented observations offer a unique opportunity to directly test sophisticated theoretical models, such as general relativistic magnetohydrodynamic simulations, against observational data. This groundbreaking achievement has ignited a surge of interest in scrutinizing black hole images illuminated by accreting plasma.

Recent observations and numerical simulations provide compelling evidence for the formation of hot spots surrounding supermassive black holes. These highly energized regions are often associated with magnetic reconnection and flux eruptions within magnetized accretion disks [19,20,21]. Notably, recurrent observations have detected hot spots in close proximity to Sgr A* [22,23,24]. Additionally, a notable instance is the detection of an orbiting hot spot within unresolved light curve data captured at the EHT’s observing frequency [25]. Furthermore, the orbital motion and polarization of these hot spots have been analyzed in [26, 27]. Crucially, the origin of these hot spots within the compact region near the Innermost Stable Circular Orbit (ISCO) makes them invaluable for probing black holes in the extreme gravity regime [25, 28].

Meanwhile, a class of Einstein-Maxwell-scalar (EMS) models has been introduced to elucidate the formation of hairy black holes [29]. These models incorporate non-minimal couplings between the scalar and Maxwell fields, inducing tachyonic instabilities capable of initiating spontaneous scalarization. Through fully non-linear numerical simulations, Herdeiro et al. have demonstrated the transition of Reissner–Nordström (RN) black holes into scalarized RN black holes [29]. This revelation has spurred extensive research within the EMS framework, exploring various areas such as different non-minimal coupling functions [30,31,32], massive and self-interacting scalar fields [33, 34], horizonless reflecting stars [35], stability analysis of scalarized black holes [36,37,38,39,40], higher dimensional scalar-tensor models [41], quasinormal modes of scalarized black holes [42, 43], two U(1) fields [44], quasitopological electromagnetism [45], topology and spacetime structure influences [46], scalarized black hole solutions in the dS/AdS spacetime [47,48,49,50,51], dynamical scalarization and descalarization [52,53,54] and rotating scalarized black hole solutions [55].

Intriguingly, scalarized RN black holes can harbor multiple photon spheres outside the event horizon within specific parameter ranges [56]. This unique feature has sparked intensive research on the optical appearances of various phenomena in their vicinity, including accretion disks [56,57,58], luminous celestial spheres [59] and infalling stars [60]. Studies have revealed that an additional photon sphere significantly amplifies observed accretion disk flux, generates beat signals in the visibility amplitude, creates triple higher-order images of a luminous celestial sphere and triggers a cascade of additional flashes from an infalling star. Furthermore, the presence of multiple photon spheres raises concerns about spacetime stability due to the potential for long-lived modes [61,62,63,64,65]. Recent work has shown that these photon spheres can induce superradiance instabilities for charged scalar perturbations [66]. Moreover, the existence of two photon spheres outside the event horizon has also been demonstrated in dyonic black holes with a quasi-topological electromagnetic term [67, 68], black holes in massive gravity [69, 70] and wormholes in the black-bounce spacetime [71,72,73]. For a comprehensive analysis of black holes with multiple photon spheres, we refer readers to [74].

This paper explores the observational characteristics of hot spots orbiting scalarized RN black holes, particularly focusing on how the presence of an additional photon sphere impacts these signatures. The subsequent sections of this paper are structured as follows: In Sect. 2, we begin with a concise review of scalarized RN black hole solutions within the EMS framework, discussing geodesic motion and gravitational lensing within these spacetimes. Section 3 is devoted to the hot spot model, followed by an analysis of time integrated images, temporal fluxes and centroids. Finally, Sect. 4 presents our conclusions. We adopt the convention \(G=c=1\) throughout the paper.

2 Scalarized RN black holes

This section first presents a concise review of the scalarized RN black hole solution within the 4-dimensional EMS model. Following this, we investigate the properties of photon spheres and ISCOs within the black hole spacetime.

2.1 Black hole solution

The EMS model, as outlined in [29], combines a gravity theory with a scalar field \(\phi \) and an electromagnetic field \(A_{\mu }\) through the action,

$$\begin{aligned} S=\frac{1}{16\pi }\int d^{4}x\sqrt{-g}\left[ \mathcal {R}-2\partial _{\mu }\phi \partial ^{\mu }\phi -f\left( \phi \right) F_{\mu \nu }F^{\mu \nu }\right] ,\nonumber \\ \end{aligned}$$
(1)

where \(\mathcal {R}\) is the Ricci scalar, and \(F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }\) is the electromagnetic field strength tensor. In this EMS model, the scalar field \(\phi \) is non-minimally coupled to the electromagnetic field \(A_{\mu }\) through the coupling function \(f\left( \phi \right) \). For the existence of scalar-free black holes like RN black holes, the coupling function must satisfy the condition \(f^{\prime }\left( 0\right) \equiv \left. df\left( \phi \right) /d\phi \right| _{\phi =0}=0\) [29, 30]. This study focuses on the exponential coupling function \(f\left( \phi \right) =e^{\alpha \phi ^{2}}\) with \(\alpha >0\). Within the RN background, the equation of motion for scalar perturbations \(\delta \phi \) is given by

$$\begin{aligned} \left( \square -\mu _{\text {eff}}^{2}\right) \delta \phi =0, \end{aligned}$$
(2)

where \(\mu _{\text {eff}}^{2}=-\alpha Q^{2}/r^{4}\). It is noteworthy that tachyonic instabilities emerge when the effective mass square \(\mu _{\text {eff}}^{2}\) becomes negative. As demonstrated in [29, 50], these instabilities can be sufficiently strong near the event horizon, inducing the formation of scalarized RN black holes from their scalar-free counterparts.

To find scalarized RN black hole solutions, we employ the following ansatz for the metric and electromagnetic field,

$$\begin{aligned} ds^{2}&=-N\left( r\right) e^{-2\delta \left( r\right) }dt^{2}+\frac{1}{N\left( r\right) }dr^{2}\nonumber \\&\quad +r^{2}\left( d\theta ^{2}+\sin ^{2}\theta d\varphi ^{2}\right) ,\nonumber \\ A_{\mu }dx^{\mu }&=\Phi \left( r\right) dt\text { and}\ \phi =\phi \left( r\right) . \end{aligned}$$
(3)

In addition, proper boundary conditions are imposed at the event horizon \(r_{h}\) and spatial infinity as

$$\begin{aligned} N\left( r_{h}\right)&=0\text {, }\delta \left( r_{h}\right) =\delta _{0}\text {, }\phi \left( r_{h}\right) =\phi _{0}\text {, }\Phi \left( r_{h}\right) =0\text {,}\nonumber \\ N\left( \infty \right)&=1\text {, }\delta \left( \infty \right) =0\text {, }\phi \left( \infty \right) =0\text {, }\Phi \left( \infty \right) =\Psi \text {.} \end{aligned}$$
(4)

Here, \(\delta _{0}\) and \(\phi _{0}\) can be used to characterize black hole solutions, and \(\Psi \) is the electrostatic potential. By specifying \(\delta _{0}\) and \(\phi _{0}\), we obtain scalarized RN black hole solutions with a non-trivial scalar field \(\phi \) using the shooting method implemented in NDSolve function of \(Wolfram\text { }\circledR Mathematica\). Black hole mass M and charge Q are determined from the asymptotic behavior of the metric functions at infinity

$$\begin{aligned} N\left( r\right)&=1-\frac{2M}{r}+\cdots ,\nonumber \\ \Phi \left( r\right)&=\Psi -\frac{Q}{r}+\cdots . \end{aligned}$$
(5)

For simplicity and generality, we express all physical quantities in units of the black hole mass by setting \(M=1\) throughout the paper.

2.2 Photon spheres

The motion of light in scalarized RN black holes is governed by the geodesic equation,

$$\begin{aligned} \frac{d^{2}x^{\mu }}{d\lambda ^{2}}+\Gamma _{\rho \sigma }^{\mu }\frac{dx^{\rho }}{d\lambda }\frac{dx^{\sigma }}{d\lambda }=0, \end{aligned}$$
(6)

where \(\lambda \) is the affine parameter, and \(\Gamma _{\rho \sigma }^{\mu }\) represents the Christoffel symbol. For null geodesics characterized by \(ds^{2}=0\), the radial component simplifies to

$$\begin{aligned} \frac{e^{-2\delta \left( r\right) }}{L^{2}}\left( \frac{dr}{d\lambda }\right) ^{2}+V_{\text {eff}}\left( r\right) =b^{-2}, \end{aligned}$$
(7)

where \(V_{\text {eff}}\left( r\right) \equiv e^{-2\delta \left( r\right) }N\left( r\right) r^{-2}\) is the effective potential, \(b\equiv \left| L\right| /E\) is the impact parameter, and L and E are the conserved angular momentum and energy of photons, respectively. In spherically symmetric black holes, unstable circular null geodesics constitute a photon sphere of radius \(r_{\text {ph}}\), determined by

$$\begin{aligned} V_{\text {eff}}\left( r_{\text {ph}}\right) =b_{\text {ph}}^{-2}\text {, }V^{\prime }\left( r_{\text {ph}}\right) =0\text {, }V^{\prime \prime }\left( r_{\text {ph}}\right) <0, \end{aligned}$$
(8)

where \(b_{\text {ph}}\) is the corresponding critical impact parameter. In other words, a local maximum of the effective potential signifies the presence of a photon sphere.

In addition, a local potential minimum gives rise to stable circular null geodesics, forming what is known as an “anti-photon sphere” [75]. Such anti-photon spheres have been observed in various spacetimes, including horizonless ultra-compact objects [76] and extreme static black holes [77]. Photons in close proximity to an anti-photon sphere are confined by potential barriers, rendering them undetectable by distant observers and, consequently, having minimal influence on black hole imaging. Nonetheless, waves trapped at anti-photon spheres can tunnel through the potential barriers and propagate towards either the event horizon or spatial infinity, potentially leading to the existence of echo signals [65] and superradiant instability [66].

Fig. 1
figure 1

The effective potential of photons (upper row) and the deflection angle \(\alpha \) as a function of the impact parameter b (lower row). Left Column: For \(\alpha =0.9\) and \(Q=1.054\), the potential exhibits a single maximum at \(r_{\text {ph}}=1.610\), marking the photon sphere with a critical impact parameter \(b_{\text {ph}}=3.673\). The deflection angle \(\alpha \) exhibits a logarithmic divergence at \(b=b_{\text {ph}}\). Right column: With \(\alpha =0.9\) and \(Q=1.070\), the potential reveals two maxima at \(r_{\text {in}}=0.204\) and \(r_{\text {out}}=1.255\), corresponding to two distinct photon spheres with critical impact parameters \(b_{\text {in}}=2.322\) and \(b_{\text {out}}=3.515\), respectively. The inset depicts a local potential minimum, corresponding to an anti-photon sphere. Between \(b_{\text {in}}\) and \(b_{\text {out}}\), the deflection angle \(\alpha \) reaches a minimum value greater than \(3\pi \), indicating that light rays traversing the region between the two photon spheres orbit the black hole at least once before escaping

Full size image

Our previous work established that scalarized RN black holes can harbor either one or two photon spheres outside the event horizon, depending on the specific values of \(\alpha \) and Q/M [56]. Figure 1 exemplifies this phenomenon through the effective potential: the upper-left panel shows a single peak for \(\alpha =0.9\) and \(Q=1.054\), while the upper-right panel reveals a double-peak structure for \(\alpha =0.9\) and \(Q=1.070\). This interesting dependence led us, in [74], to delineate the region in the \(\alpha \)-Q/M parameter space where double photon spheres emerge.

To investigate the impact of photon spheres on light deflection, we focus on the deflection angle \(\alpha \) experienced by a light ray with impact parameter b. For rays traveling from and returning to spatial infinity, the deflection angle is expressed by [78],

$$\begin{aligned} \alpha =2\int _{r_{0}}^{\infty }\frac{1}{\sqrt{b^{-2}r^{4}e^{2\delta \left( r\right) }-r^{2}N\left( r\right) }}dr-\pi , \end{aligned}$$
(9)

where \(r_{0}\), the turning point, satisfies \(V_{\text {eff}}\left( r_{0}\right) =b^{-2}\). Notably, previous studies have demonstrated that \(\alpha \) diverges logarithmically at critical impact parameters [78,79,80,81]. This divergence indicates that light rays undergo multiple circumnavigations of the black hole in the vicinity of photon spheres, essentially trapped in their gravitational influence.

The lower-left panel of Fig. 1 displays the deflection angle \(\alpha \) as a function of b for a scalarized RN black hole with \(\alpha =0.9\) and \(Q=1.054\). At large impact parameters, light rays travel far from the photon sphere, resulting in small deflection. However, as b approaches the critical value \(b_{\text {ph}}\), \(\alpha \) diverges logarithmically, reflecting the capture of light rays by the photon sphere. Note that light rays with \(b<b_{\text {ph}}\) plunge into the event horizon and are excluded from our analysis. The lower-right panel of Fig. 1 presents the deflection angle \(\alpha \) as a function of b for a scalarized RN black hole with \(\alpha =0.9\) and \(Q=1.070\). The presence of two photon spheres, marked by dashed red lines at \(b_{\text {in}}\) and \(b_{\text {out}}\) (inner and outer, respectively), distinguishes this case from the single-photon sphere case in the lower-left panel. For \(b>b_{\text {out}}\), \(\alpha \) behaves similarly to the single-photon sphere case, approaching zero with increasing impact parameter. However, due to the combined gravitational lensing effects of both photon spheres, light rays with \(b_{\text {in}}<b<b_{\text {out}}\) can undergo multiple orbital paths around the black hole, experiencing transient confinement between the two photon spheres. This orbital confinement manifests as a minimum in the deflection angle within the range \(b_{\text {in}}<b<b_{\text {out}}\).

2.3 Innermost stable circular orbit

Finally, we turn our attention to the ISCO of massive particles in scalarized RN black holes. The ISCO is widely believed to be the origin of hot spots observed in active galactic nuclei due to synchrotron radiation emitted by matter orbiting it [82,83,84]. Analogously to the null case for photons, the metric condition \(ds^{2}=-1/2\) for timelike geodesics leads to the following radial equation,

$$\begin{aligned} \frac{e^{-2\delta \left( r\right) }}{L^{2}}\left( \frac{dr}{d\lambda }\right) ^{2}+V_{\text {eff}}\left( r\right) =b^{-2}, \end{aligned}$$
(10)

where E and L represent the total energy and angular momentum per unit mass of the orbiting particle, respectively. Here, the effective potential for massive particles is defined as

$$\begin{aligned} V_{\text {eff}}\left( r\right) =e^{-2\delta \left( r\right) }N\left( r\right) \left( \frac{1}{r^{2}}+\frac{1}{L^{2}}\right) . \end{aligned}$$
(11)

Consequently, the energy per unit mass \(E_{i}\), angular momentum per unit mass \(L_{i}\) and radius \(r_{i}\) of the ISCO are identified by the conditions,

$$\begin{aligned} V_{\text {eff}}\left( r_{i}\right) =0\text {, }V_{\text {eff}}^{\prime }\left( r_{i}\right) =0\text {, }V_{\text {eff}}^{\prime \prime }\left( r_{i}\right) =0. \end{aligned}$$
(12)

Once \(r_{i}\) is determined, \(E_{i}\) and \(L_{i}\) can be obtained from explicit expressions involving the metric functions and their derivatives at \(r_{i}\),

$$\begin{aligned} E_{i}&=\sqrt{\frac{2N^{2}\left( r_{i}\right) e^{-2\delta \left( r_{i}\right) }}{2N\left( r_{i}\right) -r_{i}N^{\prime }\left( r_{i}\right) +2r_{i}N\left( r_{i}\right) \delta ^{\prime }\left( r_{i}\right) }}\text {,}\nonumber \\ \text { }L_{i}&=\sqrt{\frac{r_{i}^{3}N^{\prime }\left( r_{i}\right) -2r_{i}^{3}\delta ^{\prime }\left( r_{i}\right) N\left( r_{i}\right) }{2N\left( r_{i}\right) -r_{i}N^{\prime }\left( r_{i}\right) +2r_{i}N\left( r_{i}\right) \delta ^{\prime }\left( r_{i}\right) }}\,\text {.} \end{aligned}$$
(13)

For a hot spot orbiting the black hole at the ISCO on the equatorial plane, its four-velocity takes the form,

$$\begin{aligned} v_{e}^{\mu }=\left( \frac{E_{i}}{N\left( r_{i}\right) e^{-2\delta \left( r_{i}\right) }},0,0,\frac{L_{i}}{r_{i}^{2}}\right) . \end{aligned}$$
(14)

The corresponding angular velocity and period are \(\Omega _{e}=\sqrt{\left[ N^{\prime }\left( r_{i}\right) -2\delta ^{\prime }\left( r_{i}\right) N\left( r_{i}\right) \right] e^{-2\delta \left( r_{i}\right) }/\left( 2r_{i}\right) }\) and \(T_{e}=2\pi /\Omega _{e}\), respectively.

3 Observations of hot spot

This section explores observable signatures of hot spots orbiting scalarized RN black holes. We simplify the analysis by considering an isotropically emitting hot spot as a sphere. Utilizing the computational framework described in [85, 86], we place the observer at \(\left( r_{\text {o}},\varphi _{\text {o}}\right) =\left( 100,\pi \right) \) with an inclination angle of \(\theta _{\text {o}}\), while the hot spot, with a radius of 0.25, circles counterclockwise on the ISCO at \(r_{i}\). For optimal precision and efficiency, we employ a \(1000\times 1000\) pixel grid for each snapshot and generate 200 snapshots for a full hot spot orbit. Within the observers image plane, each pixel is associated with Cartesian coordinates \(\left( x,y\right) \),

$$\begin{aligned} x\equiv -r_{o}\Phi ,\text { }y\equiv r_{o}\Theta , \end{aligned}$$
(15)

where \(\Phi \) and \(\Theta \) are observation angles, defined as per [87]. By tracing light rays backward from the observer to the hot spot, we glean observational information for each image plane pixel. Specifically, at each time \(t_{k}\), each pixel is assigned an intensity \(I_{klm}\), collectively forming lensed images of the hot spot. Our analysis then focuses on the following image properties, as outlined in [84, 88,89,90,91],

  • Time integrated image:

    $$\begin{aligned} \left\langle I\right\rangle _{lm}=\sum \limits _{k}I_{klm}, \end{aligned}$$
    (16)

    summarizing the intensity received at each pixel.

  • Total temporal flux:

    $$\begin{aligned} F_{k}=\sum \limits _{l}\sum \limits _{m}\Delta \Omega I_{klm}, \end{aligned}$$
    (17)

    representing the total intensity received at time \(t_{k}\). Here, \(\Delta \Omega \) denotes the solid angle per pixel.

  • Temporal magnitude:

    $$\begin{aligned} m_{k}=-2.5\lg \left( \frac{F_{k}}{\min \left( F_{k}\right) }\right) , \end{aligned}$$
    (18)

    quantifying the relative brightness of each snapshot.

  • Temporal centroid:

    $$\begin{aligned} \overrightarrow{c_{k}}=F_{k}^{-1}\sum \limits _{l}\sum \limits _{m}\Delta \Omega I_{klm}\overrightarrow{r_{lm}}, \end{aligned}$$
    (19)

    indicating the center of intensity distribution in each snapshot. Here, \(\overrightarrow{r_{lm}}\) represents the position relative to the image center.

Fig. 2
figure 2

Time integrated images for a complete orbit of the hot spot, captured from an observational inclination angle of \(\theta _{\text {o}}=80^{\circ }\) (upper row) and \(50^{\circ }\) (lower row). The critical curves, outlined in white, are traced by light rays escaping the photon spheres. All intensity values are normalized to their maximum value. Left column: Single-photon sphere case with \(\alpha =0.9\) and \(Q=1.054\). The images highlight the primary, secondary and tertiary lensed image tracks positioned beyond the critical curve, stemming from the \(n=0^{>}\), \(1^{>}\) and \(2^{>}\) emissions of the hot spot, respectively. Right column: Double-photon sphere case with \(\alpha =0.9\) and \(Q=1.070\). The images unveil three image tracks outside the outer critical curve, alongside three additional tracks between the two critical curves. The two innermost tracks between the critical curves originate from \(n=4^{<>}\) light rays. For \(\theta _{\text {o}}=80^{\circ }\), they become incomplete and merge into Y-shaped patterns. The remaining track arises from \(n=5^{<>}\) light rays

Full size image
Fig. 3
figure 3

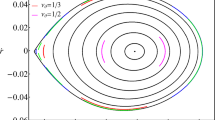
Temporal magnitudes \(m_{k}\) (upper row) and centroids \(c_{k}\) (lower row) as a function of \(t/T_{e}\). The inclination is \(\theta _{o}=80^{\circ }\). The image coordinates \(\left( x,y\right) \) of the centroids are given in units of the black hole mass M. Left column: Single-photon sphere case with \(\alpha =0.9\) and \(Q=1.054\). The green circle marks the magnitude peak dominated by the primary image. Right column: Double-photon sphere case with \(\alpha =0.9\) and \(Q=1.070\). The green circle and blue circle mark the highest and second-highest peaks, respectively. The additional peak compared to the single-photon sphere case arises from light rays orbiting between the two photon spheres

Full size image
Fig. 4
figure 4

Snapshots for the single-photon sphere (left column) and double-photon sphere (right column) cases, captured at the maximum temporal magnitude. The upper and lower rows depict the snapshots corresponding to the highest and second-highest peaks, respectively. The relative contribution of the nth-order image to the total flux \(F_{k}\) is given by \(F_{k}^{n}/F_{k}\), where \(F_{k}^{n}\) denotes the temporal flux of the nth-order image at \(t=t_{k}\). The second-highest peak in the double-photon sphere case arises primarily from the \(n=4^{<>}\) image

Full size image
Fig. 5
figure 5

Temporal magnitudes \(m_{k}\) (upper row) and centroids \(c_{k}\) (lower row) plotted against \(t/T_{e}\) for the single-photon sphere (left column) and double-photon sphere (right column) cases at an inclination of \(\theta _{o}=50^{\circ }\). The image coordinates \(\left( x,y\right) \) of the centroids are given in units of the black hole mass M. Due to the reduced influence of the Doppler effect at lower inclinations, both cases display a single peak in the temporal magnitudes, and the centroids are shifted towards the center

Full size image

3.1 Integrated images

Figure 2 displays the time integrated images of scalarized RN black holes with one or two photon spheres, viewed at inclination angles of \(80^{\circ }\) and \(50^{\circ }\). White lines mark critical curves traced by light rays escaping the photon spheres. While the single-photon sphere case shows three prominent image tracks outside the critical curve, the double-photon sphere case exhibits additional tracks between the two critical curves. To decipher the origin of these tracks, we use a numerical count n signifying the number of equatorial plane crossings during a light ray’s journey, characterizing its path and resulting image track. Note that, in double-photon sphere cases, photons can orbit between the inner and outer spheres. Therefore, superscripts > and \(<>\) denote light rays traveling outside the (outer) photon sphere and orbiting between the inner and outer photon spheres, respectively.

Focusing on an observer at \(\theta _{\text {o}}=80^{\circ }\), the upper-left panel of Fig. 2 presents the time integrated image of the hot spot for a single-photon sphere scalarized RN black hole with \(\alpha =0.9\) and \(Q=1.054\). A striking brightness asymmetry, arising from the Doppler effect, is immediately apparent. Similar to the Schwarzschild black hole case (Fig. 2 in [86]), the primary image (\(n=0^{>}\)) forms a closed semicircular track, with upper and lower segments representing the hot spot appearing behind and in front of the black hole. The smaller and dimmer track represents the secondary image (\(n=1^{>}\)) with its scarcely visible upper segment corresponding to the front-positioned hot spot and the lower segment to the back-positioned one. Unlike the Schwarzschild case, a faint and more circular tertiary track (\(n=2^{>}\)) appears near the critical curve due to the flatter potential peak of this specific configuration.

The upper-right panel of Fig. 2 depicts the time integrated image for the double-photon sphere case with \(\alpha =0.9\) and \(Q=1.070\). Familiar tracks for \(n=0^{>}\), \(1^{>}\) and \(2^{>}\) reside outside the outermost critical curve, similar to the single-photon sphere case. However, fascinatingly, additional tracks emerge between the two critical curves, originating from light rays orbiting between the inner and outer photon spheres. As revealed in Fig. 1, these orbits have a minimum value of the deflection angle \(\alpha \), setting a lower bound on n of \(n\ge 4\). Importantly, two distinct impact parameters can lead to the same \(\alpha \) above the minimum, resulting in two separate \(n=4^{<>}\) tracks. Due to this minimum \(\alpha \) value, the two \(n=4^{<>}\) tracks are incomplete and merge into Y-shaped patterns between the critical curves. A fainter \(n=5^{<>}\) track appears outside the \(n=4^{<>}\) tracks, and higher-order images become increasingly less luminous and hug the critical curves.

The lower panels of Fig. 2 present time integrated images obtained at an observation inclination of \(\theta _{\text {o}}=50^{\circ }\), revealing similarities to the \(\theta _{\text {o}}=80^{\circ }\) cases. Despite these similarities, an observer positioned at a lower inclination angle perceives a reduced degree of brightness asymmetry, accompanied by a more circular appearance of the image tracks. Moreover, for the double-photon sphere case, \(n=4^{<>}\) light rays now form two complete tracks, as the deflection angle is unable to reach its minimum value at this observation inclination.

3.2 Temporal fluxes and centorids

Figure 3 illustrates the temporal magnitudes \(m_{k}\) and centroids \(c_{k}\) as a function of time observed at \(\theta _{\text {o}}=80^{\circ }\) for scalarized RN black holes with a single photon sphere or double photon spheres. In the case of a single photon sphere, a prominent peak, labeled , is evident in the temporal magnitude plot shown in the upper-left panel of Fig. 3. The corresponding snapshot, highlighting the contributions from various images with differing values of n as tabulated, is displayed in the upper-left panel of Fig. 4. Notably, the flux at this peak is predominantly contributed by the primary images with \(n=0^{>}\), originating from the hot spot located near the leftmost portion of its orbit. This observation aligns with expectations, as the hot spot moves closer to the observer on the left side of the field of view, leading to a pronounced increase in the observed light frequency due to the Doppler effect. The lower-left panel of Fig. 3 illustrates the centroid, which mainly resides in the left half of the image plane. When the primary image experiences a Doppler-induced flux reduction in the right half of the plane, the secondary image can significantly shift the centroid towards the left. Additionally, higher-order images introduce numerical noise in regions of low flux, impacting both magnitudes and centroids.

In the double-photon sphere case, two distinct peaks are visible in the temporal magnitude plot, labeled and in the upper-right panel of Fig. 3, respectively. The snapshot corresponding to the highest peak, displayed in the upper-right panel of Fig. 4, bears similarities to the single-photon sphere case. Notably, the snapshot at the second-highest peak, presented in the lower-right panel of Fig. 4, unveils a departure from the exclusive dominance of primary images. This shift occurs as the primary image undergoes a phase of diminished flux due to the hot spot’s movement away from the observer. Consequently, the \(n=4^{<>}\) image emerges as a significant contributor to the overall flux, resulting in a pronounced local magnitude peak. Furthermore, as demonstrated in the lower-right panel of Fig. 3, the influence of higher-order images between the two critical curves tends to displace the centroid further towards the left compared to the single-photon sphere case.

Figure 5 displays the temporal magnitudes and centroids for an inclination angle of \(\theta _{o}=50^{\circ }\). In contrast to the \(\theta _{o}=80^{\circ }\) case, only a single peak is visible in the temporal magnitudes for \(\theta _{o}=50^{\circ }\). This difference arises due to the decreased impact of the Doppler effect at the lower inclination angle. Consequently, the flux becomes less frequency-dependent, enabling the primary image to dominate the total flux contribution for most of the time. Moreover, the influence of higher-order images on the centroids diminishes, causing it to shift toward the center of the primary image’s orbit.

4 Conclusions

In this paper, we have examined the observable behavior of hot spots orbiting scalarized RN black holes along the ISCOs. Intriguingly, depending on the parameters of the black hole, a scalarized RN black hole may possess either one or two photon spheres [57]. Given the substantial influence of photon spheres on black hole imaging, our observations have revealed distinctive characteristics between the single-photon sphere and double-photon sphere cases.

In the single-photon sphere case, the primary observational features align closely with those observed in the Schwarzschild black hole case [86]. Specifically, the primary image with \(n=0^{>}\) traces a closed semicircular track, culminating in a pronounced peak within the temporal flux. Conversely, in the case of double-photon spheres, photons have the capacity to orbit between the two photon spheres multiple times, resulting in the generation of additional hot spot images situated between the two critical curves. Consequently, when viewed at lower inclinations, these additional images contribute to a distinct secondary peak in the temporal flux.

Through the analysis of these image characteristics, we are able to gain deeper insights into the optical manifestations of hot spots in proximity to black holes. This understanding paves the way for the discrimination between black holes harboring a single photon sphere and those possessing multiple photon spheres. The advent of next-generation Very Long Baseline Interferometry holds promising potential for leveraging our findings as a means of exploring black holes with multiple photon spheres.