1 Introduction

Gravity, which is one of the four fundamental forces known to exist in the universe, has been widely discussed in modern physics [1]. While general relativity [2,3,4] addresses the macroscopic motion of matter on large spatial and temporal scales, quantum theory [5,6,7,8] effectively clarifies various phenomena in the microscopic domain. This accentuates the growing prominence of the contradiction between the two basic theories of physics – quantum mechanics and general relativity – centring on the inconsistency between general relativity and quantum field theory. Quantisation of gravity [9,10,11] is a significantly challenging research topic in theoretical physics. In particular, verifying any reasonable prediction of quantum gravity requires energies as high as Planck’s energy. With the current technology, such high energies are difficult to achieve. Alternatively, one could pursue experiments at lower energies that might suggest the possibility of quantum gravity or the Planck scale [12,13,14]. In 2002, researchers attempted to combine general relativity with quantum mechanics [15, 16]. The role of quantum effect in cosmology and the origin of the universe are also discussed and debated [17,18,19,20,21].

Several experimental ideas have been proposed for controlling quantum gravity [22]. A good starting point is the thought experiment proposed by Feynman during the Chapel Hill conference on gravity [23]. It is difficult to test quantum gravity proposals in practice because the quantum effects in gravitational fields are very weak. Hence, developing empirically feasible methods is essential for studying and testing the quantum nature of gravity. In 2017, a table–top experiment found that the quantum nature of gravity can be demonstrated by the interaction between gravity and two massive particles 2017 [24]. The two quantum systems were spatial superpositions of two masses, and the third system was gravity. The experiment required complete quantum control of the two massive particles. Initially, the system was not entangled. However, after the interaction of the two massive particles with a gravitational field, the entanglement in the system was proven by directly measuring the observable values of \(m_{1}\) and \(m_{2}\) [24]. When the system was in an entangled state, the gravitational field was quantised. If there was a van der Waals force [25, 26] or an electromagnetic [27, 28] interaction between the two masses, and if gravity was weaker compared to the masses [29], it cannot be concluded that gravity is quantised.

Bohr’s complementarity principle [30,31,32,33,34], a fundamental aspect of quantum mechanics, has been controversial since it was first proposed. It has a wide range of applications in physics and proposes that two mutually exclusive characteristics (wave and particle nature) cannot be simultaneously observed [35]. This was later expressed as \(P^{2}+V^{2}\leqslant 1\) [36], where P denotes the predictability of the particle path information, and V represents the visibility of the interference pattern [34]. For example, when a single photon passes through an interferometer, the particle nature of the photon is embedded in the predictability of the photon path, whereas the wave nature is shown in the interference pattern on the screen [37]. A close relationship between entanglement and \(P^{2}+V^{2}\) (duality) was discovered recently; as per this relationship, \(P^{2}+V^{2}+C^{2}=1\) for pure states [38,39,40], where C is the concurrence as a measure of two-qubit entanglement [41,42,43,44]. This relationship was proven in solid geometric projections [45]. However, in a general state, they satisfy \(P^{2}+V^{2}+C^{2}\leqslant 1\). Quantum steering between Bell nonlocality and entanglement is a nonlocal feature of quantum mechanics [46]. Additionally, the set of steerable states is a strict subset of the entangled states, as proposed by Schrödinger [47]. Furthermore, average fidelity is a measure of the expected proximity between the input and output states. Hence, the average fidelity shows how useful a given entangled state is for quantum teleportation [48, 49].

In this study, to explore whether gravity can be quantised, we investigated the gravitationally induced first-order coherence, steering violation, and maximal average fidelity between two masses in the interference framework, which are indirect indicators of the quantum nature of gravity. We explored the equivalent relationship between duality and first-order coherence in gravity. The square of the first-order coherence is equivalent to the sum of the squares of the particle and wave characteristics in the pure state. Quantum steering, which is one of the three types of nonlocal correlation [50,51,52], can also be used to demonstrate the quantum nature of gravity. We derived the complementary relationship between duality and the three-setting linear steering inequality in gravity. In addition, we explored the intrinsic relationship between duality and maximal average fidelity. Testing the first-order coherence, steering violations, and maximal average fidelity in a quantum gravity setting deepens our understanding of the quantisation of gravity.

The remainder of this paper is organised as follows. In Sect. 2, we review wave-particle duality, entanglement, and gravitationally induced duality and entanglement. In Sect. 3, we present the equivalent relationship between duality and first-order coherence. In Sect. 4, we study the trade-off relationship between duality and three-setting linear steering inequality. In Sect. 5, we explore the intrinsic relationship between duality and the maximal average fidelity. Finally, we present our conclusions in Sect. 6.

2 Preliminaries of quantum gravity

2.1 Complementary relation between entanglement and duality

As discussed earlier, an important feature of quantum theory that differs from classical theory is that gravity can be represented as a superposition of different states, and all existing schemes for quantum gravity are challenging to implement in practice. Unlike in electromagnetic fields, the quantisation effect in gravitational fields is very weak [24]. However, Marletto and Vedral [24] recently adopted a different theoretical approach to test quantum gravity, that is, to prove the quantum nature of gravity by gravitationally induced entanglement between two massive particles. The space of a two-qubit state is the product of the Hilbert spaces of the qubits. Given that each Hilbert space in this setting includes two orthogonal bases \((\left\{ \left| 0 \right\rangle ,\left| 1 \right\rangle \right\} \), the four ground states of the two-qubit Hilbert space are denoted by \( \left\{ \left| 00 \right\rangle , \left| 01 \right\rangle , \left| 10 \right\rangle , \left| 11 \right\rangle \right\} \). Therefore, the two-qubit pure state can be expressed as \(\left| \psi \right\rangle = \alpha _{0 } \left| 00 \right\rangle + \alpha _{1} \left| 01 \right\rangle +\alpha _{2}\left| 10 \right\rangle +\alpha _{3}\left| 11 \right\rangle \).

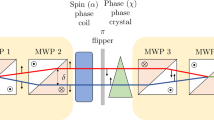
In this study, the states of two massive particles (\(m_{1}\) and \(m_{2}\)) get affected on passing through the Mach–Zender interferometers [53], as shown in Fig. 1. The upper and lower arms of the Mach–Zender interferometer is represented by 0 and 1, respectively. \(m_{1}\) and \(m_{2} \) are massive particles in the Mach–Zender interferometers. The two Mach–Zender interferometers cause both masses to be affected by the same gravitational field (for example, parallel to the Earth’s surface). In this setting, there is no interaction between \(m_{1}\) and \(m_{2} \) because of the distance between them. These two massive particles can only interact with the gravitational field. Thus, \(m_{1}\) and \(m_{2}\) are only entangled in the gravitational field.

We assigned two orthogonal bases, \(\left| 0 \right\rangle \) and \(\left| 1 \right\rangle \) to the states of the upper and lower paths of the interferometer. Each beam splitter was characterised by the reflection and transmission factors in the interferometer. We assigned arbitrary reflectance and transmittance (\(r_{1}\) and \(t_{1}\)) to the first beam splitter in the first interferometer (BS1). Similarly, the first beam splitter of the second interferometer (BS2) had the characteristics \(r_{2}\) and \(t_{2}\). These values satisfied \(r^{2} +t^{2} =1\). For a more general setup, when the ratio of BS1 to BS2 was 50 : 50, the state of each mass was \({1}/{\sqrt{2} } \left( \left| 0 \right\rangle +\left| 1 \right\rangle \right) \).

Fig. 1
figure 1

Experimental settings of gravitationally induced entanglement between two massive particles. BS1-BS4 are beam splitters, and M1-M4 are mirrors. 0 and 1 represent the upper and lower paths of interferometers, respectively. Taking the first mass as an example, when mass passes through BS1, it is transmitted or reflected. \(D_{i}\) (\(i=0\), 1) indicates a detector on path 0 or 1, and \(d_{i} \) refers to the distance between arms of interferometers. L is the length of the lower arm of each interferometer

Full size image

Therefore, the initial state of the two masses passing through the first beam splitter can be expressed as the product of the states of the first and second particle paths. That is, the system at \(t=0\) is described by the state [54],

$$\begin{aligned} \left| \psi (t=0) \right\rangle&=\left( t_{1}\left| 0 \right\rangle +r_{1}\left| 1 \right\rangle \right) \otimes \left( t_{2} \left| 0 \right\rangle +r_{2}\left| 1 \right\rangle \right) \nonumber \\&=t_{1} t_{2}\left| 00 \right\rangle +t_{1} r_{2}\left| 01 \right\rangle +r_{1} t_{2}\left| 10 \right\rangle +r_{1} r_{2}\left| 11 \right\rangle . \end{aligned}$$
(1)

The notion of complementarity has attracted widespread attention since its introduction. Based on the above description, the relationship between the duality and entanglement in the interference frame was investigated, as shown in Fig. 1.

The path information in this system (first mass) is defined as [45]

$$\begin{aligned} P=\frac{\left| p_{0}-p_{1} \right| }{\left| p_{0}+p_{1} \right| }, \end{aligned}$$
(2)

where \(p_{0}\) and \(p_{1}\) are the probabilities of the first mass detected in the upper and lower arms of the interferometer, respectively. From Eq. (2), we get \( p_{0} =\left| \alpha _{0} \right| ^{2} +\left| \alpha _{1} \right| ^{2}\) and \( p_{1} =\left| \alpha _{2} \right| ^{2} +\left| \alpha _{3} \right| ^{2}\). Herein, \(\alpha _0=t_{1}t_{2}\), \(\alpha _1=t_{1}r_{2}\), \(\alpha _2=r_{1}t_{2}\), and \(\alpha _3=r_{1}r_{2}\) are hold. \(\alpha _0\) and \(\alpha _1\) represent the probabilities that \(m_{1}\) passes through the upper path of the interferometer in Fig. 1. Thus, the particle nature of the system is given by [45]

$$\begin{aligned} P =\left( \left| \alpha _{0} \right| ^{2} +\left| \alpha _{1} \right| ^{2}\right) -\left( \left| \alpha _{2} \right| ^{2} +\left| \alpha _{3} \right| ^{2}\right) . \end{aligned}$$
(3)

However, the wave nature of a system can be quantified based on the visibility of the interference pattern [45]

$$\begin{aligned} V=\frac{p_{D}^{max}-p_{D}^{min} }{p_{D}^{max}+p_{D}^{min}}. \end{aligned}$$
(4)

\(p_{D}^{max}\) and \(p_{D}^{min}\) are the maximum and minimum probabilities of \(m_{1}\) respectively, detected by the interferometer. Therefore, the visibility of the interference pattern can be expressed as [45]

$$\begin{aligned} V=2\left| \tilde{\alpha }_{2}\alpha _{0} +\tilde{\alpha }_{3}\alpha _{1} \right| . \end{aligned}$$
(5)

Here, \(\tilde{\alpha _{i} }\) is the complex conjugate of \(\alpha _{i}\).

This relationship can be understood by considering the reduced density matrix of the system \(m_1\) as

$$\begin{aligned} {\rho _{m_1}}=\begin{pmatrix} t_{1}^{2}(r_{2}^{2}+t_{2}^{2} ) &{} r_{1}t_{1}(r_{2}^{2}+t_{2}^{2} ) \\ r_{1} t_{1} (r_{2}^{2}+t_{2}^{2} ) &{}r_{1}^{2} (r_{2}^{2}+t_{2}^{2} ) \end{pmatrix}. \end{aligned}$$
(6)

When we consider the entanglement of the system, the duality inequality \(P^{2}+V^{2}\leqslant 1\) can be reformulated as the complementary relationship \(P^{2}+V^{2}+C^{2} =1\) in the pure state. The concurrence can be determined in accordance with the purity of one of the subsystems of the two-qubit system.

$$\begin{aligned} C=\sqrt{2\left[ 1-{\text {Tr}}\left( \rho _{A\left( B \right) }^{2} \right) \right] }, \end{aligned}$$
(7)

where \(\rho _{A}\) and \( \rho _{B}\) are the reduced-density matrices of the system.

In the initial state of the system \(\left( t=0 \right) \). Using Eq. (3), we obtain the square of the path information of the two masses passing through BS1 or BS2 can be expressed as

$$\begin{aligned} P^{2}={\left| t_{1}^{2}-r_{1}^{2} \right| } ^{2} . \end{aligned}$$
(8)

From Eq. (5), the square of the visibility is given by

$$\begin{aligned} V^{2}=\left( 2r_{1}t_{1} \right) ^{2}. \end{aligned}$$
(9)

At \(t=0\), there is no interaction between the two massive particles, gravitational field, or shifting of the phase. The concurrence of the system in initial state was calculated to be zero from Eq. (7). The complementary relationship between the duality and entanglement returns is \(P^{2}+V^{2}=1\). Therefore, it is challenging to prove that the gravitational field has been quantised in its initial state.

2.2 Duality and entanglement in quantum gravity

Considering the setting of an experiment in which two masses move in the upper or lower arm of the interferometer, their interaction with the gravitational field causes a phase shift in the system. The state of the composite system before the masses enter the second beam splitter becomes

$$\begin{aligned} \left| \psi (t=T) \right\rangle&= t_{1}t_{2}e^{i\phi _{4} }\left| 00 \right\rangle +t_{1}r_{2}e^{i\phi _{3} }\left| 01 \right\rangle + r_{1}t_{2}e^{i\phi _{2} }\left| 10 \right\rangle \nonumber \\&\quad + r_{1}r_{2}e^{i\phi _{1} }\left| 11 \right\rangle . \end{aligned}$$
(10)

The four phases before the masses enter the second beam splitter (BS3 or BS4) of each interferometer can be expressed as

$$\begin{aligned}&\phi _{1} =G\tfrac{m_{1}m_{2} }{\hbar d_{2} }T, \quad \phi _{2} =G\tfrac{m_{1}m_{2} }{\hbar \left( 2d_{2}-d_{1} \right) }T,\nonumber \\&\phi _{3} =G\tfrac{m_{1}m_{2} }{\hbar d_{1} }T, \quad \phi _{4} =\phi _{1}, \end{aligned}$$
(11)

where \(\phi _{1} \) is the phase induced by the interaction between the two masses and gravity, when the distance between them is \(d_{2}\) in the interferometer. \(\phi _{2} \) is the phase induced by gravity, that is, \(m_{1} \) moves along the upper arm of the first interferometer and \(m_{2} \) moves along the lower arm of the second interferometer. Because \(m_{1} \) and \(m_{2} \) interact with gravity, the phase induced by the gravitational field is related to the positions of the masses in the interferometers. \(T=L/V\), where T is the time spent by the masses on the horizontal arm of the interferometer, L is the length of the horizontal arm, and V is the velocity of the masses.

Using Eqs. (3) and (10), the square of the predictability of path information is given by

$$\begin{aligned} P^{2}= \left( r_{1}^{2}-t_{1}^{2} \right) ^{2}. \end{aligned}$$
(12)

This result shows that the predictability of the path information of the mass in the first interferometer is related only to BS1. If the transmittance and reflectivity of BS1 are the same, that is, \(r_{1}=t_{1}=\sqrt{2}/2\), then the predictability of the path information disappears completely.

Hence, we considered the square of the visibility of the interference pattern in the first interferometer. Using Eq. (5), the square of the visibility of the first mass can be obtained as follows:

$$\begin{aligned} V^{2}=4\left( r_{1} t_{1} \right) ^{2 } \left[ r_{2}^{4}+t_{2}^{4}+2\left( r_{2}t_{2} \right) ^{2} \cos \left( \phi \right) \right] , \end{aligned}$$
(13)

here, \(\phi =2\phi _{1}-\phi _{2}-\phi _{3} \). The visibility of the interference pattern is related to the transmittance and reflectance of BS2, which are also related to the phase shift.

Finally, through Eq. (7), we obtain the square of the concurrence.

$$\begin{aligned} C^{2}=8\left( r_{1}r_{2}t_{1}t_{2} \right) ^{2} \left[ 1-\cos \left( \phi \right) \right] . \end{aligned}$$
(14)

When the phase shift is \(2n\pi \) (where n is an integer), the distances (\(d_{1}\) and \(d_{2}\)) between the two masses in different positions are the same; however, this does not occur in practice. This implies that the concurrence of the system cannot be zero when the masses interact with gravity. As the phase shift is \(n\pi \) (where n is odd), the interaction between gravity and the two masses completely destroys the interference effect of every mass. Therefore, this is the most entangled state. We can change the phase by adjusting the arm length and distance of the interferometers; simultaneously, the entanglement of the system also gets changed.

Initially, there is no entanglement (at \(t=0\)). \(m_{1}\) and \(m_{1}\) interact with the gravitational field at \(t=T\), resulting in entanglement. The quantisation of the field can be proven because of the entanglement of the system. If the masses interact with each other via van der Waals forces or other electromagnetic forces, which are much stronger than gravity, we cannot conclude that gravity is quantised [24].

If the beam splitter has a 50 : 50, the interferometer is called a symmetric Mach–Zender interferometer [55]. In an experiment [24], it was possible to select a BS2 of 50:50 to observe the quantisation of gravity. When the ratio of the transmittance and reflectivity of BS1 is 50:50, that is, \(r_{1}=t_{1}=1/\sqrt{2} \), the interaction completely destroys the interference effect of each mass, reducing the visibility of the system, making it the most entangled. If we choose BS2 with a 50 : 50 beam splitter, we obtain the following simplified relationship for the first mass:

$$\begin{aligned}&P^{2}=\left( r_{1}^{2}- t_{1}^{2} \right) ^{2}, \end{aligned}$$
(15)
$$\begin{aligned}&V^{2}=2\left( r_{1}t_{1} \right) ^{2}\left[ 1+\cos \left( \phi \right) \right] , \end{aligned}$$
(16)
$$\begin{aligned}&C^{2}=2\left( r_{1}t_{1} \right) ^{2} \left[ 1-\cos \left( \phi \right) \right] . \end{aligned}$$
(17)

This readily provides that

$$\begin{aligned} P^{2}+V^{2}+C^{2}=1. \end{aligned}$$
(18)

Therefore, gravity induces a complementary relationship between duality and entanglement. The state is entangled because of the interaction of masses and gravity, and the quantum nature of gravity can be proven by entanglement.

3 Gravitationally induced equivalence relation between duality and first-order coherence

The coherence and quantum correlations are intrinsically related [56]. Quantum resource theory opens up the possibility of establishing a quantitative relationship between coherence and nonlocal correlations [57]. This possibility is critical in quantum information processing and has inspired studies on quantitative relationships in two-qubit systems. As mentioned earlier, the quantum nature of gravity can be demonstrated by the entanglement between two masses. However, similar to entanglement, the first-order coherence of the system proves the quantum nature of gravity. A widely used measure of coherence in optical systems is the first-order coherence [50], which is similar to the degree of polarisation coherence [58]. When two subsystems are independently considered, the first-order coherence of \(\rho _{AB}\) is determined by subsystems \(\rho _{A}\) and \(\rho _{B} \) [50], expressed as

$$\begin{aligned} D_{AB}=\sqrt{\frac{D_{A}^{2}+D_{B}^{2} }{2} }. \end{aligned}$$
(19)

The first-order coherence of the subsystems \(\rho _{A}\) and \(\rho _{B}\) in the general state has the following form [41, 50]:

$$\begin{aligned} D_{A}=\sqrt{2{\text {Tr}}(\rho _{A}^{2} )-1},\quad D_{B}=\sqrt{2{\text {Tr}}(\rho _{B}^{2} )-1}, \end{aligned}$$
(20)

where each subsystem of \( \rho _{AB}\) is characterised by reduced-density matrices; that is, \(\rho _{A}={\text {Tr}}_{B}(\rho _{AB} )\) and \(\rho _{B}={\text {Tr}}_{A}(\rho _{AB} )\). When the two subsystems are coherent, \(0< D\leqslant 1\). If the two subsystems are incoherent, \(D=0 \) [41].

Similar to the relationship between the particle nature and wave nature, the complementary relationship between the first-order coherence and entanglement in the pure state is given by [41, 50]

$$\begin{aligned} D_{AB}^{2}+C_{AB}^{2}=1. \end{aligned}$$
(21)

From Eqs. (18) and (21), we obtain a relationship for the pure state, given by

$$\begin{aligned} P^{2}+V^{2}=D^{2}. \end{aligned}$$
(22)

We obtained the relationship between duality and the first-order coherence. This relationship shows that the square of the first-order coherence is synthetically equivalent to the sum of the squares of the particle and wave natures in the pure state. Because the first-order coherence of the system cannot be directly measured, the first-order coherence of the system can be obtained by measuring the predictability of the path information and visibility of the interference patterns. If the coherence of the system is not 1, the state is entangled. Thus, the quantum nature of gravity is proven.

The coherence of the system demonstrates the quantum nature of gravity. Taking the first mass as an example, \(m_{1}\) passes through BS1. \(m_{1}\) does not interact with the gravitational field, and the phase does not shift. When the first-order coherence of the system is 1 and the concurrence is 0 (Eq. (21)), the system state is separable. Accordingly, we cannot prove the quantum nature of gravity. Before \(m_{1}\) and \(m_{1}\) enter BS3 or BS4, the masses interact with the gravitational field and phases induced by the gravity shift (Eq. (11)). From Eqs. (19) and (20), we obtain the first-order coherence of the system at \(t=T\)

$$\begin{aligned} D_{1}=\sqrt{{-8r_{1}^{2}r_{2}^{2}t_{1}^{2}t_{2}^{2}+8r_{1}^{2}r_{2}^{2}t_{1}^{2}t_{2}^{2}\cos \left( \phi \right) +1 }}. \end{aligned}$$
(23)
Fig. 2
figure 2

Duality and coherence of a system as functions of the transmittance of BS1, where a green dashed line (\(P^{2}+V^{2}\) indicates the duality, and a black straight line (\(D^{2}\) indicates the coherence of the system

Full size image

The value of \(P^{2}+V^{2}\) is equal to the value of the first-order coherence \(D^{2}\) in Fig. 2, which is in complete agreement with Eq. (22). When the transmittance of BS1 is \(\sqrt{2}/2\), \(P^{2}+V^{2}\) and \(D^{2}\) reach their minimum values. They satisfy the equivalence relation at any given time. Additionally, a \(P^{2}+V^{2}\) value of less than 1 satisfies the Bohr’s complementarity principle mentioned earlier.

From Eq. (23), the first-order coherence of the system is not only related to the transmittance and reflectivity of the beam splitter, but also to the phase induced by the gravitational field. If the coherence is minimal, then the phase should be \(n\pi \) (n is an integer), and the entanglement of the system should be maximum. This demonstrates the quantum nature of gravity. The values of coherence and duality can be regulated by changing the length of the interferometer arm, distance between the arms, and position of the masses in the interferometer.

Fig. 3
figure 3

First-order coherence of a system as a function of the transmittance of BS1 or BS2 and phase. a Dependence of maximal average fidelity on the reflectance of BS1 and BS2, where the gravitationally induced phase is set to \(\phi =\pi \) and b dependence of coherence on the gravitationally induced phase and transmittance of BS1, where reflectivity of BS2 is set to \(1/\sqrt{2}\)

Full size image

The results of the first-order coherence are shown in Fig. 3. Figure 3a illustrates the dependence of coherence on the reflectance of the first beam splitters in each interferometer, where the gravitationally induced phase is set to \(\phi =\pi \). Because the reflectance of BS1 and BS2 is set to \(\sqrt{2}/2\), the first-order coherence is 0. Figure 3b describes first-order coherence of the system as a function of the reflectance of BS1 and phase induced by the gravitational field. The system has minimum coherence when the reflectance of BS1 is \(\sqrt{2}/2\) and gravitationally induced phase is \(\pi \).

Considering the interaction between the masses and gravity of the system, the interaction leads to a reduction in the first-order coherence. The first-order coherence of the system can also be adjusted by changing the arm length of the interferometer, the distance between the arms, and the transmittance or reflectivity of the beam splitter. In this experiment, the transmittance (reflectance) of both BS1 and BS2 cannot be simultaneously set to 0.

4 Gravitationally induced trade-off relation between duality and three-setting linear steering inequality

The concept of steering was first proposed by Schrödinger [47] and was later recognised as a nonlocal correlation. Subsequently, quantum steering has flourished as one of the three nonlocal correlations. A three-setting linear steering inequality is used to detect the steerability of the system, and it is considered as an exceedingly useful criterion for steering quantification. According to the hierarchical relation of the nonlocal correlation, it lies between Bell nonlocality and entanglement [46]. A set of steerable states is a strict subset of entangled states [50, 59]. Although steering is logically different from quantum entanglement and Bell nonlocality, in this study, we can still prove that the gravitational field can be quantised by the existence of a steering violation of the system.

Corollary 1

For a two-qubit pure-state system,  the relationship between duality and the three-setting linear steering inequality is given by

$$\begin{aligned} 2P^{2}+2V^{2}+S^{2}=3. \end{aligned}$$
(24)

Proof

A relationship between the first-order coherence \(D_{AB}\) and maximum violation of the three-setting linear steering inequality (\(S_{AB}\)) for an arbitrary two-qubit state is given by [50, 59]

$$\begin{aligned} D_{AB}^{2}+\frac{1}{2}S_{AB}^{2}=I_{AB}, \end{aligned}$$
(25)

where \(I_{AB}=2{\text {Tr}}\left( \rho _{AB}^{2} \right) -1/2\). In the pure state, \({\text {Tr}}\left( \rho _{AB}^{2} \right) =1\). Thus, \(D_{AB}\) and \(S_{AB}\) satisfy the new relationship

$$\begin{aligned} D_{AB}^{2}+\frac{1}{2}S_{AB}^{2}=\frac{3}{2}. \end{aligned}$$
(26)

From Eqs. (22) and (26), we can obtain the trade-off relationship between duality and the maximum violation of the three-setting linear steering inequality in Eq. (24). Thus, the proof is complete.

The maximum violation of the three-setting steering inequality for any state of the system is given by

$$\begin{aligned} S_{AB}=\sqrt{c_{1}+c_{2}+c_{3} }, \end{aligned}$$
(27)

where \(c_{i}\) (\(i=1\), 2, or 3) represents the eigenvalue of \(R^{\dagger } R\), and \(R^{\dagger }\) represents the transpose of the matrix R. \(R =\left[ r_{ij} \right] \) is the correlation matrix, where \(r_{ij}={\text {Tr}}\left[ \rho _{AB}\left( \sigma _{i}\otimes \sigma _{j} \right) \right] \). \(\sigma _{i}\) and \(\sigma _{j}\) are the Pauli matrices [56].

Using Bohr’s complementarity principle and Corollary 1, we understand that \(2P^{2}+2V^{2}\leqslant 2\) and deduce that \(S^{2}\geqslant 1\). Because the steering violation is exactly 1, we cannot prove the quantum nature of gravity. If the steering violation of the system is greater than 1, the system will violate the three-setting linear steering inequality. Furthermore, the state will become steerable, demonstrating the quantum nature of gravity. Furthermore, if the square of the steering violation of the system reaches 3, the interference effect of each mass will be destroyed completely, and the interaction between the masses and gravity will completely destroys the interference effect of both masses.

From Fig. 4, the value of \(2P^{2}+2V^{2}\) increases (decreases) with a decrease (increase) in the value of \(S^{2}\). Furthermore, the value of \(S^{2}\) is always not less than 1. Regardless of the variation in \(2P^{2}+2V^{2}\), the value of \(2P^{2}+2V^{2}+S^{2}\) remained strictly equal to 3, which is consistent with the trade-off relationship in Eq. (24). The interference effect of both masses was completely destroyed at \(\pi \) and \(3\pi \), indicating the largest steering violation.

Fig. 4
figure 4

Duality and steering of a system as functions of the phase in the setup. Red dotted, green straight, and black dotted lines represent \(2P^{2}+2V^{2}\), \(S^{2}\), and \(2P^{2}+2V^{2}+S^{2}\). The value of \(2P^{2}+2V^{2}+S^{2}\) is strictly equal to 3. No matter the variation in \(2P^{2}+2V^{2}\), \(S^{2}\) is always not less than 1

Full size image

As before, we consider the first mass as an example to prove the quantum nature of gravity by steering violations. In the initial state at \(t=0\), the masses pass through BS1 or BS2, and the steering violation is 1 according to Eqs. (1) and (27), which correspond to a non-steerable state. Thus, the system is not quantised. Therefore, quantifying the gravity and entanglement in the initial state is challenging. The reasons why steering violations cannot prove the quantum nature of gravity vary; for example, masses do not interact with the gravitational field in the initial state or with each other owing to the distance between them.

The value of the steering violation at \(t=T\) is different from that in the initial state (\(t=0\)). This is because the masses interact with the gravitational field after they pass through BS1 or BS2, causing entanglement between the masses. If \(S>1\) at \(t=T\), the state of the system is steerable. From Eqs. (10) and (27), the steering violation before the masses enter BS3 or BS4 (\(t=T\)) is given by

$$\begin{aligned} S=\sqrt{1+16r_{^{1}}^{2}r_{2}^{2}t_{2}^{2}\left[ 1-\cos \left( \phi \right) \right] -32r_{1}^{4}r_{2}^{2}t_{2}^{2}\sin \left( \frac{\phi }{2} \right) ^{2} } . \end{aligned}$$
(28)
Fig. 5
figure 5

Steering violation of a system as a function of the transmittance of BS1 or BS2 and phase. a Dependence of the steering violation on the reflectance of BS1 and BS2, where the gravitationally induced phase is set to \(\phi =\pi \) and b steering violation of the system as a function of the reflectivity of BS1 and gravitationally induced phase, where reflectivity of BS2 is set to \(1/\sqrt{2}\)

Full size image

From Eq. (28), the steering violation is related to the transmittance, reflectivity, and gravitationally induced phase of the beam splitter. The results of the steering violations are shown in Fig. 5. When the reflectance of BS1 and BS2 is near \(\sqrt{2}/2\), the steering violation of the system is high, and it is always greater than 1 Fig. 5a. Furthermore, the states can be steered. In Fig. 5b, as the phase shift is \(\pi \) and reflectance of BS2 is \(\sqrt{2}/2\), the steering violation reaches the maximum. As described above, the state is steerable, and the quantum nature of gravity can be proven. The state of the system can always be steered if the gravitationally induced phase is not \(2n\pi \) where n is an integer. When the phase is \(2n \pi \) (n is an integer), the steering violation has a minimum value of 1, which is impossible in practice.

As one of the three types of nonlocal correlations, quantum steering is logically different from entanglement and Bell nonlocality. Quantum nonlocality is a condition sufficient for the quantum nature of gravity. To measure quantum steering, we can simply measure the path information and visibility of interference patterns from Eq. (24), when they are readily available. Detecting nonclassical correlations such as steering violations is of great significance for demonstrating the quantum nature of gravity.

5 Gravitationally induced intrinsic relation between duality and maximal average fidelity

As a standard index of quantum teleportation, the average fidelity shows the usefulness of a given entangled state for quantum teleportation [48, 49, 60, 61]. Average fidelity is a measure of the expected proximity between the input and output states, but it does not provide information about fluctuations in the fidelity [48]. The maximum average fidelity is the maximum value of the average fidelity that can be achieved using standard teleportation protocols. The maximum average fidelity under all strategies for local unitary operations and standard protocols is one of the best conditions for quantum teleportation [49]. Since the upper bound for classical teleportation is 2/3 [62], the value of the maximal average, which is greater than 2/3, can be used to demonstrate the quantisation of gravity.

Corollary 2

For a two-qubit pure-state system,  the relationship between the duality and maximal average fidelity is given by

$$\begin{aligned} 2P^{2}+2V^{2}+9(2F-1)^{2} \geqslant 3. \end{aligned}$$
(29)

Proof

The three-setting linear steering inequality and maximal average fidelity satisfy the following relationship [49]:

$$\begin{aligned} F&=\frac{1}{2}\left( 1+\frac{1}{3}{\text {Tr}}\sqrt{R^{\dagger }R } \right) \geqslant \frac{1}{2}\left( 1+\frac{1}{3}\sqrt{{\text {Tr}}\left( R^{\dagger }R \right) } \right) \nonumber \\&= \frac{1}{2} \left( 1+\frac{1}{3}S_{AB} \right) , \end{aligned}$$
(30)

where \(c_{i}\) (\(i=1\), 2, and 3) is the eigenvalue of \(R^{\dagger } R\). Additionally, \(\sqrt{{\text {Tr}}\left( R^{\dagger }R \right) } =\sqrt{ {\textstyle \sum _{i=1}^{3}}c_{i} }\), which is always smaller than \({\text {Tr}}\sqrt{R^{\dagger }R} = {\textstyle \sum _{i=1}^{3}\sqrt{c_{i} } } \) [49].

Based on Corollary 1, the relationship between the three-setting linear steering inequality and duality also satisfies

$$\begin{aligned} S_{AB} =\sqrt{3-2P^{2}-2V^{2} }. \end{aligned}$$
(31)

Substituting Eq. (31) into Eq. (30), the intrinsic relationship between the duality and maximal average fidelity in Eq. (29) is obtained. Thus, the proof is complete.

How can we determine the optimal two-qubit states of quantum teleportation? Maximal average fidelity and fidelity deviations are effective [63]. Maximal average fidelity is not only useful for quantum teleportation, but can also be used to prove the quantisation of gravity. Gravity is quantised when the maximum average fidelity of the system is greater than 2/3.

Fig. 6
figure 6

The duality and maximal average fidelity of system as functions of the phase in the setup. The red straight line is \(9(2F-1)^{2}\), the green straight line is \(2P^{2}+2V^{2}\), and the black straight line \((L_{3})\) is \(2P^{2}+2V^{2}+9(2F-1)^{2}\). We can see that the value of \(L_{3}\) is no less than 3

Full size image

In Fig. 6, the trend is the same for \(L_{1}\) and \(L_{3}\). The value of duality is 0; in contrast, the values of \(L_{1}\) and \(L_{3}\) reach their maximums at this moment. This indicates that the interference effect of both masses was completely destroyed at \(\pi \) and \(3\pi \), and this exhibited the largest maximal average fidelity. As per the values shown in Fig. 6, the value of duality increases (decreases) with a decrease (increase) in the value of \(L_{1}\) and it is always not less than 3.

As before, the first mass was used as an example to demonstrate the quantum nature of gravity. In the initial state (at \(t=0\), the masses pass through BS1 or BS2. The value of the maximal average fidelity, calculated 2/3 using Eqs. (1) and (30), was which corresponds to classical teleportation. Gravity, which does not interact with masses, cannot quantised in the initial state. At \(t=T\) (before entering BS3 or BS4, \(m_{1}\) and \(m_{2}\) interact with gravity. Using Eqs. (10) and (30), we can calculate the maximal average fidelity of the system as an extremely complex function, which is not only related to the phase shift induced by the gravitational field, but also to the transmittance or reflectance of BS1 and BS2.

Fig. 7
figure 7

Maximal average fidelity of a system as a function of the transmittance of BS1 or BS2 and phase: a Dependence of maximal average fidelity on the reflectance of BS1 and BS2, where the gravitationally induced phase is set to \(\phi =\pi \) and b maximal average fidelity of the system as a function of the reflectivity of BS1 and phase induced by the gravitationally field, where reflectivity of BS2 is set to \(1/\sqrt{2}\)

Full size image

The results for the maximal average fidelity are shown in Fig. 7. When the reflectance of BS1 and BS2 is near \(\sqrt{2}/2\), the maximal average fidelity of the system is high Fig. 7a. As the reflectance of BS1 and BS2 is \(\sqrt{2}/2\), the maximal average fidelity reaches the maximum, which is 5/6. For quantum teleportation, the maximal average fidelity of the system is one of the criteria for selecting the best-performing states from a set of states. In Fig. 7b, as the phase shift \(\pi \) and reflectance of BS1 are \(\sqrt{2}/2\), respectively, the maximal average fidelity reaches the maximum, which is 5/6. Based on the value of the maximum average fidelity, it can be determined whether quantum teleportation can be performed and used to prove the quantisation of gravity in this system.

6 Conclusions

In this study, we investigated the gravitationally induced unified relationship among duality, coherence, three-setting linear steering inequality, and maximum average fidelity between two masses for a two-qubit pure state. The equivalence relation between duality and first-order coherence, which satisfied the relation \(P^{2}+V^{2}=D^{2}\) was obtained. In this study, the coherence of the system was used to prove the quantum nature of gravity; the smaller the first-order coherence, the more obvious the quantum nature of the system. Specifically, after two masses \(m_1\) and \(m_2\), which interact with the gravitational field, pass through BS1 or BS2 phase shift occurs. The first-order coherence of the system was calculated using the new phase, which was used to determine whether gravity was quantised. If the first-order coherence of the system is 0, the interference effect of the two masses is completely destroyed. Subsequently, the quantum nature of gravity was proven. Under gravitational inducement, a trade-off relationship between duality and steering violation that satisfied \(2P^{2}+2V^{2}+S^{2}=3\) is obtained. Similar to coherence and entanglement, the steering violation of the system can be used to prove the quantum nature of gravity; the larger the value of steering violation, the stronger the quantum characteristics of the system. After the two masses pass through BS1 or BS2, they interact with the gravitational field. For instance, the state is steerable when the steering violation is greater than 1, which proves that gravity is quantised. The intrinsic relation between duality and maximal average fidelity, which satisfies the relation \(2P^{2}+2V^{2}+9(2F-1)^{2} \geqslant 3\) was also obtained. As the two masses interact with the gravitational field, the maximal average fidelity is greater than 2/3, and quantum teleportation can be carried out. Additionally, quantisation of gravity can be proved in this system. We can prove the quantum nature of gravity using the coherence, steering violation, and maximal average fidelity of the system. By detecting the first-order coherence, steering violation, and maximal average fidelity in the interference frame, we can explain the connection between gravity and quantum physics in a broader and deeper discipline and help people further understand quantum gravity.