1 Introduction

The Standard Paradigm of Cosmology, namely \(\Lambda \)CDM concordance model, has been proven very successful in describing the universe evolution, at both background and perturbative levels. Nevertheless, it exhibits possible disadvantages, either theoretical or observational [1]. In the first class of potential issues one has the non-renormalizability of general relativity or the cosmological constant problem. In the second class one may find the dynamical behavior of dark energy, the realization of the inflationary phase, as well as various cosmological tensions.

Among cosmological tensions, one has the \(H_0\) one, namely the fact that the present value of the Hubble parameter is estimated by Planck collaboration to be \(H_0 = (67.27\pm 0.60)\) km/s/Mpc [2], whereas local measurements of the 2019 SH0ES collaboration (R19) lead to \(H_0 = (74.03\pm 1.42)\) km/s/Mpc. Additionally, one may have the \(\sigma _8\) tension, which is related to the matter clustering, and the fact that the Cosmic Microwave Background (CMB) estimation [2] differs from the SDSS/BOSS direct measurement [3, 4].

The first local ladder measurement of \(H_0\), obtained using the Hubble Space Telescope (HST) observations of Cepheids and SNIa, was \(72 \pm 8 \) km/s/Mpc [5]. Subsequently, dedicated efforts were made to enhance the precision of the measurements, resulting in a refined estimate of \(H_0 = 74.3 \pm 2.2 \) km/s/Mpc [6]. Additionally, in 2005, the SH0ES Project started and proceeded to advance this approach. Over the years, numerous \(H_0\) estimations have been obtained by the SH0ES collaboration, with the most recent and refined result yielding \(H_0 = 73.04 \pm 1.04 \) km/s/Mpc [7]. Hence, the \(H_0\) tension has existed since the first release of results from Planck Collaboration in 2013, which provided the estimation \(H_0 = 67.40 \pm 1.40 \) km/s/Mpc [8]. Meanwhile, the analysis of the nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations yielded a Hubble constant estimate of \(H_0 = 70.00 \pm 2.20 \) km/s/Mpc [9]. In the following years, the improvement of the data and the reduction of errors, as well as the consideration of additional datasets, has led to the worsening of the tension. For instance, as evidenced in [2], the Planck2018+lensing+BAO analysis results in \(H_0 = 67.66 \pm 0.42 \) km/s/Mpc. On the other hand, an important contribution came from recent observations from the James Webb Space Telescope, providing the strongest evidence yet that systematic errors in HST Cepheid measurements do not play a significant role in the present Hubble Tension [10]. Finally, it is interesting to note the potentially intriguing situation, where the American estimations of the current Hubble function often exceed the European ones, which could be analyzed by future epistemologists.

If these tensions are not due to unknown systematics, they probably need a modification of standard lore in order to be alleviated. There are many directions one can follow in order achieve this. In particular, since \( \theta _s=\frac{r_s}{D_A}, \) where \( r_s \propto \int _0^{t_{recom}}dt \frac{c_s(t)}{\rho (t)} \) is the sound horizon and \(D_A\propto \frac{1}{H_0} \int _{t_{recom}}^{t_{today}}dt \frac{1}{\rho (t)}\) is the angular diameter distance, one could try to change either \(r_s\) or \(D_A\) or both. Solutions that affect \(r_s\) are referred to as “early-time” solutions, and solutions that alter \(D_A\) are called “late-time” solutions. Hence, in the literature one can find a large class of solutions, including modified gravity, early dark energy, extra relativistic degrees of freedom, bulk viscous models, clustering dark energy, holographic dark energy, interacting dark energy, running vacuum models, Horndeski theories, decaying dark matter, string-inspired models, etc [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62] (for a review see [63]).

In the present work we are interested in presenting a novel alleviation of both \(H_0\) and \(\sigma _8\) tension, obtained in the framework of Tsallis cosmology [64]. Such a modified cosmological scenario arises from the application of the standard gravity-thermodynamics conjecture, namely the procedure to obtain the Friedmann equations from the first law of thermodynamics applied in the universe horizon [65,66,67], but using Tsallis non-additive entropy [68,69,70], instead of the usual Bekenstein–Hawking one. Tsallis cosmology has been shown to lead to interesting cosmological phenomenology [71,72,73,74,75,76,77,78,79,80]. Nevertheless, in the following we will show that in such a framework we can obtain phantom behavior for the effective dark-energy sector, which is one of the sufficient mechanisms that can alleviate the \(H_0\) tension, as well as an increased friction term in the matter-perturbation evolution equation, which leads to smaller \(\sigma _8\).

The plan of the work is the following: In Sect. 2 we briefly review Tsallis cosmology, both at the background and perturbative levels. Then in Sect. 3 we show how Tsallis cosmology can lead to the alleviation of both \(H_0\) and \(\sigma _8\) tensions simultaneously. Finally, in Sect. 4 we summarize the obtained results.

2 Modified cosmology through Tsallis entropy

In this section we briefly review Tsallis cosmology. Tsallis non-additive entropy [68,69,70] generalizes the standard thermodynamics to non-extensive one, and it possess the standard Boltzmann-Gibbs statistics as a limit. In a cosmological setup this is quantified by an exponent \(\delta \), and hence the Tsallis entropy can be written in the form [81]

$$\begin{aligned} S_T=\frac{\tilde{\alpha }}{4G} A^{\delta }, \end{aligned}$$
(2.1)

in units where \(\hbar =k_B = c = 1\). In the above expression G is the gravitational constant, \(A\propto L^2\) is the area of the system with characteristic length L, \(\tilde{\alpha }\) is a positive constant with dimensions \([L^{2(1-\delta )}]\) and \(\delta \) is the non-additivity parameter. As mentioned in the Introduction, in the case \(\delta =1\) and \(\tilde{\alpha }=1\), Tsallis entropy recovers the standard Bekenstein–Hawking additive entropy.

We consider a Friedmann–Robertson–Walker (FRW) metric of the form

$$\begin{aligned} ds^2=-dt^2+a^2(t)\left( \frac{dr^2}{1-kr^2}+r^2d\Omega ^2 \right) , \end{aligned}$$
(2.2)

with a(t) the scale factor, and \(k=0,+1,-1\) the spatial curvature. We substitute Tsallis entropy (2.1) into the first law of thermodynamics \(-dE=TdS\), and we perform all the steps of gravity-thermodynamics conjecture [65,66,67]. Specifically, we consider the boundary of the system to be the Universe apparent horizon \(\tilde{r}_a=(H^2+\frac{k}{a^2})^{-1}\), having temperature \(T=1/(2\pi r_h)\), and being filled by the universe matter fluid, with energy density \(\rho _m\) and pressure \(p_m\) [82,83,84,85,86,87,88,89,90,91,92,93,94,95]. Hence, this leads to (we consider only the more physically interesting case \(\delta \ne 2\)) [64]

$$\begin{aligned} -\frac{(4\pi )^{2-\delta }G}{\tilde{\alpha }}(\rho _m+p_m)=\delta \frac{\dot{H}-\frac{k}{a^2}}{\left( H^2+\frac{k}{ a^2}\right) ^{\delta -1}}, \end{aligned}$$
(2.3)

and this by integration to

$$\begin{aligned} \frac{2(4\pi )^{2-\delta }G}{3\tilde{\alpha }} \rho _m=\frac{ \delta }{2-\delta } \left( H^2+\frac{k}{a^2}\right) ^{2-\delta }-\frac{\tilde{\Lambda }}{3\tilde{\alpha }}, \end{aligned}$$
(2.4)

with dots denoting time-derivatives, and where \(\tilde{\Lambda }\) is an integration constant, which can be considered as the cosmological constant. Equations (2.3) and (2.4) are the two modified Friedmann equations for the non-extensive scenario with Tsallis entropy. Focusing on flat geometry, i.e. \(k=0\), we can re-write them into the standard form

$$\begin{aligned} H^2= & {} \frac{8\pi G}{3}\left( \rho _m+\rho _{DE}\right) \end{aligned}$$
(2.5)
$$\begin{aligned} \dot{H}= & {} -4\pi G \left( \rho _m+p_m+\rho _{DE}+p_{DE}\right) , \end{aligned}$$
(2.6)

where we have defined an effective dark energy density and pressure as [64]

$$\begin{aligned} \rho _{DE}= & {} \frac{3}{8\pi G} \left\{ \frac{\Lambda }{3}+H^2\left[ 1-\alpha \frac{ \delta }{ 2-\delta } H^{2(1-\delta ) } \right] \right\} , \end{aligned}$$
(2.7)
$$\begin{aligned} p_{DE}= & {} -\frac{1}{8\pi G}\left\{ \Lambda +2\dot{H}\left[ 1-\alpha \delta H^{2(1-\delta )} \right] \right. \nonumber \\{} & {} \left. +3H^2\left[ 1-\alpha \frac{\delta }{2-\delta }H^{ 2(1-\delta )} \right] \right\} , \end{aligned}$$
(2.8)

as well as the new constants \( \Lambda \equiv (4\pi )^{\delta -1}\tilde{\Lambda }\) and \(\alpha \equiv (4\pi )^{\delta -1}\tilde{\alpha }\). In these lines, the equation-of-state parameter for the effective dark energy is

$$\begin{aligned} w_{DE}\equiv \frac{p_{DE}}{\rho _{DE}}=-1- \frac{ 2\dot{H}\left[ 1-\alpha \delta H^{2(1-\delta )} \right] }{\Lambda +3H^2\left[ 1-\frac{\alpha \delta }{2-\delta }H^{2(1-\delta )} \right] } . \end{aligned}$$
(2.9)

We mention that for \(\delta =1\) and \( \alpha =1\) the above expressions recover the standard ones as expected.

Let us elaborate the aforementioned equations. For simplicity we consider dust matter (\(p_m=0\)) and we introduce the density parameters through

$$\begin{aligned} \Omega _m= & {} \frac{8\pi G}{3H^2} \rho _m \end{aligned}$$
(2.10)
$$\begin{aligned} \Omega _{DE}= & {} \frac{8\pi G}{3H^2} \rho _{DE}. \end{aligned}$$
(2.11)

Doing so, the Hubble parameter can be written as

$$\begin{aligned} H=\frac{\sqrt{\Omega _{m0}} H_{0}}{\sqrt{a^3 (1-\Omega _{DE})}}, \end{aligned}$$
(2.12)

where “0” denotes the present value of the corresponding quantity. In the following it proves more convenient to introduce the redshift z, defined as \( 1+z=1/a\), having imposed the present scale factor to 1. Substituting (2.7) into (2.11) and taking into account (2.12) we acquire

$$\begin{aligned} \Omega _{DE}(z)= & {} 1-H^{2}_{0}\Omega _{m0}(1+z)^3 \left\{ \frac{ (2-\delta )}{\alpha \delta }\right. \nonumber \\ {}{} & {} \left. \left[ H^{2}_{0}\Omega _{m0}(1+z)^3+\frac{\Lambda }{3} \right] \right\} ^{\frac{1}{\delta -2}}, \end{aligned}$$
(2.13)

while from (2.9) we find [64]

$$\begin{aligned}{} & {} w_{DE}(z)\nonumber \\ {}{} & {} =-1+\frac{\left\{ 3[1-\Omega _{DE}(z)]+(1+z)\Omega _{DE}'(z)\right\} \left\{ 1-\alpha \delta \left[ \frac{ H^{2}_{0}\Omega _{m0}(1+z)^3}{1-\Omega _{DE}(z)}\right] ^{1-\delta }\right\} }{[ 1-\Omega _{DE} (z)]\left\{ \frac{\Lambda [1-\Omega _{DE}(z)]}{H^{2}_{0}\Omega _{m0}(1+z)^3}+3\left\{ 1-\frac{\alpha \delta }{2-\delta }\left[ \frac{H^{2}_{0}\Omega _{m0}(1+z)^3}{1-\Omega _{DE}(z)} \right] ^{ 1-\delta }\right\} \right\} },\nonumber \\ \end{aligned}$$
(2.14)

where primes denote differentiation with respect to z. Finally, note that applying (2.13) at present time (\(z=0\)) we acquire a relation of the parameters, namely

$$\begin{aligned} \Lambda =\frac{3\alpha \delta }{2-\delta }H_0^{2(2-\delta )}-3H_0^2\Omega _{m0}, \end{aligned}$$
(2.15)

from which we deduce that our model has two extra free parameters, namely \(\alpha \) and \(\delta \).

We close this section by presenting the behavior of Tsallis cosmology at the perturbative level. Introducing as usual the matter overdensity \(\delta _m:=\delta \rho _m/\rho _m\), and focusing without loss of generality on the case \(\alpha =1\), one can show that its evolution equation is given by [96]

$$\begin{aligned}{} & {} \delta ^{\prime \prime }_{m} +\frac{2\left( 4-2\delta \right) - \left( 9-6\delta +8\pi G\Lambda H^{2\delta -4} \right) }{\left( 4-2\delta \right) (1+z)}\delta ^{\prime }_{m} \nonumber \\{} & {} \quad + \frac{3^{\frac{1}{\delta -2}}\! \left[ \left( 1-2\delta \right) \rho ^{\frac{1}{2-\delta }}_{m}-9\left( 1-\delta \right) \Lambda \rho ^{\frac{\delta -1}{2-\delta }}_{m}\right] 8\pi G }{2\left( 2-\delta \right) ^{2}H^{2}(1+z)^{2}}\delta _{m}=0,\nonumber \\ \end{aligned}$$
(2.16)

with \(\Lambda \) given by (2.15). Note that comparing to standard result, in the above expression we have a different friction term (the second term), as well as an effective Newton’s constant (the last term). Clearly, in the case \(\delta =1\), one recovers the standard result, which in the case of matter domination (\(\Omega _m\approx 1\)) gives

$$\begin{aligned} \delta ^{\prime \prime }_{m}+\frac{1}{2(1+z)}\delta ^{\prime }_{m} -\frac{3}{2(1+z)^2 } \delta _{m}=0 \end{aligned}$$
(2.17)

as expected. Lastly, after obtaining the solution for \(\delta _m(z)\), we can calculate the physically interesting observational quantity

$$\begin{aligned} f\sigma _8(z)=f(z) \,\sigma (z), \end{aligned}$$
(2.18)

with \(f(z):=-\frac{d\ln \delta _m(z)}{d\ln z}\) and \(\sigma (z):=\sigma _8\frac{\delta _m(z)}{\delta _m(0)}\) [63].

3 Alleviating \(H_{0}\) and \(\sigma _{8}\) tensions

Let us now investigate how the scenario of Tsallis cosmology can alleviate both \(H_{0}\) and \(\sigma _{8}\) tensions. As we observe, the Tsallis exponent \(\delta \) affects the background evolution, as well as the perturbation behavior. As it was in [63] and in [97, 98], one of the efficient mechanisms that can alleviate the \(H_0\) tension is to obtain an effective dark-energy equation-of-state parameter lying in the phantom regime, while one of the efficient mechanisms that can alleviate the \(\sigma _{8}\) tension is to obtain an increased friction term or a smaller effective Newton’s constant in the evolution equation of \(\delta _m\). Hence, our strategy will be to choose \(\delta \) in order to fulfill the above requirements.

We start from the fact that in \(\Lambda \)CDM cosmology the Hubble function is providing by the relation

$$\begin{aligned} H_{\Lambda CDM}(z)\equiv H_{0}\sqrt{\Omega _{m0}(1+z)^{3}+1-\Omega _{m0}}. \end{aligned}$$
(3.1)

On the other hand, in Tsallis cosmology the Hubble function is given by (2.12) with \(\Omega _{DE}(z)\) provided by (2.13). Hence, we can choose model parameters which our H(z) coincides with \(H_{\Lambda \text {CDM}}(z)\) of (3.1) at \(z= z_\textrm{CMB}\approx 1100\), namely \(H(z\rightarrow z_\textrm{CMB}) \approx H_{\Lambda \text {CDM}}(z\rightarrow z_\textrm{CMB})\), but give \(H(z\rightarrow 0) > H_{\Lambda \text {CDM}}(z\rightarrow 0)\). Finally, as usual, we desire to have the standard evolution of \(\Omega _m\) and \(\Omega _{DE}\), with the sequence of matter and dark-energy epochs, and with \(\Omega _{m0} \approx 0.31\), according to observations [2]. We mention here that the range of values \(\{\delta ,\Omega _{m0}\}\) that we are using is well within the observational bounds in these kinds of theories [64, 99].

In Fig. 1 we depict the normalized \(H(z)/(1+z)^{3}\) as a function of the redshift parameter, for \(\Lambda \)CDM scenario, as well as for Tsallis cosmology for various values of the entropic exponent \(\delta \). As we observe, for small deviations of \(\delta \) below the standard entropy value \(\delta =1\) we can have a coincidence to \(\Lambda \)CDM cosmology at high and intermediate redshifts, while at small redshifts the modified Tsallis scenario stabilizes in higher values of \(H_{0}\). More specifically, the value of \(H_{0}\) depends on \(\delta \), and it can be around \(H_{0} \approx 74\) km/s/Mpc for \(\delta = 0.993\). Hence, Tsallis cosmology, with \(\delta \) values slightly less than the standard value, can indeed alleviate \(H_0\) tension (\(\delta >1\) values do not lead to alleviation).

Fig. 1
figure 1

The normalized \(H(z)/(1 + z)^{3}\) in units of km/s/Mpc as a function of the redshift, for \(\Lambda \)CDM cosmology (black-solid) and for Tsallis cosmology for \(\alpha =1\) and for \(\delta =0.993\) (red-dotted), \(\delta =0.995\) (blue-dashed) and \(\delta =0.997\) (orange-dashed-dotted). We have imposed \(\Omega _{m0} \approx 0.31\)

Full size image
Fig. 2
figure 2

The H(z) evolution in units of km/s/Mpc as a function of the redshift, for \(\Lambda \)CDM scenario (black line) and for Tsallis cosmology with \(\alpha =1\) and \(\delta =0.993\) (red dotted line), on top of the CC data points at 2\(\sigma \) confidence level [100]. We have imposed \(\Omega _{m0} \approx 0.31\)

Full size image

As an additional verification, we confront the obtained evolution with cosmic chronometer (CC) data [101], namely datasets based on H(z) measurements through the relative ages of massive passively evolving galaxies [100]. In Fig. 2 we present H(z) for \(\Lambda \)CDM scenario and for Tsallis cosmology, on top of CC data from [100] at 2\(\sigma \) confidence level. As we see, the agreement is very good, H(z) of Tsallis cosmology lies within the CC data, exhibiting a slightly higher accelerating behavior at low redshifts, for the parameter sets \(\{\Omega _{m0}, \delta \} = \{0.31, 0.993\}\).

Fig. 3
figure 3

The evolution of the dark-energy equation-of-state parameter \(w_{DE}\) as a function of the redshift, for Tsallis cosmology with \(\alpha =1\) and \(\delta =0.993\)

Full size image
Fig. 4
figure 4

Evolution of f\(\sigma _8\) in \(\Lambda \)CDM scenario (black solid) and in Tsallis cosmology with \(\alpha =1\) and \(\delta =0.993\) (orange dashed). The blue data points are from baryonic acoustic oscillations (BAO) observations in SDSS-III DR12 [102], while the gray data points at higher redshifts are from SDSS-IV DR14 [103,104,105]

Full size image

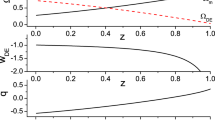
Let us now examine what is the mechanism behind the \(H_0\) tension alleviation. In Fig. 3 we present the evolution of the dark-energy equation-of-state parameter (2.14), for the value of the parameter \(\delta \) that alleviates the tension. As we observe, it lies in the phantom regime, which as we mentioned above is one of the sufficient ways to alleviate the tension [97, 98]. Note that according to (2.14) in principle \(w_{DE}(z)\) can be quintessence-like, phantom-like, or experience the phantom-divide crossing during the evolution, according to the value of \(\delta \), and this is the reason we restricted ourselves to values \(\delta \lesssim 1\), since these are needed to obtain the correct amount of phantom behavior (concerning other potential astrophysical implications of phantom behavior see [106]). Finally, note that we choose to extend Fig. 3 to negative redshifts, namely to the future, in order to show that in the scenario at hand as time passes the phantom behavior becomes less and less significant, and that the dark energy sector will asymptotically behave as a cosmological constant.

We proceed to the examination of the \(\sigma _8\) tension. As we mentioned above, the evolution equation of matter overdensity \(\delta _m\) is given by (2.16). In Fig. 4, we present the evolution of \(f\sigma _{8}\) for \(\Lambda \)CDM scenario, as well as for Tsallis cosmology, on top of observational data. As we observe, Tsallis cosmology can indeed reduce \(f\sigma _{8}\) and alleviate \(\sigma _8\) tension too, for the same parameter choice that can alleviate \(H_0\) tension. This simultaneous alleviation of the tensions is not easy to be obtained in alternative cosmological scenarios, and it is the main result of the present work.

Finally, let us examine the mechanism behind the \(\sigma _8\) tension alleviation. As we observe from (2.16), the scenario at hand has a different friction term as well as an effective Newton’s constant. One can see that under the above parameter choice, we obtain an increased friction and an effective Newton’s constant smaller than the usual one. And this is indeed one of the sufficient mechanisms to alleviate \(\sigma _8\) tension [97, 98].

4 Conclusions

We presented how Tsallis cosmology can alleviate both \(H_0\) and \(\sigma _8\) tensions simultaneously. Such a modified cosmological scenario is obtained by the application of the gravity-thermodynamics conjecture, but using the non-additive Tsallis entropy, instead of the standard Bekenstein–Hawking one. Hence, one obtains modified Friedmann equations, with extra terms that depend on the new Tsallis exponent \(\delta \) that quantifies the departure from standard entropy.

In Tsallis cosmology one acquires an effective dark-energy sector with equation-of-state parameter that can be quintessence-like or phantom-like. Additionally, at the perturbative level one extracts the evolution equation for matter overdensity, with extra terms in the friction term as well as in the effective Newton’s constant.

As we showed, for particular choice of the Tsallis parameter \(\delta \) we can obtain a phantom effective dark energy, which is known to be one of the sufficient mechanisms that can alleviate \(H_0\) tension. Interestingly enough, for the same parameter choice we obtain an increased friction term and an effective Newton’s constant smaller than the usual one, and thus the \(\sigma _8\) tension is also solved.

In summary, Tsallis cosmology can simultaneously alleviate both \(H_0\) and \(\sigma _8\) tensions. Note that in general this is not easily obtained in alternative cosmological scenarios [63]. Even within the framework of other modified entropic cosmologies this cannot be acquired, such as in the case of Barrow cosmology [94, 107] or Kaniadakis cosmology [108], due to the less freedom one has in choosing the values of the extra entropic parameters, namely \(\Delta \) and K respectively (e.g. in Barrow cosmology \(H_0\) alleviation would mathematically need \(\Delta \lesssim 0\) which is not allowed). Thus, this feature acts as a significant advantage of Tsallis modified cosmology.