Quasinormal modes of Einstein–scalar–Gauss–Bonnet black holes

Abstract

In this paper, we investigate quasinormal modes of scalar and electromagnetic fields in the background of Einstein–scalar–Gauss–Bonnet (EsGB) black holes. Using the scalar and electromagnetic field equations in the vicinity of the EsGB black hole, we study nature of the effective potentials. The dependence of real and imaginary parts of the fundamental quasinormal modes on parameter p (which is related to the Gauss–Bonnet coupling parameter $\alpha$) for different values of multipole numbers l are studied. We analyzed the effects of massive scalar fields on the EsGB black hole, which tells us the existence of quasi-resonances. In the eikonal regime, we find the analytical expression for the quasinormal frequency and show that the correspondence between the eikonal quasinormal modes and null geodesics is valid in the EsGB theory for the test fields. Finally, we study grey-body factors of the electromagnetic fields for different multipole numbers l, which deviates from Schwarzschild’s black hole.

1 Introduction

General Relativity (GR) is the simplest theory of gravitation, which is consistent with various astrophysical observations, like gravitational waves, black holes, etc. Nevertheless, GR opens some challenging problems. These are the existence of singularities at the center of the black holes, a complete theory of quantum gravity, the problem of dark matter/energy, cosmic inflation, and others. To solve these problems theorists introduce alternative approaches to gravity. There are a number of such approaches to gravity available in the literature, e.g., string-theory-inspired gravities, adding higher-order terms in the curvature tensor to the Einstein–Hilbert action of GR.

One of the well-motivated alternative theories of gravity is the EsGB theory. In this theory, the scalar field is nonminimally coupled to the Gauss–Bonnet (GB) term. The EsGB theories also arise in the low energy limit of string theory [1]. The lowest order correction to the Einstein–Hilbert action is the GB term, which is quadratic in curvature tensor, but this theory has pure divergence in 4D spacetime. Alternatively, in recent years Glavan and Lin [2] have removed the divergence in 4D GB gravity by replacing the GB parameter $\alpha$ to $\alpha /D-4$, where D is the number of spacetime dimensions. However, later it was shown that this naive regulariation scheme does not lead to the well-defined theory of gravity. Nevertheless, the black hole solutions [3, 4] obtained as results of such regularazation proved out to be also solutions in the well-defined theories [5]. On the contrary, the EsGB theories, we are interested here, are free of such kind of problems, because in EsGB theories the divergence is absent due to the coupling between the GB term and scalar fields.

Isolated black holes are very simple objects and can be described by the three parameters: mass, charge, and spin. However, the actual situation differs from this. A black hole at the center of galaxies is surrounded by matter distribution, such as an accretion disk, jets and outflows, stars, etc. Therefore, a black hole interacts with its surroundings matter distribution. Even in the absence of any matter distribution around black hole, it will interact with the vacuum and produce a pair of particles and anti-particle, which is known as Hawking radiation. Therefore, a dynamical, interacting black hole can not be described by mass, charge, and spin only, and one needs to consider the perturbations theory of black holes. There has been a growing interest in the perturbation theory of black holes [6,7,8]. There are a number of reasons for interest in proper frequencies of such out-of-equilibrium black holes, called quasinormal modes. First of all, the LIGO and VIRGO scientific collaborations detect gravitational-wave signals from black holes [9] and it is consistent with Einstein’s theories of gravity, though, due to the large uncertainty in the determining of the spin and mass of the black hole, the large window for alternative theories remains [10, 11]. The dominating influence on such a signal is expected to come from the quasinormal modes exhibiting the lowest frequency, referred to as the fundamental mode.

Various black hole solutions in higher-order theories of gravity, its quasinormal modes, and Hawking radiation are studied extensively. The EsGB gravity was studied in Refs. [12,13,14], where the most important black hole solutions were found numerically. The analytical black hole solution of EsGB theories using continued fraction approximation (CFA) and its shadow was studied in Ref. [15]. The gravitational quasinormal modes of Einstein–dilaton–Gauss–Bonnet (EdGB) solutions are studied in Refs. [16, 17]. The spontaneous scalarization, black hole sensitivities, and linear stability of the EsGB black hole are investigated in Refs. [18,19,20]. Black hole solutions in EdGB, Einstein–Wely, and Einstein cubic gravity investigated in Refs. [21,22,23,24], while its quasinormal modes and Hawking radiation are studied in Refs. [25,26,27,28,29]. In addition, quasinormal modes of Kaluza–Klein-like black holes in the Einstein–Gauss–Bonnet theory were considered in [30]. Furthermore, quasinormal modes of string-corrected d-dimensional black holes and noncommutative Schwarzschild black holes are analysed in Refs. [31,32,33,34,35,36]. The gravitational perturbations of numerically obtained EdGB black holes are studied in Ref. [16]. In the eikonal limit, the quasinormal modes for gravitational perturbations of EsGB black holes were obtained in Ref. [17]. However, the scalar and electromagnetic perturbations either of analytically or numerically obtained EsGB black hole solution are not analyzed, which provides us an opportunity to fill this gap. The scalar field will be studied not only in the massless limit, but also for the non-zero massive term. The latter has a number of motivations, because an effective mass term appears in the wave equation as a result of introduction of extra dimensions [37, 38], and magnetic fields [39, 40]. After all, massive long-lived modes and oscillatory tails [41] may contribute into the very long gravitational waves observed recently via the Time Pulsar Array [42, 43].

The paper is organized as follows. In Sect. 2, we outline the basics of EsGB theories in four dimensions and discuss the metric functions for black holes in EsGB gravity. The quasinormal modes for massless/massive scalar fields and electromagnetic fields are studied in Sect. 3 for different scalar coupling functions. Furthermore, we derived the analytical formula for quasinormal frequency in the eikonal regime. In Sect. 4, we discuss the grey-body factors for electromagnetic fields. Finally, we summarize our results in the conclusions section.

2 Einstein–scalar–Gauss–Bonnet black holes

The action for EsGB theories in 4D can be written as

$$\begin{aligned} I= \int dx^4 \sqrt{-g} \biggr [ \frac{R}{\kappa ^2} + \alpha f(\varphi ) R_{GB}^2 - \frac{1}{2} \nabla _{\mu } \varphi \nabla ^{\mu } \varphi \biggr ], \end{aligned}$$

(1)

where g is determinant of the metric $g_{\rho \sigma }$, we take $\kappa =16 \pi G c^{-4}=1$, $\alpha$ is the GB coupling constant and $R_{GB}^2$ is defined as

$$\begin{aligned} R_{GB}^2=R_{\mu \nu \rho \sigma } R^{\mu \nu \rho \sigma } -4 R_{\mu \nu } R^{\mu \nu } + R^2, \end{aligned}$$

(2)

and $f(\varphi )$ is the arbitrary smooth function of the scalar field $\varphi$, which is known as GB coupling functional. The metric of static and spherically symmetric black holes in EsGB theory can be written in the following form [15]

$$\begin{aligned} ds^2 = -g_{tt} dt^2 + g_{rr} dr^2 + r^2 \Bigl (d\theta ^2 + \sin ^2{\theta } d\phi ^2 \Bigl ), \end{aligned}$$

(3)

where the analytically approximated metric functions were found in Ref. [15]. The functions $g_{tt}$ and $g_{rr}$ are written up to fourth order for different GB coupling functional in the Appendix A. Here we consider quadratic, cubic, quartic, inverse and Logarithmic Gauss–Bonnet coupling functional.

To parameterize the family of EsGB black holes solution, we will introduce the dimension-less parameter p as

$$\begin{aligned} p \equiv \frac{96 \alpha ^2 f^{\prime }(\varphi )^2 }{r_{0}^4}, 0 \le p <1, \end{aligned}$$

(4)

where $r_{0}$ is the position of the event horizon, $\varphi _{0}$ is the scalar fields at the event horizon. In the limit $p=0$, one can obtain Schwarzschild black hole.

3 Quasinormal modes of test fields

In this paper, we consider quasinormal modes of test fields in the background of EsGB black holes. The equation for scalar, and electromagnetic in the background of the EsGB black hole is given by

$$\begin{aligned}&\frac{1}{\sqrt{-g}} \partial _{\mu } \Bigl ( \sqrt{-g} g^{\mu \nu } \partial _{\nu } \Phi \Bigl ) -m^2 \Phi =0, \end{aligned}$$

(5a)

$$\begin{aligned}&\frac{1}{\sqrt{-g}} \partial _{\mu } \Bigl ( \sqrt{-g} g^{\sigma \mu } g^{\rho \nu } F_{\rho \sigma }\Bigl ) =0, \end{aligned}$$

(5b)

where $F_{\rho \sigma } = \partial _{\rho } A_{\sigma } - \partial _{\sigma } A_{\rho }$ and $A_{\mu }$ is the vector potential. To do the separation of variables we will introduce the radial function $R_{\omega l}(r)$ and spherical harmonics $Y_{l}(\theta , \phi )$ as

$$\begin{aligned} \Phi (t,r,\theta ,\phi )= e^{\pm i \omega t} R_{\omega l}(r) Y_{l}(\theta , \phi ), \end{aligned}$$

(6)

where l is the angular number. After the separation of variables equation (5) can be written in the following Schrodinger-like wave equation [26, 44]

$$\begin{aligned} \frac{d^2 \Psi }{dr_{*}^2} + \Bigl (\omega ^2 - V_{i}(r)\Bigl ) \Psi =0, \end{aligned}$$

(7)

where $r_{*}$ is the “tortoise coordinate”, defined as

$$\begin{aligned} dr_{*}= dr \sqrt{\frac{g_{rr}}{g_{tt}}}. \end{aligned}$$

(8)

The effective potentials of scalar $(i = s)$ and electromagnetic $(i = e)$ fields in the background of EsGB black hole are given by

$$\begin{aligned} V_{s}&= \frac{g_{rr} g_{tt}^{\prime } - g_{tt} g_{rr}^{\prime }}{2r g_{rr}^2} + g_{tt} \frac{l(l+1) }{r^2} +g_{tt} m, \end{aligned}$$

(9a)

$$\begin{aligned} V_{e}&= g_{tt} \frac{l(l+1) }{r^2}. \end{aligned}$$

(9b)

The dependence of effective potential on various parameters (e.g. p and l) for massless scalar fields and electromagnetic fields are shown in Fig. 1 for cubic and logarithmic coupling functional. To express the radial coordinates in units of event horizon radius, we set $r_{0}=1$. The form of effective potential is positive definite and it diminishes at both the event horizon and infinity. For massless scalar and electromagnetic fields as we increase the parameter p height of the potential barrier decreases and the barrier height is maximum at $p=0$. It can be seen that as we increase the angular number l height of the potential barrier becomes higher. For massive scalar fields, the height of the potential barrier (Fig. 2) increases with mass and the height of the potential barrier is minimum for $m=0$. The effective potential for others coupling functional exhibits similar behaviour.

The master equation (7) can be solved using WKB approximation [45]. The wave function $\Psi$ satisfies the following boundary condition

$$\begin{aligned} \Psi \sim e^{\pm i \omega r_{*}}, \end{aligned}$$

(10)

at $r_{*} \rightarrow \pm \infty$, i.e. there are only incoming waves at the event horizon and purely outgoing waves at spatial infinity. In the asymptotic region, using the boundary condition one can solve the master equation using the WKB approximations up to the required order. Expanding the potential into the Taylor series and using the master equation, the solution of differential equation (7) is obtained near the peak of the potential. Matching these two solutions the quasinormal frequency $\omega$ is derived. Finally, the frequency can be expressed as $\omega = \text {Re}(\omega ) + i \text {Im}(\omega )$, where $\text {Re}(\omega )$ represent real oscillation frequency and $\text {Im}(\omega )$ represent damping rate. The quasinormal frequency upto 6-th order WKB method has the following form

$$\begin{aligned} \frac{i (\omega ^2 - V_{0})}{\sqrt{-2 V_{0}^{\prime \prime }}} - \sum _{i=2}^{i=6} \Lambda _{i} =n+\frac{1}{2}, \end{aligned}$$

(11)

where $\Lambda _{i}$ are the correction term up to sixth-order [45,46,47,48]. $n=0$, 1, 2 is the overtone number. To compute the quasinormal modes of massless scalar and vector fields we will use sixth-order WKB formula with Padé approximation [49, 50] $\tilde{m}=5$.

It is worth of mentioning that special attention will be devoted to the $l\gg 1$, eikonal, regime, first of all because there is a correspondence between the eikonal quasinormal modes and some parameters of the null geodesics suggested in [51] and further constrained in [52,53,54]. The correspondence is expected to be broken for gravitational perturbations of the Einstein-dilaton-Gauss–Bonnet theory [26]. Here we will check whether this correspondence is fulfilled for the test fields in the EsGB theory.

Fig. 1

Effective potential with $r_0=1$, black line denotes $p=0.0$, red line denotes $p=0.4$ and blue lines denotes $p=0.8$

Fig. 2

Effective potential for massive scalar fields with $r_0=1$, $p=0.5$, black line denotes $m=0.0$, red line denotes $m=2.0$, blue lines denotes $m=4.0$ and magenta line denotes $m=6.0$

3.1 Quadratic GB-coupling functional: $f(\varphi )=\varphi ^2$

The quasinormal modes of massless scalar $(s=0)$ and electromagnetic $(s=1)$ fields for $l=1$, 2 and $l=1$, 2, 3 are shown in Figs. 3, 4, 5, 6 and 7. From Figs. 3, 4, 5, 6 and 7 one can be seen that the behaviour of real and imaginary parts of the quasinormal frequency as a function of parameter p is almost linear for different values of l. Therefore, we use in-build Mathematica function FindFormula, to express real and imaginary parts of the quasinormal frequency as a function of parameter p for different values of l. In formula 12 and 13 the parameter p runs from $p=0.0$ to $p=0.8$. The approximate linear laws of scalar and electromagnetic fields for different values of l are given by

$$\begin{aligned} \text {Re}(\omega _{s=0, l=1})&\approx 0.586146 -0.0192317 p, \end{aligned}$$

(12a)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=1})&\approx 0.0114263 p-0.194999, \end{aligned}$$

(12b)

$$\begin{aligned} \text {Re}(\omega _{s=0, l=2})&\approx 0.967948 -0.0299163 p, \end{aligned}$$

(12c)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=2})&\approx 0.0108174 p - 0.193500. \end{aligned}$$

(12d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=1})&\approx 0.498029 -0.0176951 p, \end{aligned}$$

(13a)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=1})&\approx 0.00835913 p-0.184913, \end{aligned}$$

(13b)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=2})&\approx 0.916163 -0.0281436 p, \end{aligned}$$

(13c)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=2})&\approx 0.00940289 p-0.189931, \end{aligned}$$

(13d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=3})&\approx 1.31512 -0.0405207 p, \end{aligned}$$

(13e)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=3})&\approx 0.0103759 p-0.191264. \end{aligned}$$

(13f)

Fig. 3

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$; red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 4

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$; red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 5

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$; red line denotes real part of frequency and blue lines denote imaginary part of the frequency

Fig. 6

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$; red line denotes real part of frequency and blue lines denote imaginary part of the frequency

Fig. 7

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$; red line denotes real part of frequency and blue lines denote imaginary part of the frequency

The behaviour of real and imaginary parts of the quasinormal modes for massive scalar fields as a function of mass (m) is shown in Fig. 8. The WKB formula [45,46,47,48] can not describe the quasi resonances accurately [55], but in the eikonal regime WKB method is exact, providing sufficiently accurate results at $l \ge n$. Numerous examples of usage of the WKB method (see, for instance [50, 56, 57]) say that, the sixth-order WKB formula with Padé approximants is usually the best for the computation of the quasinormal frequency of massive scalar fields. From Fig. 8b we can see that the imaginary part of the quasinormal frequency approaches zero, which indicates the existence of arbitrarily long-lived frequencies, called quasi-resonances.

Fig. 8

The dependence of quasinormal frequency on mass (m) for massive scalar fields with $r_0=1$, $p=0.5$, red line denotes real part of frequency and blue lines denote imaginary part of the frequency

3.1.1 Analytical formula for QNMS in the eikonal regime

In the domain of high multipole numbers l (eikonal), test fields with varying spin follows a common law up to the leading order. In this context, we examine an electromagnetic field with the effective potential 9(b). In the eikonal regime, one can use the first-order WKB formula given by

$$\begin{aligned} \omega = \sqrt{V_{0} - i \Bigl ( n+ \frac{1}{2}\Bigl ) \sqrt{-2V_{0}^{\prime \prime }}}, \end{aligned}$$

(14)

where $n=0$, 1, 2 is the overtone number, $V_{0}$ is the effective potential at $r=r_{max}$ and $V_{0}^{\prime \prime }$ is the double derivative of effective potential with respect to radial coordinate r, evaluated at $r=r_{max}$. Using the Ref. [58] we find that the maximum of effective potential occurs at $r=r_{max}$ which is given by

$$\begin{aligned} r_{max}= \frac{3r_{0}}{2} +0.0387 r_{0} p + {\mathcal {O}}(p^2). \end{aligned}$$

(15)

Now, substituting $r_{max}$ and Eq. 9b into Eq. (14) one can obtain the analytical expression for quasinormal frequency in the eikonal regime as

$$\begin{aligned} \omega = \frac{(1+2l) (1-0.0258 p) - i (1+2n) (1-0.0447 p) }{3 \sqrt{3}r_{0}}.\nonumber \\ \end{aligned}$$

(16)

In the limit $p \rightarrow 0$, we obtained the analytical expression of quasinormal frequency for Schwarzschild black hole.

3.2 Cubic GB-coupling functional: $f(\varphi )=\varphi ^3$

The quasinormal modes of massless scalar $(s=0)$ and electromagnetic $(s=1)$ fields for $l=1$, 2 and $l=1$, 2, 3 are shown in Figs. 9, 10, 11, 12 and 13. From Figs. 9, 10, 11, 12 and 13 one can be seen that the behaviour of real and imaginary parts of the quasinormal frequency as a function of parameter p is almost linear for different values of l. In formula 17 and 18 the parameter p runs from $p=0.0$ to $p=0.6$. After $p=0.6$, the behaviour of real and imaginary parts of quasinormal frequency is non-linear, especially for $l=2$ (scalar fields, Fig. 10) and $l=2$, 3 (electromagnetic fields, Figs. 12, 13). The approximated linear laws of scalar and electromagnetic fields for different values of l are given by

$$\begin{aligned} \text {Re}(\omega _{s=0, l=1})&\approx 0.586345 -0.0231319 p, \end{aligned}$$

(17a)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=1})&\approx 0.0236755 p-0.258812, \end{aligned}$$

(17b)

$$\begin{aligned} \text {Re}(\omega _{s=0, l=2})&\approx 0.967896 -0.0355368 p, \end{aligned}$$

(17c)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=2})&\approx 0.0114912 p-0.193244. \end{aligned}$$

(17d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=1})&\approx 0.498397 -0.0219789 p, \end{aligned}$$

(18a)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=1})&\approx 0.0134254p - 0.202685, \end{aligned}$$

(18b)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=2})&\approx 0.916381 - 0.0344771 p, \end{aligned}$$

(18c)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=2})&\approx 0.0147288 p - 0.239645, \end{aligned}$$

(18d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=3})&\approx 1.31503 - 0.0482737 p, \end{aligned}$$

(18e)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=3})&\approx 0.0174108 p - 0.233444. \end{aligned}$$

(18f)

Fig. 9

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 10

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 11

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 12

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 13

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 14

The dependence of quasinormal frequency on mass (m) for massive scalar fields with $r_0=1$, $p=0.5$ red line denote the real part of frequency and blue lines denote the imaginary part of the frequency

The behaviour of real and imaginary parts of the quasinormal modes for massive scalar fields as a function of mass (m) is shown in Fig. 14. From Fig. 14a we can see that the real part of quasinormal frequency is an increasing function of mass m and the imaginary part of the quasinormal frequency (Fig. 14b) approaches zero, which indicates the existence of quasi-resonances.

3.2.1 Analytical formula for QNMS in the Eikonal regime

In the domain of high multipole numbers l (eikonal), test fields with varying spin follow a common law up to the leading order. In this context, we examine an electromagnetic field with the effective potential 9(b). In the eikonal regime, one can use the first-order WKB formula given in equation (14). With the help of Ref. [58] we find that the maximum of effective potential occurs at $r=r_{max}$ which is given by

$$\begin{aligned} r_{max}= \frac{3r_{0}}{2} +0.0637 r_{0} p + {\mathcal {O}}(p^2). \end{aligned}$$

(19)

Now, substituting $r_{max}$ and Eq. 9(b) into Eq. (14) one can obtain the analytical expression for quasinormal frequency in the eikonal regime for cubic GB-coupling functional as

$$\begin{aligned} \omega = \frac{(1+2l) (1-0.0596 p) - i (1+2n) (1-0.1071 p) }{3 \sqrt{3}r_{0}}.\nonumber \\ \end{aligned}$$

(20)

In the limit $p \rightarrow 0$, we obtained the analytical expression of quasinormal frequency for Schwarzschild black hole.

3.3 Quartic GB-coupling functional: $f(\varphi )=\varphi ^4$

The quasinormal modes of massless scalar $(s=0)$ and electromagnetic $(s=1)$ fields for $l=1$, 2 and $l=1$, 2, 3 are shown in Figs. 15, 16, 17, 18 and 19. From Figs. 15, 16, 17, 18 and 19 one can be seen that the behaviour of real and imaginary parts of the quasinormal frequency as a function of parameter p is almost linear for different values of l. In formula 21 and 22 the approximated analytical expression for quasinormal frequency is written down for different values of l, where parameter p runs from $p=0.0$ to $p=0.7$. After $p=0.7$, the non-linear behaviour is visible. The approximated linear laws of scalar and electromagnetic fields for different values of l are given by

$$\begin{aligned} \text {Re}(\omega _{s=0, l=1})&\approx 0.583828 -0.0130698 p, \end{aligned}$$

(21a)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=1})&\approx 0.0230895 p-0.272239, \end{aligned}$$

(21b)

$$\begin{aligned} \text {Re}(\omega _{s=0, l=2})&\approx 1.00388 -0.0383934 p, \end{aligned}$$

(21c)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=2})&\approx 0.00397625 p-0.192472. \end{aligned}$$

(21d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=1})&\approx 0.495561 -0.0117364 p, \end{aligned}$$

(22a)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=1})&\approx 0.00632363 p-0.184499, \end{aligned}$$

(22b)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=2})&\approx 0.943469 -0.0345489 p, \end{aligned}$$

(22c)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=2})&\approx 0.00445784 p-0.189155, \end{aligned}$$

(22d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=3})&\approx 1.36289 -0.0510792 p, \end{aligned}$$

(22e)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=3})&\approx 0.00418319 p-0.190336. \end{aligned}$$

(22f)

Fig. 15

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 16

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 17

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 18

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 19

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

The behaviour of real and imaginary parts of the quasinormal modes for massive scalar fields as a function of mass (m) is shown in Fig. 20 for quartic GB-coupling functional. The real part of the quasinormal frequency is shown in Fig. 20a, which is an increasing function of mass m. The imaginary part is shown in Fig. 20b and it approaches zero as mass increases. Therefore, the behaviour of the imaginary part of quasinormal frequency indicates the existence of quasi-resonances for quartic GB-coupling functional.

Fig. 20

The dependence of quasinormal frequency on mass (m) for massive fields with $r_0=1$, $p=0.5$ red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

3.3.1 Analytical formula For QNMS in the eikonal regime

In the domain of high multipole numbers l (eikonal), test fields with varying spin follow a common law up to the leading order. In this context, we examine an electromagnetic field with the effective potential 9(b). In the eikonal regime, one can use the first-order WKB formula given in Eq. (14). With the help of numerical analysis given in Ref. [58] we find that the maximum of effective potential occurs at $r=r_{max}$ which is given by

$$\begin{aligned} r_{max}= \frac{3r_{0}}{2} +0.0527 r_{0} p + {\mathcal {O}}(p^2). \end{aligned}$$

(23)

Now, substituting $r_{max}$ and Eq. 9(b) into Eq. (14) one can obtain the analytical expression for quasinormal frequency in the eikonal regime as

$$\begin{aligned} \omega = \frac{(1+2l) (1-0.0570 p) - i (1+2n) (1-0.0971 p) }{3 \sqrt{3}r_{0}}.\nonumber \\ \end{aligned}$$

(24)

In the limit $p \rightarrow 0$, we obtained the analytical expression of quasinormal frequency for Schwarzschild black hole.

3.4 Inverse GB-coupling functional: $f(\varphi )=\varphi {-1}$

The quasinormal modes of massless scalar $(s=0)$ and electromagnetic $(s=1)$ fields for $l=1$, 2 and $l=1$, 2, 3 are shown in Figs. 21, 22, 23, 24 and 25. From Figs. 21, 22, 23, 24 and 25 one can see that the behaviour of real and imaginary parts of the quasinormal frequency as a function of parameter p is almost linear for different values of l. In formula 25 and 26 the parameter p runs from $p=0.0$ to $p=0.65$. The approximated linear law of scalar and electromagnetic fields for different values of l are given by

$$\begin{aligned} \text {Re}(\omega _{s=0, l=1})&\approx 0.58558 -0.0330224 p, \end{aligned}$$

(25a)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=1})&\approx 0.0183859 p-0.194868, \end{aligned}$$

(25b)

$$\begin{aligned} \text {Re}(\omega _{s=0, l=2})&\approx 0.966147 -0.0558721 p, \end{aligned}$$

(25c)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=2})&\approx 0.0231498 p-0.215501. \end{aligned}$$

(25d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=1})&\approx 0.495763 -0.0233709 p, \end{aligned}$$

(26a)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=1})&\approx 0.0139608 p-0.184918, \end{aligned}$$

(26b)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=2})&\approx 0.915373 -0.0367994 p, \end{aligned}$$

(26c)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=2})&\approx 0.0122145 p - 0.188642, \end{aligned}$$

(26d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=3})&\approx 1.31159 -0.0728545 p, \end{aligned}$$

(26e)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=3})&\approx 0.011762 p-0.189603. \end{aligned}$$

(26f)

Fig. 21

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 22

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 23

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 24

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 25

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 26

The dependence of quasinormal frequency on mass (m) for massive scalar fields with $r_0=1$, $p=0.5$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

The behaviour of real and imaginary parts of the quasinormal modes for massive scalar fields as a function of mass (m) is shown in Fig. 26 for inverse GB-coupling functional. From Fig. 26b we can see that the imaginary part of the quasinormal frequency slowly approaches zero as mass m increases, which indicates the existence of arbitrarily long-lived frequencies, called quasi-resonances.

3.4.1 Analytical formula for QNMS in the eikonal regime

In the domain of high multipole numbers l (eikonal), test fields with varying spin follow a common law up to the leading order. In this context, we examine an electromagnetic field with the effective potential 9(b). In the eikonal regime, one can use the first-order WKB formula given in Eq. (14). Using the Ref. [58] we find that the maximum of effective potential occurs at $r=r_{max}$ which is given by

$$\begin{aligned} r_{max}= \frac{3r_{0}}{2} +0.0563 r_{0} p + {\mathcal {O}}(p^2). \end{aligned}$$

(27)

Fig. 27

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 28

Fundamental quasinormal mode $(n=0)$ for massless scalar fields with $r_0=1$, red line denotes the real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 29

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 30

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 31

Fundamental quasinormal mode $(n=0)$ for electromagnetic fields with $r_0=1$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Now, substituting $r_{max}$ and Eq. 9(b) into Eq. (14) one can obtain the analytical expression for quasinormal frequency in the eikonal regime as

$$\begin{aligned} \omega = \frac{(1+2l) (1-0.0699 p) - i (1+2n) (1-0.1201 p) }{3 \sqrt{3}r_{0}}.\nonumber \\ \end{aligned}$$

(28)

In the limit $p \rightarrow 0$, we obtained the analytical expression of quasinormal frequency for Schwarzschild black hole.

3.5 Logarithmic GB-coupling functional: $f(\varphi )=\ln {(\varphi )}$

The quasinormal modes of massless scalar $(s=0)$ and electromagnetic $(s=1)$ fields for $l=1$, 2 and $l=1$, 2, 3 are shown in Figs. 27, 28, 29, 30 and 31. From Figs. 27, 28, 29, 30 and 31 one can see that the behaviour of real and imaginary parts of the quasinormal frequency as a function of parameter p is almost linear for different values of l. In formulas 29 and 30 the parameter p runs from $p=0.0$ to $p=0.70$. The approximated linear laws for scalar and electromagnetic fields for different values of l are given by

$$\begin{aligned} \text {Re}(\omega _{s=0, l=1})&\approx 0.587079 -0.043569 p, \end{aligned}$$

(29a)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=1})&\approx 0.0231869 p-0.195646, \end{aligned}$$

(29b)

$$\begin{aligned} \text {Re}(\omega _{s=0, l=2})&\approx 0.969141 -0.0766068 p, \end{aligned}$$

(29c)

$$\begin{aligned} \text {Im}(\omega _{s=0, l=2})&\approx 0.0245713 p-0.19412. \end{aligned}$$

(29d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=1})&\approx 0.497885 -0.0368047 p, \end{aligned}$$

(30a)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=1})&\approx 0.0271431 p-0.187726, \end{aligned}$$

(30b)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=2})&\approx 0.915132 -0.0449956 p, \end{aligned}$$

(30c)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=2})&\approx 0.0277317 p-0.191956, \end{aligned}$$

(30d)

$$\begin{aligned} \text {Re}(\omega _{s=1, l=3})&\approx 1.31625 -0.103508 p, \end{aligned}$$

(30e)

$$\begin{aligned} \text {Im}(\omega _{s=1, l=3})&\approx 0.0252856 p-0.192324. \end{aligned}$$

(30f)

The behaviour of real and imaginary parts of the quasinormal modes for massive scalar fields as a function of mass (m) is shown in Fig. 32. From Fig. 32b we can see that the imaginary part of the quasinormal frequency approaches zero, which indicates the existence of quasi-resonances.

Fig. 32

The dependence of quasinormal frequency on mass (m) for massive scalar fields with $r_0=1$, $p=0.5$, red line denotes real part of frequency and blue lines denote the imaginary part of the frequency

Fig. 33

The dependence of grey-body factor on $\omega$, for the electromagnetic field $(s = 1)$, with $r_0=1$, black line denotes $p=0.0$, magenta line denotes $p=0.2$, blue line denotes $p=0.4$, red line denotes $p=0.6$ and green line denotes $p=0.8$

Fig. 34

The dependence of grey-body factor on $\omega$, for the electromagnetic field $(s = 1)$, with $r_0=1$, black line denotes $p=0.0$, magenta line denotes $p=0.2$, blue line denotes $p=0.4$, red line denotes $p=0.6$ and green line denotes $p=0.8$

Fig. 35

The dependence of grey-body factor on $\omega$, for the electromagnetic field $(s = 1)$, with $r_0=1$, black line denotes $p=0.0$, magenta line denotes $p=0.2$, blue line denotes $p=0.4$, red line denotes $p=0.6$ and green line denotes $p=0.8$

Fig. 36

The dependence of grey-body factor on $\omega$, for the electromagnetic field $(s = 1)$, with $r_0=1$, black line denotes $p=0.0$, magenta line denotes $p=0.2$, blue line denotes $p=0.4$, red line denotes $p=0.6$ and green line denotes $p=0.8$

Fig. 37

The dependence of grey-body factor on $\omega$, for the electromagnetic field $(s = 1)$, with $r_0=1$, black line denotes $p=0.0$, magenta line denotes $p=0.2$, blue line denotes $p=0.4$, red line denotes $p=0.6$ and green line denotes $p=0.8$

3.5.1 Analytical formula For QNMS in the eikonal regime

In the domain of high multipole numbers l (eikonal), test fields with varying spin follow a common law up to the leading order. In this context, we examine an electromagnetic field with the effective potential 9(b). In the eikonal regime, one can use the first-order WKB formula given in Eq. (14). Using the Ref. [58] we find that the maximum of effective potential 9(b) occurs at $r=r_{max}$ which is given by

$$\begin{aligned} r_{max}= \frac{3r_{0}}{2} +0.0544 r_{0} p + {\mathcal {O}}(p^2). \end{aligned}$$

(31)

Now, substituting $r_{max}$ and Eq. 9(b) into Eq. (14) one can obtain the analytical expression for quasinormal frequency in the eikonal regime for logarithmic GB-coupling functional as

$$\begin{aligned} \omega = \frac{(1+2l) (1-0.0690 p) - i (1+2n) (1-0.1181 p) }{3 \sqrt{3}r_{0}}.\nonumber \\ \end{aligned}$$

(32)

In the limit $p \rightarrow 0$, we obtained the analytical expression of quasinormal frequency for Schwarzschild black hole.

As one can see from this and previous analytical relations for the eikonal regime, the quasinormal modes are fully reproduced by the WKB formula and, therefore, the correspondence between eikonal qnms and null geodesics suggested in [51] is indeed valid for the test fields under consideration.

4 Grey-body factors

The strength of Hawking radiation does not fully reach a distant observer, it is partially suppressed by the effective potential surrounding the black holes and reflected to the black hole event horizon. To find the number of particles reflected due to the effective potential, it is essential to determine the grey-body factors. This involves solving the classical scattering problem to estimate the number of particles that undergo reflection.

We will investigate the wave equation (7) under the boundary conditions that allow the inclusion of incoming waves from infinity,

$$\begin{aligned} \Psi&= e^{-i \omega r_{*}} + R e^{i \omega r_{*}}, r_{*} \rightarrow \infty , \end{aligned}$$

(33a)

$$\begin{aligned} \Psi&= T e^{-i \omega r_{*}}, r_{*} \rightarrow -\infty , \end{aligned}$$

(33b)

where R and T are the reflection and transmission coefficients. This scenario is equivalent to the scattering of a wave originating from the horizon.

The nature of the effective potential is such that it decreases at both infinity, therefore we can safely apply the WKB method [45,46,47,48] to find reflection and transmission coefficients. The reflection and transmission coefficients satisfy the following relations

$$\begin{aligned} |R|^2 +|T|^2=1. \end{aligned}$$

(34)

Once the reflection coefficient is computed, we can find the transmission coefficient for each multipole number as follows

$$\begin{aligned} |A_{l}|^2 =1- |R_{l}|^2. \end{aligned}$$

(35)

Numerous approaches are available in the literature for the computation of the transmission and reflection coefficients. For an accurate computation of the transmission and reflection coefficients, we employed the 6th-order WKB formula [45,46,47,48]. In accordance with the findings presented in [45,46,47,48], the reflection coefficient can be written as

$$\begin{aligned} R= (1+e^{-2i\pi K})^{-\frac{1}{2}}, \end{aligned}$$

(36)

where K is defined by the following relations

$$\begin{aligned} K - i \frac{(\omega ^2 - V_0)}{\sqrt{-2V_{0}^{\prime \prime }}} - \sum _{i=2}^{i=6} \Lambda _{i}(K)=0, \end{aligned}$$

(37)

where $V_{0}$ is the effective potential at $r=r_{max}$, $V_{0}^{\prime \prime }$ is the double derivative of effective potential with respect to radial coordinate r, evaluated at $r=r_{max}$ and $\Lambda _i$ is the higher-order correction to the WKB formula.

4.1 Quadratic GB-coupling functional

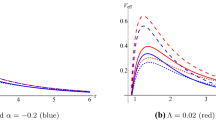
The grey-body factors for quadratic GB-coupling functional are shown in Fig. 33 as a function of $\omega$ for electromagnetic fields with different values of multiple numbers l. From Fig. 33 it can be seen that the grey-body factor is higher for EsGB black holes compared to Schwarzschild black holes. As the parameter p increases transmission rate of the particles also increases, which is consistent with the nature of the effective potential, i.e., as the parameter p increases the height of the potential barrier becomes lower resulting in a high transmission rate for the particles and vice-versa.

4.2 Cubic GB-coupling functional

The grey-body factors for cubic GB-coupling functional are shown in Fig. 34 as a function of $\omega$ for electromagnetic fields with different values of multiple numbers l. From Fig. 34 it can be seen that the grey-body factor is higher for EsGB black holes compared to Schwarzschild black holes. As the parameter p increases transmission rate of the particles also increases, which is consistent with the nature of the effective potential, i.e., as the parameter p increases the height of the potential barrier becomes lower resulting in a high transmission rate for the particles and vice-versa.

4.3 Quartic GB-coupling functional

The grey-body factors for quartic GB-coupling functional are shown in Fig. 35 as a function of $\omega$ for electromagnetic fields with different values of multiple numbers l. From Fig. 35 it can be seen that the grey-body factor is higher for EsGB black holes compared to Schwarzschild black holes. As the parameter p increases transmission rate of the particles also increases, which is consistent with the nature of the effective potential, i.e., as the parameter p increases the height of the potential barrier becomes lower resulting in a high transmission rate for the particles and vice-versa.

4.4 Inverse GB-coupling functional

The grey-body factors for inverse GB-coupling functional are shown in Fig. 36 as a function of $\omega$ for electromagnetic fields with different values of multiple numbers l. From Fig. 36 it can be seen that the grey-body factor is higher for EsGB black holes compared to Schwarzschild black holes. As the parameter p increases transmission rate of the particles also increases, which is consistent with the nature of the effective potential, i.e., as the parameter p increases the height of the potential barrier becomes lower resulting in a high transmission rate for the particles and vice-versa.

4.5 Logarithmic GB-coupling functional

The grey-body factors for logarithmic GB-coupling functional are shown in Fig. 37 as a function of $\omega$ for electromagnetic fields with different values of multiple numbers l. From Fig. 37 it can be seen that the grey-body factor is higher for EsGB black holes compared to Schwarzschild black holes. As the parameter p increases transmission rate of the particles also increases, which is consistent with the nature of the effective potential, i.e., as the parameter p increases the height of the potential barrier becomes lower resulting in a high transmission rate for the particles and vice-versa.

Here, we will write a brief analysis of how different GB-coupling functions affect the quasinormal modes of the black hole. From above analysis of the quasinormal modes of EsGB black hole as a function of parameter p, we see a strong deviation of qnms for both massless scalar and electromagnetic field compared to Schwarzschild black hole when GB-coupling functions are logarithmic. The deviation of quasinormal modes is lowest for quadratic GB-coupling functional. The transmission rate of the particles is highest for logarithmic GB-coupling functional (i.e., the strongest deviation of transmission rate occurs compared to Schwarzschild black hole) and lowest for quadratic GB-coupling functional (i.e., the lowest deviation of transmission rate occurs compared to Schwarzschild black hole).

5 Conclusions

In this study, we address previously unexplored aspects of quasinormal modes for scalar and electromagnetic fields in the vicinity of analytically obtained EsGB black holes solutions. Here, we investigate:

• The quasinormal modes of scalar and electromagnetic fields in the background of EsGB black hole for different GB coupling functional (quadratic, cubic, quartic, inverse, and Logarithmic). The dependence of the real and imaginary parts of the quasinormal modes on the parameter p is shown in Figures. For $p=0$, quasinormal modes of EsGB black hole match with Schwarzschild one. For non-zero values of p quasinormal frequency of EsGB black hole take smaller values compared to Schwarzschild black hole.

• We analyzed massive scalar fields in the EsGB background. The height of the effective potential for massive scalar fields is higher as the mass increases. For large values of mass, it shows undamped oscillations occur, which commonly known as quasi-resonances.

• We derived an analytical formula of quasinormal frequency in the eikonal regime for each GB coupling function. In the limit $p \rightarrow 0$, it reduced to the quasinormal frequency of Schwarzschild black hole. We have shown that the correspondence between the eikonal quasinormal frequencies and null geodesics [51] is hold in the EsGB theory for the test fields under consideration.

• Finally, we studied the grey-body factors for electromagnetic fields with different values of multiple numbers. Our analysis showed that for higher values of parameter p grey-body factors are larger.

Appendix A: Analytical expressions for the metric functions up to fourth order

Here, we will write down the analytical expression for the metric functions up to the fourth order in the CFA method. Therefore, the metric functions are given by

$$\begin{aligned}{} & {} g_{tt}(r) \approx \frac{{\mathcal {N}}^1}{{\mathcal {D}}^1}\left( 1- \frac{r_0}{r}\right) , \end{aligned}$$

(A1)

$$\begin{aligned}{} & {} \sqrt{g_{tt}(r)g_{rr}(r)} \approx \frac{{\mathcal {N}}^2}{{\mathcal {D}}^2}, \end{aligned}$$

(A2)

where the numerators, ${\mathcal {N}}^1$, ${\mathcal {N}}^2$ and denominators, ${\mathcal {D}}^1$, ${\mathcal {D}}^2$ are separately given for each GB coupling functional.

1.1 A.1 Quadratic GB-coupling functional: $f(\varphi )=\varphi ^2$

$$\begin{aligned}{} & {} g_{tt}(r) \approx \frac{{\mathcal {N}}^1_{eve2}}{{\mathcal {D}}^1_{eve2}}\left( 1- \frac{r_0}{r}\right) , \end{aligned}$$

(A3)

$$\begin{aligned}{} & {} \sqrt{g_{tt}(r)g_{rr}(r)} \approx \frac{{\mathcal {N}}^2_{eve2}}{{\mathcal {D}}^2_{eve2}}, \end{aligned}$$

(A4)

where

$$\begin{aligned} {\mathcal {N}}^1_{\text {eve}2}{} & {} = p^{11} \bigg (-0.027339 r^3 r_{0}+0.027339r^2r_{0}^2+0.027339 r {r_{0}}^3\nonumber \\ {}{} & {} \quad -0.027339 {r_{0}}^4\bigg )+p^{10}\bigg (-1.65064r^3{r_{0}} \nonumber \\ {}{} & {} \quad +r^4+0.639158 r^2 {r_{0}}^2 -0.349358 r {r_{0}}^3\nonumber \\ {}{} & {} \quad +0.360842 {r_{0}}^4\bigg )+p^9 \bigg (-13.5993 r^4+25.9764 r^3 {r_{0}} \nonumber \\ {}{} & {} \quad -12.2194 r^2 {r_{0}}^2+1.96871r{r_{0}}^3-2.12636 {r_{0}}^4\bigg )\nonumber \\ {}{} & {} \quad +p^8 \bigg (66.7223 r^4-136.15 r^3 {r_{0}}+68.5796 r^2 {r_{0}}^2 \nonumber \\ {}{} & {} \quad -6.96288 r {r_{0}}^3+7.81103 {r_{0}}^4\bigg ) +p^7 \bigg (-142.79 r^4\nonumber \\ {}{} & {} \quad +317.427 r^3 {r_{0}}-172.292 r^2 {r_{0}}^2+15.8938 r{r_{0}}^3 \nonumber \\ {}{} & {} \quad -18.2388 {r_{0}}^4\bigg )+p^6 \bigg (101.122 r^4-301.89 r^3 {r_{0}} \nonumber \\ {}{} & {} \quad +197.051 r^2 {r_{0}}^2-22.9918 r {r_{0}}^3+26.7025 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^5 \bigg (120.603 r^4-78.7254 r^3 {r_{0}}-38.3503 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +20.5997 r {r_{0}}^3-24.0645 {r_{0}}^4\bigg ) +p^4 \bigg (-295.148 r^4 \nonumber \\ {}{} & {} \quad +437.019 r^3 {r_{0}}-143.957 r^2 {r_{0}}^2-10.8823 r {r_{0}}^3\nonumber \\ {}{} & {} \quad +12.7195 {r_{0}}^4\bigg ) +p^3 \bigg (236.149 r^4-388.645 r^3 {r_{0}} \nonumber \\ {}{} & {} \quad +153.456 r^2 {r_{0}}^2+3.01323 r {r_{0}}^3-3.47898 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^2 \bigg (-85.9513 r^4 +147.171 r^3 {r_{0}}-61.7593 r^2 {r_{0}}^2 \nonumber \\ {}{} & {} \quad -0.319982 r {r_{0}}^3 +0.336681 {r_{0}}^4\bigg )+p \bigg (12.5012 r^4\nonumber \\ {}{} & {} \quad -21.3996 r^3 {r_{0}}+9.1727 r^2 {r_{0}}^2+0.00359074 r {r_{0}}^3 \nonumber \\ {}{} & {} \quad +0.0054195 {r_{0}}^4\bigg ) -0.608781 r^4 \nonumber \\ {}{} & {} \quad +0.894103 r^3 {r_{0}} -0.347264 r^2 {r_{0}}^2, \end{aligned}$$

(A5)

$$\begin{aligned} {\mathcal {D}}^1_{\text {eve}2}{} & {} = p^{10} r^2 \bigg ( r^2-2 r {r_{0}}+ {r_{0}}^2\bigg )\nonumber \\ {}{} & {} \quad +p^9 r^2 \bigg (-13.5993 r^2+27.6187 r {r_{0}}-14.0194 {r_{0}}^2\bigg )\nonumber \\ {}{} & {} \quad +p^8 r^2 \bigg (66.7223 r^2 \nonumber \\ {}{} & {} \quad -139.556 r {r_{0}}+72.8336 {r_{0}}^2\bigg )\nonumber \\ {}{} & {} \quad +p^7 r^2 \bigg (-142.79 r^2+319.724 r {r_{0}}\nonumber \\ {}{} & {} \quad -176.934 {r_{0}}^2\bigg )+p^6 r^2 \bigg (101.122 r^2 \nonumber \\ {}{} & {} \quad -298.896 r {r_{0}}+197.772 {r_{0}}^2\bigg )\nonumber \\ {}{} & {} \quad +p^5 r^2 \bigg (120.603 r^2-85.7535 r {r_{0}}\nonumber \\ {}{} & {} \quad -34.8151 {r_{0}}^2\bigg )+p^4 r^2 \bigg (-295.148 r^2 \nonumber \\ {}{} & {} \quad +442.573 r {r_{0}}-147.595 {r_{0}}^2\bigg )\nonumber \\ {}{} & {} \quad +p^3 r^2 \bigg (236.149 r^2-390.653 r {r_{0}}\nonumber \\ {}{} & {} \quad +154.893 {r_{0}}^2\bigg )+p^2 r^2 \bigg (-85.9513 r^2\nonumber \\ {}{} & {} \quad +147.462 r {r_{0}}-61.9667 {r_{0}}^2\bigg )\nonumber \\ {}{} & {} \quad +p r^2 \bigg (12.5012 r^2-21.4138 r {r_{0}}\nonumber \\ {}{} & {} \quad +9.17934 {r_{0}}^2\bigg )+r^2 \bigg (-0.608781 r^2\nonumber \\ {}{} & {} \quad +0.894103 r {r_{0}}-0.347264 {r_{0}}^2\bigg ), \end{aligned}$$

(A6)

$$\begin{aligned} {\mathcal {N}}^2_{\text {eve}2}{} & {} = p^9 ( r^3-2 r^2 {r_{0}}+ r {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^8 (-8.86767 r^3+17.7041 r^2 {r_{0}}-8.8364 r {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^7 (29.1248 r^3-57.7325 r^2 {r_{0}}+28.8414 r {r_{0}}^2\nonumber \\ {}{} & {} \quad -0.233666 {r_{0}}^3)\nonumber \\ {}{} & {} \quad +p^6 \bigg (-56.6765 r^3+110.257 r^2 {r_{0}}-54.735 r {r_{0}}^2 \nonumber \\ {}{} & {} \quad +1.1405 {r_{0}}^3\bigg )+p^5 \bigg (90.3253 r^3-171.817 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +83.6835 r {r_{0}}^2-2.08071 {r_{0}}^3\bigg )+p^4 \bigg (-119.877 r^3 \nonumber \\ {}{} & {} \quad +226.049 r^2 {r_{0}}-108.183 r {r_{0}}^2+1.65941 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^3 \bigg (105.82 r^3-199.251 r^2 {r_{0}}+94.4276 r {r_{0}}^2 \nonumber \\ {}{} & {} \quad -0.411268 {r_{0}}^3\bigg )+p^2 \bigg (-51.741 r^3+96.6288 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad -45.2948 r {r_{0}}^2-0.132824 {r_{0}}^3\bigg )+p \bigg (12.1153 r^3 \nonumber \\ {}{} & {} \quad -21.8254 r^2 {r_{0}}+9.91398 r {r_{0}}^2+0.058561 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad -1.22281 r^3+1.98757 r^2 {r_{0}}-0.817317 r {r_{0}}^2, \end{aligned}$$

(A7)

$$\begin{aligned} {\mathcal {D}}^2_{\text {eve}2}{} & {} = p^9 r (1. r^2-2. r {r_{0}}+1. {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^8 r (-8.86767 r^2+17.7041 r {r_{0}}-8.8364 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^7 r (29.1248 r^2-57.7325 r {r_{0}}+28.6077 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^6 r (-56.6765 r^2+110.257 r {r_{0}}-53.5872 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^5 r (90.3253 r^2-171.817 r {r_{0}}+81.5611 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^4 r (-119.877 r^2+226.049 r {r_{0}}-106.429{r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^3 r (105.82 r^2 -199.251 r {r_{0}}+93.9092 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^2 r (-51.741 r^2+96.6288 r {r_{0}}-45.3674 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p r (12.1153 r^2 -21.8254 r {r_{0}}+9.95903 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +r (-1.22281 r^2+1.98757 r {r_{0}}-0.817317 {r_{0}}^2). \end{aligned}$$

(A8)

1.2 A.2 Cubic GB-coupling functional: $f(\varphi )=\varphi ^3$

$$\begin{aligned}{} & {} g_{tt}(r) \approx \frac{{\mathcal {N}}^1_{odd3}}{{\mathcal {D}}^1_{odd3}}\left( 1- \frac{r_0}{r}\right) , \end{aligned}$$

(A9)

$$\begin{aligned}{} & {} \sqrt{g_{tt}(r)g_{rr}(r)} \approx \frac{{\mathcal {N}}^2_{odd3}}{{\mathcal {D}}^2_{odd3}}, \end{aligned}$$

(A10)

where

$$\begin{aligned} {\mathcal {N}}^1_{\text {odd}3}{} & {} = p^{12} \bigg (0.00537634 r^3 r_{0}-0.00537634 r^2 r_{0}^2\nonumber \\ {}{} & {} \quad -0.00537634 r r_{0}^3+0.00537634 r_{0}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^{11} \bigg (-0.0670504 r^3 r_{0}+0.0683756 r^2 r_{0}^2\nonumber \\ {}{} & {} \quad +0.0670504 r r_{0}^3-0.0683756 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^{10} \bigg (1. r^4 -1.70036 r^3 r_{0}+0.683358 r^2 r_{0}^2\nonumber \\ {}{} & {} \quad -0.299635 r r_{0}^3+0.316642 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^9 \bigg (-6.78182 r^4+13.1727 r^3 r_{0} \nonumber \\ {}{} & {} \quad -6.31042 r^2 r_{0}^2+0.737004 r r_{0}^3-0.817608 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^8 \bigg (17.7971 r^4-36.7027 r^3 r_{0}+18.714 r^2 r_{0}^2 \nonumber \\ {}{} & {} \quad -1.12269 r r_{0}^3+1.3156 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^7 \bigg (-21.7877 r^4+48.5071 r^3 r_{0}\nonumber \\ {}{} & {} \quad -26.4795 r^2 r_{0}^2+1.08356 r r_{0}^3 \nonumber \\ {}{} & {} \quad -1.34315 r_{0}^4\bigg )+p^6 \bigg (9.51766 r^4-26.9583 r^3 r_{0} \nonumber \\ {}{} & {} \quad +17.3344 r^2 r_{0}^2-0.638392 r r_{0}^3+0.834102 r_{0}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^5 \bigg (4.59852 r^4-2.91241 r^3 r_{0}-1.79709 r^2 r_{0}^2 \nonumber \\ {}{} & {} \quad +0.19656 r r_{0}^3-0.266067 r_{0}^4\bigg )+p^4 \bigg (-5.37404 r^4 \nonumber \\ {}{} & {} \quad +8.71817 r^3 r_{0}-3.1644 r^2 r_{0}^2\nonumber \\ {}{} & {} \quad -0.0116997 r r_{0}^3 +0.0128034 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^3 \bigg (0.540319 r^4-1.28023 r^3 r_{0} \nonumber \\ {}{} & {} \quad +0.652328 r^2 r_{0}^2-0.00618425 r r_{0}^3+0.0102582 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^2 \bigg (0.451911 r^4-0.727369 r^3 r_{0}+0.284135 r^2 r_{0}^2 \nonumber \\ {}{} & {} \quad -0.00017735 r r_{0}^3+0.000404216 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p \bigg (0.0379465 r^4-0.0549725 r^3 r_{0}\nonumber \\ {}{} & {} \quad +0.0202381 r^2 r_{0}^2-0.0000201357 r r_{0}^3 \nonumber \\ {}{} & {} \quad +0.0000179163 r_{0}^4\bigg )+0.000140052 r^4\nonumber \\ {}{} & {} \quad -0.0000971891 r^3 r_{0}, \end{aligned}$$

(A11)

$$\begin{aligned} {\mathcal {D}}^1_{\text {odd}3}{} & {} = p^{10} r^2 (1. r^2-2. r r_{0}+1. r_{0}^2)\nonumber \\ {}{} & {} \quad +p^9 r^2 (-6.78182 r^2+13.8101 r r_{0}-7.02829 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^8 r^2 (17.7971 r^2-37.355 r r_{0}+19.5579 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^7 r^2 (-21.7877 r^2+48.6892 r r_{0}-26.9117 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^6 r^2 (9.51766 r^2 -26.7448 r r_{0}+17.2901 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^5 r^2 (4.59852 r^2-3.06912 r r_{0}-1.67657 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^4 r^2 (-5.37404 r^2+8.71215 r r_{0} -3.17516 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^3 r^2 (0.540319 r^2-1.2622 r r_{0}+0.6403 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^2 r^2 (0.451911 r^2-0.725183 r r_{0}+0.28313 r_{0}^2)\nonumber \\ {}{} & {} \quad +p r^2 (0.0379465 r^2-0.0549644 r r_{0}+0.0202407 r_{0}^2) \nonumber \\ {}{} & {} \quad +r^2 (0.000140052 r^2-0.0000971891 r r_{0}), \end{aligned}$$

(A12)

$$\begin{aligned} {\mathcal {N}}^2_{\text {odd}3}{} & {} = p^9 \bigg (1. r^3-2. r^2 r_{0}+1. r r_{0}^2\bigg )\nonumber \\ {}{} & {} \quad +p^8 \bigg (-15.624 r^3+31.3197 r^2 r_{0}-15.587 r r_{0}^2\nonumber \\ {}{} & {} \quad -0.108754 r_{0}^3\bigg )+p^7 \bigg (75.8827 r^3 \nonumber \\ {}{} & {} \quad -153.129 r^2 r_{0}+75.7277 r r_{0}^2+1.51139 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^6 \bigg (-135.885 r^3+279.413 r^2 r_{0}-138.956 r r_{0}^2\nonumber \\ {}{} & {} \quad -4.46757 r_{0}^3\bigg ) \nonumber \\ {}{} & {} \quad +p^5 \bigg (72.0953 r^3-161.504 r^2 r_{0}+83.7029 r r_{0}^2\nonumber \\ {}{} & {} \quad +5.22405 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^4 \bigg (47.4153 r^3-75.3996 r^2 r_{0}+31.4976 r r_{0}^2 \nonumber \\ {}{} & {} \quad -2.47728 r_{0}^3\bigg )+p^3 \bigg (-61.6661 r^3+111.092 r^2 r_{0}\nonumber \\ {}{} & {} \quad -50.8295 r r_{0}^2+0.253284 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^2 \bigg (18.923 r^3-32.9427 r^2 r_{0} \nonumber \\ {}{} & {} \quad +14.5941 r r_{0}^2+0.0638083 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p \bigg (-2.11497 r^3+3.11041 r^2 r_{0}\nonumber \\ {}{} & {} \quad -1.13326 r r_{0}^2+0.0010564 r_{0}^3\bigg )-0.0225954 r^3 \nonumber \\ {}{} & {} \quad +0.0327384 r^2 r_{0}-0.0128335 r r_{0}^2, \end{aligned}$$

(A13)

$$\begin{aligned} {\mathcal {D}}^2_{\text {odd}3}{} & {} = p^9 r (1. r^2-2. r r_{0}+1. r_{0}^2)\nonumber \\ {}{} & {} \quad +p^8 r (-15.624 r^2+31.3197 r r_{0}-15.6957 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^7 r (75.8827 r^2-153.129 r r_{0}+77.2427 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^6 r \bigg (-135.885 r^2+279.413 r r_{0}\nonumber \\ {}{} & {} \quad -143.469 r_{0}^2\bigg )+p^5 r \bigg (72.0953 r^2-161.504 r r_{0} \nonumber \\ {}{} & {} \quad +89.0785 r_{0}^2\bigg )+p^4 r (47.4153 r^2-75.3996 r r_{0}\nonumber \\ {}{} & {} \quad +28.8021 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^3 r (-61.6661 r^2+111.092 r r_{0}-50.4318 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^2 r (18.923 r^2 -32.9427 r r_{0}+14.6226 r_{0}^2)\nonumber \\ {}{} & {} \quad +p r (-2.11497 r^2+3.11041 r r_{0}-1.13289 r_{0}^2) \nonumber \\ {}{} & {} \quad +r (-0.0225954 r^2+0.0327384 r r_{0}\nonumber \\ {}{} & {} \quad -0.0128335 r_{0}^2). \end{aligned}$$

(A14)

1.3 A.3 Quartic GB-coupling functional: $f(\varphi )=\varphi ^4$

$$\begin{aligned}{} & {} g_{tt}(r) \approx \frac{{\mathcal {N}}^1_{eve4}}{{\mathcal {D}}^1_{eve4}}\left( 1- \frac{r_0}{r}\right) , \end{aligned}$$

(A15)

$$\begin{aligned}{} & {} \sqrt{g_{tt}(r)g_{rr}(r)} \approx \frac{{\mathcal {N}}^2_{eve4}}{{\mathcal {D}}^2_{eve4}}, \end{aligned}$$

(A16)

where

$$\begin{aligned} {\mathcal {N}}^1_{\text {eve}4}{} & {} = p^{15} \bigg (1. r^4-2.089 r^3 r_{0}\nonumber \\ {}{} & {} \quad +1.089 r^2 r_{0}^2+0.0889959 r r_{0}^3-0.0889959 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^{14} \bigg (-6.89482 r^4 +14.7896 r^3 r_{0}-7.90886 r^2 r_{0}^2\nonumber \\ {}{} & {} \quad -0.757057 r r_{0}^3+0.771153 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^{13} \bigg (12.5106 r^4-29.4208 r^3 r_{0} \nonumber \\ {}{} & {} \quad +17.0451 r^2 r_{0}^2+2.92063 r r_{0}^3-3.05555 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^{12} \bigg (19.4917 r^4-29.885 r^3 r_{0}+9.84773 r^2 r_{0}^2 \nonumber \\ {}{} & {} \quad -6.69766 r r_{0}^3+7.24323 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^{11} \bigg (-115.113 r^4+224.275 r^3 r_{0}\nonumber \\ {}{} & {} \quad -107.925 r^2 r_{0}^2+9.97888 r r_{0}^3 \nonumber \\ {}{} & {} \quad -11.206 r_{0}^4\bigg )+p^{10} \bigg (198.927 r^4-410.675 r^3 r_{0}\nonumber \\ {}{} & {} \quad +210.013 r^2 r_{0}^2-9.86857 r r_{0}^3+11.562 r_{0}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^9 \bigg (-164.194 r^4+364.121 r^3 r_{0}-198.46 r^2 r_{0}^2\nonumber \\ {}{} & {} \quad +6.32619 r r_{0}^3-7.79975 r_{0}^4\bigg )+p^8 (45.2779 r^4 \nonumber \\ {}{} & {} \quad -130.919 r^3 r_{0}+85.2 r^2 r_{0}^2-2.38976 r r_{0}^3\nonumber \\ {}{} & {} \quad +3.15916 r_{0}^4)+p^7 \bigg (28.2324 r^4-33.1842 r^3 r_{0} \nonumber \\ {}{} & {} \quad +4.40023 r^2 r_{0}^2+0.342238 r r_{0}^3-0.525779 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^6 \bigg (-21.3691 r^4+38.4559 r^3 r_{0}-16.3563 r^2 r_{0}^2 \nonumber \\ {}{} & {} \quad +0.0898093 r r_{0}^3-0.104246 r_{0}^4\bigg )\nonumber \\ {}{} & {} \quad +p^5 \bigg (-0.197567 r^4-1.57336 r^3 r_{0}\nonumber \\ {}{} & {} \quad +1.45736 r^2 r_{0}^2-0.0324933 r r_{0}^3 \nonumber \\ {}{} & {} \quad +0.0403357 r_{0}^4\bigg )+p^4 \bigg (2.04375 r^4-3.45917 r^3 r_{0}\nonumber \\ {}{} & {} \quad +1.43513 r^2 r_{0}^2-0.00124132 r r_{0}^3+0.00429355 r_{0}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^3 \bigg (0.276656 r^4-0.423294 r^3 r_{0}+0.159108 r^2 r_{0}^2\nonumber \\ {}{} & {} \quad +0.0000460001 r r_{0}^3+0.000142526 r_{0}^4\bigg )\nonumber \\ {}{} & {} +p^2 \bigg (0.00912579 r^4 \nonumber \\ {}{} & {} \quad -0.0124531 r^3 r_{0}+0.0040693 r^2 r_{0}^2-5.79588 \nonumber \\ {}{} & {} \quad \times 10^{-6} r r_{0}^3+5.6289 \times 10^{-6} r_{0}^4\bigg ) \nonumber \\ {}{} & {} \quad +p \bigg (-0.0000509404 r^4+0.000117355 r^3 r_{0}\nonumber \\ {}{} & {} \quad -0.0000607436 r^2 r_{0}^2+4.44458 \times 10^{-8} r r_{0}^3 \nonumber \\ {}{} & {} \quad -6.14644 \times 10^{-8} r_{0}^4\bigg )-2.63557 \times 10^{-7} r^4\nonumber \\ {}{} & {} \quad +1.63201 \times 10^{-8} r^3 r_{0}+ 1.79379 \times 10^{-7} r^2 r_{0}^2, \end{aligned}$$

(A17)

$$\begin{aligned} {\mathcal {D}}^1_{\text {eve}4}{} & {} = p^{15} r^2 (1. r^2-2. r r_{0}+1. r_{0}^2)\nonumber \\ {}{} & {} \quad +p^{14} r^2 (-6.89482 r^2+13.948 r r_{0}-7.05321 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^{13} r^2 (12.5106 r^2-26.1315 r r_{0}+13.6209 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^{12} r^2 (19.4917 r^2-36.7725 r r_{0}+17.2808 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^{11} r^2 (-115.113 r^2 +232.465 r r_{0}-117.345 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^{10} r^2 (198.927 r^2-415.683 r r_{0}+216.716 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^9 r^2 (-164.194 r^2+364.547 r r_{0} -200.316 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^8 r^2 (45.2779 r^2-129.549 r r_{0}+84.468 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^7 r^2 (28.2324 r^2-33.7905 r r_{0}+4.977 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^6 r^2 (-21.3691 r^2+38.3498 r r_{0}-16.341 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^5 r^2 (-0.197567 r^2-1.50422 r r_{0}+1.40334 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^4 r^2 (2.04375 r^2-3.44431 r r_{0}+1.42689 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^3 r^2 (0.276656 r^2-0.422662 r r_{0}+0.158858 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^2 r^2 (0.00912579 r^2-0.0124564 r r_{0}+0.00407385 r_{0}^2)\nonumber \\ {}{} & {} \quad +p r^2 \bigg (-0.0000509404 r^2+0.000117338 r r_{0} \nonumber \\ {}{} & {} \quad -0.0000607602 r_{0}^2\bigg ) +r^2 \bigg (-2.63557 \times 10^{-7} r^2\nonumber \\ {}{} & {} \quad +1.63201 \nonumber \\ {}{} & {} \quad \times 10^{-8} r r_{0}+1.79379 \times 10^{-7} r_{0}^2\bigg ), \end{aligned}$$

(A18)

$$\begin{aligned} {\mathcal {N}}^2_{\text {eve}4}{} & {} = p^{10} \bigg (1. r^3-2. r^2 r_{0}+1. r r_{0}^2\bigg )\nonumber \\ {}{} & {} \quad +p^9 \bigg (-13.6797 r^3+27.4429 r^2 r_{0}\nonumber \\ {}{} & {} \quad -13.6766 r r_{0}^2-0.0865879 r_{0}^3\bigg ) \nonumber \\ {}{} & {} \quad +p^8 \bigg (67.4124 r^3-135.988 r^2 r_{0}\nonumber \\ {}{} & {} \quad +67.7236 r r_{0}^2+0.852114 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^7 \bigg (-148.278 r^3+302.545 r^2 r_{0}-151.49 r r_{0}^2 \nonumber \\ {}{} & {} \quad -2.77603 r_{0}^3\bigg )+p^6 \bigg (146.99 r^3-308.586 r^2 r_{0}\nonumber \\ {}{} & {} \quad +157.352 r r_{0}^2+4.22482 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^5 \bigg (-36.5144 r^3+91.761 r^2 r_{0} \nonumber \\ {}{} & {} \quad -51.9412 r r_{0}^2-3.22666 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^4 \bigg (-41.1576 r^3+69.4003 r^2 r_{0}\nonumber \\ {}{} & {} \quad -29.5381 r r_{0}^2+1.13594 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^3 \bigg (28.9496 r^3 -53.2293 r^2 r_{0}\nonumber \\ {}{} & {} \quad +24.5671 r r_{0}^2-0.117809 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +p^2 \bigg (-5.11947 r^3+9.28066 r^2 r_{0}\nonumber \\ {}{} & {} \quad -4.24613 r r_{0}^2-0.00574379 r_{0}^3\bigg ) \nonumber \\ {}{} & {} \quad +p \bigg (0.391241 r^3-0.618344 r^2 r_{0}\nonumber \\ {}{} & {} \quad +0.245794 r r_{0}^2-0.0000557057 r_{0}^3\bigg )\nonumber \\ {}{} & {} \quad +0.00525892 r^3-0.00809504 r^2 r_{0} \nonumber \\ {}{} & {} \quad +0.00330483 r r_{0}^2, \end{aligned}$$

(A19)

$$\begin{aligned} {\mathcal {D}}^2_{\text {eve}4}{} & {} = p^{10} r (1. r^2-2. r r_{0}+1. r_{0}^2)\nonumber \\ {}{} & {} \quad +p^9 r (-13.6797 r^2+27.4429 r r_{0}-13.7632 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^8 r (67.4124 r^2-135.988 r r_{0}+68.5757 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^7 r (-148.278 r^2+302.545 r r_{0}-154.267 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^6 r (146.99 r^2-308.586 r r_{0} +161.585 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^5 r (-36.5144 r^2+91.761 r r_{0}-55.1917 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^4 r (-41.1576 r^2+69.4003 r r_{0}-28.3697 r_{0}^2) \nonumber \\ {}{} & {} \quad +p^3 r (28.9496 r^2-53.2293 r r_{0}+24.4286 r_{0}^2)\nonumber \\ {}{} & {} \quad +p^2 r (-5.11947 r^2+9.28066 r r_{0}-4.24704 r_{0}^2)\nonumber \\ {}{} & {} \quad +p r (0.391241 r^2 -0.618344 r r_{0}+0.245858 r_{0}^2)\nonumber \\ {}{} & {} \quad +r (0.00525892 r^2-0.00809504 r r_{0}+0.00330483 r_{0}^2).\nonumber \\ \end{aligned}$$

(A20)

1.4 A.4 Inverse GB-coupling functional: $f(\varphi )=\varphi ^{-1}$

$$\begin{aligned}{} & {} g_{tt}(r) \approx \frac{{\mathcal {N}}^1_{inv}}{{\mathcal {D}}^1_{inv}}\left( 1- \frac{r_0}{r}\right) , \end{aligned}$$

(A21)

$$\begin{aligned}{} & {} \sqrt{g_{tt}(r)g_{rr}(r)} \approx \frac{{\mathcal {N}}^2_{inv}}{{\mathcal {D}}^2_{inv}}, \end{aligned}$$

(A22)

where

$$\begin{aligned} {\mathcal {N}}^1_{\text {inv}}{} & {} = p^{13} \bigg (0.00630915 r^3 {r_{0}}-0.00630915 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -0.00630915 r {r_{0}}^3+0.00630915 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^{12} \bigg (-0.288247 r^3 {r_{0}}+0.289835 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +0.288247 r {r_{0}}^3-0.289835 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^{11} \bigg (1. r^4+1.44067 r^3 {r_{0}}-2.51152 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -2.56824 r {r_{0}}^3+2.6391 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^{10} \bigg (-33.5247 r^4+55.6895 r^3 {r_{0}}-21.3738 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +8.14436 r {r_{0}}^3-8.93465 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^9 \bigg (139.634 r^4-272.59 r^3 {r_{0}}+130.873 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -10.712 r {r_{0}}^3+12.9426 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^8 \bigg (-211.343 r^4+445.224 r^3 {r_{0}}-232.351 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +3.40437 r {r_{0}}^3-5.11853 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^7 \bigg (104.307 r^4-239.683 r^3 {r_{0}}+134.352 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +4.79121 r {r_{0}}^3-5.8472 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^6 \bigg (36.8094 r^4-69.4903 r^3 {r_{0}}+37.49 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -4.15303 r {r_{0}}^3+5.6248 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^5 \bigg (-48.322 r^4+99.557 r^3 {r_{0}}-57.1551 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +0.840865 r {r_{0}}^3-0.70925 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^4 \bigg (12.9333 r^4-21.1041 r^3 {r_{0}}+8.6512 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -0.0658137 r {r_{0}}^3-0.217336 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^3 \bigg (0.768694 r^4-0.492765 r^3 {r_{0}}+1.99322 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +0.0218888 r {r_{0}}^3-0.0839553 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^2 \bigg (-2.1015 r^4+1.63385 r^3 {r_{0}}-0.221489 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +0.0142061 r {r_{0}}^3-0.0117263 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p \bigg (-0.155143 r^4+0.0901895 r^3 {r_{0}}-0.0282534 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +0.000352495 r {r_{0}}^3-0.000442358 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad -0.005224 r^4+0.00352893 r^3 {r_{0}}-0.000651281 r^2 {r_{0}}^2,\nonumber \\ \end{aligned}$$

(A23)

$$\begin{aligned} {\mathcal {D}}^1_{\text {inv}}{} & {} = p^{11} r^2 (1. r^2-2. r {r_{0}}+1. {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^{10} r^2 (-33.5247 r^2+67.3011 r {r_{0}}-33.7764 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^9 r^2 (139.634 r^2-287.439 r {r_{0}}+147.805 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^8 r^2 (-211.343 r^2+449.189 r {r_{0}}-237.795 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^7 r^2 (104.307 r^2-233.152 r {r_{0}}+127.187 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^6 r^2 (36.8094 r^2-74.6521 r {r_{0}}+43.2038 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^5 r^2 (-48.322 r^2+100.669 r {r_{0}}-57.9912 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^4 r^2 (12.9333 r^2-20.9337 r {r_{0}}+8.67754 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^3 r^2 (0.768694 r^2-0.696371 r {r_{0}}+1.94788 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^2 r^2 (-2.1015 r^2+1.61854 r {r_{0}}-0.227976 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p r^2 (-0.155143 r^2+0.0896651 r {r_{0}}-0.0284235 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +r^2 \bigg (-0.005224 r^2+0.00352893 r {r_{0}} \nonumber \\ {}{} & {} \quad -0.000651281 {r_{0}}^2\bigg ), \end{aligned}$$

(A24)

$$\begin{aligned} {\mathcal {N}}^2_{\text {inv}}{} & {} = p^9 \bigg (1. r^3-2.16356 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +1.01501 r {r_{0}}^2+0.148553 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^8 \bigg (-8.63116 r^3+19.3261 r^2 {r_{0}} \nonumber \\ {}{} & {} \quad -9.37725 r {r_{0}}^2-1.31772 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^7 \bigg (25.4073 r^3-61.4392 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +31.2754 r {r_{0}}^2+4.7492 {r_{0}}^3\bigg ) \nonumber \\ {}{} & {} \quad +p^6 \bigg (-25.4485 r^3+80.1206 r^2 {r_{0}}-45.5637 r {r_{0}}^2\nonumber \\ {}{} & {} \quad -9.03094 {r_{0}}^3\bigg )+p^5 \bigg (-18.958 r^3-9.26834 r^2 {r_{0}} \nonumber \\ {}{} & {} \quad +18.1535 r {r_{0}}^2+9.73502 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^4 \bigg (67.5176 r^3-88.9673 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +28.0939 r {r_{0}}^2-5.8473 {r_{0}}^3\bigg ) \nonumber \\ {}{} & {} \quad +p^3 \bigg (-62.3959 r^3+97.8017 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad -38.225 r {r_{0}}^2+1.71881 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^2 \bigg (25.6081 r^3-41.9346 r^2 {r_{0}} \nonumber \\ {}{} & {} \quad +17.3586 r {r_{0}}^2-0.140684 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p \bigg (-4.42145 r^3+6.8935 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad -2.85028 r {r_{0}}^2-0.0149354 {r_{0}}^3\bigg ) \nonumber \\ {}{} & {} \quad +0.322118 r^3-0.368892 r^2 {r_{0}}+0.119768 r {r_{0}}^2, \end{aligned}$$

(A25)

$$\begin{aligned} {\mathcal {D}}^2_{\text {inv}}{} & {} = p^9 r (1. r^2-2.16356 r {r_{0}}\nonumber \\ {}{} & {} \quad +1.16356 {r_{0}}^2)+p^8 r (-8.63116 r^2\nonumber \\ {}{} & {} \quad +19.3261 r {r_{0}}-10.695 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^7 r (25.4073 r^2-61.4392 r {r_{0}}+36.0281 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^6 r (-25.4485 r^2+80.1206 r {r_{0}}-54.6246 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^5 r (-18.958 r^2-9.26834 r {r_{0}}+27.9908 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^4 r (67.5176 r^2-88.9673 r {r_{0}}+22.0663 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^3 r (-62.3959 r^2+97.8017 r {r_{0}}-36.3316 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^2 r (25.6081 r^2-41.9346 r {r_{0}}+17.1297 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p r (-4.42145 r^2+6.8935 r {r_{0}}-2.84697 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +r (0.322118 r^2-0.368892 r {r_{0}}+0.119768 {r_{0}}^2). \end{aligned}$$

(A26)

1.5 A.5 Logarithmic GB-coupling functional: $f(\varphi )=\ln (\varphi )$

$$\begin{aligned}{} & {} g_{tt}(r) \approx \frac{{\mathcal {N}}^1_{log}}{{\mathcal {D}}^1_{log}}\left( 1- \frac{r_0}{r}\right) , \end{aligned}$$

(A27)

$$\begin{aligned}{} & {} \sqrt{g_{tt}(r)g_{rr}(r)} \approx \frac{{\mathcal {N}}^2_{log}}{{\mathcal {D}}^2_{log}}, \end{aligned}$$

(A28)

where

$$\begin{aligned} {\mathcal {N}}^1_{\text {log}}{} & {} = p^{13} \bigg (-0.0626084 r^3 {r_{0}}\nonumber \\ {}{} & {} \quad +0.0626084 r^2 {r_{0}}^2+0.0626084 r {r_{0}}^3-0.0626084 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^{12} \bigg (1. r^4-0.782889 r^3 {r_{0}}-0.230599 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -1.21711 r {r_{0}}^3+1.2306 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^{11} \bigg (-18.2212 r^4+29.3638 r^3 {r_{0}}\nonumber \\ {}{} & {} \quad -10.8868 r^2 {r_{0}}^2+7.28478 r {r_{0}}^3-7.54055 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^{10} \bigg (96.59 r^4-177.29 r^3 {r_{0}}+79.5585 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -19.3886 r {r_{0}}^3+20.5203 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^9 \bigg (-234.614 r^4+457.171 r^3 {r_{0}}-221.897 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +23.902 r {r_{0}}^3-24.2931 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^8 \bigg (282.436 r^4-551.051 r^3 {r_{0}}+275.112 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -7.20824 r {r_{0}}^3-1.91936 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^7 \bigg (-133.991 r^4+164.055 r^3 {r_{0}}-46.0945 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -13.4629 r {r_{0}}^3+41.7195 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^6 \bigg (-32.4983 r^4+341.82 r^3 {r_{0}}-300.797 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +12.9375 r {r_{0}}^3-53.4003 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^5 \bigg (34.5271 r^4-420.143 r^3 {r_{0}}+404.167 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +0.0115351 r {r_{0}}^3+31.9943 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^4 \bigg (28.0229 r^4+178.063 r^3 {r_{0}}-241.727 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -4.86976 r {r_{0}}^3-8.90541 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^3 \bigg (-30.9869 r^4-12.6459 r^3 {r_{0}}+69.661 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad +2.21647 r {r_{0}}^3+0.507243 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p^2 \bigg (8.38109 r^4-10.7164 r^3 {r_{0}}-6.17049 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -0.251471 r {r_{0}}^3+0.12598 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +p \bigg (-1.03581 r^4+2.49996 r^3 {r_{0}}-0.826428 r^2 {r_{0}}^2\nonumber \\ {}{} & {} \quad -0.0167726 r {r_{0}}^3+0.0233143 {r_{0}}^4\bigg ) \nonumber \\ {}{} & {} \quad +0.389358 r^4-0.281216 r^3 {r_{0}}+0.0686144 r^2 {r_{0}}^2,\nonumber \\ \end{aligned}$$

(A29)

$$\begin{aligned} {\mathcal {D}}^1_{\text {log}}{} & {} = p^{12} r^2 (1. r^2-2. r {r_{0}}+1. {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^{11} r^2 (-18.2212 r^2+36.6579 r {r_{0}}-18.4367 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^{10} r^2 (96.59 r^2-197.003 r {r_{0}}+100.413 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^9 r^2 (-234.614 r^2+483.3 r {r_{0}}-248.622 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^8 r^2 (282.436 r^2-565.092 r {r_{0}}+281.412 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^7 r^2 (-133.991 r^2+161.605 r {r_{0}}-19.988 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^6 r^2 (-32.4983 r^2+345.678 r {r_{0}}-336.459 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^5 r^2 (34.5271 r^2-417.829 r {r_{0}}+424.172 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^4 r^2 (28.0229 r^2+175.038 r {r_{0}}-246.175 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^3 r^2 (-30.9869 r^2-11.7993 r {r_{0}}+69.4436 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^2 r^2 (8.38109 r^2-10.8149 r {r_{0}}-6.01301 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p r^2 (-1.03581 r^2+2.54012 r {r_{0}}-0.815274 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +r^2 (0.389358 r^2-0.281216 r {r_{0}}+0.0686144 {r_{0}}^2),\nonumber \\ \end{aligned}$$

(A30)

$$\begin{aligned} {\mathcal {N}}^2_{\text {log}}{} & {} = p^9 \bigg (1. r^3-1.5934 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +0.9878 r {r_{0}}^2-0.394399 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^8 \bigg (-11.4341 r^3+18.4084 r^2 {r_{0}} \nonumber \\ {}{} & {} \quad -9.70115 r {r_{0}}^2+2.72685 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^7 \bigg (52.5869 r^3-85.6446 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +40.9887 r {r_{0}}^2-7.89466 {r_{0}}^3\bigg ) \nonumber \\ {}{} & {} \quad +p^6 \bigg (-129.875 r^3+213.791 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad -96.5185 r {r_{0}}^2+12.2873 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^5 \bigg (190.394 r^3-316.075 r^2 {r_{0}} \nonumber \\ {}{} & {} \quad +137.73 r {r_{0}}^2-10.895 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^4 \bigg (-170.683 r^3+284.439 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad -121.325 r {r_{0}}^2+5.25315 {r_{0}}^3\bigg ) \nonumber \\ {}{} & {} \quad +p^3 \bigg (92.159 r^3-152.461 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +64.1216 r {r_{0}}^2-1.0636 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p^2 \bigg (-28.3648 r^3+45.1052 r^2 {r_{0}} \nonumber \\ {}{} & {} \quad -18.6363 r {r_{0}}^2-0.0535942 {r_{0}}^3\bigg )\nonumber \\ {}{} & {} \quad +p \bigg (4.63158 r^3-6.37023 r^2 {r_{0}}\nonumber \\ {}{} & {} \quad +2.46462 r {r_{0}}^2+0.0339455 {r_{0}}^3\bigg ) \nonumber \\ {}{} & {} \quad -0.413973 r^3+0.400205 r^2 {r_{0}}-0.112264 r {r_{0}}^2, \end{aligned}$$

(A31)

$$\begin{aligned} {\mathcal {D}}^2_{\text {log}}{} & {} = p^9 r (1. r^2-1.5934 r {r_{0}}+0.593401 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^8 r (-11.4341 r^2+18.4084 r {r_{0}}-6.9743 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^7 r (52.5869 r^2-85.6446 r {r_{0}}+33.0761 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^6 r (-129.875 r^2+213.791 r {r_{0}}-84.1127 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^5 r (190.394 r^2-316.075 r {r_{0}}+126.509 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^4 r (-170.683 r^2+284.439 r {r_{0}}-115.594 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p^3 r (92.159 r^2-152.461 r {r_{0}}+62.6652 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +p^2 r (-28.3648 r^2+45.1052 r {r_{0}}-18.518 {r_{0}}^2) \nonumber \\ {}{} & {} \quad +p r (4.63158 r^2-6.37023 r {r_{0}}+2.46727 {r_{0}}^2)\nonumber \\ {}{} & {} \quad +r (-0.413973 r^2+0.400205 r {r_{0}}-0.112264 {r_{0}}^2).\nonumber \\ \end{aligned}$$

(A32)