1 Introduction

In the present cosmological context [1,2,3,4], the accelerated expansion [5] plays a fundamental role, opening a variety of research directions in science and technology. Although the accelerated expansion has been discovered at the end of the last millennium [6, 7], it remained an open problem [8] in cosmological theories, driving the background dynamics of the Universe. This phenomenon, coined as dark energy, has been probed using different observational techniques [9,10,11,12,13,14,15]. The simplest possible theoretical model is the \(\Lambda \)CDM model [16], a cosmological scenario which extends the Einstein–Hilbert action by adding a cosmological constant \(\Lambda \), leading to a theoretical representation having a constant equation of state [17]. The \(\Lambda \)CDM model can explain the dark energy phenomenon at the level of background dynamics [18, 19], representing a possible theoretical representation as an approximate effective theory. However, this model is not fully compatible to the evolution of the Universe [20,21,22,23,24] and cannot explain several properties of the dark energy equation of state [25,26,27,28]. Consequently, various scalar tensor theories of gravitation have been proposed [29,30,31,32,33], aiming towards a more complete theory of gravitation compatible to the evolution of our Universe [30].

In these theories the f(R) model appeared as a natural extension [34,35,36], based on the scalar curvature. This model can explain different aspects related to the evolution of the Universe, representing a possible direction in scalar tensor theories [37, 38]. Later, various theories have appeared, based on different specific invariants [39,40,41,42,43,44]. Another particular representation is related to the presence of scalar fields [45,46,47,48,49,50], specific components which are also compatible to the accelerated expansion, driving the dark energy phenomenon. These fields can also be coupled to different specific invariants, in a non–minimally representation [51,52,53,54,55]. Hence, in the modified gravity theories, the accelerated expansion represents a curious phenomenon which is compatible to different representations [56], a compatibility acting on the fundamental geometry of space and time.

In the modified gravity theories a specific model has been developed recently, denoted as the Einsteinian cubic gravity [57]. This model was introduced in an attempt of obtaining a more general theory of gravitation, by considering a linearization technique [57]. Furthermore, a more generic gravity theory in a four dimensional space–time has been proposed [58], a specific model which can explain the current accelerated expansion of the Universe. The dynamical analysis [59] for such a theory has been investigated in Refs. [60,61,62], analyzing specific properties of the background expansion. The inclusion of higher order invariants in the gravity theories has attracted a lot of attention in the recent years [63,64,65,66,67,68,69]. In Ref. [70] the authors have considered different data sets, constraining the generic f(P) cubic gravity theories using a machine learning approach. Also, the non–minimal coupling of the scalar fields with cubic invariants has been investigated recently [71,72,73]. The inclusion of such higher order terms has applications in the inflationary epoch [74,75,76,77], in the study of black holes solutions [78,79,80,81], with various ramifications in different aspects of cosmological theories [82,83,84].

In modified gravity theories [16] a particular characteristic is related to astrophysical observations, analyzing the compatibility between the predicted values and the specific late time observations. Hence, the ability of the corresponding models to act closely and in a compatible manner with recent observations [85] is a crucial aspect. In recent years several works [86,87,88,89,90,91] were dedicated to the study of modified gravity theories by considering an observational perspective. Recently, in Ref. [86] Big Bang nucleosynthesis has been considered in the observational study of a particular modified gravity theory in teleparallel gravity. Another approach is related to the black hole formation in the early radiation epoch [92]. Furthermore, gravitational waves can be used as a probe for modified gravity theories [93], distinguishing the viable theories from an observational perspective. Moreover, N–body simulations [94] can be used together with cosmological data in order to investigate several properties related to the structure formation. In [95] the authors use a variety of cosmological probes (CMB, BAO, Pantheon data from Supernovae Type Ia, RSD) for the analysis of observational constraints in the case of specific dark matter and dark energy models. As can be noted, in the recent literature several approaches have been dedicated to the study of modified gravity theories from the viewpoint of astrophysical observations, representing an important tool associated to the accelerated expansion phenomenon.

In the present paper we shall further investigate the cubic gravity theory by adopting an observational perspective [96], considering different data sets, based on cosmic chronometers (CC), baryon acoustic oscillations (BAO), and supernovae (SNe). The approach will analyze the extension of the \(\Lambda \)CDM model towards a higher order gravity theory, considering a linear representation which takes into account a cubic invariant based on third order contractions of the Riemann tensor. This enables us to further examine the physical implications of such higher order terms in this geometric setup, obtaining viable constraints from the viewpoint of current observations. Hence, our model is based on a particular extension of the Einstein–Hilbert action, embedding viable geometrical manifestations in the proposed action, originating from specific cubic components [96, 97]. As discussed in [61] the cubic components are expected to influence the dynamics at early times, while at late times the cosmological constant mainly drives the accelerated expansion. In this regard, the non–negligible deviations from the \(\Lambda \)CDM model which are compatible with recent observations might result from higher order geometrical corrections.

The paper is organized as follows. In Sect. 2 we briefly discuss the present extension of the \(\Lambda \)CDM model, presenting the corresponding fields equations which are obtained by varying the action with respect to the inverse metric. Then, in Sect. 3 we discuss the basic ingredients used in order to apply the Markov–Chain–Monte–Carlo (MCMC) sampling, analyzing the obtained results. Lastly, in Sect. 4 we give a short summary and the final concluding remarks.

2 The cosmological model

In the following, we shall briefly present the cosmological model studied in the manuscript. We have considered a higher order extension of the \(\Lambda \)CDM model by embedding a specific cubic invariant in the corresponding action, based on third order contractions of the Riemann tensor. Hence, the theoretical scenario is assumed to be described by the following action [57, 58]:

$$\begin{aligned} S=S_m+\int d^4x \sqrt{-g} \Bigg ( \frac{1}{2}(R-2 \Lambda )+\alpha P\Bigg ), \end{aligned}$$
(1)

where \(S_m\) represents the action corresponding to the matter component, R the scalar curvature, \(\alpha \) a constant parameter, and P a higher order invariant which encodes the specific third order contractions of the Riemann tensor,

$$\begin{aligned} P= & {} \beta _1 R_{\mu \quad \nu }^{\quad \rho \quad \sigma }R_{ \rho \quad \sigma }^{\quad \gamma \quad \delta }R_{\gamma \quad \delta }^{\quad \mu \quad \nu }+\beta _2 R_{\mu \nu }^{\rho \sigma }R_{\rho \sigma }^{\gamma \delta }R_{\gamma \delta }^{\mu \nu }\nonumber \\{} & {} +\beta _3 R^{\sigma \gamma }R_{\mu \nu \rho \sigma }R_{\quad \quad \gamma }^{\mu \nu \rho }+\beta _4 R R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }\nonumber \\{} & {} +\beta _5 R_{\mu \nu \rho \sigma }R^{\mu \rho }R^{\nu \sigma } \nonumber \\{} & {} +\beta _6 R_{\mu }^{\nu }R_{\nu }^{\rho }R_{\rho }^{\mu }+\beta _7 R_{\mu \nu }R^{\mu \nu }R+\beta _8 R^3. \end{aligned}$$
(2)

In the previous relation \(\beta _i\) (\(i={1,..,8}\)) are constant coefficients specific to the cubic gravity theory. As can be seen, the model extends the fundamental Einstein–Hilbert scenario by considering non–negligible cubic components in the proposed action. If we take into account the following relations [57, 58],

$$\begin{aligned} \beta _7= & {} \frac{1}{12}\big [3\beta _1-24\beta _2-16\beta _3-48\beta _4-5\beta _5-9\beta _6\big ], \end{aligned}$$
(3)
$$\begin{aligned} \beta _8= & {} \frac{1}{72}\big [-6\beta _1+36\beta _2+22\beta _3+64\beta _4+3\beta _5+9\beta _6\big ], \end{aligned}$$
(4)
$$\begin{aligned} \beta _6= & {} 4\beta _2+2\beta _3+8\beta _4+\beta _5, \end{aligned}$$
(5)

we obtain the specific cubic gravity theory which encodes third order contractions of the Riemann tensor. In this case we use the specific redefinition,

$$\begin{aligned} {\bar{\beta }}=(-\beta _1+4\beta _2+2\beta _3+8\beta _4), \end{aligned}$$
(6)

obtaining the following representation for the higher order term [57, 58]:

$$\begin{aligned} P=6{\bar{\beta }}H^4 (2H^2+3\dot{H}), \end{aligned}$$
(7)
Fig. 1
figure 1

The posterior distributions for the relevant cosmological parameters in the case of cosmic chronometers and baryon acoustic oscillations observations

Full size image

in the case of a homogeneous and isotropic Universe characterized by the Robertson–Walker metric,

$$\begin{aligned} ds^2=-dt^2+a^2(t) \delta _{ik}dx^i dx^k, \end{aligned}$$
(8)

with a(t) the cosmic scale factor. As can be noted, the action that we are proposing extends the \(\Lambda \)CDM model by embedding higher order corrections based on specific third order contractions of the Riemann tensor. The cubic term added in the action represents a non-topological invariant constructed in such a way that leads to second order Friedmann equations. Hence, the Eqs. (3)–(6) assure compatibility between the specific form of the higher order term and the requirements related to a second order theory. Note that in the final representation of the higher order invariant the terms containing \(\beta _5\) parameter cancel out, leading to a simple expression of the non-topological component. If we consider the variation of the previous action (1) with respect to the inverse metric, we obtain the following modified Friedmann relations [57, 58]:

$$\begin{aligned}{} & {} 3H^2=\rho _m+\rho _{g}, \end{aligned}$$
(9)
$$\begin{aligned}{} & {} 3H^2+2\dot{H}=-p_m-p_{g}, \end{aligned}$$
(10)

with \(\rho _g\) the density of the geometrical dark energy component, and \(p_g\) the corresponding pressure,

$$\begin{aligned} \rho _g= & {} 6 \alpha {\bar{\beta }} H^6 +\Lambda \end{aligned}$$
(11)
$$\begin{aligned} p_g= & {} -6 \alpha {\bar{\beta }} H^4 (H^2+2 \dot{H})-\Lambda . \end{aligned}$$
(12)

Note that the final field equations in the covariant form are not displayed in the manuscript, due to the complex form of formulas involved. The dedicated reader can find the final field equations in the Appendix of Ref. [58]. Moreover, for this model the standard continuity equation is satisfied. In what follows we can redefine the specific cubic constant, \(\beta =\alpha {\bar{\beta }}\), obtaining simpler expressions for the previous relations. Finally, we can write the associated density parameters as usual,

$$\begin{aligned} \Omega _m= & {} \frac{\rho _m}{3 H^2}, \end{aligned}$$
(13)
$$\begin{aligned} \Omega _g= & {} \frac{\rho _g}{3 H^2}, \end{aligned}$$
(14)

satisfying the corresponding constraint,

$$\begin{aligned} \Omega _m+\Omega _g=1. \end{aligned}$$
(15)
Fig. 2
figure 2

One dimensional posterior distribution for the \(\beta \) parameter in the case of CC + BAO observations

Full size image
Fig. 3
figure 3

The variation of the Hubble parameter in the case of CC + BAO observations

Full size image
Fig. 4
figure 4

The evolution of the dark energy equation of state for the best fitted values in the case of CC + BAO observations

Full size image

3 Observational properties for the cubic gravity theory

3.1 Generic properties

In order to study the higher order gravity theory from an observational perspective, we need to express the dynamical equations in a comprehensible manner. Combining the Eqs. (9) and (10), we arrive at the following expression:

$$\begin{aligned} -3 H^2+6 \beta H^6+\Lambda =\dot{H}(2-12 \beta H^4). \end{aligned}$$
(16)

Next, we introduce the redshift variable defined as:

$$\begin{aligned} z(t)=\frac{1}{a(t)}-1, \end{aligned}$$
(17)

changing the dependence from the cosmic time to redshift. In this case, the time derivative of the Hubble parameter can be expressed as follows:

$$\begin{aligned} \dot{H}=(-H)H'(1+z), \end{aligned}$$
(18)

where the prime indicates the derivative with respect to the redshift variable. The Eq. (16) takes the following form:

$$\begin{aligned} 3 H^2-6 \beta H^6-\Lambda =H H' (1+z)(2-12 \beta H^4). \end{aligned}$$
(19)

Next, we introduce the dimensionless Hubble parameter defined as:

$$\begin{aligned} E(z)=\frac{H(z)}{H_0}, \end{aligned}$$
(20)

expressing the evolution of the cosmological system in an autonomous manner,

$$\begin{aligned} E'=\frac{3 H_0^2E^2-6 \beta E^6 H_0^6-\Lambda }{E H_0^2(1+z)(2-12 \beta E^4 H_0^4)}. \end{aligned}$$
(21)

We now introduce the density parameter associated to the cosmological constant \(\Lambda \) at the present time,

$$\begin{aligned} \Omega _{\Lambda }=\frac{\Lambda }{3 H_0^2}, \end{aligned}$$
(22)

the density parameter for the matter component,

$$\begin{aligned} \Omega _{m0}=\frac{\rho _m(z=0)}{3 H_0^2}, \end{aligned}$$
(23)

and the density parameter corresponding to the higher order corrections of the \(\Lambda \)CDM model,

$$\begin{aligned} \Omega _{c0}=2 \beta H_0^4, \end{aligned}$$
(24)

satisfying the following constraint at \(z=0\):

$$\begin{aligned} \Omega _{m0}+\Omega _{\Lambda }+ \Omega _{c0}=1. \end{aligned}$$
(25)

Hence, the evolution of the dynamical cosmological system can be expressed as follows:

$$\begin{aligned} E'=\frac{3 E^2-6 \beta E^6 H_0^4-3\Omega _{\Lambda }}{2 E (1+z)(1-6 \beta E^4 H_0^4)}. \end{aligned}$$
(26)

In order to emulate the evolution of the cosmological model we solve the ordinary differential Eq. (26) taking into account that at the present time (\(z=0\)) we have the initial condition,

$$\begin{aligned} E(z=0)=\frac{H(z=0)}{H_0}=1. \end{aligned}$$
(27)

As can be noted, the corresponding evolution (26) depends on the present value of the Hubble parameter (\(H_0\)), the current density parameter associated to the cosmological constant \(\Lambda \), and the \(\beta \) parameter, a constant expressing the strength of the higher order corrections based on third order contractions of the Riemann tensor.

In order to study the present cosmological model, we have considered specific observations based on cosmic chronometers (CC), baryon acoustic oscillations (BAO), and Ia supernovae (SNe). This allows us to further constrain the corresponding free parameters in the Eq. (26), \((H_0, \Omega _{\Lambda }, \beta )\). For the observational analysis, we have considered data from CC, BAO, and SNe [96], obtaining possible viable constraints associated to the higher order corrections due to the specific contractions of the Riemann tensor. In our analysis we have defined the associated chi-squared functions. For the CC + BAO data the chi-square has the following form:

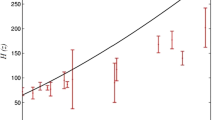
$$\begin{aligned} \chi ^2_{CC+BAO}=\sum _{i=1}^{31(CC)+26(BAO)}\left( \frac{H_o(z_i)-H_m(z_i)}{\sigma _{i}}\right) ^2, \end{aligned}$$
(28)

where \(H_o\) represents the observed value of the Hubble parameter having the corresponding uncertainty \(\sigma _i\) at the redshift \(z_i\), while \(H_m\) denotes the value obtained from the present cosmological model (obtained by numerical evolution of the Eq. (26)). The results of the Markov chain Monte-Carlo sampling for the CC + BAO data have been presented in Figs. 1, 2, 3 and 4. In order to obtain these figures, we have used the Cobaya package [96, 98] considering the following value for the Gelman-Rubin criterion \(R-1=0.001\). Secondly, for the CC + BAO + SNe dataset we have further defined a more general chi–square function,

$$\begin{aligned} \chi ^2_{CC+BAO+SNe}=\chi ^2_{CC+BAO}+\chi ^2_{SNe}, \end{aligned}$$
(29)

where

$$\begin{aligned} \chi ^2_{SNe}= & {} \sum _{z_1}\sum _{z_2} \left( m_o(z_1)-m_m(z_1))\right) C^{-1}(z_1,z_2)(m_o(z_2)\nonumber \\{} & {} -m_m(z_2)), \end{aligned}$$
(30)

with m the apparent magnitude having the specific covariance matrix \(C(z_1,z_2)\). As in the previous case, the subscript (o) is associated to the observations, while (m) corresponds to the values obtained using the present cosmological model [96, 98]. For the second sampling, in the case of CC + BAO + SNe data set, we have used 1048 supernovae type Ia events from the Pantheon data [99]. The results of the second analysis are presented in Figs. 5, 6, 7, 8, 9 and 10. In what follows we shall briefly discuss the obtained results specific for the higher order contractions of the Riemann tensor. In Fig. 1 we present the posterior distributions and the corresponding confidence intervals for the higher order corrections of the \(\Lambda \)CDM model by taking into account data from cosmic chronometers and baryon acoustic oscillations. In this case we note that the density parameter associated to the matter content \(\Omega _{m0}\) has a higher value, while the density parameter corresponding to the higher order corrections \(\Omega _{c0}\) is negative and \(\propto 10^{-3}\). In Fig. 2 we present one dimensional distribution associated to the \(\beta \) parameter, observing that \(\beta \propto 10^{-11}\). The variation of the best fitted value corresponding to the Hubble parameter is presented in Fig. 3, while the corresponding equation of state for the geometrical dark energy component is displayed in Fig. 4. From the evolution of the geometrical dark energy equation of state (\(w_g=p_g / \rho _g\)) we observe that at late times the plot follows closely the \(\Lambda \)CDM model, while at early time the deviation corresponds to a super–accelerated regime. The best fitted values obtained suggest that the main source of cosmic acceleration is related to the cosmological constant, while the higher order corrections based on the third order contractions of the Riemann tensor represent the origin of the super–accelerated regime, explaining the early times dynamics and the non–negligible deviations from the phantom divide line in the near past.

Fig. 5
figure 5

The posterior distributions for the relevant cosmological parameters in the case of CC + BAO + SNe observations

Full size image

For the CC + BAO + SNe observations we have presented the corresponding confidence intervals in Fig. 5, observing that the value of the present Hubble parameter is higher in this case (as compared to CC + BAO data set), having a lower value of the matter density parameter (\(\Omega _{m0}\)) at the present time. The results indicate that the density parameter corresponding to the higher order contractions of the Riemann tensor is negative and non–negligible, closely proportional to \(\Omega _{c0} \propto 10^{-3}\). The result is almost consistent with the CC + BAO data set, suggesting a compatibility between the two data sets. Furthermore, from Fig. 6 we see that the value of the \(\beta \) parameter is \(\propto 10^{-11}\), a result consistent with the previous data set. In Fig. 7 we have displayed the associated one dimensional posterior distribution for the absolute magnitude. Next, in Figs. 8 and 9 we have showed the compatibility of the best fitted results with respect to observations, for the variation of the associated Hubble parameter and the corresponding apparent magnitude. Lastly, in Fig. 10 we have displayed the evolution of the dark energy equation of state, observing the presence of the super–accelerated regime in the near past. The results are consistent with the CC + BAO data sets, noting that for the Pantheon data the regime is less super–accelerated. The obtained values for the two data sets are also displayed in Table 1, summarizing the present results. The evolution of the matter density parameter is presented in Fig. 11 for the best fitted values in the case of CC+BAO and CC+BAO+Sne observations.

Fig. 6
figure 6

One dimensional posterior distribution for the \(\beta \) parameter in the case of CC + BAO + SNe observations

Full size image

We have also calculated the specific values of the Akaike information criterion (AIC),

$$\begin{aligned} AIC=2 k -2 Log(L_{max}), \end{aligned}$$
(31)

and Bayesian information criterion (BIC),

$$\begin{aligned} BIC=k Log (N) -2 Log(L_{max}). \end{aligned}$$
(32)

In these formulas \(L_{max}\) denotes the maximum likelihood, N is associated to data, while k corresponds to the number of parameters in the sampling. The results are shown in Table 3, where the displayed results are obtained by subtracting the corresponding value from the result specific to the \(\Lambda \)CDM model. The results show that from the viewpoint of \(\chi ^2\) statistic and the Akaike information criterion the present model is preferred with respect to the \(\Lambda \)CDM model. This result is valid for the two data sets, CC + BAO, and CC + BAO + SNe. However, considering the Bayesian information criterion, the situation is different. For CC + BAO data, the model is slight better than the \(\Lambda \)CDM model, while for the Pantheon systematic the \(\Lambda \)CDM model is still favored. As can be seen, those two data sets are in tension with each other, affecting the obtained results. Hence, the present model is favored by the data coming from cosmic chronometers and baryon acoustic oscillations. The extension of the \(\Lambda \)CDM model towards the higher order gravity theories based on third order contractions of the Riemann tensor represents a possible and viable scenario which can explain the accelerated expansion, with the main source of cosmic acceleration driven by the cosmological constant.

Fig. 7
figure 7

One dimensional posterior distribution for the M parameter in the case of CC + BAO + SNe observations

Full size image
Fig. 8
figure 8

The variation of the Hubble parameter in the case of CC + BAO + SNe observations

Full size image
Fig. 9
figure 9

The variation of the apparent magnitude of the supernovae in the case of the best fitted values of the cubic model for CC + BAO + SNe observations (left panel). The \(\Lambda \)CDM model is presented in the right panel

Full size image

3.2 Cosmographic parameters

In what follows, we shall discuss the evolution of several cosmographic parameters, analyzing different dynamical properties. Before proceeding, we note that the cosmographic analysis is a very important tool in the study of cosmological systems, describing various dynamical effects. The first cosmographic parameter is the deceleration parameter, defined as follows:

$$\begin{aligned} q=-1+(1+z)\frac{H'}{H}. \end{aligned}$$
(33)

Here the prime \('\) denotes differentiation with respect to the redshift variable. The evolution of the deceleration parameter is presented in Fig. 12. For this, we can note that a positive value is associated to a deceleration epoch, while a negative one implies cosmic acceleration at the level of background dynamics. The late time acceleration of the Universe is clearly presented in the figure, observing some specific deviations at early times.

The second dynamical measure is represented by the jerk parameter,

$$\begin{aligned} j=1-2(1+z)\frac{H'}{H}+(1+z)^2\frac{{H'}^2}{H^2}+(1+z)^2 \frac{H''}{H}. \end{aligned}$$
(34)

For this parameter the sign is very important, being associated to transitive dynamical effects. Hence, a transitive epoch of the Universe at the level of background dynamics corresponds to a positive sign. The evolution of the jerk parameter appears in Fig. 13. We note that the current value of \(j_0=1\), acting closely near the cosmological constant boundary value. However, at early time the dynamical evolution is quite different if cubic constraints are taken into consideration.

The snap parameter

$$\begin{aligned} s= & {} 1-3(1+z)\frac{H'}{H}+3(1+z)^2\frac{{H'}^2}{H^2}+(1+z)^3\frac{{H'}^3}{H^3}\nonumber \\{} & {} +(-4)(1+z)^3 \frac{H'H''}{H^2}+(1+z)^2\frac{H''}{H}-(1+z)^3\frac{H'''}{H},\nonumber \\ \end{aligned}$$
(35)

involves the values of higher order derivatives, describing possible deviations from the \(\Lambda \)CDM model, depicted in Fig. 14. A clear distinction is observed in the case of CC+BAO data, since the sign of the corresponding parameter is switched in the late stages of evolution.

The Om(z) diagnostic represents a specific measure defined as follows:

$$\begin{aligned} Om(z)=\frac{E^2-1}{(1+z)^3-1}, \end{aligned}$$
(36)

presented in Fig. 15. For this, we can note that the model acts closely as the \(\Lambda \)CDM model in the case of CC+BAO+SNe observations, with non negligible deviations in the case of CC+BAO data, acting closely as a phantom field. The graph is consistent with the evolution of the dark energy equation of state, indicating that the model acts closely as a cosmological constant at late times, without crossing the phantom divide line boundary in the near past.

Fig. 10
figure 10

The dark energy equation of state for the best fitted values in the case of CC + BAO + SNe observations

Full size image
Table 1 The confidence intervals for the higher order gravity theory based on cubic contractions of the Riemann tensor
Full size table
Table 2 The confidence intervals for the \(\Lambda \)CDM model
Full size table
Table 3 The AIC and BIC values corresponding to the present cosmological scenario
Full size table
Fig. 11
figure 11

The evolution of the matter density parameters for the best fitted values in the case of CC + BAO / CC + BAO + SNe observations

Full size image
Fig. 12
figure 12

The evolution of the deceleration parameter for the best fitted values in the case of CC + BAO / CC + BAO + SNe observations

Full size image
Fig. 13
figure 13

The evolution of the jerk parameter for the best fitted values in the case of CC + BAO / CC + BAO + SNe observations

Full size image
Fig. 14
figure 14

The evolution of the snap parameter for the best fitted values in the case of CC + BAO / CC + BAO + SNe observations

Full size image
Fig. 15
figure 15

The evolution of the Om diagnostic for the best fitted values in the case of CC + BAO / CC + BAO + SNe observations

Full size image

4 Summary and conclusions

In the present paper we have studied a modified gravity theory which extends the fundamental \(\Lambda \)CDM model by embedding viable geometrical constituents based on third order contractions of the Riemann tensor. This cosmological model represents a novel approach in the modified gravity theories, taking into account a specific invariant which leads to second order equations in the Friedmann relations. After briefly describing the proposed action and the corresponding modified Friedmann relations, we have introduced the dimensionless Hubble parameter, expressing the evolution of the dynamical system in a proper manner. The present study is devoted to the analysis of the particular extension of the \(\Lambda \)CDM model from an observational perspective, investigating specific viable constraints for the cubic gravity model in the linear order. The analysis takes into account data from cosmic chronometers, baryon acoustic oscillations, and supernovae of Ia type as the Pantheon data set. After expressing the corresponding \(\chi ^2\) specific functions, we have used the Cobaya package for the Markov chain Monte-Carlo sampling. The results of our analysis have been discussed in the previous sections for the CC + BAO and CC + BAO + SNe data sets.

From the statistical analysis it is clear that a realistic modified gravity theory should go beyond the \(\Lambda \)CDM model, the simplest cosmological scenario. In our approach we have considered higher order terms in the proposed action, based on third order contractions of the Riemann tensor. In the previous section we have seen that in the case of CC + BAO and CC + BAO + SNe data sets, the inclusion of such higher order terms is mildly preferred and fully compatible to recent cosmological data. However, the problem of \(H_0\) tension is still present in the current analysis, due to the deviations of the corresponding observables.

In the case of CC + BAO data set we have observed that the values corresponding to the best fitted parameters are comparable with the specific values for the \(\Lambda \)CDM model. Hence, the value of the present Hubble parameter \(H_0\) is quite lower for the CC + BAO data set, while the matter density parameter at the present time \(\Omega _{m0}\) has a higher value. The density parameter associated to the higher order contractions of the Riemann tensor \(\Omega _{c0}\) is negative, with the \(\beta \) parameter negative and proportional to \(\beta \propto 10^{-11}\). All of these suggests that the present higher order extension of the \(\Lambda \)CDM model acts in the early evolution of the Universe, diminishing the accelerated expansion in the early matter era. This is consistent with the study of phase–space structure performed in [61], the de–Sitter attractor is mainly driven by the cosmological constant term. It is also interesting to note that the dark energy equation of state associated to the geometrical component has a phantom behavior, without the inclusion of the scalar fields with a negative kinetic energy.

The results for the CC + BAO + SNe data sets show that the inclusion of the higher order contractions of the Riemann tensor leads to a slightly lower value for the Hubble parameter at the present time (compared to the \(\Lambda \)CDM model). Moreover, the best fitted value for the matter density parameter \(\Omega _{m0}\) is higher with respect to the corresponding value specific for the \(\Lambda \)CDM model, suggesting that the inclusion of the cubic components slightly moderate the accelerated expansion in the near past. The present analysis has also considered the Akaike information criterion and the Bayesian information criterion for the previous mentioned data sets. We note that for the Akaike information criterion the inclusion of cubic contractions of the Riemann tensor is slightly preferred for the two data sets. However, in the case of Bayesian information criterion the results are not conclusive. For the CC + BAO data, the higher order contractions of the Riemann tensor are very slightly preferred, while for the Pantheon data the \(\Lambda \)CDM model is still favored. We mention that for the CC + BAO + SNe data sets the geometrical dark energy component has a phantom behavior, acting bellow the cosmological constant boundary. However, the inclusion of the Pantheon data moderate the cosmic expansion, with the corresponding variation less accelerated. In this case the value of the density parameter associated to the higher order contractions of the Riemann tensor \(\Omega _{c0}\) is still negative and comparable to the previous values.

The present cosmological model can be further extended in a variety of approaches. For example, one can consider an extension of the corresponding action beyond the linear order, discussing the full compatibility of the f(P) gravity theory with different observations. Moreover, the statistical analysis can also take into account various data sets, defining a more stringent \(\chi ^2\) function. This would allow us to obtain a more realistic theoretical model which includes higher order terms fully compatible to recent cosmological data. All of these questions are open and left for a different investigation in the near future.