Massive scalar field perturbations of black holes surrounded by dark matter

Abstract

We consider scalar field perturbations in the background of black holes immersed in perfect fluid dark matter (PFDM). We find, by using the sixth-order Wentzel–Kramers–Brillouin (WKB) approximation, that the longest-lived modes are those with a higher angular number for a scalar field mass smaller than a critical value, known as the anomalous decay rate of the quasinormal modes, while beyond this critical value the opposite behavior is observed. Moreover, we show that it is possible to recover the real part of the quasinormal frequencies (QNFs), the imaginary part of the QNFs, and the critical scalar field mass of the Schwarzschild background for different values of the PFDM intensity parameter k. For values of k smaller than these values, the abovementioned quantities are greater than the Schwarzschild background. However, beyond these values of k, these quantities are smaller than the Schwarzschild background.

1 Introduction

The recent observations of gravitational waves (GWs) produced as a result of the relativistic collision of two compact objects have opened up the possibility of studying the nature and properties of compact objects. In the near future, following the recent LIGO detections [1,2,3,4,5], GW astronomy will provide us a better understanding of the gravitational interaction and astrophysics of these objects. The recent observations do not yet probe the detailed structure of the spacetime of compact objects beyond the photon sphere; however, one expects that the properties of these objects will be revealed in the years to come with future GW observations. In particular, the expectation is to precisely detect the ringdown phase, which is governed by a series of damped oscillatory modes at early times, known as quasinormal modes (QNMs) [6,7,8,9]. It is expected that the future GW observations will provide some information on the nature and physics of the near-horizon region of black holes (BHs). The existence of any structure at near-horizon scales would generate a series of “echoes” of the primary gravitational wave signal produced during the ringdown phase [10, 11].

In general relativity, one of the most important compact objects is the BH, and one of the most distinguishable features of BHs is the event horizon. The event horizon, which is a causal boundary, prevents us from entering the BH. Black holes in our Universe may be affected by astronomical environments, such as dark matter (DM) near BHs [12,13,14]. It is believed that 90% of galaxies are composed of DM [15]. The abnormally high velocities of stars at the outskirts of galaxies imply that visible disks of galaxies are immersed in a much larger, roughly spherical halo of DM [16, 17]. DM does not interact with the electromagnetic field, and therefore the propagation of light is possible inside the dark matter halo. Various studies have been performed to determine whether the black hole shadow could be affected by the tidal forces induced by invisible matter ([18,19,20]). However, the results look highly model-dependent, as a particular equation of state was considered for the dark matter. The most reliable way to detect dark matter outside the BH is to study the gravitational wave signal, produced during the ringdown phase, generating a series of echoes. Various models of black holes surrounded by dark matter have been studied [21,22,23,24].

On the other hand, recent astrophysical observations show an accelerating expansion of the Universe [25,26,27], implying the presence of a state with negative pressure. The negative pressure could originate from the presence of a barotropic perfect fluid which corresponds to the dark energy or to the presence of a cosmological constant. The state equation is given by the relation between the pressure p and the energy density $\rho$, $w=p/\rho$, and the recent observations suggest that the equation of state lies in a narrow strip around $w =-1$ [28, 29], where $w =-1$ corresponds to a cosmological constant $\Lambda$ and $w <-1$ is allowed [30, 31]. Considering that the Universe is filled with a barotropic perfect fluid corresponding to dark energy, an equation of state $w <-1$ can be realized with the presence of a phantom field. The phantom dark energy has the property that the dominant energy condition is violated so that the energy density and curvature may grow to infinity in a finite time, which is referred to as the Big Rip singularity [31, 32]. The introduction of dark matter may explain the discrepancy between the predicted rotation curves of galaxies when only including luminous matter and the actual (observed) rotation curves that differ significantly [33,34,35].

A spherical halo of dark matter around the Schwarzschild BH has been considered for testing the gravitational response of black holes in the astrophysical environment [36,37,38], and also for studying the shadow [39]. Dark matter possesses some mass which can be modeled as an additional effective mass in the mass function of a BH. One then expects that the ringdown profile will be modified due to new physics near the surface/event horizon and echoes to be generated due to matter at some distance from the black hole. This allows us to understand how the echoes of the surface of the BH are affected by the astrophysical environment at a distance. We expect the straightforward calculations for the time-domain profiles of such a system to support the expectations that if the echoes are observed, they should most likely be ascribed to some new physics near the event horizon rather than some “environmental” effect. An exact and fully relativistic solution of the Einstein field equations was discussed in [40] which describes a black hole in the center of an anisotropic dark matter halo without the need for adding any Newtonian potential for the dark matter, and metric perturbations in these spacetimes were also studied [41].

Static, spherically symmetric exact solutions of Einstein equations with the quintessential matter having a negative equation of state surrounding a black hole charged or not was presented in [42, 43]. A condition of additivity and linearity in the energy–momentum tensor was introduced, allowing us to obtain the known solutions for the electromagnetic static field, implying a relativistic relation between the energy density and pressure. A real phantom field minimally coupled to gravity was introduced in [44], with the aim of investigating the possibility that galactic dark matter exists in a scenario with a phantom field responsible for the dark energy, where there is a static and spherical approximate solution for this kind of the galaxy system with a supermassive black hole at its center. The phantom field defined in an effective theory is valid only at low energies, in order to avoid the well-known quantum instability of the vacuum at high frequencies.

The aim of this work is to study the propagation of massive scalar fields in a BH spacetime surrounded by perfect fluid dark matter (PFDM) for the highest values of $\ell$ in order to see whether there is an anomalous decay rate of QNMs for the photon sphere modes [45]. The QNMs give an infinite discrete spectrum which consists of complex frequencies, $\omega = \omega _R + i\omega _I$, where the real part $\omega _R$ determines the oscillation timescale of the modes, while the complex part $\omega _I$ determines their exponentially decaying timescale. If the background consists of Schwarzschild and Kerr BHs, it is found that for gravitational perturbations, the longest-lived modes are always those with the lowest angular number $\ell$. This is understood from the fact that the more energetic modes with a high angular number $\ell$ would have faster decay rates. The anomalous behavior occurs when the longest-lived modes are those with the highest angular number, and this can occur with a massive probe scalar field. There is a critical mass of the scalar field where the behavior of the decay rate of the QNMs is inverted and can be obtained from the condition $\mathrm{{Im}}(\omega )_{\ell }=\mathrm{{Im}}(\omega )_{\ell +1}$ in the eikonal limit, that is, when $\ell \rightarrow \infty$. The anomalous behavior in the quasinormal frequencies (QNFs) is possible in asymptotically flat, asymptotically de Sitter (dS), and asymptotically anti-de Sitter (AdS) spacetime; however, we observed that the critical mass exists for asymptotically flat and asymptotically dS spacetime, and it is not present in asymptotically AdS spacetime for large and intermediate BHs. Such behavior has also been studied for scalar fields [46,47,48,49,50,51,52,53,54,55] as well as charged scalar fields [56, 57] and fermionic fields [58]. The anomalous decay in accelerating black holes was studied in [59].

The QNMs for a massless scalar field and their connection to the shadow radius in the background of a modified Schwarzschild BH were studied in [60]. Modification of the background BH was due to the presence of the PFDM surrounding the BH encoded by the parameter k. It was shown that the QNM spectra deviate from those of a Schwarzschild BH due to the presence of the PFDM. Moreover, for any $k > 0$, the real part and the absolute value of the imaginary part of the QNFs increase, which means that the field perturbations in the presence of PFDM decay more rapidly compared to a Schwarzschild vacuum BH. It was also shown that there exists a reflecting point $k_0$ corresponding to maximal values for the real part of QNM frequencies. Namely, as the PFDM parameter k increases in the interval $k < k_0$, the QNFs increase and reach their maximum values at $k = k_0$. In addition, it was shown that $k_0$ is also a reflecting point for the shadow radius. In the physical context, QNFs are associated with the value of the effective potential and its derivatives evaluated at its maximum point. For asymptotically flat black holes, this radius corresponds to the radius of the photon sphere or the radius of unstable null geodesics. Furthermore, as shown in [45], utilizing the Wentzel–Kramers–Brillouin (WKB) approximation and establishing the connection between unstable null geodesics and QNFs in the eikonal limit, the following relation was found for the real part of the QNFs: $\omega _\mathrm{{real}}=l\sqrt{\frac{f(r_{c})}{r_{c}^{2}}}$, where $r_{c}$ is the radius of unstable null geodesics or the photon sphere. Additionally, it was demonstrated in [60,61,62,63] that the black hole shadow radius can be related to the real part of QNFs in the eikonal limit: $\omega _\mathrm{{real}}=\frac{l}{R_{s}}$, where $R_{s}=\frac{r_{c}}{\sqrt{f(r_{c})}}$. As indicated in the article [60], the shadow radius attains its lowest value for $k=k_{0}=0.81$, which, according to the expression for $\omega _\mathrm{{real}}$, corresponds to the largest quasinormal oscillation (real part). This aligns with the results obtained with the WKB method. It is worth noting that if the event horizon decreases, it will lead to a reduction in the shadow radius and, consequently, higher values for the oscillation frequencies.

However, the analysis in [60] was carried out for low values of $\ell$, and it is known that the WKB method provides better accuracy for larger $\ell$ (and $\ell > n$, where n is the overtone). In this study, we consider larger values of $\ell$, and we show that there is a value of the parameter k for which the real part of the QNFs is maximum, which is associated with a reflecting point in the context of the BH shadow. Additionally, our results show that there is a value of the parameter k for which the absolute value of the imaginary part of the QNFs is greatest. As we will see, there is a value of $k \ne 0$ that reproduces the real and the imaginary part of the QNFs of the Schwarzschild background separately, but there is not a value of k that can reproduce the same QNF as that of the Schwarzschild background. Also, we show the existence of an anomalous behavior of the decay rate for the background considered. Moreover, there is a value of $k \ne 0$ that reproduces the critical scalar field mass of the Schwarzschild background.

The work is organized as follows. In Sect. 2, we give the setup of the theory. Then, in Sect. 3, we study the scalar perturbations, and in Sect. 4, we study the photon sphere modes. Finally, conclusions and final remarks are presented in Sect. 5.

2 The setup of the theory

One of the first works that discussed static spherically symmetric exact solutions of Einstein equations with the dark matter surrounding a black hole was in [42]. A condition of additivity and linearity in the energy–momentum tensor was introduced, which allows one to obtain correct limits to the known solutions implying the relativistic relation between the energy density and pressure. The solution which was found is

$$\begin{aligned} \textrm{d}s^2= & {} \left[ 1-\frac{r_g}{r}-\sum _n \left( \frac{r_n}{r} \right) ^{3w_n+1} \right] \,\textrm{d}t^2\nonumber \\{} & {} -\frac{\textrm{d}r^2}{\displaystyle \left[ 1-\frac{r_g}{r}-\sum _n \left( \frac{r_n}{r} \right) ^{3w_n+1} \right] } \nonumber \\{} & {} - r^2(\textrm{d}\theta ^2 -\sin ^2\theta \, \textrm{d}\phi ^2)~, \end{aligned}$$

(1)

where $r_g = 2 M$, M is the black hole mass, $r_n$ are the dimensional normalization constants, and $w_n$ are the dark matter state parameters

$$\begin{aligned} p_n=w_n \rho _n~. \end{aligned}$$

(2)

This work was further extended in [43], in which a scalar field was introduced. Then the state describing the dark matter with the negative pressure was considered as a perfect fluid approximation of a scalar field with an appropriate potential. Thus, introducing a scalar field $\varphi$ with the Lagrangian equal to

$$\begin{aligned} {{\mathcal {L}}} = \frac{1}{2}\, g^{\mu \nu }\,\partial _\mu \varphi \,\partial _\nu \varphi -V(\varphi )~, \end{aligned}$$

(3)

with identification

$$\begin{aligned} \rho _\mathrm{{DM}} = - g^{tt}[\partial _r \varphi (r)]^2, \end{aligned}$$

the dark matter modified metric (1) was reproduced.

The possibility that a phantom field is responsible for the dark matter was further investigated in [44]. A spherically approximate solution of a dark matter galaxy was obtained with a supermassive black hole at its center. The solution of the metric functions is satisfied with $g_{tt} = - g_{rr}^{-1}$, and the observation of the rotational stars moving in circular orbits in a spiral galaxy constrained the background of the phantom field to be spatially inhomogeneous, having an exponential potential.

The action of real phantom field minimally coupled to gravity was given by

$$\begin{aligned} S= & {} \int d^4x\sqrt{-g}\left[ \frac{R}{2\kappa ^2} +\frac{1}{2}g^{uv}\partial _{u}\Phi \partial _{v}\Phi \right. \nonumber \\{} & {} \left. -V(\Phi )+\mathcal {L}_{m}\right] ~, \end{aligned}$$

(4)

where R is the Ricci scalar, ${\kappa ^2} = 8 {\pi G}$, with G being the Newton constant, and $V(\phi )$ is the phantom field potential. The term $\mathcal {L}_{m}$ accounts for the massive dark matter in the galaxy.

The black hole solution is described by the metric

$$\begin{aligned} \mathrm{{d}}s^2=-f(r)\mathrm{{d}}t^2+\frac{\mathrm{{d}}r^2}{f(r)}+r^2(\mathrm{{d}}\theta ^2+\sin ^2\theta \mathrm{{d}}\phi ^2), \end{aligned}$$

(5)

where

$$\begin{aligned} f(r)=1-\frac{2M}{r}+\frac{k}{r}\ln \left( \frac{r}{|k|}\right) , \end{aligned}$$

(6)

M is the black hole mass, and k is a parameter describing the intensity of the PFDM. The above metric function is similar to the metric function with the parameter k specifying the presence of the phantom scalar field acting as its scalar charge. It was found that because the infalling phantom particles have a total negative energy, the accretion of the phantom energy is related to the decrease of the black hole mass.

Using (5) as the background metric with the metric function (6), massless scalar field and electromagnetic field perturbations were carried out in [60]. It was found that the presence of the PFDM parameter k results in a deviation of quasinormal mode spectra from those of a Schwarzschild black hole, and it was shown that the field perturbations in the presence of PFDM decay more rapidly compared to a Schwarzschild vacuum black hole.

3 Scalar field perturbations

We first show in Fig. 1 the behavior of the event horizon radius $r_h$ of the BH as a function of the parameter k (in the following we consider $k > 0$) using the metric function (6). We can observe that when the BH mass M increases, the event horizon radius increases. Also, the event horizon is lowest for $k=k_h=\frac{2M}{1+e}$. Namely, as the PFDM parameter k increases in the interval $k < k_h$, $r_h$ decreases and reaches its minimum value at $k = k_h$. Then, for $k > k_h$, $r_h$ increases when the parameter k increases. It is worth noting that there is a value of k for which the event horizon radius is the same as the Schwarzschild BH, and beyond this value of k, the event horizon is greater than the Schwarzschild background.

Fig. 1

The behavior of the event horizon radius $r_h$ as a function of the PFDM intensity parameter k. The black line is for $M=0.5$, the blue line for $M=1.0$, and the red line for $M=3.0$

The QNMs of scalar perturbations in the background of the metric (5) are given by the scalar field solution of the Klein–Gordon equation

$$\begin{aligned} \frac{1}{\sqrt{-g}}\partial _{\mu } \left( \sqrt{-g}g^{\mu \nu }\partial _{\nu } \varphi \right) =m^{2}\varphi , \end{aligned}$$

(7)

with suitable boundary conditions for a BH geometry. In the above expression, m is the mass of the scalar field $\varphi$. Now, by means of the following ansatz

$$\begin{aligned} \varphi =e^{-i\omega t} R(r) Y(\Omega ) , \end{aligned}$$

(8)

the Klein–Gordon equation reduces to

$$\begin{aligned}{} & {} \frac{1}{r^2}\frac{\mathrm{{d}}}{\mathrm{{d}}r}\left( r^2f(r)\frac{\mathrm{{d}}R}{\mathrm{{d}}r}\right) +\left( \frac{\omega ^2}{f(r)} -\frac{\kappa ^{2}}{r^2}-m^{2}\right) R(r)=0,\nonumber \\ \end{aligned}$$

(9)

where we defined $-\kappa ^{2}=-\ell (\ell +1)$, with $\ell =0,1,2,...$, which represents the eigenvalues of the Laplacian on the two-sphere, and $\ell$ is the multipole number. Now, defining $R(r)=\frac{F(r)}{r}$ and by using the tortoise coordinate $r^*$ given by $\mathrm{{d}}r^*=\frac{\mathrm{{d}}r}{f(r)}$, the Klein–Gordon equation can be written as a one-dimensional Schrödinger-like equation,

$$\begin{aligned} \frac{\mathrm{{d}}^{2}F(r^*)}{\mathrm{{d}}r^{*2}}-V_\mathrm{{eff}}(r)F(r^*)=-\omega ^{2}F(r^*), \end{aligned}$$

(10)

with an effective potential $V_{\text {eff}}(r)$, which parametrically expressed, $V_\mathrm{{eff}}(r^*)$, is given by

$$\begin{aligned} V_\mathrm{{eff}}(r)=\frac{f(r)}{r^2} \left( \kappa ^{2} + m^2 r^2+f^\prime (r)r\right) . \end{aligned}$$

(11)

In Fig. 2, we show its behavior for different values of the parameters. Note that a potential barrier occurs in each case, with its maximum value increasing when $\ell$ or m increases. For $0<k \le 0.81$, the maximum in the potential increases when k increases, but for $k>0.81$, the maximum of the potential decreases when k increases; thus it is possible to recover the height of the potential for the Schwarzschild case ($k\approx 3.50$) but with a larger event horizon.

Fig. 2

The effective potential $V_\mathrm{{eff}}$ as a function of r, with $M=1$. The left panel is for massless scalar field $m=0$, $k=0.01$, and $\ell =20,40,60$. The central panel is for $\ell =20$, $k=0.01$, and $m=0,1.0,2.0$. The right panel is for $\ell =20$, $m=0$, and $k=0.01, 0.50, 1.00, 2.00, 3.50, 5.00$

Fig. 3

The behavior of the potentials $V_\mathrm{{Sch}}$, $V_\mathrm{{dM}}$, and $V=V_\mathrm{{Sch}}+V_\mathrm{{dM}}$ as a function of r with $m=1$, $M=1$, and $\ell =20$. The black line is for V, the blue line for $V_\mathrm{{Sch}}$, and the red line for $V_\mathrm{{dM}}$. The left panel is for $k=0.5$ and $r_h=1.463$, the central panel is for $k=2.0$ and $r_h=2$, and the right panel is for $k=5.0$ and $r_h=3.618$

Fig. 4

The behavior of the potentials $V_\mathrm{{Sch}}$, $V_\mathrm{{dM}}$, and $V=V_\mathrm{{Sch}}+V_\mathrm{{dM}}$ as a function of r with $M=1$ and $\ell =20$. The black line is for V, the blue line for $V_\mathrm{{Sch}}$, and the red line for $V_\mathrm{{dM}}$. The left panel is for $k=0.5$ and $r_h=1.463$, the central panel is for $k=2.0$ and $r_h=2$, and the right panel is for $k=5.0$ and $r_h=3.618$. The continuous line is for a massless scalar field $m=0$, the dashed line is for $m=2.0$, and the dotted line is for $m=5.0$

The effective potential can be split as $V_\mathrm{{eff}}(r)= V_\mathrm{{Sch}}(r) + V_\mathrm{{dM}}(r)$, where

$$\begin{aligned} V_\mathrm{{Sch}}(r)= & {} -\frac{(2 M-r) \left( l (l+1) r +m^2 r^3+2 M\right) }{r^4}, \end{aligned}$$

(12)

$$\begin{aligned} V_\mathrm{{dM}}(r)= & {} \frac{k \left( \log \left( \frac{r}{k}\right) \left( -k \log \left( \frac{r}{k}\right) \!+\!k\!+\!\left( l^2\!+\!l\!-\!1\right) r\!+\!m^2 r^3\!+\!4M\right) \!-\!2 M\!+\!r\right) }{r^4}.\nonumber \\ \end{aligned}$$

(13)

Fig. 5

The behavior of the critical scalar field mass $m_{c}$ for the fundamental mode $n=0$ as a function of k. The black line is for $M=0.5$, the blue line for $M=1.0$, and the red line for $M=3.0$

Fig. 6

The behavior of $\mathrm{{Re}}(\omega )$ (left panel) and $\mathrm{{Im}}(\omega )$ (right panel) for the fundamental mode ($n=0$) as a function of the PFDM intensity parameter k with $M=1$ and $\ell =20$. The black line is for a massless scalar field ($m=0$), and the blue line is for a massive scalar field ($m=1.0$)

Table 1 QNFs for $M =1$, $\ell =20$, $m=0$, and different values of k and n

Table 2 The fundamental QNFs for $M =1$, $m=0$, and different values of k and $\ell$

Table 3 QNFs for $M =1$, $\ell =20$, $m=0$, and different values of k and n

Table 4 The fundamental QNFs for $M=1$, $m=0$, and different values of k and $\ell$

In Fig. 3, we plot their behavior. For k = 0.5 (left panel), the event horizon is located at $r_h=1.463$. Note that near the horizon, the blue line representing $V_\mathrm{{Sch}}$ is negative until $r=2M$, and the red line representing $V_\mathrm{{dM}}$ is positive. Beyond $r=2M$, both potentials are positive ($V_\mathrm{{Sch}}$, and $V_\mathrm{{dM}}$). Then, for $k=2.0$ (central panel) and $r > rh$ with $r_h=2.0$, both potentials are positive ($V_\mathrm{{Sch}}$ and $V_\mathrm{{dM}}$). For $k=5.0$ (right panel) and $r > rh$ with $r_h=3.618$), beyond the horizon, the blue line ($V_\mathrm{{Sch}}$) is positive and the red line ($V_\mathrm{{dM}}$) is negative. Beyond $V_\mathrm{{dM}}=0$, both potentials are positive ($V_\mathrm{{Sch}}$, $V_\mathrm{{dM}}$). It is worth mentioning that for large values of r, $V_\mathrm{{dM}}$ goes to zero and $V_\mathrm{{eff}}(r)$ goes to $V_\mathrm{{Sch}}$.

Fig. 7

The behavior of $\mathrm{{Re}}(\omega )$ (left panel) and $\mathrm{{Im}}(\omega )$ (right panel) for the fundamental mode ($n=0$) as a function of the event horizon $r_h$ with $M=1$ and $\ell =20$. The black line is for a massless scalar field ($m=0$), and the blue line is for a massive scalar field ($m=1.0$)

Fig. 8

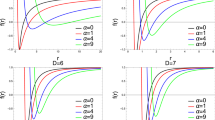
The behavior of $-\mathrm{{Im}}(\omega )$ for the fundamental mode ($n=0$) as a function of the scalar field mass m for different values of the parameter $\ell =20,40,60$ with $M=1$ and $k=0.07$ (left panel), $k=1.0$ (central panel), and $k=8.0$ (right panel). Here, the WKB method gives $m_{c}\approx 0.08$, $m_{c}\approx 0.13$, and $m_{c}\approx 0.05$, respectively

Fig. 9

The behavior of $-\mathrm{{Im}}(\omega )$ for the first overtone ($n=1$) as a function of the scalar field mass m for different values of the parameter $\ell =20,40,60$ with $M=1$ and $k=0.07$ (left panel), $k=1.0$ (central panel), and $k=8.0$ (right panel). Here, the WKB method gives $m_{c}\approx 0.17$, $m_{c}\approx 0.27$, and $m_{c}\approx 0.10$, respectively

As we can see from the above figure, at a fixed value of the scalar field mass $m=1$, the PFDM at large distances does not contribute, and we recover the Schwarzschild black hole, while near the horizon, the k parameter of the PFDM plays a decisive role. Varying the parameter k from $k=0.5$ to $k=5$, there is an interplay of the potentials from negative to positive values, indicating how the PFDM from small to large values interacts with the Schwarzschild black hole.

In Fig. 4, we show the effect of the scalar field mass on the potential for the three cases previously analyzed ($k=0.5,2.0,5.0$). We observe that the absolute value of each potential, $V_\mathrm{{eff}}(r)$, $V_\mathrm{{Sch}}$, and $V_\mathrm{{dM}}$, increases when the scalar field mass increases, and this occurs near the horizon of the black hole. We also observe that the largest increase of the absolute value of each potential occurs at intermediate values of the PFDM parameters k. Also, when $r\rightarrow \infty$, we find from Eqs. (11), (12), and (13) that the asymptotic behavior of the potentials is given by $V_\mathrm{{eff}}(r)\rightarrow m^2$, $V_\mathrm{{Sch}}\rightarrow m^2$, and $V_\mathrm{{dM}} \rightarrow 0$ as expected.

4 Photon sphere modes

In this section, in order to gain analytical insight into the behavior of the QNFs in the eikonal limit $\ell \rightarrow \infty$, we use the method based on the Wentzel–Kramers–Brillouin (WKB) approximation introduced by Mashhoon [64] and by Schutz and Iyer [65]. Iyer and Will computed the third-order correction [66], and then it was extended to the sixth order [67], and recently up to the 13th order [68], see also [69].

Table 5 Fundamental QNFs for $M =1$ and different values of k and m. Bold letters indicate the longest-lived modes

Table 6 Fundamental QNFs for $M =1$ and different values of k and m. Bold letters indicate the longest-lived modes

This method has been used to determine the QNFs for asymptotically flat and asymptotically de Sitter black holes. This is because the WKB method can be used for effective potentials which have the form of potential barriers that approach a constant value at the horizon and spatial infinity [9]. However, only the photon sphere modes can be obtained with this method. The QNMs are determined by the behavior of the effective potential near its maximum value $V(r^*_{\max })$. The Taylor series expansion of the potential around its maximum is given by

$$\begin{aligned} V(r^*)= V(r^*_{\max })+ \sum _{i=2}^{\infty } \frac{V^{(i)}}{i!} (r^*-r^*_{\max })^{i} , \end{aligned}$$

(14)

where

$$\begin{aligned} V^{(i)}= \frac{\mathrm{{d}}^{i}}{\mathrm{{d}} r^{*i}}V(r^*)|_{r^*=r^*_{\max }} \end{aligned}$$

(15)

corresponds to the ith derivative of the potential with respect to $r^*$ evaluated at the position of the maximum of the potential $r^*_{\max }$. Using the WKB approximation up to third order beyond the eikonal limit, the QNFs are given by the following expression: [70]

$$\begin{aligned} \omega ^2= & {} V(r^*_{\max }) -2 i U , \end{aligned}$$

(16)

where

$$\begin{aligned} U= & {} N\sqrt{-V^{(2)}/2}+\frac{i}{64} \left( -\frac{1}{9} \frac{V^{(3)2}}{V^{(2)2}}(7+60N^2) +\frac{V^{(4)}}{V^{(2)}}(1+4 N^2) \right) \\{} & {} +\frac{N}{2^{3/2} 288} \Bigg ( \frac{5}{24} \frac{V^{(3)4}}{(-V^{(2)})^{9/2}} (77+188N^2) \\{} & {} +\frac{3}{4} \frac{V^{(3)2} V^{(4)}}{(-V^{(2)})^{7/2}}(51+100N^2)\\{} & {} +\frac{1}{8}\frac{V^{(4)2}}{(-V^{(2)})^{5/2}}(67+68N^2) +\frac{V^{(3)}V^{(5)}}{(-V^{(2)})^{5/2}}(19+28N^2)\\{} & {} +\frac{V^{(6)}}{(-V^{(2)})^{3/2}}(5+4N^2) \Bigg ), \end{aligned}$$

and $N=n+1/2$, with $n=0,1,2,\dots$ being the overtone number. The imaginary and real parts of the QNFs can be written as

$$\begin{aligned} \omega _I^2= & {} - (\mathrm{{Im}}(U)+V/2) +\sqrt{(\mathrm{{Im}}(U)+V/2)^2+\mathrm{{Re}}(U)^2} , \nonumber \\\end{aligned}$$

(17)

$$\begin{aligned} \omega _R^2= & {} -\mathrm{{Re}}(U)^2 / \omega _I^2 , \end{aligned}$$

(18)

respectively, where $\mathrm{{Re}}(U)$ is the real part of U, and $\mathrm{{Im}}(U)$ is its imaginary part. Now, defining $L^2= \ell (\ell +1)$, we find that for large values of L, the maximum of the potential is approximately at

$$\begin{aligned} r_{\max } \approx r_{0}+\frac{1}{L^2}r_{1}, \end{aligned}$$

(19)

where

$$\begin{aligned} r_{0} =\frac{3}{2} k W\left( \frac{2}{3}e^{\frac{2M}{k}+\frac{1}{3}}\right) , \end{aligned}$$

(20)

W(x) is the Lambert function, and

$$\begin{aligned} r_{1}=\frac{2r_{0}(k^{2}+12 kM+16M^{2}-2(2k+3M)r_{0} +m^{2}(k+2M)r_{0}^{3})+2k r_{0}\log (\frac{r_{0}}{k}) (-6k-16M+3r_{0}-m^{2}r_{0}^{3}+4k\log (\frac{r_{0}}{k}))}{2r_{0}(2k-6M+4r_{0}+3k\log (\frac{r_{0}}{k}))}. \end{aligned}$$

(21)

Thus, the potential evaluated at $r^*_{\max }$ is given by

$$\begin{aligned} V(r^*_{\max })\approx & {} \frac{(-2M+r_{0}+ k\log (\frac{r_{0}}{k}))}{r_{0}^{3}}L^{2}\nonumber \\{} & {} +\frac{1}{9r_{0}^{4}}\Biggl (-3(29 k^{2}+66 kM+60M^{2}) +4(-7k+6M)r_{0}-14r_{0}^{2}\nonumber \\{} & {} -18m^{2}(k+2M)r_{0}^{3}+3m^{2}r_{0}^{4}\nonumber \\{} & {} +3k\log \bigg (\frac{r_{0}}{k}\bigg )(33k+60M-4r_{0}+6m^{2}r_{0}^{3} -15k\log (\frac{r_{0}}{k}))\nonumber \\{} & {} +\frac{(3k+2r_{0})(61 k^{2}+4r_{0}^{2}(7+3m^{2}r_{0}^{2}) +kr_{0}(82+15m^{2}r_{0}^{2}))}{2k+6M-4r_{0} 3k\log (\frac{r_{0}}{k})}\Biggr ) .\nonumber \\ \end{aligned}$$

(22)

The higher-order derivatives $V^{(i)}(r*_{\max })$ with $i=2,3,4,5,6$ are presented in Appendix A. Thus, by using these terms and Eq. (A11), we can find an analytical expression for the critical scalar field mass $m_c$, which is too lengthy to be presented here, because it is obtained from the term proportional to $1/L^2$ in $\omega$. However, we plot its behavior as a function of k in Fig. 5. We can observe that when the BH mass M increases, the critical scalar field mass decreases. Also, there is a value of $k_c$ corresponding to a maximal value for the critical scalar field mass. Namely, as the PFDM parameter k increases in the interval $k < k_c$, $m_c$ increases and reaches maximum values at $k = k_c$. Then, for $k > k_c$, the $m_c$ decreases when the parameter k increases. Remarkably, there is a value of the PFDM parameter k for which the critical scalar field mass is the same as that for the Schwarzschild BH; beyond this value of k, the critical scalar field mass is smaller than that of the Schwarzschild background. This behavior of the scalar field mass m and the PFDM parameter k indicates that there is an interplay between the real matter and the phantom matter affecting the mass of the background Schwarzschild black hole.

Now we plot in Fig. 6 the behavior of the real and imaginary parts of the QNFs as a function of the PFDM intensity parameter k. We can observe that there is a value of the parameter $k_0\approx 0.81$ for which the real part of the QNFs is maximum, which is associated with a reflecting point in the context of the BH shadow. Namely, as the PFDM parameter k increases in the interval $k < k_0$, the QNFs increase and reach their maximum values at $k = k_0$, as was pointed out in Ref. [60] for low values of $\ell$. Then, for $k > k_0$, the real part of the QNF decreases when the parameter k increases. Remarkably, there is a value of the PFDM parameter k for which the real part of the QNF is the same as that for the Schwarzschild BH, beyond which the frequency of oscillation is smaller than for the Schwarzschild case. A similar behavior occurs for the absolute value of the imaginary part of the QNF. Also, it is possible to observe that for a massive scalar field, the real part of the QNFs increases and the absolute value of the imaginary part of the QNFs decreases in comparison with the massless scalar field.

We show in the following tables that the real part of the QNFs have a maximum at $k_0 \approx 0.81$, and this value does not depend on n (see Table 1) or $\ell$ (see Table 2). Note also that the imaginary part of the QNFs have a maximum at $k \approx 1.19$, and this value also does not depend on n (see Table 3) or $\ell$ (see Table 4).

Now, we show the relation of QNFs to the location of the horizon in Fig. 7. We can observe a maximum value of the real part of the QNFs at $r_h \approx 1.502$ and for the imaginary part at $r_h \approx 1.622$. Also, it is possible to observe that for massive scalar fields, the real part of the QNFs increases and the absolute value of the imaginary part of the QNFs decreases in comparison to massless scalar fields.

Now, in order to show the anomalous behavior, we plot in Figs. 8 and 9 the behavior of $-\mathrm{{Im}}(\omega )$ as a function of m by using the sixth-order WKB method for $n=0$ and $n=1$, respectively. We can observe an anomalous decay rate, i.e., for $m<m_c$, the longest-lived modes are those with the highest angular number $\ell$, whereas for $m>m_c$, the longest-lived modes are those with the smallest angular number. Also, when the overtone number n increases, the parameter $m_c$ increases. In addition, it can be observed that the behavior of the critical scalar field mass with respect to the parameter k agrees with Fig. 5.

Finally, in order to analyze the behavior of the longest-lived modes with respect to the scalar field mass and the PFDM parameter k, we show in Tables 5 and 6 some fundamental QNFs for $M=1$ and different values of m and k. Firstly, it is possible to observe the anomalous behavior of the decay rate of the QNFs previously described. Bold letters show the longest-lived modes. Additionally, a particular behavior can be observed for fixed values of the scalar field mass, see $m=0.08$ and $m=0.09$. In these cases, for small values of the PFDM parameter k (see $k=0.01,0.07$), the longest-lived modes are those with the smallest angular number. As the k parameter increases (see $k=1,2$), the longest-lived modes are those with the highest angular number, and then for the largest values of k (see $k=5,10$), the longest-lived modes are those with the smallest angular number.

5 Conclusions

In this work, we studied the propagation of massive scalar fields in the background of BHs immersed in perfect fluid dark matter through the QNFs by using the WKB method to determine whether there is an anomalous decay behavior in the QNMs as has been observed in other BH backgrounds. Here, we considered the photon sphere modes, which are complex.

With regard to the photon sphere modes, we showed that there is a value of the parameter $k=k_0$ for which the real part of the QNFs is maximum, which is associated with a reflecting point in the context of a BH shadow. Namely, as the PFDM parameter k increases in the interval $k < k_0$, the QNFs increase and reach their maximum values at $k = k_0$. Then, for $k > k_0$, the real part of the QNF decreases when the parameter k increases. Remarkably, there is a value of the PFDM parameter k for which the real part of the QNF is the same as that for the Schwarzschild BH; beyond this value of k, the frequency of oscillation is smaller than for the Schwarzschild case. A similar behavior occurs for the absolute value of the imaginary part of the QNF. However, there is not a value of k for which it would be possible to recover the QNFs for the Schwarzschild background, i.e., the real and imaginary parts of the QNFs. In addition, for a massive scalar field, the real part of the QNFs increases and the absolute value of the imaginary part of the QNFs decreases in comparison with a massless scalar field.

We showed the existence of an anomalous decay rate of QNMs. That is, the absolute values of the imaginary part of the QNFs decay when the angular harmonic numbers increase if the mass of the scalar field is smaller than a critical mass. On the contrary, they grow when the angular harmonic numbers increase if the mass of the scalar field is larger than the critical mass, and they also increase with the overtone number n for $\ell \ge n$. Also, the critical scalar field mass decreases when the BH mass M increases, and there is a value of $k_c$ corresponding to a maximal value for the critical scalar field mass. Namely, as the PFDM parameter k increases in the interval $k < k_c$, the $m_c$ increases and reaches maximum values at $k = k_c$. Then, for $k > k_c$, the $m_c$ decreases when the parameter k increases. Remarkably, there is a value of the PFDM parameter k for which the critical scalar field mass is the same as that for the Schwarzschild BH, beyond which the critical scalar field mass is smaller than for the Schwarzschild background.

We have also reported a particular behavior for fixed values of the scalar field mass ($m=0.08, 0.09$), where for small values of the PFDM parameter k ($k=0.01,0.07$), the longest-lived modes are those with the smallest angular number. As the k parameter increases ($k=1,2$), the longest-lived modes are those with the highest angular number, and then for the largest values of k ($k=5,10$), the longest-lived modes are those with smallest angular number. Also, in order to show that the scale of the location of the horizon is not important because the behavior for ${\bar{k}}<1$ is similar to the behavior for ${\bar{k}}>1$, with ${\bar{k}}=k/r_h$, we have included a dimensionless analysis, see Appendix B.

It would be interesting to consider charged black holes immersed in perfect fluid dark matter that represent Reissner–Nordström–dS BHs when the PFDM parameter $k\rightarrow 0$ in order to determine whether it is possible to avoid the existence of unstable modes for $l=0$ for a value of the parameter k for a charged massive scalar field. Also, with regard to the study of superradiance as well as the existence of bound states which could trigger an instability, work in this direction is in progress.

Appendices

Appendix A: higher-order derivatives of the potential

In order to explicitly set forth the terms of the WKB approximation outlined in Sect. IV, we present the higher-order derivatives $V^{(i)}(r*_{\max })$ with $i=2,3,4,5,6$ of the potential.

$$\begin{aligned} V^{(0)}= & {} V_{02} L^2 + V_{00} + \mathcal {O}(L^{-2}),\nonumber \\ V^{(2)}= & {} V_{22}L^2 + V_{20} + \mathcal {O}(L^{-2}), \nonumber \\ V^{(3)}= & {} V_{32}L^2 + \mathcal {O}(L^0),\nonumber \\ V^{(4)}= & {} V_{42}L^2+ \mathcal {O}(L^0),\nonumber \\ V^{(5)}= & {} V_{52}L^2 + \mathcal {O}(L^0),\nonumber \\ V^{(6)}= & {} V_{62}L^2 +\mathcal {O}(L^0), \end{aligned}$$

(A1)

where

$$\begin{aligned} V_{00}= & {} \frac{\eta \left( -\eta +k+m^2 r_0^3+4 M-3 r_1-r_0\right) -\left( 2 M-r_0\right) \left( k+m^2 r_0^3+2 M\right) +r_1 \left( k+6 M-2 r_0\right) }{r_0^4}, \end{aligned}$$

(A2)

$$\begin{aligned} V_{02}= & {} \frac{-2M+r_{0}+\eta }{r_{0}^{3}}, \end{aligned}$$

(A3)

$$\begin{aligned} V_{22}= & {} \frac{\left( \eta -2 M+r_0\right) \left( k^2+ \eta \left( 15 \eta -11 k+20 (r_0-3 M)\right) +22 k M-9 k r_0+60 M^2-40 M r_0+6 r_0^2\right) }{r_0^7}, \end{aligned}$$

(A4)

$$\begin{aligned} V_{20}= & {} \frac{1}{r_0^9}\Bigg (r_0 r_1 \left( -8 \eta +k+16 M-7 r_0\right) \nonumber \\{} & {} \left( k^2+\eta \left( 15 \eta -11 k+20 \left( r_0-3 M\right) \right) \right. \nonumber \\{} & {} \left. +22 k M-9 k r_0+60 M^2-40 M r_0+6 r_0^2\right) \nonumber \\{} & {} -r_0 \left( -\eta +2 M-r_0\right) \Bigg (k^3+\eta \Bigg (-18 k^2\nonumber \\{} & {} +\eta \left( -24 \eta +48 k+3 m^2 r_0^3+144 M-35 r_0+15 r_1\right) \nonumber \\{} & {} +k \left( -5 m^2 r_0^3-192 M+64 r_0+19 r_1\right) \nonumber \\{} & {} -4 M \left( 3 m^2 r_0^3-35 r_0+15 r_1\right) \nonumber \\{} & {} +2 r_0 \left( m^2 r_0^3-6 r_0+20 r_1\right) -288 M^2\Bigg )\nonumber \\{} & {} +k^2 \left( m^2 r_0^3+36 M-15 r_0-10 r_1\right) \nonumber \\{} & {} +k\Bigg (2 M \left( 5 m^2 r_0^3-64 r_0-19 r_1\right) \nonumber \\{} & {} +r_0 \left( -3 m^2 r_0^3+19 r_0+2 r_1\right) +192 M^2\Bigg )\nonumber \\{} & {} +4 M^2 \left( 3 m^2 r_0^3-35 r_0+15 r_1\right) \nonumber \\{} & {} -4 M r_0 \left( m^2 r_0^3-6 r_0+20 r_1\right) +192 M^3+18 r_0^2 r_1\Bigg )\Bigg ), \end{aligned}$$

(A5)

$$\begin{aligned} V_{32}= & {} -\frac{1}{{r_0^9}}\left( \eta -2 M+r_0\right) \nonumber \\{} & {} \Bigg (-k^3+\eta \Bigg (29 k^2+\eta \left( 105 \eta -122 k+210 \left( r_0-3 M\right) \right) \nonumber \\{} & {} +488 k M-190 k r_0+1260 M^2\nonumber \\{} & {} -840 M r_0+130 r_0^2\Bigg )+k^2 \left( 26 r_0-58 M\right) \nonumber \\{} & {} +k\left( -488 M^2+380 M r_0-71 r_0^2\right) -840 M^3+840 M^2 r_0\nonumber \\{} & {} -260 M r_0^2+24 r_0^3\Bigg ), \end{aligned}$$

(A6)

$$\begin{aligned} V_{42}= & {} \frac{1}{r_0^{11}}(\eta -2 M+r_0) \Bigg (k^4+134 k^3 M\nonumber \\{} & {} +r_0^2\left( 443 k^2+5014 k M+9520 M^2\right) +2508 k^2 M^2\nonumber \\{} & {} +\eta \Bigg (-67 k^3+\eta \Bigg (627 k^2+3\nonumber \\{} & {} \eta \left( 315 \eta -506 k+840 \left( r_0-3 M\right) \right) \nonumber \\{} & {} +k \left( 9108 M-3441 r_0\right) \nonumber \\{} & {} +140 \left( 162 M^2-108 M r_0+17 r_0^2\right) \Bigg )\nonumber \\{} & {} +76 k^2 \left( 14 r_0-33 M\right) \nonumber \\{} & {} +k \left( -18216 M^2+13764 M r_0-2507 r_0^2\right) \nonumber \\{} & {} +28 \left( -1080 M^3+1080 M^2 r_0-340 M r_0^2+33 r_0^3\right) \Bigg )\nonumber \\{} & {} -r_0 \left( 63 k^3+2128 k^2 M+13764 k M^2+20160 M^3\right) \nonumber \\{} & {} +12144 k M^3-4 r_0^3 (145 k+462 M)+15120 M^4+120 r_0^4\Bigg ), \nonumber \\\end{aligned}$$

(A7)

$$\begin{aligned} V_{52}= & {} -\frac{1}{r_0^{13}}\left( \eta -2 M+r_0\right) \Bigg (-k^5-290 k^4 M-10472 k^3 M^2\nonumber \\{} & {} -103752 k^2 M^3+r_0^3 \left( 6631 k^2+62608 k M+105728 M^2\right) \nonumber \\{} & {} -2 r_0^2 \left( 1037 k^3+25459 k^2 M+136464 k M^2+176400 M^3\right) \nonumber \\{} & {} +\eta \Bigg (145 k^4+10472 k^3 M\nonumber \\{} & {} +r_0^2 \left( 25459 k^2+272928 k M+529200 M^2\right) +155628 k^2 M^2\nonumber \\{} & {} +\eta \Bigg (-2618 k^3+3 \eta \Bigg (4323 k^2+\eta \Bigg (3465 \eta -7141 k\nonumber \\{} & {} -11550 \left( 3 M-r_0\right) \Bigg )+k \left( 57128 M-21150 r_0\right) \nonumber \\{} & {} +2100 \left( 66 M^2-44 M r_0+7 r_0^2\right) \Bigg )\nonumber \\{} & {} +k^2 \left( 31787 r_0-77814 M\right) \nonumber \\{} & {} -12 k \left( 42846 M^2-31725 M r_0+5686 r_0^2\right) \nonumber \\{} & {} -56\left( 14850 M^3-14850 M^2 r_0+4725 M r_0^2-472 r_0^3\right) \Bigg )\nonumber \\{} & {} -2 r_0 \left( 2341 k^3+63574 k^2 M+380700 k M^2+554400 M^3\right) \nonumber \\{} & {} +685536 k M^3-56 r_0^3 (559 k+1888 M)+831600 M^4\nonumber \\{} & {} +7308 r_0^4\Bigg )+4 r_0 \left( 35 k^4+2341 k^3 M+31787 k^2 M^2\nonumber \right. \\{} & {} \left. +126900 k M^3+138600 M^4\right) -342768 k M^4\nonumber \\{} & {} -232 r_0^4 (22 k+63 M)-332640 M^5+720 r_0^5\Bigg ), \end{aligned}$$

(A8)

$$\begin{aligned} V_{62}= & {} \frac{1}{r_0^{15}}\left( \eta -2 M+r_0\right) \nonumber \\{} & {} \Bigg (k^6+606 k^5 M{+}38956 k^4 M^2{+}687280 k^3 M^3{+}4411392 k^2 M^4\nonumber \\{} & {} +r_0^4 \left( 96087 k^2+790304 k M+1214640 M^2\right) \nonumber \\{} & {} -2 r_0^3 \Bigg (26415 k^3+519972 k^2 M+2413912 k M^2+2821280 M^3\Bigg )\nonumber \\{} & {} +8 r_0^2 \Bigg (1037 k^4+47202 k^3 M+512376 k^2 M^2\nonumber \\{} & {} +1763502 k M^3+1732500 M^4\Bigg )\nonumber \\{} & {} +\eta \Bigg (-303 k^5+4 k^4 \left( 4505 r_0-9739 M\right) \nonumber \\{} & {} -24 k^3\left( 42955 M^2-36978 M r_0+7867 r_0^2\right) \nonumber \\{} & {} -12 k^2 \Bigg (735232 M^3-876564 M^2 r_0\nonumber \\{} & {} +341584 M r_0^2-43331 r_0^3\Bigg )\nonumber \\{} & {} +\eta \Bigg (9739 k^4+12 k^3 \left( 42955 M-18489 r_0\right) \nonumber \\{} & {} +24 k^2 \left( 275712 M^2-219141 M r_0+42698 r_0^2\right) \nonumber \\{} & {} +\eta \Bigg (-85910 k^3+3 \eta \Bigg (91904 k^2+\eta \Bigg (45045 \eta -113623 k\nonumber \\{} & {} -180180 \left( 3 M-r_0\right) \Bigg )+k \left( 1136230 M-414567 r_0\right) \nonumber \\{} & {} +11550 \left( 234 M^2-156 M r_0+25 r_0^2\right) \Bigg )\nonumber \\{} & {} +k^2 \left( 876564 r_0-2205696 M\right) \nonumber \\{} & {} -6 k \left( 2272460 M^2-1658268 M r_0+293917 r_0^2\right) \nonumber \\{} & {} -3080 \left( 7020 M^3-7020 M^2 r_0+2250 M r_0^2-229r_0^3\right) \Bigg )\nonumber \\{} & {} +4 k \Bigg (6817380 M^3-7462206 M^2 r_0+2645253 M r_0^2 \nonumber \\{} & {} -301739 r_0^3\Bigg )+420 \left( 77220 M^4-102960 M^3 r_0\right. \nonumber \\{} & {} \quad \left. +49500 M^2r_0^2-10076 M r_0^3+723 r_0^4\right) \Bigg )\nonumber \\{} & {} -8 k \left( 3408690 M^4-4974804 M^3 r_0\right. \nonumber \\{} & {} \left. +2645253 M^2 r_0^2-603478 M r_0^3+49394 r_0^4\right) \nonumber \\{} & {} -48 \left( 540540 M^5-900900 M^4 r_0+577500 M^3 r_0^2\right. \nonumber \\{} & {} \left. -176330 M^2 r_0^3+25305 M r_0^4-1338 r_0^5\right) \Bigg )\nonumber \\{} & {} -r_0 \Bigg (297 k^5+36040 k^4 M +887472 k^3 M^2+7012512 k^2 M^3\nonumber \\{} & {} +19899216 k M^4+17297280 M^5\Bigg )+10907808 k M^5\nonumber \\{} & {} -4 r_0^5 (12215 k+32112 M)+8648640 M^6+5040 r_0^6\Bigg ),\nonumber \\ \end{aligned}$$

(A9)

with

$$\begin{aligned} \eta =k\log \left( \frac{r_{0}}{k}\right) . \end{aligned}$$

(A10)

On the other hand, our interest is to evaluate the QNFs for large values of L, so we expand the frequencies as a power series in L. It is important to keep in mind that in the eikonal limit, the leading term is linear in L, and for $k=0$, we should recover the Schwarzschild black hole frequencies. Next we consider the following expression in powers of L

$$\begin{aligned} \omega =\omega _{1m}L+\omega _{0}+\omega _{1}L^{-1} +\omega _{2}L^{-2} + \mathcal {O}(L^{-3}), \end{aligned}$$

(A11)

where

$$\begin{aligned} \omega _{1m}= & {} \frac{1}{r_0}\sqrt{\frac{-2M+r_{0}+\eta }{r_{0}}}, \end{aligned}$$

(A12)

$$\begin{aligned} \omega _0= & {} -\frac{i\sqrt{2} }{4 r_0^2 }\sqrt{-k^2-\eta \left( 15 \eta -11 k +20 \left( r_0-3 M\right) \right) -22 k M+9 k r_0-60 M^2+40 M r_0-6 r_0^2} , \end{aligned}$$

(A13)

$$\begin{aligned} \omega _1= & {} \frac{1}{38880 r_0^{5/2} \sqrt{\eta -2 M+r_0}}\nonumber \\{} & {} \times \Bigg (-52110 \eta ^2+6 \Bigg (-645 k^2+3240 r_1\nonumber \\{} & {} \left( k+6 M-2 r_0\right) -13905 k M+5959 k r_0\nonumber \\{} & {} -6480 m^2 M r_0^3+3240 m^2 r_0^4-34740 M^2\nonumber \\{} & {} +21000 M r_0-2241 r_0^2\Bigg )\nonumber \\{} & {} +\frac{1}{\chi }\Bigg (9 k^3 (5110 M-541 k)\nonumber \\{} & {} +6 k^2 r_0 (12347 M-5736 k)-3 \eta \left( 7665 k^3+12347 k^2r_0 \right. \nonumber \\{} & {} \left. +5757 k r_0^2+700 r_0^3\right) +14 r_0^3 (300 M-1453 k)\nonumber \\{} & {} +2 k r_0^2 (17271 M-23194 k)-2420 r_0^4\Bigg )\nonumber \\{} & {} +\frac{1}{\chi ^2}\Bigg (11 \Bigg (549 k^5 (k+22 M) +3 k^4 r_0 (13808 M-1213 k)\nonumber \\{} & {} +2 k^3 r_0^2 (27635 M-8257 k)+k^2 r_0^3 (35628 M-23939 k)\nonumber \\{} & {} -\eta \left( 33 k^2+47 k r_0+16 r_0^2\right) \nonumber \\{} & {} \times \left( 183 k^3+367 k^2 r_0+226 k r_0^2+40 r_0^3\right) \nonumber \\{} & {} +40 r_0^5 (32 M-129 k)+k r_0^4 (10992 M-16145 k) -624 r_0^6\Bigg )\Bigg ) \nonumber \\{} & {} +45 \eta \times \left( 927 k+8 \left( 54 m^2 r_0^3+579 M-175 r_0-162 r_1\right) \right) \Bigg ),\nonumber \\ \end{aligned}$$

(A14)

with

$$\begin{aligned} \chi= & {} k^2+\eta (15 \eta -11 k+20 (r_0-3 M))\nonumber \\{} & {} +22 k M-9 k r_0+60 M^2-40 M r_0+6 r_0^2. \end{aligned}$$

(A15)

$$\begin{aligned} \omega _2= & {} \mu ^{-1}i \Bigg (216 r_0 \delta ^6-1728 \Bigg (\left( m^2 r_0^3-r_0+k+4 M-\eta -3 r_1\right) \eta \nonumber \\{} & {} -\left( 2 M-r_0\right) \left( m^2 r_0^3+k+2 M\right) +\left( k+6 M-2 r_0\right) r_1\Bigg ) r_0 \delta ^5 \nonumber \\{} & {} -108 r_0 \alpha \delta ^4 +1728 \Bigg (r_0 r_1 \left( k+16 M-8 \eta -7 r_0\right) \delta \nonumber \\{} & {} -r_0 \left( 2 M-\eta -r_0\right) \Bigg (k^3+\left( m^2 r_0^3-15 r_0+36 M-10 r_1\right) k^2\nonumber \\{} & {} +\Bigg (192 M^2+2 \left( 5 m^2 r_0^3-64 r_0-19 r_1\right) M\nonumber \\{} & {} +r_0 \left( -3 m^2 r_0^3+19 r_0+2 r_1\right) \Bigg ) k \nonumber \\{} & {} +192 M^3+\eta \Bigg (-18 k^2+\left( -5 m^2 r_0^3 +64 r_0-192 M+19 r_1\right) k\nonumber \\{} & {} -288 M^2+\eta \left( 3 m^2 r_0^3-35 r_0+48 k+144 M-24 \eta +15 r_1\right) \nonumber \\{} & {} -4 M \left( 3 m^2 r_0^3-35 r_0+15 r_1\right) \nonumber \\{} & {} +2 r_0 \left( m^2 r_0^3-6 r_0+20 r_1\right) \Bigg )\nonumber \\{} & {} +18 r_0^2 r_1+4 M^2 \left( 3 m^2 r_0^3-35 r_0+15 r_1\right) \nonumber \\{} & {} -4 M r_0 \left( m^2 r_0^3-6 r_0+20 r_1\right) \Bigg )\Bigg ) \delta ^4\nonumber \\{} & {} +132 \sigma ^2 r_0 \delta ^3+36 \Bigg (k^6+606 M k^5+38956 M^2 \nonumber \\{} & {} \times k^4+687280 M^3 k^3+4411392 M^4 k^2\nonumber \\{} & {} +10907808 M^5 k+8648640 M^6\nonumber \\{} & {} +5040 r_0^6-4 (12215 k+32112 M) r_0^5\nonumber \\{} & {} +\left( 96087 k^2+790304 M k+1214640 M^2\right) r_0^4\nonumber \\{} & {} -2 \left( 26415 k^3+519972 M k^2+2413912 M^2 k+2821280 M^3\right) \nonumber \\{} & {} \times r_0^3+8 \Bigg (1037 k^4+47202 M k^3+512376 M^2 k^2\nonumber \\{} & {} +1763502 M^3 k+1732500 M^4\Bigg ) r_0^2\nonumber \\{} & {} +\eta \Bigg (-303 k^5+4 \left( 4505 r_0-9739 M\right) k^4\nonumber \\{} & {} -24 \Bigg (42955 M^2-36978 r_0 M\nonumber \\{} & {} +7867 r_0^2\Bigg ) k^3-12 \Bigg (735232 M^3-876564 r_0 M^2\nonumber \\{} & {} +341584 r_0^2 M-43331 r_0^3\Bigg ) \nonumber \\{} & {} \times k^2-8 \Bigg (3408690 M^4-4974804 r_0 M^3\nonumber \\{} & {} +2645253 r_0^2 M^2-603478 r_0^3 M+49394 r_0^4\Bigg ) k\nonumber \\{} & {} +\eta \Bigg (9739 k^4+12 \left( 42955 M-18489 r_0\right) k^3\nonumber \\{} & {} +24 \left( 275712 M^2-219141 r_0 M+42698 r_0^2\right) k^2\nonumber \\{} & {} +4 \left( 6817380 M^3-7462206 r_0 M^2+2645253 r_0^2 M-301739 r_0^3\right) k\nonumber \\{} & {} +\eta \Bigg (-85910 k^3+\left( 876564 r_0-2205696 M\right) k^2\nonumber \\{} & {} -6 \left( 2272460 M^2+293917 r_0^2-1658268 Mr_0\right) k\nonumber \\{} & {} +3 \eta \Bigg (91904 k^2+\left( 1136230 M-414567 r_0\right) k\nonumber \\{} & {} +\eta \left( -113623 k+45045 \eta -180180 \left( 3 M-r_0\right) \right) \nonumber \\{} & {} +11550 \left( 234 M^2-156 r_0 M+25 r_0^2\right) \Bigg )\nonumber \\{} & {} -3080\left( 7020 M^3-7020 r_0 M^2+2250 r_0^2 M -229r_0^3\right) \Bigg )\nonumber \\{} & {} +420 \left( 77220 M^4-102960 r_0 M^3+49500 r_0^2 M^2 \right. \nonumber \\{} & {} \left. -10076 r_0^3 M+723 r_0^4\right) \Bigg )\nonumber \\{} & {} -48 \Bigg (540540 M^5-900900 r_0 M^4\nonumber \\{} & {} +577500 r_0^2 M^3-176330 r_0^3 M^2+25305 r_0^4 M-1338 r_0^5\Bigg )\Bigg )\nonumber \\{} & {} -\Bigg (297 k^5+36040 M k^4+887472 M^2 k^3\nonumber \\{} & {} +7012512 M^3 k^2+19899216 M^4 k+17297280 M^5\Bigg ) r_0\Bigg ) r_0 \delta ^3\nonumber \\{} & {} -63 r_0 \alpha ^2 \delta ^2-156 r_0 \sigma \Bigg (-k^5-290 M k^4-10472 M^2 k^3\nonumber \\{} & {} -103752 M^3 k^2-342768 M^4 k-332640 M^5+720 r_0^5\nonumber \\{} & {} -232 (22 k+63 M) r_0^4+\left( 6631 k^2+62608 M k+105728 M^2\right) r_0^3\nonumber \\{} & {} -2 \left( 1037 k^3+25459 M k^2+136464 M^2 k+176400 M^3\right) r_0^2\nonumber \\{} & {} +\eta \Bigg (145 k^4+10472 M k^3+155628 M^2 k^2+685536 M^3 k\nonumber \\{} & {} +831600 M^4+7308 r_0^4-56 (559 k+1888 M) r_0^3\nonumber \\{} & {} +\left( 25459 k^2+272928 M k+529200 M^2\right) r_0^2\nonumber \\{} & {} +\eta \Bigg (-2618 k^3+\left( 31787 r_0-77814 M\right) k^2\nonumber \\{} & {} -12 \left( 42846 M^2-31725 r_0 M+5686 r_0^2\right) k\nonumber \\{} & {} +3 \eta \left( 4323 k^2+\left( 57128 M-21150 r_0\right) k \right. \nonumber \\{} & {} \left. +\eta \left( -7141 k+3465 \eta -11550 \left( 3 M-r_0\right) \right) \right. \nonumber \\{} & {} \left. +2100\left( 66 M^2-44 r_0 M+7 r_0^2\right) \right) \nonumber \\{} & {} -56 \left( 14850 M^3-14850 r_0 M^2+4725 r_0^2 M-472 r_0^3\right) \Bigg )\nonumber \\{} & {} -2 \left( 2341 k^3+63574 M k^2+380700 M^2 k +554400 M^3\right) r_0\Bigg )\nonumber \\{} & {} +4 \left( 35 k^4+2341 M k^3+31787 M^2 k^2\right. \nonumber \\{} & {} \left. +126900 M^3 k+138600 M^4\right) r_0\Bigg ) \delta ^2-155 r_0 \sigma ^4+342 \alpha \delta \sigma ^2 r_0\Bigg ),\nonumber \\ \end{aligned}$$

(A16)

with

$$\begin{aligned} \mu= & {} 6912 r_0^4 \left( -2 M+\eta +r_0\right) \delta ^4 \sqrt{-2\delta }, \end{aligned}$$

(A17)

$$\begin{aligned} \xi= & {} 15 \eta -11 k+20 \left( r_0-3 M\right) , \end{aligned}$$

(A18)

$$\begin{aligned} \delta= & {} \eta \xi +k^2+22 k M-9 k r_0+60 M^2-40 M r_0+6 r_0^2, \nonumber \\\end{aligned}$$

(A19)

$$\begin{aligned} \sigma= & {} -k^3+\eta \left( 29 k^2+\eta \left( 105 \eta -122 k+210 \left( r_0-3 M\right) \right) \right. \nonumber \\{} & {} \left. +488 k M -190 k r_0+1260 M^2-840 M r_0+130 r_0^2\right) \nonumber \\{} & {} +k^2 \left( 26 r_0-58 M\right) {+}k \left( -488 M^2{+}380 M r_0-71 r_0^2\right) \nonumber \\{} & {} -840 M^3+840 M^2 r_0-260 M r_0^2+24 r_0^3, \end{aligned}$$

(A20)

$$\begin{aligned} \alpha= & {} k^4+134 k^3 M+r_0^2 \left( 443 k^2+5014 k M +9520 M^2\right) \nonumber \\{} & {} +2508 k^2 M^2+\eta \Bigg (-67 k^3+\eta \Bigg (627 k^2+3 \eta \nonumber \\{} & {} \times \left( 315 \eta -506 k+840 \left( r_0-3 M\right) \right) \nonumber \\{} & {} +k \left( 9108 M-3441 r_0\right) \nonumber \\{} & {} +140 \left( 162 M^2-108 M r_0+17 r_0^2\right) \Bigg )\nonumber \\{} & {} +76 k^2 \left( 14 r_0-33 M\right) \nonumber \\{} & {} +k \left( -18216 M^2+13764 M r_0-2507 r_0^2\right) \nonumber \\{} & {} +28 \left( -1080 M^3+1080 M^2 r_0-340 M r_0^2+33 r_0^3\right) \Bigg )\nonumber \\{} & {} -r_0 \left( 63 k^3+2128 k^2 M+13764 k M^2+20160 M^3\right) \nonumber \\{} & {} +12144 k M^3-4 r_0^3 (145 k+462 M)\nonumber \\{} & {} +15120 M^4+120 r_0^4. \end{aligned}$$

(A21)

Appendix B: dimensionless analysis

Fig. 10

The effective potential ${\bar{V}}_\mathrm{{eff}}$ as a function of ${\bar{r}}$. The left panel is for a massless scalar field with ${\bar{m}}=0$, ${\bar{k}}=0.01$, and $\ell =20,40,60$. The central panel is for $\ell =20$, ${\bar{k}}=0.01$, and ${\bar{m}}=0,1.0,2.0$. The right panel is for $\ell =20$, ${\bar{m}}=0$, and ${\bar{k}}=0.01, 0.50, 1.00, 2.00, 3.50, 5.00$

Scaling by the event horizon radius $r_h$, that is, by considering ${\bar{r}}=r/r_h$, ${\bar{k}}=k/r_h$, and ${\bar{m}}=mr_h$, the metric function and the effective potential can be written as

$$\begin{aligned} f({\bar{r}})= & {} 1-\frac{1}{{\bar{r}}}+\frac{{\bar{k}}}{{\bar{r}}}\ln ({\bar{r}}), \end{aligned}$$

(B1)

$$\begin{aligned} {\bar{V}}_\mathrm{{eff}}({\bar{r}})= & {} \frac{f({\bar{r}})}{{\bar{r}}^2} \left( \kappa ^{2} + {\bar{m}}^2 {\bar{r}}^2 + {\bar{r}}f^\prime ({\bar{r}})\right) = r_h^2 V_\mathrm{{eff}}(r)~, \end{aligned}$$

(B2)

respectively. Here, the prime denotes a derivative with respect to ${\bar{r}}$. In Fig. 10, we show the behavior of the effective potential for different values of the parameters. Note that a potential barrier occurs in each case, with its maximum value increasing when $\ell$ or ${\bar{m}}$ increases. However, ${\bar{V}}_\mathrm{{eff}}({\bar{r}})$ has a different behavior than ${V}_\mathrm{{eff}}({r})$; the maximum value of the potential barrier increases when ${\bar{k}}$ increases.

Fig. 11

The behavior of the critical scalar field mass ${\bar{m}}_{c}$ for the fundamental mode $n=0$ as a function of ${\bar{k}}$. The continuous line is for the exact value of ${\bar{m}}_{c}$, and the dotted line is for the approximate expression of ${\bar{m}}_{c}$ via Eq. (B3)

Fig. 12

The behavior of $\mathrm{{Re}}({\bar{\omega }})$ (left panel) and $\mathrm{{Im}}({\bar{\omega }})$ (right panel) for the fundamental mode ($n=0$) as a function of the parameter ${\bar{k}}$, and $\ell =20$. The black line is for ${\bar{m}}=0$, and the blue line is for ${\bar{m}}=10$

Also, it is possible to find the critical mass parameter ${\bar{m}}_c$, which for small values of ${\bar{k}}$ is given perturbatively by the expansion

$$\begin{aligned} {\bar{m}}_c= & {} \frac{1}{27}\sqrt{\frac{137}{10}} + {\bar{k}} \left( \frac{77}{30 \sqrt{1370}} +\frac{1}{27} \sqrt{\frac{137}{10}} \ln \left( \frac{3}{2}\right) \right) \nonumber \\{} & {} + {\bar{k}}^2 \left( -\frac{450343}{277425 \sqrt{1370}}\right. \nonumber \\{} & {} +\frac{1}{27} \sqrt{\frac{137}{10}} \ln ^2\left( \frac{3}{2}\right) \nonumber \\{} & {} \left. +\frac{4}{135} \sqrt{\frac{2}{685}} \ln \left( \frac{3}{2}\right) \right) +O\left( {\bar{k}}^3\right) . \end{aligned}$$

(B3)

We plot its behavior as a function of ${\bar{k}}$ in Fig. 11. We can observe that when the parameter ${\bar{k}}$ increases, the critical mass ${\bar{m}}_c$ increases, and for ${\bar{k}}=0$, we recover the value of the Schwarzschild black hole.

Now, we plot in Fig. 12 the behavior of the real and imaginary parts of ${\bar{\omega }}=\omega r_h$ as a function of the parameter ${\bar{k}}$, separately. Here, both the real part and absolute value of the imaginary part of ${\bar{\omega }}$ increase when the parameter ${\bar{k}}$ or ${\bar{m}}$ increases, i.e., there is a corresponding elevation in both oscillation frequency and damping. Specifically, when ${\bar{k}} > 1$, it signifies a scenario predominantly governed by dark matter, as this condition is equivalent to $k > r_h$. In this context, the influence of dark matter manifests as an augmentation in both the oscillation frequency and damping of the QNFs.

Now, in order to show the anomalous behavior, we plot in Figs. 13 and 14 the behavior of $-\mathrm{{Im}}({\bar{\omega }})$ as a function of ${\bar{m}}$ by using the sixth-order WKB method for $n=0$ and $n=1$, respectively. We can observe an anomalous decay rate, i.e., for ${\bar{m}}<{\bar{m}}_c$, the longest-lived modes are those with the highest angular number $\ell$, whereas for ${\bar{m}}>{\bar{m}}_c$, the longest-lived modes are those with the smallest angular number. Also, when the overtone number n increases, the parameter ${\bar{m}}_c$ increases. In addition, it can be observed that the behavior of the critical parameter ${\bar{m}}_c$ with respect to the parameter ${\bar{k}}$ agrees with Fig. 11.

Fig. 13

The behavior of $-\mathrm{{Im}}({\bar{\omega }})$ for the fundamental mode ($n=0$) as a function of ${\bar{m}}$ for different values of the parameter $\ell =20,40,60$, with ${\bar{k}}=0.07$ (left panel), ${\bar{k}}=1.0$ (central panel), and ${\bar{k}}=8.0$ (right panel). Here, the WKB method gives ${\bar{m}}_{c}\approx 0.15$, ${\bar{m}}_{c}\approx 0.24$, and ${\bar{m}}_{c}\approx 0.62$, respectively

Fig. 14

The behavior of $-\mathrm{{Im}}({\bar{\omega }})$ for the first overtone ($n=1$) as a function of ${\bar{m}}$ for different values of the parameter $\ell =20,40,60$, with $M=1$, ${\bar{k}}=0.07$ (left panel), ${\bar{k}}=1.0$ (central panel), and ${\bar{k}}=8.0$ (right panel). Here, the WKB method gives ${\bar{m}}_{c}\approx 0.30$, ${\bar{m}}_{c}\approx 0.48$, and ${\bar{m}}_{c}\approx 1.19$, respectively

The above description of ${\bar{V}}_\mathrm{{eff}}({\bar{r}})$, ${\bar{m}}_c$, $\mathrm{{Re}}({\bar{\omega }})$, and $\mathrm{{Im}}({\bar{\omega }})$ shows that the scale of the location of the horizon is not important, because the behavior for ${\bar{k}}<1$ is similar to the behavior for ${\bar{k}}>1$, with ${\bar{k}}=k/r_h$.