1 Introduction

An important field in experimental researches for exploring physics beyond the Standard Model (BSM) is the electric dipole moments of leptons (l-EDMs). Predictions of the Standard Model (SM) for l-EDMs, which violates the CP symmetry, are very tiny to detect by the current experiments [1, 2]. For example, the present upper bound of electron-EDMs is

$$\begin{aligned} |d_e|<8.7 \times 10^{-29}~(\textrm{e}.\textrm{cm}), \end{aligned}$$
(1)

by ACME Collaboration in ThO molecules at the 90% confidence level [3, 4], while the prediction of SM as an order of \(10^{-40}~(\mathrm e.cm)\) [2]. Moreover, the Muon g-2 experiment at Brookhaven National Laboratory (BNL) bounds the muon-EDMs [5] as:

$$\begin{aligned} |d_{\mu }| < 1.8 \times 10^{-19}~(\mathrm e.cm), \end{aligned}$$
(2)

while the several experiments have plans to improve it in the order of \( 10^{-21}~(\mathrm e.cm)\), such as the Fermilab Muon g-2 [6] and the J-PARC Muon g-2/EDM [7]. The Paul Scherrer Institute (PSI) also plans to probing the order of magnitude as \(6 \times 10^{-23}~(\mathrm e.cm)\) [8]. About tau-EDMs, the present limit is obtained by the correlation of spin-momentum in the process \(e^{+}e^{-} \rightarrow \gamma ^{*} \rightarrow \tau ^{+}\tau ^{-}\) [9] in the Belle experiment by

$$\begin{aligned} |d_{\tau }|<10^{-17}~(\mathrm e.cm), \end{aligned}$$
(3)

which Belle II experiment should improve it two order of magnitude, namely \(10^{-19}~(\mathrm e.cm)\) [10]. Hence, any observation of l-EDMs can be a signal of the new physics BSM [11,12,13].

On the other hand, D. Colladay and V. A. Kostelecky put forward a Standard Model Extension (SME) that have some extra terms in SM to interpret the violating the symmetries of Lorentz and CPT by several constant coefficients which called Lorentz violation (LV) parameters [14]. SME have been provided for a long time a framework to study of phenomenological effects of LV, for example, the anomalous magnetic dipole moments (AMDMs) [15,16,17] and EDMs of particles [18,19,20,21] are considered. Furthermore, many researches in terrestrial [22,23,24,25,26] and astrophysical [27,28,29,30] systems have extensively considered, where the comprehensive list of constraints can be found in Ref. [31].

There is a CP violation source in the QEDE can give the contributions to the l-EDMs at tree levels [21]. In this paper, we introduce the LV parameter, which can induce the l-EDMs in the QEDE framework and show the connection between this LV parameter and l-EDMs at high energy limit. We consider the electron-positron annihilation (\(e^{+}e^{-}\rightarrow l^{+}l^{-} \)) with new vertex of l-EDMs, where the collision experiments in high energy physics provide a way to test of LV theory [32, 33]. Consequently, we investigate that the breaking of Lorentz symmetry comes from l-EDMs, leads to modification of the cross section in the center of mass frame and constraints the corresponding LV parameter by the current and future terrestrial experiments.

The paper is organized as follows. In Sect. 2, we briefly introduce the CPT-even term, \(d_{\mu \nu }\), in QEDE that can appear the CP violation to find the l-EDMs. We consider the electron-positron annihilation via l-EDMs (i.e. muon and tau) at leading order in Sect. 3 to investigate the cross section effects at high energy limit. We find new bounds on the corresponding LV parameters from the colliders such as LEP, ILC, CLIC, and FCCee. We derive the angular distribution of Bhabha scattering in the presence of Lorentz violating by implying electron-EDMs in Sect. 4 and estimate the new bound on the corresponding LV parameter with using the available terrestrial experiments. Moreover, we obtain constraints on combination of LV parameter with considering the time and location dependence of l-EDMs in the LV background. We make some final remarks in the last section.

2 EDMs of leptons in the QEDE theory

The Lagrangian density of QEDE is parameterized for Leptons as follows (\(\hbar =c=1\)):

$$\begin{aligned} {\mathcal {L}}^{QEDE}=\bar{\psi }(i\Gamma _{\mu }\overleftrightarrow {D}^{\mu }-M)\psi , \end{aligned}$$
(4)

where

$$\begin{aligned} \Gamma _{\mu }= & {} \gamma _{\mu }+c_{\mu \nu }\gamma ^{\nu }-d_{\mu \nu }\gamma ^{\nu }\gamma ^{5} +e_{\mu }+if_{\mu }\gamma ^{5}+\frac{1}{2}g_{\lambda \nu \mu }\sigma ^{\lambda \nu },\nonumber \\ M= & {} m+a_{\mu }\gamma ^{\mu }-b_{\mu }\gamma ^{\mu }\gamma ^{5} +\frac{1}{2}H_{\mu \nu }\sigma ^{\mu \nu }+im_{5}\gamma ^{5}. \end{aligned}$$
(5)

The terms with parameters \(\{a_{\mu },b_{\mu },e_{\mu },f_{\mu },g_{\lambda \nu \mu }\}\) violate CPT symmetry while those with \(\{c_{\mu \nu },d_{\mu \nu },H_{\mu \nu }\}\) preserve CPT symmetry. The LV parameters that appear in the \(\Gamma _{\mu }\) are dimensionless and depend on the momentum of particle, and others in the M have dimensions of mass and are momentum independent by renormalization in the QEDE theory [34]. The LV parameters \(f_{\mu }\) and \(d_{\mu \nu }\) can produce the l-EDMs [21] in non-relativistic limit, where \(f_{\mu }\) can absorb with a redefinition of fermion field [35]. Therefore, we consider only \(d_{\mu \nu }\) parameter as a source of CP violation in the QEDE theory. The effective QEDE theory in the presence of the LV parameter, \(d_{\mu \nu }\) would be given by

$$\begin{aligned} {{{\mathcal {L}}}}^{EDM}_{QEDE}= & {} i\frac{1}{2} \bar{\psi } \gamma ^\mu \overleftrightarrow {D}_{\mu } \psi - m_{l}\bar{\psi }\psi \nonumber \\{} & {} +i\frac{1}{2}\,d_{\mu \nu }\bar{\psi }\gamma _{5} \gamma ^{\mu }\overleftrightarrow {D}^{\nu }\psi , \end{aligned}$$
(6)

where the \( d_{\mu \nu } \) parameter not only modifies Dirac equation but also breaks the spin degeneracy, while there are two dispersion relations and spinors for both particles and antiparticles [36, 37].

The general form factors can be written in the presence of \(d_{\mu \nu }\) is:

$$\begin{aligned} \mathcal{{F_\mu }}(q^2)= & {} F_1(q^{2}).\Big [\,\gamma _\mu +\gamma _5\gamma ^\nu d_{\mu \nu }\Big ]+F_2(q^{2}).\Big [\,\,i\frac{\sigma _{\mu \nu }q^\nu }{2m_{l}}\Big ]\nonumber \\{} & {} +F_3(q^{2}).\Big [(q_\mu -\frac{q^2}{2m_{l}}\gamma _\mu )\gamma _5 +\frac{q^2}{2m_{l}}d_{\mu \nu }\gamma ^\nu \Big ]\nonumber \\{} & {} +F_4(q^{2}).\Big [\,\, \sigma _{\mu \nu } \frac{q^\nu }{2m_{l}}\gamma _5\Big ]+(F_{d})_{\mu }(q^{2}), \end{aligned}$$
(7)

where \(q_{\mu } = p'_{\mu }-p_{\mu }\) is the transition momentum and \(m_{l}\) is the lepton mass. \(F_{1}\) is the usual electric charge, \(F_{2}\) magnetic dipole moment, \(F_{3}\) anapole (axial charge), and \(F_{4}\) electric dipole moment form factors. It should be mention that the \(F_{d}\) form factor denotes all the new form factors that can be defined with \(d_{\mu \nu }\) parameter and given in Ref. [21]. Calculating the vertex function correction at leading order in the QEDE framework shows that the \(F_{4}\) form factor leads to non-zero l-EDMs (\(d_l\)) at high energy limit, which is given by

$$\begin{aligned} d_l=-\frac{F_4({q^2=0})}{2m_{l}}, \end{aligned}$$
(8)

where

$$\begin{aligned} F_4(p,d)= & {} \frac{275\alpha }{18\pi }\Bigg \{\frac{p.d^s.p}{m_{l}^2} \Bigg \}. \end{aligned}$$
(9)

Therefore, the connection between l-EDMs (\(d_{l}\)) and LV parameter (\(d_{\mu \nu }\)) would be as follows:

$$\begin{aligned} \mid d_l\mid= & {} \frac{275\alpha }{36\pi }\Bigg \{\frac{p.d^s.p}{m_{l}^3} \Bigg \}, \end{aligned}$$
(10)

where \(\alpha \) is the fine structure constant and \( d^{s} \) denotes the symmetric part of \( d_{\mu \nu } \) parameter. In fact, the effects l-EDMs is valid when \( (\frac{p}{m_{l}})^{2} \mid d^{s}\mid \le 1\) in the LV theory. The Eq. (10) shows that the l-EDMs could be found at tree level, whereas it could enhance at high energy in the LV background. This feature encourage us to find the upper bounds of LV parameter by considering the current and future experiments for both l-EDMs measurements and colliders.

3 Lepton-pair production via l-EDMs in the LV background

The process \(e^{+}e^{-}\rightarrow l^{+}l^{-} \), where \( l=\mu ,\tau \) is one of the simple reaction in the QED and most important in high energy physics. We attempt to explore the LV effects through l-EDMs (\(d_{l}\)) in the cross section of this process. We take into account the Lagrangian density related to l-EDMs in the effective theory as

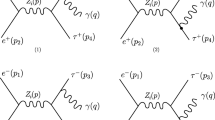
$$\begin{aligned} {\mathcal {L}}^{EDM}_{eff}=-i\frac{1}{2} d_{l}\bar{\psi }\gamma _5\sigma ^{\mu \nu }\psi F_{\mu \nu }, \end{aligned}$$
(11)

where \( \sigma ^{\mu \nu } =\frac{i}{2}[\gamma ^{\mu },\gamma ^{\nu }]\), and \(F_{\mu \nu } \) is the electromagnetic field. One can easily find the CP-odd EDM vertex that is shown by a cross circle in Fig. 1 is \(-ied_{l}\sigma ^{\mu \nu }\gamma ^{5}q_{\nu }\), where \( d_l \) refers to the l-EDMs. It is worthwhile to note that there is also a weak Dipole Moments (wDM) vertex (\(d^{w}_l\)) as well as the l-EDM vertex (\(d_{l}\)), whereas the wDM is coupled to the weak boson field (\(Z^{0}\)) [38, 39]. In this work, however, we ignore it because its effect in our regime is so small.

Fig. 1
figure 1

Photon-Lepton interaction with the l-EDMs vertex (\(d_{l}\))

Full size image

Accordingly, there are two distributions from SM and new physics with \(d_{l}\) for un-polarized \( e^{+}e^{-} \) annihilation process at leading order, which are shown in the Fig. 2. The total squared amplitude at tree level can be written by using perturbation method as follows:

$$\begin{aligned} |M|^2= & {} |M_{SM}+M_{d}|^2=|M_{SM}|^2+|M_{d}|^2+2|M^{*}_{SM}M_{d}|, \nonumber \\ \end{aligned}$$
(12)

where

$$\begin{aligned} M_{SM}= & {} -\frac{e^{2}}{q^{2}}\bigg (\bar{v}(p')\gamma ^{\mu }u(p)\bigg ) \times \bigg (\bar{u}(k)\gamma _{\mu }v(k')\bigg )\nonumber \\{} & {} -\frac{g^{2}}{(4\cos \theta _{\omega })^{2}(q^{2}-M_{Z}^{2})} \bigg (\bar{v}(p')\gamma ^{\mu }(a_{v}-\gamma _{5})u(p)\bigg )\nonumber \\{} & {} \times \bigg (\bar{u}(k)\gamma _{\mu }(a_{v}-\gamma _{5})v(k')\bigg ), \end{aligned}$$
(13)
$$\begin{aligned} M_{d}= & {} -\frac{e^{2}d_{l}}{q^{2}}\bigg (\bar{v}(p')\gamma ^{\mu }u(p)\bigg ) \bigg (\bar{u}(k)\sigma _{\mu \alpha }q^{\alpha }\gamma ^{5}v(k')\bigg ).\nonumber \\ \end{aligned}$$
(14)

Here, \(a_{v}=1-4\sin ^{2}\theta _{\omega }\) and \( \theta _{\omega } \) denotes the Weinberg angle. One can compute the averaged squared amplitude for each parts as follows:

$$\begin{aligned} |\overline{M_{SM}}|^2= & {} e^{4}\bigg (1+\frac{m_{l}^2}{E^2}+\big (1-\frac{m_{l}^{2}}{E^{2}}\big )\cos ^{2}\theta \bigg )\nonumber \\{} & {} +\dfrac{g^{4}}{(4\cos \theta _{\omega })^{4}(1-\dfrac{M_{Z}^{2}}{4E^{2}})^{2}}\nonumber \\{} & {} \times \bigg ((a_{v}^{2}+1)^{2}(1+\cos ^{2}\theta )+8a_{v}^{2}\cos \theta \bigg ), \end{aligned}$$
(15)
$$\begin{aligned} |\overline{M_{d}}|^2= & {} 4e^{4}d_{l}^{2}E^{2}(1-\frac{m_{l}^2}{E^2})\sin ^2{\theta }, \end{aligned}$$
(16)

where E is the total energy of particles and \( \theta \) is the deviation angle from collision direction in the center of mass frame. Therefore, the corresponding total cross section can be driven as follows:

$$\begin{aligned} \sigma (e^{+}e^{-}\rightarrow l^{+}l^{-})= & {} \frac{4\pi \alpha ^{2}}{3s}\bigg (1+\frac{1}{16\sin ^{2}2\theta }\frac{s^2}{(s-M_{Z}^{2})^2}\bigg )\nonumber \\{} & {} +\frac{2\pi \alpha ^{2}d_{l}^{2}}{3}, \end{aligned}$$
(17)

while s refers to the Mandelstam variable and there is any distribution from the crossing terms. Equation (17) shows that one can find the usual cross section in the SM frame by applying \(d_{l}\longrightarrow 0\). In the high energy regime, \( \sqrt{s}>>M_{Z} \), the distribution of cross section in the SM is maximum \(\sigma _{SM}=\frac{4\pi \alpha ^{2}}{3s}\), and the modification term corresponding the l-EDMs effect (\(\sigma _{d}\)) is given by

$$\begin{aligned} \sigma _{d}(p,d_{\mu \nu })= & {} \frac{2\pi \alpha ^{2}d_{l}^{2}(p,d_{\mu \nu })}{3}. \end{aligned}$$
(18)

Therefore, by taking LV parameter \(d_{\mu \nu }\), the effects of l-EDMs at high energy would be importance. To show that, let us considering the deviation of cross section induced by l-EDMs as

$$\begin{aligned} \left| \dfrac{\Delta \sigma }{\sigma _{SM}}\right| =\left| \dfrac{\sigma _{EXP}-\sigma _{SM}}{\sigma _{SM}}\right| \sim \left| \dfrac{\sigma _{d}}{\sigma _{SM}}\right| , \end{aligned}$$
(19)

where \(|\dfrac{\sigma _{d}}{\sigma _{SM}}|=\frac{1}{2}sd^{2}_{l}\), and \(d_l\) obeys of Eq. (10). The electron-positron collider (LEP) at CERN reported the experimental cross section from pair production of both muon and tau channels, for example, at center of mass \(\sqrt{s}=207~\mathrm GeV\) [40, 41]. The deviation introduced in Eq. (19) should be as order of \(10^{-3}\) and \(~10^{-2}\) for muon and tau, respectively. By using Eqs. (10) and (19), one can find that the upper bounds on corresponding LV parameters, which are gathered in Table 1.

Fig. 2
figure 2

\(e^{+}e^{-}\rightarrow l^{+}l^{-} \) process with the l-EDMs vertex (\(d_{l}\))

Full size image
Table 1 Upper bounds on \(d_{\mu \nu } \) from the LEP experiment where \( \sqrt{s}=207~\mathrm GeV \)
Full size table

It is important to note that one can predict the upper bounds on LV parameters from future colliders, see Table 2, such as ILC (International Linear Collider) [42], CLIC (Compact Linear Collider) [43, 44], and FCCee (Future Circular Collider) [45] as the next generation of colliders that proposed with center of mass \(500~\mathrm GeV \), \( 3~\mathrm TeV\), and \( 400~\mathrm GeV \), respectively.

Table 2 Upper bounds on \( d_{\mu \nu } \) from the next generation colliders
Full size table

4 Bhabha scattering via electron-EDMs in the LV background

To calculate the un-polarized differential cross section for Bhabha scattering in the QEDE, the contributions should be considered are shown in Fig. 3. There are the usual SM distributions (s-channel and t-channel) plus the extra ones, which are from the electron-EDMs vertex at leading order.

The corresponding SM magnitude is represented by

$$\begin{aligned} |M_{SM}|= & {} |M(\gamma ,s)+M(\gamma ,t)\nonumber \\{} & {} +M(Z,s)+M(Z,t)|, \end{aligned}$$
(20)

where it can be driven easily as follows:

$$\begin{aligned} M_{SM}= & {} -\frac{e^{2}}{q_{s}^{2}}\bigg [\bar{v}(p')\gamma ^{\mu }u(p)\times \bar{u}(k)\gamma _{\mu }v(k')\bigg ]\nonumber \\{} & {} -\frac{e^{2}}{q_{t}^{2}}\bigg [\bar{u}(p')\gamma ^{\mu }u(p)\times \bar{v}(k)\gamma _{\mu }v(k')\bigg ]\nonumber \\{} & {} -\frac{g^{2}}{(4\cos \theta _{\omega })^{2}(q_{s}^{2}-M_{Z}^{2})}\nonumber \\{} & {} \times \bigg [\bar{v}(p')\gamma ^{\mu }(a_{v}-\gamma _{5})u(p)\times \bar{u}(k)\gamma _{\mu }(a_{v}-\gamma _{5})v(k')\bigg ]\nonumber \\{} & {} -\frac{g^{2}}{(4\cos \theta _{\omega })^{2}(q_{t}^{2}-M_{Z}^{2})}\nonumber \\{} & {} \times \bigg [\bar{u}(p')\gamma ^{\mu }(a_{v}-\gamma _{5})u(p)\times \bar{v}(k)\gamma _{\mu }(a_{v}-\gamma _{5})v(k')\bigg ].\nonumber \\ \end{aligned}$$
(21)
Fig. 3
figure 3

Bhabha scattering with the electron-EDMs vertex for both s-channel and t-channel

Full size image

The electron-EDMs contributions can be written as

$$\begin{aligned} |M_{d}|= & {} |2M_{d}(\gamma ,s)+2M_{d}(\gamma ,t)\nonumber \\{} & {} +M_{dd}(\gamma ,s)+M_{dd}(\gamma ,t)|, \end{aligned}$$
(22)

where \( M_{d}(\gamma ) \) and \( M_{dd}(\gamma )\) refer to one and two electron-EDMs vertexes, respectively. The corresponding magnitude is given by

$$\begin{aligned} M_{d}= & {} -\dfrac{2e^{2}d_{e}q^{\alpha }_{s}}{q_{s}^{2}}\bigg [(\bar{v}(p') \gamma ^{\mu }u(p))\times (\bar{u}(k)\sigma _{\mu \alpha }\gamma ^{5}v(k'))\bigg ]\nonumber \\{} & {} -\dfrac{2e^{2}d_{e}q_{t}^{\alpha }}{q_{t}^{2}}\bigg [(\bar{u}(p') \gamma ^{\mu }u(p))\times (\bar{v}(k)\sigma _{\mu \alpha }\gamma ^{5}v(k'))\bigg ]\nonumber \\{} & {} -\dfrac{2e^{2}d_{e}^{2}q_{s\alpha }q_{s}^{\beta }}{q_{s}^{2}} \bigg [(\bar{v}(p')\sigma ^{\mu \alpha }\gamma ^{5}u(p))\nonumber \\{} & {} \times (\bar{u}(k)\sigma _{\mu \beta }\gamma ^{5}v(k'))\bigg ]\nonumber \\{} & {} -\dfrac{2e^{2}d_{e}^{2}q_{t\alpha }q_{t}^{\beta }}{q_{t}^{2}} \bigg [(\bar{u}(p')\sigma ^{\mu \alpha }\gamma ^{5}u(p))\nonumber \\{} & {} \times (\bar{v}(k)\sigma _{\mu \beta }\gamma ^{5}v(k'))\bigg ], \end{aligned}$$
(23)

here, \(q_{s}\) and \(q_{t}\) refer to transition momentum in s-channel and t-channel, receptively. By applying the straightforward method to calculate the un-polarized cross section for the QED process, the total differential cross section in the center of mass can be rewritten by

$$\begin{aligned} \frac{d\sigma }{d\Omega }= \left( \frac{d\sigma }{d\Omega }\right) _{SM}+\left( \frac{d\sigma }{d\Omega }\right) _{d}+\left( \frac{d\sigma }{d\Omega }\right) _{SM \times d}, \end{aligned}$$
(24)

where \((\frac{d\sigma }{d\Omega })_{SM \times d} \) refers to the differential cross section related to interface of SM and electron-EDMs. The usual differential cross section at the lowest order of SM in the Bhabha scattering calculated in Ref. [46] as

$$\begin{aligned} \left( \frac{d\sigma }{d\Omega }\right) _{SM}= & {} \frac{\alpha ^{2}}{16E^{2}}F(\theta ), \end{aligned}$$
(25)

where \(F(\theta )=\bigg (\frac{3+\cos ^{2}\theta }{1-\cos \theta }\bigg )^{2}\).

The new contributions of electron-EDMs terms can be found as follows:

$$\begin{aligned} \bigg (\frac{d\sigma }{d\Omega }\bigg )_{d}= & {} -2\dfrac{\alpha ^{2}d_{e}^{2}}{s}\nonumber \\{} & {} \times \bigg (-\frac{t^{2}}{u}+2\frac{s^{2}}{u}+2u -\frac{u^{2}}{s}+2s+2\frac{t^{2}}{s}\bigg ),\end{aligned}$$
(26)
$$\begin{aligned} \bigg (\frac{d\sigma }{d\Omega }\bigg )_{SM \times d}= & {} \dfrac{\alpha ^{2}d_{e}^{2}}{16s}\bigg (-2\frac{s^{2}}{u} -8u+8\frac{t^{2}}{u}+16t-10\frac{t^{2}}{s}\bigg )\nonumber \\{} & {} +\dfrac{g^{2}\alpha d_{e}^{2}(a_{v}^{2}-1)}{64\pi s(4\cos \theta _{\omega })^{2}}\nonumber \\{} & {} \times \bigg (\dfrac{-2s^{2}-8u^{2}+8t^{2}+16tu}{u-M_{Z}^{2}}+\dfrac{10t^{2}}{s-M_{Z}^{2}}\bigg ), \end{aligned}$$
(27)

which \( e=g\sin \theta _{\omega } \), \( E=2E_{c.m} \), and \( \theta \) is the collision angle in the Bhabha scattering. By using the usual Mandestam variables, the modifications in the angular distributions come from the electron-EDMs is given by

$$\begin{aligned} \bigg (\frac{d\sigma }{d\Omega }\bigg )_{d}+\bigg (\frac{d\sigma }{d\Omega }\bigg )_{SM \times d}= & {} -\frac{\alpha ^{2}d^{2}_{e}}{2}G(\theta )+\frac{\alpha ^{2}d^{2}_{e}}{16}H(\theta )\nonumber \\{} & {} +\frac{\alpha ^{2}d^{2}_{e}}{64\times 16}K(\theta _{\omega })J(\theta ), \end{aligned}$$
(28)

with

$$\begin{aligned} G(\theta )= & {} \dfrac{{\cos ^{3}\theta }+{\cos ^{2}\theta }+23\cos \theta +13}{1+\cos \theta },\nonumber \\ H(\theta )= & {} \dfrac{-5{\cos ^{3}\theta }+13{\cos ^{2}\theta }+21\cos \theta -9}{1+\cos \theta },\nonumber \\ J(\theta )= & {} \dfrac{16(-2\cos ^{2}\theta +4\cos \theta -1)}{1+\cos \theta +\frac{M^{2}_{Z}}{2E^{2}}}\nonumber \\{} & {} +\dfrac{10(1-\cos \theta )^{2}}{1-\dfrac{M_{Z}^{2}}{4E^{2}}}, \end{aligned}$$
(29)

while the Weinberg angle function can be described by

$$\begin{aligned} K(\theta _{\omega })=\dfrac{4(1-4\sin ^{2}\theta _{\omega })^{2}-1}{\sin ^{2}2\theta _{\omega }}. \end{aligned}$$
(30)

The expressions (25–29) indicate that the electron-EDMs (\(d_{e}\)) provides the new angular distributions in the differential cross section, which may sensitive to new physics. It is worthwhile to mention that the usual Bhabha scattering distribution can be recovered by using \(d_{e}\longrightarrow 0\). To determine the upper bound for the corresponding LV parameter (\(d^{e}_{LV}\)), we use the Eq. (10) and the maximum energy beam \( \sqrt{s}=207~\mathrm GeV \) by the LEP collaboration on precision tests for Bhabha scattering which is available in Refs. [40, 41]. The upper bound on LV parameter, namely \( d_{LV}^{e} < 3.6 \times 10^{-17} \) can be obtained by the beam direction \( cos\theta =0 \). Here, we set \((\frac{d\sigma }{d\Omega })_{SM}\sim 2\dfrac{\alpha ^{2}}{s}\) and \((\frac{d\sigma }{d\Omega })_{d}~\sim 8\alpha ^{2}d^{2}_{e}\), which cause the corresponding deviation should be as \(4sd^{2}_{e}\). This bound finds from the terrestrial experiment can be compatible with similar ones achieved in Ref. [31]. Moreover, we suggest upper bounds from future colliders, see Table 3, which are very tight compare with astrophysical bounds, one can see Ref. [31].

Table 3 Upper bounds on \( d_{\mu \nu }^{e} \) from future experiments, where \(cos\theta {=}0\)
Full size table

5 Time and location dependence on l-EDMs in the LV theory

We use a transformation between the non-rotating (the standard Sun-centered) and rotating (the Earth) frames to show the time and location dependence of LV parameter. It is given by \(\hat{x}_{i}=R_{iJ}\hat{X}_{J}\),

$$\begin{aligned} R_{iJ}=\left( \begin{array}{ccc} \cos {\chi }\cos {\Omega t} &{} \quad \cos {\chi }\sin {\Omega t} &{}\quad -\sin {\chi } \\ -\sin {\Omega t} &{}\quad \cos {\Omega t} &{} \quad 0 \\ \sin {\chi }\cos {\Omega t} &{} \quad \sin {\chi }\sin {\Omega t} &{} \quad \cos {\chi }\\ \end{array} \right) . \end{aligned}$$
(31)

Here, \(\hat{x_{i}}=(\hat{x}, \hat{y}, \hat{z})\) is the rotating basis and \(\hat{X_{J}}=(\hat{X}, \hat{Y}, \hat{Z})\) is the non-rotating basis, where \(\hat{Z}\) refers to along the north direction parallel to the Earth’s axis and \(\hat{z}\) is normal to surface of the Earth [47]. It should note that \( \Omega \sim 2\pi /(23\mathrm h~56\mathrm m)\) is the Earth’s sidereal rotation frequency, and \(\chi \) denotes to the angle between \(\hat{Z}\) and \(\hat{z}\). Since LV parameters are determined by the non-rotating frame, it is valuable to show them with function of time and location parameters. At this point, l-EDMs in Eq. (10) can be expressed by

$$\begin{aligned} d_l= & {} 4.8 \times 10^{-16}\dfrac{1}{m_{l}^3}\nonumber \\{} & {} \times \Bigg \{p^{2}_{0}d_{00}+p^{2}_{x}d_{xx}+p^{2}_{y}d_{yy}+p^{2}_{z}d_{zz}\Bigg \} (\mathrm e.cm), \end{aligned}$$
(32)

where by taking into account the values of muon particle inside a storage ring for instant at BNL, one can rewrite the muon-EDMs (\(l=\mu \)) in LV background as

$$\begin{aligned} d^{BNL}_\mu= & {} 2.4 \times 10^{-16}\dfrac{p_{0}^{2}}{m_{\mu }^3}\nonumber \\{} & {} \times \Bigg \{2d_{00}+d_{xx}+d_{yy}\Bigg \} (\mathrm e.cm), \end{aligned}$$
(33)

which muon is traveling in the x–y plane with energy \(p_{0}>> m_{\mu }\), \( p_{z}=0 \), and \(p^{2}_{x}=p^{2}_{y}\). The expression \(2d_{00}+d_{xx}+d_{yy} \) with transforming such as \(d_{ij}=R_{iI}R_{jJ}d_{IJ}\) can be found as

$$\begin{aligned} 2d_{00}+d_{xx}+d_{yy}= & {} 2d_{TT}+(1-\sin ^2\chi \cos ^2\Omega t)d_{XX}\nonumber \\{} & {} +(1-\sin ^2\chi \sin ^2\Omega t)d_{YY}+\sin ^2\chi d_{ZZ}\nonumber \\{} & {} -\frac{1}{2}\sin ^2\chi \sin 2\Omega t(d_{XY}+d_{YX})\nonumber \\{} & {} -\frac{1}{2}\sin 2\chi \cos \Omega t(d_{XZ}+d_{ZX})\nonumber \\{} & {} -\frac{1}{2}\sin 2\chi \sin \Omega t(d_{YZ}+d_{ZY}), \end{aligned}$$
(34)

here the time dependence leads to day-night asymmetry for muon-EDMs (\(d_{\mu }\)). For muon inside a ring with an energy around \(3~\mathrm GeV \) in the location of \( \chi \sim 49.1^{\circ } \), one can estimate a bound on the combination of LV parameter (\( d_{\mu \nu } \)) for muon particle as the order of:

$$\begin{aligned} d_{TT}+0.36(d_{XX}+d_{YY})+0.28d_{ZZ}< 4.15 \times 10^{-8}, \end{aligned}$$
(35)

whereas the upper experimental bound on muon-EDMs is \( 1.8 \times 10^{-19}~(\mathrm e.cm)\). For experiments J-PARC and PSI, where \(p_{0}(= 0.3~\mathrm GeV\sim m_{\mu })\), we obtain

$$\begin{aligned} d^{J-PARC}_\mu&=4.8 \times 10^{-16}\dfrac{p_{0}^{2}}{m_{\mu }^3}d_{00}~ (\mathrm e.cm), \end{aligned}$$
(36)

where muon-EDMs is independent of time (and location) and also impose the upper bounds on the corresponding LV parameter, namely \(d^{\mu }_{TT}<2.08\times 10^{-7}\), and \(d^{\mu }_{TT}<2.08\times 10^{-9}\) for the sensitivity of J-PARC and PSI experiments, respectively. These bounds on \( d_{\mu \nu } \) parameters may consider in the muon sector from the terrestrial experiments, see Ref. [31]. These bounds show that by improving the sensitivity of \(d_{\mu }\) and muon energy in the ring, one has the tight bounds on combination of LV parameter.

Moreover, we employ a similar analysis for tau-EDMs (\(l=\tau \)), which probed from electron-positron collider in the Belle experiment. One can rewrite the corresponding EDMs as follows:

$$\begin{aligned} d^{Belle}_\tau&=4.8 \times 10^{-16}\dfrac{p_{0}^{2}}{m_{\tau }^3}\Bigg \{d_{00}+d_{zz}\Bigg \} (\mathrm e.cm), \end{aligned}$$
(37)

where we consider the tau particle produces with \(p_{x}=p_{y}=0\), and energy \(p_{0}>>m_{\tau }\). The combination of LV parameter can be extracted in the non-rotating frame by

$$\begin{aligned} d_{00}+d_{zz}= & {} d_{TT}+\sin ^2\chi \cos ^2\Omega td_{XX}\nonumber \\{} & {} +\sin ^2\chi \sin ^2\Omega td_{YY}+\cos ^2\chi d_{ZZ}\nonumber \\{} & {} +\frac{1}{2}\sin ^2\chi \sin 2\Omega t(d_{XY}+d_{YX})\nonumber \\{} & {} +\frac{1}{2}\sin 2\chi \cos \Omega t(d_{XZ}+d_{ZX})\nonumber \\{} & {} +\frac{1}{2}\sin 2\chi \sin \Omega t(d_{YZ}+d_{ZY}), \end{aligned}$$
(38)

where the upper bound for tau sector is found at \(\chi \sim 36.2^{\circ }\) [9] as

$$\begin{aligned} d_{TT}+0.17(d_{XX}+d_{YY})+0.65d_{ZZ}< 2.08 \times 10^{-4}, \end{aligned}$$
(39)

whereas this combination can be restricted by \(10^{-6}\) for the Belle II experiment [10].

6 Conclusion

Standard Model Extension as a frame to follow the effects of Lorentz violation has provided to the l-EDMs at tree level. The operator \( d_{\mu \nu } \) in the QEDE that could reflect the CP violation and l-EDMs at the non-relativistic limit. The l-EDMs could be enhanced in the LV background, specifically when considering cross section of electron-positron annihilation. It is shown in this paper that the cross section depends on the energy of particle in the LV background. By utilizing the LEP data, we found that the bounds on \(|d^{e}_{LV}| < 3.6 \times 10^{-17} \), \( |d^{\mu }_{LV}|< 9.5 \times 10^{-10} \), and \( |d^{\tau }_{LV}|< 1.5 \times 10^{-6} \) for electron, muon, tau particles, respectively. Furthermore, we estimated that these bounds may be tight in future colliders, see Tables 2 and 3. Finally, we discussed about time and location dependence of l-EDMs (\(d_{l}\)) which are limited the components of \(d_{\mu \nu }\) in muon sector as order of \(d_{TT}+0.36(d_{XX}+d_{YY})+0.28d_{ZZ}< 4.15 \times 10^{-8}\), \(d^{\mu }_{TT}<2.08\times 10^{-7}\), and \(d^{\mu }_{TT}<2.08\times 10^{-9}\) from BNL, J-PARC, and PSI experiments, respectively. Similarly, the combinations of LV in tau sector (\(d^{\tau }_{LV}\)) are bounded as \(d_{TT}+0.17(d_{XX}+d_{YY})+0.65d_{ZZ}< 2.08 \times 10^{-4}\) and \(d_{TT}+0.17(d_{XX}+d_{YY})+0.65d_{ZZ}< 2.08 \times 10^{-6}\) through Belle, and Belle II experiments. The bounds in both muon and tau sectors of \(d_{\mu \nu }\) are first time from terrestrial experiments and may be strong ones with the accurate experiment data in future.