Heavy quarks in polarised deep-inelastic scattering at the electron-ion collider

Abstract

We extend the FONLL general-mass variable-flavour-number scheme to the case of longitudinally polarised DIS structure functions, accounting for perturbative corrections up to $\mathcal {O}\left( \alpha _s^2\right)$. We quantify the impact of charm quark mass and higher-order perturbative corrections on projected measurements of inclusive and charm-tagged longitudinal asymmetries at the Electron-Ion Collider (EIC) and at the Electron-ion collider in China (EicC). We demonstrate how the inclusion of these corrections is essential to compute predictions with an accuracy that matches the projected precision of the measurements. The computation is made publicly available through the open-source EKO and YADISM programs.

1 Introduction

The production of charm quarks in unpolarised deep-inelastic scattering (DIS) contributes significantly to the inclusive structure functions measured by HERA [1, 2]. In particular, it can amount to up to 25% at small values of the proton momentum fraction x and at small to moderate values of the momentum transfer $Q^2$. The accurate determination of parton distribution functions (PDFs) [3,4,5] from experimental data therefore requires to include charm mass effects in the computation of DIS cross sections. Indeed, all modern PDF determinations [1, 6,7,8,9] account for these effects either with the fixed-flavour-number (FFN) scheme [10] or with a general-mass variable-flavour-number (GM-VFN) scheme [11,12,13]. The latter combines power-suppressed mass corrections proportional to $m_c^2/Q^2$ with resummation of collinear logarithms of the form $\ln (Q^2/m_c^2)$, where $m_c$ is the charm quark mass. GM-VFN schemes provide an accurate description of charm structure functions for all values of $Q^2$.

The production of charm quarks in polarised DIS is in principle subject to similar considerations. Until now, however, a zero-mass variable flavour number (ZM-VFN) scheme, whereby charm production is modelled in terms of a massless charm PDF, has been used in all modern polarised PDF determinations [14,15,16,17]. The reason being that charm mass effects are small in the kinematic region covered by the available polarised DIS datasets, which furthermore are less precise than their unpolarised counterparts.

This state of affairs will change with the upcoming Electron-Ion Collider [18], which is expected to start taking data in the 2030 s. The EIC will be sensitive to polarised DIS structure functions and asymmetries down to $x\sim 10^{-4}$ for both inclusive and charm-tagged measurements with unprecedented precision. Similar considerations apply to the proposed Electron-ion collider in China (EicC) [19]. The theoretical interpretation of these upcoming high-precision measurements demands, in analogy with the unpolarised case, to properly account for charm mass effects and higher-order perturbative corrections.

The goal of this paper is to present a unified computational framework in which longitudinally polarised structure functions, cross sections, and asymmetries can be determined using a state-of-the-art treatment of higher-order QCD and charm-quark corrections. In particular, this is achieved by extending the FONLL GM-VFN scheme, developed for unpolarised DIS in [12, 20], to the polarised case. The FONLL scheme matches the massive fixed-flavour computation, accurate when $Q^2\sim m_c^2$, with the massless computation, accurate when $Q^2\gg m_c^2$. Our computational framework is made available through the open-source EKO [21] and YADISM [22] software.

We deploy this framework to evaluate predictions for inclusive and charm-tagged longitudinally polarised asymmetries in the kinematic region covered by the EIC and EicC. We specifically quantify the impact of including higher-order and charm-quark corrections in the computation, and we demonstrate their comparative relevance to properly match the expected precision of these measurements. The theoretical accuracy of our framework therefore represents an important input to analyse future EIC and EicC data, in particular to determine polarised PDFs.

The outline of this paper is as follows. In Sect. 2 we summarise the theoretical framework underpinning the calculation of massless and massive polarised structure functions up to $\mathcal {O}\left( \alpha _s^2\right)$ accuracy, and discuss their combination into the FONLL scheme. In Sect. 3 we assess the phenomenological relevance of heavy quark mass effects and higher-order QCD corrections on predictions for inclusive and charm-tagged longitudinally polarised asymmetries at the EIC and EicC. In particular, we compare these corrections to the projected experimental uncertainties for these observables. A summary is provided in Sect. 4. The paper is supplemented with two appendices. Appendix A presents a benchmark of the implementation of polarised DGLAP evolution in EKO against PEGASUS [23]. Appendix B revisits the role of target mass corrections in polarised structure functions, and compares their impact with that associated with heavy quark and higher-order corrections.

2 Polarised structure functions in a general-mass scheme

In this section we discuss how the FONLL scheme can be extended to the polarised case. We first review the definition of polarised structure functions. We then discuss the details of the FONLL scheme in the polarised case and its implementation in EKO and YADISM. We finally present numerical results in different regions of x and $Q^2$ to validate the implementation of the scheme, and highlight the role played by charm mass effects, by higher-order corrections, and by the choice of input polarised PDFs.

2.1 Polarised structure functions revisited

Let us consider lepton-proton polarised DIS where both the lepton and the proton beams are longitudinally polarised. The differential cross section can be expressed in terms of the polarised structure functions $g_1$, $g_L$, and $g_4$ as

$$\begin{aligned}&\frac{d^2 \Delta \sigma ^j(x,Q^2)}{dx dy} = \frac{4 \pi \alpha ^2}{xyQ^2} \xi ^j \left\{ - \left[ 1 + (1-y)^2\right] g_4^j(x,Q^2) \right. \nonumber \\&\quad + y^2 g_L^j(x,Q^2) + (-1)^p 2x \left[ 1 - (1-y)^2\right] \nonumber \\&\quad \times \left. g_1^j(x,Q^2) \right\} , \end{aligned}$$

(2.1)

with $p= 1$ for leptons and $p = 0$ for anti-leptons. The index j distinguishes charged current (CC) interactions, with $\xi ^\textrm{CC}=2$, from neutral current (NC) interactions, with $\xi ^\textrm{NC}=1$. The inelasticity y is given by $y=Q^2/(2x m_N E_{\ell })$ for fixed-target scattering and $y=Q^2/xs$ for collider scattering; $m_N$ is the proton mass, $E_{\ell }$ is the lepton beam energy, and s is the square of the centre-of-mass energy. In Eq. (2.1), we neglect the polarised structure functions $g_2$ and $g_3$, which are suppressed by powers of $W^2/Q^2$, with W being the invariant mass of the hadronic final state.

Provided $Q^2$ is large enough, polarised structure functions can be factorised as a convolution between perturbative polarised coefficient functions, $\Delta C^j_{i, k}(x,\alpha _s)$, and non-perturbative, process-independent polarised PDFs, $\Delta q_k(x,Q^2)$ (for quarks), and $\Delta g(x,Q^2)$ (for the gluon). These polarised PDFs are defined as the difference between the PDFs of partons with the same and with the opposite helicity as compared to the direction of the proton spin, e.g. for quarks

$$\begin{aligned} \Delta q_k(x,Q^2) = q_k^{\uparrow \uparrow }(x,Q^2) - q_k^{\uparrow \downarrow }(x,Q^2) \, , \end{aligned}$$

(2.2)

and likewise for the gluon, where the first arrow indicates the direction of the proton spin and the second the partonic helicity. As reviewed in Appendix A, these polarised PDFs satisfy polarised DGLAP evolution equations in analogy with their unpolarised counterparts. At leading twist, this factorised convolution for the polarised structure functions reads

$$\begin{aligned} \begin{aligned} g_1^j(x,Q^2)&= \int _{x}^{1} \frac{dz}{z} \Bigg [ \sum _{k={1}}^{n_f} \Delta q_k^+\left( \frac{x}{z},Q^2\right) \Delta C^j_{1, k}(z,\alpha _s) \\&\quad + \Delta g\left( \frac{x}{z},Q^2\right) \Delta C^j_{1,g}(z,\alpha _s) \Bigg ] , \\ g_i^j(x,Q^2)&= \int _{x}^{1} \frac{dz}{z} \Bigg [ \sum _{k={1}}^{n_f} \Delta q_k^-\left( \frac{x}{z},Q^2\right) \Delta C^j_{i, k}(z,\alpha _s) \Bigg ], \\&\quad i= 4,L , \end{aligned} \end{aligned}$$

(2.3)

with $n_f$ the number of active quark flavours and $\Delta q_k^\pm = \Delta q_k \pm \Delta {\bar{q}}_k$ defining the usual sea and valence quark flavour combinations. Being leading-twist, Eq. (2.3) does not include target mass corrections (TMCs), which are reviewed in Appendix B.

The dominant contribution to the double differential cross section Eq. (2.1) is provided by the parity-conserving $g_1$ structure function. Therefore, we will henceforth focus only on this specific structure function. Furthermore, we restrict ourselves to the electromagnetic case, in which a virtual photon is exchanged in the hard scattering. Nevertheless, our discussion can be generalised to the other polarised structure functions.

Rearranging the quark PDFs in linear combinations which are convenient for DGLAP evolution, see Appendix A, the structure function $g_1$ can be expressed as

$$\begin{aligned} g_1 (x, Q^2)&= \left( \frac{1}{n_f} \sum _{k=1}^{n_f} e_{q_k}^2 \right) \int _{x}^{1} \frac{dz}{z} \Bigg [\Delta \Sigma \left( \frac{x}{z}, Q^2 \right) \Delta C_1^{\textrm{PS}} \nonumber \\&\quad \times \left( z, \alpha _s\right) + \Delta g \left( \frac{x}{z} , Q^2 \right) \Delta C_{1,g}\left( z,\alpha _s\right) \Bigg ] \nonumber \\&\quad + \sum _{k=1}^{n_f} e_{q_k}^2 \int _{x}^{1} \frac{dz}{z} \Delta q_k^+ \left( \!\frac{x}{z},Q^2\!\right) \Delta C_1^{\textrm{NS}} \left( z, \alpha _s\right) , \end{aligned}$$

(2.4)

where $e_{q_k}$ is the fractional quark charge. The polarised structure function $g_1 (x, Q^2)$ is therefore decomposed into three contributions proportional to the quark non-singlet (NS), gluon, and quark pure singlet (PS) coefficient functions. The latter is defined as the difference between the singlet (S) and NS coefficient functions, $\Delta C_1^{\textrm{PS}} = \Delta C_1^{\textrm{S}} - \Delta C_1^{\textrm{NS}}$.

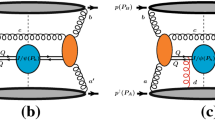
Equation (2.4) assumes that all active quarks at the scale $Q^2$ can be treated as massless. However, quark mass effects cannot be neglected when the value of $Q^2$ is close to the value of a heavy quark mass $m_h$. Such effects can be included by modifying the expressions for the coefficient functions, so that $g_1$ reads as

$$\begin{aligned}&g_1 (x, Q^2, m_h^2) \!=\! \left( \! \frac{1}{n_f} \sum _{k=1}^{n_f} e_{q_k}^2 \!\right) \int _{x}^{1} \frac{dz}{z} \left[ \Delta \Sigma \left( \! \frac{x}{z}, Q^2 \!\right) \Delta C_1^{\textrm{PS}}\right. \nonumber \\&\left. \quad \times \left( z, \alpha _s, \frac{m_h^2}{Q^2}\right) + \Delta g \left( \frac{x}{z} , Q^2 \right) \Delta C_{1,g}\left( z,\alpha _s,\frac{m_h^2}{Q^2}\right) \right] \nonumber \\&\quad + \sum _{k=1}^{n_f} e_{q_k}^2 \int _{x}^{1} \frac{dz}{z} \Delta q_{k}^+ \left( \frac{x}{z},Q^2\right) \Delta C_1^{\textrm{NS}} \nonumber \\&\quad \times \left( z, \alpha _s,\frac{m_h^2}{Q^2}\right) . \end{aligned}$$

(2.5)

The polarised structure function is then recast into light, heavy, and light-heavy contributions

$$\begin{aligned} g_1(x,Q^2,m_h^2)= & {} g_{1}^{(\ell )}(x,Q^2) + g_{1}^{(h)}(x,Q^2,m_h^2/Q^2) \nonumber \\{} & {} + g_{1}^{(\ell h)}(x,Q^2,m_h^2/Q^2) , \end{aligned}$$

(2.6)

where $g_{1}^{(\ell )}$ indicates the contributions from diagrams where only light quark lines are present, $g_{1}^{(h)}$ those from diagrams where the heavy quark couples to the virtual gauge boson, and $g_{1}^{(\ell h)}$ those which contain heavy quark lines but where a light quark couples to the virtual boson.

The separation between light and heavy structure functions in Eq. (2.6) is hence affected by an ambiguity concerning in which category one should assign the $g_{1}^{(\ell h)}$ contribution, involving heavy quarks in the final state but where only light quarks couple to the virtual boson. This ambiguity is irrelevant for the inclusive structure function, but it affects the heavy quark structure functions.

The case of charm production is of particular phenomenological interest. The experimental definition of the charm structure function $g_1^c$ is based on tagging charm quarks (or charmed hadrons) in the final state, hence it would include $g_{1}^{(\ell h)}$. However, the theoretical infrared-safe definition of $g_1^c$ coincides with $g_{1}^{(h)}$, and contains only diagrams where the charm quark couples with the virtual boson. Here we adopt the same convention as in [12], and define the charm structure function exclusively in terms of $g_{1}^{(h)}$, while the $g_{1}^{(\ell h)}$ contribution enters only the total structure function. The latter term is non-zero only starting at $\mathcal {O}\left( \alpha _s^2\right)$ and is small in the region relevant for both current and future measurements. In the $n_f=3$ massive scheme, the charm structure function at the first non-trivial order is expressed in terms of the gluon polarised PDF,

$$\begin{aligned} g_1^c (x, Q^2,m_c^2)= e_c^2\int _{x}^{1} \frac{dz}{z} \Delta g \left( \frac{x}{z} , Q^2 \right) \Delta C^{c}_{1,g} \left( z,\alpha _s,\frac{m_c^2}{Q^2}\right) , \end{aligned}$$

(2.7)

with the first non-zero term of the gluon coefficient function $\Delta C_{1,g}$ being $\mathcal {O}\left( \alpha _s\right)$.

The massless coefficient functions entering the polarised structure function $g_1$, Eq. (2.4), have been computed at NNLO in [24] and recently at N$^3$LO in [25].¹ The massive coefficient functions entering Eq. (2.5) are available up to $\mathcal {O}(\alpha _s^2)$ [29] together with their corresponding asymptotic limit $Q^2 \gg m_h^2$ [30,31,32,33,34,35]. In Table 1 we summarise which polarised neutral-current DIS coefficient functions are available in the literature and which we have implemented in YADISM. For each perturbative order (NLO, NNLO, and N$^3$LO) we indicate the light-to-light (“light”), light-to-heavy (“heavy”), heavy-to-heavy (“intrinsic”), and “asymptotic” ($Q^2 \gg m_h^2$) contributions. As we will see next, all the perturbative ingredients required to implement FONLL at $\mathcal {O}(\alpha _s^2)$ are available and implemented. Whereas, in principle, Eq. (2.7) could be extended to account for a polarised intrinsic charm component, as done for the unpolarised case [36], we neglect it here and set it to zero. The implementation of the massless polarised coefficient functions and structure functions in YADISM has been benchmarked against APFEL[37] and APFEL++[38] up to $\mathcal {O}(\alpha _s^2)$, finding satisfactory agreement [22].

Table 1 Overview of polarised neutral-current DIS coefficient functions available in the literature and implemented in YADISM (blue), available in the literature (only for $g_1$), but not implemented in YADISM (yellow), and not available in the literature (red). For each perturbative order (NLO, NNLO, and N$^3$LO) we indicate the light-to-light (“light”), light-to-heavy (“heavy”), heavy-to-heavy (“intrinsic”), and “asymptotic” ($Q^2 \gg m_h^2$ limit) coefficients functions which have been implemented and benchmarked

2.2 The FONLL scheme for polarised structure functions

The FONLL scheme was originally proposed in [39] to account for heavy quark mass effects in D- and B-meson production in hadronic collisions, and was later generalised to unpolarised DIS [12], eventually taking into account an intrinsic charm contribution [20]. The basic idea underlying FONLL is best exemplified in the case of charm quark mass effects. There FONLL combines the massive (three-flavor-number, 3FN) and massless (four-flavor-number, 4FN) schemes through a suitable matching procedure. Since both the 3FN and the 4FN schemes are well defined factorisation schemes, the FONLL framework has the advantage that it can be generally applied to any (un)polarised electro- and hadro-production processes without the need to rely on alternative factorisation schemes. Whereas henceforth we will focus on charm, the discussion can be readily generalised to the case of bottom, as well as to that of multiple heavy quarks.

In analogy with the unpolarised case, a generic polarised structure function in the FONLL scheme with four active quarks can be written as:

$$\begin{aligned} g^{\textrm{FONLL}} (x, Q^2) = g^{[4]}(x, Q^2) + g^{[3]}(x, Q^2) - g^{[3,0]}(x, Q^2), \end{aligned}$$

(2.8)

where the 3FN- and 4FN-scheme structure functions are respectively given by:

$$\begin{aligned} g^{[3]}(x, Q^2)&= \int _{x}^{1} \frac{dz}{z} \sum _{i=g,q,\bar{q}} \Delta f_i^{[3]} \left( \frac{x}{z}, Q^2 \right) \nonumber \\ {}&\quad \times \Delta C_i^{[3]} \left( z, \alpha _s^{[3]}, \frac{m_c^2}{Q^2} \right) \, , \end{aligned}$$

(2.9)

$$\begin{aligned} g^{[4]}(x, Q^2)&= \int _{x}^{1} \frac{dz}{z} \sum _{i=g,q,\bar{q},c,\bar{c}} \Delta f_i^{[4]} \left( \frac{x}{z}, Q^2 \right) \nonumber \\ {}&\quad \times \Delta C_i^{[4]} \left( z, \alpha _s^{[4]} \right) \, , \end{aligned}$$

(2.10)

with q and c denoting the light quarks and the charm quark, respectively. The PDFs and strong coupling entering the 3FN structure function in Eq. (2.8) can be expressed in terms of their 4FN counterparts, by means of the matching relations provided below. The asymptotic limit ($Q^2\gg m_c^2$) of the massive calculation, $g^{[3,0]}$, ensures that terms appearing in both the 3FN and 4FN schemes cancel out for virtualities much higher than that charm quark mass, and it is given by

$$\begin{aligned} g^{[3,0]}(x, Q^2)&= \int _{x}^{1} \frac{dz}{z} \sum _{i=g,q,\bar{q}} \Delta f_i^{[3]} \left( \frac{x}{z}, Q^2 \right) \Delta C_i^{[3,0]}\nonumber \\&\quad \times \left( z, \alpha _s^{[3]}, \log \frac{m_c^2}{Q^2} \right) , \end{aligned}$$

(2.11)

where $\Delta C_i^{[3,0]}$ is the massless (asymptotic) limit of the polarised massive coefficient function, in which only the collinear logarithms $\log (m^2_c/Q^2)$ are retained and mass-suppressed terms are neglected.

As pointed out in [12], there is some flexibility in choosing the perturbative accuracy at which heavy quark mass terms are included in the 3FN and 4FN schemes. In particular, three different variants can be considered: FONLL-A, in which both 3FN and 4FN expressions are computed at $\mathcal {O}(\alpha _s)$; FONLL-B, in which the 3FN expression is computed at $\mathcal {O}(\alpha _s^2)$ while the 4FN is computed at $\mathcal {O}(\alpha _s)$; and FONLL-C, in which both 3FN and 4FN expressions are computed at $\mathcal {O}(\alpha _s^2)$.

It is clear from Eq. (2.8) that in the asymptotic limit the FONLL expression reduces to the 4FN scheme owing to the fact that the difference term $\left( g^{[3]} - g^{[3,0]} \right)$ vanishes by construction. On the other hand, in the threshold region $m^2_c\sim Q^2$, the difference term $g^{[d]} \equiv \left( g^{[4]} - g^{[3,0]} \right)$ vanishes only up to higher-order perturbative corrections, which can be numerically large. Different options are available to reduce the impact of a non-vanishing value of $g^{[d]}$ near the threshold region so that the 3FN calculation is recovered. One option, known as $\chi$-scaling, consists in replacing the lower integration limit x in the convolutions entering $g^{[d]}$, namely Eqs. (2.10) and (2.11), with a scaling variable $\chi =x(1+4m_c^2/Q^2)$, motivated by the physical threshold for charm quark pair production.

Fig. 1

Comparison of the polarised proton PDFs from the NNPDFpol1.1 [14], JAM17 [17], and DSSV14 [16] NLO determinations at $Q=2$ GeV. Error bands indicate the corresponding $68\%$ CL PDF uncertainties, evaluated over the Monte Carlo replicas provided by each group. We note that the polarised charm PDF has been set to zero in the DSSV14 Monte Carlo grid

In FONLL, one adopts instead a damping prescription, which is based on rewriting Eq. (2.8) as

$$\begin{aligned} g^{\textrm{FONLL}} (x, Q^2)&= g^{[3]}(x, Q^2) + D\left( \frac{m^2_c}{Q^2} \right) g^{[d]}(x,Q^2), \nonumber \\ D\left( \frac{m^2_c}{Q^2} \right)&\equiv \Theta \left( Q^2 - m^2_c \right) \left( 1 - \frac{m^2_c}{Q^2} \right) ^2. \end{aligned}$$

(2.12)

The definition of the damping factor D in Eq. (2.12) ensures that the difference term $g^{[d]}$, formally of higher order, is suppressed close to the threshold region $m^2_c \sim Q^2$, without affecting the required cancellation between $g^{[3]}$ and $g^{[3,0]}$ in the asymptotic limit $Q^2\gg m_c^2$. In this work, when presenting results for the polarised FONLL structure functions, we adopt the threshold damping prescription Eq. (2.12). For unpolarised structure functions, the numerical impact of this threshold damping prescription is large in FONLL-A, and otherwise small in FONLL-B and FONLL-C. In the polarised case, instead, one finds minimal effects of the damping prescription for all FONLL variants.

The two expressions in Eqs. (2.9) and (2.10) are alternative definitions of the polarised structure functions that depend on the PDFs and strong coupling. As mentioned previously, in order to evaluate the FONLL expression in Eq. (2.8), the massive 3FN structure function needs to be expressed in terms of $\Delta f_i^{[4]}$ and $\alpha _s^{[4]}$. The relations between the PDFs and strong coupling in the two schemes are defined at some fixed matching scale $\mu _c$ and the corresponding results at a generic scale $Q^2\ne \mu _c^2$ can be obtained using the DGLAP evolution equations, see Appendix A. These matching conditions are given by

$$\begin{aligned} \alpha _s^{[4]} (\mu ^2_c)&= \alpha _s^{[3]} (\mu ^2_c) + \sum _{n=2}^{\infty } c_n \left( \alpha _s^{[3]} (\mu ^2_c)\right) ^n, \end{aligned}$$

(2.13)

$$\begin{aligned} \Delta f_i^{[4]} (x, \mu ^2_c)&= \int _{x}^{1} \frac{dz}{z} \sum _{j=g,q,\bar{q}} \Delta f_j^{[3]} \left( \frac{x}{z}, \mu _c^2 \right) \Delta K_{ij} \nonumber \\&\quad \times \left( z, \alpha _s^{[4]}(\mu _c^2), \frac{\mu _c^2}{m_c^2} \right) . \end{aligned}$$

(2.14)

Note that although it is customary to match at the charm mass scale, $\mu _c=m_c$, this is not required.

Fig. 2

The inclusive polarised structure function $g_1(x,Q^2)$ at three fixed values of x ($x=10^{-3},10^{-2}$, and 0.1) as a function of $Q^2$. The central value of the NNPDFpol1.1 NLO polarised PDF set is used as input. From top to bottom, we display results corresponding to the FONLL-A, -B, and -C calculations. In each plot, we also display results obtained in the ZM-VFN and massive 3FN schemes. The vertical grey line indicates the value of $m_c^2$ at which the 3FN and 4FN schemes are matched

Fig. 3

Same as Fig. 2 for the charm polarised structure function $g_1^c$

The matching coefficients $c_n$ in Eq. (2.13) for the strong coupling are known up to four loops [40]. The polarised matching coefficients $\Delta K_{ij}$ in Eq. (2.14) admit a perturbative expansion in $\alpha _s^{[4]}$ whose terms in the series are computed by comparing the computations of the coefficient functions in the 3FNS and 4FNS. The components of $\Delta K_{ij}$ for any values of i and j are known up to $\mathcal {O}(\alpha _s^2)$ [34]. The expression of the zeroth order matching coefficients are trivial, $\Delta K_{ij}^{(0)} = \delta _{ij}$. At $\mathcal {O}(\alpha _s)$, only $\Delta K_{ij}^{(1)}$ components with $i=g,c,\bar{c}$ and $j=g$ contribute, while all other components that involve quark lines are nonzero only starting at $\mathcal {O}(\alpha _s^2)$.

2.3 Numerical results

The formalism described in Sect. 2.2 together with the theoretical ingredients listed in Sect. 2.1 has been implemented in YADISM, enabling the calculation of FONLL polarised structure functions at $\mathcal {O}\left( \alpha _s\right)$ and $\mathcal {O}\left( \alpha ^2_s\right)$. In the following we present numerical results for the polarised structure function $g_1$ and $g_1^c$. After a review of the features of the current polarised PDF sets, we check their expected $Q^2$ behaviour, their perturbative stability, and their dependence on the input polarised PDF set.

2.3.1 Polarised PDFs

We present results for FONLL structure functions using alternately two different determinations of polarised PDFs: NNPDFpol1.1 [14] and JAM17 [17]. These two PDF sets are compared in Fig. 1 at $Q=2$ GeV as a function of x, where the error bands indicate the $68\%$ CL PDF uncertainties. For completeness, we also include in this comparison the widely-used DSSV14 polarised PDF set, in particular its Monte Carlo variant presented in [16]. We show the up and down valence quarks, gluon, total quark singlet, strangeness, and charm polarised PDFs. In DSSV14, the fit is performed in a ZM-VFN scheme but the resulting charm PDF is set to zero in the released LHAPDF grids.

Three observations are relevant in light of the subsequent discussion. First, polarised PDFs are suppressed at small x, in contrast with their unpolarised counterparts in the singlet sector, implying that in general spin asymmetries (defined as ratios of polarised over unpolarised observables) are strongly suppressed in this small-x region. Second, while there is a broad agreement between the three groups considered for $\Delta u_V$, $\Delta d_V$, and $\Delta \Sigma$, there are larger differences for the $\Delta g$, $\Delta s^+$ and $\Delta c^+$. In particular, the polarised gluon PDF (which drives perturbative charm production) is poorly known at small x and displays large uncertainties which then feed into the polarised charm PDF. Third, the polarised gluon PDF peaks at higher values of x and with a larger magnitude in NNPDFpol1.1 as compared to JAM17. The same qualitative behaviour appears in the polarised charm PDF.

All of these remarks indicate that the bulk of the PDF dependence of polarised structure functions and asymmetries, both inclusive and charm-tagged, will be related to differences at the level of the gluon and charm polarised PDFs.

2.3.2 $Q^2$ dependence

Figures 2 and 3 display respectively the inclusive and charm polarised structure functions, $g_1(x,Q^2)$ and $g_1^c(x,Q^2)$, for three fixed values of x ($x=10^{-3},10^{-2},$ and 0.1) as a function of $Q^2$. The central value of the NNPDFpol1.1 NLO polarised PDF set is used as input. From top to bottom, we display results corresponding to the FONLL-A, -B, and -C. By construction, the first two are accurate to NLO ($\mathcal {O}\left( \alpha _s\right)$-accurate), while the last is accurate to NNLO ($\mathcal {O}\left( \alpha _s^2\right)$-accurate). In each plot, we also display results obtained in the ZM-VFN (only for $Q^2\ge m_c^2$) and massive 3FN schemes. The vertical grey line indicates the value of $m_c^2$ at which the 3FN and 4FN schemes are matched.

From these comparisons, one verifies that the FONLL calculation interpolates between the massive calculation at low $Q^2$ (close to the charm mass) and the massless calculation valid for large $Q^2\gg m_c^2$. For both $g_1$ and $g_1^c$, charm mass effects can be significant at a scale close to the value of the charm quark mass. For $g_1$, at $x\sim 10^{-3}$ and $Q^2 = m_c^2$, the massless NLO (NNLO) calculation overestimates the matched FONLL calculation by up to 15% (25%). For $g_1^c$, mass effects cannot be neglected until relatively large $Q^2$, given that only for the FONLL calculation converges to the massless one. Interestingly, this holds true also for relatively large x values, such as $x=0.1$, though in this region $g_1^c$ is relatively small in absolute terms. From Fig. 3 one also notes that, depending on the value of x and on the perturbative order, the matched FONLL calculation deviates from the 3FN scheme calculation already for moderate values of $Q^2$, indicating how a purely massive calculation will in general be inadequate to describe data unless close to threshold. The behaviour of this near-threshold region exhibits in general a very mild dependence on the choice made for the damping of subleading terms, see Sect. 2.2.

Overall, we conclude that in the kinematic region defined by GeV$^2$ charm quark mass effects cannot be neglected in the computation of either the inclusive or charm structure functions. For larger GeV$^2$ values, instead, the massless and FONLL calculations coincide. This said, it is important to emphasise that a partial cancellations of charm mass effects may occur if the polarised structure functions are normalised to their unpolarised counterparts, as happens in the definition of the experimentally measured spin asymmetries. We will revisit this issue in Sect. 3, where we will compare heavy quark mass effects in inclusive and charm-tagged spin asymmetries to the projected precision of EIC and EicC pseudodata.

2.3.3 Perturbative stability and PDF dependence

The FONLL structure functions displayed in Figs. 3 and 2 exhibit a clear dependence on the perturbative accuracy of the calculation. To showcase these differences in a more direct manner, Figs. 4 and 5 display a comparison between the FONLL-A (NLO) and FONLL-C (NNLO) calculations for the inclusive $g_1(x,Q^2)$ and charm-tagged $g_1^c(x,Q^2)$ polarised structure functions, respectively, for three different values of $Q^2$ near the matching scale. In both cases, the top and bottom panels show the predictions using, respectively, the NNPDFpol1.1 and JAM17 polarised PDF sets as input. Error bands correspond to $68\%$ CL PDF uncertainties.

Fig. 4

Comparison between the FONLL-A and FONLL-C calculations of the inclusive polarised structure function $g_1(x,Q^2)$. We display results for NNPDFpol1.1 (top panels) and JAM17 (bottom panels) as a function of x for three different values of $Q^2$. Error bands correspond to $68\%$ CL PDF uncertainties

Fig. 5

Same as Fig. 4 for the charm structure function $g_1^c(x,Q^2)$

Fig. 6

The inclusive longitudinal double spin asymmetry $A_{||}$, defined in Eq. (3.2), computed at NNLO accuracy with either the ZM-VFN or the FONLL-C schemes using the NNPDFpol1.1 [14], JAM17 [17], and DSSV14 [15, 16] polarised PDF sets. Points correspond to a subset of the pseudodata discussed in Sect. 3.1, specifically to the low-$Q^2$ bins of the EIC electron-proton beam energy configuration 10$\otimes$100 GeV. Error bars, indicated on top of the FONLL-C result, correspond to the projected experimental uncertainties

Fig. 7

The charm longitudinal asymmetry $A^c_1$, defined in Eq. (3.4) computed at NLO accuracy with either the ZM-VFN or the FONLL-A schemes using the NNPDFpol1.1 [14] (left) and JAM17 [17] (right) polarised PDF sets. Points correspond to the pseudodata discussed in Sect. 3.1, at different values of x and $Q^2$. Error bars, indicated on top of the FONLL-C result, correspond to the projected experimental uncertainties

Fig. 8

Same as Fig. 7 at NNLO

Fig. 9

Same as Fig. 7 for the EicC

Figures 5 and 4 indicate that NNLO corrections to both $g_1(x,Q^2)$ and $g_1^c(x,Q^2)$ are moderate for and sizeable for , irrespective of the PDF set used. Concerning the inclusive structure function $g_1$, the NNLO (FONLL-C) computation leads to a suppression of the structure function with respect to its NLO (FONLL-A) counterpart. Concerning the charm structure function $g_1^c$, the NNLO (FONLL-C) computation leads to a negative and large (in absolute value) structure function in the near-threshold region, whereas the NLO (FONLL-A) computation leaves it slightly positive in the same region. Interestingly, NNPDFpol1.1 PDF uncertainties are sufficiently large to encompass these large differences for .

The sensitivity of $g_1(x,Q^2)$ and $g_1^c(x,Q^2)$ on the input PDF set is generally mild: the aforementioned features qualitatively hold when either the NNPDFpol1.1 or JAM17 PDF sets are used as input. Small differences are observed, e.g. the shift between FONLL-A and FONLL-C predictions is larger in JAM17 than in NNPDFpol1.1. Given that for the sake of the comparison the PDFs have been kept fixed in both the FONLL-A and -C calculations, one expects that the observed differences may be reduced once the PDFs are refitted to NNLO accuracy and in the presence of the constraints provided by future electron-proton colliders.

3 Charm mass effects in polarised DIS at electron-ion colliders

In this section we quantify the impact of charm mass effects on polarised DIS measurements at future polarised electron-ion colliders, in particular at the EIC and the EicC. We discuss first the observables and pseudodata sets considered, then the computation of the corresponding theoretical predictions, and finally the comparison between the two. In particular, we assess the significance of charm mass corrections in comparison to the size of the projected experimental uncertainties and of the higher-order QCD corrections.

3.1 Observables and pseudodata sets

We consider pseudodata sets for the double-spin asymmetry $A_\parallel$ forecast at the EIC, and for the polarised charm asymmetry $A_1^c$ forecast at the EIC and EicC. The double-spin asymmetry $A_\parallel$ is defined as the ratio of the polarised to unpolarised differential cross sections,

$$\begin{aligned} A_\parallel (x,Q^2) = \frac{d^2\Delta \sigma (x,Q^2)}{d^2\sigma (x,Q^2)} =\frac{d^2\sigma ^{\rightarrow \Rightarrow }-d^2\sigma ^{\rightarrow \Leftarrow }}{d^2\sigma ^{\rightarrow \Rightarrow } +d^2\sigma ^{\rightarrow \Leftarrow }}, \end{aligned}$$

(3.1)

where the numerator (denominator) is the difference between (sum of) differential cross sections for which the nucleon is polarised along ($\Rightarrow$) or opposite ($\Leftarrow$) the polarisation direction of the lepton beam ($\rightarrow$). Neglecting target mass corrections, $\mathcal {O}(m_N^2/Q^2)$, which are expected to be immaterial for EIC and EicC kinematics,² the asymmetry $A_\parallel$ becomes proportional to the virtual photo-absorption asymmetry $A_1$,

$$\begin{aligned} A_{||}(x,Q^2) = \mathcal {D}(y) A_1(x,Q^2), \end{aligned}$$

(3.2)

where $\mathcal {D}(y)=[y(2-y)]/[y^2+2(1-y)]$ is the photon de-polarisation factor, and y is the inelasticity. Within the same kinematic approximation, the photo-absorption asymmetry $A_1$ reads

$$\begin{aligned} A_1(x,Q^2)=\frac{g_1(x,Q^2)}{F_1(x,Q^2)}, \end{aligned}$$

(3.3)

where $F_1$ is the unpolarised structure function corresponding to $g_1$. Likewise, we define the charm photo-absorption asymmetry as

$$\begin{aligned} A_1^c(x,Q^2)=\frac{g_1^c(x,Q^2)}{F_1^c(x,Q^2)}. \end{aligned}$$

(3.4)

For the inclusive double-spin asymmetry $A_{||}$ at the EIC, we use the projections obtained in [41]. These were recently produced in the context of the performance study of the ATHENA detector, now integrated into the ePIC detector which will be installed at interaction point IP6 of the EIC. These projections consider five different beam energy configurations for electron-proton scattering, each one assuming one year of running: $5\otimes 41~\textrm{GeV}$, $5\otimes 100~\textrm{GeV}$, $10\otimes 100~\textrm{GeV}$, $10\otimes 275~\textrm{GeV}$, and $18\otimes 275~\textrm{GeV}$, where the first (second) number indicates the electron (proton) energy. These five scenarios correspond, respectively, to centre-of-mass energies of $\sqrt{s}=29$, 45, 63, 105 and 140 GeV, and to integrated luminosities of $\mathcal {L}=4.4$, 61, 79, 100, and 15.4 fb$^{-1}$. In all cases, the kinematic coverage considered is $Q^2 \ge 1$ GeV$^2$ and $0.01< y < 0.95$. The systematic uncertainties include a point-by-point uncorrelated systematic uncertainty (1.5%), a normalisation uncertainty (5%), and a systematic uncertainty of $10^{-4}$ due to the relative luminosity. Electron and proton beam polarisations between 70% and 80% are assumed.

For the charm photo-absorption asymmetry $A_1^c$, Eq. (3.4), at the EIC and at the EicC, we use projections from [42] and [43], respectively. In the case of the EIC, these projections correspond to three different beam energy configurations: $5\otimes 41~\textrm{GeV}$, $5\otimes 100~\textrm{GeV}$, and $18\otimes 275~\textrm{GeV}$. The corresponding centre-of-mass energies are $\sqrt{s}=43$, 67, and 211 GeV. An integrated luminosity of $\mathcal {L}=100$ fb$^{-1}$ is assumed for all three configurations. Electron and proton beam polarisations are of $80\%$ and $70\%$, respectively. In the case of the EicC, projections correspond to two different beam energy configurations: $3.5\otimes 20~\textrm{GeV}$, and $5\otimes 25~\textrm{GeV}$. The corresponding centre-of-mass energy is $\sqrt{s}=15$ GeV and 22 GeV, and the integrated luminosity is $\mathcal {L}=100$ fb$^{-1}$. For both the EIC and the EicC, the total experimental uncertainties provided in [42, 43] include statistical, systematic, and luminosity uncertainties added in quadrature.

In all cases, we ignore the central values of the aforementioned pseudodata sets as provided in Refs. [41,42,43]. We retain instead only their projections for the experimental uncertainties as a function of each bin in x and Q. The projected central values of the pseudodata are then replaced with our own theoretical predictions, obtained as described next.

3.2 Theoretical predictions

We compute theoretical predictions for the inclusive and charm spin asymmetries corresponding to the pseudodata sets discussed above by using alternately the ZM-VFN or the FONLL schemes, specifically FONLL-A at NLO and FONLL-C at NNLO, see Sect. 2 for details. We neglect a possible polarised intrinsic charm component in the proton, TMCs, electroweak corrections, and corrections due to hadronisation of charm quarks into D mesons. These corrections are expected to be of similar size in unpolarised and polarised scattering, therefore they will almost completely cancel in the relevant asymmetries. The renormalisation and factorisation scales, $\mu _R$ and $\mu _F$, are set equal to the DIS virtuality, $\mu _R=\mu _F=Q$. The same theoretical settings are adopted consistently in the computation of both the unpolarised and polarised structure functions entering the asymmetry.

We use the following sets of polarised PDFs: NNPDFpol1.1 [14], DSSV14 [15, 16], and JAM17 [17] for the computation of inclusive asymmetries; NNPDFpol1.1 and JAM17 for the computation of charm asymmetries. In the latter case, we do not use the DSSV14 PDF set because the polarised charm quark and anti-quark PDFs are identically set to zero in the released LHAPDF grid.³ By varying the input PDF set one can verify that, whereas predictions change consistently with Fig. 1, our assessment of the impact of charm-quark mass corrections does not depend on the specific choice of polarised PDF set. In all cases, we take the NNLO unpolarised PDF set from the NNPDF4.0 determination [9] to evaluate the denominator of the spin asymmetries.

We consider these settings suitable to quantify the role of charm quark mass effects in EIC spin asymmetries. They may not necessarily correspond to the optimal settings that one would adopt to include actual EIC measurements in a global fit of helicity-dependent PDFs.

Fig. 10

Same as Fig. 9 at NNLO

3.3 Comparisons with EIC and EicC projections

We now compare the accuracy of theoretical predictions obtained in the ZM-VFN and FONLL schemes against the expected precision of the pseudodata sets discussed above. In particular, we investigate whether differences in the former are larger than the latter. We discuss in turn the inclusive longitudinal double-spin asymmetry $A_{||}$ and the charm photo-absorption asymmetry $A_1^c$.

3.3.1 Inclusive double-spin asymmetry

Figure 6 shows the inclusive longitudinal double spin asymmetry $A_{||}$, Eq. (3.2), computed at NNLO accuracy with either the ZM-VFN or the FONLL-C schemes. The three aforementioned PDF sets are used. Error bars, indicated on top of the FONLL-C result, correspond to the projected experimental uncertainties, see Sect. 3.1. We display only pseudodata points corresponding to the low-$Q^2$ bins of the EIC electron-proton dataset associated to the beam energy configuration 10$\otimes$100 GeV. For these bins and this beam energy configuration, quark mass effects are the largest. We explicitly checked that, at higher values of $Q^2$ or for different beam energy configurations, the FONLL-C calculation smoothly reduces to the ZM-VFN.

From Fig. 6 one observes that predictions obtained with either the ZM-VFN or the FONLL-C schemes may differ significantly, especially in the bins with the lowest values of $Q^2$. Predictions obtained with the former typically undershoot the ones obtained with the latter. Whereas the magnitude of the predictions depend on the input polarised PDF set, especially in the small-x region beyond the coverage of available data, the impact of charm mass effects is much larger than the projected experimental uncertainties. As expected, as $Q^2$ increases, the difference between predictions obtained with the ZM-VFN or the FONLL-C schemes becomes negligible. We therefore conclude that the inclusion of charm mass corrections in the computation of the inclusive double-spin asymmetry is essential to properly match the forecast EIC measurements within their precision and robustly interpret them in terms of the underlying spin decomposition of the proton [44].

3.3.2 Charm photo-absorption longitudinal asymmetry

Figures 7 and 8 show the charm longitudinal asymmetry $A^c_1$, Eq. (3.4), computed at NLO and NNLO accuracy, respectively. Predictions are obtained either with the ZM-VFN or the appropriate FONLL schemes (FONLL-A at NLO and FONLL-C at NNLO). They correspond to the EIC pseudodata discussed in Sect. 3.1. The NNPDFpol1.1 and JAM17 PDF sets are used. Error bars, indicated on top of the FONLL-C result, correspond to the projected experimental uncertainties. Figures 9 and 10 are as Figs. 7 and 8 for the EicC pseudodata. In all of these figures, each point corresponds to a different bin in x and $Q^2$; due to the DIS kinematics, increasing values of x correlate with increasing values of $Q^2$.

As in the case of the inclusive double spin asymmetry, we remark that predictions obtained with either the ZM-VFN of the FONLL schemes, given a perturbative order, may differ significantly. Differences, as expected, are generally larger when $Q^2$ is smaller. As in the case of the inclusive double-spin asymmetry, these are fairly independent from the input PDF set, and can be larger than the projected experimental uncertainty. We therefore conclude, also in this case, that the inclusion of charm mass corrections is essential to correctly interpret future collider data.

We finally note that, for both the EIC and EicC, there are marked differences in predictions obtained at NLO and NNLO. These can be traced back to the large perturbative corrections that affect the polarised charm structure function $g_1^c$ at low $Q^2$, and, albeit to a lesser extent, also its unpolarised counterpart $F_1^c$. For instance, at $x\sim 0.01$ and $Q^2\sim 5$ GeV$^2$, one has (using NNPDFpol1.1 as input) that $g_1^c\sim 0.004$ with FONLL-A but $g_1^c\sim -0.05$ with FONLL-C (Fig. 5): not only a change of an order of magnitude in size but also a change of sign. These large perturbative corrections to charm production in polarised electron-proton collisions are also relevant for the inclusive structure function, which is reduced from $g_1\sim 0.47$ at NLO to $\sim 0.23$ at NNLO (Fig. 4), again considering $x\sim 0.01$ and $Q^2\sim 5$ GeV$^2$.

In light of all of these considerations, we generally remark that the intermediate-to-large-$Q^2$, large-x region, especially for the higher energy beam configurations, are the most promising to measure a non-vanishing polarised charm asymmetry, which may be as large as a few percent. Such a sizeable asymmetry will provide valuable information on both the mechanisms of heavy quark production in polarised DIS, as well as on the underlying distribution of the proton spin among its partonic constituents.

4 Summary

In this work we have presented a comprehensive framework enabling the calculation of polarised structure functions and asymmetries in deep-inelastic scattering up to $\mathcal {O}\left( \alpha _s^2\right)$ and accounting for charm quark mass effects. This framework mirrors state-of-the-art theory calculations in polarised DIS and is implemented in the open-source EKO and YADISM software. We have shown that FONLL structure functions successfully match the massless and massive calculations, and that they display good perturbative convergence. By comparing our predictions with projected pseudodata corresponding to the upcoming US- and China-based electron-ion colliders, we have found that charm mass effects are significant and must be accounted for to achieve a robust description of both inclusive and charm-tagged polarised asymmetries at these future facilities.

Our results constitute the first step towards a new global determination of polarised PDFs accurate to NNLO within the NNPDF framework. This will possibly include not only polarised DIS measurements, but also W gauge boson production and semi-inclusive DIS measurements, for which NNLO computations have been completed recently [45,46,47]. Aside from this goal, our results represent an important ingredient for the precision phenomenology program at the upcoming EIC, making it possible to robustly access precious information on the spin structure of the proton from the interpretation of its inclusive and charm-tagged polarised structure function measurements.

Appendices

Polarised DGLAP evolution

Helicity-dependent PDFs obey DGLAP evolution equations, which, in x space, read as

$$\begin{aligned} \frac{d}{d \ln Q^2} \Delta f_i(x, Q^2)= & {} \sum _k \int _x^1 \frac{dz}{z} \Delta P_{ik}\left( \frac{x}{z}, \alpha _s(Q^2)\right) \nonumber \\{} & {} \times \Delta f_k (x, Q^2) \, \end{aligned}$$

(A.1)

with $\Delta P_{ik}(x, \alpha _s)$ being the polarised splitting functions and i, k partonic flavour indexes running over all active quark flavours and the gluon. DGLAP equations can, for convenience, be expressed in Mellin space

$$\begin{aligned}&\frac{d}{d \ln Q^2} \Delta f_i(N, Q^2) \nonumber \\ {}&\quad = - \sum _k\Delta \gamma _{ik}(N, \alpha _s(Q^2)) \Delta f_k (N, Q^2) \ , \end{aligned}$$

(A.2)

where convolutions are replaced by products. The quantities $\Delta \gamma _{ik}$, called polarised anomalous dimensions, are defined by

$$\begin{aligned} \Delta \gamma _{ik}(N, \alpha _s(Q^2)) = - \int _0^1 dx\,x^{N-1} \Delta P_{ik}(x, \alpha _s(Q^2)) ,\nonumber \\ \end{aligned}$$

(A.3)

and likewise for the Mellin space PDFs $\Delta q_k (N, Q^2)$. Solving the coupled system of Eqs. (A.1) or (A.2) is most efficiently done by rotating to a convenient flavour basis. Specifically, one defines the polarised total quark singlet PDF as

$$\begin{aligned} \Delta \Sigma (x,Q^2)= & {} \sum _{i=1}^{n_f} \Delta q_i^+(x,Q^2) = \sum _{i=1}^{n_f} \left( \Delta q_i(x,Q^2) \right. \nonumber \\{} & {} \left. + \Delta \bar{q}_i(x,Q^2)\right) , \end{aligned}$$

(A.4)

which evolves coupled with the polarised gluon $\Delta g$, while all other quark combinations evolve independently in terms of non-singlet evolution equations.

The polarised splitting functions $\Delta P_{ik}$ can be evaluated in perturbative QCD,

$$\begin{aligned} \Delta P_{ik}(x,\alpha _s(Q^2)) = \sum _{n=0}^m \alpha _s^{n+1}(Q^2) \Delta P_{ik}^{(n)}(x) \, . \end{aligned}$$

(A.5)

The complete set of $\Delta P_{ik}$ has been computed at NLO in [48] and then at NNLO in [49,50,51]. At leading order, the polarised quark-to-quark splitting function is identical to its unpolarised counterpart, $\Delta P_{qq}^{(0)} = P_{qq}^{(0)}$. Symmetry considerations imply that polarised non-singlet splitting functions coincide with the spin-averaged ones to all orders after they are swapped as follows:

$$\begin{aligned} \Delta P_{\textrm{NS},\pm }^{(n)}(x) = P_{\textrm{NS},\mp }^{(n)}(x) \qquad \forall \, n \, . \end{aligned}$$

(A.6)

Furthermore, helicity conservation implies that the first moment of the gluon-to-quark splitting function vanishes

$$\begin{aligned} \int _0^{1} x \Delta P_{qg}(x,\alpha _s(Q^2)) dx = 0 \ , \end{aligned}$$

(A.7)

to all orders in perturbation theory.

Fig. 11

The percentage difference with respect to the Les Houches polarised PDF evolution benchmark tables for the EKO and PEGASUS predictions, obtained by evolving polarised PDFs from $Q^2=2$ GeV$^2$ to $Q^2=10^4$ GeV$^2$. Evolution is carried out at NLO (the highest accuracy at which the polarized LH tables are available) in a VFNS with $n_f^{\mathrm{(max)}} = 5$ active quark flavours. We show results for the evolution benchmarks corresponding to the polarised quark singlet $\Delta \Sigma (x,Q^2)$ (left) and gluon $\Delta g(x,Q^2)$ PDFs (right)

As in the case of unpolarised DGLAP evolution, one also has to account for the fact that the number of active quark flavours $n_f$ depends on the scale $Q^2$. In a VFN scheme, ignoring intrinsic heavy quark contributions, heavy flavour polarised PDFs are entirely generated at the scale $\mu _h$ from matching conditions relating schemes with $n_f$ and $n_f+1$ active quarks. At the scale $Q^2 = \mu _h^2$, these matching relations take the general form

$$\begin{aligned} \Delta f_i^{[n_f+1]} (x, \mu ^2_h)= & {} \int _{x}^{1} \frac{dz}{z} \sum _{j=g,q,\bar{q}} \Delta f_j^{[n_f]} \left( \frac{x}{z}, \mu _h^2 \right) \Delta K_{ij} \nonumber \\{} & {} \times \left( z, \alpha _s^{[n_f+1]}(\mu _h^2), \frac{\mu _h^2}{m_h^2} \right) , \end{aligned}$$

(A.8)

where the sum over j includes only the $n_f$ light quark flavours. The polarised operator matrix elements $\Delta K_{ij}$ have been computed up to $\mathcal {O}\left( \alpha _s^2\right)$ (NNLO) accuracy [34]. Equation (A.8) can be generalized to the case of intrinsic heavy quarks being present at scales $Q^2< \mu ^2_h$.

Helicity-dependent QCD calculations performed in dimensional regularisation have to address the issue of the definition of the $\gamma _5$ Dirac matrix in $d \ne 4$ space-time dimensions, which enters through the helicity projection operators. Usually, an ad-hoc renormalisation scheme, called Larin scheme, is defined for convenience and then quantities are mapped to the M-scheme by means of finite transformation. This technical point becomes relevant for higher-order QCD calculations involving polarised partons.

The calculation of polarised structure functions discussed in Sect. 2 requires polarised PDFs evolved up to NNLO. For this reason, polarised DGLAP evolution up to this accuracy has been implemented in EKO [21]. The necessary VFN scheme matching conditions, which were computed only very recently, are implemented in a public piece of software for the first time in this work.

Fig. 12

Results of evolving the Les Houches benchmark polarised toy PDFs [52] between $Q^2=2$ GeV$^2$ and $Q^2=10^4$ GeV$^2$ with EKO in the VFNS scheme with up to $n_f=5$. We compare the results of polarised evolution at three different perturbative orders, LO, NLO, and NNLO, for the same fixed input PDF

We have benchmarked our implementation of polarised evolution in EKO  with other public codes, in particular with PEGASUS [23] and APFEL [37], and with the Les Houches (LH) evolution benchmark tables [52], finding good agreement in all cases considered. Depending on the case, the benchmark is restricted to the NLO VFN scheme or to NNLO in the FFN scheme. In Fig. 11 we show the percentage difference between the results of polarised PDFs evolved from $Q^2=2$ GeV$^2$ to $Q^2=10^4$ GeV$^2$ with EKO, PEGASUS, or the LH tables. Polarised DGLAP evolution is carried out at NLO (the highest accuracy at which the LH tables are available) in a VFNS with $n_f^{\mathrm{(max)}} = 5$ active quark flavours. We show results corresponding to the polarised quark singlet $\Delta \Sigma (x,Q^2)$ and gluon $\Delta g(x,Q^2)$ PDFs. Excellent agreement between the EKO evolution, the reference LH tables, and PEGASUS is found, with differences at the $\mathcal {O}(10^{-5})$ level. A similar agreement is achieved for other quark flavour combinations not shown here.

We finally assess the perturbative convergence of DGLAP evolution for a fixed boundary condition up to this accuracy. In Fig. 12 we display the results of evolving the LH polarised toy PDFs [52] between $Q^2=2$ GeV$^2$ and $Q^2=10^4$ GeV$^2$ with EKO in the VFNS scheme with up to $n_f^{\mathrm{(max)}}=5$. We compare polarised evolution at three different perturbative orders, LO, NLO, and NNLO, in all cases with the same input PDF. We note that the LH toy PDF set assumes $\Delta \bar{u} = \Delta \bar{d}$, while polarised evolution induces a breaking of this relation at NLO and beyond.

From this comparison, one observes how the perturbative series converges. Differences between NNLO and NLO are smaller than those between NLO and LO for all values of x and flavour combinations. NLO corrections are large, for instance up to a factor 2 for the small-x gluon and sea quarks and up to a 50% for the sea quarks in the intermediate x region. NNLO corrections are much smaller, at the few percent level at most. Although small, these corrections are of the same size or larger as the projected experimental uncertainties of the forthcoming EIC and EicC measurements. Therefore, NNLO corrections to polarised PDF evolution must be included in theoretical predictions entering the interpretation of the data at these future facilities.

Fig. 13

Comparisons of the exact implementation of TMCs in $g_1(x,Q^2)$, Eq. (B.1) with the approximated implementation of Eq. (B.3) for different values of $Q^2$. The polarised structure functions are computed using FONLL-C using NNPDFpol1.1 as input PDF set

Fig. 14

The impact of TMCs on the $g_1(x,Q^2)$ structure function evaluated with FONLL-A as a function of x for fixed $Q^2$ (upper panels) and as a function of $Q^2$ for fixed x (lower panels), normalised to the calculation without TMCs, using the NNPDFpol1.1 polarised PDF set as input

Fig. 15

Same as Fig. 14 in the case where structure functions are evaluated with FONLL-C

Target mass corrections in polarised DIS

In this Appendix, we discuss the implementation of target mass corrections (TMCs) to the computation of the polarised structure functions $g_1$ in YADISM. We also study their numerical impact in comparison to charm quark corrections accounted for in the FONLL scheme.

The leading-twist definition of the polarised structure function $g_1$, Eq. (2.4), is valid in the Bjorken-scaling limit where $Q^2 \rightarrow \infty$ and x is fixed. At low $Q^2$ values, power-suppressed (highest-twist) corrections to the spin-dependent structure functions can have large effects in some kinematic regions. A subset of the total higher-twist contribution can be evaluated in terms of closed-form expressions using the Operator Product Expansion (OPE). The complete TMC expressions for polarised structure functions arising from twist-2 and twist-3 operators have been derived in [53]. Equation (2.4) is then modified as

$$\begin{aligned} \tilde{g}_1 \left( x ,Q^2\right)&= \frac{1}{\left( 1+\gamma ^2\right) ^{3 / 2}} \frac{x}{\xi } g_1(\xi ,Q^2)\nonumber \\&\quad +\frac{\gamma ^2}{\left( 1+\gamma ^2\right) ^2} \int _{\xi }^1 \frac{d v}{v}\left[ \frac{x+\xi }{\xi } \right. \nonumber \\&\quad \left. +\frac{\gamma ^2-2}{2 \sqrt{1+\gamma ^2}} \log \left( \frac{v}{\xi }\right) \right] g_1 (v,Q^2) \, , \end{aligned}$$

(B.1)

in terms of the so-called Nachtmann variable,

$$\begin{aligned} \xi = \frac{2 x}{1+\sqrt{1+\gamma ^2}} \quad \text {with} \quad \gamma ^2 = 4 x^2 \frac{m_N^2}{Q^2}. \end{aligned}$$

(B.2)

It is clear from Eq. (B.1) that in the asymptotic limit, $Q^2 \rightarrow \infty$, one has that $\xi =x$ and $\gamma =0$ so that the leading-twist expression is recovered.

The target mass corrected structure function in Eq. B.1 involves integrals, $k_1 = \int dv/v g_1(v)$ and $k_2 = \int dv/v \log (v/ \xi ) g_1(v)$, which can be numerically difficult to evaluate. As done in the case of unpolarised TMCs [54], upper bounds for the size of these integrals can be computed. Given that the non-leading terms $k_1$ and $k_2$ constitute a small correction to the leading term and that $g_1(v)$ decreases as a function of v, we can evaluate the terms at the lower integration limit. That is, the two integrals have as upper bounds $k_1 < g_1 \int dv /v$ and $k_2 < g_1 \int dv/v \log (v/ \xi )$. By analytically evaluating these two integrals, one arrives at the following approximation:

$$\begin{aligned}&\tilde{g}_1^{\textrm{approx}} \left( x ,Q^2\right) \nonumber \\ {}&= g_1(\xi ,Q^2) \left[ \frac{1}{\left( 1+\gamma ^2\right) ^{3 / 2}} \frac{x}{\xi } + \frac{\gamma ^2}{\left( 1+\gamma ^2\right) ^2} \right. \nonumber \\&\quad \times \left. \left( \frac{x+\xi }{\xi } (1 - \xi ) +\frac{\gamma ^2-2}{4 \sqrt{1+\gamma ^2}} \log ^2 \left( \frac{1}{\xi } \right) \right) \right] , \end{aligned}$$

(B.3)

with the key benefit that the dependence on the leading-twist structure function is now factorised.

Figure 13 compares the TMC-corrected structure function $\widetilde{g}_1(x,Q^2)$ using the FONLL-C scheme evaluated with the exact, Eq. (B.1), and with the approximated, Eq. (B.3), implementations. These comparisons show that the difference between the exact and approximated expressions is larger at small $Q^2$, reaching up to $25\%$ for $Q^2=2~\textrm{GeV}^2$, but it decreases as $Q^2$ increases. Therefore, the target-mass corrected expression given by Eq. B.3 is a good approximation at high momentum scale.

The impact of TMCs on the $g_1(x,Q^2)$ polarised structure function is displayed in Fig. 14 (with FONLL-A) and in Fig. 15 (with FONLL-C), where the target-mass corrected structure function is normalised to its leading-twist counterpart. The NNPDFpol1.1 polarised PDF set is used as input. As can be seen, the ratio is close to unity at small x and large $Q^2$, while it quickly increases at large x and large $Q^2$. For instance, at $x=0.5$, the impact of TMCs on the structure function $g_1$ can grow from about $5 \%$ at $Q^2=5$ GeV$^2$ to about $15\%$ at $Q^2=2$ GeV$^2$. As expected, these effects decrease as x decreases (2-$3\%$ at $x=0.25$) but they increase dramatically as x increases ($30\%$ at x=0.75). In general, TMCs depend only moderately on the perturbative order.

The results of Figs. 14 and 15 highlight how TMCs are in general also required to achieve an accurate description of polarised DIS structure functions, especially for measurements sensitive to the large-x, small-$Q^2$ kinematic region. This region is not primarily probed by the EIC and the EicC. Furthermore, owing to the fact that TMCs for the unpolarised structure function $F_1$ and the polarised $g_1$ structure function have similar structure, TMCs mostly cancel in the asymmetry $A_1$ [55]. For these reasons, TMCs are not included in the results presented in Sects. 2 and 3.