Resonant entanglement of photon beams by a magnetic field

Abstract

In spite of the fact that photons do not interact with an external magnetic field unless nonlinearity of QED is taken into account, the latter field may indirectly affect photons in the presence of a charged environment. This opens up an interesting possibility to continuously control the entanglement of photon beams without using any crystalline devices. We study this possibility in the framework of an adequate QED model. In an approximation it was discovered that such entanglement has a resonant nature, namely, a peak behavior at certain magnetic field strengths, depending on characteristics of photon beams direction of the magnetic field and parameters of the charged medium. Numerical calculations illustrating the above-mentioned resonant behavior of the entanglement measure and some concluding remarks are presented.

1 Introduction

Entanglement phenomenon is associated with a quantum non-separability of parts of a composite system. Entangled states appear in studying principal questions of quantum theory, they are considered as key elements in quantum information theory in quantum computations and quantum cryptography technologies; see e.g. Refs. [1, 2]. In laboratory conditions the entanglement of photon beams is usually created and studied using some kind of crystalline devices. In spite of the fact that photons do not interact with an external magnetic field, the latter field may indirectly affect photons in the presence of a charged environment. This opens up an interesting possibility to continuously control the entanglement of photon beams. Studying this possibility in the framework of an adequate QED model, we have discovered that such entanglement has a resonant nature, namely, a peak behavior at certain magnetic field strengths depending on characteristics of photon beams and parameters of the charged medium. This is the study presented in this article. The article is organized as follows: In Sect. 2, we outline details of the above-mentioned QED model. This model describes a photon beam that consists of photons with two different frequencies, moving in the same direction and interacting with a quantized charged scalar field (KG field) placed in a constant magnetic field. Particles of the KG field we call electrons in what follows and the totality of the electrons is called the electron medium. Photons with each frequency may have two possible linear polarizations. In the beginning, we consider the electron subsystem consisting of only one charged particle. Both quantized fields (electromagnetic and the KG one) are placed in a box of the volume $V=L^{3}$ and periodic conditions are supposed. We believe that in this case the model already describes the photons interacting with many identical electrons, and the quantity $\rho =V^{-1}$ may be interpreted as the density of the electron medium. In this article, we essentially correct exact solutions used in our previous consideration of similar models; see Ref. [3] and references there. In a certain approximation, solutions of the model correspond to two independent subsystems, one of which is a quasi-electron medium and another one is a set of some quasi-photons. In the new solutions the orders of smallness of contributions to quasi-photon states used in calculating the entanglement measures are accurately determined and an adequate expression for the spectrum of quasi-electrons derived. Namely, the latter made it possible to detect the resonant behavior of the entanglement measure at some resonant values of the external magnetic field. Finally, in Sect. 4, numerical calculations illustrating the above-mentioned resonant behavior of the entanglement measure and some concluding remarks are presented. Technical details related to Hamiltonian diagonalization are placed in the Appendix A.

2 QED model and its solutions

Consider photons with two different momenta ${\textbf{k}}_{s}=\kappa _{s} {\textbf{n}},$ $s=1,2$ (frequencies), moving in the same direction ${\textbf{n}} =\left( 0,0,1\right)$ and interacting with quantized charged scalar particles-electrons placed in a constant magnetic field ${\textbf{B}}=B{\textbf{n}},$ $B>0,$ potentials of which in the Landau gauge are: ${\textbf{A}}_{\textrm{ext}}( {\textbf{r}})=\left( -Bx^{(2)},0,0\right) .$ In what follows, we use the system of units where $\hbar =c=1.$ The operator potentials $\hat{A}^{\mu }\left( {\textbf{r}}\right) ,$ $\mu =0,\ldots ,3;$ ${\textbf{r}}=\left( x^{(1)},x^{(2)},x^{(3)}=z\right)$ of the photon beam are chosen in the Coulomb gauge, $\hat{A}^{\mu }({\textbf{r}}) =( 0,\hat{{\textbf{A}}} ({\textbf{r}})),$ ${\textrm{div}}\hat{{\textbf{A}}}({\textbf{r}})=0,$ in fact, they depend only on z, 

$$\begin{aligned}{} & {} \hat{{\textbf{A}}}\left( {\textbf{r}}\right) =\sum _{s=1,2}\sum _{\lambda =1,2} \sqrt{\frac{1}{2\kappa _{s}V}}\left[ \hat{a}_{s,\lambda }\exp \left( i\kappa _{s}z\right) \right. \nonumber \\{} & {} \qquad \left. +\hat{a}_{s,\lambda }^{\dagger }\exp \left( -i\kappa _{s}z\right) \right] {\textbf{e}}_{\lambda }, \nonumber \\{} & {} \left[ \hat{a}_{s,\lambda },\hat{a}_{s^{\prime },\lambda ^{\prime }}\right] =0,\ \left[ \hat{a}_{s,\lambda },\hat{a}_{s^{\prime },\lambda ^{\prime }}^{\dagger }\right] =\delta _{s,s^{\prime }}\delta _{\lambda ,\lambda ^{\prime }}. \end{aligned}$$

(1)

Here $\hat{a}_{s,\lambda }$ and $\hat{a}_{s,\lambda }^{\dagger }$ are creation and annihilation operators of the free photons from the beam, ${\textbf{e}}_{\lambda }$ are real polarization vectors, $({\textbf{e}}_{\lambda } {\textbf{e}}_{\lambda ^{\prime }})=\delta _{\lambda ,\lambda ^{\prime }},$ $( {\textbf{ne}}_{\lambda })=0,$ $\lambda ,\lambda ^{\prime }=1,2,$ $s,s^{\prime }=1,2.$ We choose the polarization vector in the form ${\textbf{e}}_{1}=(1,0,0),$ ${\textbf{e}}_{2}=(0,1,0).$ The photon Fock space ${\mathfrak {H}}_{{\gamma }}$ is constructed by the creation and annihilation operators and by the vacuum vector $\left| 0\right\rangle _{ {\gamma }},$ $\hat{a}_{s,\lambda }\left| 0\right\rangle _{{\gamma }}=0,$ $\forall s,\lambda .$ Photon vectors are denoted as $\left| \Psi \right\rangle _{{\gamma }},$ $\left| \Psi \right\rangle _{{\gamma }}\in {\mathfrak {H}}_{{\gamma }}.$ The Hamiltonian of free photon beam reads:

$$\begin{aligned}{} & {} \hat{H}_{{\gamma }}=\sum _{s=1,2}\sum _{\lambda =1,2}\kappa _{s}\hat{a} _{s,\lambda }^{\dagger }\hat{a}_{s,\lambda }\,\nonumber \\{} & {} \kappa _{s}=\kappa _{0}d_{s},\ \kappa _{0}=2\pi L^{-1},\ d_{s}\in {\mathbb {N}}. \end{aligned}$$

(2)

Electrons are described by a scalar field $\varphi \left( {\textbf{r}}\right)$ interacting with the external constant magnetic field $A_{\textrm{ext}}^{\mu }({\textbf{r}}).$ The magnetic field does not violate the vacuum stability. After the canonical quantization, the scalar field and its canonical momentum $\pi ({\textbf{r}})$ become operators $\hat{\varphi }({\textbf{r}})$ and $\hat{\pi }({\textbf{r}}).$ The corresponding Heisenberg operators $\hat{\varphi }(x)$ and $\hat{\pi }(x),$ $x=(x^{\mu })=(t,{\textbf{r}}),$ satisfy the equal-time nonzero commutation relations $[\hat{\varphi }(x),\hat{\pi } (x^{\prime })]_{t=t^{\prime }}=i\delta ({\textbf{r}}-{\textbf{r}}^{\prime }).$ These operators act in the electron Fock space ${\mathfrak {H}}_{\textrm{e}}$ constructed by a set of creation and annihilation operators of the scalar particles and by a corresponding vacuum vector $\left| 0\right\rangle _{ \textrm{e}}.$ Electron vectors are denoted as $\left| \Psi \right\rangle _{\textrm{e}},$ $\left| \Psi \right\rangle _{\textrm{e}}\subset {\mathfrak {H}}_{\textrm{e}}.$

The Fock space ${\mathfrak {H}}$ of the complete system is a tensor product of the photon Fock space and the electron Fock space, ${\mathfrak {H}}={\mathfrak {H}}_{{\gamma }}\otimes {\mathfrak {H}}_{\textrm{e}}.$ Vectors from the Fock space ${\mathfrak {H}}$ are denoted by $\left| \Psi \right\rangle ,$ $\left| \Psi \right\rangle \in {\mathfrak {H}}.$

The Hamiltonian of the complete system (composed of the photon and the electron subsystems) has the following form:

$$\begin{aligned}&\hat{H}=\int \left\{ \hat{\pi }^{+}({\textbf{r}})\hat{\pi }({\textbf{r}})\right. \nonumber \\&\qquad \left. +\hat{ \varphi }^{+}\left( {\textbf{r}}\right) \left[ \hat{\textbf{P}}^{2}({\textbf{r}} )+m^{2}\right] \hat{\varphi }\left( {\textbf{r}}\right) \right\} d{\textbf{r}}+ \hat{H}_{{\gamma }}, \nonumber \\&\hat{\textbf{P}}({\textbf{r}})=\hat{\textbf{p}}+e\left[ \hat{{\textbf{A}}}(z)+ {\textbf{A}}_{\textrm{ext}}({\textbf{r}})\right] ,\nonumber \\&\hat{\textbf{p}}=-i\nabla ,\ e>0. \end{aligned}$$

(3)

Consider the amplitude-vector (AV) $\varphi (x)=\ _{\textrm{e}}\left\langle 0\right| \hat{\varphi }({\textbf{r}})\left| \Psi \left( t\right) \right\rangle ,$ which is on the one hand a function on x (the projection of a vector $\left| \Psi \left( t\right) \right\rangle$ onto a one-electron state), on the other side AV is a vector in the photon Fock space. In the similar manner, one could introduce many-electron or positron amplitudes and interpreted them as AVs of photons interacting with many charged particles. However, we neglect the existence of such amplitudes in the accepted further approximation, they are related to processes of pair creation. In such an approximation, one can demonstrate that AV $\varphi (x)$ satisfies the following equation:

$$\begin{aligned} \left[ (i\partial _{t}-\hat{H}_{{\gamma }})^{2}-\hat{\textbf{P}}^{2}( {\textbf{r}})-m^{2}\right] \varphi (x)=0. \end{aligned}$$

(4)

It is convenient to pass from the AV $\varphi (x)$ to a AV $\Phi (x)=U_{ {\gamma }}\left( t\right) \varphi (x),$ $U_{{\gamma }}\left( t\right) =\exp ( i\hat{H}_{{\gamma }}t),$ which satisfies a KG like equation (KGE):

$$\begin{aligned}&\left[ \hat{P}_{\mu }\hat{P}^{\mu }-m^{2}\right] \Phi (x)=0,\nonumber \\&\hat{P}^{\mu }=\hat{P}^{\mu }\left( x\right) =i\partial ^{\mu }+e\left[ \hat{A}^{\mu }(u)+A_{\textrm{ext}}^{\mu }({\textbf{r}})\right] , \nonumber \\&\hat{A}^{\mu }(u)=\left( 0,\hat{{\textbf{A}}}(u)\right) ,\quad u=t-z,\nonumber \\&\hat{{\textbf{A}}}(u)=U_{{\gamma }}\left( t\right) \hat{{\textbf{A}}}(z)U_{{\gamma }}^{-1}\left( t\right) \nonumber \\&\quad =\frac{1}{e}\sum _{s=1,2}\sum _{\lambda =1,2}\sqrt{\frac{\varepsilon }{ 2\kappa _{s}}}\left[ \hat{a}_{s,\lambda }\exp \left( -i\kappa _{s}u\right) \right. \nonumber \\&\qquad \left. + \hat{a}_{s,\lambda }^{\dagger }\exp \left( i\kappa _{s}u\right) \right] {\textbf{e}}_{\lambda }, \end{aligned}$$

(5)

where $\varepsilon =\alpha \rho ,$ $\alpha =e^{2}/\hbar c=1/137,$ and $\rho$ is the density of the electron media. The quantity $\varepsilon$ characterizes the strength of the interaction between the charged particles and the photon beam. We suppose that both $\varepsilon$ and $\alpha$ are small, this supposition defines the above mentioned approximation.

One can see that in the model under consideration, we have three commuting integrals of motion $\hat{G}_{\mu }=i\partial _{\mu }+n_{\mu }\hat{H}_{ {\gamma }},$ $\mu =0,$ 1,  3;  $n^{\mu }=(1,{\textbf{n}});$ $\hat{G} _{0}$ can be interpreted as the operator of the total energy and $\hat{G} _{\mu },$ $\mu =1,$ 3 as momenta operators in the directions $x^{1}$ and z.

Recall that $\hat{I}$ is an integral of motion if its mean value

$$\begin{aligned}&\left( \varphi ,\hat{I}\varphi \right) =\int \varphi ^{*}\left( x\right) \left( i\overleftrightarrow {\partial _{0}}-2eA_{0}\right) \hat{I}\varphi \left( x\right) d{\textbf{r}},\\&\overleftrightarrow {\partial _{0}}= \overrightarrow{\partial _{0}}-\overleftarrow{\partial _{0}}, \end{aligned}$$

with respect to any $\varphi$ satisfying the KGE does not depend on time. If $\hat{I}$ is an integral of motion, then $\left[ \hat{I},\hat{P}_{\mu } \hat{P}^{\mu }\right] =0.$

If $\hat{I}$ is an integral of motion, then, apart from satisfying the KGE, the wave function could be choose as an eigenfunction of $\hat{I}.$ Then we look for AV $\Phi (x)$ that are also eigenvectors for the integrals of motion $\hat{G}_{\mu },$

$$\begin{aligned}{} & {} \left[ \hat{P}_{\mu }\hat{P}^{\mu }-m^{2}\right] \Phi (x)=0, \nonumber \\{} & {} \hat{G}_{\mu }\Phi (x)=g_{\mu }\Phi (x),\quad \mu =0,1,3, \end{aligned}$$

(6)

where $g_{0}$ is the total energy and $g_{1,3}$ are momenta in $x^{1}$ and z directions. From Eq. (6) it follows

$$\begin{aligned}{} & {} \left[ \hat{P}_{\mu }\hat{P}^{\mu }-m^{2}\right] \Phi (x)\nonumber \\{} & {} \quad =\frac{1}{2(ng)}[ \hat{H}_{{\chi }}\left( u\right) -(g_{0}-g_{3})/2]\Phi (x),\nonumber \\{} & {} \hat{H}_{{\chi }}\left( u\right) =\hat{H}_{{\gamma }}+\frac{1 }{2(ng)}\left\{ \left[ eBx^{(2)}-g^{1}-e\hat{A}^{1}\left( u\right) \right] ^{2}\right. \nonumber \\{} & {} \qquad \left. +\left[ i\partial _{2}-eA^{2}\left( u\right) \right] ^{2}+m^{2}\right\} , \end{aligned}$$

(7)

where $(ng)=g_{0}+g_{3}.$ Consequently, the operator $\hat{H}_{{\chi }}\left( u\right)$ commutes with the operator $\hat{P}_{\mu }\hat{P}^{\mu }$ on solutions $\Phi (x),$ and therefore is an integral of motion.

A solution to Eq. (6) has form

$$\begin{aligned} \Phi (x)= & {} \exp \left[ -i(g_{0}t+g_{1}x^{(1)}+g_{3}z)\right] \nonumber \\{} & {} \times \hat{U}_{{\gamma }}\left( u\right) \chi (x^{(2)}), \end{aligned}$$

(8)

where the function $\chi (x^{(2)})$ must satisfy the following equation:

$$\begin{aligned} \hat{H}_{{\chi }}(0)\chi (x^{(2)})=\frac{g_{0}-g_{3}}{2}\chi (x^{(2)}). \end{aligned}$$

(9)

In order to solve the latter equation, we pass to a description of the electron motion in the magnetic field in an adequate Fock space, see Ref. [4]. We introduce new creation $\hat{a}_{0}^{\dagger }$ and annihilation $\hat{a}_{0}$ Bose operators, $[\hat{a}_{0},\hat{a} _{0}^{\dagger }]=1,$

$$\begin{aligned}&\hat{a}_{0}=(2)^{-1/2}\left( \eta +\partial _{\eta }\right) ,\nonumber \\&\hat{a}_{0}^{\dagger }=(2)^{-1/2}\left( \eta -\partial _{\eta }\right) ,\ (eB)^{1/2}\eta =\left( eBx^{(2)}-g^{1}\right) , \nonumber \\&x^{(2)}=\sqrt{\frac{1}{2eB}}\left( \hat{a}_{0}-\hat{a}_{0}^{\dagger }\right) +g^{1},\nonumber \\&\partial _{2}=\sqrt{\frac{eB}{2}}\left( \hat{a}_{0}+\hat{a} _{0}^{\dagger }\right) ,\quad \hat{a}_{0}\left| 0\right\rangle _{\textrm{e}}=0. \end{aligned}$$

(10)

These operators commute with all the photon operators $a_{s,\lambda }^{\dagger }$ and $\hat{a}_{s,\lambda },$ $s=1,2,$ $\lambda =1,2.$ We denote the totality of the free photon and the introduced electron creation and annihilation operators as $a_{s,\lambda }^{\dagger }$ and $\hat{a} _{s,\lambda },$ $s=0,1,2,$ where $\hat{a}_{0,\lambda }^{\dagger }=\hat{a} _{0}^{\dagger }\delta _{\lambda ,1}$ and $\hat{a}_{0,\lambda }=\hat{a} _{0}\delta _{\lambda ,1}.$ The corresponding vacuum vector $\left| 0\right\rangle$ reads:

$$\begin{aligned} \left| 0\right\rangle =\left| 0\right\rangle _{{\gamma } }\otimes \left| 0\right\rangle _{\textrm{e}},\ \hat{a}_{s,\lambda }\left| 0\right\rangle =0,\quad s=0,1,2. \end{aligned}$$

(11)

The operator $\hat{H}_{{\chi }}\left( 0\right)$ can be represented as a quadratic form in terms this totality of the creation and annihilation operators,

$$\begin{aligned}{} & {} \hat{H}_{{\chi }}(0)=\sum _{s,s^{\prime }=0,1,2}\sum _{\lambda ,\lambda ^{\prime }=1,2}A_{s,\lambda ;s^{\prime },\lambda ^{\prime }}a_{s,\lambda }^{\dagger }\hat{a}_{s^{\prime },\lambda ^{\prime }}\nonumber \\{} & {} \quad +\frac{1}{ 2}\left( B_{s,\lambda ;s^{\prime },\lambda ^{\prime }}\hat{a}_{s,\lambda }^{\dagger }\hat{a}_{s^{\prime },\lambda ^{\prime }}^{\dagger }+B_{s,\lambda ;s^{\prime },\lambda ^{\prime }}^{*}\hat{a}_{s,\lambda }\hat{a} _{s^{\prime },\lambda ^{\prime }}\right) \nonumber \\{} & {} \quad +\frac{m^{2}}{2ng}+\frac{\omega }{2}+\frac{\epsilon }{2}\sum _{s=1,2}\kappa _{s}^{-1},\ \omega =\frac{eB}{ng},\ \epsilon =\frac{\varepsilon }{ng}, \nonumber \\{} & {} A_{s,\lambda ;s^{\prime },\lambda ^{\prime }}=\left[ \omega (2-\lambda )\delta _{0,s}+\kappa _{s}\left( 1-\delta _{0,s}\right) \right] \delta _{s,s^{\prime }}\delta _{\lambda ,\lambda ^{\prime }}\nonumber \\{} & {} \quad +\frac{\epsilon }{2 \sqrt{\kappa _{s}\kappa _{s^{\prime }}}}\left( 1-\delta _{0,s}\right) \left( 1-\delta _{0,s^{\prime }}\right) \delta _{\lambda ,\lambda ^{\prime }} \nonumber \\{} & {} \quad -\frac{\left| ng\right| }{ng}\frac{\sqrt{\epsilon \omega }}{2} \left[ \frac{(+i)^{\lambda -1}}{\sqrt{\kappa _{s}}}\left( 1-\delta _{0,s}\right) \delta _{0,s^{\prime }}\delta _{\lambda ^{\prime },1}\right. \nonumber \\{} & {} \quad \left. +\frac{ (-i)^{\lambda ^{\prime }-1}}{\sqrt{\kappa _{s^{\prime }}}}\left( 1-\delta _{0,s^{\prime }}\right) \delta _{0,s}\delta _{\lambda ,1}\right] , \nonumber \\{} & {} B_{s,\lambda ;s^{\prime },\lambda ^{\prime }}=\frac{\epsilon }{2\sqrt{ \kappa _{s}\kappa _{s^{\prime }}}}\left( 1-\delta _{0,s}\right) \left( 1-\delta _{0,s^{\prime }}\right) \delta _{\lambda ,\lambda ^{\prime }}\nonumber \\{} & {} \quad -\frac{\left| ng\right| }{ng}\frac{\sqrt{\epsilon \omega }}{2} \left[ \frac{(-i)^{\lambda -1}}{\sqrt{\kappa _{s}}}\left( 1-\delta _{0,s}\right) \delta _{0,s^{\prime }}\delta _{\lambda ^{\prime },1}\right. \nonumber \\{} & {} \quad \left. +\frac{ (-i)^{\lambda ^{\prime }-1}}{\sqrt{\kappa _{s^{\prime }}}}\left( 1-\delta _{0,s^{\prime }}\right) \delta _{0,s}\delta _{\lambda ,1}\right] . \end{aligned}$$

(12)

As it is demonstrated in Appendix A, there exists a linear canonical transformation of the operators $a_{s,\lambda }^{\dagger }$ and $\hat{a} _{s,\lambda },$ $s=0,1,2,$ given by Eqs. (A1) which diagonalizes the Hamiltonian $\hat{H}_{{\chi }}\left( 0\right) ,$

$$\begin{aligned}&\hat{H}_{{\chi }}\left( 0\right) =\hat{H}_{\textrm{e}}(0)+\hat{H}_{\mathrm {q-ph}}(0),\nonumber \\&\hat{H}_{\textrm{e}}(0)=\tau _{0}c_{0}^{\dagger }c_{0}+\frac{m^{2}}{2(ng)}+\frac{\omega }{2}, \nonumber \\&\hat{H}_{\mathrm {q-ph}}(0)=\sum _{s=1,2}\sum _{\lambda =1,2}\tau _{s,\lambda }c_{s,\lambda }^{\dagger }c_{s,\lambda }\nonumber \\&\quad -\sum _{s,k=0,1,2}\sum _{\lambda ,\lambda ^{\prime }=1,2}\tau _{k,\lambda ^{\prime }}\left| v_{s,\lambda ;k,\lambda ^{\prime }}\right| ^{2} +\frac{\epsilon }{2}\sum _{s=1,2}\kappa _{s}^{-1}, \nonumber \\ \end{aligned}$$

(13)

where the quantities $\tau _{k,\lambda }$ satisfy the conditions $\tau _{0}(\epsilon =0)=\omega ,$ $\tau _{k,\lambda }(\epsilon =0)=\kappa _{k}$ being positive roots of the equation

$$\begin{aligned}&\sum _{s=1,2}\frac{\epsilon }{\tau _{k,\lambda }^{2}-\kappa _{s}^{2}}=1+\frac{ \left( -1\right) ^{\lambda }\omega }{\tau _{k,\lambda }}, \nonumber \\&\tau _{0,\lambda }=\tau _{0}\delta _{\lambda ,1},\quad k=0,1,2. \end{aligned}$$

(14)

It is possible to demonstrate that after an unitary transformation, the integral of motion $\hat{H}_{{\chi }}\left( u\right)$ can be separated in two parts $\hat{H}_{\mathrm {q-ph}}(u)$ and $\hat{H}_{\textrm{e}}(u)$:

$$\begin{aligned}{} & {} \hat{H}_{{\chi }}(u)=\hat{U}_{{\gamma }}\left( u\right) \hat{ H}_{{\chi }}\left( 0\right) \hat{U}_{{\gamma }}\left( u\right) ^{-1}\nonumber \\{} & {} \quad =\hat{H}_{\mathrm {q-ph}}(u)+\hat{H}_{\textrm{e}}(u), \nonumber \\{} & {} \hat{H}_{\mathrm {q-ph}}(u)=\hat{U}_{{\gamma }}\left( u\right) \hat{H}_{\mathrm {q-ph}}(0)\hat{U}_{{\gamma }}\left( u\right) ^{-1},\nonumber \\{} & {} \hat{H}_{\textrm{e}}(u)=\hat{U}_{{\gamma }}\left( u\right) \hat{H}_{\textrm{e}}(0)\hat{U}_{{\gamma }}\left( u\right) ^{-1}, \nonumber \\{} & {} \left[ \hat{H}_{\textrm{e}}(u),\hat{H}_{{\chi }}(u)\right] =0\nonumber \\{} & {} \left[ \hat{H}_{\mathrm {q-ph}}(u),\hat{H}_{{\chi }}(u)\right] =0. \end{aligned}$$

(15)

Each of these parts are also integrals of motion due to relations Eqs. (7), (9) and (15). The operator $\hat{H}_{\textrm{e}}$ corresponds to the quasi-electron subsystem, while the operator $\hat{H}_{\mathrm {q-ph}}$ to the subsystem of quasi-photons.

It is useful to consider operators $\hat{\mathcal {P}}_{\mu },$

$$\begin{aligned}{} & {} \hat{\mathcal {P}}_{\mu }=\hat{G}_{\mu }\ -n_{\mu }\hat{H}_{\mathrm {q-ph}}\left( u\right) \nonumber \\{} & {} \quad =i\partial _{\mu }-n_{\mu }\left[ \hat{H}_{\mathrm {q-ph}}\left( u\right) -\hat{H}_{{\gamma }}\right] , \nonumber \\{} & {} \left[ \hat{\mathcal {P}}_{\mu },\hat{\mathcal {P}}_{\nu }\right] =0,\quad \mu ,\nu =0,1,2, \end{aligned}$$

(16)

witch are also integrals of motion. If we assume that at $\epsilon \rightarrow 0$ the photons do not interact with the electronic medium, then in such a limit the operators $\hat{\mathcal {P}}_{\mu }$ are the energy–momentum operators of a the free electrons $i\partial _{\mu },$ and the operator $n_{\mu }\hat{H}_{\mathrm {q-ph}}\left( u\right)$ is the energy–momentum operator of the free photons $\hat{H}_{{\gamma }}.$ It is therefore appropriate to refer to $\hat{\mathcal {P}}_{\mu }$ as the quasi-electron energy–momentum, and to $n_{\mu }\hat{H}_{\mathrm {q-ph}}\left( u\right)$ as the energy–momentum of the quasi-photons.

Then we can choose AV $\Phi (x)$ to be eigenvectors for the integrals of motion $\hat{H}_{\textrm{e}}\left( u\right) ,$ $\hat{H}_{\mathrm {q-ph}}(u)$ and $\hat{\mathcal {P}}_{\mu },$

$$\begin{aligned} \hat{H}_{\textrm{e}}(u)\Phi (x)= & {} E_{\textrm{e}}\Phi (x),\nonumber \\ \hat{H}_{\mathrm {q-ph}}(u)\Phi (x)= & {} E_{\mathrm {q-ph}}\Phi (x),\nonumber \\ \hat{\mathcal {P}}_{\mu }\ \Phi (x)= & {} p_{\mu }\Phi (x). \end{aligned}$$

(17)

Further, we interpret the eigenvalues $p_{\mu }$ as momenta of quasi-electrons. It follows from Eq. (17) that $\Phi (x)$ is an eigenvector for the operator $\hat{H}_{{\chi }}(u),$

$$\begin{aligned} \hat{H}_{{\chi }}(u)\Phi (x)=E\Phi (x),\ E=E_{\textrm{e}}+E_{\mathrm {q-ph}}. \end{aligned}$$

(18)

Substituting (8) into Eq. (18), we obtain an equation for the function $\chi (x^{2}),$

$$\begin{aligned} \hat{H}_{{\chi }}(0)\chi (x^{(2)})=E\chi (x^{(2)}), \end{aligned}$$

(19)

which has the following solutions:

$$\begin{aligned}&\chi (x^{(2)})=\left| \phi _{\textrm{e}}\right\rangle \otimes \left| \Phi _{\mathrm {q-ph}}\right\rangle ,\nonumber \\&\left| \Phi _{\mathrm {q-ph}}\right\rangle =\prod _{\lambda =1,2}\frac{\left( \hat{c}_{1,\lambda }^{\dagger }\right) ^{N_{1,\lambda }}}{\sqrt{N_{1,\lambda }!}}\left| 0\right\rangle _{{\textrm{c}}_{1}} \prod _{\lambda ^{\prime }=1,2}\frac{\left( \hat{c}_{2,\lambda ^{\prime }}^{\dagger }\right) ^{N_{2,\lambda ^{\prime }}}}{\sqrt{ N_{2,\lambda ^{\prime }}!}}\left| 0\right\rangle _{{\textrm{c}}_{2}}, \nonumber \\&\left| \phi _{\textrm{e}}\right\rangle =\frac{\left( \hat{c} _{0}^{\dagger }\right) ^{N_{0}}}{\sqrt{N_{0}!}}\left| 0\right\rangle _{ {\textrm{c}}_{0}},\ \hat{c}_{0}\left| 0\right\rangle _{c_{0}}=0,\ \ c_{s,\lambda }\left| 0\right\rangle _{{\textrm{c}}_{s}}=0,\nonumber \\&E_{\textrm{e}}=\tau _{0}N_{0}+\frac{m^{2}}{2(ng)}+\frac{\omega }{2},\ \ N_{0}\in {\mathbb {N}}, \nonumber \\&E_{\mathrm {q-ph}}=\sum _{s=1,2}\sum _{\lambda =1,2}\tau _{s,\lambda }N_{s,\lambda }\nonumber \\&\qquad -\sum _{s,k=0,1,2}\sum _{\lambda ,\lambda ^{\prime }=1,2}\tau _{k,\lambda ^{\prime }}\left| v_{s,\lambda ;k,\lambda ^{\prime }}\right| ^{2}\nonumber \\&\qquad +\frac{\epsilon }{2}\sum _{s=1,2}\kappa _{s}^{-1},\ \ N_{s,\lambda }\in {\mathbb {N}}. \end{aligned}$$

(20)

Equations (17), (9) and (19) are consistent if

$$\begin{aligned}&g_{0}=p_{0}+E_{\mathrm {q-ph}},\quad g_{1}=p_{1},\quad g_{3}=p_{3}-E_{\mathrm {q-ph}},\\&E=\frac{g_{0}-g_{3}}{2}, \end{aligned}$$

which implies:

$$\begin{aligned}&E_{\textrm{e}}+E_{\mathrm {q-ph}}\ =\frac{g_{0}-g_{3}}{2}=\frac{p_{0}-p_{3}}{2 }+E_{\mathrm {q-ph}},\nonumber \\&\left( ng\right) =\left( np\right) , \end{aligned}$$

(21)

and

$$\begin{aligned} E_{\textrm{e}}=\frac{p_{0}-p_{3}}{2}. \end{aligned}$$

(22)

Taking into account Eq. (20) from (22) we obtain the spectrum of quasi-electrons in the constant magnetic field:

$$\begin{aligned}&p_{0}^{2}=2eB\left( \frac{\tau _{0}}{\omega }N_{0}+\frac{1}{2}\right) +p_{3}^{2}+m^{2},\nonumber \\&\omega =\frac{eB}{(np)}. \end{aligned}$$

(23)

Since $\tau _{0}(\epsilon =0)=\omega ,$ the well-known spectrum of a relativistic spinless particle in the constant magnetic field, follows from Eq. (23),

$$\begin{aligned} \bar{p}_{0}^{2}=2eB\left( N_{0}+\frac{1}{2}\right) +p_{3}^{2}+m^{2}. \end{aligned}$$

(24)

For small $\varepsilon$ the roots $\tau _{k,\lambda }$ are:

$$\begin{aligned}{} & {} \tau _{k,\lambda }=\kappa _{k}+\frac{\omega _{0}}{2eB\left( \kappa _{k}+(-1)^{\lambda }\omega _{0}\right) }\varepsilon +O(\varepsilon ^{2})\,\nonumber \\{} & {} \quad k,\lambda =1,2, \end{aligned}$$

(25)

$$\begin{aligned}{} & {} \tau _{0}=\omega _{0}\left\{ 1-\varepsilon \frac{\omega _{0}}{eB}\left( \frac{\omega _{0}N_{0}}{\bar{p}_{0}}-1\right) \right. \nonumber \\{} & {} \quad \left. \times \sum _{s^{\prime }=1,2}\left( \omega _{0}^{2}-\kappa _{s^{\prime }}^{2}\right) ^{-1}\right\} +O(\varepsilon ^{2}),\nonumber \\{} & {} \omega _{0}=\frac{eB}{\bar{p}_{0}+p_{3}}. \end{aligned}$$

(26)

In this approximation, the spectrum of the quasi-electrons in the constant magnetic field has form:

$$\begin{aligned} p_{0}&=\bar{p}_{0}+\epsilon \frac{\omega _{0}N_{0}}{\bar{p}_{0}}\left( \frac{ \omega _{0}N_{0}}{\bar{p}_{0}}-1\right) \sum _{s^{\prime }=1,2}\left( \omega _{0}^{2}-\kappa _{s^{\prime }}^{2}\right) ^{-1}\nonumber \\&\quad +O(\varepsilon ^{2}). \end{aligned}$$

(27)

Using Eqs. (25) and (26) we obtain for small $\varepsilon$ expressions for matrices (A11) defining the canonical transformation (A1):

$$\begin{aligned}{} & {} u_{s,\lambda ;k,\sigma }=-\left\{ \delta _{\lambda ,1}\delta _{s,0}\delta _{\lambda ,\sigma }\delta _{s,k}\right. \nonumber \\{} & {} \quad \left. +\frac{\textrm{sgn}\left[ \omega _{0}+(-1)^{\lambda }\kappa _{s}\right] }{\sqrt{2}}\left[ \delta _{\lambda ,1}+i(-1)^{\sigma }\delta _{\lambda ,2}\right] \right. \nonumber \\{} & {} \quad \left. \times \left( 1-\delta _{s,0}\right) \delta _{s,k}\right. \nonumber \\{} & {} \quad +\left. \frac{\omega _{0}\sqrt{\varepsilon }}{\sqrt{2eB\kappa _{k}} \left| \omega _{0}-\kappa _{k}\right| }\delta _{s,0}\left( 1-\delta _{k,0}\right) \delta _{\sigma ,1}\right\} +O(\varepsilon ), \nonumber \\{} & {} v_{s,\lambda ;s^{\prime },\lambda ^{\prime }}=\left\{ \frac{(-i)^{\lambda -1}\omega _{0}\sqrt{\varepsilon }}{\sqrt{2eB\kappa _{s}}\left( \omega _{0}+\kappa _{s}\right) }\left( 1-\delta _{s,0}\right) \delta _{s,k}\right. \nonumber \\{} & {} \quad \left. -\delta _{s,0}\left( 1-\delta _{k,0}\right) \delta _{\lambda ,1}\delta _{\sigma ,2} \frac{\omega _{0}\sqrt{\varepsilon }}{\sqrt{2eB\kappa _{k}}\left( \omega _{0}+\kappa _{k}\right) }\right. \nonumber \\{} & {} \quad +\left. \sqrt{\frac{\kappa _{k}}{\kappa _{s}}}\frac{\omega _{0}\left[ \delta _{\lambda ,1}+i(-1)^{\sigma }\delta _{\lambda ,2}\right] \varepsilon }{2eB\sqrt{2}\left( \kappa _{s}+\kappa _{k}\right) \left| \omega _{0}+\left( -1\right) ^{\sigma }\kappa _{k}\right| }\right. \nonumber \\{} & {} \quad \left. \times \left( 1-\delta _{s,0}\right) \left( 1-\delta _{k,0}\right) \right\} +O(\varepsilon ). \end{aligned}$$

(28)

Substituting $\chi (x^{2})$ given by Eq. (20) in Eq. (8) for $\Phi (x),$ for small $\varepsilon$ we obtain:

$$\begin{aligned}{} & {} \Phi (x)=\left| \Phi _{\textrm{e}}\right\rangle \otimes \left| \Phi _{\mathrm {q-ph}}\right\rangle +O(\varepsilon ), \nonumber \\{} & {} \left| \Phi _{\textrm{e}}\right\rangle =\exp \left\{ -i\left( p_{0}t+p_{1}x^{(1)}+p_{3}z\right) \right\} \nonumber \\{} & {} \quad \times \frac{\left( \hat{c}_{0}^{\dagger }\right) ^{N_{0}}}{\sqrt{N_{0}!}}\left| 0\right\rangle _{{\textrm{c}} _{0}}. \end{aligned}$$

(29)

3 Photon entanglement problem

3.1 General

We recall that a qubit is a two-level quantum-mechanical system with state vectors (two columns) $\left| \psi \right\rangle =\left( \psi _{1},\psi _{2}\right) ^{T}\in$ ${\mathcal {H}}={\mathbb {C}}^{2},$ $\langle \psi ^{\prime }\left| \psi \right\rangle =\psi _{1}^{\prime *}\psi _{1}+\psi _{2}^{\prime *}\psi _{2}.$ An orthogonal basis $\left| a\right\rangle ,$ $a=0,$ 1 in ${\mathcal {H}}$ is: $\left| 0\right\rangle =\left( 1,0\right) ^{T},$ $\left| 1\right\rangle =\left( 0,1\right) ^{T},$ $\langle a\left| a^{\prime }\right\rangle =\delta _{aa^{\prime }},$ $\sum _{a=0,1}\vert a \rangle \langle a\vert = I,$ where $I={\textrm{diag}}\left( 1,1\right) .$ E.g. two levels can be taken as spin up and spin down of an electron; or two polarizations of a single photon. A system, composed of two qubit subsystems A and B with the Hilbert space ${\mathcal {H}}_{AB}={\mathcal {H}}_{A}\otimes {\mathcal {H}}_{B}$ where ${\mathcal {H}}_{A/B}={\mathbb {C}}^{2}$ is a four level system. If $\left| a\right\rangle _{A}$ and $\left| b\right\rangle _{B},$ a,  $b=0,$ 1,  are orthonormal bases in ${\mathcal {H}}_{A}$ and ${\mathcal {H}}_{B}$ respectively, then $\left| \alpha b\right\rangle =\left| a\right\rangle \otimes \left| b\right\rangle$ is a complete and orthonormalized basis in ${\mathcal {H}}_{AB},$ $\left| \alpha b\right\rangle =\left| a\right\rangle \otimes \left| b\right\rangle =\left( a_{1}b_{1},a_{1}b_{2},a_{2}b_{1},a_{2}b_{2}\right) ^{T}.$ The so-called computational basis $\left| \Theta \right\rangle _{s},$ $s=1,2,3,4,$ reads:

$$\begin{aligned}&\left| \Theta \right\rangle _{1}=\left| 00\right\rangle =\left( \begin{array}{cccc} 1&0&0&0 \end{array} \right) ^{T},\nonumber \\&\left| \Theta \right\rangle _{2}=\left| 01\right\rangle =\left( \begin{array}{cccc} 0&1&0&0 \end{array} \right) ^{T}, \nonumber \\&\left| \Theta \right\rangle _{3}=\left| 10\right\rangle =\left( \begin{array}{cccc} 0&0&1&0 \end{array} \right) ^{T},\nonumber \\&\left| \Theta \right\rangle _{4}=\left| 11\right\rangle =\left( \begin{array}{cccc} 0&0&0&1 \end{array} \right) ^{T}. \end{aligned}$$

(30)

A pure state $\left| \Psi \right\rangle _{AB}\in {\mathcal {H}}_{AB}$ is called separable iff it can be represented as: $\left| \Psi \right\rangle _{AB}=\left| \Psi \right\rangle _{A}\otimes \left| \Psi \right\rangle _{B},$ $\left| \Psi \right\rangle _{A}\in {\mathcal {H}} _{A},$ $\left| \Psi \right\rangle _{B}\in {\mathcal {H}}_{B}.$ Otherwise, it is entangled. An entanglement measure $M\left( \left| \Psi \right\rangle _{AB}\right)$ of the state $\left| \Psi \right\rangle _{AB}$ is real and positive. This measure is zero for separable states, and is 1 for maximally entangled states. In what follows, we use the information measure

$$\begin{aligned}&M\left( \vert \Psi \rangle _{AB}\right) =S\left( \hat{\rho }_{A}\right) =S\left( \hat{\rho }_{B}\right) ,\nonumber \\&S\left( \hat{\rho }_{A/B}\right) = -{\textrm{tr}}\left( \hat{\rho }_{A/B}\log \hat{\rho }_{A/B}\right) , \nonumber \\&\hat{\rho }_{A}={\textrm{tr}}_{B}\hat{\rho }_{AB}= \sum _{b}\langle b\vert \hat{\rho }_{AB}\vert b\rangle ,\nonumber \\&\hat{\rho }_{B}={\textrm{tr}}_{A}\hat{\rho }_{AB}= \sum _{a}\langle a\vert \hat{\rho }_{AB}\vert a\rangle , \end{aligned}$$

(31)

where $S\left( \hat{\rho }\right) =-{\textrm{tr}}\left( \hat{\rho }\log \hat{\rho }\right)$ is von Neumann entropy of $\hat{\rho }.$ One can see that $S\left( \rho _{A}\right) =S\left( \rho _{B}\right) .$ Although the entanglement measure of a pure state is always zero, its reduced statistical operators have nonzero entanglement measures.

For a the pure state $\left| \Psi \right\rangle _{AB}=\sum _{s=1}^{4}\upsilon _{s}\left| \Theta \right\rangle _{s},$ we obtain:

$$\begin{aligned}{} & {} \hat{\rho }_{AB}=\ _{AB}\vert \Psi \rangle \langle \Psi \vert \ _{AB}\\{} & {} \quad =\left[ \upsilon _{1}\left| 00\right\rangle +\upsilon _{2}\left| 01\right\rangle +\upsilon _{3}\left| 10\right\rangle +\upsilon _{4}\left| 11\right\rangle \right] \\{} & {} \qquad \times \left[ \upsilon _{1}^{*}\langle 00\vert +\upsilon _{2}^{*} \langle 01\vert +\upsilon _{3}^{*}\langle 10\vert +\upsilon _{4}^{*}\langle 11\vert \right] . \end{aligned}$$

Then

$$\begin{aligned}&\hat{\rho }_{A}=\ _{B}\langle 0\vert \hat{\rho }_{AB}\left| 0\right\rangle _{B}+\ _{B}\langle 1\vert \hat{\rho }_{AB} \left| 1\right\rangle _{B}\nonumber \\&\quad =\vert \upsilon _{1}\vert ^{2}\left| 0\right\rangle \langle 0\vert +\upsilon _{1}\upsilon _{3}^{*}\left| 0\right\rangle \langle 1\vert +\vert \upsilon _{2}\vert ^{2}\left| 0\right\rangle \langle 0\vert \nonumber \\&\qquad +\upsilon _{2}\upsilon _{4}^{*}\left| 0\right\rangle \langle 1\vert +\upsilon _{3}\upsilon _{1}^{*}\left| 1\right\rangle \langle 0\vert +\vert \upsilon _{3}\vert ^{2}\left| 1\right\rangle \langle 1\vert \nonumber \\&\qquad +\upsilon _{4}\upsilon _{2}^{*}\left| 1\right\rangle \langle 0\vert +\vert \upsilon _{4}\vert ^{2}\left| 1\right\rangle \langle 1\vert \nonumber \\&\quad = \begin{pmatrix} \rho ^{(A)}_11 &{} \rho ^{(A)}_12\\ \rho ^{(A)}_21 &{} \rho ^{(A)}_22 \end{pmatrix},\nonumber \\&\rho _{11}^{\left( A\right) }=\vert \upsilon _{1}\vert ^{2}+\vert \upsilon _{2}\vert ^{2},\ \rho _{12}^{\left( A\right) }=\upsilon _{1}\upsilon _{3}^{*}+\upsilon _{2}\upsilon _{4}^{*}, \nonumber \\&\rho _{21}^{\left( A\right) }=\upsilon _{3}\upsilon _{1}^{*}+\upsilon _{4}\upsilon _{2}^{*},\quad \rho _{22}^{\left( A\right) }=\vert \upsilon _{3}\vert ^{2}+\vert \upsilon _{4}\vert ^{2}. \end{aligned}$$

(32)

Calculating the entanglement measure, we may use eigenvalues of the matrix $\hat{\rho }_{A},$

$$\begin{aligned}&\hat{\rho }^{\left( A\right) }P_{a}=\lambda _{a}P_{a},\nonumber \\&\lambda _{a}=\frac{1 }{2}\left( \vert \upsilon _{1}\vert ^{2}+\vert \upsilon _{2}\vert ^{2}+\vert \upsilon _{3}\vert ^{2}+\vert \upsilon _{4}\vert ^{2}+\left( -1\right) ^{a}y\right) , \nonumber \\&P_{a}=\left( \begin{array}{c} \frac{\vert \upsilon _{1}\vert ^{2}+\vert \upsilon _{2}\vert ^{2}-\vert \upsilon _{4}\vert ^{2}-\vert \upsilon _{3}\vert ^{2}+\left( -1\right) ^{a}y}{2\left( \upsilon _{3}\upsilon _{1}^{*}+\upsilon _{4}\upsilon _{2}^{*}\right) } \\ 1 \end{array} \right) ,\nonumber \\&M\left( \left| \Psi \right\rangle _{AB}\right) =-\sum _{a=1,2}\lambda _{a}\log _{2}\lambda _{a}=H(z), \nonumber \\&H(z)=-\left[ z\log _{2}z+\left( 1-z\right) \log _{2}(1-z)\right] ,\nonumber \\&z=\left( 1+y\right) /2, \nonumber \\&y =\left[ \left( \vert \upsilon _{1}\vert ^{2}+\vert \upsilon _{2}\vert ^{2}-\vert \upsilon _{4}\vert ^{2}-\vert \upsilon _{3}\vert ^{2}\right) ^{2}\right. \nonumber \\&\quad \left. + 4 \vert \upsilon _{1}\upsilon _{3}^{*}+\upsilon _{2}\upsilon _{4}^{*}\vert ^{2}\right] ^{1/2},\quad \left( 0\log _{2}0\equiv 0\right) . \end{aligned}$$

(33)

Function H(z) is the so-called binary entropy function; see e.g. Refs. [5, 6].

3.2 Entanglement of photons with anti-parallel polarizations in the model under consideration

Here using solutions of the model under consideration constructed in Sect. 2, we study the entanglement of photons with anti-parallel polarizations by the electron medium and by the external magnetic field.

Consider the state $\left| \Phi _{\mathrm {q-ph}}\right\rangle$ describing quasi-photons, with different frequencies and with anti-parallel polarizations, $\lambda _{1}$ and $\lambda _{2}\ne \lambda _{1},$ i.e., $N_{1,3-\lambda _{1}}=N_{2,3-\lambda _{2}}=0,$ $N_{1,\lambda _{1}}=N_{2,\lambda _{2}}=1$:

$$\begin{aligned}&\left| \Phi _{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\right\rangle = \hat{c}_{1,\lambda _{1}}^{\dagger }\hat{c}_{2,\lambda _{2}}^{\dagger }\left| 0\right\rangle _{{\textrm{c}}},\nonumber \\&\left| 0\right\rangle _{{\textrm{c}}}=\left| 0\right\rangle _{{\textrm{c}} _{1}}\otimes \left| 0\right\rangle _{{\textrm{c}}_{2}},\quad \hat{c} _{s,\lambda }\left| 0\right\rangle _{{\textrm{c}}}=0, \end{aligned}$$

(34)

where $s=1,2.$

With account taken of Eqs. (A1) and (28) we can see that the last equation (34) implies for small $\varepsilon$:

$$\begin{aligned} \left| 0\right\rangle _{{\textrm{c}}}&=\left| 0\right\rangle - \frac{\omega _{0}\sqrt{\varepsilon }}{2eB}\left[ \sum _{s=1,2}\frac{i\hat{a} _{s,1}^{\dagger }+\hat{a}_{s,2}^{\dagger }}{\sqrt{\kappa _{s}}\left( \omega _{0}+\kappa _{s}\right) }\right] \hat{a}_{0}^{\dagger }\left| 0\right\rangle \nonumber \\&\quad +O(\varepsilon ). \end{aligned}$$

(35)

Then, it follows from Eq. (35) that $\left| 0\right\rangle _{ {\textrm{c}}}=\left| 0\right\rangle +O(\sqrt{\varepsilon }).$ Taking into account expansion (A1) for state (34), we obtain:

$$\begin{aligned}{} & {} \left| \Phi _{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\right\rangle = \hat{c}_{1,\lambda _{1}}^{\dagger }\hat{c}_{2,\lambda _{2}}^{\dagger }\left| 0\right\rangle +O(\sqrt{\varepsilon })\nonumber \\{} & {} \quad =\sum _{s,s^{\prime }=1,2}\sum _{\lambda ,\lambda ^{\prime }=1,2}u_{s,\lambda ;2,\lambda _{2}}u_{s,\lambda ;1,\lambda _{1}}\hat{a}_{s^{\prime },\lambda ^{\prime }}^{\dagger }\hat{a}_{s,\lambda }^{\dagger }\left| 0\right\rangle \nonumber \\{} & {} \qquad +u_{0,1;2,\lambda _{2}}\sum _{s=1,2}\sum _{\lambda =1,2}u_{s,\lambda ;1,\lambda _{1}}\hat{a}_{s,\lambda }^{\dagger }\hat{a}_{0}^{\dagger }\left| 0\right\rangle \nonumber \\{} & {} \qquad +\left( \sum _{s=0,1,2}\sum _{\lambda =1,2}u_{s,\lambda ;2,\lambda _{2}}v_{s,\lambda ,1,\lambda _{1}}^{*}\right) \left| 0\right\rangle \nonumber \\{} & {} \qquad +O(\sqrt{\varepsilon }), \nonumber \\{} & {} \quad \left\| \Phi _{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\right\| ^{2}=1+O(\sqrt{\varepsilon }). \end{aligned}$$

(36)

We believe that the corresponding free photon nonentangled beam after passing through the macro region, which consists of the electron media in the presence of the magnetic field, is deformed to this form, and there exists an analyzer detecting a two photon state for measuring the entanglement of the initial free photons. The two photon state $\vert \tilde{\Phi }_{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\rangle$ is represented by the first term in Eq. (36),

$$\begin{aligned}&\left| \tilde{\Phi }_{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\right\rangle =D\nonumber \\&\quad \times \sum _{s,s^{\prime }=1,2}\sum _{\lambda ,\lambda ^{\prime }=1,2}u_{s,\lambda ;2,\lambda _{2}}u_{s^{\prime },\lambda ^{\prime };1,\lambda _{1}}\hat{a}_{s^{\prime },\lambda ^{\prime }}^{\dagger }\hat{a}_{s,\lambda }^{\dagger }\left| 0\right\rangle ,\nonumber \\&\left\| \tilde{\Phi }_{\mathrm {q-ph}}\right\| ^{2}=1, \end{aligned}$$

(37)

where D is a normalization factor. It follows from Eq. (28) that $u_{s,\lambda ;2,\lambda _{2}}u_{s,\lambda ^{\prime };1,\lambda _{1}}=O( \varepsilon \left( \Delta \kappa \right) ^{-1}).$ Then at $\Delta \kappa =\left| \kappa _{2}-\kappa _{1}\right| \gg 1,$ the two photon state (37) can be reduced to the following form:

$$\begin{aligned}{} & {} \left| \tilde{\Phi }_{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\right\rangle \nonumber \\{} & {} \quad =D\sum _{\lambda ,\lambda ^{\prime }}\left[ u_{1,\lambda } \tilde{u}_{2,\lambda ^{\prime }}+u_{2,\lambda ^{\prime }}\tilde{u} _{1,\lambda }\right] \hat{a}_{1,\lambda }^{+}\hat{a}_{2,\lambda ^{\prime }}^{+}\left| 0\right\rangle \nonumber \\{} & {} \qquad +O\left( \left( \Delta \kappa \right) ^{-1}\right) , \nonumber \\{} & {} u_{s,\lambda }=u_{s,\lambda ;1,\lambda _{2}},\ \ \tilde{u}_{s,\lambda }=u_{s,\lambda ;2,\lambda _{1}}. \end{aligned}$$

(38)

In terms of the computational basis,

$$\begin{aligned}&\left| \vartheta _{1}\right\rangle =a_{1,1}^{+}a_{2,1}^{+}\left| 0\right\rangle ,\ \left| \vartheta _{2}\right\rangle =a_{1,1}^{+}a_{2,2}^{+}\left| 0\right\rangle ,\\&\left| \vartheta _{3}\right\rangle =a_{1,2}^{+}a_{2,1}^{+}\left| 0\right\rangle ,\ \left| \vartheta _{4}\right\rangle =a_{1,1}^{+}a_{2,1}^{+}\left| 0\right\rangle , \end{aligned}$$

Fig. 1

The entanglement measure as a function of the magnetic field

Fig. 2

The entanglement measure M(2, 1) as a function of the electron medium density

the state (38) can be rewritten as follows:

$$\begin{aligned}{} & {} \left| \tilde{\Phi }_{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\right\rangle =D\sum _{j=1}^{4}\upsilon _{j}\left| \vartheta _{j}\right\rangle ,\ \nonumber \\{} & {} D=\left( \sum _{i=1}^{4}\vert \upsilon _{i}\vert ^{2}\right) ^{-1/2}, \nonumber \\{} & {} \upsilon _{1}=u_{1,1}\tilde{u}_{2,1}+u_{2,1}\tilde{u}_{1,1},\nonumber \upsilon _{4}=\upsilon _{1}, \nonumber \\{} & {} \upsilon _{2}=u_{1,1}\tilde{u}_{2,2}+u_{2,2}\tilde{u}_{1,1},\quad \upsilon _{3}=-\upsilon _{2}. \end{aligned}$$

(39)

Let us calculate the entanglement measure $M(\lambda _{1},\lambda _{2})=M(\vert \tilde{\Phi }_{\mathrm {q-ph}}(\lambda _{1},\lambda _{2})\rangle )$ of the state $\vert \tilde{\Phi }_{\mathrm {q-ph} }(\lambda _{1},\lambda _{2})\rangle$ as the von Neumann entropy of the reduced density operator $\hat{\rho }^{\left( 1\right) }$ of the subsystem of the first photon,

$$\begin{aligned}{} & {} M(\lambda _{1},\lambda _{2})=-{\textrm{tr}}\left( \hat{\rho }^{\left( 1\right) }\log _{2}\hat{\rho }^{\left( 1\right) }\right) \nonumber \\{} & {} \quad =-\sum _{a=1,2}\mu _{a}\log _{2}\mu _{a}\ \nonumber \\{} & {} \quad =-\left[ z\log _{2}z+\left( 1-z\right) \log _{2}(1-z)\right] , \end{aligned}$$

(40)

where $\mu _{a},$ $a=1,2,$ are eigenvalues of the operator $\hat{\rho }^{\left( 1\right) }.$ In fact, we have to calculate the quantity y to obtain the entanglement measure $M(\lambda _{1},\lambda _{2}).$ At small $\varepsilon$ they read:

$$\begin{aligned}{} & {} y=1-\beta \varepsilon ^{4}+O(\varepsilon ^{5}), \nonumber \\{} & {} \beta =\frac{\left( \bar{p}_{0}/\Delta \kappa \right) ^{4}}{8(\omega _{0}+(-1)^{\lambda _{1}}\kappa _{1})^{2}(\omega _{0}+(-1)^{\lambda _{2}}\kappa _{2})^{2}},\nonumber \\{} & {} M(\lambda _{1},\lambda _{2})=-2\beta \varepsilon ^{4}\log _{2}\varepsilon \nonumber \\{} & {} \quad +\frac{\beta }{2\ln 2}\left( 1-\ln \frac{\beta }{2}\right) \varepsilon ^{4}+O(\varepsilon ^{5}). \end{aligned}$$

(41)

Further, it is convenient for us to choose a reference frame relative to which the momentum $p_{3}$ of electrons in the charged medium is zero, $p_{3}=0.$ Then the quantity $\omega _{0}$ is related to the magnetic field B as:

$$\begin{aligned} \omega _{0}=\frac{eB}{\sqrt{2eB\left( N_{0}+1/2\right) +m^{2}}}. \end{aligned}$$

(42)

We note that the quantity y given by Eq. (41) is singular, if

$$\begin{aligned} \omega _{0}=\left\{ \begin{array}{ll} \kappa _{1},&{}\quad \text {if}\ \lambda _{1}=1,\ \lambda _{2}=2 \\ \kappa _{2},&{}\quad \text {if}\ \lambda _{1}=2,\ \lambda _{2}=1. \end{array} \right. \end{aligned}$$

(43)

The corresponding to such $\omega _{0}$ strengths of the magnetic field B,  will be called resonant ones. There exist two such resonant values, $B=B_{1}$ at $\omega _{0}=\kappa _{1}$ for $\lambda _{1}=1$ and $B=B_{2}$ at $\omega _{0}=\kappa _{2}$ for $\lambda _{1}=2$:

$$\begin{aligned} B_{1}= & {} \frac{\kappa _{1}}{e}\sqrt{(N_{0}+1/2)^{2}\kappa _{1}^{2}+m^{2}}\nonumber \\{} & {} +\left( N_{0}+1/2\right) \kappa _{1}^{2}, \nonumber \\ B_{2}= & {} \frac{\kappa _{2}}{e}\sqrt{(N_{0}+1/2)^{2}\kappa _{2}^{2}+m^{2}}\nonumber \\{} & {} +\left( N_{0}+1/2\right) \kappa _{2}^{2}. \end{aligned}$$

(44)

When $B=B_{1},$ the expansions

$$\begin{aligned} \tau _{1,2}= & {} \kappa _{1}+\frac{\kappa _{1}\varepsilon }{2(\kappa _{1}+\kappa _{2})eB_{1}}+O(\varepsilon ^{2}), \nonumber \\ \tau _{2,1}= & {} \kappa _{2}-\sqrt{\frac{\kappa _{1}\varepsilon }{2eB_{1}}} +O(\varepsilon ) \end{aligned}$$

(45)

take place. Similarly, when $B=B_{2},$ the expansions

$$\begin{aligned} \tau _{1,2}= & {} \kappa _{1}+\frac{\kappa _{2}\varepsilon }{2(\kappa _{1}+\kappa _{2})eB_{2}}+O(\varepsilon ^{2}), \nonumber \\ \tau _{2,1}= & {} \kappa _{2}-\sqrt{\frac{\kappa _{2}\varepsilon }{2eB_{2}}} +O(\varepsilon ) \end{aligned}$$

(46)

hold. They have a different character than the one given by Eqs. (25) for similar roots. We suppose that at $B=B_{1}$ or $B=B_{2}$ analytical properties of roots (25) change as functions of the parameter $\varepsilon .$

From (45) and (46), we find that when a resonant value B is reached, the entanglement manifests itself already in a lower order in $\varepsilon$ compared to expression (41). For $B=B_{1},$ we have:

$$\begin{aligned}{} & {} y=1-\delta _{1}\varepsilon ^{3}+O(\varepsilon ^{4}),\nonumber \\{} & {} \delta _{1}=\frac{1}{ 4(\Delta \kappa )^{4}(\kappa _{1}+\kappa _{2})^{2}}\left( \frac{\kappa _{1}}{ eB_{1}}\right) ^{3}, \nonumber \\{} & {} M(\lambda _{1},\lambda _{2})=-\frac{3}{2}\delta _{1}\varepsilon ^{3}\log _{2}\varepsilon \nonumber \\{} & {} \quad +\frac{\delta _{1}}{2\ln 2}\left( 1-\ln \frac{\delta _{1}}{2} \right) \varepsilon ^{3}+O(\varepsilon ^{4}), \end{aligned}$$

(47)

whereas for $B=B_{2},$ we obtain:

$$\begin{aligned}{} & {} y=1-\delta _{2}\varepsilon ^{3}+O(\varepsilon ^{4}),\nonumber \\{} & {} \delta _{2}=\frac{1 }{4(\Delta \kappa )^{4}(\kappa _{1}+\kappa _{2})^{2}}\left( \frac{\kappa _{2} }{eB_{2}}\right) ^{3}, \nonumber \\{} & {} M(\lambda _{1},\lambda _{2})=-\frac{3}{2}\delta _{2}\varepsilon ^{3}\log _{2}\varepsilon \nonumber \\{} & {} \quad +\frac{\delta _{2}}{2\ln 2}\left( 1-\ln \frac{\delta _{2}}{2} \right) \varepsilon ^{3}+O(\varepsilon ^{4}). \end{aligned}$$

(48)

It can be seen that if the photon polarizations are the same, $\lambda _{1}=\lambda _{2}$ then the entanglement measure is equal to zero, $M(1,1)=M(2,2)=0.$

4 Illustrative numerical calculations and some final remarks

In our numerical calculations, we consider all the electrons in the charge medium located on zero Landau level $N_{0}=0$ and the beam of two photons with polarization $\lambda _{1}=2$ and $\lambda _{2}=1.$ It follows from Eq. (41) that the resonant entanglement is related to the frequency of that photon whose polarization vector is directed along the Ox axis at $B>0.$ If you change the direction of the magnetic field, $B<0,$ then the resonant entanglement will be related to the frequency of that photon whose polarization vector is directed along the Oy axis. Therefore in the case under consideration we have the resonant value of the magnetic field is $B=B_{2},$ see Eq. (44).

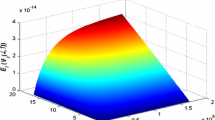
On the first plot the entanglement measure M (2, 1) is calculated as a function of the magnetic field B for the fixed first photon frequency $\nu _{1}=10^{3}~\text {nm},$ and different second photon frequency $\nu _{2}=2\pi \kappa _{2}^{-1}.$ The electron density is chosen to be $\rho =10^{14}{\mathrm {el\ m}}^{-3}$ (Fig. 1).

We see that the entanglement measure increases with increasing the magnetic field strength $B<B_{{2}}.$ When the magnetic field reaches its resonant value $B=B_{2},$ the entanglement measure experiences a jump. A further increase in the magnetic field $B>B_{{2}}$ leads to a smooth decrease in the entanglement. We also see that the entanglement measure decreases as the difference in photon frequencies increases. In the work [3] the entanglement of two photons in the absence of a magnetic field was considered and it was shown that the measure of the entanglement is the same for $\lambda _{1}=1,$ $\lambda _{2}=2$ and $\lambda _{1}=2,$ $\lambda _{2}=1.$ Here it is demonstrated that the presence of the magnetic field removes the degeneracy in photon polarizations and the entanglement measure depends on the direction of photon polarizations in the beam. Increasing the magnetic field strength increases entanglement, as long as the magnetic field value is below a certain resonant value, which is determined by the frequency of the photon having polarization $\lambda =1,$ see Eq. (44). The resonant value of B increases with decreasing of photon frequencies. But these values are not large, for example, for photons with frequencies $\nu _{2}$ corresponding to the ultraviolet range 380 nm–10 nm, the resonant values range from 6 to 225 A/m.

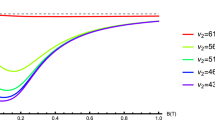
On the second plot the entanglement measure M (2, 1) is calculated as a function of the electron medium density for the fixed first photon frequency $\nu _{1}=10^{3}~\text {nm},$ and different second photon frequencies $\nu _{2}.$ The magnetic field B is chosen to be $B=2$ A/m which is less the corresponding resonant values (Fig. 2).

Note that the measure of entanglement increases with increasing density of the electronic medium and with increasing of pre-resonance values of the magnetic field. In our calculations the entanglement measure does not exceed 0.1. However, such a magnitude of the entanglement is usual in laboratory experiments, for example, similar magnitudes appear when an entangled biphoton Fock state of photons is scattered inside an optical cavity; see Refs. [7, 8].

We stress that performed numerical calculations are intended to illustrate the existence of a possible resonant entanglement within the framework of the chosen model and the approximations made. On the other hand, if our consideration motivates possible experiments to detect the effect of resonant entanglement then there may be an incentive to refine the corresponding model, in particular, the analytical formulas (41), (47) and (48) under weaker restrictions on the density of the electron medium and frequencies of the photons.

Appendix A: Diagonalization of the operator \(\hat{H}_{{\chi }}\left( 0\right) \)

Here we are going to construct a linear canonical transformation from the operators $a_{s,\lambda }^{\dagger }$ and $\hat{a}_{s,\lambda },$ $s=0,1,2,$ to some new Bose operators $\hat{c}_{s,\lambda }^{\dagger }$ and $\hat{c} _{s,\lambda },$ $s=0,1,2,$

$$\begin{aligned}{} & {} \hat{c}_{s,\lambda }=\sum _{s'=0,1,2;}\sum _{\lambda ' =1,2}u_{s^{\prime },\lambda ^{\prime };s,\lambda }^{*}\hat{a}_{s^{\prime },\lambda ^{\prime }}\nonumber \\{} & {} \quad +v_{s^{\prime },\lambda ^{\prime };s,\lambda }\hat{a}_{s^{\prime },\lambda ^{\prime }}^{\dagger },\ \ \hat{c}_{0,\lambda }=\hat{c} _{0}\delta _{\lambda ,1}, \nonumber \\{} & {} \hat{c}_{s,\lambda }^{\dagger }=\sum _{s=0,1,2;}\sum _{\lambda =1,2}u_{s^{\prime },\lambda ^{\prime };s,\lambda }\hat{a}_{s^{\prime },\lambda ^{\prime }}^{\dagger }\nonumber \\{} & {} \quad +v_{s^{\prime },\lambda ^{\prime };s,\lambda }^{*}\hat{a}_{s^{\prime },\lambda ^{\prime }},\ \ \hat{c}_{0,\lambda }^{\dagger }=\hat{c}_{0}^{\dagger }\delta _{\lambda ,1}, \end{aligned}$$

(A1)

$$\begin{aligned}{} & {} \left[ \hat{c}_{s,\lambda },\hat{c}_{s^{\prime },\lambda ^{\prime }}\right] =\left[ \hat{c}_{s,\lambda }^{\dagger },\hat{c}_{s^{\prime },\lambda ^{\prime }}^{\dagger }\right] =0, \nonumber \\{} & {} \left[ \hat{c}_{s,\lambda },\hat{c} _{s^{\prime },\lambda ^{\prime }}^{\dagger }\right] =\delta _{s,s^{\prime }}\delta _{\lambda ,\lambda ^{\prime }}, \end{aligned}$$

(A2)

in terms of which operator (12) takes the following diagonal form:

$$\begin{aligned}&\hat{H}_{{\chi }}(0)=\sum _{s=0,1,2}\sum _{\lambda =1,2}\tau _{s,\lambda }\hat{c}_{s,\lambda }^{\dagger }\hat{c}_{s,\lambda }+\tilde{H}_{0},\nonumber \\&\tau _{0,\lambda }=\tau _{0}\delta _{\lambda ,1},\ \ \tau _{s,\lambda }>0,\ \ \tilde{H}_{0}=\text {const}. \end{aligned}$$

(A3)

It is known that for the linear transformation (A1) to be canonical (namely, Eqs. (A2) hold true) it is required that the matrices $u=\left( u_{s,\lambda ;s^{\prime },\lambda ^{\prime }}\right)$ and $v=\left( v_{s,\lambda ;s^{\prime },\lambda ^{\prime }}\right)$ must satisfy the set of equations

$$\begin{aligned} uu^{\dagger }-vv^{\dagger }=1,\quad vu^{T}=uv^{T}; \end{aligned}$$

(A4)

(see Ref. [9]). We note that we are looking for the those canonical transformations that diagonalizes the Hamiltonian $\hat{H}_{ {\chi }}(0)$ transforming it to form (A3). In this case with account taken of Eqs. (A2) and (A3) we obtain:

$$\begin{aligned} \left[ \hat{H}_{{\chi }}(0),\hat{c}_{s,\lambda }\right] =-\tau _{s,\lambda }\hat{c}_{s,\lambda }. \end{aligned}$$

(A5)

Substituting Eqs. (12) and (A1) into Eq. (A5), we obtain the following system of equations

$$\begin{aligned}{} & {} \left( A-\tau \right) u^{+}-Bv^{T}=0,\quad \tau =\left( \tau _{s,\lambda }\right) , \nonumber \\{} & {} \left( A+\tau \right) v^{T}-B^{+}u^{+}=0, \nonumber \\{} & {} A=\left( A_{s,\lambda ;s^{\prime },\lambda ^{\prime }}\right) ,\quad B=\left( B_{s,\lambda ;s^{\prime },\lambda ^{\prime }}\right) . \end{aligned}$$

(A6)

In contrast to Eqs. (A4), it is linear in the matrices u and v which allows one relatively easy its analysis. One can see that system (A6) is joint if positive numbers $\tau =(\tau _{s,\lambda })$ for each possible set $s=0,1,2$ and $\lambda =1,2$ satisfy the equations:

$$\begin{aligned}{} & {} \left( \sum _{s=1,2}\frac{\epsilon }{\tau ^{2}-\kappa _{s}^{2}}-1+\frac{\omega }{\tau }\right) \nonumber \\{} & {} \qquad \times \left( \sum _{s^{\prime }=1,2}\frac{\epsilon }{\tau ^{2}-\kappa _{s^{\prime }}^{2}}-1-\frac{\omega }{\tau }\right) =0,\nonumber \\{} & {} \qquad \text {if } \epsilon \ne 0, \end{aligned}$$

(A7)

$$\begin{aligned}{} & {} \quad \left( \tau -\kappa _{1}\right) ^{2}(\tau -\kappa _{2})^{2}\nonumber \\{} & {} \qquad \times \left[ \left( \frac{\omega }{\tau }\right) ^{2}-1\right] =0,\quad \text {if } \epsilon =0. \end{aligned}$$

(A8)

We now suppose that roots $\tau$ of Eq. (A7) are at the same time, solutions of the equation

$$\begin{aligned} \sum _{s^{\prime }=1,2}\frac{\epsilon }{\tau _{s,\lambda }^{2}-\kappa _{s^{\prime }}^{2}}=1+\frac{(-1)^{\lambda }\omega }{\tau _{s,\lambda }} \end{aligned}$$

(A9)

with the initial conditions:

$$\begin{aligned}&\left. \tau _{0,1}\right| _{\epsilon \rightarrow 0}=\omega ,\quad \left. \tau _{s,1}\right| _{\epsilon \rightarrow 0}=\kappa _{s},\nonumber \\&\left. \tau _{s,2}\right| _{\epsilon \rightarrow 0}=\kappa _{s}. \end{aligned}$$

(A10)

Thus, we define three positive roots $\tau _{0,1},$ $\tau _{1,1},$ and $\tau _{2,1}$ for $\lambda =1$ and two different positive roots $\tau _{1,1}$ and $\tau _{1,2}$ for $\lambda =2.$ Due to condition (A10), these five roots must be reduced to roots of Eq. (A8) as $\epsilon \rightarrow 0.$

Solving now Eqs. (A6), we obtain the set:

$$\begin{aligned}{} & {} u_{s,\lambda ;k,\sigma }=\left[ \left( \sqrt{\frac{\tau _{k,\sigma }}{\kappa _{s}}}+\sqrt{\frac{\kappa _{s}}{\tau _{k,\sigma }}}\right) \right. \nonumber \\{} & {} \quad \left. \times \frac{ \delta _{\lambda ,1}-i\left( -1\right) ^{\sigma }\delta _{\lambda ,2}}{ 2\left( \tau _{k,\sigma }^{2}-\kappa _{s}^{2}\right) }\left( 1-\delta _{s,0}\right) \right. \nonumber \\{} & {} \quad \left. -\delta _{s,0}\delta _{1,\lambda }\delta _{1,\sigma }\sqrt{ \frac{\omega }{\epsilon r_{k,\sigma }^{3}}}\right] \left( 1-\delta _{\sigma ,2}\delta _{k,0}\right) q_{k,\sigma }, \nonumber \\{} & {} v_{s,\lambda ;k,\sigma }=\left[ \left( \sqrt{\frac{\tau _{k,\sigma }}{\kappa _{s}}}-\sqrt{\frac{\kappa _{s}}{\tau _{k,\sigma }}}\right) \right. \nonumber \\{} & {} \quad \left. \times \frac{ \delta _{\lambda ,1}+i\left( -1\right) ^{\sigma }\delta _{\lambda ,2}}{ 2\left( \tau _{k,\sigma }^{2}-\kappa _{s}^{2}\right) }\left( 1-\delta _{s,0}\right) \right. \nonumber \\{} & {} \quad \left. -\delta _{s,0}\delta _{1,\lambda }\delta _{1,\sigma }\sqrt{ \frac{\omega }{\epsilon r_{k,\sigma }^{3}}}\right] \left( 1-\delta _{\sigma ,2}\delta _{k,0}\right) q_{k,\sigma }. \end{aligned}$$

(A11)

Substituting it into Eqs. (A4) and taking into account Eq. (A9), we derive the following expressions for the quantities $q_{k,\sigma }$:

$$\begin{aligned} q_{k,\sigma }=\left[ \frac{\left( -1\right) ^{\sigma -1}\omega }{\epsilon \tau _{k,\sigma }^{3}}+2\sum _{s=1,2}\left( \tau _{k,\sigma }^{2}-\kappa _{s}^{2}\right) ^{-2}\right] ^{-1/2}. \end{aligned}$$

We can verify that the Eqs. $\det u\ne 0$ and $\det v\ne 0$ hold true such that transformation (A1) is an reversible.

Let us return to Eq. (A3) and finally determine the form of the constant $\tilde{H}_{0}.$ To this end, we consider the vacuum mean (with respect to vacuum (11)) of the operator $\hat{H}_{{\chi }}(0)$ in its initial form (12),

$$\begin{aligned} \left\langle 0\left| \hat{H}_{{\chi }}(0)\right| 0\right\rangle =\frac{m^{2}}{2ng}+\frac{\omega }{2}+\frac{\epsilon }{2} \sum _{s=1,2}\kappa _{s}^{-1}. \end{aligned}$$

(A12)

With account taken of Eqs. (A1) and (A3), we obtain:

$$\begin{aligned}&\left\langle 0\left| \hat{H}_{{\chi }}(0)\right| 0\right\rangle =\tilde{H}_{0}\nonumber \\&\quad +\sum _{s,k=0,1,2}\sum _{\lambda ,\lambda ^{\prime }=1,2}\tau _{k,\lambda ^{\prime }}\left| v_{s,\lambda ;k,\lambda ^{\prime }}\right| ^{2}. \end{aligned}$$

(A13)

Comparing RHS of Eqs. (A12) and (A13), we obtain the constant $\tilde{H}_{0},$

$$\begin{aligned} \tilde{H}_{0}= & {} \frac{m^{2}}{2ng}+\frac{\omega }{2}\nonumber \\{} & {} -\sum _{s,k=0,1,2}\sum _{ \lambda ,\lambda ^{\prime }=1,2}\tau _{k,\lambda ^{\prime }}\left| v_{s,\lambda ;k,\lambda ^{\prime }}\right| ^{2}\nonumber \\{} & {} +\frac{\epsilon }{2}\sum _{s=1,2}\kappa _{s}^{-1}. \end{aligned}$$

(A14)