1 Introduction

Relativistic stellar structure is a field with a century-long history that traces its origins back to Schwarzschild’s pivotal findings in 1916. Schwarzschild unveiled both the universal vacuum exterior solution and the initial interior [1] stellar solution [2] with the aim of establishing a cohesive connection between these solutions, effectively describing the entirety of a star’s interior and exterior regions. For a considerably long period, it was conventional to consider the interior of stars as being composed of a perfect fluid, with equal radial and tangential pressures.

The growing interest in anisotropic fluids, characterized by non-equal radial and tangential pressures, is well-founded. Recent research has demonstrated that enforcing local isotropy is overly restrictive and can unduly limit the modeling of self-gravitating objects. Moreover, local pressure anisotropy can arise from a diverse range of physical phenomena commonly encountered in compact objects. Therefore, it is of paramount importance to explore potential methods for deriving exact solutions that describe anisotropic fluid distributions. For an in-depth exploration of the origins and consequences of local anisotropy in astrophysical objects, readers are encouraged to consult [3,4,5,6,7,8,9,10,11].

The pursuit of a rigorous definition of complexity has been a goal shared by many workers across various branches of science. Among the numerous definitions proposed to date, most have relied on concepts such as information and entropy. They are built on the intuitive notion that complexity should somehow quantify a fundamental characteristic of the structures within a system [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. In a recent study [30, 31], a novel definition of complexity was introduced for spherically symmetric static self-gravitating fluids. This new concept of complexity is rooted in the fundamental assumption that a system’s lowest complexity corresponds to a fluid distribution that is homogeneous in terms of energy density and exhibits isotropic pressure. Consequently, a complexity factor with a value of zero is assigned to such a distribution. The candidate for measuring the degree of complexity that naturally emerges from this assumption is a quantity denoted as \(Y_{TF}\) and referred to as the complexity factor. The primary motivation behind this proposal lies in the fact that the scalar function \(Y_{TF}\) encompasses contributions from both the inhomogeneity in energy density and the local anisotropy in pressure. These contributions combine in a highly specific manner, resulting in a vanishing value for \(Y_{TF}\) in the case of a homogeneous and locally isotropic fluid distribution. Additionally, in the context of a charged fluid, this scalar also accounts for the influence of electric charge. It’s worth noting that the defined complexity factor not only vanishes for the simple configuration mentioned earlier but can also become zero when the two terms in its definition, involving density inhomogeneity and anisotropic pressure, mutually cancel each other out. Therefore, a state of vanishing complexity may correspond to a variety of distinct systems. Complexity has been further expanded to include modified gravity theories within the context of general relativity, as demonstrated in various studies [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50].

Numerous significant efforts have been made to investigate the characteristics of physically plausible solutions that describe relativistic compact objects in static, stationary, or collapsing states. Currently known exact solutions have been derived by introducing certain constraints. These constraints may involve imposing symmetry conditions on the metric, introducing coupled field equations, establishing meaningful equations of state for the matter variables, or defining specific algebraic properties of the Riemann tensor.

The primary objective of this paper is to provide a comprehensive and detailed comparative analysis of five distinct approaches, as outlined in the abstract, that are commonly utilized to obtain exact interior solutions to the Einstein field equations (EFEs) in the context of spherically symmetric fluid distributions. It is essential to note that such solutions serve as the fundamental building blocks for modeling compact objects. One of these approaches is rooted in the concept of vanishing complexity, as recently defined in [30, 31]. This definition has proven to be an invaluable tool for investigating the structure of self-gravitating systems. Several authors have obtained interior solutions for compact stars using the vanishing complexity approach in diverse settings [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73].

Another approach, known as the embedding class one approach employing the Karmarkar condition [74], has also been extensively utilized for discovering exact solutions for fluid distributions [6]. The Karmarkar initial embedding motivation transitions into a geometric method that generates matter configurations capable of representing compact astrophysical objects. Its primary appeal lies in its ability to ensure the embedding of a 4-dimensional Riemannian space into a 5-dimensional Pseudo-Euclidean space. various workers have obtained interior solutions for compact stars using the embedding class one approach [4, 75,76,77,78,79,80,81,82,83,84,85,86,87,88].

Conformally flat anisotropic spheres exhibit the intriguing property of possessing a vanishing Weyl tensor [89], which is also fruitful for finding exact solutions to the EFEs. This property leads to a differential equation for the metric functions \(\lambda \) and \(\nu \), which bears a similarity to the Karmarkar condition or the isotropic case. Some solutions related to the conformally flat approach can be found in [90,91,92,93,94,95,96,97,98].

The systematic utilization of spacetime symmetries is also a valuable approach for tackling the field equations. An illustrative case of this is the utilization of conformal symmetries. Notably, conformal Killing vectors generate conserved quantities along null geodesics, and the presence of conformal symmetry frequently places restrictions on the metric functions, resulting in the discovery of novel exact solutions for the field equations governing gravitating objects. Essentially, the conformal Killing vector approach also results in a bridge equation that connects metric potentials. Early instances of relativistic systems featuring a conformal Killing vector are exemplified by the models introduced by Herrera and Ponce de Leon [99]. Additional works on this topic can be found in [100,101,102,103,104,105,106,107,108,109]. In the realm of wormhole solutions, recent research has highlighted the increased effectiveness of employing conformal symmetry in their modeling [110, 111]. For a comprehensive survey of various metrics that have been used to study exact solutions of the Einstein field equations, one can refer to [112].

The aforementioned approaches involve integrating bridge equations between metric potentials into the three field equations. This integration provides the flexibility of selecting a generating function to derive solutions, a key advantage that allows the entire system to be created by choosing a single metric potential. In contrast to the conventional approach, which typically assumes two generating functions, this method streamlines the process and offers the distinct benefit of solving highly non-linear EFEs without requiring an equation of state. To be considered physically realistic, these models must satisfy various regularity, matching, and stability conditions. The feasibility of each approach depends on the selection of an appropriate seed metric potential function.

In [113], the authors introduced the Karmarkar scalar condition, which is formulated in terms of the structure scalars derived from the orthogonal decomposition of the Riemann tensor. This technique establishes an algebraic relationship among the physical variables rather than a differential equation involving the metric coefficients. Using the Karmarkar scalar condition, they developed a method to determine all attainable class I static spherical solutions for embedding, as long as the energy density profile is known. In our analysis, we thoroughly examine the physical behavior of all models. We ensure that the standard physical requirements, necessary for a star model to be considered physically admissible, are met. Additionally, we conduct stability assessments to guarantee the stability of these models. Based on our findings, we suggest that the vanishing complexity approach appears to be a suitable method for obtaining exact solutions to the Einstein field equations.

This paper is structured as follows: in Sect. 2, we begin with a brief overview of the Einstein field equations. Sections 2.1 to 2.5 lay the groundwork for discussing the conformally flat condition, the complexity factor, the condition of vanishing complexity, the embedding of class one spacetime satisfying the Karmarkar condition, and the conformally killing vector approach along with Karmarkar scalar condition. Section 3 focuses on describing the boundary conditions. In Sect. 4, particularly in Sects. 4.1–4.5, we provide a novel interior solution based on the previously mentioned approaches and determine the arbitrary constants associated with each approach. Sections 5–8 are dedicated to a comprehensive exploration of the physical characteristics of the well-behaved solution. This includes a detailed analysis of stability, red-shift profiles, the anisotropic parameter, energy conditions, and various other standard physical parameters. Finally, in Sect. 9, we provide a summary of our key findings and offer a concise conclusion to the paper.

2 The system of Einstein field equations

The Einstein field equations (EFEs) are formulated by minimizing the Einstein-Hilbert (EH) action with respect to the metric tensor. The EH action is defined as:

$$\begin{aligned} S_{EH} = \int \sqrt{-g}~ d^4x \left( \frac{1}{16\pi }~{\mathcal {R}}+{\mathcal {L}}_m \right) . \end{aligned}$$
(1)

In this equation: \({\mathcal {R}}\) represents the Ricci scalar invariant, defined as \({\mathcal {R}} = g^{\mu \eta } {\mathcal {R}}_{\mu \eta }\). \({\mathcal {L}}_m\) denotes the Lagrangian density for matter fields. g is the determinant of the metric tensor, given by \(g = \text {det}[g_{\mu \eta }]\). The relationship between the matter stress-energy tensor \(T_{\mu \eta }\) and the Lagrangian \({\mathcal {L}}_m\) is expressed by the equation:

$$\begin{aligned} T_{\mu \eta } = -\frac{2}{\sqrt{-g}} \frac{\delta (\sqrt{-g}~{\mathcal {L}}_m)}{\delta g^{\mu \eta }}. \end{aligned}$$
(2)

The interior of a relativistic star is described by a Schwarzschild-like line element given as:

$$\begin{aligned} ds^2= & {} e^{\nu (r)}dt^2 - e^{\lambda (r)}dr^2 - r^2(d\theta ^2 + \sin ^2{\theta }\,d\phi ^2), \end{aligned}$$
(3)

where, \(e^{\nu (r)}\) and \(e^{\lambda (r)}\) are arbitrary functions serving as the metric potentials, which determine the geometry of the spacetime within the star.

To describe the anisotropic stellar fluid within this model, the energy-momentum tensor \(T_{\mu \eta }\) is given by:

$$\begin{aligned} T_{\mu \eta }= & {} (p_t+\rho )v_{\mu }v_\eta -p_t g_{\mu \eta }+(p_r-p_t)\chi _\mu \chi _\eta . \end{aligned}$$
(4)

In this context, the physical parameters \(\rho \), \(p_r\), and \(p_t\) correspond to the energy density, radial pressure measured in the direction of the spacelike vector, and transverse pressure orthogonal to \(p_r\), respectively.

The EFEs for the metric (3) and the energy-momentum tensor (4), using units where \(G=c=1\), are given as follows:

$$\begin{aligned} 8\pi \rho= & {} \frac{1 - e^{-\lambda }}{r^2} + \frac{\lambda 'e^{-\lambda }}{r}, \end{aligned}$$
(5)
$$\begin{aligned} 8\pi p_r= & {} \frac{\nu ' e^{-\lambda }}{r} - \frac{1 - e^{-\lambda }}{r^2}, \end{aligned}$$
(6)
$$\begin{aligned} 8\pi p_t= & {} \frac{e^{-\lambda }}{4}\left( 2\nu '' + {\nu '}^2 - \nu '\lambda ' + \frac{2\nu '}{r}-\frac{2\lambda '}{r}\right) . \end{aligned}$$
(7)

Here, \((')\) represents differentiation with respect to the radial coordinate r. By using (6) and (7), we can derive the anisotropy measure as follows:

$$\begin{aligned} \Delta= & {} p_t-p_r. \end{aligned}$$
(8)

2.1 Conformally flat condition (CFC)

A spacetime is deemed conformally flat when its Weyl tensor is null. The vanishing of the Weyl tensor signifies that the spacetime lacks significant local gravitational tidal effects, and it can be mathematically transformed, in a conformal manner, into a flat spacetime. In spherically symmetric spacetimes, where only one independent component of the Weyl tensor exists, the conformally flat condition reduces to a single equation given by [89]:

$$\begin{aligned} \frac{\nu ^{\prime \prime }}{2}+ \frac{\nu ^{\prime 2}}{4}--\frac{\nu ^{\prime }\lambda ^{\prime }}{4}-\frac{\nu ^{\prime }-\lambda ^{\prime }}{2r}+\frac{1-e^\lambda }{r^2}=0. \end{aligned}$$
(9)

Following Herrera et al. [89] above equation reduces to

$$\begin{aligned} \frac{\nu ^{\prime }}{2}-\frac{1}{r}= \frac{e^{\lambda /2}}{r} \sqrt{1-c^{2}r^{2}e^{-\nu }}, \end{aligned}$$
(10)

with \(c^{2}=-C_{1}\).

Further integration of (10) leads to the following bridge equation

$$\begin{aligned} e^{\nu }={c}^2r^2\cosh ^{2} \left( \int \frac{e^{\lambda /2}}{r}dr+ Log(d) \right) , \end{aligned}$$
(11)

where c and d are constants of integration.

2.2 Vanishing complexity condition (VCC)

The criterion of the vanishing complexity factor was originally introduced by Herrera within the framework of general relativity, as outlined in [30]. Herrera, in the wake of Bel’s work [114], explored the following tensors (for further insights see [115]):

$$\begin{aligned} Y_{\alpha \beta }= & {} R_{\alpha \gamma \beta \delta }\,u^{\gamma }\,u^{\delta },\\ Z_{\alpha \beta }= & {} ^\star R_{\alpha \gamma \beta \delta }\,u^{\gamma }\,u^{\delta } = \frac{1}{2} \,{\eta }_{{\alpha \gamma \epsilon \mu }} \, R^{\epsilon \mu }\,_{\beta \delta } \,u^{\gamma }u^{\delta },\\ X_{\alpha \beta }= & {} ^\star R^{\star }_{\alpha \gamma \beta \delta }\,u^{\gamma }\,u^{\delta }= \frac{1}{2} \, {\eta _{\alpha \gamma }\,^{\epsilon \mu }} {R^{\star }}_{\epsilon \mu \beta \delta }\,u^{\gamma }\,u^{\delta }, \end{aligned}$$

where \(^\star R_{\alpha \gamma \beta \delta }\) and \(^\star R^{\star }_{\alpha \gamma \beta \delta }\) are the left and double dual tensors. The orthogonal splitting of the Riemann tensor can be expressed in terms of the tensors defined above, as discussed in [115].

In the context of the physical variables, the explicit expressions for these three tensors \(Y_{\alpha \beta },\, Z_{\alpha \beta }\) and \(X_{\alpha \beta }\) were calculated in [30] as follows:

$$\begin{aligned} Y_{\alpha \beta }= & {} \frac{4\pi }{3}[\rho + (p_r+ 2p_t)]h_{\alpha \beta } + 4\pi \Pi _{\alpha \beta } + E_{\alpha \beta },\\ Z_{\alpha \beta }= & {} 0,\\ X_{\alpha \beta }= & {} \frac{8\pi }{3}\rho \, h_{\alpha \beta } + 4\pi \Pi _{\alpha \beta } - E_{\alpha \beta }. \end{aligned}$$

Indeed, using the tensors \(X^{\alpha \beta }\) and \(Y^{\alpha \beta }\), Herrera defined four scalar functions denoted as \(X_T,\, X_{TF}, \,Y_T\), and \(Y_{TF}\), to express these tensors. Furthermore, a fifth scalar linked to the tensor \(Z^{\alpha \beta }\) vanishes in the static case (kindly see [30]) and can be expressed as follows:

$$\begin{aligned} X_T= & {} 8\pi \rho , \end{aligned}$$
(12)
$$\begin{aligned} X_{TF}= & {} 4\pi \Pi - E \end{aligned}$$
(13)
$$\begin{aligned} Y_T= & {} 4\pi (\rho + 3p_r - 2\Pi ), \end{aligned}$$
(14)
$$\begin{aligned} Y_{TF}= & {} 4\pi \Pi +E. \end{aligned}$$
(15)

Here \(\Pi =p_r-p_t=-\Delta \), where \(\Delta \) is referred to as the local anisotropy of pressure and is determined by sum of \(X_{TF}\) and \(Y_{TF}\). The expression of E is related to the electric part of the Weyl Tensor, defined as

$$\begin{aligned} E=&{} -\frac{e^{-\lambda }}{4}\left( \nu ''+\frac{\nu '^2-\lambda '\nu '}{2}-\frac{\nu '-\lambda '}{r}+\frac{2(1-e^{\lambda })}{r^2}\right) . \end{aligned}$$
(16)

The complexity factor \(Y_{TF}\) for the system described by (3)–(7) can be expressed as

$$\begin{aligned} Y_{TF}= & {} 8 \pi \Pi - \frac{4\pi }{r^3} \int _0^r y^3~\frac{d\rho (y)}{dy} \,dy. \end{aligned}$$
(17)

The condition \(Y_{TF}=0\) serves as a criterion for vanishing complexity. By utilizing the EFEs and the condition given in (17), the expression of anisotropy is obtained as:

$$\begin{aligned} \Delta =-\Pi =p_t-p_r= & {} \frac{1}{2r^3} \int _0^r y^3\frac{d\rho (y)}{dy} \,dy. \end{aligned}$$
(18)

The expression in (18) can be treated as a non-local equation of state that can be employed as a valid criterion for determining the physical parameters while solving the EFEs.

Substituting the expressions of EFEs into (17) yields the vanishing factor \(Y_{TF}\) as

$$\begin{aligned} Y_{TF} = \frac{\nu '(r\lambda '-r \nu ')+2-2r\nu ''}{4re^\lambda }. \end{aligned}$$
(19)

Further, the vanishing complexity condition becomes

$$\begin{aligned} \nu '[r(\lambda '-\nu ')+2]-2r\nu ''=0. \end{aligned}$$
(20)

The above Eq. (20) can be represented as an exact differential equation

$$\begin{aligned} \frac{d}{dr}\left( {\nu \over 2} + \log \nu '-{\lambda \over 2}-\log r \right)= & {} 0. \end{aligned}$$

On integrating the above equation, we get the following relation

$$\begin{aligned} \frac{\nu }{2} + \log \nu '-\frac{\lambda }{2}-\log r= & {} C_1. \end{aligned}$$
(21)

It can also be rewritten as

$$\begin{aligned} \nu ' e^{\nu /2} = C_2\, r\, e^{\lambda /2}, \end{aligned}$$
(22)

where \(C_1\) and \(C_2\) are constants.

The relation (22) between the metric potentials can further be expressed as:

$$\begin{aligned} e^{\nu }=\Bigg (B+A \int r \,\sqrt{e^{\lambda }}~dr\Bigg )^2, \end{aligned}$$
(23)

where A and B are integration constants.

2.3 Embedding class I condition (ECC) or the Karmarkar condition

When the Karmarkar condition, as outlined in [74], is fulfilled, it allows for the embedding of a four-dimensional curved space-time within a five-dimensional pseudo-Euclidean space. This condition is expressed as follows [116]:

$$\begin{aligned} R_{0303}R_{1212} -R_{0101}R_{2323} -R_{0313}R_{0212} = 0. \end{aligned}$$
(24)

This condition offers a geometrical framework for applying equations of state that establish the relationship between radial and tangential pressures.

The metric (3) describes a spacetime that satisfies the Karmarkar condition (24) can be written as

$$\begin{aligned}&2\nu ^{\prime \prime }\textrm{e}^{\nu } -\left( (\nu ^{\prime })^2 + 2\nu ^{\prime \prime }\right) \textrm{e}^{(\nu -\lambda )} -\nu ^{\prime }\textrm{e}^{\nu } \left( \lambda ^{\prime }-\nu ^{\prime } \right) \\&\quad -\left( \textrm{e}^{\lambda } -2\right) {\dot{\lambda }}^2 +{\dot{\nu }}{\dot{\lambda }}\left( \textrm{e}^{\lambda } -1\right) -2\ddot{\lambda }\left( \textrm{e}^{\lambda } - 1\right) = 0. \end{aligned}$$

In the static scenario, it gives rise to the following differential equation [117]:

$$\begin{aligned} \frac{2\nu ^{''}}{\nu '}+\nu '=\frac{\lambda 'e^{\lambda }}{e^{\lambda }-1}. \end{aligned}$$
(25)

After integrating (25), the relationship between \(\nu \) and \(\lambda \) takes the form:

$$\begin{aligned} e^{\nu }=\left( C+D\int _{0}^{r}\sqrt{e^{\lambda }-1}~dr\right) ^2, \end{aligned}$$
(26)

where C and D represent integration constants.

2.4 Conformally killing vector condition (CKVC)

We consider the interior of a star under conformal motion through a non-static conformal killing vector as follows:

$$\begin{aligned} L_\xi g_{ij} = g_{ij;k}\xi ^k + g_{kj}\xi ^k_{\,;i} + g_{ik}\xi ^k_{\,;j} = \psi g_{ij}. \end{aligned}$$
(27)

Here, L represents the Lie derivative operator, \(\xi \) is the four-vector along which the derivative is taken, \(\psi \) is the conformal factor, and \(g_{ij}\) are the metric potentials. It’s important to note that when \(\psi \) equals 0, the equation gives rise to a Killing vector, while for \(\psi \) as a constant, it represents a homothetic vector. In a more general scenario, when \(\psi \) takes the form \(\psi (x, t)\), we obtain conformal vectors. This versatile approach allows for a broader exploration of spacetime geometry by utilizing conformal killing vectors.

In accordance with the work of Herrera et al. [100], we assume that \(\xi \) is non-static, while \(\psi \) remains static, as defined by the following equations:

$$\begin{aligned} \quad \xi = \alpha (t, r)\partial _t + \beta (t, r)\partial _r, \end{aligned}$$
(28)
$$\begin{aligned} \quad \psi = \psi (r) . \end{aligned}$$
(29)

The set of Eqs. (3) (27), (28), and (29) gives rise to the following expressions for \(\alpha \), \(\beta \), \(\psi \), and \(\lambda \):

$$\begin{aligned} \alpha = A_k + \frac{1}{2}kt, \end{aligned}$$
(30)
$$\begin{aligned} \beta = \frac{1}{2}B_k re^{-\lambda /2}, \end{aligned}$$
(31)
$$\begin{aligned} \psi = B_k e^{-\lambda /2}, \end{aligned}$$
(32)
$$\begin{aligned} \quad e^\nu = {P^2r^2}\exp \left( -2*Q\int \frac{e^{\lambda /2}}{r} dr\right) , \end{aligned}$$
(33)

where \(A_k\), \(B_k\), P and \(Q=\frac{k}{B_k}\) are arbitrary constants. The Eq. (33) represents the bridge equation between both the metric potentials [109].

2.5 Karmarkar scalar condition

The coordinate dependence of the Karmarkar condition can be circumvented within the tetrad framework by projecting the Riemann tensor as shown below [113]:

$$\begin{aligned} R_{\alpha \beta \mu \nu }V^\alpha V^\mu S^\beta S^\nu R_{\gamma \delta \sigma \rho } K^\gamma K^\sigma L^\delta L^\rho \nonumber \\ -R_{\alpha \beta \mu \nu }V^\alpha V^\mu K^\beta K^\nu R_{\gamma \delta \sigma \rho } L^\gamma L^\sigma S^\delta S^\rho \nonumber \\ -R_{\alpha \beta \mu \nu }V^\alpha K^\mu S^\beta S^\nu R_{\gamma \delta \sigma \rho } V^\gamma L^\sigma K^\delta L^\rho = 0. \end{aligned}$$
(34)

Given the following equations under the assumption of spherical symmetry:

$$\begin{aligned} Y_0= & {} 4\pi (\rho +3P), \quad Y_1={{\mathcal {E}}}_1-4\pi \Pi _1, \ X_0=8\pi \rho , \nonumber \\ X_1= & {} -({{\mathcal {E}}}_1+4\pi \Pi _1) \mathrm {~and} Z= 4 \pi {{\mathcal {F}}}, \end{aligned}$$
(35)

the above system simplifies to a straightforward algebraic scalar relation among several physical variables, given by:

$$\begin{aligned} Y_0 X_1+(X_0+X_1)Y_1=-3Z^2. \end{aligned}$$
(36)

It’s worth noting that this scalar relation among the physical variables remains valid for any dynamic and dissipative spherical matter distribution (see [113] for more details).

3 Boundary conditions

Most celestial objects are assumed to exist in a vacuum or nearly vacuum spacetime. At the boundary between these spacetimes, suitable matching conditions are assumed to exist between the internal spacetime and external vacuum region. In this scenario, the Schwarzschild spacetime provides an efficient exterior solution, i.e.,

$$\begin{aligned} ds^2= & {} -\bigg (1-\frac{2 M}{r}\bigg )\,dt^2+\frac{dr^2}{1-2 M/r} \nonumber \\{} & {} +r^2 \Big (d\theta ^2 +\sin ^2\theta \,d\phi ^2 \Big ). \end{aligned}$$
(37)

Here, M is the total mass of the object. For the system to be continuous over the boundary \(r = R\), we use the Darmois-Israel-boundary condition, which yields the following two fundamental matching conditions [118, 119]:

$$\begin{aligned} 1-\frac{2 M}{R}= & {} e^{\nu (R)},~~~ \end{aligned}$$
(38)
$$\begin{aligned} 1-\frac{2 M }{R}= & {} e^{-\lambda (R)},~~~ \end{aligned}$$
(39)

and other matching condition we have considered is given by

$$\begin{aligned} p_r(R)= & {} 0. \end{aligned}$$
(40)

These conditions are used to calculate arbitrary constants involved in the solution.

4 New interior solution through diverse approaches

4.1 Solution via conformally flat condition

To construct the model, we assume a new metric potential \(g_{rr}=e^{\lambda }\) specified by

$$\begin{aligned} e^{\lambda }= & {} \frac{b^2}{\left( b-a r^2\right) ^2}. \end{aligned}$$
(41)

Here, a and b are non-negative constants.

By substituting the value of \(e^{\lambda }\) from (41) into (11), we derive the expression for \(e^{\nu }\), denoted as \(e^{\nu _1}\) for this specific model, as follows:

$$\begin{aligned} e^{\nu _1}= & {} \frac{c^2 \left( r^2 \left( d^2-a\right) +b\right) ^2}{4 d^2 \left( b-a r^2\right) }, \end{aligned}$$
(42)

where c and d are integrating constants.

By plugging in the metric potentials defined in (41) and (42), we can compute the expressions for \(\rho _1\), \(p_{r_1}\), \(p_{t_1}\) and \(\Delta _1\):

$$\begin{aligned}{} & {} \rho _1 = \frac{a \left( 6 b-5 a r^2\right) }{b^2}, \end{aligned}$$
(43)
$$\begin{aligned}{} & {} p_{r_1} =\frac{3 a^2 r^4 \left( d^2-a\right) +4 b^2 \left( d^2-a\right) +a b r^2 \left( 7 a-8 d^2\right) }{b^2 \left( r^2 \left( d^2-a\right) +b\right) },\nonumber \\ \end{aligned}$$
(44)
$$\begin{aligned}{} & {} p_{t_1} =\frac{5 a^2 r^4 \left( d^2-a\right) +4 b^2 \left( d^2-a\right) +a b r^2 \left( 9 a-8 d^2\right) }{b^2 \left( r^2 \left( d^2-a\right) +b\right) }, \nonumber \\ \end{aligned}$$
(45)
$$\begin{aligned}{} & {} \Delta _1 = p_{t_1}-p_{r_1}. \end{aligned}$$
(46)

The expressions for mass (m(r)), compactification (u(r)), surface red-shift \(z_{s_1}(r)\) and gravitational red-shift \(z_{r_1}(r)\) are as follows:

$$\begin{aligned}{} & {} m(r) = \frac{r}{2} (1-e^{-\lambda }) = -\frac{a r^3 \left( a r^2-2 b\right) }{2 b^2}, \end{aligned}$$
(47)
$$\begin{aligned}{} & {} u(r) = \frac{m(r)}{r} = -\frac{a r^2 \left( a r^2-2 b\right) }{2 b^2}, \end{aligned}$$
(48)
$$\begin{aligned}{} & {} z_{s}(r) = \frac{1}{\sqrt{1-2u}} = \frac{a r^2}{b-a r^2}, \end{aligned}$$
(49)
$$\begin{aligned}{} & {} z_{r_1}(r) = \frac{1}{\sqrt{e^{\nu _1}}} -1 = \frac{2}{\sqrt{\frac{c^2 \left( r^2 \left( d^2-a\right) +b\right) ^2}{d^2 \left( b-a r^2\right) }}}-1. \end{aligned}$$
(50)

It is important to note that the expressions for mass, compactification, and surface red-shift values are identical to those presented above for the next three approaches.

4.1.1 Evaluation of arbitrary constants

The expressions of the constants are derived from the boundary conditions in (38–40) in conformally flat condition approach as

$$\begin{aligned}{} & {} a=\frac{b R^3-\sqrt{b^2 R^5 (R-2 M)}}{R^5} \end{aligned}$$
(51)
$$\begin{aligned}{} & {} c=\frac{\sqrt{a} \sqrt{R-2 M} \sqrt{-\left( 2 b-3 a R^2\right) \left( 4 b-3 a R^2\right) \left( 2 b-a R^2\right) }}{2 \sqrt{-b^2 R \left( b-a R^2\right) ^2}} \nonumber \\ \end{aligned}$$
(52)
$$\begin{aligned}{} & {} d=-\frac{\sqrt{a} \sqrt{\left( 4 b-3 a R^2\right) \left( a R^2-b\right) }}{\sqrt{-3 a^2 R^4+8 a b R^2-4 b^2}} . \end{aligned}$$
(53)

4.2 Solution via vanishing complexity condition

To construct the model, we adopt the same seed solution for \(e^{\lambda }\) as specified in (41). By substituting the value of \(e^{\lambda }\) into (23), we derive the expression for \(e^{\nu }\), denoted as \(e^{\nu _2}\) for this particular model, as follows:

$$\begin{aligned} e^{\nu _2}= & {} \left( B-\frac{A b \log \left( b-a r^2\right) }{2 a}\right) ^2, \end{aligned}$$
(54)

where A and B are integrating constants.

Substituting the metric potentials given by (41) and (54), the expressions of \(\rho _2,~ p_{r_2}, ~p_{t_2}\) and \(\Delta _2\) can be calculated as

$$\begin{aligned}{} & {} \rho _2 = \frac{a \left( 6 b-5 a r^2\right) }{b^2}, \end{aligned}$$
(55)
$$\begin{aligned}{} & {} p_{r_2} =\frac{a \left( -\frac{4 A b \left( b-a r^2\right) }{A b \log \left( b-a r^2\right) -2 a B}+a r^2-2 b\right) }{b^2}, \end{aligned}$$
(56)
$$\begin{aligned}{} & {} p_{t_2} =\frac{\left( 2 a \left( b-a r^2\right) \right) \left( \frac{2 A b}{2 a B-A b \log \left( b-a r^2\right) }-1\right) }{b^2} , \end{aligned}$$
(57)
$$\begin{aligned}{} & {} \Delta _2 = p_{t_2}-p_{r_2}. \end{aligned}$$
(58)

The equation for gravitational red-shift is derived as follows:

$$\begin{aligned}{} & {} z_{r_2}(r) = \frac{1}{\sqrt{e^{\nu _2}}} -1 = \frac{2}{\sqrt{\frac{c^2 \left( r^2 \left( d^2-a\right) +b\right) ^2}{d^2 \left( b-a r^2\right) }}}-1. \end{aligned}$$
(59)

4.2.1 Evaluation of arbitrary constants

The expressions for the constants are determined by utilizing boundary conditions given in (38–40) under the vanishing complexity condition approach. Specifically, the expression for the constant a is provided in (51), while the expressions for the remaining constants are calculated as follows:

$$\begin{aligned}{} & {} A=\frac{a \sqrt{R-2 M} \left( a R^2-2 b\right) }{2 \sqrt{b^2 R \left( b-a R^2\right) ^2}} \end{aligned}$$
(60)
$$\begin{aligned}{} & {} B= \frac{b \sqrt{R-2 M} \left( \left( a R^2-2 b\right) \log \left( b-a R^2\right) +4 a R^2-4 b\right) }{4 \sqrt{b^2 R \left( b-a R^2\right) ^2}}. \nonumber \\ \end{aligned}$$
(61)

4.3 Solution via embedding class I condition

To generate the model, we utilize the identical seed solution for \(e^{\lambda }\) as defined in (41). Upon substituting this value of \(e^{\lambda }\) into (26), we can express \(e^{\nu }\) for this model as \(e^{\nu _3}\) in the following manner:

$$\begin{aligned} e^{\nu _3}= & {} \left( C-\frac{D \left( \sqrt{2 b-a r^2}-\sqrt{b} \tanh ^{-1}\left( \frac{\sqrt{2 b-a r^2}}{\sqrt{b}}\right) \right) }{\sqrt{a}}\right) ^2,\nonumber \\ \end{aligned}$$
(62)

where C and D are integrating constants.

Substituting the metric potentials given by (41) and (62), the expressions of \(\rho _3,~ p_{r_3}, ~p_{t_3}\) and \(\Delta _3\) can be calculated as

$$\begin{aligned}{} & {} \rho _3 = \frac{a \left( 6 b-5 a r^2\right) }{b^2}, \end{aligned}$$
(63)
$$\begin{aligned}{} & {} p_{r_3} =-\frac{a \sqrt{2 b-a r^2} \left( \sqrt{b} D h_1 \sqrt{2 b-a r^2}+h_2\right) }{b^2 \left( -D \sqrt{2 b-a r^2}+\sqrt{a} C+\sqrt{b} D h_1\right) }, \end{aligned}$$
(64)
$$\begin{aligned}{} & {} p_{t_3} =\frac{a \left( b-a r^2\right) \left( 2 \sqrt{b} D h_1 \sqrt{2 b-a r^2}+h_3\right) }{b^2 \sqrt{2 b-a r^2} \left( D \sqrt{2 b-a r^2}-\sqrt{a} C-\sqrt{b} D h_1\right) },\nonumber \\, \end{aligned}$$
(65)
$$\begin{aligned}{} & {} \Delta _3 = p_{t_3}-p_{r_3}. \end{aligned}$$
(66)

where

$$\begin{aligned} h_1=\tanh ^{-1}\left( \frac{\sqrt{2 b-a r^2}}{\sqrt{b}}\right) \end{aligned}$$
(67)
$$\begin{aligned} h_2 = \sqrt{a} C \sqrt{2 b-a r^2}+3 a D r^2-4 b D \end{aligned}$$
(68)
$$\begin{aligned} h_3 = 2 \sqrt{a} C \sqrt{2 b-a r^2}+5 a D r^2-8 b D. \end{aligned}$$
(69)

The expression for gravitational red-shift is determined from the equation:

$$\begin{aligned}{} & {} z_{r_3}(r) = \frac{1}{\sqrt{e^{\nu _2}}} -1. \end{aligned}$$
(70)

4.3.1 Evaluation of arbitrary constants:

The constants’ expressions are obtained by applying the boundary conditions presented in (38–40) within the framework of the embedding class I condition approach. To be specific, the Eq. (51) defines the constant a, while the expressions for the other constants are established as follows:

$$\begin{aligned}{} & {} C=\frac{\sqrt{2 M-R} \left( \sqrt{b} h_1(R) \left( 2 b-a R^2\right) +\sqrt{2 b-a R^2} \left( 3 a R^2-4 b\right) \right) }{2 \sqrt{R} \sqrt{\left( b-a R^2\right) ^2} \sqrt{a R^2-2 b}} \nonumber \\ \end{aligned}$$
(71)
$$\begin{aligned}{} & {} D = \frac{\sqrt{a} \sqrt{2 M-R} \sqrt{a R^2-2 b}}{2 \sqrt{R} \sqrt{\left( b-a R^2\right) ^2}} . \end{aligned}$$
(72)

4.4 Solution via conformally killing vector condition

To create the model, we employ the identical seed solution for \(e^{\lambda }\) as provided in (41). By substituting the value of \(e^{\lambda }\) into (33), we derive the expression for \(e^{\nu }\), denoted as \(e^{\nu _4}\) for this specific model, as follows:

$$\begin{aligned} e^{\nu _4}= & {} P^2 r^{2-2 Q} \left( b-a r^2\right) ^Q, \end{aligned}$$
(73)

where P and Q are integrating constants.

Substituting the metric potentials given by (41) and (73), the expressions of \(\rho _4,~ p_{r_4}, ~p_{t_4}\) and \(\Delta _4\) can be calculated as

$$\begin{aligned}{} & {} \rho _4 = \frac{a \left( 6 b-5 a r^2\right) }{b^2}, \end{aligned}$$
(74)
$$\begin{aligned}{} & {} p_{r_4} =\frac{3 a^2 r^2}{b^2}+\frac{2 a (Q-3)}{b}+\frac{2-2 Q}{r^2}, \end{aligned}$$
(75)
$$\begin{aligned}{} & {} p_{t_4} =\frac{5 a^2 r^2}{b^2}+\frac{2 a (Q-3)}{b}+\frac{(Q-1)^2}{r^2}, \end{aligned}$$
(76)
$$\begin{aligned}{} & {} \Delta _4 = p_{t_4}-p_{r_4}. \end{aligned}$$
(77)

Gravitational red-shift is determined by the following equation:

$$\begin{aligned}{} & {} z_{r_4}(r) = \frac{1}{\sqrt{e^{\nu _4}}} -1=\frac{1}{\sqrt{P^2 r^{2-2 Q} \left( b-a r^2\right) ^Q}}-1. \end{aligned}$$
(78)

4.4.1 Evaluation of arbitrary constants

The expression for the constant a is described in (51), and the other constants are calculated from the boundary conditions (38–40) for conformally killing vector condition approach as follows:

$$\begin{aligned}{} & {} P =-\frac{\sqrt{R-2 M}}{R^{3/2}} \nonumber \\{} & {} \times \sqrt{\left( b-a R^2\right) ^{\frac{\left( 3 a^2 R^4-6 a b R^2+2 b^2\right) \left( 2 \log (R)-\log \left( b-a R^2\right) \right) }{2 b \left( b-a R^2\right) \log \left( b-a R^2\right) }}} \end{aligned}$$
(79)
$$\begin{aligned}{} & {} Q = \frac{1}{2} \left( -\frac{3 a R^2}{b}+\frac{b}{a R^2-b}+3\right) . \end{aligned}$$
(80)

4.5 Solution via the Karmarkar scalar condition

In [113], the authors established the following relation:

$$\begin{aligned} X = \frac{3}{r^3}\int X_0 r^2 dr. \end{aligned}$$
(81)

The above equation shows that all metrics depend on a single physical parameter, namely, the energy density (\(X_0\)).

By setting \(X_0 = \frac{a \left( 6 b - 5 a r^2\right) }{b^2}\), we obtain the expressions X and the metric potential \(e^{\lambda }=B^2(r,t)\) in static case as

$$\begin{aligned} X= & {} \frac{3 a \left( 2 b r^3-a r^5\right) }{b^2 r^3} \end{aligned}$$
(82)
$$\begin{aligned} B^2(r,0)= & {} \frac{1}{1 - \frac{r^2}{3}X} = \frac{b^2}{\left( b - a r^2\right) ^2}. \end{aligned}$$
(83)

The Eq. (83) matches with the assumed metric potential given in (41).

5 Discussion on geometrical, physical variables and stability analysis

We can assess the physical validity of solutions for a compact stellar structure by examining various physical conditions, considering the given parameter values \(a = 0.302095 \times 10^{-2}\)/km\(^2\) and \(b = 0.9\)/km\(^2\). These parameter values are associated with a compact star having a mass of \(2.65 M_{\odot }\) and a radius of \(R = 9.8\) km. In the upcoming sections, we will provide a comprehensive analysis of these conditions. We now summarize the conditions that collectively ensure that solutions to the EFEs in general relativity accurately describe the behavior of relativistic objects, such as compact stars, and that these objects remain physically stable under various perturbations and conditions.

5.1 Continuity of metrics

This condition ensures that the metric (description of spacetime) inside the star matches smoothly with the metric outside the star at the stellar surface. This is important for maintaining a consistent description of spacetime around the star.

5.2 Regularity conditions for stellar interior

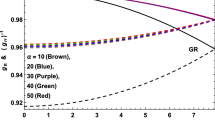
The regularity conditions impose specific constraints on various properties within the interior of the celestial object. These conditions require that all metric potentials, density, and pressures maintain non-negative and finite values throughout the entire star. Moreover, at the center of the object, these metric potentials must satisfy particular conditions: \(e^{\nu (r)}\) evaluated at \(r=0\) should yield a finite value, and \(e^{-\lambda (r)}\) evaluated at \(r=0\) should equal 1. These constraints are essential to ensure that the metric potentials adhere to the initial fundamental boundary conditions, as depicted for all four methods in Fig. 1. Furthermore, pressures and density should decrease monotonically from the center of the star towards its surface, reflecting the typical behavior of stars. Additionally, at the boundary of the star (its surface), the radial pressure (\(p_r\)) should become zero. This condition ensures that the star’s outer layers do not exert an inward force. Figure 2 illustrates how radial (\(p_r\)) and tangential (\(p_t\)) pressures vary with radial distance (r) for the conformally flat Condition (CFC) and vanishing complexity condition (VCC). Meanwhile, Fig. 3 focuses on the same pressure variations but for the embedding class I condition (ECC) and conformally killing vector condition (CKVC) approaches. Figure 4 presents density (\(\rho (r)\)) profile as a function of radial distance, providing a comprehensive view of the models generated through all four approaches.

Fig. 1
figure 1

Profiles of the metric potential \(e^{\nu }(r)\) with respect to r for the models generated through (i) CFC [green color], (ii) VCC [pink color], (iii) ECC [yellow color], and (iv) CKVC [blue color] approaches

Full size image
Fig. 2
figure 2

Variations of \(p_r\) and \(p_t\) with respect to r for the models generated through (i) CFC [green color], and (ii) VCC [pink color]

Full size image
Fig. 3
figure 3

Variations of \(p_r\) and \(p_t\) with respect to r for the models generated through (iii) ECC [yellow color], and (iv) CKVC [blue color]

Full size image
Fig. 4
figure 4

Profile of \(\rho (r)\) with respect to r for the models generated through all four approaches

Full size image

5.3 Complexity factor

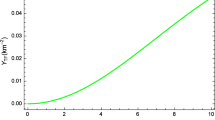
Figure 5 illustrates the evolution of the complexity factor within the context of the vanishing complexity condition (VCC).

Fig. 5
figure 5

Profile of the complexity factor \((Y_{TF})\) with respect to r obtained using VCC approach

Full size image

5.4 Zeldovich’s criterion and the finite central parameters

According to Zeldovich’s criterion, it is expected that the physical parameters \(\rho \), \(p_r\), and \(p_t\) within the central region of the celestial object remain non-negative and comply with the condition specified in [120], which is represented as:

$$\begin{aligned} p_{r_c}/\rho _c \le 1. \end{aligned}$$
(84)

The profiles presented in Fig. 6 for the first two methods and Fig. 7 for the remaining two methods provide visual confirmation that the CFC, VCC, and ECC models presented in this study meet the requirements of Zeldovich’s criterion. However, the CKVC model fails to satisfy the criteria as \({p_t/\rho }\) takes on negative values.

Fig. 6
figure 6

Variations of \(\frac{p_r}{\rho }\) and \(\frac{p_t}{\rho }\) with respect to r for the models generated through (i) CFC [green color], and (ii) VCC [pink color] approaches

Full size image
Fig. 7
figure 7

Variations of \({p_r\over \rho }\) and \({p_t\over \rho }\) with respect to r for the models generated through (iii) ECC [yellow color], and (iv) CKVC [blue color] approaches

Full size image

5.5 Bondi adiabatic index

In their work, Harrison et al. [121] and Zeldovich and Novikov [122] streamlined Chandrasekhar’s stability condition within the framework of radial perturbation theory. This simplification results in a mass-central density relationship given by

$$\begin{aligned} M(\rho _c) \propto \rho _c^{3(\Gamma -4/3)/2}, \end{aligned}$$
(85)

a relationship that is crucial for ensuring the presence of a positive and non-vanishing characteristic frequency as required for stability.

The relativistic adiabatic index, as provided by [123], is given by:

$$\begin{aligned} \Gamma = \frac{\rho + p_r}{p_r} \frac{dp_r}{d\rho }. \end{aligned}$$
(86)

According to Bondi [124], for a stable Newtonian sphere, it is required that \(\Gamma > 4/3\). However, when considering the presence of pressure anisotropy, this condition is modified into a more generalized form, as described by [125]:

$$\begin{aligned} \Gamma > \frac{4}{3} + \left[ -\frac{4\Delta _c}{3 |p^{'}{r_c}|r} + \frac{\rho _c p_{r_c}}{2 |p^{'}_{r_c}|}r\right] . \end{aligned}$$
(87)

Here, \(\Delta _{c}\) and \(\rho _c\) represent anisotropy and energy density at the center in static equilibrium, respectively. The terms enclosed in square brackets account for both anisotropic and relativistic corrections, both of which have positive values. These corrections contribute to an increased unstable range of \(\Gamma \), as discussed in [126]. In general, if \(\Gamma > 4/3\), the system is considered stable under gravitational collapse. The adiabatic index profiles for the first three approaches exhibit stable and expected behavior, as visualized in Fig. 8. In contrast, the profile associated with the fourth approach, known as the conformally killing vector condition (CKVC), shows unexpected behavior.

Fig. 8
figure 8

Profiles of adiabatic index (\(\Gamma (r)\)) for the models generated through (i) CFC (green color), (ii) VCC (pink color), and (iii) ECC (Dark yellow color) approaches

Full size image

5.6 Stability equilibrium conditions

The modified Tolman–Oppenheimer–Volkoff (TOV) equation, which describes an anisotropic fluid distribution, was originally formulated by [127] as follows:

$$\begin{aligned} \underbrace{-{\nu ' \over 2}(\rho +p_r)}_{F_g}-\underbrace{{dp_r \over dr}}_{F_h}+\underbrace{{2\Delta \over r}}_{F_a}=0. \end{aligned}$$
(88)

In this equation, the symbols \(F_g\), \(F_h\), and \(F_a\) represent the gravitational, hydrostatic, and anisotropic forces, respectively, that act upon the stellar object. The profiles presented in Fig. 9 for the first two approaches and in Fig. 10 for the remaining two approaches provide a visual representation of how the gravitational force \(F_g\) dominates over both the anisotropic force \(F_a\) and the hydrostatic force \(F_h\). As a result, the system maintains static equilibrium, where the gravitational force effectively counteracts the combined influence of the anisotropic and hydrostatic forces.

Fig. 9
figure 9

Variations of balancing forces with respect to r for the models generated through (i) CFC (green color), and (ii) VCC (pink color) approaches

Full size image
Fig. 10
figure 10

Variation of balancing forces with respect to r for the models generated through (iii) ECC [yellow color], and (iv) CKVC [blue color] approaches

Full size image

6 Red-shift profiles

In the realm of spherically symmetrical stellar structures, we have computed the functions characterizing gravitational red-shift (\(z_g(r)\)) and surface red-shift (\(z_s(r)\)) for the stellar system through all four approaches, as detailed in Sect. 3 above. We utilized the following expressions to derive these values:

$$\begin{aligned} z_r(r)= & {} \frac{1}{\sqrt{e^{\nu }}}-1\nonumber , \\ \end{aligned}$$
(89)
$$\begin{aligned} z_s(r)= & {} \frac{1}{\sqrt{1-2u(r)}}-1. \end{aligned}$$
(90)

It is interesting to note that the gravitational red-shift (\(z_g(r)\)) and the surface red-shift (\(z_s(r)\)) for the compact object exhibit contrasting behaviors with respect to the radial coordinate (r). Specifically, as r increases, \(z_g(r)\) decreases, while \(z_s(r)\) increases, as illustrated in Fig. 11. Simultaneously, both the mass function m(r) and the parameter u(r) display an increasing trend with r. The variations in mass (m(r)) and compactification (u(r)) for the models generated through all four approaches are depicted in Fig. 12.

Fig. 11
figure 11

Profiles of red-shift with respect to r for the models generated through (i) CFC [green color], (ii) VCC [pink color], (iii) ECC [yellow color], and (iv) CKVC [blue color] approaches

Full size image
Fig. 12
figure 12

Variation of m(r) and u(r) with respect to r for the models generated through all four approaches

Full size image

7 Anisotropic parameter insights

In physically relativistic models, a notable feature of the pressure distribution within a compact star is the behavior of the pressure anisotropy (\(\Delta (r)\)). This behavior is characterized by the fact that \(\Delta (r)\) starts at zero at the center of the star, denoted as \(\Delta (0) = 0\). As one progresses outward from the center, \(\Delta (r)\) gradually increases, eventually reaching a positive value as it approaches the stellar object’s boundary. This phenomenon signifies that anisotropic pressure generates a repulsive force within the compact star, owing to the presence of a positive anisotropy constant. To visually represent this characteristic, Fig. 13 provides a graphical depiction of the variation of \(\Delta (r)\) across the entire stellar object. However, it is important to recognize that this behavior is not consistent when employing different methods. In the case of the embedding class I condition (ECC), there are discontinuities observed at specific points in the pressure anisotropy profile. Also, in the conformally killing vector condition (CKVC) method, the anisotropy does not exhibit the same behavior within the specified range. Therefore, the consistency of this behavior can vary depending on the specific method used for modeling.

Fig. 13
figure 13

Profiles of anisotropy (\(\Delta (r)\)) with respect to r for the models generated through (i) CFC [green color], (ii) VCC [pink color], and (iii) ECC [yellow color] approaches

Full size image

8 Energy conditions

To ensure the physical stability of a static model for the star’s interior, it is imperative that the following energy conditions are met: (i) The null energy condition (NEC): \(\rho - p_r \ge 0\), (ii) The weak energy conditions: \(\rho - p_r \ge 0\), \(\rho \ge 0\) (WEC\(_r\)), and \(\rho - p_t \ge 0\), \(\rho \ge 0\) (WEC\(_t\)), (iii) The strong energy condition (SEC): \(\rho - p_r - 2p_t \ge 0\). The illustration in Fig. 14 pertains to the first two methods, while Fig. 15 corresponds to the remaining two methods. These figures provide clear evidence that all of these energy conditions are rigorously satisfied within the confines of the compact star.

Fig. 14
figure 14

Variations of energy conditions with respect to r for the models generated through (i) CFC (green color), and (ii) VCC (pink color) approaches

Full size image
Fig. 15
figure 15

Variations of energy conditions with respect to r for the models via (iii) ECC [yellow color], and (iv) CKVC [blue color] approaches

Full size image

8.1 Causality and Hererra cracking conditions

The Hererra cracking method, as described in [128, 129], is employed to assess the stability of anisotropic stars when subjected to radial perturbations. The conditions for cracking and causality are expressed as follows:

$$\begin{aligned} -1< {v_t^2}-{v_r^2} \le 0, \end{aligned}$$
(91)

which can be further elaborated as:

$$\begin{aligned} \frac{dp_t}{d\rho }=\frac{dp_r}{d\rho }+\frac{d\Delta }{d\rho }=\frac{dp_r}{d\rho }+\frac{d\Delta }{dr}\frac{dr}{d\rho }, \end{aligned}$$
(92)
$$\begin{aligned} v_r^2-v_t^2=-\frac{d\Delta }{dr}\frac{dr}{d\rho }. \end{aligned}$$
(93)

The profiles depicted in Fig. 16 for the first three methods and Fig. 17 for the same three methods demonstrate that the radial and tangential velocities meet the conditions \(0 < v_r^2, v_t^2 \le 1\) and \(-1 < v_t^2 - v_r^2 \le 0\) throughout the entire stellar object. These conditions align with the causality requirement and indicate potential stability for the model under examination. However, it’s worth noting that the CKVC method does not exhibit consistency with these values in either context.

Fig. 16
figure 16

Profiles of \( v_r^2~ \& ~v_t^2\) with respect to r for the models generated through (i) CFC [green color], (ii) VCC [pink color], and (iii) ECC [yellow color] approaches

Full size image
Fig. 17
figure 17

Profiles of \(v_t^2-v_r^2\) with respect to r for the models generated through (i) CFC [green color], (ii) VCC [pink color], and (iii) ECC [yellow color] approaches

Full size image

8.2 Static stability criteria

In the context of non-rotating, spherically symmetric equilibrium stellar models, the static stability criteria specify that the mass of compact stars should increase in response to small radial pulsations in their central density. Mathematically, this behavior is expressed by the following equation:

$$\begin{aligned} \frac{\partial M}{\partial \rho _c}>0. \end{aligned}$$
(94)

These criteria ensure the static and stable nature of the model. They were originally proposed independently by [121, 122] for stable stellar models. The total mass equation is given by:

$$\begin{aligned} M=m(R) = -\frac{a R^3 \left( a R^2-2 b\right) }{2 b^2}. \end{aligned}$$
(95)

The expression of mass concerning the central density (\(a=\frac{b \rho _c }{6}\)) takes the form:

$$\begin{aligned} M(\rho _c)= & {} -\frac{1}{72} \rho _c R^3 \left( \rho _c R^2-12\right) . \end{aligned}$$
(96)

Moreover,

$$\begin{aligned} \frac{\partial M}{\partial \rho _c}= & {} -\frac{\rho _c R^5}{72}-\frac{1}{72} R^3 \left( \rho _c R^2-12\right) >0, \end{aligned}$$
(97)

demonstrating compliance with the static stability criterion (94) for the solutions yielded by all four models in the interval [0, 0.063] of \(\rho _c\). The variation in mass with central density for models generated using all four approaches is depicted in Fig. 18.

Fig. 18
figure 18

Variation of mass with central density for the models generated through all four approaches

Full size image

9 Discussions and conclusions: key findings

Table 1 Physical parameter values for compact star of mass \(M=2.65 M_\odot \), radius \(R=9.8\) km for \(a=0.00302095\)/km\(^2\) and \(b=0.9\)/km\(^2\) of the solution obtained via conformally flat condition (CFC), vanishing complexity condition (VCC), embedding class I condition (ECC) and conformally killing vector condition (CKVC) approaches
Full size table
Table 2 Physical viability for compact star of mass \(M=2.13 M_\odot \), Radius \(R=9.8\) and parameters \(a=0.00232526\)/km\(^2\) and \(b=0.9\)/km\(^2\)) of the solution obtained via CFC, VCC, ECC and CKVC approaches
Full size table

The following findings and observations are derived from the above analysis:

  1. 1.

    The compact star, with a mass of \(2.65 M_{\odot }\) and a radius of \(R=9.8\) km, and parameter values \(a=0.00232526\) /km\(^2\) and \(b=0.9\)/km\(^2\), satisfies all the physical, geometrical, and stability conditions in the CFC and VCC models. However, in the ECC model with the same parameter values, while it meets all conditions except for the tangential pressure (\(p_t\)), which is not defined at certain points within the interval [9.5, R] as indicated in the Fig. 3. This failure to define \(p_t\) leads to non-compliance with the causality condition, as both \(v_r^2\) and \(v_t^2\) exceed the value of 1, as shown in the Fig. 16. Additionally, the modified TOV equation is not satisfied due to the lack of definition for anisotropy and anisotropic force at some points within the interval [0, R], as illustrated in the Fig. 13. In the CKVC model, there are issues with both \(p_t\) and \({p_t\over \rho }\) taking negative values, resulting in a failure to meet the causality condition, the Herrera cracking condition, and exhibiting an increasing tendency of anisotropy. However, this model fulfills all other physical and geometrical conditions.

  2. 2.

    The profiles of Fig. 3 also exhibit that in the CKVC models the physical variables \(p_r\), \(p_t\) take infinity at \(r=0\). In the remaining three models (CFC, VCC and ECC) have a finite central pressure and decreasing outward (Fig. 2). For these three solutions, the ECC model provides higher central density as compared to the VCC, CFC models with the same central density, surface pressure, surface redshift, compactification factor (Table 1).

  3. 3.

    The parameter \(\Gamma (r)\) provides stability of the celestial object. The central values of \(\Gamma (r)\) explains the gravitational collapsing behavior of the models. In the present models, CFC has the lowest central adiabatic index 4.76117, whereas it becomes infinity for CKVC model which provide an unstable solution. At the end, the ECC class model is more stable one as compare to VCC, CFC models (Table 1). In summary, the CFC and VCC models with the specified parameters satisfy all conditions, while the ECC model encounters problems with tangential pressure, causality, and TOV equations. The CKVC model presents issues with negative pressure values, failing to meet the causality and Herrera cracking conditions while exhibiting an increasing anisotropy tendency, but it adheres to all other physical and geometrical conditions. The physical parameter values for the compact star, as determined using all four approaches, are presented in Table 1.

  4. 4.

    For the compact star with a mass of \(2.13 M_{\odot }\), a radius of \(R=9.8\) km, and parameters \(a=0.00232526\)/km\(^2\) and \(b=0.9\)/km\(^2\), the VCC model satisfies all physical, geometrical, and stability conditions. However, the CFC model fulfills all those conditions except the causality condition, as the tangential sound speed \(v_t^2\) is negative (Fig. 19). For the same parameter values, the ECC model meets all conditions, including the causality condition. However, it has an issue where the physical variable \(p_r\) is not regular at some points in the interval [9.577, R]. Furthermore, it fails to satisfy the TOV equations as anisotropy and anisotropic forces are not regular at certain points in the range [0, R]. In the CKVC model, both the tangential pressure \(p_t\) and the ratio \({p_t\over \rho }\) take negative values. This model also fails to meet the causality condition, the Herrera cracking condition, and exhibits an increasing tendency of anisotropy. Nevertheless, it satisfies all other physical and geometrical conditions. In summary, the VCC model appears to be the most physically consistent and stable among the models discussed, as it satisfies all conditions without any specific issues mentioned. The CFC and ECC models have exhibited some violations in their physical properties, while the CKVC model seems to have significant issues with causality, stability, and anisotropy. Table 2 presents a format outlining the criteria used to evaluate the physical viability of solutions obtained through the examination of compact stars via four distinct computational methodologies.

  5. 5.

    Upon conducting a graphical analysis for various compact stars with a mass range from \(2.55 M_{\odot }\) to \(2.65 M_{\odot }\) and a fixed radius of \(R=9.8\) km, the CFC and VCC satisfy all well-behaved conditions. However, the ECC and CKVC models fail to satisfy the causality condition. When the mass of the compact star below \(2.55 M_{\odot }\), the tangential velocity in the CFC model becomes negative, leading to a violation of the causality condition. Additionally, when the mass of the compact star is less than or equal to \(2.15 M_{\odot }\), the ECC model adheres to the causality condition, but the CFC model fails to meet this requirement. An in-depth analysis of the matter type relevant to all the solutions, offering detailed insights into \(M-R\) curves by employing observed neutron star masses to predict radii, can similarly be undertaken following the methodology outlined in [73].

Fig. 19
figure 19

Profiles of \( v_r^2~ \& ~v_t^2\) with respect to r for the models generated through (i) CFC [green color], (ii) VCC [pink color], and (iii) ECC [yellow color] approaches for compact star of Mass \(M=2.13 M_\odot \), Radius \(R=9.8\)

Full size image